Redes neurais em trading: Aprendizado hierárquico de características em nuvens de pontos

Introdução

Um conjunto geométrico de pontos consiste em coleções de pontos no espaço euclidiano. Como um conjunto, esses dados devem ser invariantes em relação às permutações de seus membros. Além disso, a métrica de distância define vizinhanças locais, que podem apresentar diferentes propriedades. Por exemplo, a densidade e outros atributos dos pontos podem variar de uma região a outra.

No artigo anterior, vimos que o método PointNet codifica cada ponto no espaço e, em seguida, agrega todos os objetos individuais em uma assinatura global da nuvem de pontos. O PointNet não captura a estrutura local. No entanto, o uso da estrutura local se mostrou essencial para o sucesso das arquiteturas convolucionais. Modelos convolucionais recebem dados brutos definidos em grades regulares e são capazes de capturar objetos em escalas progressivamente maiores ao longo de uma hierarquia com múltiplas resoluções. Em níveis mais baixos, os neurônios possuem campos receptivos menores, enquanto em níveis mais altos, esses campos são maiores. A abstração de padrões locais ao longo da hierarquia melhora a generalização.

Uma abordagem semelhante foi aplicada ao modelo PointNet++, apresentado no artigo "PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space". A ideia central por trás do PointNet++ é dividir o conjunto de pontos em regiões locais sobrepostas com base na métrica de distância do espaço subjacente. Assim como as redes convolucionais, o PointNet++ extrai características locais, capturando estruturas geométricas sutis de pequenas regiões. Esses objetos locais são então agrupados em elementos maiores e processados para obter representações de nível superior. Esse processo se repete até que todas as características do conjunto de pontos sejam extraídas.

Ao projetar o PointNet++, os autores do método abordam dois problemas: a divisão do conjunto de pontos e a abstração de conjuntos de pontos ou características locais por meio do aprendizado local de funções. Esses dois problemas estão interligados, pois, ao dividir o conjunto de pontos, é necessário criar estruturas comuns entre as subdivisões para permitir o compartilhamento dos pesos das características locais treinadas, semelhante ao que ocorre em modelos convolucionais. Os autores do método escolheram o PointNet como unidade de aprendizado local, pois essa arquitetura é eficiente para processar conjuntos de pontos desordenados e extrair características semânticas. Além disso, essa arquitetura resiste a danos nos dados brutos. Como bloco de construção fundamental, o PointNet abstrai conjuntos de pontos locais ou objetos em representações de nível superior. Dentro dessa representação, o PointNet++ aplica o PointNet recursivamente à segmentação hierárquica dos dados brutos.

Um dos desafios que ainda persiste está no método de criação das subdivisões sobrepostas da nuvem de pontos. Cada região é definida como uma esfera de vizinhança no espaço euclidiano, cujos parâmetros incluem a posição do centroide e a escala. Para cobrir uniformemente todo o conjunto, os centroides são escolhidos a partir dos pontos brutos, seguindo um algoritmo de amostragem dos pontos mais distantes. Em comparação com modelos convolucionais volumétricos, que escaneiam o espaço em etapas fixas, os campos receptivos locais do PointNet++ dependem tanto dos dados brutos quanto da métrica utilizada, o que aumenta sua eficiência.

1. Algoritmo PointNet++

Na arquitetura do PointNet, é utilizada apenas uma operação MaxPooling para agregar todo o conjunto de pontos. Os autores do PointNet++, por sua vez, desenvolveram uma arquitetura hierárquica de agrupamento de pontos, com abstração progressiva das regiões locais ao longo da hierarquia.

A estrutura hierárquica proposta consiste em uma série de níveis de abstração predefinidos. Em cada nível, a nuvem de pontos é processada e abstraída para gerar um novo conjunto de dados com menos elementos. Cada nível de abstração é composto por três camadas principais: a camada de Amostragem, a camada de Agrupamento e a camada PointNet. A camada de Amostragem seleciona um subconjunto de pontos da nuvem de pontos original e determina os centroides das regiões locais. Em seguida, a camada de Agrupamento forma conjuntos locais de pontos, identificando objetos "vizinhos" ao redor dos centroides. A camada PointNet utiliza uma versão reduzida do PointNet para codificar padrões das regiões locais em vetores de características.

O nível de abstração recebe como entrada uma matriz N×(d+C), que contém N pontos com d dimensões de coordenadas e C dimensões de características. A saída é uma matriz N′×(d+C′, em que N′ representa pontos subamostrados e C′ representa a dimensão do novo vetor de características, que captura o contexto local de maneira mais generalizada.

Os autores do PointNet++ propõem o uso de amostragem iterativa dos pontos mais distantes para selecionar os centroides. Em comparação com a amostragem aleatória, essa abordagem permite uma melhor cobertura do conjunto de pontos para o mesmo número de centroides. Ao contrário das redes convolucionais, que escaneiam um espaço vetorial independente da distribuição dos dados, a estratégia de amostragem proposta gera campos receptivos adaptados aos dados brutos.

Os dados brutos para a camada de Agrupamento consistem em uma nuvem de pontos de tamanho N×(d+C) e nas coordenadas do conjunto de centroides de tamanho N′×d. A saída dessa camada são grupos de conjuntos de pontos organizados no formato N′×K×(d+C), onde cada grupo corresponde a uma região local, e K representa o número de pontos na vizinhança do centroide.

É importante notar que K pode variar de um grupo para outro, mas a camada PointNet subsequente é capaz de converter uma quantidade flexível de pontos em um vetor de características do objeto local com tamanho fixo.

Nas redes neurais convolucionais, a região local de um pixel é composta por pixels cujos índices no array estão dentro de uma distância específica de Manhattan (tamanho do kernel) a partir do pixel central. Já em uma nuvem de pontos extraída de um espaço métrico, as vizinhanças dos pontos são determinadas com base em uma métrica de distância.

Durante o processo de agrupamento, o modelo encontra todos os pontos que estão dentro de um determinado raio a partir do ponto de referência (o limite superior de K é definido como um hiperparâmetro).

Na camada PointNet, os dados de entrada são N′ regiões locais de pontos com tamanho N′×K×(d+C). Na saída, cada região local é representada por seu centroide e um objeto local que codifica a vizinhança do centroide. O tamanho do tensor resultante é N′×(d+C).

As coordenadas dos pontos dentro da região local são inicialmente convertidas para um sistema de coordenadas local relativo ao centroide:

para i = 1, 2,…, K e j = 1, 2,…, d, onde representa a coordenada do centroide.

Os autores do método utilizam o PointNet como bloco de construção fundamental para o aprendizado local de padrões. O uso de coordenadas relativas em conjunto com objetos pontuais permite capturar as relações espaciais entre os pontos dentro da região local.

Com frequência, a densidade das nuvens de pontos não é uniforme em diferentes regiões. Essa heterogeneidade representa um desafio significativo para o aprendizado de características a partir de um conjunto de pontos. Características aprendidas a partir de regiões densas podem não ser bem generalizadas para áreas com amostragem esparsa. Por conseguinte, modelos treinados em nuvens de pontos esparsas podem ter dificuldade em reconhecer estruturas locais de granularidade fina.

Idealmente, é necessário analisar a nuvem de pontos com o máximo de precisão possível para capturar os mínimos detalhes em regiões com alta densidade de amostragem. No entanto, essa abordagem minuciosa não é eficiente em áreas com baixa densidade de pontos, pois os padrões locais podem ser distorcidos devido à escassez de valores. Nesses casos, é necessário buscar modelos em uma escala maior dentro de uma vizinhança ampliada. Para atingir esse objetivo, os autores do PointNet++ propõem camadas PointNet adaptáveis à densidade, treinadas para combinar objetos de regiões em diferentes escalas conforme a variação da densidade da amostragem original.

No PointNet++, cada nível de abstração extrai múltiplos padrões locais em diferentes escalas e os combina de maneira inteligente de acordo com a densidade local dos pontos. O artigo original apresenta dois tipos de camadas adaptativas à densidade.

Uma abordagem simples, mas eficaz, para capturar padrões em múltiplas escalas é aplicar camadas de agrupamento com diferentes escalas, seguidas pela atribuição de PointNets correspondentes para extrair as características de cada escala. Os objetos em diferentes escalas são então combinados em um único objeto multiescalar.

Nesse processo, a rede é treinada para aprender uma estratégia otimizada de combinação de características em múltiplas escalas. Isso é feito descartando aleatoriamente pontos da amostragem original com uma probabilidade aleatória para cada instância.

A abordagem descrita acima exige alto poder computacional, pois envolve a execução do PointNet local em grandes vizinhanças para cada ponto centroide. Um método alternativo, que evita esse alto custo computacional e, ao mesmo tempo, mantém a capacidade de agregação adaptativa da informação de acordo com as propriedades distributivas dos pontos, consiste na concatenação de dois vetores. Um dos vetores é obtido somando os objetos dentro de cada sub-região no nível inferior Li-1, utilizando um determinado nível de abstração. O outro vetor é uma característica extraída pela aplicação direta de um único PointNet sobre todos os pontos brutos da região local.

Em áreas de baixa densidade, o primeiro vetor pode ser menos confiável que o segundo, pois a sub-região utilizada no cálculo do primeiro vetor contém menos pontos, o que pode comprometer sua precisão em razão da escassez de amostragem. Nessa situação, o segundo vetor deve ter maior peso. Por outro lado, quando a densidade da região é alta, o primeiro vetor fornece informações mais detalhadas, pois tem a capacidade de realizar verificações recursivas em alta resolução nos níveis mais baixos.

Esse método é mais eficiente em termos computacionais, pois evita a necessidade de extrair características em vizinhanças de grande escala nos níveis mais baixos.

Na camada de abstração, o conjunto original de pontos é subamostrado. No entanto, em tarefas de segmentação, como a rotulação semântica de pontos, é desejável obter características para todos os pontos originais. Uma solução possível é manter a amostragem de todos os pontos como centroides em todos os níveis de abstração definidos, o que, no entanto, gera um alto custo computacional. Outra abordagem consiste em propagar as características dos pontos subamostrados para os pontos originais.

A visualização original do método PointNet++ é apresentada a seguir.

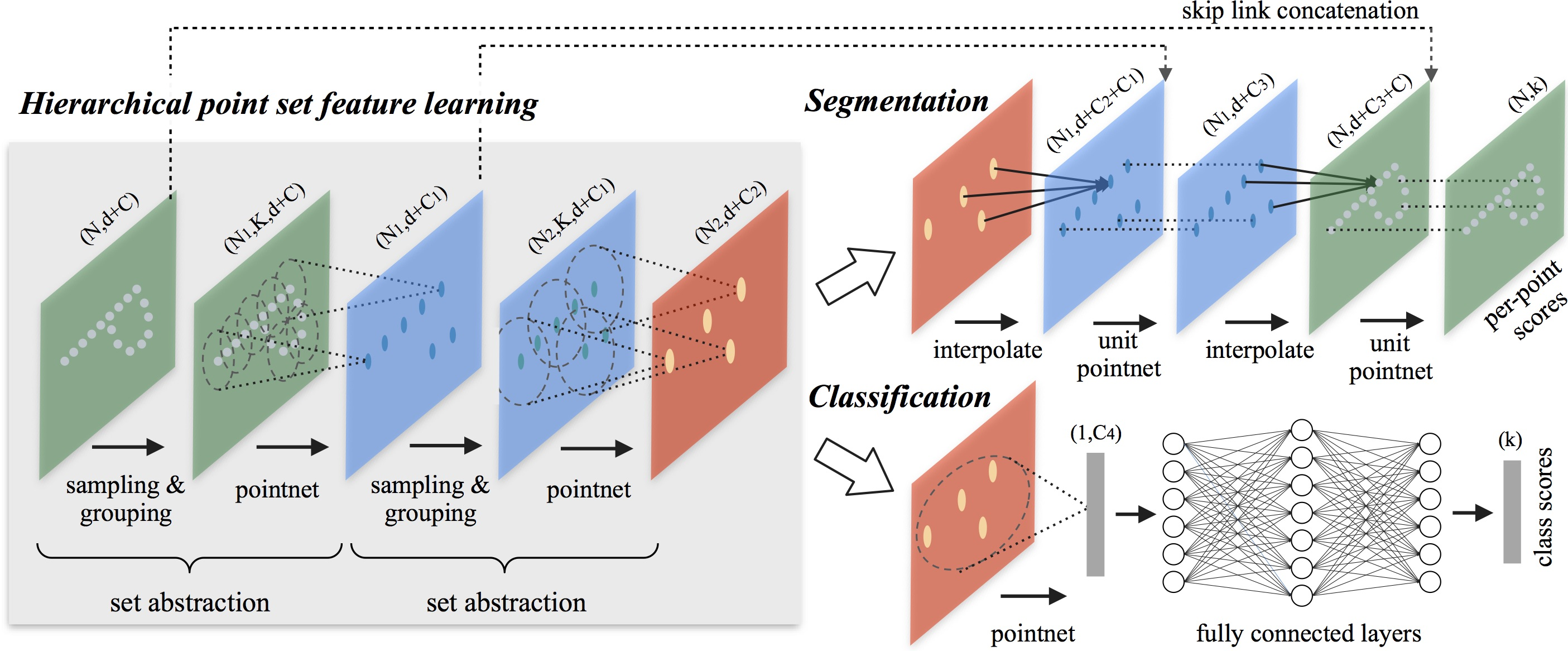
2. Implementação em MQL5

Após revisar os aspectos teóricos do método PointNet++, passamos à parte prática do nosso artigo, na qual implementamos nossa interpretação das abordagens propostas utilizando MQL5. Vale destacar que nossa implementação difere da versão original descrita anteriormente em alguns aspectos. No entanto, abordaremos todos os detalhes.

Dividimos nosso trabalho em dois blocos. Primeiro, criaremos a camada de subamostragem local dos dados, que combinará as camadas de Amostragem e Agrupamento descritas anteriormente. Em seguida, construiremos uma classe de nível superior, que reunirá os blocos individuais em um único algoritmo PointNet++.

2.1 Adição de um programa OpenCL

O algoritmo de subamostragem local será implementado na classe CNeuronPointNet2Local. No entanto, antes de começarmos a trabalhar nela, precisamos expandir a funcionalidade do nosso programa OpenCL.

Para isso, criaremos o kernel CalcDistance, no qual determinaremos a distância entre os pontos da nuvem analisada.

É importante observar que a distância será calculada no espaço multidimensional das características descritivas de cada ponto. O resultado do kernel será uma matriz N×N cujos valores são nulos na diagonal.

Nos parâmetros do kernel, receberemos ponteiros para dois buffers de dados (dados brutos e espaço para armazenamento dos resultados) e uma constante que especificará a dimensionalidade do vetor de características de cada ponto.

__kernel void CalcDistance(__global const float *data,
                           __global float *distance,
                           const int dimension
                          )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const int total = (int)get_local_size(1);

No corpo do kernel, identificamos a thread no espaço de tarefas.

A saída esperada é uma matriz quadrada, então criaremos um espaço de tarefas bidimensional com o tamanho correspondente. Dessa forma, cada thread calculará um único elemento da matriz de resultados.

Aqui encontramos a primeira divergência em relação ao algoritmo original. Não determinaremos os centroides das regiões locais iterativamente. Em nossa implementação, cada ponto da nuvem atuará como centroide de sua própria região local. Para garantir a adaptabilidade do tamanho das regiões, normalizaremos as distâncias até cada ponto da nuvem. Para realizar essa normalização, será necessário um intercâmbio de dados entre as threads individuais. Para isso, criaremos grupos de trabalho locais organizados ao longo das linhas da matriz de resultados do kernel.

Para realizar a troca de dados dentro do grupo de trabalho, criamos um array local.

   __local float Temp[LOCAL_ARRAY_SIZE];
   int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);

Definimos também constantes de deslocamento para os elementos necessários nos buffers de dados.

   const int shift_main = main * dimension;
   const int shift_slave = slave * dimension;
   const int shift_dist = main * total + slave;

Em seguida, implementamos um laço para calcular a distância entre dois objetos no espaço multidimensional.

//--- calc distance
   float dist = 0;
   if(main != slave)
     {
      for(int d = 0; d < dimension; d++)
         dist += pow(data[shift_main + d] - data[shift_slave + d], 2.0f);
     }

Vale destacar que os cálculos são realizados apenas para os elementos fora da diagonal, pois a distância de um ponto para ele mesmo é sempre "0". Assim, evitamos desperdício de recursos computacionais com cálculos desnecessários.

Na próxima etapa, determinamos a maior distância dentro do grupo de trabalho. Primeiro, coletamos os valores máximos dos blocos individuais em um array local.

//--- Look Max
   for(int i = 0; i < total; i += ls)
     {
      if(!isinf(dist) && !isnan(dist))
        {
         if(i <= slave && (i + ls) > slave)
            Temp[slave - i] = max((i == 0 ? 0 : Temp[slave - i]), dist);
        }
      else
         if(i == 0)
            Temp[slave] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Depois, identificamos o maior valor dentro desse array.

   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(slave < count && (slave + count) < ls)
        {
         if(Temp[slave] < Temp[slave + count])
            Temp[slave] = Temp[slave + count];
         Temp[slave + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Após encontrar a maior distância relativa ao ponto analisado, normalizamos todas as distâncias calculadas dividindo-as por esse valor. Como resultado, todas as distâncias entre pontos são transformadas para o intervalo [0, 1].

//--- Normalize
   if(Temp[0] > 0)
      dist /= Temp[0];
   if(isinf(dist) || isnan(dist))
      dist = 1;
//--- result
   distance[shift_dist] = dist;
  }

Os valores normalizados são então armazenados nos elementos correspondentes do buffer global de resultados.

É claro que entendemos que a maior distância entre duas amostras individuais pode variar de caso a caso. Ao normalizar os valores dentro de escalas locais, acabamos perdendo essa diferença. No entanto, esse é justamente o princípio por trás da adaptação dos campos receptivos.

Se um ponto analisado estiver dentro de uma região densa da nuvem, a maior distância será determinada por um dos pontos localizados na borda dessa região. Por outro lado, se o ponto analisado estiver na extremidade da nuvem, o ponto mais distante provavelmente estará na borda oposta. Nesse segundo caso, a distância será maior, o que significa que o campo receptivo também será maior.

Além disso, espera-se que a densidade de pontos seja maior no interior da nuvem do que em suas extremidades. Nessa situação, faz sentido aumentar os campos receptivos nas bordas da nuvem de pontos analisada.

Os autores do PointNet++ propõem, então, calcular os deslocamentos locais dos pontos em relação ao centroide correspondente e aplicar um mini-PointNet a esses subconjuntos locais de dados. No entanto, por trás da aparente simplicidade dessa abordagem, há um problema significativo de implementação.

Como mencionado anteriormente, o número de elementos em cada região local varia e não é conhecido previamente. Isso levanta a questão do dimensionamento dos buffers de dados. Podemos, é claro, estabelecer um limite máximo para a quantidade de pontos no campo receptivo e definir um buffer com "margem de segurança", mas essa abordagem resulta em um maior consumo de memória e aumenta a complexidade computacional de todo o modelo. Como consequência, o treinamento se torna mais difícil e o desempenho da rede diminui.

Em vez disso, aplicamos uma abordagem mais simples e universal. Eliminamos o cálculo dos deslocamentos locais e utilizamos uma única matriz de parâmetros de peso para todos os elementos, de forma semelhante ao PointNet convencional, para o aprendizado das características dos pontos. No entanto, realizamos a operação de MaxPooling dentro dos campos receptivos. Para isso, criamos um novo kernel chamado FeedForwardLocalMax, cujos parâmetros incluem ponteiros para três buffers de dados: características dos pontos, distâncias normalizadas entre os pontos e o buffer de resultados. Além disso, adicionamos uma constante que define o raio do campo receptivo.

__kernel void FeedForwardLocalMax(__global const float *matrix_i,
                                  __global const float *distance,
                                  __global float *matrix_o,
                                  const float radius
                                 )
  {
   const size_t i = get_global_id(0);
   const size_t total = get_global_size(0);
   const size_t d = get_global_id(1);
   const size_t dimension = get_global_size(1);

Planejamos executar esse kernel dentro de um espaço de tarefas bidimensional. O primeiro eixo representa o número de elementos na nuvem de pontos, enquanto o segundo eixo representa a dimensionalidade das características de cada elemento. No corpo do kernel, identificamos imediatamente a thread atual em ambas as dimensões do espaço de tarefas. Nesse caso, cada thread opera de maneira independente, tornando desnecessário criar grupos de trabalho e trocar dados entre eles.

Em seguida, definimos constantes de deslocamento nos buffers de dados.

   const int shift_dist = i * total;
   const int shift_out = i * dimension + d;

Depois, implementamos um laço para determinar o valor máximo.

   float result = -3.402823466e+38;
   for(int k = 0; k < total; k++)
     {
      if(distance[shift_dist + k] > radius)
         continue;
      int shift = k * dimension + d;
      result = max(result, matrix_i[shift]);
     }
   matrix_o[shift_out] = result;
  }

Vale destacar que, antes de verificar o valor do próximo elemento, sempre garantimos que ele esteja dentro do campo receptivo correspondente ao elemento da nuvem de pontos.

Após a conclusão das iterações do laço, armazenamos o valor obtido no buffer de resultados.

De maneira semelhante, criamos o kernel de propagação reversa CalcInputGradientLocalMax, que distribui o gradiente do erro para os elementos correspondentes. Os algoritmos dos kernels de propagação para frente e reversa são bastante semelhantes. Convido você a analisá-los por conta própria. O código completo de todos os kernels está disponível no anexo. Agora, partimos para a implementação do programa principal.

2.2 Classe de subamostragem local

Realizamos o trabalho preparatório no que diz respeito à implementação OpenCL e agora passamos para a construção da classe de subamostragem local. Durante a implementação dos kernels no programa OpenCL, já discutimos parcialmente os princípios de construção dos algoritmos. Agora, ao desenvolver os métodos da classe CNeuronPointNet2Local, exploraremos esses conceitos em maior profundidade e analisaremos sua implementação no código. A seguir, apresentamos a estrutura da nova classe.

class CNeuronPointNet2Local   :  public CNeuronConvOCL
  {
protected:
   float                fRadius;
   uint                 iUnits;
   //---
   CBufferFloat         cDistance;
   CNeuronConvOCL       cFeatureNet[3];
   CNeuronBatchNormOCL  cFeatureNetNorm[3];
   CNeuronBaseOCL       cLocalMaxPool;
   CNeuronConvOCL       cFinalMLP;
   //---
   virtual bool         CalcDistance(CNeuronBaseOCL *NeuronOCL);
   virtual bool         LocalMaxPool(void);
   virtual bool         LocalMaxPoolGrad(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPointNet2Local(void) {};
                    ~CNeuronPointNet2Local(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint window_out, float radius,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNet2LocalOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Na estrutura acima, podemos observar vários objetos internos de camadas neurais e duas variáveis, cujo propósito será explicado ao longo da implementação dos métodos da classe.

Também notamos um conjunto de métodos já conhecidos, que podem ser sobrescritos. Além disso, há três métodos cujos nomes coincidem com os kernels criados anteriormente:

• CalcDistance(CNeuronBaseOCL *NeuronOCL);
• LocalMaxPool(void);
• LocalMaxPoolGrad(void).

Como você já deve ter percebido, esses são os métodos responsáveis por enfileirar os kernels para execução. Esse é um algoritmo que já analisamos anteriormente, então não vamos nos aprofundar nele nesta parte do artigo.

Também vale ressaltar que estamos herdando a classe do CNeuronConvOCL, que representa uma camada convolucional. Essa situação não é muito comum em nossa prática e se deve ao processamento independente das características dos grupos locais.

Todos os objetos internos da classe são declarados estaticamente, o que nos permite manter o construtor e o destrutor da classe vazios. A inicialização de uma nova instância do objeto é feita através do método Init.

bool CNeuronPointNet2Local::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                 uint window, uint units_count, uint window_out, float radius, 
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, 128, 128, window_out, 
                                        units_count, 1, optimization_type, batch))
      return false;

Os parâmetros desse método incluem as principais constantes que definem a arquitetura do objeto. Todas elas correspondem a parâmetros semelhantes de uma camada convolucional, com a adição de um novo parâmetro: radius, que define o raio da janela receptiva do elemento.

No corpo do método, chamamos diretamente o método com o mesmo nome da classe-mãe, que já possui o controle necessário dos dados recebidos e a inicialização dos objetos herdados. É importante destacar que os valores passados para o método da classe-mãe são ligeiramente diferentes dos recebidos do programa externo. Isso ocorre devido às particularidades do uso dos objetos herdados, algo que explicaremos com mais detalhes ao implementar o método de propagação para frente, feedForward.

Após a execução bem-sucedida das operações da classe-mãe, armazenamos algumas das constantes obtidas, enquanto outras já foram salvas no decorrer da execução das operações herdadas.

   fRadius = MathMax(0.1f, radius);
   iUnits = units_count;

A seguir, iniciamos a configuração dos objetos internos. O primeiro passo é criar um buffer para armazenar as distâncias entre os objetos analisados na nuvem de pontos. Como mencionado anteriormente, esse buffer será uma matriz quadrada.

   cDistance.BufferFree();
   if(!cDistance.BufferInit(iUnits * iUnits, 0) ||
      !cDistance.BufferCreate(OpenCL))
      return false;

Para a extração de características dos pontos, criamos um bloco composto por três camadas convolucionais e três camadas de normalização em lote, seguindo a mesma lógica da extração de características no PointNet. Não implementamos um bloco de projeção dos dados brutos, pois assumimos que essa funcionalidade já está presente na classe de nível superior.

   if(!cFeatureNet[0].Init(0, 0, OpenCL, window, window, 64, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[0].Init(0, 1, OpenCL, 64 * iUnits, iBatch, optimization))
      return false;
   cFeatureNetNorm[0].SetActivationFunction(LReLU);
   if(!cFeatureNet[1].Init(0, 2, OpenCL, 64, 64, 128, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[1].Init(0, 3, OpenCL, 128 * iUnits, iBatch, optimization))
      return false;
   cFeatureNetNorm[1].SetActivationFunction(LReLU);
   if(!cFeatureNet[2].Init(0, 4, OpenCL, 128, 128, 256, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[2].Init(0, 5, OpenCL, 256 * iUnits, iBatch, optimization))
      cFeatureNetNorm[2].SetActivationFunction(None);

Também criamos uma camada para armazenar os resultados do MaxPooling local.

   if(!cLocalMaxPool.Init(0, 6, OpenCL, cFeatureNetNorm[2].Neurons(), optimization, iBatch))
      return false;

Além disso, adicionamos uma camada MLP para processar os resultados finais.

   if(!cFinalMLP.Init(0, 7, OpenCL, 256, 256, 128, iUnits, 1, optimization, iBatch))
      return false;
   cFinalMLP.SetActivationFunction(LReLU);

O segundo nível da arquitetura será baseado na funcionalidade herdada.

Vale destacar que, ao contrário do PointNet convencional, utilizamos camadas convolucionais também na saída. Isso se deve ao processamento independente dos descritores das regiões locais.

Por fim, ao concluir as operações do método de inicialização, especificamos explicitamente que a classe não usará uma função de ativação e retornamos um valor booleano indicando o sucesso da operação à função chamadora.

   SetActivationFunction(None);
   return true;
  }

Após concluir a inicialização do novo objeto, passamos à construção dos algoritmos de propagação para frente no método feedForward. Os parâmetros desse método incluem um ponteiro para o objeto contendo os dados brutos.

bool CNeuronPointNet2Local::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CalcDistance(NeuronOCL))
      return false;

Como mencionado anteriormente, não realizamos a projeção dos dados para um espaço canônico dentro desta classe. Essa operação será executada no nível superior, se necessário. Portanto, iniciamos diretamente o cálculo das distâncias entre os elementos dos dados brutos.

Em seguida, criamos um laço para o cálculo das características dos elementos analisados.

   CNeuronBaseOCL *temp = NeuronOCL;
   uint total = cFeatureNet.Size();
   for(uint i = 0; i < total; i++)
     {
      if(!cFeatureNet[i].FeedForward(temp))
         return false;
      if(!cFeatureNetNorm[i].FeedForward(cFeatureNet[i].AsObject()))
         return false;
      temp = cFeatureNetNorm[i].AsObject();
     }

Depois, realizamos as operações de MaxPooling para as regiões locais dos pontos.

   if(!LocalMaxPool())
      return false;

Ao final das operações do método, aplicamos um MLP independente de duas camadas aos descritores de todas as regiões locais.

   if(!cFinalMLP.FeedForward(cLocalMaxPool.AsObject()))
      return false;
   if(!CNeuronConvOCL::feedForward(cFinalMLP.AsObject()))
      return false;
//---
   return true;
  }

O primeiro nível do MLP utiliza a camada interna cFinalMLP. Já as operações da segunda camada são realizadas por meio da funcionalidade herdada da classe-mãe.

É importante monitorar o processo em cada etapa para garantir que as operações sejam concluídas corretamente. Após a execução bem-sucedida de todas as operações, retornamos um valor lógico indicando o sucesso da execução para a função chamadora.

Os algoritmos de propagação reversa são implementados nos métodos calcInputGradients e updateInputWeights. O primeiro método distribui o gradiente do erro para todos os elementos de acordo com sua influência no resultado final. Sua lógica segue exatamente a estrutura do método de propagação para a frente, mas com as operações realizadas em ordem inversa. O segundo método é responsável pela atualização dos parâmetros treináveis do modelo. Aqui, simplesmente chamamos os métodos correspondentes dos objetos internos que contêm os parâmetros de aprendizado. Ambos os algoritmos são diretos e fáceis de compreender, portanto sugiro que você os analise por conta própria. Lembro que o código completo desta classe e de todos os seus métodos está disponível no anexo.

2.3 Criação do algoritmo PointNet++

Já realizamos um grande volume de trabalho e agora chegamos à etapa final da implementação. Neste momento, reunimos os blocos isolados em um único algoritmo, o PointNet++. Essa tarefa será realizada dentro da classe CNeuronPointNet2OCL, cuja estrutura é apresentada abaixo.

class CNeuronPointNet2OCL   :  public CNeuronPointNetOCL
  {
protected:
   CNeuronPointNetOCL   *cTNetG;
   CNeuronBaseOCL       *cTurnedG;
   //---
   CNeuronPointNet2Local caLocalPointNet[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
public:
                     CNeuronPointNet2OCL(void) {};
                    ~CNeuronPointNet2OCL(void) ;
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint output, bool use_tnets,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNet2OCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Por mais surpreendente que possa parecer, esta classe declara apenas dois objetos estáticos para a discretização local dos dados e dois objetos dinâmicos, que serão inicializados caso seja necessário projetar os dados para um espaço canônico. Essa simplicidade estrutural se deve ao fato de herdarmos a funcionalidade do PointNet convencional, onde grande parte dos procedimentos já foi implementada.

Como mencionado anteriormente, os objetos dinâmicos são inicializados apenas quando necessário. Portanto, deixamos o construtor da classe vazio. No entanto, no destrutor, verificamos a existência de ponteiros válidos para os objetos dinâmicos e os removemos caso necessário.

CNeuronPointNet2OCL::~CNeuronPointNet2OCL(void)
  {
   if(!!cTNetG)
      delete cTNetG;
   if(!!cTurnedG)
      delete cTurnedG;
  }

A inicialização do objeto da classe ocorre, como de costume, no método Init. Os parâmetros desse método incluem as constantes principais que definem a arquitetura da classe. Todas essas constantes foram mantidas integralmente da classe-mãe.

bool CNeuronPointNet2OCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,

                               uint window, uint units_count, uint output, bool use_tnets, 
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronPointNetOCL::Init(numOutputs, myIndex, open_cl, 64, units_count, 
                                output, use_tnets, optimization_type, batch))
      return false;

No corpo do método, chamamos diretamente o método equivalente da classe-mãe. Em seguida, verificamos se é necessário criar os objetos responsáveis pela projeção dos dados brutos no espaço canônico.

//--- Init T-Nets
   if(use_tnets)
     {
      if(!cTNetG)
        {
         cTNetG = new CNeuronPointNetOCL();
         if(!cTNetG)
            return false;
        }
      if(!cTNetG.Init(0, 0, OpenCL, window, units_count, window * window, false, optimization, iBatch))
         return false;

Caso seja necessário, primeiro criamos os objetos apropriados e, em seguida, os inicializamos.

      if(!cTurnedG)
        {
         cTurnedG = new CNeuronBaseOCL();
         if(!cTurned1)
            return false;
        }
      if(!cTurnedG.Init(0, 1, OpenCL, window * units_count, optimization, iBatch))
         return false;
     }

Se o usuário não especificar a necessidade de projeção dos dados, verificamos se há ponteiros válidos para esses objetos. Se houver, removemos os objetos desnecessários.

   else
     {
      if(!!cTNetG)
         delete cTNetG;
      if(!!cTurnedG)
         delete cTurnedG;
     }

Depois disso, inicializamos dois objetos de discretização local dos dados, cada um com um raio de campo receptivo diferente, e concluímos a execução do método.

   if(!caLocalPointNet[0].Init(0, 0, OpenCL, window, units_count, 64, 0.2f, optimization, iBatch))
      return false;
   if(!caLocalPointNet[1].Init(0, 0, OpenCL, 64, units_count, 64, 0.4f, optimization, iBatch))
      return false;
//---
   return true;
  }

Vale ressaltar que começamos com um campo receptivo pequeno e o aumentamos gradualmente. No entanto, não expandimos o campo receptivo até cobrir toda a nuvem de pontos, pois essa função já é herdada da classe PointNet convencional.

Após concluir o método de inicialização do objeto da classe, passamos à construção do algoritmo de propagação para frente no método feedForward.

bool CNeuronPointNet2OCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- LocalNet
   if(!cTNetG)
     {
      if(!caLocalPointNet[0].FeedForward(NeuronOCL))
         return false;
     }

Os parâmetros desse método incluem um ponteiro para o objeto que contém os dados brutos. Inicialmente, é verificada a necessidade de projeção dos dados brutos para um espaço canônico. O procedimento segue a mesma lógica implementada na classe PointNet original. Se a projeção dos dados não for necessária, o ponteiro é encaminhado diretamente para o método de propagação para frente da primeira camada de discretização local dos dados.

Caso contrário, primeiro geramos a matriz de projeção dos dados.

   else
     {
      if(!cTurnedG)
         return false;
      if(!cTNetG.FeedForward(NeuronOCL))
         return false;

Em seguida, projetamos os dados brutos multiplicando-os pela matriz de projeção.

      int window = (int)MathSqrt(cTNetG.Neurons());
      if(IsStopped() ||
         !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), 
                                    NeuronOCL.Neurons() / window, window, window))
         return false;

Somente após essa transformação, passamos os valores resultantes para o método de propagação para frente da camada de discretização dos dados.

      if(!caLocalPointNet[0].FeedForward(cTurnedG.AsObject()))
         return false;
     }

Depois, realizamos a discretização com um campo receptivo maior.

   if(!caLocalPointNet[1].FeedForward(caLocalPointNet[0].AsObject()))
      return false;

Por fim, transmitimos os dados enriquecidos para o método de propagação para frente da classe-mãe, onde é determinado o descritor da nuvem de pontos analisada como um todo.

   if(!CNeuronPointNetOCL::feedForward(caLocalPointNet[1].AsObject()))
      return false;
//---
   return true;
  }

Como podemos observar, graças à estrutura complexa de herança, conseguimos construir um método de propagação bastante conciso para nossa nova classe. Os algoritmos dos métodos de propagação reversa também são compactos. Sugiro que você os analise por conta própria no anexo. Lembro que o código completo de todas as classes e módulos utilizados na preparação deste artigo está disponível no mesmo anexo. Lá também estão incluídos os códigos completos dos programas de treinamento dos modelos e sua interação com o ambiente. Vale mencionar que esses últimos foram transferidos integralmente do artigo anterior, sem nenhuma modificação. Além disso, a arquitetura dos modelos foi praticamente preservada. De fato, apenas um tipo de camada foi alterado no Codificador do estado do ambiente, mantendo todos os outros parâmetros inalterados.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPointNet2OCL;
   descr.window = BarDescr;                        // Variables
   descr.count = HistoryBars;                      // Units
   descr.window_out = LatentCount;                 // Output Dimension
   descr.step = int(true);                         // Use input and feature transformation
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Isso torna ainda mais interessante analisar os resultados do treinamento da nova política do Ator.

3. Testes

Agora concluímos a implementação de nossa interpretação das abordagens propostas pelos autores do PointNet++. Chegou o momento de avaliar a eficácia dessa implementação com dados históricos reais. Assim como no estudo anterior, os modelos serão treinados com os dados históricos do EURUSD para todo o ano de 2023. O intervalo de tempo será H1, e os parâmetros de todos os indicadores permanecerão nos valores padrão. O teste do modelo treinado será realizado no Strategy Tester do MetaTrader 5.

Como mencionado anteriormente, nossa nova abordagem difere da anterior apenas em uma camada. Além disso, essa nova camada é apenas uma versão aprimorada da solução anterior. Isso torna a comparação entre os dois modelos ainda mais interessante. Para garantir uma comparação o mais justa possível, treinamos os modelos utilizando exatamente o mesmo conjunto de dados da pesquisa anterior.

Geralmente, recomendo atualizar periodicamente o conjunto de dados de treinamento para obter melhores resultados com o aprendizado do modelo. Apenas assim a amostragem permanecerá alinhada à política atual do Ator, permitindo uma avaliação mais precisa de suas ações e ajustes mais eficientes na estratégia. No entanto, neste caso específico, não posso deixar de lado a oportunidade de comparar dois métodos semelhantes e avaliar a eficácia do aprendizado hierárquico. No artigo anterior, treinamos uma política de Ator capaz de gerar lucro a partir desse conjunto de dados. Agora, esperamos que a nova abordagem obtenha resultados semelhantes.

Ao final do treinamento, a nova arquitetura foi capaz de aprender uma política que gerava lucro tanto no conjunto de treinamento quanto no conjunto de teste. Os resultados do teste da nova abordagem são apresentados a seguir.

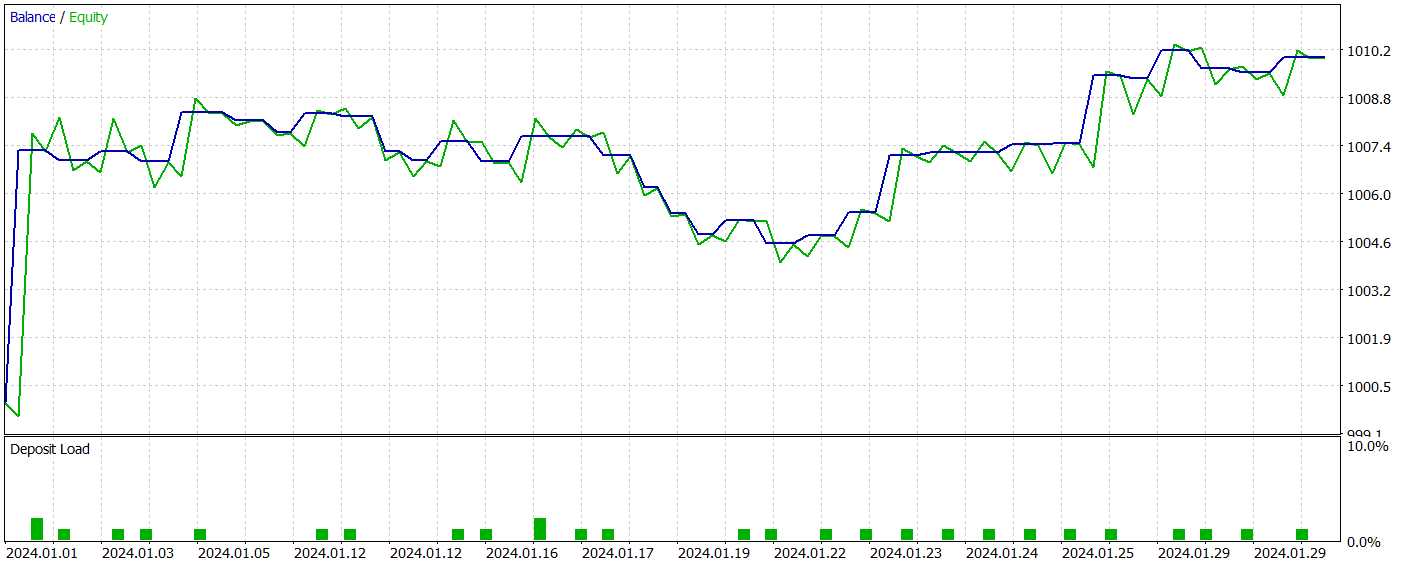
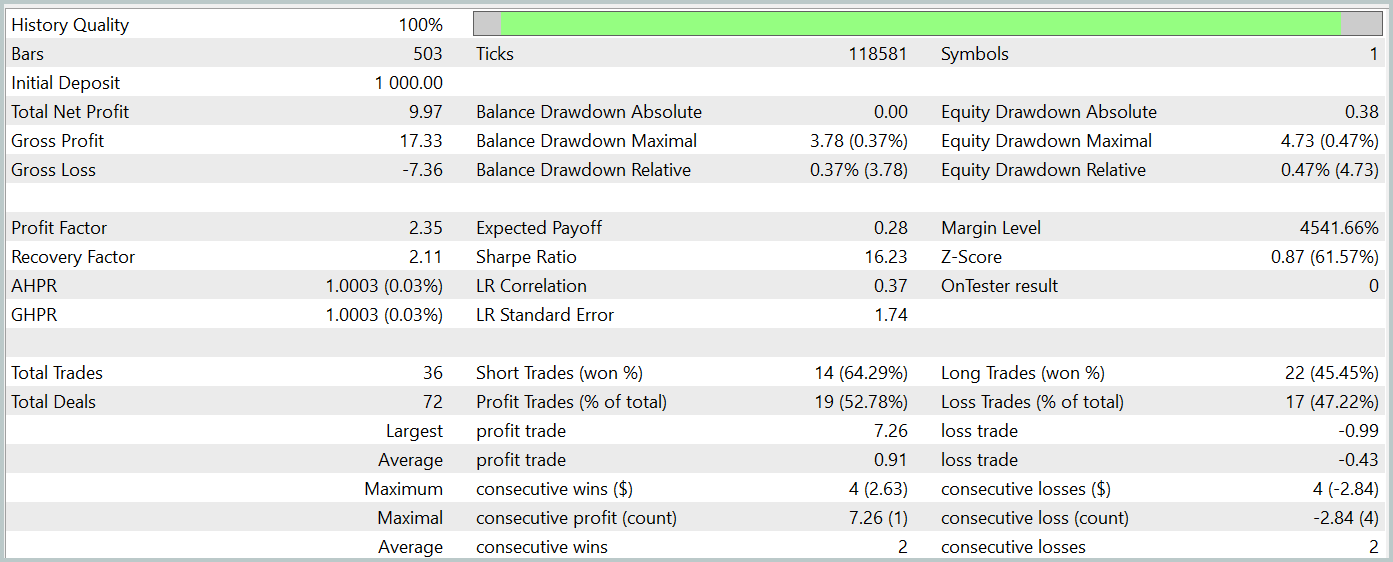
É preciso dizer que comparar os resultados de ambas as arquiteturas não é uma tarefa fácil. Durante o período de teste, ambas as versões geraram aproximadamente o mesmo lucro. As variações na drawdown do saldo e do equity permaneceram dentro da margem de erro. No entanto, a nova abordagem executou um número menor de operações e apresentou um leve aumento no fator de lucro.

No entanto, o número reduzido de operações realizadas por ambas as abordagens não permite tirar conclusões definitivas sobre sua eficácia em períodos mais longos.

Considerações finais

O uso do método PointNet++ permite analisar de maneira eficiente padrões locais e globais em dados financeiros complexos, considerando sua estrutura multidimensional. O aprimoramento no processamento de dados pontuais melhora a precisão das previsões e a estabilidade das estratégias de trading, o que pode resultar em decisões mais bem fundamentadas e bem-sucedidas em mercados dinâmicos.

Na parte prática deste artigo, implementamos nossa interpretação das abordagens propostas pelos autores do PointNet++. Durante os testes, a arquitetura conseguiu gerar lucro na amostra de teste. No entanto, os programas apresentados têm um caráter exclusivamente demonstrativo e servem apenas para ilustrar o funcionamento do método.

Referências

• PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de Modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criar uma rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL