Klassische Strategien neu interpretieren (Teil VIII): Währungsmärkte und Edelmetalle zum USDCAD

In dieser Artikelserie wollen wir die breite Palette möglicher Anwendungen von KI in Handelsstrategien erkunden. Unser Ziel ist es, Sie mit den Informationen zu versorgen, die Sie benötigen, um eine fundierte Entscheidung zu treffen, bevor Sie Ihr Kapital in eine KI-basierte Strategie investieren. Wir hoffen, dass Sie eine Strategie finden können, die für Ihre Risikotoleranz geeignet ist.

Überblick über die Handelsstrategie

In der heutigen Diskussion werden wir die Beziehungen zwischen der Währung und den Edelmetallmärkten aufdecken. Edelmetalle sind ein wesentlicher Bestandteil jeder modernen Wirtschaft. Der Grund dafür ist ihr breites industrielles Einsatzspektrum, das von der Elektronik bis zur Gesundheitsfürsorge reicht. Preisschwankungen bei Edelmetallen führen zu einer Inflation bei den Herstellern von Fertigerzeugnissen, was zu einem Rückgang der inländischen Produktion führen kann, oder andererseits zu einer sinkenden Nachfrage in den Ländern, die diese Metalle exportieren.

Gold ist eines der wichtigsten Exportgüter Kanadas und Amerikas. Die natürliche Korrosionsbeständigkeit von Gold sorgt dafür, dass es sowohl bei Entwicklern empfindlicher elektronischer Geräte als auch bei Juwelieren sehr gefragt ist. Palladium hingegen wird von vielen Industriezweigen nachgefragt, insbesondere von der Automobilindustrie. In einem Auto gibt es mehr als 20 verschiedene Bauteile, die Katalysatoren benötigen. Die bekanntesten sind die in den Auspuffrohren eingebauten Katalysatoren. Jeder dieser Konverter enthält zum Teil erhebliche Mengen an Palladium.  Kanada und Amerika sind beide führende Exporteure von Fahrzeugen. Daher werden sich die Preise dieser Edelmetalle in gewissem Maße auf die Inlandsproduktion dieser beiden Länder auswirken.

In der Vergangenheit war die Korrelation zwischen dem Goldpreis und dem Dollar invers. Wenn sich der Dollar schlecht entwickelte, tendierten die Anleger dazu, alle Positionen, die sie auf den Dollar gesetzt hatten, zu schließen und ihr Geld stattdessen in Gold abzusichern. In den Tagen der quantitativen Lockerung, die wir jetzt erleben, sind die Zusammenhänge jedoch nicht mehr so eindeutig.

Überblick über die Methodik

Wir möchten, dass unser Computer seine eigene Strategie aus den Preisen dieser drei Märkte lernt. Natürlich haben wir eine gewisse Neigung, an Strategien zu glauben, die uns gefallen oder intuitiv Sinn machen, und nicht an Strategien, die dies nicht tun. Durch das algorithmische Erlernen einer Strategie ist unser Computer jedoch in der Lage, Zusammenhänge zu erkennen, für die wir vielleicht ein ganzes Leben gebraucht hätten, um sie zu entdecken. Es könnte aber auch die Grenzen der Genauigkeit unserer Strategie aufzeigen.

Bewertung der Zuverlässigkeit der Edelmetallmärkte bei der Vorhersage der Devisenmärkte. Wir haben versucht, den USDCAD-Wechselkurs anhand von 3 Gruppen von Prädiktoren zu prognostizieren:

1. Kurse für das Währungspaar USDCAD
2. Kurse von XAUUSD und XPDUSD
3. Ein Satz der oben genannten.

Wir haben alle unsere Daten direkt aus dem MetaTrader 5-Terminal mit Hilfe eines angepassten Skripts, das wir in MQL5 geschrieben haben, geholt. Wir haben die Daten in eine CSV-Datei geschrieben und sie in Python verarbeitet. Darüber hinaus wurden signifikante negative Korrelationsniveaus beobachtet, -0,5 zwischen XAUUSD und USDCAD und schließlich -,66 zwischen XPDUSD und USDCAD. Allerdings wurde nur eine mäßige direkte Korrelation zwischen den beiden Metallen festgestellt (0,37).

Wir haben versucht, die Daten zu visualisieren. Aus den Daten konnten wir jedoch keine erkennbaren Zusammenhänge ablesen. Wir haben versucht, die Daten in höheren Dimensionen darzustellen, indem wir ein 3D-Punktdiagramm verwendeten, aber ohne Erfolg. Die Daten scheinen schwer zu trennen zu sein.

Daraufhin haben wir mehrere Modelle zur Prognose des USDCAD-Wechselkurses unter Verwendung der drei zuvor beschriebenen Gruppen von Prädiktoren trainiert. Das Modell mit der besten Leistung war das lineare Modell unter Verwendung der ersten Gruppe von Prädiktoren. Da das lineare Modell jedoch keine einstellbaren Parameter hat, wählten wir das zweitbeste Modell, den Linear Support Vector Regressor (LSVR), als unser bestes Modell aus.

Wir haben die Hyperparameter des LSVR-Modells erfolgreich angepasst, ohne dass es zu einer Überanpassung an das Trainingsset kam, was durch die Tatsache belegt wird, dass wir das Standard-LSVR-Modell bei unbekannten Daten übertrafen. Leider ist es uns nicht gelungen, das lineare Modell mit denselben Validierungsdaten zu übertreffen. Wir verwendeten den durchschnittlichen RMSE, der durch 5-fache Zeitreihen-Kreuzvalidierung ohne zufälliges Verschieben berechnet wurde, um die Modellauswahl sowohl beim Training als auch bei der Validierung durchzuführen.

Anschließend exportierten wir unser angepasstes LSVR-Modell in das ONNX-Format und erstellten unseren eigenen Expert Advisor mit integrierter KI unter Verwendung von MQL5.

Datenerhebung

Ich habe ein praktisches Skript beigefügt, mit dem Sie Daten von Ihrem MetaTrader 5 Terminal abrufen können. Starten Sie das Skript einfach auf dem Chart, das Sie analysieren möchten, und legen Sie los.

Das Skript fragt einfach so viele Balken ab, wie Sie in der Eingabe angeben, und schreibt sie im CSV-Format. Das Aufschreiben der Zeit ist wichtig, weil wir sie später verwenden werden, wenn wir unsere CSV-Dateien in Python zu einem zusammengefassten Datenrahmen zusammenfügen wollen. Wir werden unsere Daten nur an den Tagen zusammenführen, die sie alle gemeinsam haben.

Beachten Sie, dass wir die Eigenschaft einschließen: „#property script_show_inputs“: Wenn Sie diese Eigenschaft nicht in Ihre Skripte aufnehmen, können Sie die Skripteingaben nicht anpassen.

//+------------------------------------------------------------------+
//|                                                     ProjectName  |
//|                                     Copyright 2020, CompanyName  |
//|                                     http://www.companyname.net   |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link          "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//---Amount of data requested
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
//---File name
   string file_name = "Market Data " + Symbol() + ".csv";

//---Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
        {
        if(i == size)
        {
        FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

        else
        {
        FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                iOpen(Symbol(),PERIOD_CURRENT,i),
                iHigh(Symbol(),PERIOD_CURRENT,i),
                iLow(Symbol(),PERIOD_CURRENT,i),
                iClose(Symbol(),PERIOD_CURRENT,i));
        }
        }

  }
//+------------------------------------------------------------------+

Nun, da unsere Daten fertig sind, können wir mit der Bereinigung der Daten in Python beginnen.

Datenbereinigung

Zunächst importieren wir die benötigten Standardbibliotheken.

#Import the libraries we need
import pandas as pd
import numpy as np

Dies ist die Version der Bibliothek, die wir in dieser Demonstration verwenden.

#Display library versions
print(f"Pandas version {pd.__version__}")
print(f"Numpy version {np.__version__}")

Pandas Version 2.2.1
Numpy Version 1.26.4

Nun lesen wir die CSV-Daten ein, die wir abgerufen haben.

#Read in the data we need
usdcad = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data USDCAD.csv")
usdcad = usdcad[::-1]
xauusd = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data XAUUSD.csv")
xauusd = xauusd[::-1]
xpdusd = pd.read_csv("\\home\\volatily\\.wine\\drive_c\\Program Files\\MetaTrader 5\\MQL5\\Files\\Market Data XPDUSD.csv")
xpdusd = xpdusd[::-1]

Wir verwenden die Zeitspalte als Index

#Set the time column as the index
usdcad.set_index("Time",inplace=True)
xauusd.set_index("Time",inplace=True)
xpdusd.set_index("Time",inplace=True)

und führen die Daten zusammen.

#Let's merge the data
merged_data = usdcad.merge(xauusd,suffixes=('',' XAU'),left_index=True,right_index=True)
merged_data = merged_data.merge(xpdusd,suffixes=('',' XPD'),left_index=True,right_index=True)

So sehen unsere Daten aus.

merged_data

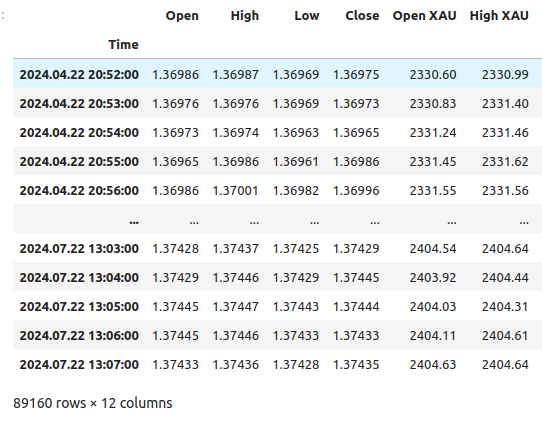
Abb. 1: Unser zusammengeführter Datenrahmen

Wir müssen festlegen, wie weit wir in die Zukunft blicken wollen.

#Define the forecast horizon
look_ahead = 20

Wir definieren die 3 Gruppen von Prädiktoren, die wir testen möchten.

#Define the predictors and target
ohlc_predictors = ['Open','High','Low','Close']
new_predictors = ['Open XAU','High XAU','Low XAU','Close XAU','Open XPD','High XPD','Low XPD','Close XPD']
predictors = ohlc_predictors + new_predictors

Kennzeichnung der Daten.

#Let's add labels to the data
merged_data["Target"] = merged_data["Close"].shift(-look_ahead)

Erstellen wir auch die Kennzeichnungen, die bei der Visualisierung der Daten hilfreich sind. Diese Kennzeichnungen fassen die Veränderungen auf den einzelnen Märkten zusammen.

#Let's also add labels to help us visualize the relationships
merged_data["Binary Target"] = np.nan
merged_data["XAU Target"] = np.nan
merged_data["XPD Target"] = np.nan

#Define the target values
#Changes in the USDCAD Exchange rate
merged_data.loc[merged_data["Close"] > merged_data["Target"],"Binary Target"] = 0
merged_data.loc[merged_data["Close"] < merged_data["Target"],"Binary Target"] = 1
#Changes in the price of Gold
merged_data.loc[merged_data["Close XAU"] > merged_data["Close XAU"].shift(-look_ahead),"XAU Target"] = 0
merged_data.loc[merged_data["Close XAU"] < merged_data["Close XAU"].shift(-look_ahead),"XAU Target"] = 1
#Changes in the price of Palladium
merged_data.loc[merged_data["Close XPD"] > merged_data["Close XPD"].shift(-look_ahead),"XPD Target"] = 0
merged_data.loc[merged_data["Close XPD"] < merged_data["Close XPD"].shift(-look_ahead),"XPD Target"] = 1

#Drop any NA values
merged_data.dropna(inplace=True)

Explorative Datenanalyse

Um unsere Daten zu visualisieren, werden wir zunächst die erforderlichen Bibliotheken importieren.

#Explorartory data analysis
import seaborn as sns
import matplotlib.pyplot as plt

Anzeige der Bibliotheksversionen.

#Display library version
print(f"Seaborn version: {sns.__version__}")

Version Seaborn: 0.13.2

Zunächst setzen wir den Index unseres zusammengeführten Datenrahmens zurück.

#Reset the index
merged_data.reset_index(inplace=True)

Erstellen wir nun eine Korrelations-Heatmap. Wie wir sehen können, besteht eine signifikant starke Korrelation zwischen den beiden Edelmetallen und dem USDCAD-Paar. Dies steht im Einklang mit unserer grundlegenden Analyse der Rolle, die diese Metalle für das Bruttoinlandsprodukt beider Länder spielen. Leider führte dies nicht zu einer besseren Leistung beim Versuch, den USDCAD-Wechselkurs zu prognostizieren.

#Correlation heatmap
fig , ax = plt.subplots(figsize=(7,7))
sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True,ax=ax)

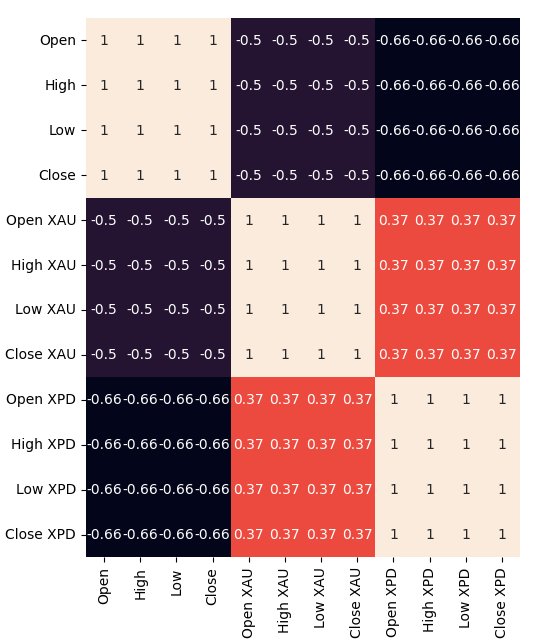
Abb. 2: Unsere Heatmap der Korrelation

Wir haben zwei kategoriale Diagramme erstellt, die alle Fälle zusammenfassen, in denen der Gold- oder Palladiumpreis gestiegen (Spalte 1) oder gefallen ist (Spalte 2). Von dort aus haben wir die einzelnen Punkte eingefärbt, um anzuzeigen, ob der USDCAD-Wechselkurs gestiegen ist (orangefarbene Punkte) oder gefallen ist (blaue Punkte). Wie man sehen kann, haben wir eine Mischung aus beiden Ergebnissen in beiden Spalten. Dies könnte darauf hindeuten, dass die Veränderungen des USDCAD-Wechselkurses unabhängig von den Veränderungen bei den von uns ausgewählten Edelmetallen sind.

#Let's create categorical plots
sns.catplot(data=merged_data,x="XAU Target",y="Close",hue="Binary Target")

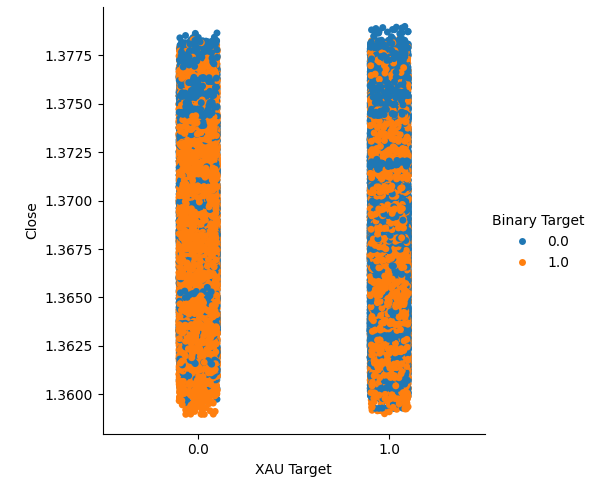
Abb. 3: Kategorische Darstellung des Goldpreises und des USDCAD-Schlusskurses

#Let's create categorical plots
sns.catplot(data=merged_data,x="XPD Target",y="Close",hue="Binary Target")

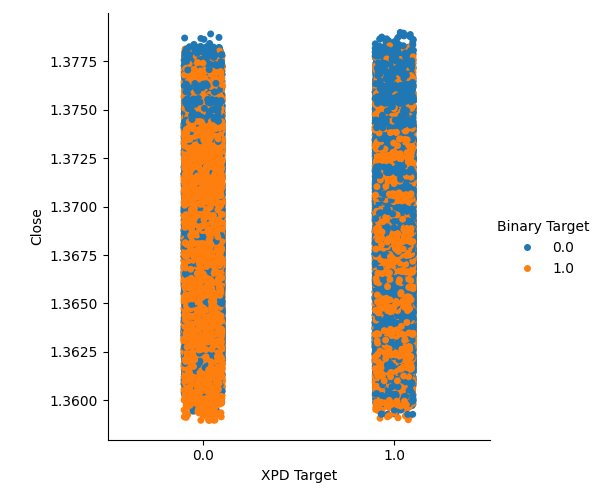
Abb. 4: Kategorische Darstellung des Palladiumpreises gegen den USDCAD-Preis

Anschließend erstellten wir Streudiagramme, um die Varianz zwischen dem Schlusskurs des Palladium- und USDCAD-Marktes zu visualisieren. Leider ergab sich daraus kein erkennbarer Zusammenhang, den wir uns zunutze machen können. Wir färbten jeden Punkt mit der gleichen orangefarbenen und blauen Farbkarte wie oben beschrieben.

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XPD",y="Close",hue="Binary Target")

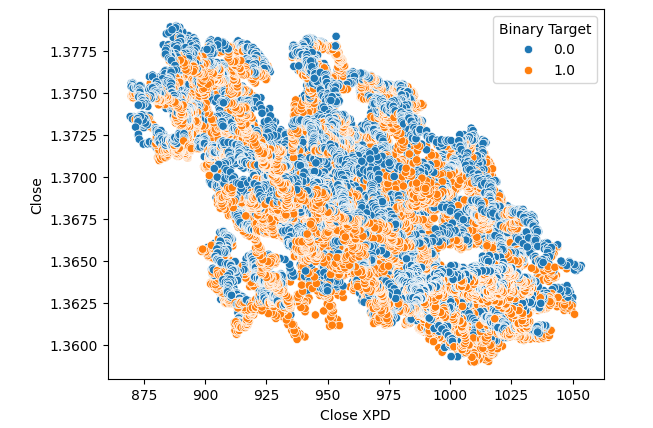
Abb. 5: Streudiagramm von XPDUSD gegen USDCAD

Keine Verbesserungen ergaben sich, als wir den Goldpreis anstelle des Palladiumpreises in das Streudiagramm einfügten.

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XAU",y="Close",hue="Binary Target")

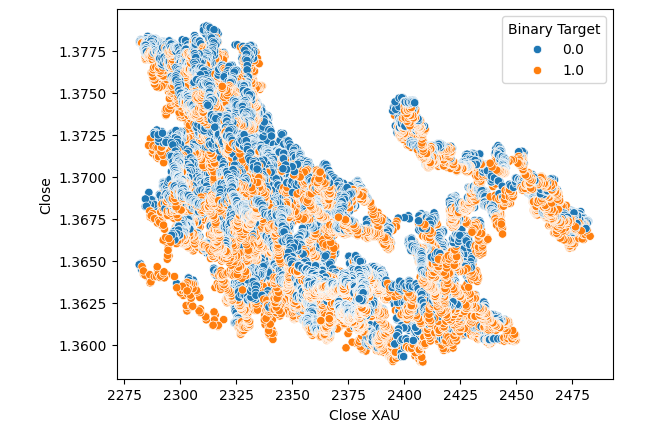
Abb. 6: Ein Streudiagramm des XAUUSD gegen den USDCAD-Schluss

Wir dachten daran, eine Beziehung zwischen den beiden Metallen selbst zu testen. Der Zusammenhang war für uns jedoch noch nicht offensichtlich. Wir haben ein Streudiagramm des Goldpreises gegenüber dem Palladiumpreis erstellt und die Veränderung des USDCAD-Paares zur Einfärbung der einzelnen Punkte verwendet, aber das brachte keine Verbesserung.

#Let's visualize scatter plots
sns.scatterplot(data=merged_data,x="Close XPD",y="Close XAU",hue="Binary Target")

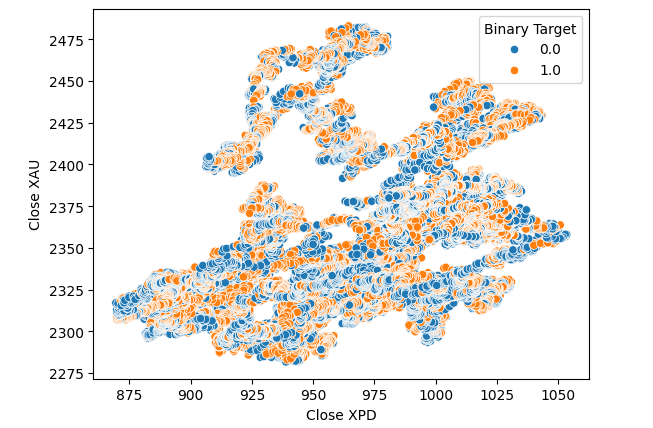
Abb. 7: Ein Streudiagramm von XAUUSD gegen XPDUSD

Manchmal können Beziehungen verborgen sein, da wir nicht genügend Variablen gleichzeitig betrachten, um die Auswirkungen zu erkennen. Wir haben ein 3D-Diagramm mit den Schlusskursen von Palladium, Gold und dem USDCAD erstellt. Leider zeigte das Ergebnis, dass es sich um Cluster in den Daten handelte, die eine geringe Trennschärfe aufwiesen und im Wesentlichen das wiederholten, was wir bereits wissen.

#Visualizing 3D data
fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111,projection='3d')
colors = ['blue' if movement == 0 else 'orange' for movement in merged_data.loc[0:1100,"Binary Target"]]
ax.scatter(merged_data.loc[0:1100,"Close"],merged_data.loc[0:1100,"Close XAU"],merged_data.loc[0:1100,"Close XPD"],c=colors)

#Set labels
ax.set_xlabel('USDCAD')
ax.set_ylabel('XAUUSD')
ax.set_zlabel('XPDUSD')

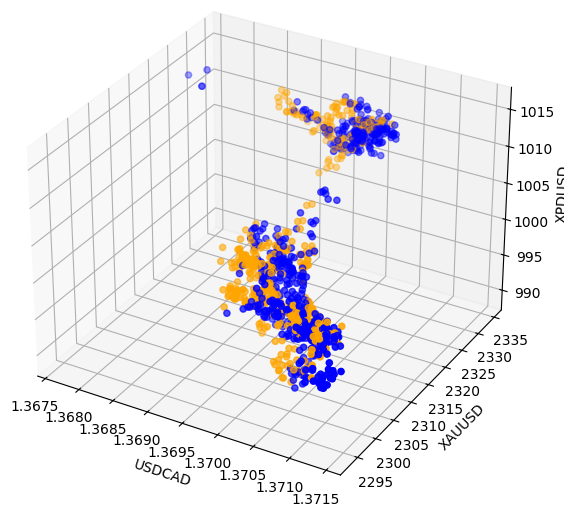
Abb. 8: Visualisierung unserer Marktdaten in 3D

Datenmodellierung

Beginnen wir nun mit der Modellierung unserer Daten. Zunächst importieren wir die Standardbibliotheken.

#Modelling the data
import sklearn
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import RobustScaler

Anzeige der Bibliotheksversion.

#Print library version
print(f"Sklearn version {sklearn.__version__}")

Sklearn version 1.4.1.post1

Bevor wir mit dem Training von Modellen beginnen, müssen wir die Daten zunächst skalieren und standardisieren.

#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)

Nun werden wir die Daten in zwei Hälften aufteilen, eine für Training und Optimierung und die zweite für Validierung und Test auf Überanpassung.

#Split the data
train_X,test_X,train_y,test_y = train_test_split(scaled_data,merged_data.loc[:,"Target"],shuffle=False,test_size=0.5)

Importieren wir nun die Modelle

#Preparing to model the data
from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor , GradientBoostingRegressor , BaggingRegressor
from sklearn.svm import LinearSVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import root_mean_squared_error

und jetzt erstellen wir das geteilte Zeitreihenobjekt.

#Create the time series split object
tscv = TimeSeriesSplit(gap=look_ahead,n_splits=5)

Wir speichern die Modelle in einer Liste, damit wir sie iterativ durchgehen können.

#Create a list of models
models = [
        LinearRegression(),
        RandomForestRegressor(),
        GradientBoostingRegressor(),
        BaggingRegressor(),
        LinearSVR(),
        KNeighborsRegressor(),
        MLPRegressor(hidden_layer_sizes=(100,10))
]

Wir erstellen einen Datenrahmen, um unsere Genauigkeitsstufen zu speichern.

#List of models
columns = [
        "Linear Regression",
        "Random Forest",
        "Gradient Boost",
        "Bagging",
        "Linear SVR",
        "K-Neighbors",
        "Neural Network"
]

#Create a dataframe to store our error metrics
ohlc_error = pd.DataFrame(columns=columns,index=np.arange(0,5))
new_error = pd.DataFrame(columns=columns,index=np.arange(0,5))
all_error = pd.DataFrame(columns=columns,index=np.arange(0,5))

Wir definieren die zu verwendenden Prädiktoren.

#Setting the current predictors
current_predictors = predictors

Wir führen eine Kreuzvalidierung von jedem Modell mit den oben definierten Prädiktoren durch.

#Perform cross validation
for j in np.arange(0,len(models)):
        model = models[j]
        for i,(train,test) in enumerate(tscv.split(train_X)):
        model.fit(train_X.loc[train[0]:train[-1],current_predictors],train_y.loc[train[0]:train[-1]])
        all_error.iloc[i,j] = root_mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],current_predictors]))

Betrachten wir unsere Fehlerniveaus unter Verwendung gewöhnlicher OHLC-Daten. Aus unseren Visualisierungen und den zusammenfassenden Statistiken geht hervor, dass das Modell der linearen Regression bei dieser Aufgabe am besten abgeschnitten hat.

ohlc_error

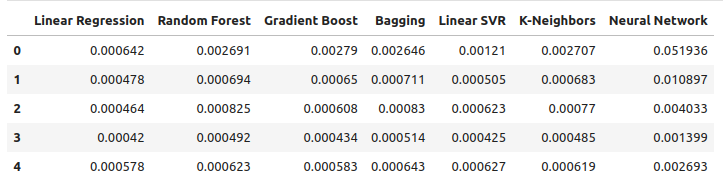
Abb. 9: Unsere Fehlergrenzen bei der Vorhersage mit OHLC USDCAD-Daten

Darstellung der Daten.

ohlc_error.plot()

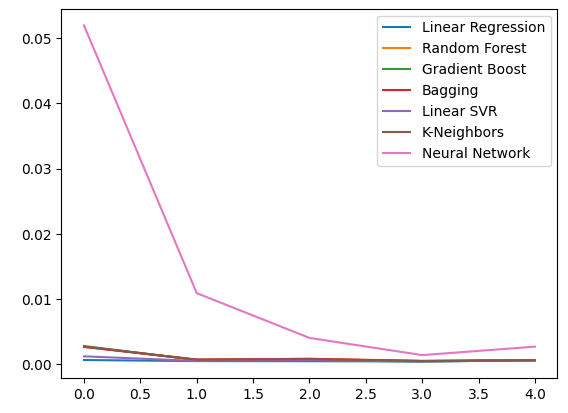
Abb. 10: Unsere Modellgenauigkeit bei Verwendung des ersten Satzes von Prädiktoren

Erstellen von Box-Plots.

fig = plt.figure(figsize=(5,5))
plt.boxplot(ohlc_error)

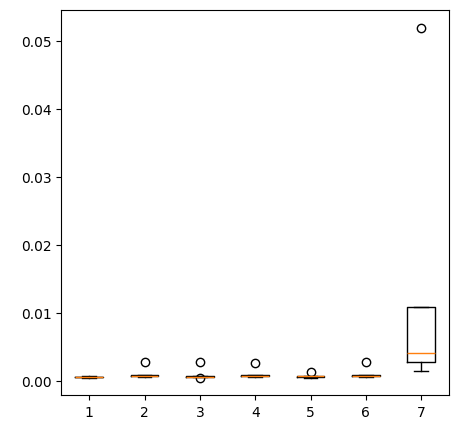
Abb. 11: Unsere Modellgenauigkeit bei Vorhersagen mit der ersten Gruppe von Prädiktoren

Betrachten wir unsere Fehlerquote bei der Verwendung der Edelmetalle zur Prognose des USDCAD-Wechselkurses. Die lineare Regression ist immer noch das beste Modell, allerdings nicht mehr mit großem Abstand.

new_error

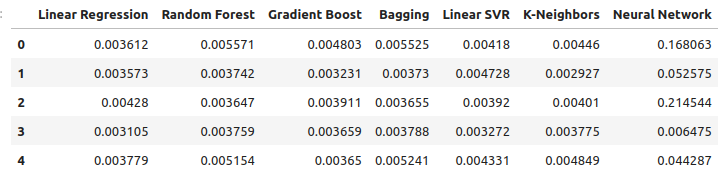
Abb. 12: Unsere neuen Fehlerstufen

Darstellung der neuen Fehlerniveaus.

new_error.plot()

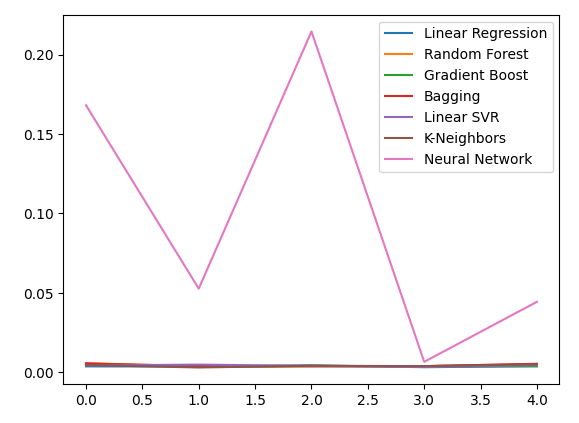
Abb. 13: Unsere neuen Fehlerstufen

Erstellung eines Box-Plots der neuen Ergebnisse.

fig = plt.figure(figsize=(5,5))
plt.boxplot(new_error)

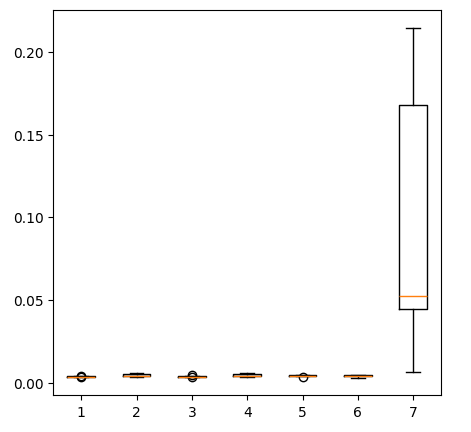
Abb. 14: Unsere Fehlerquote bei der Verwendung von Edelmetallmarktdaten

Betrachten wir nun unsere Leistung unter Verwendung aller verfügbaren Daten. Wir stellen nach wie vor fest, dass das lineare Modell deutlich besser abschneidet als alle anderen Modelle, die wir haben. Versuchen wir nun, das zweitbeste Modell, die LinearSVR, so zu optimieren, dass es die lineare Regression übertrifft.

all_error

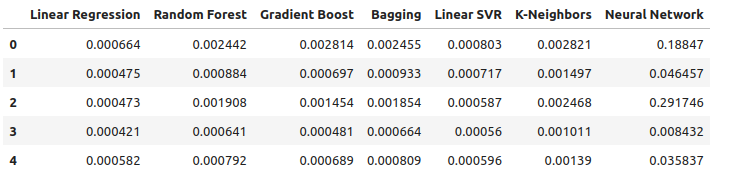
Abb. 15: Unsere Genauigkeit bei der Verwendung aller uns vorliegenden Daten

Aufzeichnung der Fehlerniveaus.

all_error.plot()

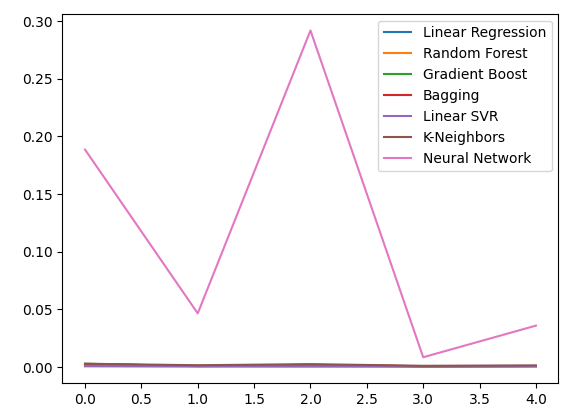
Abb. 16: Liniendiagramme unserer Genauigkeit bei Verwendung aller uns vorliegenden Daten

Die Erstellung eines Box-Plots der Fehlerniveaus, die wir unter Verwendung aller uns vorliegenden Daten erhalten haben, zeigt, dass die einfache lineare Regression immer noch die beste Wahl ist.

fig = plt.figure(figsize=(5,5))
plt.boxplot(all_error)

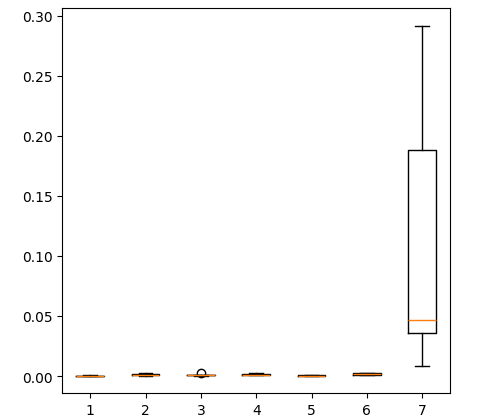
Abb. 17: Box-Plots unserer Genauigkeit bei Verwendung aller uns vorliegenden Daten

Die mittleren Fehlerwerte unserer Modelle über alle 5 Validierungssätze hinweg zeigen deutlich, dass das lineare Modell bisher unsere beste Wahl ist. Die LinearSVR ist jedoch nicht weit davon entfernt.

all_error.mean()

Linear Regression 0.000523
Random Forest      0.001333
Gradient Boost       0.001227
Bagging                  0.001343
Linear SVR             0.000653
K-Neighbors            0.001837
Neural Network       0.114188
dtype: object

Das Merkmal Bedeutung

Bevor wir mit der Optimierung unseres Modells beginnen, sollten wir zunächst beurteilen, welche Merkmale wichtig erscheinen. Wir hoffen, dass unsere Daten in Bezug auf den Edelmetallmarkt ihren Wert in diesem Test zeigen werden. Wir werden zunächst die Werte der gegenseitigen Information (MI) testen. Der MI ist ein Maß dafür, wie viel Gewissheit man über den Wert des Ziels erhält, wenn man den Wert eines der Prädiktoren kennt. Der MI wird auf einer logarithmischen Skala berechnet, daher ist ein MI-Wert über 2 in der Praxis selten anzutreffen.

Wir beginnen mit dem Import der benötigten Bibliotheken.

#Mutual information score
from sklearn.feature_selection import mutual_info_regression

Nun berechnen wir die MI-Scores für jeden unserer Prädiktoren.

#Prepare the data for plotting
mi = mutual_info_regression(train_X,train_y)
mi = mi.reshape(1,12)
mi_scores = pd.DataFrame(mi,columns=predictors)

Die Darstellung unserer MI-Scores deutet darauf hin, dass die Daten des USDCAD-Marktes möglicherweise informativer sind als alle Daten des Edelmetallmarktes. Dies wird durch unseren Kreuzvalidierungstest bestätigt, bei dem wir festgestellt haben, dass das lineare Modell, das nur die Notierungen des USDCAD-Marktes verwendet, den geringsten Fehler aufweist.

#Prepare the data for plotting
mi = mutual_info_regression(train_X,train_y)
mi = mi.reshape(1,12)
mi_scores = pd.DataFrame(mi,columns=predictors)
#Plot the scores
mi_scores.plot.bar()

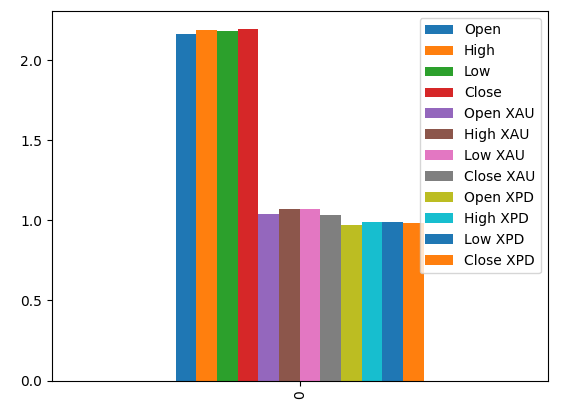
Abb. 18: Gegenseitige Informationswerte für unsere 3 Datensätze

Als Nächstes werden wir die SHAP-Werte berechnen. SHAP-Werte sind Black-Box-Erklärer, die uns helfen, die globale Bedeutung von Merkmalen in unseren maschinellen Lernmodellen zu identifizieren.

Importieren der SHAP-Bibliothek.

#The Linear SVR appears to be performing second best
import shap

Initialisieren des LSVR-Modells.

#Initialize the model
model = LinearSVR()
model.fit(train_X,train_y)

Berechnen der SHAP-Werte.

#Compute SHAP values
explainer = shap.Explainer(model,train_X)
explanations = explainer(train_X)

Anzeigen der globale Bedeutung des Merkmals.

#Plot SHAP values
shap.plots.violin(explanations)

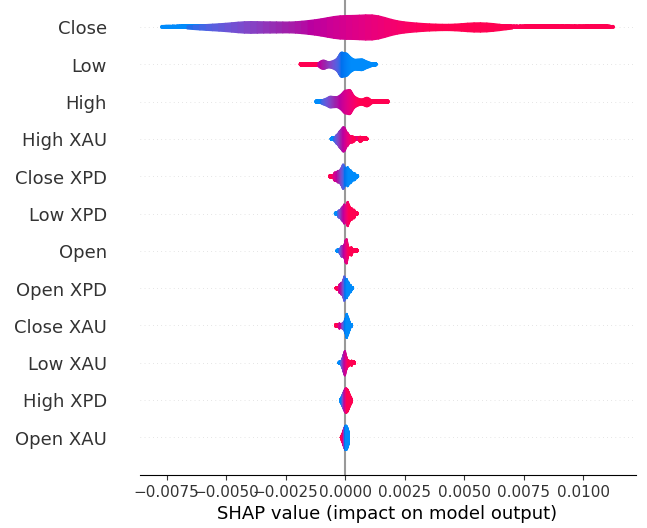
Abb. 19: Unsere SHAP-Bedeutungsstufen

Unsere SHAP-Erklärungen stimmen nicht mit unserer Bewertung der gegenseitigen Information überein. Wir haben das Problem der unterschiedlichen Einschätzungen in früheren Artikeln ausführlich behandelt. Das Beste, was man dazu sagen kann, ist, dass die Bedeutung von Merkmalen schwierig einzuschätzen sein kann und mit Vorsicht zu genießen ist. Beide Erklärungen legen jedoch nahe, dass die Edelmetallmärkte einige nützliche Informationen enthalten.

Anpassen der Hyperparameter

Durch die Anpassung unseres Modells können wir bei ungesehenen Daten bessere Ergebnisse erzielen, als dies mit dem Standardmodell möglich wäre.

Um unser Modell abzustimmen, müssen wir zunächst die benötigten Bibliotheken importieren.

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

Initialisieren wir nun das Modell.

#Reinitialize the model
model = LinearSVR()

Dann legen wir unsere Tuning-Parameter fest. Wir übergeben das Modell und ein Verzeichnis möglicher Parameterwerte, gefolgt von der Gesamtzahl der Iterationen, die wir durchführen möchten. Wir möchten eine 5-fache Kreuzvalidierung durchführen, um den negativen mittleren quadratischen Fehler zu messen, d. h. wir wählen das Modell mit dem geringsten Validierungsfehler aus. Schließlich ermöglicht die Einstellung von n_jobs auf minus 1 die parallele Durchführung der Suche auf allen verfügbaren CPU-Kernen.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "epsilon" : [0,10,100,1000],
        "tol":[0.01,0.001,0.0001,0.00001,0.0000001],
        "C":[1,10,100,1000,10000],
        "loss":['epsilon_insensitive', 'squared_epsilon_insensitive']  
        },
        n_iter=1000,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Anpassen des Tuners.

#Let's fit the tuner
tuner_results = tuner.fit(train_X,train_y)

Die besten Parameter, die wir gefunden haben.

#Let's see the best parameters we found
tuner_results.best_params_

{'tol': 1e-05, 'loss': 'squared_epsilon_insensitive', 'epsilon': 0, 'C': 10000}

Test auf Überanpassung

Um die Überanpassung zu testen, müssen wir zunächst unsere Modelle initialisieren.

#Testing for overfitting
benchmark =  LinearRegression()
default_lsvr = LinearSVR()
customized_lsvr = LinearSVR(tol=1e-05,loss='squared_epsilon_insensitive',epsilon=0,C=10000)

Wir setzen nun die Indizes zurück, damit wir eine Kreuzvalidierung durchführen können.

#Reset the indexes
test_y = test_y.reset_index()
test_X = test_X.reset_index()

Wir formatieren die Daten

#Format the data
test_y = test_y.loc[:,"Target"]
test_X = test_X.loc[:,predictors]

und erstellen die Datenrahmen, um unsere Fehlerstufen zu speichern.

#Create dataframes to store our error levels
test_error = pd.DataFrame(columns=["Linear Regression","LSVR","Customized LSVR"],index=[0,1,2,3,4])

Wir trainieren die Modelle anhand der Trainingsmenge

#Fit the models on the training set
benchmark.fit(train_X,train_y)
default_lsvr.fit(train_X,train_y)
customized_lsvr.fit(train_X,train_y)

und speichern die Modelle in einer Liste.

models = [benchmark,default_lsvr,customized_lsvr]

Die Kreuzvalidierung jedes Modells mit den Testdaten.

for j in np.arange(0,len(models)):
        model = models[j]
        for i,(train,test) in enumerate(tscv.split(test_X)):
        model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1]])
        test_error.iloc[i,j] = root_mean_squared_error(test_y.loc[test[0]:test[-1]],model.predict(test_X.loc[test[0]:test[-1],:]))

Unser Testfehler.

test_error

Lineare Regression	LSVR	Angepasster LSVR
0.000598	0.000542	0.000743
0.000472	0.000573	0.000722
0.000318	0.000451	0.000333
0.000341	0.000366	0.000499
0.00043	0.000839	0.00043

Nach unserer durchschnittlichen Leistung über alle 5 Faltungen hinweg, war unser lineares Modell immer noch das leistungsfähigste Modell. Es ist uns jedoch gelungen, das Standardmodell zu übertreffen.

#Let's calculate our mean performances
test_error.mean()

Linear Regression      0.000432
LSVR                          0.000554
Customized LSVR      0.000545
dtype: object

Visualisierung unseres Testfehlers.

#Let's visualize our error
test_error.plot()

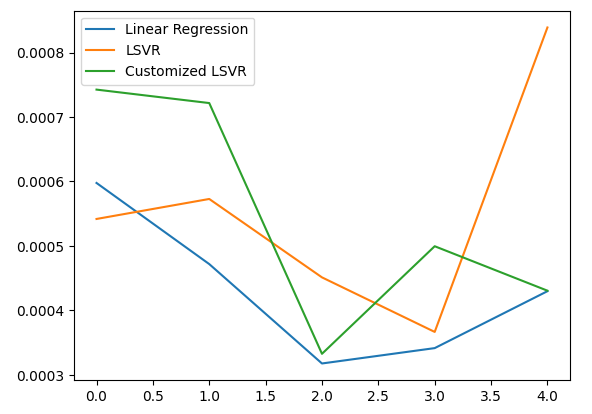
Abb. 20: Visualisierung unseres Testfehlers

Erstellung eines Box-Plots der Fehlerquoten unserer Tests.

#Create a boxplot of the error
sns.boxplot(data=test_error)

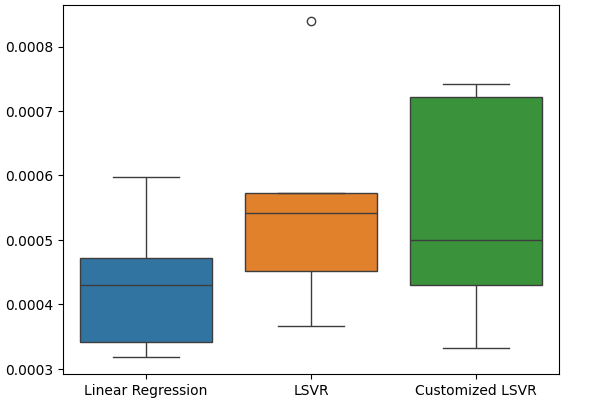
Abb. 21: Visualisierung unseres Testfehlers

Vorbereiten des Modells für den Export nach ONNX

Bevor wir unser Modell in das ONNX-Format exportieren können, müssen wir die Daten zunächst skalieren und standardisieren, indem wir den Mittelwert subtrahieren und durch die Standardabweichung dividieren. Anschließend werden wir unsere Skalierungsfaktoren in CSV ausgeben, damit wir das Verfahren in MQL5 reproduzieren können.

Zunächst erstellen wir den Datenrahmen, in dem unsere Skalierungsfaktoren gespeichert werden.

#Let's scale our data
scaling_factors = pd.DataFrame(columns=predictors,index=['mean','standard deviation'])
X = merged_data.loc[:,predictors]
y = merged_data.loc[:,"Target"]

Dann speichern wir den Mittelwert und die Standardabweichung und führen schließlich das Skalierungsverfahren durch.

#Let's fill each column
for i in np.arange(0,len(predictors)):
        scaling_factors.iloc[0,i] = X.iloc[:,i].mean()
        scaling_factors.iloc[1,i] = X.iloc[:,i].std()
        X.iloc[:,i] = ( ( X.iloc[:,i] - scaling_factors.iloc[0,i] ) / scaling_factors.iloc[1,i])

Wir speichern die Skalierungsfaktoren.

#Save the scaling factors as a CSV
scaling_factors.to_csv("/home/volatily/.wine/drive_c/Program Files/MetaTrader 5/MQL5/Files/usd_cad_xau_xpd_scaling_factors.csv")

Exportieren des Modells nach ONNX

ONNX steht für Open Neural Network Exchange (ONNX) und ist ein quelloffener, interoperabler Rahmen für maschinelles Lernen, der es Entwicklern ermöglicht, Modelle für maschinelles Lernen in einem sprachunabhängigen Rahmen zu erstellen, auszutauschen und einzusetzen. Dies wird erreicht, indem jedes Modell für maschinelles Lernen als Baum von Knoten und Graphen dargestellt wird, der mit jeder Sprache, die die ONNX-API unterstützt, wieder zum ursprünglichen Modell zusammengesetzt werden kann.

Zunächst werden wir die benötigten Bibliotheken importieren.

#Let's prepare to export our model to ONNX format
import onnx
import netron
import skl2onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Anzeige der Bibliotheksversionen.

#Display library versions
print(f"Onnx version: {onnx.__version__}")
print(f"Netron version: {netron.__version__}")
print(f"Skl2onnx version: {skl2onnx.__version__}")

Onnx-Version: 1.15.0
Netron-Version: 7.8.0
Skl2onnx-Version: 1.16.0

Nun werden wir die Eingabetypen unseres Modells definieren.

#Define the input type
initial_types = [('float_input',FloatTensorType([1,12]))]

Trainieren wir das Modell mit allen Daten, die wir haben.

#Train the model on all the data we have
customized_lsvr = LinearSVR(tol=1e-05,loss='squared_epsilon_insensitive',epsilon=0,C=10000)
customized_lsvr.fit(X,y)

Konvertieren des Modells in das ONNX-Format.

#Covert the sklearn model
onnx_model = convert_sklearn(customized_lsvr,initial_types=initial_types)

Speichern des ONNX-Modells.

#Save the onnx model
onnx_name = "USDCAD XAUUSD XPDUSD M1 Float.onnx"
onnx.save(onnx_model,onnx_name)

Sehen wir uns das ONNX-Modell an.

#View the onnx model
netron.start(onnx_name)

Abb. 22: Visualisierung unseres ONNX-Modells in netron

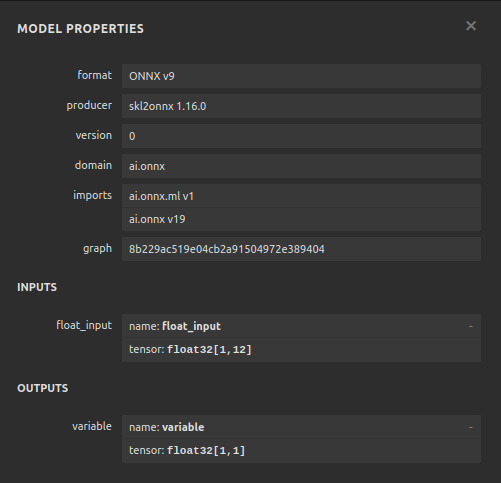
Abb. 23: Die Parameter des ONNX-Modells stimmen mit unseren Erwartungen für den Input und Output des Modells überein

Implementation in MQL5

Um einen AI-integrierten Expert Advisor in MQL5 zu implementieren, müssen wir zunächst das ONNX-Modell laden, das wir zuvor exportiert haben.

//+------------------------------------------------------------------+
//|                                                    USDCAD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Resources                                                        |
//+------------------------------------------------------------------+
#resource  "\\Files\\USDCAD XAUUSD XPDUSD M1 Float.onnx" as const uchar onnx_buffer[];

Als Nächstes müssen wir die Handelsbibliothek laden, damit wir Positionen öffnen und schließen können.

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

Lassen Sie uns auch einige globale Variablen definieren, die wir in unserem Programm benötigen werden.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long onnx_model;
double mean_values[12],std_values[12];
vectorf model_output = vectorf::Zeros(1);
int model_forecast,state;
double ask,bid;

Lassen Sie uns die Hilfsfunktionen definieren, die wir in unserem Programm verwenden werden. Wir brauchen eine Funktion, die für das Laden unseres ONNX-Modells und das Setzen seiner Eingabe- und Ausgabeformen verantwortlich ist. Dazu verwenden wir eine Funktion, die true zurückgibt, wenn sie erfolgreich war, und false, wenn nicht. Unsere Funktion erstellt zunächst das Modell aus dem zuvor erstellten Puffer und versucht dann, die Eingabe- und Ausgabeformen festzulegen und zu validieren.

//+------------------------------------------------------------------+
//| This function is responsible for loading our ONNX model          |
//+------------------------------------------------------------------+
bool load_onnx(void)
  {
//--- First we must create the model from the buffer
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Now we shall define our I/O shape
   ulong input_shape [] = {1,12};
   ulong output_shape []  = {1,1};

   if(!OnnxSetInputShape(onnx_model,0,input_shape))
        {
        Comment("Failed to set ONNX input shape!");
        return(false);
        }

   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
        {
        Comment("Failed to set ONNX output shape!");
        return(false);
        }

//--- Everything went fine
   return(true);
  }
//+------------------------------------------------------------------+

Diese Funktion liest die CSV-Datei mit unseren Skalierungswerten und speichert sie in den von uns definierten global skalierten Arrays.

//+------------------------------------------------------------------+
//| This function will read our scaling factors and store them       |
//+------------------------------------------------------------------+
bool load_scaling_factors(void)
  {
//--- Read in the file
   string file_name = "usd_cad_xau_xpd_scaling_factors.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols).

//--- Check the result
   if(result != INVALID_HANDLE)
        {
        Print("Opened the file");
        //--- Store the values of the file

        int counter = 0;
        string value = "";

        while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end
        {

        if(counter > 100)  //if you aim to read 10 values set a break point after 10 elements have been read
                break; //stop the reading progress

        value = FileReadString(result);
        Print("Trying to read string: ",value," count value: ",counter);

        //--- Check where we are
        if((counter >= 14) && (counter < 26))
        {
                mean_values[counter - 14] = (float) value;
        }
        //--- Check where we are
        if((counter >= 27) && (counter < 39))
        {
                std_values[counter - 27] = (float) value;
        }
        //--- Reading a new row
        if(FileIsLineEnding(result))
        {
                Print("row++");
        }

        counter++;
        }
        //---Close the file
        ArrayPrint(mean_values);
        ArrayPrint(std_values);
        FileClose(result);
        return(true);
        }
//--- We failed to find the file
   else
        {
        Comment("Failed to find the file containing scaling factors");
        return(false);
        }
  }

Außerdem benötigen wir eine Funktion, die für das Abrufen der aktualisierten Kursnotierungen vom Markt zuständig ist.

//+------------------------------------------------------------------+
//| Update market prices                                             |
//+------------------------------------------------------------------+
void update_market_prices(void)
  {
   ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK);
   bid = SymbolInfoDouble(_Symbol,SYMBOL_BID);
  }

Schließlich brauchen wir noch eine Funktion, mit der wir die Vorhersagen aus unserem Modell abrufen können. Unsere Vorhersagefunktion skaliert zunächst die Daten, bevor sie sie an unser Modell weitergibt.

//+------------------------------------------------------------------+
//| Model predict                                                    |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- First fetch the market data

   vectorf model_input  =
        {
        iOpen("USDCAD",PERIOD_CURRENT,0),iHigh("USDCAD",PERIOD_CURRENT,0),iLow("USDCAD",PERIOD_CURRENT,0),iClose("USDCAD",PERIOD_CURRENT,0),
        iOpen("XAUUSD",PERIOD_CURRENT,0),iHigh("XAUUSD",PERIOD_CURRENT,0),iLow("XAUUSD",PERIOD_CURRENT,0),iClose("XAUUSD",PERIOD_CURRENT,0),
        iOpen("XPDUSD",PERIOD_CURRENT,0),iHigh("XPDUSD",PERIOD_CURRENT,0),iLow("XPDUSD",PERIOD_CURRENT,0),iClose("XPDUSD",PERIOD_CURRENT,0)
        };

//--- Now standardize and scale the data
   for(int i =0; i < 12; i++)
        {
        model_input[i] = ((model_input[i] - mean_values[i]) / std_values[i]);
        }

//--- Now fetch a prediction from our model
   OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output);

//--- Store our model's forecat
   if(model_output[0] > iClose("USDCAD",PERIOD_CURRENT,0))
        {
        model_forecast = 1;
        }
   else
        if(model_output[0] < iClose("USDCAD",PERIOD_CURRENT,0))
        {
        model_forecast = -1;
        }
  }

Bei der Initialisierung unseres Expert Advisors laden wir zunächst unsere ONNX-Datei und lesen dann die Skalierungswerte ein. Wenn eines dieser Verfahren fehlschlägt, brechen wir den gesamten Prozess ab.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- This function will load our ONNX model
   if(!load_onnx())
        {
        return(INIT_FAILED);
        }

//--- This function will load our scaling factors
   if(!load_scaling_factors())
        {
        return(INIT_FAILED);
        }
//---
   return(INIT_SUCCEEDED);
  }

Wenn unser Expert Advisor aus dem Chart entfernt wurde, sollten wir die nicht mehr benötigten Ressourcen freigeben.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we do not need
   OnnxRelease(onnx_model);
   ExpertRemove();
  }

Wenn wir schließlich Änderungen der Geld- und Briefkurse erhalten, speichern wir den aktualisierten Preis im Speicher und holen eine neue Vorhersage von unserem KI-Modell.  Wenn wir keine offenen Positionen haben, nehmen wir die von unserem KI-Modell vorgeschlagene Position ein. Wenn wir jedoch eine offene Position haben, prüfen wir, ob die Vorhersage unseres KI-Modells nicht gegen unsere aktuelle Position verstößt.

void OnTick()
  {
//--- Update the market prices
   update_market_prices();

//--- Fetch a forecast from our model
   model_predict();

//--- Find a trading oppurtunity
   if(PositionsTotal() == 0)
        {
        if(model_forecast == -1)
        {
        Trade.Sell(0.2,_Symbol,ask,0,0,"USDCAD AI");
        state = -1;
        }

        else
        if(model_forecast == 1)
        {
                Trade.Buy(0.2,_Symbol,ask,0,0,"USDCAD AI");
                state = 1;
        }
        }

//--- Check for reversals
   if(PositionsTotal() > 0)
        {
        if(state != model_forecast)
        {
        Alert("Reversal detected by our AI system, closing all positions now!");
        Trade.PositionClose(_Symbol);
        }
        }

  }
//+------------------------------------------------------------------+

Abb. 24: Unser Expertenratgeber in Aktion

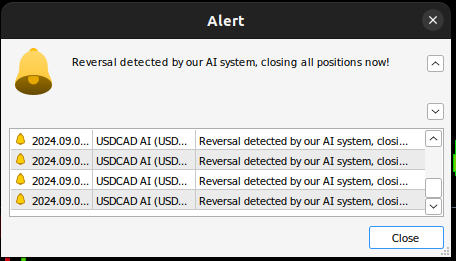
Abb. 25: Unser KI-System hat eine mögliche Umkehrung erkannt

Schlussfolgerung

Im heutigen Artikel haben wir gezeigt, wie Sie verborgene Beziehungen aufdecken können, die zwischen miteinander verbundenen Märkten bestehen können. Es sei jedoch darauf hingewiesen, dass unsere empirische Analyse zeigt, dass wir möglicherweise besser dran sind, wenn wir nur gewöhnliche Marktdaten und einfachere lineare Modelle verwenden. Das mag stimmen, denn wie wir alle wissen, können Marktdaten verrauscht sein. Und bei verrauschten Daten sind einfachere Modelle in der Regel besser als komplexere Modelle, weil die komplexen Modelle empfindlich auf die Schwankungen in den Eingabedaten reagieren.