
Neuronale Netze im Handel: Hierarchische Vektortransformer (Letzter Teil)
Einführung
Im vorangegangenen Artikel haben wir uns mit der theoretischen Beschreibung des Algorithmus Hierarchical Vector Transformer (HiVT) vertraut gemacht, der für die Bewegungsvorhersage durch mehrere Agenten für autonom fahrende Fahrzeuge vorgeschlagen wurde. Diese Methode bietet einen effektiven Ansatz zur Lösung des Vorhersageproblems, indem das Problem in Phasen lokaler Kontextextextraktion und globaler Interaktionsmodellierung zerlegt wird.
Hier ist ein kurzer Überblick über die Methode. Das Problem der Zeitreihenprognose wird von den Autoren der HiVT-Methode in 3 Stufen gelöst. In der ersten Phase extrahiert das Modell lokale kontextuelle Merkmale von Objekten. Die gesamte Szene wird in eine Reihe lokaler Regionen unterteilt, die jeweils auf einen einzigen zentralen Agenten ausgerichtet sind.
In der zweiten Stufe werden globale, weiträumige Abhängigkeiten der Szene durch die Übertragung von Informationen zwischen agenten-zentrierten lokalen Bereichen erfasst.
Die kombinierten, lokalen und globalen Darstellungen ermöglichen es dem Decoder, die zukünftigen Trajektorien aller Agenten in einem einzigen Vorwärtsdurchlauf des Modells vorherzusagen.
Im Folgenden wird die Visualisierung der Methode durch den Autor vorgestellt.
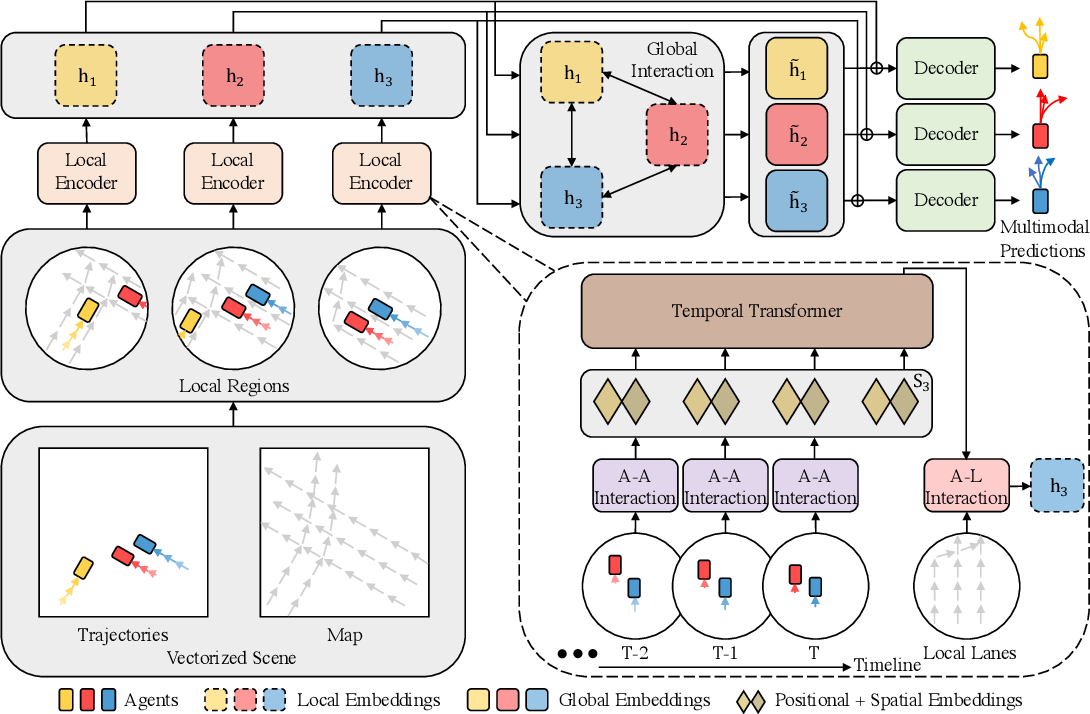
Darüber hinaus haben wir im vorangegangenen Artikel recht umfangreiche Vorarbeiten geleistet, bei denen einzelne Blöcke des vorgeschlagenen Algorithmus implementiert wurden. In diesem Artikel werden wir die begonnene Arbeit zu Ende führen und die einzelnen disparaten Blöcke zu einer einzigen komplexen Struktur zusammenfügen.
1. Zusammenbau von HiVT
Wir werden unsere Vision der Ansätze, die von den HiVT-Autoren vorgeschlagen wurden, im Rahmen der Klasse CNeuronHiVTOCL umsetzen. Die Funktionsweise des Kerns wird von der Basisklasse CNeuronBaseOCL (voll verbundene Schicht) abgeleitet. Seine vollständige Struktur wird im Folgenden dargestellt.
class CNeuronHiVTOCL : public CNeuronBaseOCL { protected: uint iHistory; uint iVariables; uint iForecast; uint iNumTraj; //--- CNeuronBaseOCL cDataTAD; CNeuronConvOCL cEmbeddingTAD; CNeuronTransposeRCDOCL cTransposeATD; CNeuronHiVTAAEncoder cAAEncoder; CNeuronTransposeRCDOCL cTransposeTAD; CNeuronLearnabledPE cPosEmbeddingTAD; CNeuronMVMHAttentionMLKV cTemporalEncoder; CNeuronLearnabledPE cPosLineEmbeddingTAD; CNeuronPatching cLineEmbeddibg; CNeuronMVCrossAttentionMLKV cALEncoder; CNeuronMLMHAttentionMLKV cGlobalEncoder; CNeuronTransposeOCL cTransposeADT; CNeuronConvOCL cDecoder[3]; // Agent * Traj * Forecast CNeuronConvOCL cProbProj; CNeuronSoftMaxOCL cProbability; // Agent * Traj CNeuronBaseOCL cForecast; CNeuronTransposeOCL cTransposeTA; //--- virtual bool Prepare(const CNeuronBaseOCL *history); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override ; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronHiVTOCL(void) {}; ~CNeuronHiVTOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, uint num_traj, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronHiVTOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Die vorgestellte Struktur des Objekts CNeuronHiVTOCL enthält die Deklaration der bereits bekannten Liste überschreibbarer Methoden und eine ganze Reihe von internen Objekten, deren Funktionalitäten wir bei der Implementierung von Algorithmen der überschreibbaren Methoden erkunden werden.
Wir deklarieren alle internen Objekte als statisch und können daher den Konstruktor und Destruktor der Klasse leer lassen. Alle verschachtelten Objekte und Variablen werden in der Methode Init initialisiert.
bool CNeuronHiVTOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, uint num_traj, ENUM_OPTIMIZATION optimization_type, uint batch) { if(units_count < 2 || !CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * forecast, optimization_type, batch)) return false;
In den Methodenparametern erhalten wir die wichtigsten Konstanten, die es uns ermöglichen, die Architektur des initialisierten Objekts eindeutig zu identifizieren. Im Hauptteil der Methode rufen wir die entsprechende Methode der übergeordneten Klasse auf. Wie Sie wissen, implementiert sie die Initialisierung aller geerbten Objekte und Variablen.
Bitte beachten Sie, dass wir eine direkte Überprüfung der Anzahl der Elemente in der analysierten Sequenz zu den in der Methode der Elternklasse implementierten Kontrollen hinzufügen. In diesem Fall muss es mindestens 2 davon geben. Der Grund dafür ist, dass wir bei der Vektorisierung des Ausgangszustands, die der HiVT-Algorithmus vornimmt, mit der Wertedynamik arbeiten werden. Um die Veränderung des Wertes zu berechnen, benötigen wir also 2 Referenzen: die des aktuellen und des vorherigen Zeitschritts.
Nach erfolgreicher Übergabe des Steuerblocks innerhalb der Initialisierungsmethode speichern wir die erhaltenen Parameter der Blockarchitektur in lokalen Variablen.
iVariables = window; iHistory = units_count - 1; iForecast = forecast; iNumTraj = MathMax(num_traj, 1);
Als Nächstes initialisieren wir die internen Objekte. Die Reihenfolge der Initialisierung interner Objekte entspricht der Reihenfolge der Verwendung von Objekten innerhalb des Algorithmus für den Vorwärtsdurchgang. Auf diese Weise können wir den zu erstellenden Algorithmus noch einmal durcharbeiten und sicherstellen, dass die Erstellung von Objekten sowohl ausreichend als auch notwendig ist.
Zunächst erstellen wir ein Objekt der inneren Schicht, um die Vektordarstellung des analysierten Zustands der Umgebung zu erfassen.
Ich möchte daran erinnern, dass hier der Vektor der Beschreibung jedes einzelnen Elements der univariaten Sequenz in einem separaten Zeitschritt gleich der doppelten Anzahl der analysierten univariaten Sequenzen ist. Denn jedes Element der Sequenz ist durch eine Bewegung im zweidimensionalen Raum und eine Veränderung der Position der übrigen Agenten in Bezug auf das zu analysierende Element gekennzeichnet.
Wir erstellen einen solchen Beschreibungsvektor für jedes Element aller analysierten univariaten Sequenzen in jedem Zeitschritt.
if(!cDataTAD.Init(0, 0, OpenCL, 2 * iVariables * iVariables * iHistory, optimization, iBatch)) return false;
Bitte beachten Sie, dass wir bei der Implementierung des HiVT-Algorithmus mit dreidimensionalen Tensoren arbeiten und ihr Bild in einem eindimensionalen Datenpuffer speichern. Um die aktuelle Dimension in den Namen der Objekte anzugeben, fügen wir ein 3-stelliges Suffix hinzu:
- T (Time) — die Dimension der Zeitschritte;
- A (Agent) — die Dimension des Agenten (univariate Zeitreihe); in unserem Fall ist es der analysierte Parameter;
- D (Dimension) — die Dimension f des Vektors, der ein Element der univariaten Folge beschreibt.
Als Nächstes werden wir eine Faltungsschicht verwenden, um Einbettungen der resultierenden Vektorbeschreibungen zu erstellen.
if(!cEmbeddingTAD.Init(0, 1, OpenCL, 2 * iVariables, 2 * iVariables, window_key, iVariables * iHistory, 1, optimization, iBatch)) return false;
In diesem Fall verwenden wir zur Erzeugung von Einbettungen 1 Parametermatrix, die wir auf alle Elemente der multimodalen Sequenz anwenden. Daher geben wir die Anzahl der analysierten Blöcke einer bestimmten Schicht als das Produkt aus der Anzahl der univariaten Sequenzen und der Tiefe der analysierten Geschichte an.
Nach der Erzeugung von Einbettungen, die dem HiVT-Algorithmus folgen, müssen wir die lokalen Abhängigkeiten zwischen den Agenten innerhalb eines Zeitschritts analysieren. Wie im vorigen Artikel beschrieben, müssen wir vor diesem Schritt die Originaldaten transponieren.
if(!cTransposeATD.Init(0, 2, OpenCL, iHistory, iVariables, window_key, optimization, iBatch)) return false;
Erst dann können wir die Aufmerksamkeitsklassen verwenden, um Abhängigkeiten zwischen den Agenten in der lokalen Gruppe zu erkennen.
if(!cAAEncoder.Init(0, 3, OpenCL, window_key, window_key, heads, (heads + 1) / 2, iVariables, 2, 1, iHistory, optimization, iBatch)) return false;
Achten Sie bitte auf die folgenden beiden Momente. Zunächst haben wir nach der Transposition der Daten die Zeichenfolge im Suffix des Objektnamens in ATD geändert, was der Dimensionalität des dreidimensionalen Tensors am Ausgang der Datentranspositionsebene entspricht.
Zweitens wollen wir die Funktionsweise unserer Aufmerksamkeitsblöcke untersuchen. Ursprünglich waren sie für die Arbeit mit zweidimensionalen Tensoren konzipiert, bei denen jede Zeile den Beschreibungsvektor eines einzelnen Sequenzelements darstellt. Im Wesentlichen geht es darum, Abhängigkeiten zwischen den Zeilen der analysierten Matrix zu ermitteln - was man als „vertikale Aufmerksamkeit“ bezeichnen kann. Später haben wir das Erkennen von Abhängigkeiten innerhalb einzelner univariater Sequenzen einer multimodalen Zeitreihe eingeführt. In der Praxis haben wir die ursprüngliche Matrix in mehrere identische Matrizen unterteilt, die jeweils weniger unitäre Zeitreihen enthalten. Diese neuen Matrizen übernahmen die Anzahl der Zeilen aus der ursprünglichen Matrix, während ihre Spalten gleichmäßig auf sie verteilt wurden. Strukturell entspricht dies der Dimensionalität unseres dreidimensionalen Tensors. Die erste Dimension stellt die Anzahl der Zeilen in der ursprünglichen Datenmatrix dar. Die zweite Dimension gibt die Anzahl der kleineren Matrizen an, die für die unabhängige Analyse verwendet werden. Die dritte Dimension stellt die Größe des Beschreibungsvektors für ein einzelnes Sequenzelement dar. Unter Berücksichtigung der vorherigen Transposition des Einbettungstensors aus den Originaldaten definieren wir die Anzahl der unitären Sequenzen als die Größe der analysierten Sequenz im aktuellen Aufmerksamkeitsblock. Die Tiefe der analysierten historischen Daten wird in dem Parameter angegeben, der die Anzahl der Variablen darstellt. Dieser Ansatz ermöglicht es uns, Abhängigkeiten zwischen einzelnen Variablen innerhalb eines einzigen Zeitschritts zu analysieren.
In dieser Implementierung des Abhängigkeitsanalyseblocks von Agent-Agent habe ich zwei Aufmerksamkeitsschichten verwendet und für jede interne Schicht einen Schlüssel-Wert-Tensor (Key-Value) erzeugt. Die Anzahl der Aufmerksamkeitsköpfe im Schlüssel-Wert-Tensor ist halb so groß wie die des entsprechenden Parameters im Abfrage-Tensor (Query).
Außerdem ist zu beachten, dass wir in diesem Fall mit dem CNeuronHiVTAAEncoder einen Aufmerksamkeitsblock mit der Funktion zur Verwaltung von Merkmalen verwenden.
Nach der Anreicherung der Sequenzelementeinbettungen mit Abhängigkeiten zwischen Agenten innerhalb einer lokalen Gruppe ermöglicht der HiVT-Algorithmus die Analyse von zeitlichen Abhängigkeiten innerhalb einzelner unitärer Sequenzen. In diesem Stadium müssen wir die Daten in ihre ursprüngliche Darstellung zurückversetzen.
if(!cTransposeTAD.Init(0, 4, OpenCL, iVariables, iHistory, window_key, optimization, iBatch)) return false;
Dann fügen wir eine vollständig trainierbare Positionskodierung hinzu.
if(!cPosEmbeddingTAD.Init(0, 5, OpenCL, iVariables * iHistory * window_key, optimization, iBatch)) return false;
Als Nächstes verwenden wir den Aufmerksamkeitsblock CNeuronMVMHAttentionMLKV um zeitliche Abhängigkeiten zu erkennen.
if(!cTemporalEncoder.Init(0, 6, OpenCL, window_key, window_key, heads, (heads + 1) / 2, iHistory, 2, 1, iVariables, optimization, iBatch)) return false;
Trotz der Unterschiede in der Architektur der Aufmerksamkeitsblöcke für lokale und zeitliche Abhängigkeit verwenden wir dieselben Parameter, um sie zu initialisieren.
In einem nächsten Schritt schlagen die HiVT-Autoren vor, die Einbettungen der Agenten mit Informationen über den Straßenkarte anzureichern. Ich denke, niemand bezweifelt, dass der Zustand der Straße, ihre Markierungen und Kurven einen gewissen Einfluss auf die Handlungen des Agenten haben. In unserem Fall gibt es keine klaren Leitlinien für die Begrenzung von Änderungen der Werte der analysierten Parameter. Natürlich gibt es Bereiche mit akzeptablen Werten für einzelne Oszillatoren. Der RSI kann zum Beispiel nur Werte im Bereich von 0 bis 100 annehmen. Dies ist jedoch ein Einzelfall.
Wir verwenden also die historischen Daten, die uns vorliegen, um die wahrscheinlichste Veränderung zu ermitteln. Wir werden die Darstellung der Straßenkarte durch Einbettungen von tatsächlichen kleinen Segmenten von Trajektorien ersetzen, die wir mit Hilfe einer Daten-Patching-Schicht erstellen werden.
if(!cLineEmbeddibg.Init(0, 7, OpenCL, 3, 1, 8, iHistory - 1, iVariables, optimization, iBatch)) return false;
Beachten Sie, dass wir bei der Vektorisierung des aktuellen Zustands die Dynamik der Parameteränderung über einen Zeitschritt verwendet haben. Bei der Einbettung tatsächlicher kleiner Abschnitte der Trajektorie verwenden wir jedoch Blöcke von 3 Elementen mit einem Schritt von 1. Auf diese Weise wollen wir die Abhängigkeiten zwischen der Dynamik des Indikators bei einem bestimmten Schritt und der möglichen Fortsetzung der Trajektorie ermitteln.
Dann fügen wir den resultierenden Einbettungen eine vollständig trainierbare Positionskodierung hinzu.
if(!cPosLineEmbeddingTAD.Init(0, 8, OpenCL, cLineEmbeddibg.Neurons(), optimization, iBatch)) return false;
Dann reichern wir die aktuellen Einbettungen der Agenten mit Informationen über Trajektorien an. Hierfür verwenden wir den Kreuzaufmerksamkeitsblock CNeuronMVCrossAttentionMLKV mit zwei inneren Schichten.
if(!cALEncoder.Init(0, 9, OpenCL, window_key, window_key, heads, 8, (heads + 1) / 2, iHistory, iHistory - 1, 2, 1, iVariables, iVariables, optimization, iBatch)) return false;
Es mag den Anschein erwecken, als würden wir hier nacheinander zwei ähnliche Operationen durchführen: die Identifizierung zeitlicher Abhängigkeiten und die Analyse von Abhängigkeiten zwischen Agenten und Trajektorien. In beiden Fällen analysieren wir die Abhängigkeiten zwischen dem aktuellen Zustand des Agenten und der Darstellung der Parameter desselben Indikators in anderen Zeitintervallen. Aber hier gibt es einen schmalen Grat. Im ersten Fall vergleichen wir ähnliche Zustände des Agenten in verschiedenen Zeitschritten. Im zweiten Fall haben wir es mit bestimmten Mustern der Trajektorie zu tun, die ein etwas größeres Zeitintervall abdecken.
Dies vervollständigt den Block der lokalen Abhängigkeitsanalyse, der im Wesentlichen die Einbettung des Agentenstatus auf umfassende Weise erweitert. Der nächste Schritt des HiVT-Algorithmus ist die Analyse der langfristigen Abhängigkeiten der Szene im globalen Interaktionsblock.
if(!cGlobalEncoder.Init(0, 10, OpenCL, window_key*iVariables, window_key*iVariables, heads, (heads+1)/2, iHistory, 4, 2, optimization, iBatch)) return false;
Hier verwenden wir einen Aufmerksamkeitsblock mit 4 internen Ebenen. Um Abhängigkeiten zu analysieren, verwenden wir eine Darstellung nicht einzelner Agenten, sondern der gesamten Szene.
Dann müssen wir die kommende Abfolge der vorhergesagten Werte modellieren. Die Vorhersage der kommenden Sequenz wird wie bisher im Rahmen einzelner univariater Sequenzen durchgeführt. Zu diesem Zweck müssen wir zunächst die aktuellen Daten transponieren.
if(!cTransposeADT.Init(0, 11, OpenCL, iHistory, window_key * iVariables, optimization, iBatch)) return false;
Zur Vorhersage der nachfolgenden Werte für die gesamte Planungstiefe schlagen die Autoren von HiVT die Verwendung eines MLP vor. In unserem Fall wird diese Arbeit in einem Block von 3 aufeinanderfolgenden Faltungsschichten durchgeführt, von denen jede ein eigenes Fenster mit analysierten Daten und eine eigene Aktivierungsfunktion erhält.
if(!cDecoder[0].Init(0, 12, OpenCL, iHistory, iHistory, iForecast, window_key * iVariables, optimization, iBatch)) return false; cDecoder[0].SetActivationFunction(SIGMOID); if(!cDecoder[1].Init(0, 13, OpenCL, iForecast * window_key, iForecast * window_key, iForecast * window_key, iVariables, optimization, iBatch)) return false; cDecoder[1].SetActivationFunction(LReLU); if(!cDecoder[2].Init(0, 14, OpenCL, iForecast * window_key, iForecast * window_key, iForecast * iNumTraj, iVariables, optimization, iBatch)) return false; cDecoder[2].SetActivationFunction(TANH);
In der ersten Phase arbeiten wir im Rahmen der einzelnen Elemente der Einbettungsbeschreibung des Zustands eines einzelnen Agenten, wobei wir die Größe der Sequenz von der Tiefe der analysierten Geschichte bis zum Planungshorizont ändern.
Anschließend analysieren wir globale Abhängigkeiten innerhalb einzelner Agenten über den gesamten Planungshorizont, ohne die Tensorgröße zu verändern.
Erst in der letzten Phase sagen wir für jede einzelne univariate Zeitreihe mehrere mögliche Szenarien voraus. Die Anzahl der Varianten der vorhergesagten Trajektorien wird von einem externen Programm in den Methodenparametern festgelegt.
Eine Besonderheit des vorgeschlagenen Ansatzes ist die Prognose mehrerer möglicher Szenarien. Wir brauchen jedoch einen Mechanismus zur Auswahl der wahrscheinlichsten Trajektorie. Daher projizieren wir die erhaltenen Trajektorien zunächst auf die Dimension der Anzahl der vorhergesagten Trajektorien für jeden Agenten.
if(!cProbProj.Init(0, 15, OpenCL, iForecast * iNumTraj, iForecast * iNumTraj, iNumTraj, iVariables, optimization, iBatch)) return false;
Dann verwenden wir eine SoftMax-Funktion, um die erhaltenen Projektionen in den Wahrscheinlichkeitsbereich zu übertragen.
if(!cProbability.Init(0, 16, OpenCL, iForecast * iNumTraj * iVariables, optimization, iBatch)) return false; cProbability.SetHeads(iVariables); // Agent * Traj
Indem wir die zuvor vorhergesagten Bahnen mit ihren Wahrscheinlichkeiten abwägen, erhalten wir die durchschnittliche Bahn der kommenden Bewegung unseres Agenten.
if(!cForecast.Init(0, 17, OpenCL, iForecast * iVariables, optimization, iBatch)) return false;
Jetzt müssen wir nur noch die vorhergesagten Werte in die Dimensionen der Originaldaten umrechnen. Wir implementieren die Funktionsweise durch die Umsetzung von Daten.
if(!cTransposeTA.Init(0, 18, OpenCL, iVariables, iForecast, optimization, iBatch)) return false;
Um die Datenkopiervorgänge zu reduzieren und die Nutzung der Speicherressourcen zu optimieren, definieren wir die Ergebnis- und Fehlergradienten-Pufferzeiger unseres Blocks zu ähnlichen Puffern der letzten internen Datenumsetzungsschicht um.
SetOutput(cTransposeTA.getOutput(),true); SetGradient(cTransposeTA.getGradient(),true); //--- return true; }
Dann schließen wir die Methodenoperation ab, indem wir das logische Ergebnis der Methodenoperationen an das aufrufende Programm zurückgeben.
Nachdem wir die Initialisierung des Klassenobjekts abgeschlossen haben, gehen wir in der feedForward-Methode zum Aufbau des Vorwärtsdurchgangs-Algorithmus für unsere Klasse über.
bool CNeuronHiVTOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!Prepare(NeuronOCL)) return false;
In den Methodenparametern erhalten wir einen Zeiger auf ein Objekt, das die Originaldaten enthält. Wir übergeben den empfangenen Zeiger sofort an die Methode Prepare, die die Ausgangsdaten vorbereitet. Diese Methode ist ein „Wrapper“ für den Aufruf des Datenvektorisierungskerns HiVTPrepare. Wir haben den Algorithmus in einem früheren Artikel besprochen. Wir haben uns bereits verschiedene Methoden für die Warteschlangenbildung von OpenCL-Programmkernen angesehen. Der Algorithmus der Prepare-Methode weist keine besonderen Merkmale auf. Deshalb verzichte ich in diesem Artikel auf die Beschreibung seines Algorithmus. Sie können sie mit dem im Anhang enthaltenen Code selbständig studieren.
Als Nächstes erzeugen wir auf der Grundlage der erhaltenen Vektordarstellungen in jedem einzelnen Zeitschritt Agenteneinbettungen.
if(!cEmbeddingTAD.FeedForward(cDataTAD.AsObject())) return false;
Wir setzen sie um.
if(!cTransposeATD.FeedForward(cEmbeddingTAD.AsObject())) return false;
Und wir ergänzen lokale Abhängigkeiten im Rahmen der Analyse von Agent-Agent-Repräsentationen.
if(!cAAEncoder.FeedForward(cTransposeATD.AsObject())) return false;
Im nächsten Schritt ergänzen wir die Agenten-Zustandseinbettungen um zeitliche Abhängigkeiten an. Dazu transponieren wir zunächst den aktuellen Datentensor.
if(!cTransposeTAD.FeedForward(cAAEncoder.AsObject())) return false;
Wir fügen dem Text Positionsmarkierungen hinzu.
if(!cPosEmbeddingTAD.FeedForward(cTransposeTAD.AsObject())) return false;
Und dann rufen wir die Vorwärtsdurchgangsmethode unseres zeitlichen Aufmerksamkeitsmoduls im Kontext der einzelnen Agenten auf.
if(!cTemporalEncoder.FeedForward(cPosEmbeddingTAD.AsObject())) return false;
Nach erfolgreicher Ausführung der zeitlichen Aufmerksamkeitsoperationen erhalten wir einen Tensor von Einbettungen der analysierten Daten, der mit lokalen und zeitlichen Abhängigkeiten angereichert ist. Nun müssen wir die resultierenden Einbettungen mit Informationen über mögliche Bewegungsmuster anreichern. Zu diesem Zweck erstellen wir zunächst Einbettungen der Muster der zu analysierenden historischen Bewegung.
if(!cLineEmbeddibg.FeedForward(NeuronOCL)) return false;
Wir fügen den resultierenden Mustereinbettungen eine Positionskodierung hinzu.
if(!cPosLineEmbeddingTAD.FeedForward(cLineEmbeddibg.AsObject())) return false;
Im Kreuzaufmerksamkeitsmodul reichern wir die Einbettungen unserer Agenten mit Informationen über verschiedene Bewegungsmuster an.
if(!cALEncoder.FeedForward(cTemporalEncoder.AsObject(), cPosLineEmbeddingTAD.getOutput())) return false;
Wir wenden das globale Aufmerksamkeitsmodul auf den Tensor der angereicherten Agenteneinbettungen an.
if(!cGlobalEncoder.FeedForward(cALEncoder.AsObject())) return false;
Darauf folgt ein Block zur Vorhersage der kommenden Agentenbewegung. Ich möchte daran erinnern, dass wir die späteren Werte der analysierten Parameter in Form von univariaten Sequenzen prognostizieren wollen. Daher transponieren wir zunächst den gegebenen Datentensor.
if(!cTransposeADT.FeedForward(cGlobalEncoder.AsObject())) return false;
Als Nächstes führen wir einen Vorwärtsdurchgang unseres dreischichtigen MLP-Blocks für die Datenvorhersage durch.
if(!cDecoder[0].FeedForward(cTransposeADT.AsObject())) return false; if(!cDecoder[1].FeedForward(cDecoder[0].AsObject())) return false; if(!cDecoder[2].FeedForward(cDecoder[1].AsObject())) return false;
Hier ist die Besonderheit der HiVT-Methode zu beachten. Der MLP, der die kommende Bewegung vorhersagt, gibt nicht nur eine, sondern mehrere Varianten für die mögliche Fortsetzung der analysierten Ausgangsreihe aus. Wir müssen die Wahrscheinlichkeiten für jede Variante der vorhergesagten Bewegung bestimmen. Zu diesem Zweck werden wir zunächst prädiktive Trajektorien erstellen.
if(!cProbProj.FeedForward(cDecoder[2].AsObject())) return false;
Mit Hilfe der SoftMax-Funktion übersetzen wir die erhaltenen Projektionen in den Wahrscheinlichkeitsbereich.
if(!cProbability.FeedForward(cProbProj.AsObject())) return false;
Nun müssen wir nur noch den Tensor der vorhergesagten Trajektorien mit ihren Wahrscheinlichkeiten multiplizieren.
if(IsStopped() || !MatMul(cDecoder[2].getOutput(), cProbability.getOutput(), cForecast.getOutput(), iForecast, iNumTraj, 1, iVariables)) return false;
Als Ergebnis dieser Operation erhalten wir für jede univariate Reihe der analysierten multimodalen Sequenz einen Tensor von durchschnittlich gewichteten Trajektorien für den gesamten Planungshorizont.
Am Ende unserer Vorwärtsdurchgangsmethode transponieren wir den vorhergesagten Wertetensor, damit er mit den Messungen der ursprünglichen Daten übereinstimmt.
if(!cTransposeTA.FeedForward(cForecast.AsObject())) return false; //--- return true; }
Wie üblich geben wir einen booleschen Wert an das aufrufende Programm zurück, der den Erfolg der Methodenoperationen angibt.
Damit schließen wir die Implementierung des Vorwärtsdurchgangs-Algorithmus für die HiVT-Methode ab und gehen zur Entwicklung der Rückwärtsdurchgangs-Methoden für unsere Klasse über. Wie Sie wissen, besteht der Rückwärtsdurchgangs-Algorithmus aus zwei Hauptkomponenten:
- Verteilung des Gradientenfehlers auf alle Elemente je nach ihrem Einfluss auf das Endergebnis. Diese Funktion ist in der Methode calcInputGradients implementiert.
- Anpassung der trainierbaren Modellparameter zur Minimierung des Gesamtverlustes, die in der Methode updateInputWeights durchgeführt wird.
Wir beginnen die Implementierung der Rückwärtsdurchgangs-Algorithmen mit der Entwicklung der Gradientenfehlerverteilungsmethode calcInputGradients. Die Logik dieser Methode spiegelt die Logik des Vorwärtsdurchgangs-Algorithmus vollständig wider, mit der Ausnahme, dass alle Operationen in umgekehrter Reihenfolge durchgeführt werden.
bool CNeuronHiVTOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Als Eingabeparameter erhält diese Methode einen Zeiger auf das Objekt der vorhergehenden Schicht - dieselbe Schicht, die die Eingabedaten während des Feedforward-Durchgangs geliefert hat. In diesem Fall müssen wir jedoch den Fehlergradienten zurückgeben, um sicherzustellen, dass er den Einfluss der ursprünglichen Eingabedaten auf das Endergebnis widerspiegelt.
Im Hauptteil der Methode wird sofort die Relevanz des empfangenen Zeigers geprüft. Wenn der Zeiger ungültig ist, wäre die Ausführung der Methodenoperationen sinnlos.
Sobald die Validierungsprüfungen erfolgreich bestanden sind, wird der Fehlergradient entsprechend verteilt.
Auf der Ausgangsebene der aktuellen Schicht ist der Fehlergradient bereits in dem entsprechenden Puffer unserer Klasse gespeichert. Sie wurde dort bei der Ausführung der entsprechenden Methode in der nachfolgenden Schicht aufgezeichnet. Aufgrund des zuvor implementierten Puffer-Swapping-Mechanismus ist der erforderliche Fehlergradient bereits im Puffer der letzten Datenumsetzungsschicht vorhanden. Von hier aus beginnen wir mit der Übertragung des Fehlergradienten auf die Ebene der gewichteten durchschnittlichen Vorhersagetrajektorienschicht für univariate Zeitreihen.
if(!cForecast.calcHiddenGradients(cTransposeTA.AsObject())) return false;
Wie Sie sich erinnern, haben wir im Vorwärtsdurchgang die gewichteten durchschnittlichen Trajektorien durch Multiplikation des Tensors mehrerer vorhergesagter Trajektorien mit dem Vektor der entsprechenden Wahrscheinlichkeiten erhalten. Dementsprechend müssen wir im Prozess des Rückwärtsdurchgangs den Fehlergradienten sowohl auf den Tensor der Menge der vorhergesagten Trajektorien als auch auf den Wahrscheinlichkeitsvektor verteilen.
if(IsStopped() || !MatMulGrad(cDecoder[2].getOutput(), cDecoder[2].getGradient(), cProbability.getOutput(), cProbability.getGradient(), cForecast.getGradient(), iForecast, iNumTraj, 1, iVariables)) return false;
Wir werden den Wahrscheinlichkeitsfehlergradienten an die Projektionsschicht der vorhergesagten Trajektorien weitergeben.
if(!cProbProj.calcHiddenGradients(cProbability.AsObject())) return false;
Zur Erstellung der Projektionen haben wir die Vorhersagetrajektorien selbst verwendet. Anschließend wird der Fehlergradient in der Regel auf die Ebene der Vorhersagetrajektorien übertragen.
Es ist jedoch zu beachten, dass der Fehlergradient für die Menge der Vorhersagetrajektorien bereits von der gewichteten durchschnittlichen Trajektorie im vorherigen Schritt übergeben wurde. Ein direkter Aufruf der Methode calcHiddenGradients der entsprechenden Schicht würde den zuvor übertragenen Fehlergradienten überschreiben und den Puffer durch neue Werte ersetzen. In solchen Fällen verwenden wir in der Regel Hilfsdatenpuffer, in denen die Werte aus zwei Datenströmen summiert werden, um alle Informationen zu erhalten. In diesem speziellen Fall wurde jedoch beschlossen, den Fehlergradienten nicht weiter in die Datenprojektionsschicht zu übertragen. Ziel dieses Ansatzes ist es, die Vorhersage nachfolgender Trajektorien „sauber“ zu halten und Verzerrungen zu vermeiden, die durch die mit der Relevanz einzelner Trajektorien verbundenen probabilistischen Verteilungsfehler verursacht werden.
Stattdessen propagieren wir den Fehlergradienten der Vorhersagetrajektorien durch die MLP-Schicht des Vorhersageblocks.
if(!cDecoder[1].calcHiddenGradients(cDecoder[2].AsObject())) return false; if(!cDecoder[0].calcHiddenGradients(cDecoder[1].AsObject())) return false;
Wir transponieren den resultierenden Fehlergradiententensor und leiten ihn durch den globalen Interaktionsblock.
if(!cTransposeADT.calcHiddenGradients(cDecoder[0].AsObject())) return false; if(!cGlobalEncoder.calcHiddenGradients(cTransposeADT.AsObject())) return false; if(!cALEncoder.calcHiddenGradients(cGlobalEncoder.AsObject())) return false;
Vom globalen Interaktionsblock wird der Fehlergradient dann an den Block für die lokale Abhängigkeitsanalyse weitergeleitet.
Zur Erinnerung: Dieser Block führt eine umfassende Analyse der gegenseitigen Abhängigkeiten zwischen den einzelnen lokalen Objekten durch. Hier leiten wir den empfangenen Fehlergradienten zunächst durch den Agenten-Trajektorien-Kreuzaufmerksamkeitsblock, bis hinunter zur Ebene der zeitlichen Abhängigkeitsanalyse und der Positionskodierung von Bewegungsmustereinbettungen.
if(!cTemporalEncoder.calcHiddenGradients(cALEncoder.AsObject(), cPosLineEmbeddingTAD.getOutput(), cPosLineEmbeddingTAD.getGradient(), (ENUM_ACTIVATION)cPosLineEmbeddingTAD.Activation())) return false;
Wir propagieren den Fehlergradienten durch Positionskodierungsoperationen.
if(!cLineEmbeddibg.calcHiddenGradients(cPosLineEmbeddingTAD.AsObject())) return false;
Und dann geben wir sie an die Quelldatenebene weiter.
if(!NeuronOCL.calcHiddenGradients(cLineEmbeddibg.AsObject())) return false;
Für den zweiten Datenstrom propagieren wir zunächst den Fehlergradienten durch den Block zur Analyse der zeitlichen Abhängigkeit.
if(!cPosEmbeddingTAD.calcHiddenGradients(cTemporalEncoder.AsObject())) return false;
Danach passen wir den erhaltenen Fehlergradienten in der Positionskodierung an.
if(!cTransposeTAD.calcHiddenGradients(cPosEmbeddingTAD.AsObject())) return false;
Anschließend werden die Daten transponiert und der Gradient durch den Block der Agenten-Abhängigkeitsanalyse propagiert.
if(!cAAEncoder.calcHiddenGradients(cTransposeTAD.AsObject())) return false; if(!cTransposeATD.calcHiddenGradients(cAAEncoder.AsObject())) return false;
Am Ende der Methodenoperationen transponieren wir die Daten in die ursprüngliche Darstellung und übertragen den Fehlergradienten durch die Einbettungserzeugungsschicht auf die Vektordarstellung der ursprünglichen Daten.
if(!cEmbeddingTAD.calcHiddenGradients(cTransposeATD.AsObject())) return false; if(!cDataTAD.calcHiddenGradients(cEmbeddingTAD.AsObject())) return false; //--- return true; }
Wie üblich geben wir einen booleschen Wert an das aufrufende Programm zurück, der das Ergebnis der Ausführung der Methodenoperationen angibt.
In diesem Stadium haben wir den Fehlergradienten auf alle Modellelemente entsprechend ihrem Einfluss auf das Endergebnis verteilt. Nun müssen wir die trainierbaren Modellparameter anpassen, um den Gesamtfehler zu minimieren. Diese Funktion ist in der Methode updateInputWeights implementiert.
Es ist wichtig zu beachten, dass alle trainierbaren Parameter unserer neuen Klasse CNeuronHiVTOCL in ihren internen Objekten gespeichert sind. Allerdings enthalten nicht alle internen Objekte trainierbare Parameter. Sie sind zum Beispiel nicht in den Datenumsetzungsebenen enthalten. Daher interagieren wir bei dieser Methode nur mit Objekten, die trainierbare Parameter enthalten. Um sie anzupassen, genügt es, die entsprechende Methode jedes internen Objekts aufzurufen.
Wie Sie sehen können, ist die Logik dieser Methode recht einfach, sodass wir in diesem Artikel nicht den vollständigen Code zur Verfügung stellen werden. Sie können sie mit dem im Anhang enthaltenen Code selbständig studieren. Die Anhänge enthalten auch den vollständigen Quellcode unserer neuen Klasse und alle ihre Methoden.
2. Modell der Architektur
Wir haben die Entwicklung der Klasse CNeuronHiVTOCL und ihrer Methoden abgeschlossen. Die Klasse implementiert unsere Interpretation der von den Autoren der HiVT-Methode vorgeschlagenen Ansätze. Nun ist es an der Zeit, das neue Objekt in die Architektur unseres Modells zu integrieren.
Wie zuvor binden wir das Vorhersageobjekt für die zukünftige Bewegung der analysierten multimodalen Reihen in das Environmental State Encoder-Modell ein. Der architektonische Aufbau dieses Modells wird in der Methode CreateEncoderDescriptions definiert. Diese Methode empfängt einen Zeiger auf ein dynamisches Array-Objekt, in dem wir die Architektur des generierten Modells aufzeichnen.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Im Methodenrumpf prüfen wir die Relevanz des empfangenen Zeigers und erstellen gegebenenfalls eine neue Instanz des dynamischen Arrays. Danach gehen wir zu einer sequentiellen Beschreibung der architektonischen Lösung für jede Schicht unseres Modells über.
Um die Ausgangsdaten zu erhalten, verwenden wir eine vollständig verbundene Basisschicht von ausreichender Größe.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Wir planen, rohe, unbearbeitete Daten in das Modell einzugeben. Um solche Daten in eine vergleichbare Form zu bringen, verwenden wir Batch-Normalisierungsschichten.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Nach der anfänglichen Verarbeitung übertragen wir die ursprünglichen Daten sofort in unseren neuen Block, der nach den Ansätzen der HiVT-Methode erstellt wurde.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronHiVTOCL; { int temp[] = {BarDescr, NForecast, 6}; // {Variables, Forecast, NumTraj} ArrayCopy(descr.windows, temp); } descr.window_out = EmbeddingSize; // Inside Dimension descr.count = HistoryBars; // Units descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Hier wiederholen wir praktisch ähnliche Parameter aus früheren Arbeiten. Es wird nur 1 neuer Blockparameter hinzugefügt, der die Anzahl der Varianten der vorhergesagten Trajektorien bestimmt. In diesem Fall verwenden wir 6.
Am Ausgang des Blocks von CNeuronHiVTOCL erwarten wir fertige Prognosewerte für die analysierten multimodalen Zeitreihen. Es gibt jedoch einen Vorbehalt. Um den effizienten Betrieb des Modells mit einer multimodalen Zeitreihe zu organisieren, haben wir alle ihre Werte in eine vergleichbare Form gebracht. Dementsprechend erhielten wir die vorhergesagten Werte in einer ähnlichen Form. Um die erhaltenen Prognosewerte mit den üblichen Werten der Originaldaten in Einklang zu bringen, fügen wir ihnen die statistischen Parameter der Verteilung hinzu, die bei der Normalisierung der Rohdaten entfernt wurden.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Danach werden wir die erzielten Ergebnisse im Frequenzbereich koordinieren.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Die Architekturen der Modelle Akteur (Actor) und Kritiker (Critic) bleiben unverändert. Das Gleiche gilt für Modellschulungsprogramme. Deshalb werden wir im Rahmen dieses Artikels nicht näher darauf eingehen. Der vollständige Quellcode aller in dieser Studie verwendeten Programme ist jedoch in den beigefügten Materialien für weitere Untersuchungen verfügbar.
3. Tests
Wir haben die Umsetzung unserer Interpretation der HiVT-Methode abgeschlossen. Nun ist es an der Zeit, die Wirksamkeit unserer Lösungen zu bewerten. Zunächst müssen wir die Modelle anhand echter historischer Daten trainieren und dann die trainierten Modelle an einem Datensatz testen, der nicht Teil des Trainingssatzes war.
Für das Training verwenden wir historische EURUSD-Daten auf dem H1-Zeitrahmen für das gesamte Jahr 2023.
Die Schulung wird offline durchgeführt. Daher müssen wir zunächst den erforderlichen Trainingsdatensatz zusammenstellen. Weitere Einzelheiten zu diesem Verfahren finden Sie in unserem Artikel über die Real-ORL Methode. Für das Training unseres Environmental State Encoders haben wir einen Datensatz verwendet, der während des Betriebs früherer Modelle gesammelt wurde.
Wie Sie wissen, arbeitet das State Encoder-Modell nur mit historischen Kursbewegungsdaten und analysierten Indikatoren, die unabhängig von den Aktionen des Agenten sind. Daher ist es in diesem Stadium nicht notwendig, den Trainingsdatensatz regelmäßig zu aktualisieren, da neu hinzugefügte Trajektorien keine zusätzlichen Informationen für den Encoder liefern. Wir setzen den Trainingsprozess fort, bis wir die gewünschten Ergebnisse erzielt haben.
Die Testergebnisse des trainierten Modells werden unten dargestellt.
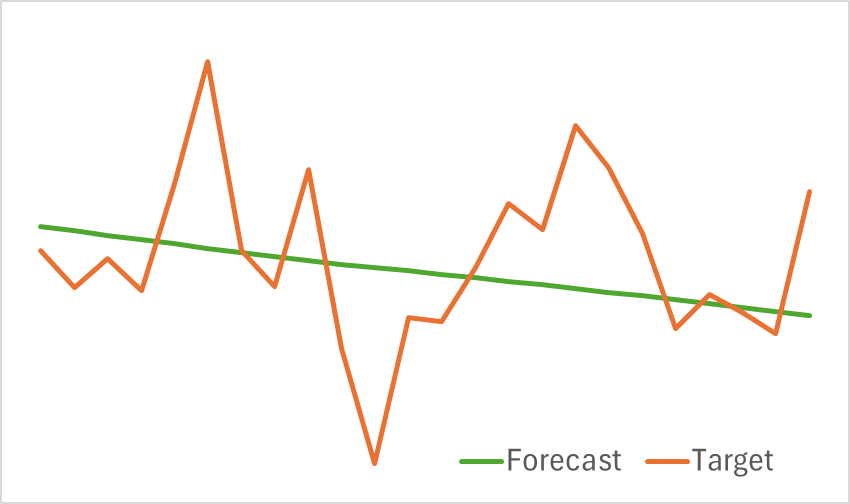
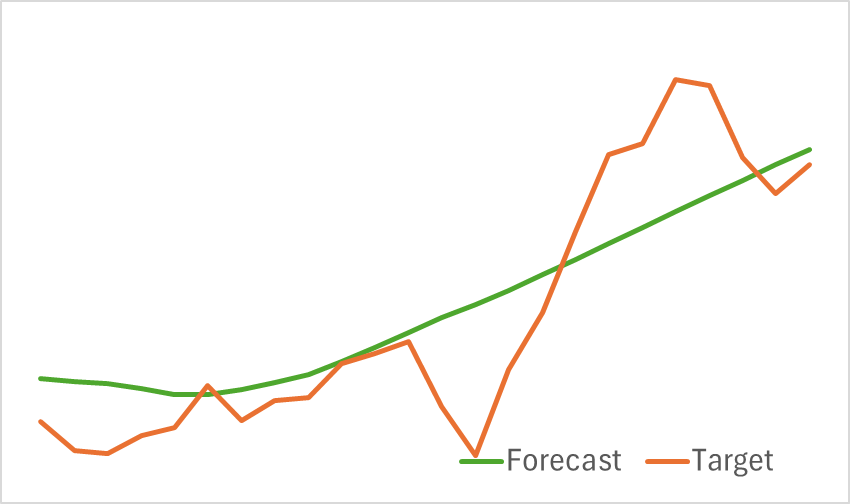
Wie aus den beigefügten Grafiken ersichtlich ist, erfasst unser Modell effektiv die wichtigsten Trends bei den bevorstehenden Preisbewegungen.
Als Nächstes gehen wir zur zweiten Stufe des Trainings über, die sich auf das Training der gewinnmaximierenden Verhaltenspolitik des Akteurs und der Belohnungsfunktion des Kritikers konzentriert. Im Gegensatz zum Encoder hängt das Training des Akteurs wesentlich von den Aktionen ab, die er in der Umgebung ausführt. Um effektives Lernen zu gewährleisten, müssen wir den Trainingsdatensatz auf dem neuesten Stand halten. Daher aktualisieren wir den Datensatz regelmäßig, um die aktuelle Politik des Akteurs widerzuspiegeln.
Das Training wird fortgesetzt, bis sich der Fehler des Modells auf einem bestimmten Niveau stabilisiert. Zu diesem Zeitpunkt tragen weitere Aktualisierungen des Datensatzes nicht mehr zur Optimierung der Politik des Akteurs bei.
Wir evaluieren die Effektivität des trainierten Modells mit dem MetaTrader 5 Strategietester, indem wir historische Daten vom Januar 2024 verwenden, während alle anderen Parameter unverändert bleiben. Die Testergebnisse des trainierten Modells werden unten dargestellt.
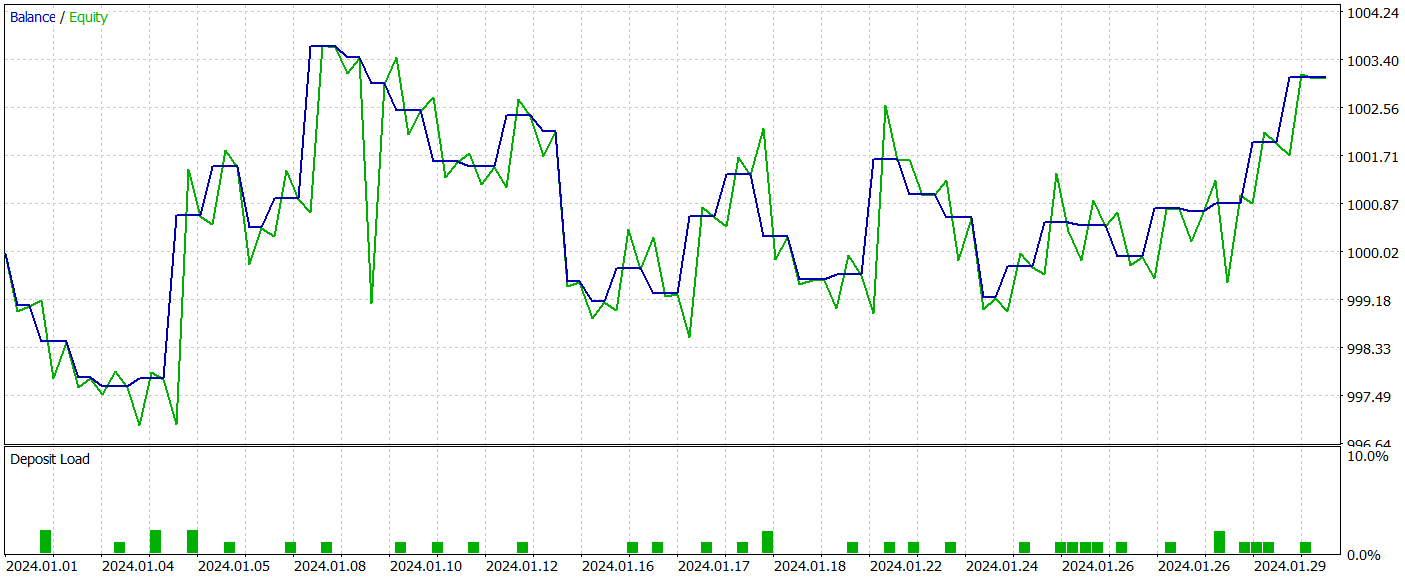
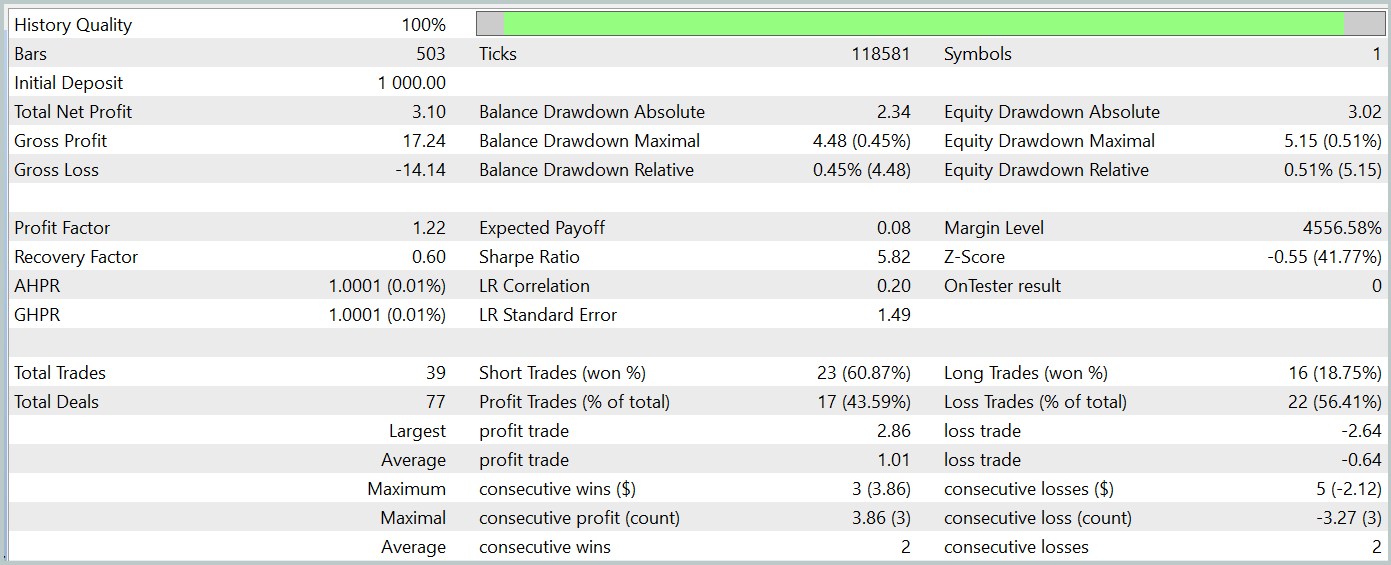
Wie die Ergebnisse zeigen, hat unser Trainingsprozess erfolgreich eine Akteurspolitik hervorgebracht, die in der Lage ist, sowohl auf Trainings- als auch auf Testdaten Gewinne zu erzielen. Während des Testzeitraums führte das Modell 39 Handelsgeschäfte aus, von denen über 43 % mit Gewinn abgeschlossen wurden. Der Anteil der Handelsgeschäfte mit Gewinn war etwas geringer als der Anteil derer mit Verlust. Der durchschnittliche und der maximale Gewinn pro Handel überstiegen jedoch die entsprechenden Verluste, sodass das Modell den Test mit einem kleinen Nettogewinn abschließen konnte. Der Gewinnfaktor wurde mit 1,22 angegeben.
Es ist jedoch zu beachten, dass die erzielten Ergebnisse aufgrund des Fehlens eines eindeutigen Trends in der beobachteten Saldenlinie und der begrenzten Anzahl von Handelsgeschäfte möglicherweise nicht vollständig repräsentativ sind.
Schlussfolgerung
In diesem Artikel haben wir die HiVT-Methode mit MQL5 erfolgreich umgesetzt. Wir haben den vorgeschlagenen Algorithmus in das Environmental State Encoder-Modell integriert. Anschließend haben wir die Modelle trainiert und getestet. Die Testergebnisse haben gezeigt, dass die HiVT-Methode die Markttrends effektiv erfasst. Sie lieferte auch ein ausreichendes Maß an Vorhersagequalität, um die Entwicklung einer profitablen Handelspolitik für den Agenten zu unterstützen.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Trainings-EA des Encoders |
| 5 | Test.mq5 | Expert Advisor | Trainings-EA für das Model |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15713
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronale Netze im Handel: Hierarchische Vektortransformer (HiVT)
Neuronale Netze im Handel: Hierarchische Vektortransformer (HiVT)
 Von der Grundstufe bis zur Mittelstufe: WHILE- und DO WHILE-Anweisungen
Von der Grundstufe bis zur Mittelstufe: WHILE- und DO WHILE-Anweisungen
 Implementierung eines Schnellfeuer-Handelsstrategie-Algorithmus mit parabolischem SAR und einfachem gleitenden Durchschnitt (SMA) in MQL5
Implementierung eines Schnellfeuer-Handelsstrategie-Algorithmus mit parabolischem SAR und einfachem gleitenden Durchschnitt (SMA) in MQL5
 Entwicklung eines Replay-Systems (Teil 62): Abspielen des Dienstes (III)
Entwicklung eines Replay-Systems (Teil 62): Abspielen des Dienstes (III)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.