
Redes neuronales en el trading: Transformador vectorial jerárquico (Final)
Introducción
En el artículo anterior, introdujimos la descripción teórica del algoritmo de Transformador Vectorial Jerárquico (HiVT), propuesto para la predicción del movimiento multiagente en el campo de los vehículos de conducción autónoma. Este método ofrece un enfoque eficaz para resolver el problema de la predicción de series temporales descomponiendo el problema principal en etapas de extracción del contexto local y la modelización global de las interacciones.
Permítame recordarles que el problema de la previsión de series temporales lo resuelven los autores del método HiVT en 3 etapas. En el primer paso, el modelo extrae las características contextuales locales de los objetos. El escenario completo se divide en un conjunto de áreas locales, cada una de ellas centrada en torno a un agente central.
En la segunda etapa, las dependencias globales de largo alcance se capturan en el escenario mediante la transferencia de información entre regiones locales centradas en el agente.
Las representaciones locales y globales resultantes permiten al descodificador predecir las futuras trayectorias de todos los agentes en una única pasada directa del modelo.
A continuación le presentamos la visualización del método por parte del autor.
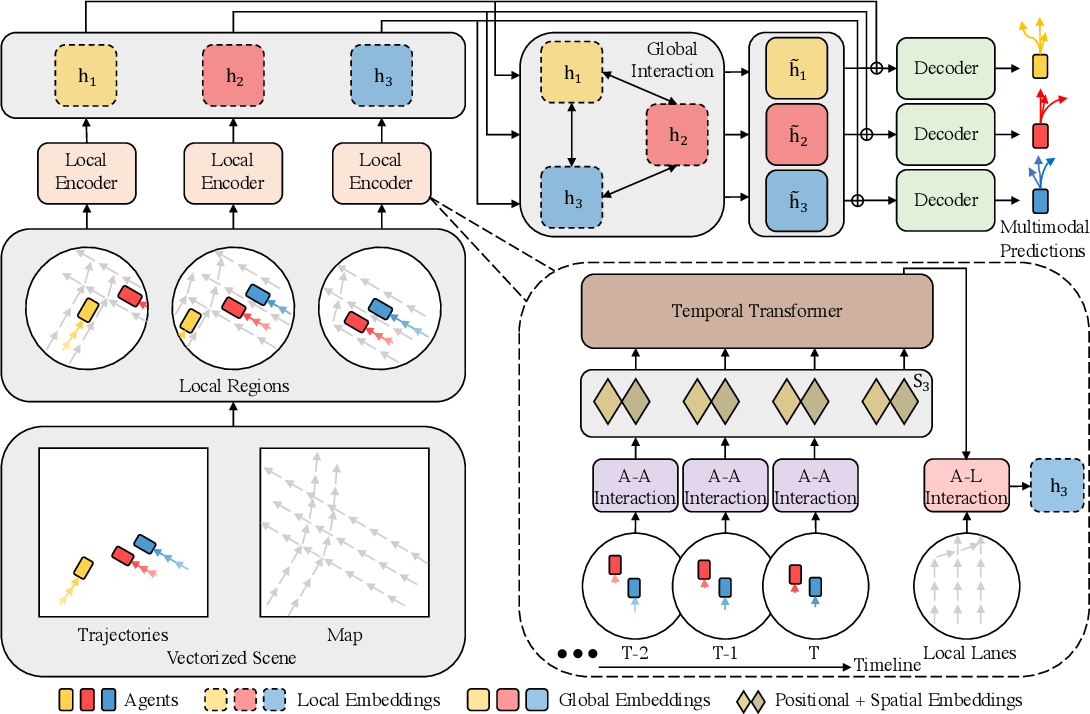
Además, en el artículo anterior, realizamos un trabajo preparatorio bastante extenso, durante el cual implementamos bloques individuales del algoritmo propuesto. Y ahora tendremos que completar el trabajo que hemos empezado, uniendo bloques separados y dispares en una única estructura integrada.
1. Montamos el HiVT
Implementaremos nuestra visión de los enfoques propuestos por los autores del método HiVT dentro de la clase CNeuronHiVTOCL. La funcionalidad básica de nuestra nueva clase se heredará de la capa CNeuronBaseOCL totalmente conectada. Y su estructura completa será la siguiente.
class CNeuronHiVTOCL : public CNeuronBaseOCL { protected: uint iHistory; uint iVariables; uint iForecast; uint iNumTraj; //--- CNeuronBaseOCL cDataTAD; CNeuronConvOCL cEmbeddingTAD; CNeuronTransposeRCDOCL cTransposeATD; CNeuronHiVTAAEncoder cAAEncoder; CNeuronTransposeRCDOCL cTransposeTAD; CNeuronLearnabledPE cPosEmbeddingTAD; CNeuronMVMHAttentionMLKV cTemporalEncoder; CNeuronLearnabledPE cPosLineEmbeddingTAD; CNeuronPatching cLineEmbeddibg; CNeuronMVCrossAttentionMLKV cALEncoder; CNeuronMLMHAttentionMLKV cGlobalEncoder; CNeuronTransposeOCL cTransposeADT; CNeuronConvOCL cDecoder[3]; // Agent * Traj * Forecast CNeuronConvOCL cProbProj; CNeuronSoftMaxOCL cProbability; // Agent * Traj CNeuronBaseOCL cForecast; CNeuronTransposeOCL cTransposeTA; //--- virtual bool Prepare(const CNeuronBaseOCL *history); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override ; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronHiVTOCL(void) {}; ~CNeuronHiVTOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, uint num_traj, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronHiVTOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
En la estructura presentada de nuestro objeto CNeuronHiVTOCL vemos la declaración de la lista de métodos redefinidos y una serie de objetos internos cuya funcionalidad conoceremos durante la implementación de los algoritmos de los métodos redefinidos.
Declararemos todos los objetos internos estáticamente, lo cual nos permitirá dejar el constructor y el destructor de la clase "vacíos". La inicialización directa de todos los objetos y variables anidados se realizará en el método Init.
bool CNeuronHiVTOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, uint num_traj, ENUM_OPTIMIZATION optimization_type, uint batch) { if(units_count < 2 || !CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * forecast, optimization_type, batch)) return false;
En los parámetros del método obtendremos las constantes básicas que nos permitirán identificar unívocamente la arquitectura del objeto que se está inicializando, mientras que en el cuerpo del método llamaremos directamente al método homónimo de la clase padre. Como ya sabrá, es donde se inicializan todos los objetos y variables heredados.
Aquí cabe destacar que añadiremos una comprobación directa del número de elementos de la secuencia analizada a los controles implementados en el método de la clase padre. En este caso, debería haber al menos 2, ya que durante la vectorización del estado de origen que proporciona el algoritmo HiVT, operaremos sobre la dinámica de los indicadores. Y para calcular el cambio en un indicador, necesitaremos 2 de sus valores: en el paso temporal actual y en el anterior.
Después de pasar con éxito el bloque de control de nuestro método de inicialización, almacenaremos los parámetros resultantes de la arquitectura del bloque en variables internas.
iVariables = window; iHistory = units_count - 1; iForecast = forecast; iNumTraj = MathMax(num_traj, 1);
A continuación, inicializaremos los objetos internos. El orden de inicialización de los objetos internos se corresponderá con la secuencia de utilización de los objetos dentro del algoritmo de pasada directa del algoritmo considerado. Este planteamiento nos permitirá seguir elaborando el algoritmo que debemos construir y asegurarnos de que los objetos creados son tanto suficientes como necesarios.
Primero crearemos un objeto de capa interna para registrar la representación vectorial del estado del entorno analizado.
Recordemos que aquí el vector de descripción de cada elemento individual de una secuencia unitaria en un paso temporal independiente será igual al doble del número de secuencias unitarias analizadas. Y es que cada elemento de la secuencia se caracteriza por un movimiento en el espacio bidimensional y un cambio en la posición de los demás agentes con respecto al elemento analizado.
Luego crearemos dicho vector de descripción para cada elemento de todas las secuencias unitarias analizadas en cada paso temporal.
if(!cDataTAD.Init(0, 0, OpenCL, 2 * iVariables * iVariables * iHistory, optimization, iBatch)) return false;
Nótese que al implementar el algoritmo HiVT, construimos el trabajo con tensores tridimensionales cuya imagen almacenamos en un búfer de datos unidimensional. Y para indicar la dimensionalidad actual en los nombres de los objetos, añadiremos un sufijo de 3 caracteres:
- T (Time) — dimensionalidad de los pasos temporales;
- A (Agent) — dimensionalidad del agente (serie temporal unitaria), en nuestro caso, del parámetro analizado;
- D (Dimension) — dimensionalidad del vector que describe un elemento de una secuencia unitaria.
A continuación, usaremos la capa de convolución para crear las incorporaciones de las descripciones vectoriales resultantes.
if(!cEmbeddingTAD.Init(0, 1, OpenCL, 2 * iVariables, 2 * iVariables, window_key, iVariables * iHistory, 1, optimization, iBatch)) return false;
En este caso, utilizaremos 1 matriz de parámetros para generar las incorporaciones, que aplicaremos a todos los elementos de la secuencia multimodal. Por consiguiente, especificaremos el número de bloques analizados de esta capa como el producto del número de secuencias unitarias por la profundidad de la historia analizada.
Tras generar las incorporaciones, el algoritmo HiVT permitirá analizar las dependencias locales entre agentes en un único paso temporal. Como ya comentamos en el artículo anterior, antes de realizar este paso deberemos transponer los datos de origen.
if(!cTransposeATD.Init(0, 2, OpenCL, iHistory, iVariables, window_key, optimization, iBatch)) return false;
Solo entonces podremos utilizar las clases de atención de que disponemos para identificar las dependencias entre los agentes del grupo local.
if(!cAAEncoder.Init(0, 3, OpenCL, window_key, window_key, heads, (heads + 1) / 2, iVariables, 2, 1, iHistory, optimization, iBatch)) return false;
Aquí hay dos puntos a considerar. En primer lugar, tras la transposición de datos, cambiaremos la secuencia de caracteres del sufijo del nombre del objeto por ATD, que se corresponde con la dimensionalidad del tensor 3D en la salida de la capa de transposición de datos.
En segundo lugar, eche un vistazo a la funcionalidad de nuestros bloques de atención. Originalmente los diseñamos para trabajar con tensores bidimensionales en los que cada fila representa un vector que describe un elemento de una secuencia. Y de hecho identificamos las dependencias entre las filas de la matriz analizada; por así decirlo, ejecutamos una "atención vertical". Posteriormente, añadimos la detección de dependencias dentro de secuencias unitarias individuales de una serie temporal multimodal. En la práctica, dividimos la matriz original en varias matrices idénticas de series unitarias menores para analizarlas. Las nuevas matrices heredaron el número de filas de la matriz original: dividimos uniformemente sus columnas entre sí. En esencia, esto se corresponde con la dimensionalidad de nuestro tensor tridimensional. La primera dimensión será el número de filas de la matriz original de datos analizados. La segunda dimensión indicará el número de matrices menores para análisis independientes. Y la tercera dimensión representará la dimensionalidad del vector de descripción de un elemento de la secuencia analizada. Considerando la pretransposición del tensor de incorporación de los datos de origen, especificaremos el número de secuencias unitarias como el tamaño de la secuencia analizada del bloque de atención actual. Al mismo tiempo, especificaremos la profundidad de la historia analizada de los datos de origen en el parámetro del número de variables. Así, conseguiremos el efecto de analizar las dependencias entre variables individuales en 1 paso temporal.
En esta implementación del bloque de análisis de dependencia Agente-Agente, hemos usado 2 capas de atención con generación de tensor Key-Value para cada capa interna. En ese caso, el número de cabezas de atención del tensor Key-Value es 2 veces menor que el parámetro similar para el tensor Query.
Nótese que en este caso estamos utilizando un bloque de atención con función de control de asociación de características CNeuronHiVTAAEncoder.
Tras enriquecer la incorporación de elementos de secuencia con dependencias entre agentes del grupo local, el algoritmo HiVT permite analizar las dependencias temporales dentro de elementos individuales de secuencias unitarias. Aquí deberemos devolver los datos a la representación original.
if(!cTransposeTAD.Init(0, 4, OpenCL, iVariables, iHistory, window_key, optimization, iBatch)) return false;
A continuación, añadiremos una codificación posicional totalmente entrenable.
if(!cPosEmbeddingTAD.Init(0, 5, OpenCL, iVariables * iHistory * window_key, optimization, iBatch)) return false;
Y utilizaremos el bloque de atención CNeuronMVMHAtenciónMLKV para identificar las dependencias temporales.
if(!cTemporalEncoder.Init(0, 6, OpenCL, window_key, window_key, heads, (heads + 1) / 2, iHistory, 2, 1, iVariables, optimization, iBatch)) return false;
A pesar de las diferencias en la arquitectura de los bloques de atención de dependencia local y temporal, usaremos los mismos parámetros para inicializarlos.
Como siguiente paso, los autores del método HiVT proponen enriquecer las incorporaciones de los Agentes con información sobre mapas de carreteras. Creo que nadie dudará de que el estado de la carretera, sus señales y giros imponen cierta impronta a las acciones del agente. En nuestro caso, no existen directrices explícitas para limitar la variación de los valores de los parámetros analizados. Obviamente, existen zonas de valores aceptables de osciladores individuales. Por ejemplo, el RSI solo puede tomar valores entre 0 y 100. Pero eso es más bien un caso especial.
Por consiguiente, utilizaremos los datos históricos de que disponemos para determinar el cambio más probable. Sustituiremos la representación cartográfica por incorporaciones de pequeños segmentos de trayectoria reales que crearemos utilizando la capa de parcheado de datos.
if(!cLineEmbeddibg.Init(0, 7, OpenCL, 3, 1, 8, iHistory - 1, iVariables, optimization, iBatch)) return false;
Tenga en cuenta que al vectorizar el estado actual, utilizaremos la dinámica del cambio de parámetros en 1 paso temporal. Y al incorporar pequeños segmentos reales de la trayectoria, utilizaremos bloques de 3 elementos con un paso 1. De este modo queremos revelar las dependencias entre la dinámica del indicador en un paso individual y la posible continuación de la trayectoria.
A las incorporaciones resultantes, añadiremos una codificación posicional totalmente entrenable.
if(!cPosLineEmbeddingTAD.Init(0, 8, OpenCL, cLineEmbeddibg.Neurons(), optimization, iBatch)) return false;
Y, a continuación, enriqueceremos las incorporaciones actuales de los Agentes con información sobre la trayectoria. Para ello, utilizaremos el bloque de atención cruzada CNeuronMVCrossAttentionMLKV con dos capas internas.
if(!cALEncoder.Init(0, 9, OpenCL, window_key, window_key, heads, 8, (heads + 1) / 2, iHistory, iHistory - 1, 2, 1, iVariables, iVariables, optimization, iBatch)) return false;
Aquí puede parecer que estamos realizando secuencialmente 2 operaciones similares: identificar las dependencias temporales y analizar las dependencias entre agentes y trayectorias. En ambos casos, analizamos las dependencias del estado actual del Agente con la representación de los parámetros del mismo indicador en otros segmentos temporales. Pero aquí existe una línea muy fina. En el primer caso, emparejaremos estados similares del agente en distintos pasos temporales, mientras que en el segundo, trataremos con unos patrones de trayectoria que abarcan un intervalo de tiempo algo mayor.
Con esto concluiremos el bloque de análisis de dependencias locales, que esencialmente enriquece de forma exhaustiva la incorporación del estado del Agente. El siguiente paso del algoritmo HiVT consistirá en analizar las dependencias a largo plazo del escenario en el bloque de interacción global.
if(!cGlobalEncoder.Init(0, 10, OpenCL, window_key*iVariables, window_key*iVariables, heads, (heads+1)/2, iHistory, 4, 2, optimization, iBatch)) return false;
Aquí utilizaremos un bloque de atención con 4 capas interiores. En este caso, utilizaremos la representación de todo el escenario en lugar de Agentes individuales para analizar las dependencias.
Y luego solo nos quedará modelizar la próxima secuencia de valores previstos. Al igual que antes, la predicción de la secuencia siguiente se realizará dentro de secuencias unitarias individuales. Para ello, primero tendremos que transponer los datos actuales.
if(!cTransposeADT.Init(0, 11, OpenCL, iHistory, window_key * iVariables, optimization, iBatch)) return false;
Además, los autores del método HiVT proponen usar un MLP para predecir los valores posteriores para toda la profundidad de planificación. En nuestro caso, este trabajo se realizará en un bloque de 3 capas convolucionales consecutivas, cada una de las cuales ha recibido una ventana única de datos analizados y su propia función de activación.
if(!cDecoder[0].Init(0, 12, OpenCL, iHistory, iHistory, iForecast, window_key * iVariables, optimization, iBatch)) return false; cDecoder[0].SetActivationFunction(SIGMOID); if(!cDecoder[1].Init(0, 13, OpenCL, iForecast * window_key, iForecast * window_key, iForecast * window_key, iVariables, optimization, iBatch)) return false; cDecoder[1].SetActivationFunction(LReLU); if(!cDecoder[2].Init(0, 14, OpenCL, iForecast * window_key, iForecast * window_key, iForecast * iNumTraj, iVariables, optimization, iBatch)) return false; cDecoder[2].SetActivationFunction(TANH);
En la primera etapa, trabajaremos dentro de los elementos individuales de la incorporación de la descripción del estado del Agente individual, cambiando el tamaño de la secuencia desde la profundidad de la historia analizada hasta el horizonte de planificación.
A continuación, analizaremos las dependencias globales dentro de los agentes individuales para todo el horizonte de planificación sin cambiar el tamaño del tensor.
Solo en la última etapa pronosticaremos a la vez varias evoluciones posibles para cada serie temporal unitaria individual. El número de variantes de trayectorias de previsión se fijará mediante un programa externo en los parámetros del método.
A este respecto, cabe señalar que la previsión de múltiples escenarios supone una característica distintiva del enfoque propuesto. Sin embargo, necesitaremos un mecanismo para seleccionar la trayectoria más probable. Por consiguiente, primero haremos una proyección de las trayectorias obtenidas a la dimensionalidad del número de trayectorias previstas para cada agente.
if(!cProbProj.Init(0, 15, OpenCL, iForecast * iNumTraj, iForecast * iNumTraj, iNumTraj, iVariables, optimization, iBatch)) return false;
Y con la ayuda de la función SoftMax trasladaremos las proyecciones obtenidas al dominio de la probabilidad.
if(!cProbability.Init(0, 16, OpenCL, iForecast * iNumTraj * iVariables, optimization, iBatch)) return false; cProbability.SetHeads(iVariables); // Agent * Traj
Ponderando las trayectorias predichas previamente por sus probabilidades, obtendremos la trayectoria media del próximo movimiento de nuestro Agente.
if(!cForecast.Init(0, 17, OpenCL, iForecast * iVariables, optimization, iBatch)) return false;
Todo lo que deberemos hacer es llevar los valores predichos a la dimensionalidad de los datos de origen. Implementaremos esta función transponiendo los datos.
if(!cTransposeTA.Init(0, 18, OpenCL, iVariables, iForecast, optimization, iBatch)) return false;
Para reducir las operaciones de copiado de datos y optimización del uso de los recursos de memoria, redefiniremos los punteros de los búferes de gradiente de resultados y errores de nuestro bloque a los búferes similares de la última capa interna de transposición de datos.
SetOutput(cTransposeTA.getOutput(),true); SetGradient(cTransposeTA.getGradient(),true); //--- return true; }
Y finalizar el método retornando el resultado lógico de las operaciones del método al programa que realiza la llamada.
Una vez hayamos terminado de inicializar el objeto de clase, pasaremos a construir el algoritmo de pasada directa de nuestra clase en el método feedForward.
bool CNeuronHiVTOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!Prepare(NeuronOCL)) return false;
En los parámetros del método, obtendremos un puntero al objeto que contiene los datos de origen. Y transmitiremos inmediatamente el puntero resultante al método Prepare de preparación de los datos de origen. Este método es una "envoltura" para llamar al kernel de vectorización de datos HiVTPrepare, cuyo algoritmo analizamos en el artículo anterior. Ya hemos visto muchas veces métodos distintos para poner los kernels de los programas OpenCL en la cola de ejecución. Y el algoritmo del método Prepare no se distinguirá por ninguna peculiaridad ni escollo. Por lo tanto, en el ámbito de este artículo, omitiremos la descripción de su algoritmo. No obstante, podrá consultarlo usted mismo en el archivo adjunto.
A continuación, basándonos en las representaciones vectoriales obtenidas, generaremos las incorporaciones de los Agentes en cada paso temporal individual.
if(!cEmbeddingTAD.FeedForward(cDataTAD.AsObject())) return false;
Luego las transpondremos.
if(!cTransposeATD.FeedForward(cEmbeddingTAD.AsObject())) return false;
Y las enriqueceremos con las dependencias locales en el marco del análisis de las representaciones Agente-Agente.
if(!cAAEncoder.FeedForward(cTransposeATD.AsObject())) return false;
Después enriqueceremos las incorporaciones de los estados de los agentes añadiendo dependencias temporales. Para ello, primero transpondremos el tensor de datos actual.
if(!cTransposeTAD.FeedForward(cAAEncoder.AsObject())) return false;
Le añadiremos etiquetas de codificación de posición.
if(!cPosEmbeddingTAD.FeedForward(cTransposeTAD.AsObject())) return false;
Y llamaremos al método de pasada directa de nuestro módulo de atención temporal según agentes individuales.
if(!cTemporalEncoder.FeedForward(cPosEmbeddingTAD.AsObject())) return false;
Tras realizar con éxito las operaciones de atención temporal, obtendremos un tensor de incorporación de los datos analizados enriquecido con dependencias locales y temporales. Y ahora tendremos que enriquecer las incorporaciones resultantes con información sobre posibles patrones de movimiento. Para ello, primero crearemos las incorporaciones de los patrones del movimiento histórico analizado.
if(!cLineEmbeddibg.FeedForward(NeuronOCL)) return false;
Luego añadiremos la codificación posicional a las incorporaciones de los patrones resultantes.
if(!cPosLineEmbeddingTAD.FeedForward(cLineEmbeddibg.AsObject())) return false;
Y en el módulo de atención cruzada, enriqueceremos las incorporaciones de nuestros agentes con información sobre distintos patrones de movimiento.
if(!cALEncoder.FeedForward(cTemporalEncoder.AsObject(), cPosLineEmbeddingTAD.getOutput())) return false;
Después aplicaremos el módulo de atención global al tensor de agentes de incorporación enriquecidos.
if(!cGlobalEncoder.FeedForward(cALEncoder.AsObject())) return false;
A esto le seguirá un bloque para predecir el próximo movimiento de los agentes. Permítame recordarle que tenemos previsto pronosticar los valores posteriores de los parámetros analizados en cuanto a secuencias unitarias. Por ello, primero transpondremos el tensor de datos existente.
if(!cTransposeADT.FeedForward(cGlobalEncoder.AsObject())) return false;
Después realizaremos una pasada directa de nuestro bloque de predicción de datos MLP de tres capas.
if(!cDecoder[0].FeedForward(cTransposeADT.AsObject())) return false; if(!cDecoder[1].FeedForward(cDecoder[0].AsObject())) return false; if(!cDecoder[2].FeedForward(cDecoder[1].AsObject())) return false;
Aquí deberemos recordar las peculiaridades del método HiVT. A la salida de la previsión MLP del próximo movimiento obtendremos no una, sino varias opciones de posible continuación de la serie inicial analizada. Y tendremos que determinar las probabilidades de realización de cada variante del movimiento previsto. Para ello, primero realizaremos trayectorias predictivas.
if(!cProbProj.FeedForward(cDecoder[2].AsObject())) return false;
Y con la ayuda de la función SoftMax traduciremos las proyecciones obtenidas al área de valores probabilísticos.
if(!cProbability.FeedForward(cProbProj.AsObject())) return false;
Ahora solo tendremos que multiplicar el tensor de las trayectorias previstas por sus probabilidades.
if(IsStopped() || !MatMul(cDecoder[2].getOutput(), cProbability.getOutput(), cForecast.getOutput(), iForecast, iNumTraj, 1, iVariables)) return false;
Como resultado de esta operación, obtendremos un tensor de trayectorias medias ponderadas a lo largo de todo el horizonte de planificación para cada fila unitaria de la secuencia multimodal analizada.
Y al final de las operaciones de nuestro método de pasada directa, realizaremos una transposición del tensor de valor predictivo para alinearlo con las medidas de los datos de origen analizados.
if(!cTransposeTA.FeedForward(cForecast.AsObject())) return false; //--- return true; }
Como es habitual, retornaremos al programa que realiza la llamada el valor lógico del resultado de las operaciones del método.
Aquí terminaremos nuestro trabajo de implementación del algoritmo de pasada directa del método HiVT y pasaremos a construir los métodos de pasada inversa de nuestra clase. Como ya sabe, el algoritmo de pasada inversa consta de 2 bloques principales:
- La distribución del gradiente de error a todos los elementos según su influencia en el resultado final. Esta funcionalidad se implementa en el método calcInputGradients.
- La corrección de los parámetros entrenados del modelo para minimizar su rendimiento global, lo cual se implementa en el método updateInputWeights.
Empezaremos a implementar algoritmos de pasada inversa construyendo el método de distribución de gradientes de error calcInputGradients. El algoritmo de este método se construirá en total conformidad con el algoritmo de pasada directa, solo que todas las operaciones se realizarán en orden inverso.
bool CNeuronHiVTOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En los parámetros de este método obtendremos el puntero al objeto de la capa anterior, que nos ha transmitido los datos de origen durante la pasada directa. Y en este caso, tendremos que transmitirle el gradiente de error según la influencia de los datos de entrada en el resultado final.
En el cuerpo del método comprobaremos directamente la relevancia del puntero recibido. De lo contrario, las operaciones de este método carecerán de sentido.
Una vez superado con éxito el bloque de control, procederemos a realizar las operaciones de distribución directa del gradiente de error.
El gradiente de error al nivel de resultados de la capa actual ya está contenido en el búfer correspondiente de nuestra clase. Se escribió allí al realizar las operaciones de un método similar de la capa posterior. Y gracias al intercambio de búferes de datos realizado antes, el gradiente de error que necesitamos ya está contenido en el búfer de la última capa de transposición de datos. Comenzaremos nuestro trabajo transfiriendo el gradiente de error a la capa de trayectorias predictivas medias ponderadas de series unitarias.
if(!cForecast.calcHiddenGradients(cTransposeTA.AsObject())) return false;
Como recordará, en el proceso de pasada directa, obtuvimos las trayectorias medias ponderadas multiplicando el tensor de varias trayectorias previstas por el vector de probabilidades correspondientes. En consecuencia, durante el proceso de pasada inversa, tendremos que distribuir el gradiente de error tanto en el tensor del conjunto de trayectorias predichas como en el vector de probabilidad.
if(IsStopped() || !MatMulGrad(cDecoder[2].getOutput(), cDecoder[2].getGradient(), cProbability.getOutput(), cProbability.getGradient(), cForecast.getGradient(), iForecast, iNumTraj, 1, iVariables)) return false;
Luego pasaremos el gradiente de error de las probabilidades a la capa de proyección de las trayectorias proyectadas.
if(!cProbProj.calcHiddenGradients(cProbability.AsObject())) return false;
Y utilizaremos las propias trayectorias proyectadas para obtener las proyecciones. Y además, tendríamos que transmitir el gradiente de error al nivel de las trayectorias predictivas.
Pero aquí conviene señalar que ya hemos transferido antes el gradiente de error del paso de la trayectoria media ponderada al nivel del tensor del conjunto de trayectorias predictivas. Y una llamada directa al método calcHiddenGradients de la capa correspondiente eliminará el gradiente de error previamente pasado y sobrescribirá el búfer con nuevos valores. Por lo general, en estos casos se utilizan búferes de datos auxiliares y, a continuación, se suman los valores de los 2 flujos de datos. Sin embargo, en este caso hemos decidido no seguir pasando el gradiente de error de la capa de proyección de datos. De esta forma, queremos mantener "limpia" la predicción de las trayectorias posteriores sin que sus valores se vean distorsionados por errores en la distribución de probabilidad de la relevancia de las trayectorias individuales.
Por lo tanto, ejecutaremos el gradiente de error de las trayectorias de predicción a través del MLP del bloque de predicción.
if(!cDecoder[1].calcHiddenGradients(cDecoder[2].AsObject())) return false; if(!cDecoder[0].calcHiddenGradients(cDecoder[1].AsObject())) return false;
Luego transpondremos el tensor de gradiente de error obtenido en la salida y lo pasaremos por el bloque de interacción global.
if(!cTransposeADT.calcHiddenGradients(cDecoder[0].AsObject())) return false; if(!cGlobalEncoder.calcHiddenGradients(cTransposeADT.AsObject())) return false; if(!cALEncoder.calcHiddenGradients(cGlobalEncoder.AsObject())) return false;
Desde el bloque de interacción global, el gradiente de error pasará al bloque de análisis de dependencia local.
Permítame recordarle que en este bloque se realiza un análisis exhaustivo de las dependencias mutuas entre objetos locales individuales. Y aquí pasaremos primero el gradiente de error resultante a través del bloque de atención cruzada Agente-Trayectoria al nivel del bloque de análisis de dependencia temporal y codificación de la posición de incorporaciones de patrones de movimiento.
if(!cTemporalEncoder.calcHiddenGradients(cALEncoder.AsObject(), cPosLineEmbeddingTAD.getOutput(), cPosLineEmbeddingTAD.getGradient(), (ENUM_ACTIVATION)cPosLineEmbeddingTAD.Activation())) return false;
Luego descenderemos el gradiente de error a través de las operaciones de codificación posicional.
if(!cLineEmbeddibg.calcHiddenGradients(cPosLineEmbeddingTAD.AsObject())) return false;
Y lo llevaremos al nivel de los datos de origen.
if(!NeuronOCL.calcHiddenGradients(cLineEmbeddibg.AsObject())) return false;
En el segundo flujo de datos, primero pasaremos el gradiente de error por el bloque de análisis de dependencia temporal.
if(!cPosEmbeddingTAD.calcHiddenGradients(cTemporalEncoder.AsObject())) return false;
A continuación, corregiremos el gradiente de error resultante según la operación de codificación de la posición.
if(!cTransposeTAD.calcHiddenGradients(cPosEmbeddingTAD.AsObject())) return false;
Después transpondremos los datos y pasaremos el gradiente a través del bloque de análisis de dependencia Agente-Agente.
if(!cAAEncoder.calcHiddenGradients(cTransposeTAD.AsObject())) return false; if(!cTransposeATD.calcHiddenGradients(cAAEncoder.AsObject())) return false;
Al final de las operaciones del método, transpondremos los datos a la representación original y pasaremos el gradiente de error a través de la capa de generación de incorporaciones hasta la representación vectorial de los datos de origen.
if(!cEmbeddingTAD.calcHiddenGradients(cTransposeATD.AsObject())) return false; if(!cDataTAD.calcHiddenGradients(cEmbeddingTAD.AsObject())) return false; //--- return true; }
Y retornaremos el resultado lógico de las operaciones al programa que realiza la llamada.
En este paso, distribuiremos el gradiente de error entre todos los elementos del modelo en función de su influencia en el resultado final. Y ahora tendremos que ajustar los parámetros entrenados del modelo en la dirección de la minimización del error global del modelo. Acto seguido, implementaremos esta funcionalidad en el método updateInputWeights.
Y aquí deberemos recordar que todos los parámetros entrenables de nuestra nueva clase CNeuronHiVTOCL estarán contenidos en sus objetos internos. Pero no todos los objetos internos contendrán parámetros entrenables. Por ejemplo, no se encontrarán en las capas de transposición de datos. Por lo tanto, en este método, solo trabajaremos con objetos que contengan parámetros entrenables. Y para ajustarlos, bastará con llamar al método homónimo del objeto interno correspondiente.
Como puede ver, el algoritmo del método es bastante sencillo, por lo que no ofreceremos su código completo en el marco de este artículo. No obstante, podrá consultarlo usted mismo en el archivo adjunto. El código completo de nuestra nueva clase y todos sus métodos también se dará allí.
2. Arquitectura del modelo
Ya hemos completado nuestro trabajo de construcción de la nueva clase CNeuronHiVTOCL y sus métodos. Esta clase implementará nuestra visión de los enfoques propuestos por los autores del método HiVT. Y ahora es el momento de implementar el nuevo objeto en la arquitectura de nuestro modelo.
Al igual que antes, introduciremos el objeto de predicción del movimiento posterior de la serie multimodal analizada en el modelo del codificador de estados del entorno. La solución arquitectónica de este modelo se presentará en el método CreateEncoderDescriptions. En los parámetros de este método obtendremos el puntero a un objeto de array dinámico en el que escribiremos la solución arquitectónica del modelo generado.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
En el cuerpo del método comprobaremos la relevancia del puntero obtenido y, de ser necesario, crearemos una nueva instancia del array dinámico. A continuación, describiremos de forma secuencial la arquitectura de cada capa de nuestro modelo.
Para ello, usaremos una capa básica completamente conectada de tamaño suficiente para obtener los datos de origen.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Tenemos previsto introducir en el modelo datos "brutos" sin procesar. Y para que tengan un aspecto comparable, usaremos capas de normalización por lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Tras el tratamiento inicial, transferiremos directamente los datos de origen a nuestro nuevo bloque construido utilizando los enfoques del método HiVT.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronHiVTOCL; { int temp[] = {BarDescr, NForecast, 6}; // {Variables, Forecast, NumTraj} ArrayCopy(descr.windows, temp); } descr.window_out = EmbeddingSize; // Inside Dimension descr.count = HistoryBars; // Units descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Aquí repetiremos prácticamente los parámetros similares de trabajos anteriores. Solo se añadiremos 1 nuevo parámetro de bloque, que definirá el número de variantes de las trayectorias previstas. En este caso, utilizaremos 6.
A la salida del bloque CNeuronHiVTOCL, esperamos recibir los valores de previsión ya listos de las series temporales multimodales analizadas. No obstante, deberemos considerar un pequeño detalle: Para organizar el funcionamiento eficaz del modelo con una serie temporal multimodal, hemos reunido todos sus valores en una forma comparable. Y en consecuencia, hemos obtenido los valores de previsión de forma similar. Para aproximar los valores previstos resultantes a las medidas habituales de los datos de origen, les añadiremos los parámetros de distribución estadística extraídos al normalizar los datos "brutos".
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
A continuación, coordinaremos los resultados obtenidos en el dominio de la frecuencia.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
La arquitectura de los modelos del Actor y el Crítico no ha cambiado. Lo mismo puede decirse de los programas de entrenamiento del modelo. Por ello, en el marco de este artículo no nos detendremos en su análisis. No obstante, encontrará el código completo de todos los programas utilizados en la elaboración de este artículo en el anexo para su propio estudio.
3. Simulación
Ya hemos implementado nuestra propia visión de los enfoques propuestos por los autores del método HiVT. Ahora es el momento de probar la eficacia de las soluciones que hemos aplicado. Para ello, primero deberemos entrenar los modelos con datos históricos reales y luego probar los modelos entrenados en un conjunto de datos fuera de la muestra de entrenamiento.
Para el entrenamiento del modelo usaremos los datos históricos del marco temporal EURUSD H1 para todo el año 2023.
El entrenamiento de los modelos lo realizaremos offline. Por lo tanto, tendremos que recoger la muestra de entrenamiento necesaria antes de empezar a entrenar. Podrá obtener más información sobre este proceso en el artículo sobre el método Real-ORL. Nosotros, en cambio, utilizaremos la muestra de entrenamiento recogida por modelos anteriores para entrenar nuestro codificador de estados del entorno.
Como ya sabrá, el modelo del Codificador del estado de la cuenta trabaja solo con los datos históricos de los movimientos de precios y los indicadores analizados que son independientes de las acciones realizadas por el Agente. Por ello, en esta fase del entrenamiento del modelo, no necesitaremos actualizar periódicamente la muestra de entrenamiento, ya que las nuevas trayectorias añadidas no proporcionarán información adicional a nuestro Codificador. Y ejecutaremos el proceso de entrenamiento hasta obtener los resultados deseados.
A continuación le presentamos los resultados de la prueba del modelo entrenado.
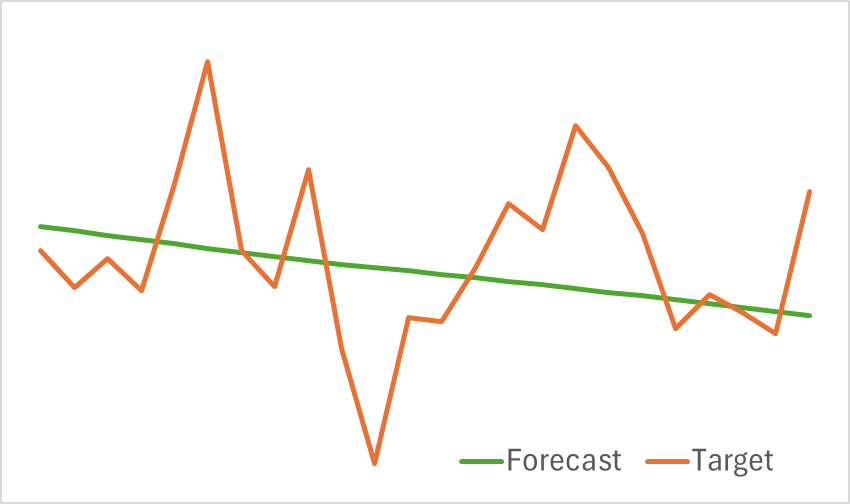
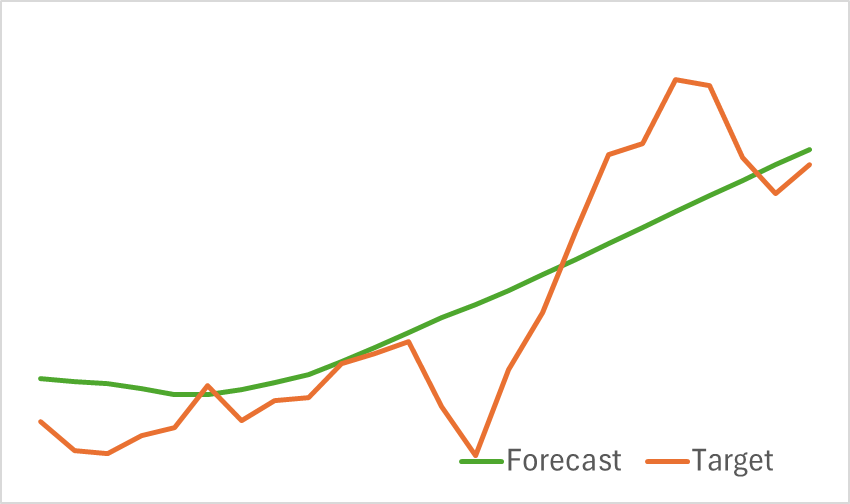
Como podemos ver en los gráficos anteriores, el modelo que hemos montado puede captar las principales tendencias de los próximos movimientos de precios con bastante eficacia.
A continuación, pasaremos a la segunda etapa del entrenamiento del modelo: el entrenamiento de la política de comportamiento rentable del Actor y de la función de recompensa del Crítico. Obviamente, en este caso, las recompensas reales del entorno dependerán en gran medida de las acciones realizadas por el Actor. Por lo tanto, para que el proceso de entrenamiento resulte sea eficaz, deberemos mantener actualizada la muestra de entrenamiento. Así que deberemos actualizar periódicamente los datos de la muestra de entrenamiento para reflejar las políticas actuales del Actor.
Los modelos se entrenarán hasta que el error del modelo se fije prácticamente en algún nivel. Y la nueva actualización de la muestra de entrenamiento no conducirá a una optimización de la política de comportamiento del Actor en el entrenamiento posterior.
Probamos la eficiencia del modelo entrenado en el simulador de estrategias de MetaTrader 5 con los datos históricos de enero de 2024 con todos los demás parámetros intactos. A continuación le presentamos los resultados de la prueba del modelo entrenado.
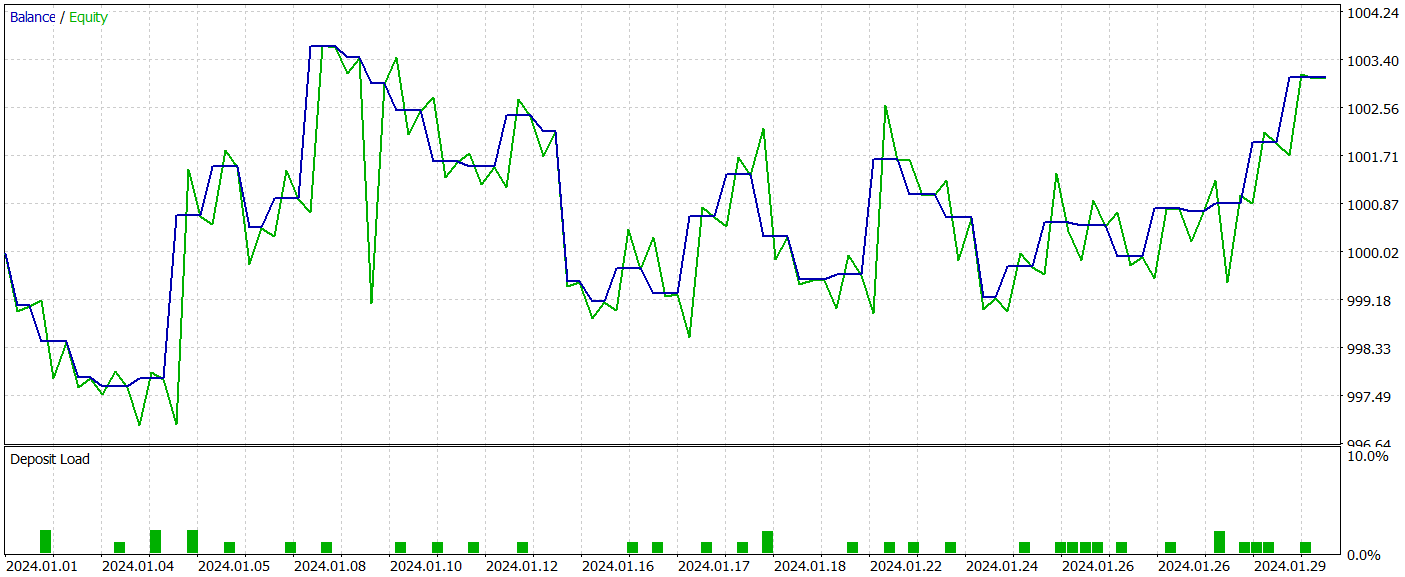

Como se desprende de los resultados de las pruebas anteriores, durante el entrenamiento hemos podido obtener una política del Actor capaz de generar beneficios tanto en los datos de entrenamiento como en los de prueba. Durante el periodo de prueba, el modelo ha realizado 39 transacciones comerciales y más del 43% de ellas se han cerrado con beneficios. Sí, la proporción de transacciones rentables es ligeramente inferior a la de no rentables. Sin embargo, gracias a que el tamaño de las transacciones rentables máximas y medias supera el mismo indicador de las transacciones perdedoras, hemos logrado completar la prueba con un pequeño beneficio. Al mismo tiempo, el factor de beneficio se ha fijado en 1,22.
No obstante, debemos señalar que, debido a la ausencia de una tendencia clara en la línea de balance observada por nosotros y al número reducido de transacciones en el proceso de prueba, los resultados obtenidos difícilmente pueden calificarse de representativos.
Conclusión
En este artículo, hemos completado la implementación de los enfoques propuestos por los autores del método HiVT usando MQL5. Asimismo, hemos implementado el algoritmo propuesto en el modelo del Codificador del estado del entorno. A continuación hemos entrenado y probado los modelos. Los resultados de las pruebas han demostrado la capacidad del método HiVT de captar eficazmente las tendencias de los próximos movimientos de precios. Y la calidad de predicción del próximo movimiento puede resultar suficiente para entrenar una política rentable para el comportamiento del agente.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | StudyEncoder.mq5 | Asesor | Asesor de entrenamiento del Codificador |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15713
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Métodos de William Gann (Parte II): Creación del indicador Cuadrado de Gann
Métodos de William Gann (Parte II): Creación del indicador Cuadrado de Gann
 Redes neuronales en el trading: Análisis de nubes de puntos (PointNet)
Redes neuronales en el trading: Análisis de nubes de puntos (PointNet)
 Gráficos del índice del dólar y del índice del euro — ejemplo de servicio en MetaTrader 5
Gráficos del índice del dólar y del índice del euro — ejemplo de servicio en MetaTrader 5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso