
交易中的神经网络:层次化向量变换器(终章)
概述
在上一篇文章中,我们领略了层次化矢量变换器(HiVT)算法的理论描述,其是为汽车智驾预测多个体运动而提出的。该方法将问题分解为局部上下文提取、和全局互动等几个阶段建模,提供了一种解决预测问题的有效方式。
以下是该方法的简述。HiVT 方法的作者分 3 个阶段解决了时间序列预测问题。在第一阶段,模型提取对象的局部上下文特征。整个场景被划分为一组局部区域,每个区域都以一个个体为中心。
在第二阶段,在以个体为中心的局部区域之间传输信息,并记录场景上的全局大范围依赖性。
组合的局部和全局表示,令解码器能够在模型的单次前向通验中预测所有个体的未来轨迹。
作者对该方法的可视化如下所示。
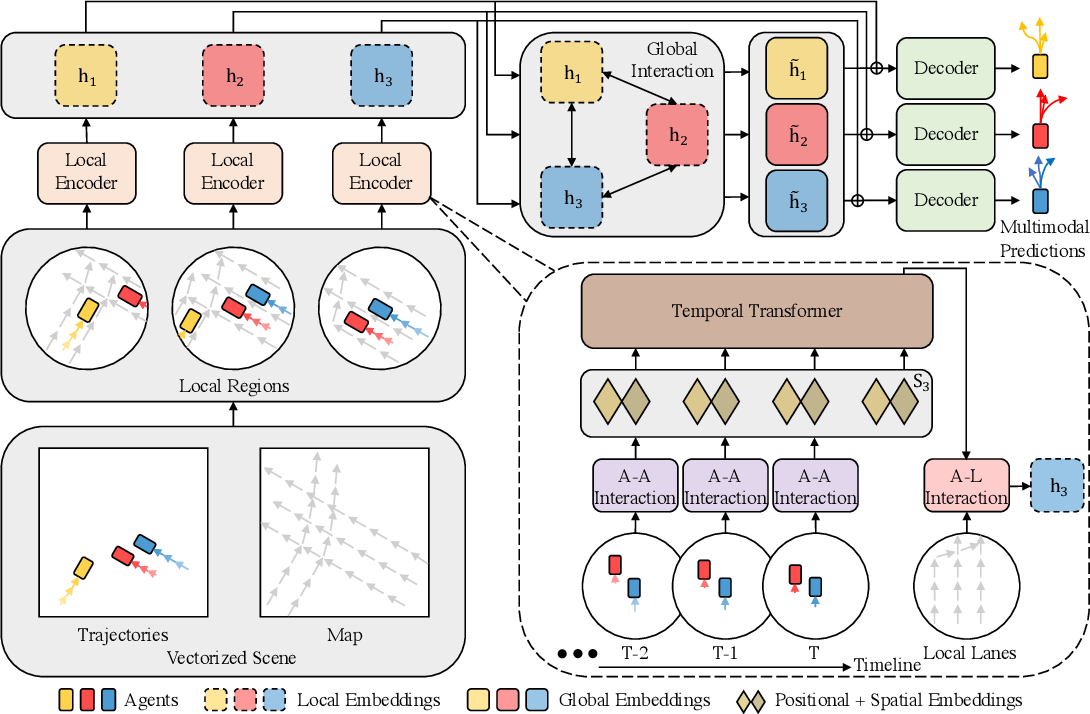
此外,在上一篇文章中,我们进行了相当广泛的准备工作,在此期间,实现了所提议算法的各个模块。在本文中,我们将完成我们的初创工作,将各个不同的模块合并到一个复杂的单一结构之中。
1. 汇编 HiVT
我们将在 CNeuronHiVTOCL 类的框架内实现 HiVT 作者所提议方式的愿景。核心功能将继承自基本全连接层类 CNeuronBaseOCL。其完整结构如下所示。
class CNeuronHiVTOCL : public CNeuronBaseOCL { protected: uint iHistory; uint iVariables; uint iForecast; uint iNumTraj; //--- CNeuronBaseOCL cDataTAD; CNeuronConvOCL cEmbeddingTAD; CNeuronTransposeRCDOCL cTransposeATD; CNeuronHiVTAAEncoder cAAEncoder; CNeuronTransposeRCDOCL cTransposeTAD; CNeuronLearnabledPE cPosEmbeddingTAD; CNeuronMVMHAttentionMLKV cTemporalEncoder; CNeuronLearnabledPE cPosLineEmbeddingTAD; CNeuronPatching cLineEmbeddibg; CNeuronMVCrossAttentionMLKV cALEncoder; CNeuronMLMHAttentionMLKV cGlobalEncoder; CNeuronTransposeOCL cTransposeADT; CNeuronConvOCL cDecoder[3]; // Agent * Traj * Forecast CNeuronConvOCL cProbProj; CNeuronSoftMaxOCL cProbability; // Agent * Traj CNeuronBaseOCL cForecast; CNeuronTransposeOCL cTransposeTA; //--- virtual bool Prepare(const CNeuronBaseOCL *history); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override ; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronHiVTOCL(void) {}; ~CNeuronHiVTOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, uint num_traj, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronHiVTOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
所呈现的 CNeuronHiVTOCL 对象结构包含已熟悉的可重写方法清单的声明,和一连串内部对象,我们将在实现可重写方法的算法期间探索其功能。
我们将所有内部对象声明为静态,如此我们就可将类的构造函数和析构函数留空。所有嵌套对象和变量都在 Init 方法中初始化。
bool CNeuronHiVTOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, uint num_traj, ENUM_OPTIMIZATION optimization_type, uint batch) { if(units_count < 2 || !CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * forecast, optimization_type, batch)) return false;
在方法参数中,我们接收主要常量,这些常量允许我们唯一标识初始化对象的架构。在方法主体中,我们调用父类的相关方法。如您所知,它实现了所有继承对象和变量的初始化。
请注意,我们将把所分析序列中元素数量的直接检查添加到已在父类方法实现的控制当中。在这种情况下,必须至少有 2 个。这是因为由 HiVT 算法提供的初始状态矢量化过程中,我们配以动态值进行操作。因此,为了计算数值的变化,我们需要 2 个引用:在当前、和前一个时间步。
在初始化方法中成功通过控制模块之后,我们将接收到的模块架构参数保存在局部变量当中。
iVariables = window; iHistory = units_count - 1; iForecast = forecast; iNumTraj = MathMax(num_traj, 1);
接下来,我们初始化内部对象。内部对象的初始化顺序与前馈通验算法中对象的使用顺序相呼应。这种方式令我们能够再一次贯通正在构造的算法,并确保创建对象的充分性和必要性。
首先,我们将创建一个内层对象来记录已分析环境状态的向量表示。
我要提醒您,此处单变量序列的每个独立元素在一个分离时间步的描述向量,等于所分析单变量序列数量的两倍。因为序列的每个元素都以二维空间中的运动,以及其余个体相对于被分析元素的位置变化为特征。
我们在每个时间步都为全部所分析单变量序列的每个元素创建这样的描述向量。
if(!cDataTAD.Init(0, 0, OpenCL, 2 * iVariables * iVariables * iHistory, optimization, iBatch)) return false;
请注意,在实现 HiVT 算法时,我们以三维张量构建工作,将它们的图像保存在一维数据缓冲区之中。为了在对象名称中指示当前维度,我们添加了一个 3 个字符的后缀:
- T (Time) ― 时间步的维度;
- A (Agent) ― 个体的维度(单变量时间序列);在我们的例子中,它是所分析的参数;
- D (Dimension) — 维度 f,描述单变量序列元素上的向量。
接下来,我们将用卷积层来创建结果向量描述的嵌入。
if(!cEmbeddingTAD.Init(0, 1, OpenCL, 2 * iVariables, 2 * iVariables, window_key, iVariables * iHistory, 1, optimization, iBatch)) return false;
在这种情况下,为了生成嵌入,我们用到 1 个参数矩阵,我们将其应用于多模态序列的所有元素。因此,我们将给定层的所分析模块数量表示为单变量序列数量乘以所分析历史深度的乘积。
生成嵌入之后,按照 HiVT 算法,我们需要在一个时间步内分析个体之间的局部依赖关系。如上一篇文章所述,在执行该步骤之前,我们需要转置原始数据。
if(!cTransposeATD.Init(0, 2, OpenCL, iHistory, iVariables, window_key, optimization, iBatch)) return false;
只有这样,我们才能使用注意力类来识别局部组中个体之间的依赖关系。
if(!cAAEncoder.Init(0, 3, OpenCL, window_key, window_key, heads, (heads + 1) / 2, iVariables, 2, 1, iHistory, optimization, iBatch)) return false;
请注意以下两个时刻。首先,在转置数据之后,我们将对象名称后缀中的字符序列修改为 ATD,这与数据转置层输出时三维张量的维数相对应。
其次,我们来检查注意力模块的功能。最初,它们被设计为搭配二维张量工作,其中每行代表一个单序列元素的描述向量。本质上,我们识别所分析矩阵各行之间的依赖关系 — 执行可以描述为“垂直注意力”。后来,我们引入了多模态时间序列的独立单变量序列内的依赖关系检测。在实践中,我们将原始矩阵划分为几个雷同的矩阵,每个矩阵包含较少的幺正序列。这些新矩阵继承了原始矩阵的行数,而它们的列沿它们均匀分布。结构上,这与我们的三维张量的维数一致。第一个维度表示原始数据矩阵中的行数。第二个维度表示用于独立分析的较小矩阵的数量。第三个维度表示单个序列元素的描述向量的大小。考虑到原始数据中嵌入张量的先验转置,我们将幺正序列的数量定义为当前注意力模块中所分析序列的大小。顺便,在表示变量数量的参数中指定所分析历史数据的深度。这种方式令我们能够在单一时间步内分析独立变量之间的依赖关系。
在该个体-个体依赖性分析模块的实现中,我使用了两个注意力层,为每个内层生成一个键-值张量。键-值张量中的注意力头数量是查询张量中等效参数的一半。
此外,要注意,在本例中,我们使用了配有 CNeuronHiVTAAEncoder 特征管理函数的注意力模块。
在依据局部组内个体之间的依赖关系丰富序列元素嵌入后,HiVT 算法提供了对独立幺正序列内的时间依赖关系的分析。在该阶段,我们需要将数据返回至其原始表述。
if(!cTransposeTAD.Init(0, 4, OpenCL, iVariables, iHistory, window_key, optimization, iBatch)) return false;
然后我们加上完全可训练的定位编码。
if(!cPosEmbeddingTAD.Init(0, 5, OpenCL, iVariables * iHistory * window_key, optimization, iBatch)) return false;
接下来,我们使用注意力模块 CNeuronMVMHAttentionMLKV 来识别时态依赖关系。
if(!cTemporalEncoder.Init(0, 6, OpenCL, window_key, window_key, heads, (heads + 1) / 2, iHistory, 2, 1, iVariables, optimization, iBatch)) return false;
尽管局部和时态依赖注意力模块的架构不同,但我们使用相同的参数来初始化它们。
在下一步中,HiVT 作者提议配合有关路线图的信息来丰富个体嵌入。我认为没有人会怀疑道路的状况、标记和弯道会给个体的动作留下一定的印记。在我们的例子中,没有明确的指导方针来限制所分析参数的数值变化。当然,独立振荡器是有可接受数值区域的。例如,RSI 只能取 0 到 100 范围内的数值。但这是一个孤立的案例。
故此,我们将依据我们拥有的历史数据来判定最可能的变化。我们将用实际的小轨迹分段的嵌入来替换路线图表示,即我们将用数据补片层来创建。
if(!cLineEmbeddibg.Init(0, 7, OpenCL, 3, 1, 8, iHistory - 1, iVariables, optimization, iBatch)) return false;
注意,在矢量化当前状态时,我们所用的参数变化动态覆盖一个时间步。但当嵌入实际的轨迹小分区时,我们使用 3 个元素的模块,步长为 1。以该方式,我们想辨别指标在特定步骤的动态与可能的轨迹延续之间的依赖关系。
然后,我们将完全可训练的定位编码添加到生成的嵌入之中。
if(!cPosLineEmbeddingTAD.Init(0, 8, OpenCL, cLineEmbeddibg.Neurons(), optimization, iBatch)) return false;
然后,我们据有关轨迹的信息来丰富当前的个体嵌入。为此,我们采用含有两个内层的交叉注意力模块 CNeuronMVCrossAttentionMLKV。
if(!cALEncoder.Init(0, 9, OpenCL, window_key, window_key, heads, 8, (heads + 1) / 2, iHistory, iHistory - 1, 2, 1, iVariables, iVariables, optimization, iBatch)) return false;
于此,我们看似正在按顺序执行两个类似的操作:识别时间依赖关系,和分析个体与轨迹之间的依赖关系。在这两种情况下,我们分析代理当前状态的依赖关系,并在其它时间间隔内采用同一指标的参数表示。但此处还有一行。在第一种情况下,我们比较个体在各个时间步的相似状态。在第二种情况下,我们正在应对某些覆盖稍大时间间隔的轨迹形态。
局部依赖关系分析模块就这样完成了,其本质上以综合举措丰富了个体状态嵌入。HiVT 算法的下一步是分析全局互动模块中场景的长期依赖关系。
if(!cGlobalEncoder.Init(0, 10, OpenCL, window_key*iVariables, window_key*iVariables, heads, (heads+1)/2, iHistory, 4, 2, optimization, iBatch)) return false;
此处我们用到一个含 4 个内层的注意力模块。为了分析依赖关系,我们所用的并非单独的个体表示,而是整个场景。
然后,我们需要针对即将到来的预测值序列建模。如前,针对即将到来序列的预测,是在独立单变量序列的框架内实现的。为此,我们首先需要转置当前数据。
if(!cTransposeADT.Init(0, 11, OpenCL, iHistory, window_key * iVariables, optimization, iBatch)) return false;
进而,为了预测整个规划深度的后续数值,HiVT 方法的作者建议使用一个 MLP。在我们的例子中,这项工作是在 3 个连续卷积层模块中执行的,每个卷积层都接收一个独有的所分析数据窗口,和其自己的激活函数。
if(!cDecoder[0].Init(0, 12, OpenCL, iHistory, iHistory, iForecast, window_key * iVariables, optimization, iBatch)) return false; cDecoder[0].SetActivationFunction(SIGMOID); if(!cDecoder[1].Init(0, 13, OpenCL, iForecast * window_key, iForecast * window_key, iForecast * window_key, iVariables, optimization, iBatch)) return false; cDecoder[1].SetActivationFunction(LReLU); if(!cDecoder[2].Init(0, 14, OpenCL, iForecast * window_key, iForecast * window_key, iForecast * iNumTraj, iVariables, optimization, iBatch)) return false; cDecoder[2].SetActivationFunction(TANH);
在第一阶段,我们是在单独个体状态的嵌入描述的各个元素的框架内工作,将序列的大小从所分析历史的深度,更改为规划的横向范围。
然后,我们分析整个规划横向范围内每位个体的全局依赖关系,且无需更改张量大小。
只有在最后阶段,我们才预测每个独立单变量时间序列的若干可能场景。所预测轨迹的变体数量由外部程序在方法参数中指定。
此处应当注意的是,预测若干种可能的场景是所提议方式的一个别致特点。不过,我们需要一种机制来选择最可能的轨迹。因此,我们首先将获得的轨迹投影到每位个体预测轨迹数的维度。
if(!cProbProj.Init(0, 15, OpenCL, iForecast * iNumTraj, iForecast * iNumTraj, iNumTraj, iVariables, optimization, iBatch)) return false;
然后,我们使用 SoftMax 函数将获得的投影转换至概率域。
if(!cProbability.Init(0, 16, OpenCL, iForecast * iNumTraj * iVariables, optimization, iBatch)) return false; cProbability.SetHeads(iVariables); // Agent * Traj
按其概率来为先前预测的轨迹配重,我们获得个体即将到来的平均移动轨迹。
if(!cForecast.Init(0, 17, OpenCL, iForecast * iVariables, optimization, iBatch)) return false;
现在,我们只需要将预测值转换到原始数据的维度。我们通过转置数据来实现功能。
if(!cTransposeTA.Init(0, 18, OpenCL, iVariables, iForecast, optimization, iBatch)) return false;
为了减少数据复制操作,并优化内存资源用法,我们重新定义了模块结果和误差梯度缓冲区指针,指向最后一个内部数据转置层的类似缓冲区。
SetOutput(cTransposeTA.getOutput(),true); SetGradient(cTransposeTA.getGradient(),true); //--- return true; }
然后我们将方法操作的逻辑结果返回给调用程序,完成方法操作。
类对象完成初始化工作之后,我们转到 feedForward 方法中为类构建前馈算法。
bool CNeuronHiVTOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!Prepare(NeuronOCL)) return false;
在方法参数中,我们接收一个指向包含原始数据的对象指针。我们立即将收到的指针传递给准备初始数据的 Prepare 方法。该方法是一个 “包装器”,用来调用数据矢量化内核 HiVTPrepare。我们在上一篇文章中讨论过它的算法。我们已考察过 OpenCL 程序内核的各种排队方法。Prepare 方法的算法没有任何特殊之处。因此,在本文中我将省略对其算法的描述。您可用附件中提供的代码自行研究它。
接下来,基于获得的向量表示,我们在每个独立的时间步生成个体嵌入。
if(!cEmbeddingTAD.FeedForward(cDataTAD.AsObject())) return false;
我们把它们转置。
if(!cTransposeATD.FeedForward(cEmbeddingTAD.AsObject())) return false;
然后我们在个体-个体表示的分析框架内丰富局部依赖关系。
if(!cAAEncoder.FeedForward(cTransposeATD.AsObject())) return false;
在下一步中,我们通过添加临时依赖项来丰富个体状态嵌入。为此,我们首先转置当前数据张量。
if(!cTransposeTAD.FeedForward(cAAEncoder.AsObject())) return false;
我们把定位编码标记加入其中。
if(!cPosEmbeddingTAD.FeedForward(cTransposeTAD.AsObject())) return false;
然后我们在独立个体的境况中调用我们的时态注意力模块的前馈方法。
if(!cTemporalEncoder.FeedForward(cPosEmbeddingTAD.AsObject())) return false;
时态注意力运算成功执行之后,我们获得了所分析数据的嵌入张量,丰富了局部和时态依赖性。现在我们需要依据有关可能的运动形态信息来丰富生成的嵌入。为此,我们首先创建所分析历史运动形态的嵌入。
if(!cLineEmbeddibg.FeedForward(NeuronOCL)) return false;
我们将定位编码添加到生成的形态嵌入之中。
if(!cPosLineEmbeddingTAD.FeedForward(cLineEmbeddibg.AsObject())) return false;
在交叉注意力模块中,我们用有关各种运动形态的信息丰富个体嵌入。
if(!cALEncoder.FeedForward(cTemporalEncoder.AsObject(), cPosLineEmbeddingTAD.getOutput())) return false;
我们将全局注意力模块应用于丰富个体嵌入的张量。
if(!cGlobalEncoder.FeedForward(cALEncoder.AsObject())) return false;
接下来的模块是预测即将到来的个体移动。我要提醒您,我们计划根据单变量序列预测所分析参数的后续值。因此,我们首先转置给定的数据张量。
if(!cTransposeADT.FeedForward(cGlobalEncoder.AsObject())) return false;
接下来,我们运行三层 MLP 模块的前馈通验,进行数据预测。
if(!cDecoder[0].FeedForward(cTransposeADT.AsObject())) return false; if(!cDecoder[1].FeedForward(cDecoder[0].AsObject())) return false; if(!cDecoder[2].FeedForward(cDecoder[1].AsObject())) return false;
此处我们应当记住 HiVT 方法的特殊性。MLP 预测即将到来的走势的输出不是一个,而是所分析初始序列可能延续的若干个变体。我们必须判定所预测运动的每个变体的概率。为此,我们将首先制作预测轨迹。
if(!cProbProj.FeedForward(cDecoder[2].AsObject())) return false;
使用 SoftMax 函数,我们将获得的投影转换至概率域。
if(!cProbability.FeedForward(cProbProj.AsObject())) return false;
现在我们只需将预测轨迹的张量乘以它们的概率。
if(IsStopped() || !MatMul(cDecoder[2].getOutput(), cProbability.getOutput(), cForecast.getOutput(), iForecast, iNumTraj, 1, iVariables)) return false;
结果如是,我们获得了所分析多模态序列的每个单变量序列的整个规划横向范围的平均加权轨迹张量。
在我们的前馈方法运算结束时,我们转置预测值张量,以便匹配原始数据的衡量度。
if(!cTransposeTA.FeedForward(cForecast.AsObject())) return false; //--- return true; }
如常,我们给调用程序返回一个布尔值,表明方法操作成功。
据此,我们总结了 HiVT 方法的前向通验算法的实现,并转到为我们的类开发后向通验方法。如您所知,向后通验算法由两个主要部件组成:
- 所有元素的梯度误差分布基于它们对最终结果的影响。该功能是在 calcInputGradients 方法中实现。
- 调整可训练模型参数,从而把整体损失最小化,这在 updateInputWeights 方法中执行。
我们从开发梯度误差分布方法 calcInputGradients 来开始实现后向通验算法。该方法的逻辑完全镜像前向通验算法的逻辑,只是所有操作都以相反的顺序执行。
bool CNeuronHiVTOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
作为输入参数,该方法接收指向上一层对象的指针 — 在前馈通验期间提供输入数据的同一层。不过,在这种情况下,我们需要将误差梯度传回给它,确保它反映了原始输入数据对最终结果的影响。
在方法主体中,我们立即检查接收指针的相关性。如果指针无效,则执行方法操作将毫无意义。
成功通过验证检查之后,我们将继续相应地分派误差梯度。
在当前层的输出级别,误差梯度已存储在我们类的相应缓冲区当中。它是在后续层中执行等效方法期间记录在那里的。由于先前实现的缓冲区交换机制,所需的误差梯度在最终数据转置层的缓冲区中已就绪。自此处,我们开始将误差梯度传播到单变量时间序列的加权平均预测轨迹层的级别。
if(!cForecast.calcHiddenGradients(cTransposeTA.AsObject())) return false;
如您所忆,在前向通验中,我们通过将若干个预测轨迹的张量乘以相应的概率向量来获得加权平均轨迹。相应地,在反向传播通验过程中,我们必须在预测轨迹集的张量和概率向量上分派误差梯度。
if(IsStopped() || !MatMulGrad(cDecoder[2].getOutput(), cDecoder[2].getGradient(), cProbability.getOutput(), cProbability.getGradient(), cForecast.getGradient(), iForecast, iNumTraj, 1, iVariables)) return false;
我们将概率误差梯度传递给预测轨迹的投影层。
if(!cProbProj.calcHiddenGradients(cProbability.AsObject())) return false;
为了获得投影,我们使用了预测轨迹本身。在此之后,我们典型情况下会将误差梯度传递到预测轨迹级别。
不过,重点要注意,预测轨迹集的误差梯度已经从上一步的加权平均轨迹中传递过来。直接调用相应层的 calcHiddenGradients 方法将覆盖之前传送的误差梯度,即用新值替换缓冲区。如此这般,我们典型情况下会用到辅助数据缓冲区,汇总来自两个数据流的数值,以保留所有信息。然而,在这个特定实例中,我决定不将误差梯度进一步传递到数据投影层。这种方式的目标是保持对后续轨迹的预测“干净”,防止由独立轨迹的相关性有关的概率分布误差引起扭曲。
代之,我们将预测轨迹的误差梯度传播到预测模块的 MLP 层。
if(!cDecoder[1].calcHiddenGradients(cDecoder[2].AsObject())) return false; if(!cDecoder[0].calcHiddenGradients(cDecoder[1].AsObject())) return false;
我们转置得到的误差梯度张量,并将其传递给全局互动模块。
if(!cTransposeADT.calcHiddenGradients(cDecoder[0].AsObject())) return false; if(!cGlobalEncoder.calcHiddenGradients(cTransposeADT.AsObject())) return false; if(!cALEncoder.calcHiddenGradients(cGlobalEncoder.AsObject())) return false;
然后从全局互动模块中,误差梯度被传递到局部依赖性分析模块。
如是提醒,该模块对各个局部对象之间的相互依赖关系进行全面分析。在此,我们首先将接收到的误差梯度经由个体-轨迹交叉注意力模块,往下直至时态依赖分析和运动形态嵌入的定位编码级别。
if(!cTemporalEncoder.calcHiddenGradients(cALEncoder.AsObject(), cPosLineEmbeddingTAD.getOutput(), cPosLineEmbeddingTAD.getGradient(), (ENUM_ACTIVATION)cPosLineEmbeddingTAD.Activation())) return false;
我们经由定位编码操作传播误差梯度。
if(!cLineEmbeddibg.calcHiddenGradients(cPosLineEmbeddingTAD.AsObject())) return false;
然后我们将其传递到源数据级别。
if(!NeuronOCL.calcHiddenGradients(cLineEmbeddibg.AsObject())) return false;
对于第二个数据流,我们首先通过时态依赖性分析模块传播误差梯度。
if(!cPosEmbeddingTAD.calcHiddenGradients(cTemporalEncoder.AsObject())) return false;
之后,我们在定位编码运算中调整获得的误差梯度。
if(!cTransposeTAD.calcHiddenGradients(cPosEmbeddingTAD.AsObject())) return false;
然后我们转置数据,并经由个体-个体依赖性分析模块传播梯度。
if(!cAAEncoder.calcHiddenGradients(cTransposeTAD.AsObject())) return false; if(!cTransposeATD.calcHiddenGradients(cAAEncoder.AsObject())) return false;
在方法运算结束时,我们将数据转置为原始表示,并通过嵌入生成层将误差梯度传播到原始数据的向量表示。
if(!cEmbeddingTAD.calcHiddenGradients(cTransposeATD.AsObject())) return false; if(!cDataTAD.calcHiddenGradients(cEmbeddingTAD.AsObject())) return false; //--- return true; }
如常,我们向调用程序返回一个布尔值,指示方法操作的执行结果。
在该阶段,我们根据误差梯度对最终结果的影响,将误差梯度分派给所有模型单元。现在,我们需要调整可训练模型参数,以便把总体误差最小化。该功能在 updateInputWeights 方法中实现。
重点需注意,我们的新类 CNeuronHiVTOCL 的所有可训练参数都存储在其内部对象当中。不过,并非所有内部对象都包含可训练的参数。例如,数据转置层不包括它们。因此,在该方法中,我们只与包含可训练参数的对象进行互动。为了调整它们,只需调用每个内部对象的相应方法足矣。
如您所见,该方法的逻辑非常简单,故在本文中我们不会提供其完整代码。您可用附件中提供的代码自行研究它。附件还包括新类,及其所有方法的完整源代码。
2. 模型架构
我们已经完成了 CNeuronHiVTOCL 类及其方法的开发。该类实现了我们对 HiVT 方法作者所提议方式的解释。现在,是时候将新对象集成到我们的模型架构当中了。
如前,我们将所分析多模态序列未来运动的预测对象合并到环境状态编码器模型之中。该模型的架构设计在 CreateEncoderDescriptions 方法中定义。该方法接收指向动态数组对象的指针,我们在其中记录生成的模型架构。
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
在方法主体中,我们检查接收指针的相关性,并在必要时创建动态数组的新实例。之后,我们转至针对模型每一层的架构方案进行顺序描述。
为了获得初始数据,我们使用足够大小的全连接基层。
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
我们计划将原生的、未处理的数据输入到模型当中。为了将这些数据转换为可比较的形式,我们使用批量归一化层。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
初始处理之后,我们立即将原始数据传送到使用 HiVT 方法构建的新模块。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronHiVTOCL; { int temp[] = {BarDescr, NForecast, 6}; // {Variables, Forecast, NumTraj} ArrayCopy(descr.windows, temp); } descr.window_out = EmbeddingSize; // Inside Dimension descr.count = HistoryBars; // Units descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
在此,我们实际上重复了以前工作中的类似参数。只添加了 1 个新的模块参数,它判定所预测轨迹的变体数量。在本例中,我们取 6。
在 CNeuronHiVTOCL 模块的输出中,我们期望收到所分析多模态时间序列的现成预测值。但有一个警告。为了规划具有多模态时间序列的模型有效运行,我们将其所有数值转换为可比较的形式。相应地,我们获得的预测值也按类似形式。为了令获得的预测值与原始数据的正常数值保持一致,我们将向它们添加在原始数据归一化期间删除的分布统计参数。
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
之后,我们将在频域中校正获得的结果。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
参与者和评论者模型的架构保持不变。模型训练计划亦如此。因此,我们不会在本文的框架内详论它们。不过,本研究中用到的所有程序的完整源代码都可在随附的素材中找到,以供进一步探索。
3. 测试
我们已完成了对 HiVT 方法的解释实现。现在是时候评估我们解决方案的有效性了。首先,我们需要在真实的历史数据上训练模型,然后在不属于训练集的数据集上测试已训练模型。
对于训练,我们采用 EURUSD 的 2023 年全年 H1 时间帧的历史 数据。
训练离线进行。因此,我们首先需要编译所需的训练数据集。有关该过程的更多详细信息,请参阅我们关于 真实-ORL 方法的文章。为了训练我们的环境状态编码器,我们用到先前模型运行期间收集的数据集。
如您所知,状态编码器模型仅适用于历史价格走势数据和分析指标,其独立于个体的动作。因此,在该阶段,没有必要定期更新训练数据集,因为新添加的轨迹不会为编码器提供额外的信息。我们继续训练过程,直至达成预期结果。
训练模型的测试结果如下所示。
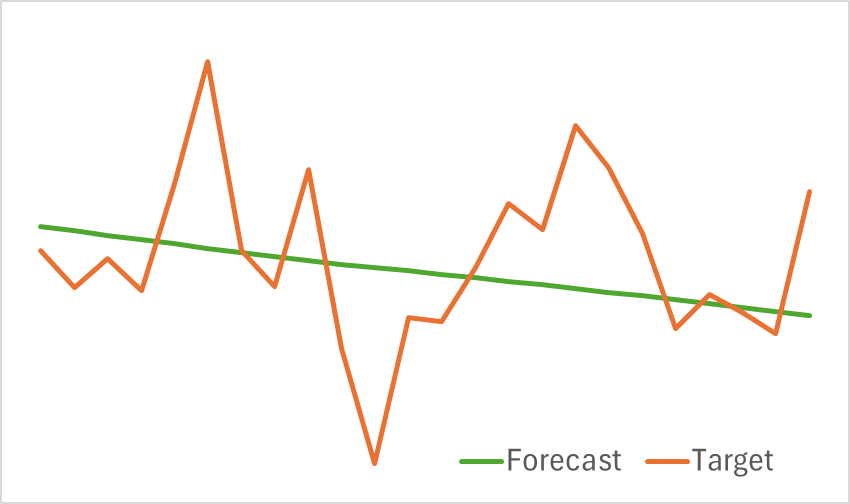
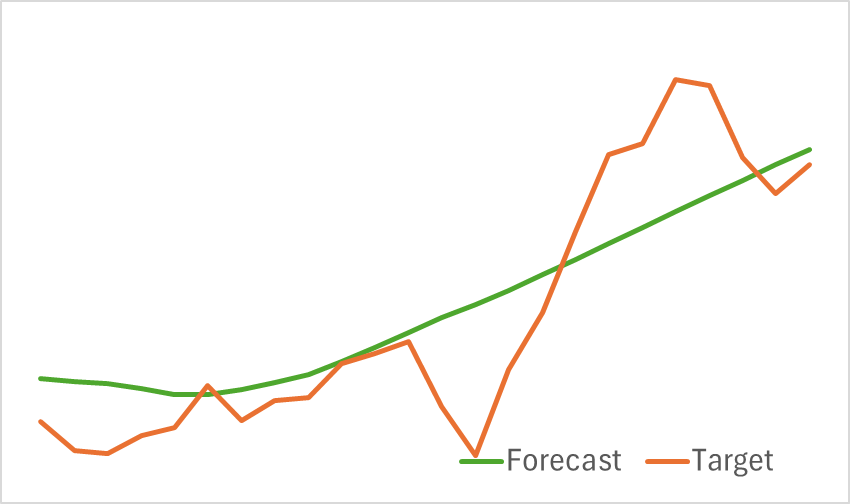
从提供的图表中可见,我们的模型有效地捕捉了即将到来的价格走势的关键趋势。
接下来,我们进入训练的第二阶段,重点是训练参与者的盈利最大化行为政策,和评论者的奖励函数。不像编码器,参与者的训练在很大程度上取决于它在环境中执行的动作。为了确保有效的学习,我们必须保持训练数据集最新。因此,我们会定期更新数据集,从而反映参与者的当前政策。
训练会持续,直至模型的误差稳定在某个水平。此刻,进一步的数据集更新对于优化参与者的政策不再具有贡献。
我们利用 MetaTrader 5 策略测试器评估训练模型的有效性,应用 2024 年 1 月的历史数据,同时保持所有其它参数不变。训练模型的测试结果如下所示。
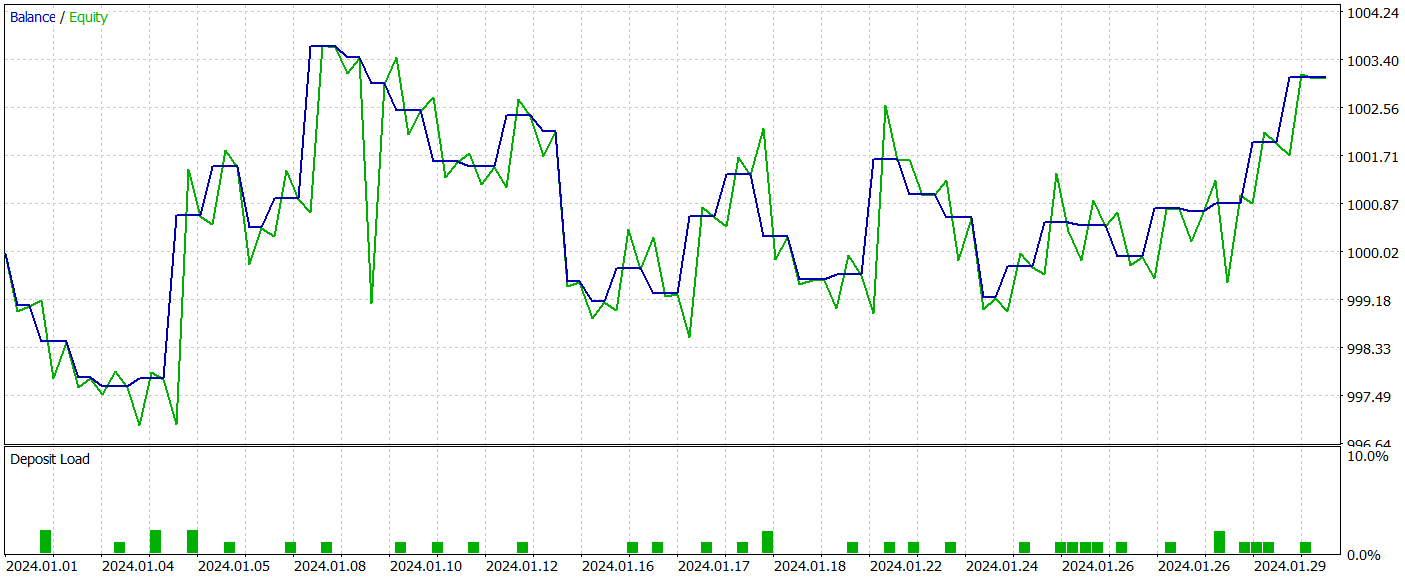
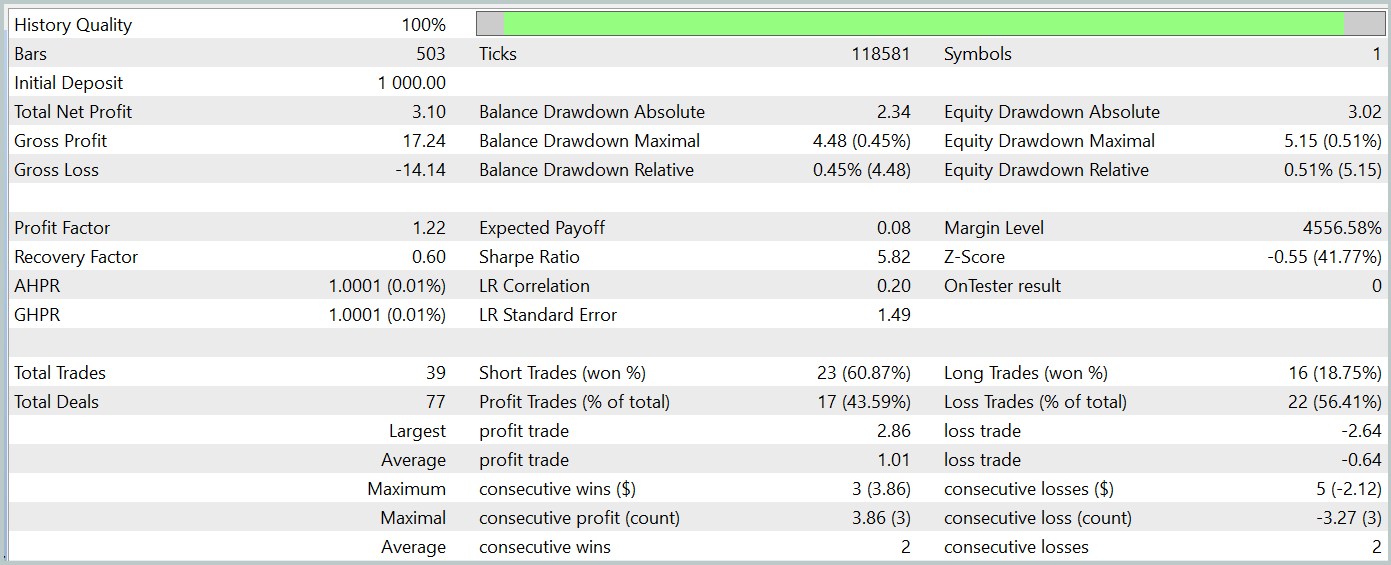
正如结果所示,我们的训练过程成功地产生了一个能够在训练和测试数据上均产生盈利的参与者政策。在测试期间,该模型执行了 39 笔交易,其中超过 43% 的交易以盈利收场。盈利交易的比例略低于亏损交易。然而,每笔交易的平均和最大盈利均超过了相应亏损,令模型能够以较小的净盈利完成测试。盈利因子记录为 1.22。
不过,重点要注意,由于观察到的余额线缺乏明确的趋势,并且交易数量有限,因此获得的结果可能无法代表全部。
结束语
在本文中,我们成功实现了 MQL5 版本的 HiVT 方法。我们将所提议算法集成到环境状态编码器模型之中。然后,我们继续训练和测试模型。测试结果表明,HiVT 方法有效地捕捉到市场趋势。它还提供了足够的预测品质水平,支持个体制定可盈利的交易政策。
参考
文章中所用程序
| # | 发行 | 类型 | 说明 |
|---|---|---|---|
| 1 | Research.mq5 | 智能系统 | 收集样本的 EA |
| 2 | ResearchRealORL.mq5 | 智能系统 | 利用 Real ORL方法收集样本的 EA |
| 3 | Study.mq5 | 智能系统 | 模型训练 EA |
| 4 | StudyEncoder.mq5 | 智能系统 | 编码器训练 EA |
| 5 | Test.mq5 | 智能系统 | 模型测试 EA |
| 6 | Trajectory.mqh | 类库 | 系统状态描述结构 |
| 7 | NeuroNet.mqh | 类库 | 创建神经网络的类库 |
| 8 | NeuroNet.cl | 函数库 | OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/15713
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 您应当知道的 MQL5 向导技术(第 36 部分):依据马尔可夫(Markov)链的 Q-学习
您应当知道的 MQL5 向导技术(第 36 部分):依据马尔可夫(Markov)链的 Q-学习
 美元和欧元指数图表 — MetaTrader 5 服务示例
美元和欧元指数图表 — MetaTrader 5 服务示例
 创建 MQL5-Telegram 集成 EA 交易(第 4 部分):模块化代码函数以增强可重用性
创建 MQL5-Telegram 集成 EA 交易(第 4 部分):模块化代码函数以增强可重用性
 在任何市场中获得优势(第五部分):联邦储备经济数据库(FRED)欧元兑美元( EURUSD)可替代数据
在任何市场中获得优势(第五部分):联邦储备经济数据库(FRED)欧元兑美元( EURUSD)可替代数据