
Neuronale Netze im Handel: Eine komplexe Methode zur Vorhersage einer Trajektorie (Traj-LLM)
Einführung
Die Vorhersage künftiger Preisbewegungen auf den Finanzmärkten spielt eine entscheidende Rolle bei den Entscheidungsprozessen der Händler. Hochwertige Prognosen ermöglichen es den Händlern, fundiertere Entscheidungen zu treffen und Risiken zu minimieren. Die Vorhersage künftiger Preisentwicklungen ist jedoch aufgrund der chaotischen und stochastischen Natur der Märkte mit zahlreichen Herausforderungen verbunden. Selbst die fortschrittlichsten Prognosemodelle sind oft nicht in der Lage, alle Faktoren, die die Marktdynamik beeinflussen, angemessen zu berücksichtigen, wie z. B. plötzliche Veränderungen im Verhalten der Teilnehmer oder unerwartete externe Ereignisse.
In den letzten Jahren hat die Entwicklung der künstlichen Intelligenz, insbesondere im Bereich der großen Sprachmodelle (LLMs), neue Wege für die Lösung einer Vielzahl komplexer Aufgaben eröffnet. LLMs haben bemerkenswerte Fähigkeiten bei der Verarbeitung komplexer Informationen und der Modellierung von Szenarien gezeigt, die dem menschlichen Denken ähneln. Diese Modelle werden erfolgreich in verschiedenen Bereichen eingesetzt, von der Verarbeitung natürlicher Sprache bis hin zur Vorhersage von Zeitreihen, was sie zu vielversprechenden Instrumenten für die Analyse und Vorhersage von Marktbewegungen macht.
Ich möchte Ihnen den Traj-LLM-Algorithmus vorstellen, der in der Veröffentlichung „Traj-LLM: A New Exploration for Empowering Trajectory Prediction with Pre-trained Large Language Models“ vorgestellt wurde. Traj-LLM wurde entwickelt, um Aufgaben im Bereich der Vorhersage der Trajektorie für autonome Fahrzeuge zu lösen. Die Autoren schlagen vor, LLMs zu verwenden, um die Genauigkeit und Anpassungsfähigkeit der Vorhersage zukünftiger Trajektorien von Verkehrsteilnehmern zu verbessern.
Darüber hinaus kombiniert Traj-LLM die Leistungsfähigkeit großer Sprachmodelle mit innovativen Ansätzen zur Modellierung zeitlicher Abhängigkeiten und Interaktionen zwischen Objekten und ermöglicht so genauere Prognose der Trajektorie auch unter komplexen und dynamischen Bedingungen. Dieses Modell verbessert nicht nur die Vorhersagegenauigkeit, sondern bietet auch neue Möglichkeiten, mögliche Zukunftsszenarien zu analysieren und zu verstehen. Wir gehen davon aus, dass die Anwendung der von den Autoren vorgeschlagenen Methodik zur Bewältigung unserer Aufgaben beitragen und die Qualität unserer Prognosen für künftige Preisentwicklungen verbessern wird.
1. Traj-LLM-Algorithmus
Die Traj-LLM-Architektur besteht aus vier integralen Komponenten:
- Lückenhafte kontextuelle gemeinsame Kodierung,
- Modellierung der Interaktion auf hoher Ebene,
- Fahrbahnbezogenes, probabilistisches Lernen,
- Laplace-Multimodal-Dekoder.
Die Autoren der Methode Traj-LLM schlagen vor, die Fähigkeiten von LLM für die Fahrbahnvorhersage zu nutzen, wodurch die Notwendigkeit einer expliziten Echtzeit-Merkmalstechnik entfällt. Die spärliche, kontextuelle, gemeinsame Kodierung transformiert zunächst Agenten- und Szenenmerkmale in eine Form, die von LLMs interpretiert werden kann. Diese Repräsentationen werden dann in vortrainierte LLMs eingegeben, um die Interaktionsmodellierung auf hoher Ebene durchzuführen. Zur Nachahmung menschenähnlicher kognitiver Funktionen und zur weiteren Verbesserung des Szeneverständnisses in Traj-LLM wird ein fahrbahnbezogenes, probabilistisches Lernen über ein Mamba-Modul eingeführt. Schließlich wird der multimodale Laplace-Decoder eingesetzt, um zuverlässige Vorhersagen zu erstellen.
Der erste Schritt in Traj-LLM ist die Codierung der raum-zeitlichen Rohdaten der Szene, wie z.B. Agentenstatus und Fahrbahninformationen. Für jede dieser Schichten wird ein Einbettungsmodell mit einer rekurrenten Schicht und einem MLP verwendet, um mehrdimensionale Merkmale zu extrahieren. Die resultierenden Tensoren hi und fl werden dann an ein Fusion-Submodul weitergeleitet, das den komplexen Informationsaustausch zwischen Agentenzuständen und Fahrbahn in lokalisierten Bereichen ermöglicht. Bei diesem Prozess wird ein Token-Einbettungsmechanismus verwendet, der sich an die Architektur von LLM anpasst.
Der Fusionsprozess verwendet einen mehrköpfigen Selbstbeobachtungsmechanismus, um die Merkmale Agent-Agent zusammenzuführen. Darüber hinaus umfasst die Zusammenführung der Funktionen von Agent-Fahrbahn und Fahrbahn-Agent die Aktualisierung der Ansichten von Agent und Fahrbahn unter Verwendung eines mehrköpfigen Kreuzaufmerksamkeits-Mechanismus mit Skip-Verbindungen. Formal kann dieser Prozess wie folgt dargestellt werden:

Danach werden hi und fl kombiniert, um spärliche kontextuelle gemeinsame Kodierungen gi zu bilden, die intuitiv die Abhängigkeiten erfassen, die für die lokalen rezeptiven Felder der vektorisierten Entitäten relevant sind. Dieser Kodierungsansatz soll LLMs in die Lage versetzen, Trajektoriendaten effektiv zu interpretieren und so die Fähigkeiten von LLMs zu erweitern.
Trajektorienübergänge folgen Mustern, die durch übergeordnete Bedingungen bestimmt werden, die von verschiedenen Szenenelementen abgeleitet werden. Um diese Wechselwirkungen zu untersuchen, erforschen die Autoren die Fähigkeit von LLMs, Abhängigkeiten zu modellieren, die mit Aufgaben zur Vorhersage von Trajektories verbunden sind. Trotz der Ähnlichkeiten zwischen Trajektoriendaten und natürlichsprachlichen Texten gilt die direkte Verwendung von LLMs zur Verarbeitung spärlicher kontextueller gemeinsamer Kodierungen als ineffizient. Denn die vortrainierten LLMs sind in erster Linie für Textdaten optimiert. Ein alternativer Vorschlag ist eine umfassende Umschulung aller LLMs. Dieser Prozess erfordert beträchtliche Rechenressourcen, sodass er kaum durchführbar ist. Eine andere, effektivere Lösung ist die Verwendung der Methode der parametereffizienten Feinabstimmung (PEFT) zur Feinabstimmung von vortrainierten LLMs.
Die Autoren von Traj-LLM verwenden Parameter aus vortrainierten NLP-Transformer-Architekturen, insbesondere GPT-2, für die Interaktionsmodellierung auf hoher Ebene. Sie schlagen vor, alle bereits trainierten Parameter einzufrieren und neue, trainierbare Parameter mit Hilfe einer Low-Rank-Adaptation-Technik (LoRA) einzuführen. LoRA wird auf die Entitäten Abfrage (Query) und Schlüssel (Key) des LLM-Aufmerksamkeitsmechanismus angewendet.
So werden die spärlichen, kontextuellen, gemeinsamen Kodierungen gi in ein LLM eingegeben, das aus einer Reihe von vortrainierten Transformer-Blöcken besteht, die mit LoRA verbessert wurden. Dieses Verfahren führt zu hochrangigen Interaktionsdarstellungen zi.
![]()
Die Ausgaben des vortrainierten LLM werden über ein MLP transformiert, um den Dimensionen von gi zu entsprechen, was zu den endgültigen Interaktionszuständen si auf hoher Ebene führt.
Die meisten erfahrenen Fahrer konzentrieren sich auf eine begrenzte Anzahl relevanter Fahrbahnabschnitte, die ihr künftiges Handeln maßgeblich beeinflussen. Um diese menschenähnliche, kognitive Funktion nachzubilden und das Verständnis der Szene in Traj-LLM weiter zu verbessern, verwenden die Autoren der Methode ein fahrbahnbezogenes, probabilistisches Lernen, um die Wahrscheinlichkeit des Abgleichs von Bewegungszuständen mit Fahrbahnsegmenten kontinuierlich zu bewerten. Das Modell gleicht die Trajektorie des Zielagenten in jedem Zeitschritt t∈{1,…,tf} mithilfe einer Mamba-Schicht mit den Fahrbahninformationen ab. Als selektives strukturiertes Zustandsraummodell (SSM) verfeinert und verallgemeinert Mamba die relevanten Informationen. Dies ist vergleichbar mit der Art und Weise, wie menschliche Autofahrer wichtige Hinweise aus der Umgebung, z. B. mögliche Fahrbahnen, selektiv verarbeiten, um ihre Entscheidungen zu treffen.
In der vorgeschlagenen Architektur umfasst die Mamba-Schicht einen Mamba-Block, eine dreischichtige Normalisierung und ein positionsbezogenes Vorwärtsdurchgangsnetz. Der Mamba-Block erweitert zunächst die Dimensionalität durch lineare Projektionen und erzeugt so unterschiedliche Darstellungen für zwei parallele Datenströme. Ein Zweig durchläuft eine Faltung und SiLU-Aktivierung, um fahrbahnbezogene Abhängigkeiten zu erfassen. Im Kern enthält der Mamba-Block ein selektives Zustandsraummodell mit diskretisierten Parametern, die auf den Eingangsdaten basieren. Um die Stabilität zu verbessern, werden Instanznormalisierung und Restverbindungen hinzugefügt, was zu latenten Repräsentationen führt.
Anschließend verbessert ein positionsbezogenes Vorwärtsdurchgangsnetz die Modellierung von fahrbahngetreuen Bewertungen in der verborgenen Dimension. Auch hier werden Instanznormalisierung und Restverbindungen angewandt, um fahrbahnbezogenen Trainingsvektoren zu erzeugen, die dann an eine MLP-Schicht weitergegeben werden.
Wie bereits erwähnt, konzentrieren sich erfahrene Fahrer auf wichtige Fahrbahnsegmente, um effiziente Entscheidungen zu treffen. Daher werden die besten Kandidatenfahrbahnen sorgfältig ausgewählt und zu einem Satz ℳ zusammengefasst.
Das fahrbahnbezogene, probabilistische Lernen wird als Klassifizierungsaufgabe modelliert, wobei der binäre Kreuzentropieverlust ℒlane zur Optimierung der Wahrscheinlichkeitsschätzung verwendet wird.
Die Visualisierung der Autoren der Methode Traj-LLM ist unten dargestellt.
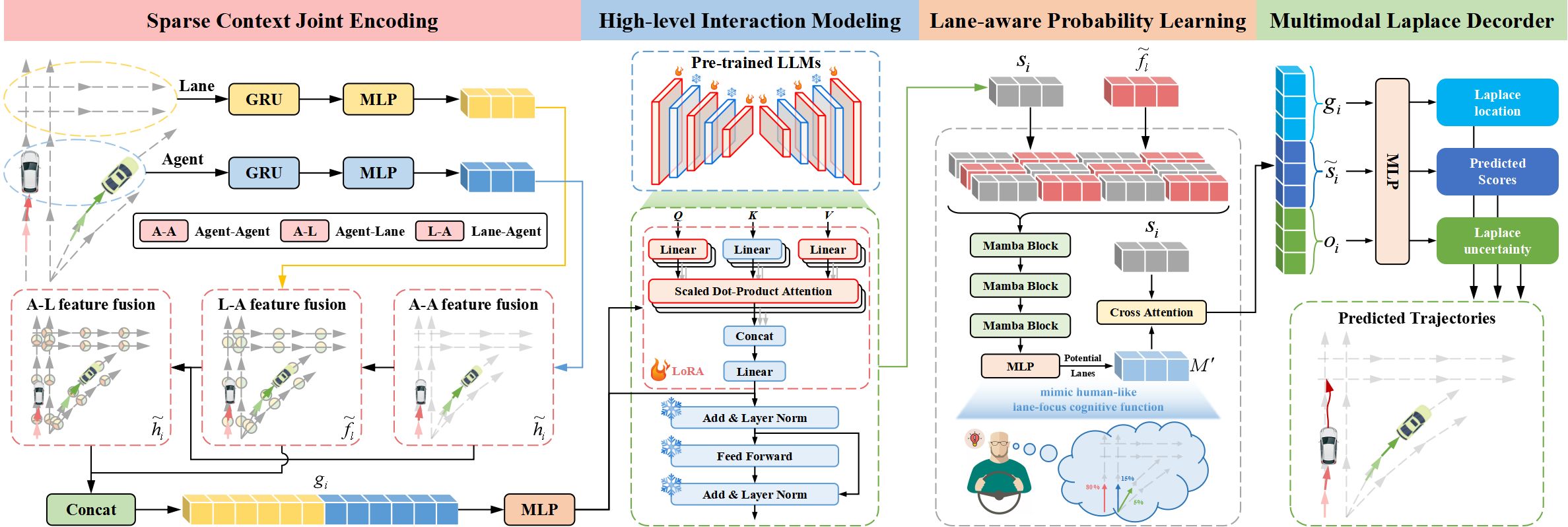
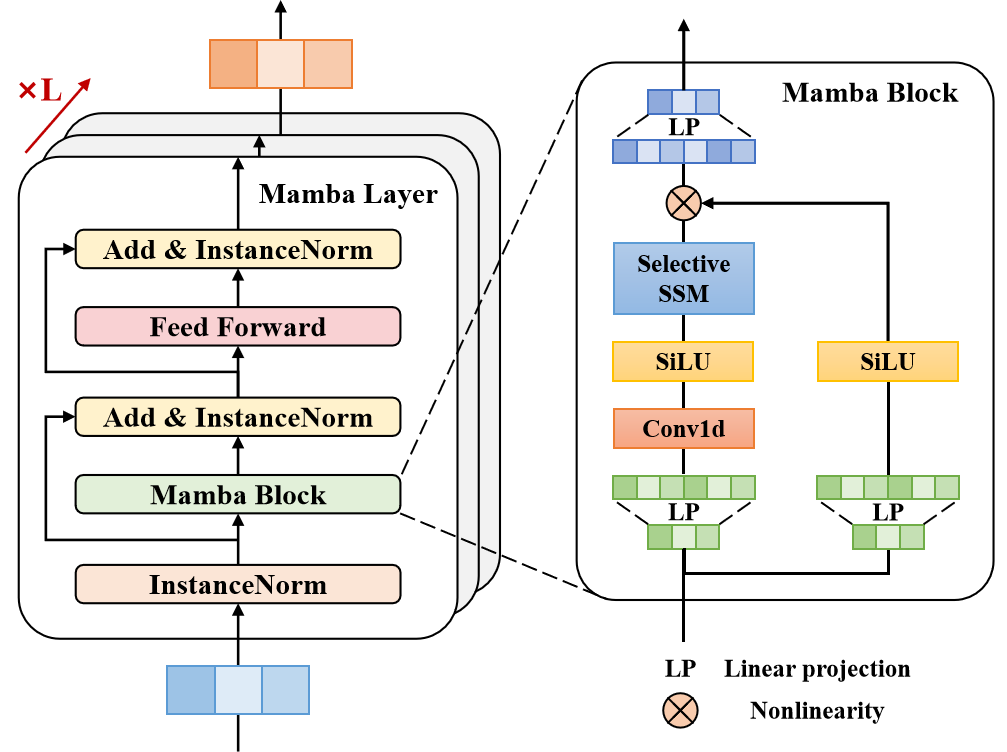
2. Implementation in MQL5
Nach der Besprechung der theoretischen Aspekte der Methode Traj-LLM gehen wir zum praktischen Teil unseres Artikels über, in dem wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umsetzen. Der Algorithmus Traj-LLM ist ein komplexer Rahmen, der mehrere architektonische Komponenten integriert, von denen wir einige bereits in früheren Arbeiten kennengelernt haben. So können wir bei der Konstruktion des Algorithmus auf bestehende Module zurückgreifen. Es werden jedoch zusätzliche Änderungen erforderlich sein.
2.1 Anpassen des Algorithmus-Blocks von LSTM
Schauen wir uns die oben dargestellte Visualisierung der Methode Traj-LLM an. Die rohen Eingabedaten durchlaufen zunächst den spärlichen, kontextuellen, gemeinsamen Kodierungsblock, der eine rekurrente Schicht und einen MLP umfasst. Unsere Bibliothek enthält bereits die rekurrente Schicht CNeuronLSTMOCL. Sie verarbeitet jedoch die Eingabedaten als eine einzige, einheitliche Darstellung des Umweltzustands. Im Gegensatz dazu schlagen die Autoren der Methode eine unabhängige Kodierung der einzelnen Agenten und Fahrbahnzustände vor. Daher müssen wir für jeden Datenkanal eine unabhängige Kodierung organisieren. Nun, wir könnten für jeden Kanal ein eigenes CNeuronLSTMOCL-Objekt instanziieren. Dies würde jedoch zu einer unkontrollierbaren Zunahme der internen Objekte und der sequenziellen Verarbeitung führen, was sich negativ auf die Leistung des Modells auswirken würde.
Eine zweite Lösung besteht darin, die bestehende rekurrente Schichtklasse CNeuronLSTMOCL zu modifizieren. Dies erfordert Änderungen auf der Seite von OpenCL. Der Vorwärtsdurchgang unserer rekurrenten Schicht ist im Kernel LSTM_FeedForward implementiert. Um Operationen in univariaten Sequenzen zu implementieren, werden wir keine Änderungen an den externen Parametern des Kernels vornehmen. Um die parallele Verarbeitung von Daten einzelner univariater Sequenzen zu organisieren, werden wir dem Aufgabenraum eine weitere Dimension hinzufügen.
__kernel void LSTM_FeedForward(__global const float *inputs, int inputs_size, __global const float *weights, __global float *concatenated, __global float *memory, __global float *output) { uint id = (uint)get_global_id(0); uint total = (uint)get_global_size(0); uint id2 = (uint)get_local_id(1); uint idv = (uint)get_global_id(2); uint total_v = (uint)get_global_size(2);
Ich möchte daran erinnern, dass die Funktionsweise des LSTM-Blocks auf vier Entitäten basiert, deren Werte von internen Schichten errechnet werden:
- Forget Gate — verantwortlich für das Verwerfen von irrelevanten Informationen
- Input Gate — zuständig für die Aufnahme neuer Informationen
- Output Gate — verantwortlich für die Erzeugung des Ausgangssignals
- New Content — stellt die Kandidatenwerte für die Aktualisierung des Zellstatus dar
Der Algorithmus zur Berechnung dieser Einheiten ist einheitlich und folgt der Struktur einer vollständig verbundenen Schicht. Der einzige Unterschied liegt in den Aktivierungsfunktionen, die auf jeder Stufe angewendet werden. Daher haben wir in unserer Implementierung die Berechnung dieser Entitäten so konzipiert, dass sie in parallelen Threads innerhalb einer Arbeitsgruppe verarbeitet werden. Um den Datenaustausch zwischen Threads zu ermöglichen, verwenden wir ein Array, das dem lokalen Speicher zugeordnet ist.
__local float Temp[4];
Als Nächstes definieren wir die Verschiebungskonstanten in den globalen Datenpuffern.
float sum = 0; uint shift_in = idv * inputs_size; uint shift_out = idv * total; uint shift = (inputs_size + total + 1) * (id2 + id);
Bitte beachten Sie die folgenden Punkte. Wir implementieren den Prozess der Arbeit des rekurrenten Blocks mit unabhängigen Kanälen. Nach der Konstruktionslogik des Algorithmus Traj-LLM enthalten jedoch alle unabhängigen Informationskanäle vergleichbare Daten, ob es sich nun um Informationen über den Zustand verschiedener Agenten oder über vorhandene Verkehrsfahrbahnen handelt. Daher ist es logisch, eine einzige Gewichtsmatrix zu verwenden, um Informationen aus verschiedenen Datenkanälen zu kodieren, was es uns ermöglicht, vergleichbare Einbettungen am Ausgang zu erhalten.
Die Kanalkennung wirkt sich also auf den Offset in den Quell- und Ergebnispuffern aus. Dies hat jedoch keine Auswirkungen auf die Verschiebung der Gewichtsmatrix.
Als Nächstes erstellen wir eine Schleife zur Berechnung der gewichteten Summe der verborgenen Zustände.
for(uint i = 0; i < total; i += 4) { if(total - i > 4) sum += dot((float4)(output[shift_out + i], output[shift_out + i + 1], output[shift_out + i + 2], output[shift_out + i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += output[shift_out + k] * weights[shift + k]; }
Und wir fügen den Einfluss der Eingabedaten hinzu.
shift += total; for(uint i = 0; i < inputs_size; i += 4) { if(total - i > 4) sum += dot((float4)(inputs[shift_in + i], inputs[shift_in + i + 1], inputs[shift_in + i + 2], inputs[shift_in + i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += inputs[shift_in + k] * weights[shift + k]; } sum += weights[shift + inputs_size];
Wir wenden die entsprechende Aktivierungsfunktion auf den erhaltenen Wert an.
if(isnan(sum) || isinf(sum)) sum = 0; if(id2 < 3) sum = Activation(sum, 1); else sum = Activation(sum, 0);
Danach speichern wir die Ergebnisse der Operationen und synchronisieren die Arbeitsgruppen-Threads.
Temp[id2] = sum; concatenated[4 * shift_out + id2 * total + id] = sum; //--- barrier(CLK_LOCAL_MEM_FENCE);
Jetzt müssen wir nur noch das Ergebnis der Arbeit des LSTM-Blocks berechnen, das gleichzeitig der verborgene Zustand einer bestimmten Zelle ist.
if(id2 == 0) { float mem = memory[shift_out + id + total_v * total] = memory[shift_out + id]; float fg = Temp[0]; float ig = Temp[1]; float og = Temp[2]; float nc = Temp[3]; //--- memory[shift_out + id] = mem = mem * fg + ig * nc; output[shift_out + id] = og * Activation(mem, 0); } }
Die Ergebnisse der Operationen werden in den entsprechenden Elementen der globalen Datenpuffer gespeichert.
Ähnliche Änderungen haben wir an den Kerneln der Rückwärtsdurchgänge vorgenommen. Die wichtigsten davon waren im Kernel LSTM_HiddenGradient. Wie beim Vorwärts-Kernel ändern wir die Zusammensetzung der externen Parameter nicht und passen nur den Aufgabenbereich an.
__kernel void LSTM_HiddenGradient(__global float *concatenated_gradient, __global float *inputs_gradient, __global float *weights_gradient, __global float *hidden_state, __global float *inputs, __global float *weights, __global float *output, const int hidden_size, const int inputs_size) { uint id = get_global_id(0); uint total = get_global_size(0); uint idv = (uint)get_global_id(1); uint total_v = (uint)get_global_size(1);
Alle unabhängigen Kanäle arbeiten mit einer Gewichtsmatrix. Daher müssen wir für die Gewichtungskoeffizienten die Fehlergradienten aus allen unabhängigen Kanälen sammeln. Jeder Datenkanal arbeitet in einem eigenen Thread, den wir zu Arbeitsgruppen zusammenfassen werden. Für den Datenaustausch zwischen Threads wird ein Array im lokalen Speicher verwendet.
__local float Temp[LOCAL_ARRAY_SIZE]; uint ls = min(total_v, (uint)LOCAL_ARRAY_SIZE);
Als Nächstes definieren wir Offsets in den Datenpuffern.
uint shift_in = idv * inputs_size; uint shift_out = idv * total; uint weights_step = hidden_size + inputs_size + 1;
Wir erstellen eine Schleife über den verketteten Puffer der Eingabedaten. Zunächst aktualisieren wir nur den verborgenen Zustand.
for(int i = id; i < (hidden_size + inputs_size); i += total) { float inp = 0; if(i < hidden_size) { inp = hidden_state[shift_out + i]; hidden_state[shift_out + i] = output[shift_out + i]; }
Und dann bestimmen wir den Fehlergradienten auf der Eingangsebene.
else { inp = inputs[shift_in + i - hidden_size]; float grad = 0; for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; grad += temp * (1 - temp) * weights[i + g * weights_step]; } for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; grad += temp * (1 - pow(temp, 2.0f)) * weights[i + g * weights_step]; } inputs_gradient[shift_in + i - hidden_size] = grad; }
Hier berechnen wir auch den Fehlergradienten auf der Gewichtsebene. Zunächst setzen wir die Werte des lokalen Arrays zurück.
for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE);
Achten Sie darauf, die Arbeit der Arbeitsgruppen-Threads zu synchronisieren.
Als Nächstes wird der Gesamtfehlergradient aus allen Datenkanälen ermittelt. Im ersten Schritt speichern wir einzelne Werte in einem lokalen Array.
for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - temp) * inp; barrier(CLK_LOCAL_MEM_FENCE); }
Wir gehen davon aus, dass es in den analysierten Daten eine relativ geringe Anzahl unabhängiger Kanäle geben wird. Daher sammeln wir die Summe der Array-Werte in einem Thread und speichern dann den resultierenden Wert im globalen Datenpuffer.
if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[i + g * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); }
In ähnlicher Weise erfassen wir den Fehlergradienten für die Gewichte von New Content.
for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[4 * shift_out + g]; if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE); for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - pow(temp, 2.0f)) * inp; barrier(CLK_LOCAL_MEM_FENCE); } if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[i + g * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); } }
Dabei ist zu beachten, dass wir bei der Ausführung der Hauptschleifenoperationen die Bayes'schen Verzerrungsgewichtungsfaktoren aus den Augen verloren haben. Um die entsprechenden Fehlergradienten zu berechnen, führen wir zusätzliche Operationen nach dem obigen Schema durch.
for(int i = id; i < 4 * hidden_size; i += total) { if(idv < ls) Temp[idv % ls] = 0; barrier(CLK_LOCAL_MEM_FENCE); float temp = concatenated_gradient[4 * shift_out + (i + 1) * hidden_size]; if(i < 3 * hidden_size) { for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += temp * (1 - temp); barrier(CLK_LOCAL_MEM_FENCE); } } else { for(uint v = 0; v < total_v; v += ls) { if(idv >= v && idv < v + ls) Temp[idv % ls] += 1 - pow(temp, 2.0f); barrier(CLK_LOCAL_MEM_FENCE); } } if(idv == 0) { temp = Temp[0]; for(int v = 1; v < ls; v++) temp += Temp[v]; weights_gradient[(i + 1) * weights_step] = temp; } barrier(CLK_LOCAL_MEM_FENCE); } }
Besondere Aufmerksamkeit sollte den Thread-Synchronisationspunkten gewidmet werden. Ihre Zahl muss mindestens so groß sein, dass das korrekte Funktionieren des Algorithmus gewährleistet ist. Zu viele Synchronisationspunkte verschlechtern die Leistung und verlangsamen den Betrieb. Außerdem können falsch platzierte Synchronisierungspunkte, die nicht von allen Threads erreicht werden, dazu führen, dass das Programm nicht mehr reagiert.
Damit schließen wir unseren Überblick über die Code-Anpassungen von OpenCL ab, die notwendig sind, um LSTM-Blockoperationen unter unabhängigen Datenkanälen zu organisieren. Was spezifische Bearbeitungen am Rande des Hauptprogramms betrifft, so möchte ich Sie ermutigen, diese selbst zu erkunden. Der vollständige Code der aktualisierten Klasse CNeuronLSTMOCL und alle ihre Methoden sind im Anhang enthalten.
2.2 Bau des Mamba-Blocks
Der nächste Schritt unserer Vorbereitungsarbeiten ist der Bau des Mamba-Blocks. Der Name dieses Blocks erinnert absichtlich an die Methode, die wir im vorherigen Artikel besprochen haben. Die Autoren von Traj-LLM erweitern die Verwendung von Zustandsraummodellen (SSM) und schlagen eine Blockarchitektur vor, die mit einem Encoder für einen Transformer verglichen werden kann. Aber in diesem Fall wird die Selbstaufmerksamkeit durch die Architektur von Mamba ersetzt.
Um den vorgeschlagenen Algorithmus zu implementieren, wird eine neue Klasse CNeuronMambaBlockOCL geschaffen, deren Struktur im Folgenden dargestellt wird.
class CNeuronMambaBlockOCL : public CNeuronBaseOCL { protected: uint iWindow; CNeuronMambaOCL cMamba; CNeuronBaseOCL cMambaResidual; CNeuronConvOCL cFF[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronMambaBlockOCL(void) {}; ~CNeuronMambaBlockOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMambaBlockOCL; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Die Kernfunktionalität wird von der Basisklasse CNeuronBaseOCL(fully connected layer) abgeleitet. Wir werden die bekannte Liste virtueller Methoden außer Kraft setzen.
Innerhalb der Struktur unserer neuen Klasse können wir interne Objekte hervorheben, deren Funktionalität wir Schritt für Schritt erkunden werden, wenn wir mit der Implementierung von Methoden fortfahren. Alle Objekte werden statisch deklariert. So können wir den Konstruktor und den Destruktor der Klasse „leer“ lassen. Die Initialisierung aller internen Objekte und Variablen wird innerhalb von Init durchgeführt.
Wie bereits erwähnt, ähnelt der Mamba-Block in seiner Architektur dem Encoder eines Transformers. Diese Ähnlichkeit zeigt sich auch in den Parametern der Initialisierungsmethode, die eine klare und strukturierte Definition der internen Architektur des Blocks liefern.
bool CNeuronMambaBlockOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Innerhalb des Methodenkörpers rufen wir die gleichnamige Methode der Elternklasse auf, die bereits einen minimal notwendigen Block für die Parametervalidierung und die Initialisierung aller geerbten Objekte enthält.
Nach erfolgreicher Ausführung der Initialisierungsmethode der übergeordneten Klasse speichern wir die Größe des Datenanalysefensters in einer lokalen Variable zur weiteren Verwendung.
iWindow = window;
Dann geht es an die Initialisierung der internen Objekte. Zunächst initialisieren wir die Schicht des Zustandsraums von Mamba.
if(!cMamba.Init(0, 0, OpenCL, window, window_key, units_count, optimization, iBatch)) return false;
Daran schließt sich eine vollverknüpfte Schicht an, deren Puffer wir für die Speicherung der normalisierten Ergebnisse der selektiven Zustandsraumanalyse mit Restverknüpfung verwenden wollen.
if(!cMambaResidual.Init(0, 1, OpenCL, window * units_count, optimization, iBatch)) return false; cMambaResidual.SetActivationFunction(None);
Danach fügen wir einen Block FeedForward hinzu.
if(!cFF[0].Init(0, 2, OpenCL, window, window, 4 * window, units_count, 1, optimization, iBatch)) return false; cFF[0].SetActivationFunction(LReLU); if(!cFF[1].Init(0, 2, OpenCL, 4 * window, 4 * window, window, units_count, 1, optimization, iBatch)) return false; cFF[1].SetActivationFunction(None);
Dann organisieren wir das Ersetzen von Zeigern in Datenpuffern, um unnötige Kopiervorgänge zu vermeiden.
SetActivationFunction(None); SetGradient(cFF[1].getGradient(), true); //--- return true; }
Beachten Sie, dass wir hier nur den Zeiger auf den Fehlergradientenpuffer ersetzen. Dies ist darauf zurückzuführen, dass während des Vorwärtsdurchgangs vor der Übertragung der Ergebnisse an den Schichtausgang eine zusätzliche Restverbindung und Normalisierung der erhaltenen Ergebnisse organisiert wird.
Vergessen Sie nicht, die Ergebnisse der einzelnen Arbeitsschritte zu überwachen. Am Ende der Methode geben wir das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurück.
Nach der Initialisierung des Klassenobjekts geht es an die Konstruktion des Algorithmus für den Vorwärtsdurchgang, der in der Methode feedForward implementiert ist. Es ist ganz einfach.
bool CNeuronMambaBlockOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cMamba.FeedForward(NeuronOCL)) return false;
In den Methodenparametern erhalten wir einen Zeiger auf das Objekt der vorherigen Schicht, das uns die Eingabedaten übergibt. Und im Hauptteil der Methode übergeben wir den erhaltenen Zeiger sofort an das selektive Modell des Zustandsraums.
Nach erfolgreichem Abschluss der Operationen der Direktpass-Methode der inneren Schicht summieren wir die erhaltenen Ergebnisse und die ursprünglichen Daten, gefolgt von einer Normalisierung der Werte.
if(!SumAndNormilize(cMamba.getOutput(), NeuronOCL.getOutput(), cMambaResidual.getOutput(), iWindow, true)) return false;
Als Nächstes kommt der Block mit dem Vorwärtsdurchgang.
if(!cFF[0].FeedForward(cMambaResidual.AsObject())) return false; if(!cFF[1].FeedForward(cFF[0].AsObject())) return false;
Wir organisieren die Restverbindung mit anschließender Datennormalisierung.
if(!SumAndNormilize(cMambaResidual.getOutput(), cFF[1].getOutput(), getOutput(), iWindow, true)) return false; //--- return true; }
Die Methoden der Rückwärtsdurchgänge haben auch einen recht einfachen Algorithmus, und ich schlage vor, sie für ein unabhängiges Studium so zu belassen. Ich möchte Sie daran erinnern, dass Sie im Anhang den vollständigen Code dieser Klasse und alle ihre Methoden finden.
Damit sind die vorbereitenden Arbeiten abgeschlossen und wir können mit der Konstruktion des allgemeinen Algorithmus der Methode von Traj-LLM fortfahren.
2.3 Zusammenfügen der einzelnen Blöcke zu einem kohärenten Algorithmus
Oben haben wir die Vorarbeit geleistet und unsere Bibliothek um die fehlenden „Bausteine“ ergänzt, die wir zum Aufbau des Traj-LLM-Algorithmus innerhalb der Klasse CNeuronTrajLLMOCL verwenden werden. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronTrajLLMOCL : public CNeuronBaseOCL { protected: //--- State Encoder CNeuronLSTMOCL cStateRNN; CNeuronConvOCL cStateMLP[2]; //--- Variables Encoder CNeuronTransposeOCL cTranspose; CNeuronLSTMOCL cVariablesRNN; CNeuronConvOCL cVariablesMLP[2]; //--- Context Encoder CNeuronLearnabledPE cStatePE; CNeuronLearnabledPE cVariablesPE; CNeuronMLMHAttentionMLKV cStateToState; CNeuronMLCrossAttentionMLKV cVariableToState; CNeuronMLCrossAttentionMLKV cStateToVariable; CNeuronBaseOCL cContext; CNeuronConvOCL cContextMLP[2]; //--- CNeuronMLMHAttentionMLKV cHighLevelInteraction; CNeuronMambaBlockOCL caMamba[3]; CNeuronMLCrossAttentionMLKV cLaneAware; CNeuronConvOCL caForecastMLP[2]; CNeuronTransposeOCL cTransposeOut; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronTrajLLMOCL(void) {}; ~CNeuronTrajLLMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronTrajLLMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Wie Sie sehen, überschreiben wir in der Klassenstruktur dieselben virtuellen Methoden. Allerdings zeichnet sich diese Klasse durch eine wesentlich größere Anzahl interner Objekte aus, was bei einer derart komplexen Architektur durchaus zu erwarten ist. Der Zweck dieser deklarierten Objekte wird deutlich werden, wenn wir mit der Implementierung der Klassenmethoden fortfahren.
Alle internen Objekte der Klasse werden als statisch deklariert. Folglich bleiben der Konstruktor und der Destruktor leer. Die Initialisierung aller deklarierten Objekte wird in der Methode Init durchgeführt.
In den Methodenparametern erhalten wir die Hauptkonstanten, die zur Initialisierung der verschachtelten Objekte verwendet werden. Hier sehen wir die Namen der Parameter, die uns bereits bekannt sind. Bitte beachten Sie jedoch, dass einige von ihnen unterschiedliche Funktionen für einzelne interne Objekte enthalten können.
bool CNeuronTrajLLMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * forecast, optimization_type, batch)) return false;
Einer bereits etablierten Tradition folgend, besteht der erste Schritt innerhalb der Init-Methode darin, die gleichnamige Methode der Elternklasse aufzurufen. Wie Sie wissen, führt diese Methode bereits eine grundlegende Parametervalidierung und Initialisierung aller geerbten Objekte durch. Nach der erfolgreichen Ausführung der Methode der übergeordneten Klasse fahren wir mit der Initialisierung der deklarierten internen Objekte fort.
Ausgehend von den Erfahrungen bei der Erstellung früherer Modelle gehen wir davon aus, dass der Input für das Modell eine Matrix ist, die die aktuelle Marktsituation beschreibt. Jede Zeile dieser Matrix enthält eine Reihe von Parametern, die eine einzelne Marktkerze charakterisieren, einschließlich der entsprechenden Werte der analysierten Indikatoren.
Gemäß dem Traj-LLM-Algorithmus werden die erhaltenen Eingabedaten zunächst an den Block „Sparse Context Encoder“ weitergeleitet, der einen Agenten-Encoder und einen Fahrbahn-Encoder umfasst. In unserem Fall handelt es sich um Geber für Umweltzustände (einzelne Balkendaten) und historische Trajektorien analysierter Parameter (Indikatoren).
Der Zustandscodierer wird aus einem rekurrenten Block zur Analyse einzelner Balken und zwei nachfolgenden Faltungsschichten aufgebaut, die die MLP-Operation innerhalb unabhängiger Informationskanäle umsetzen.
//--- State Encoder if(!cStateRNN.Init(0, 0, OpenCL, window_key, units_count, optimization, iBatch) || !cStateRNN.SetInputs(window)) return false; if(!cStateMLP[0].Init(0, 1, OpenCL, window_key, window_key, 4 * window_key, units_count, optimization, iBatch)) return false; cStateMLP[0].SetActivationFunction(LReLU); if(!cStateMLP[1].Init(0, 2, OpenCL, 4 * window_key, 4 * window_key, window_key, units_count, optimization, iBatch)) return false;
Die Methodenparameter umfassen die wichtigsten Konstanten, die für die Initialisierung eingebetteter Objekte verwendet werden. Hier sehen wir vertraute Parameternamen, aber es ist wichtig zu beachten, dass einige von ihnen unterschiedliche Funktionen für bestimmte interne Objekte haben können.
//--- Variables Encoder if(!cTranspose.Init(0, 3, OpenCL, units_count, window, optimization, iBatch)) return false; if(!cVariablesRNN.Init(0, 4, OpenCL, window_key, window, optimization, iBatch) || !cVariablesRNN.SetInputs(units_count)) return false; if(!cVariablesMLP[0].Init(0, 5, OpenCL, window_key, window_key, 4 * window_key, window, optimization, iBatch)) return false; cVariablesMLP[0].SetActivationFunction(LReLU); if(!cVariablesMLP[1].Init(0, 6, OpenCL, 4 * window_key, 4 * window_key, window_key, window, optimization, iBatch)) return false;
Es ist wichtig zu beachten, dass nach dem Traj-LLM-Algorithmus eine gemeinsame Analyse von Agenten und Fahrbahnen durchgeführt wird. Die Ausgabe der Encoder ergibt daher Vektoren, die einzelne Elemente der Sequenzen (Umweltzustände oder historische Trajektorien der analysierten Indikatoren) mit identischen Dimensionen darstellen. Gleichzeitig sind unterschiedliche Sequenzlängen zulässig, da die Anzahl der analysierten Umweltzustände oft nicht gleich der Anzahl der analysierten Parameter ist, die diese Zustände beschreiben.
Im nächsten Schritt des Traj-LLM-Algorithmus werden die Ausgaben der Kodierer an den Fusionsblock weitergeleitet, wo eine umfassende Analyse der Abhängigkeiten zwischen den einzelnen Sequenzelementen mit Hilfe der Mechanismen von Selbstaufmerksamkeit und Kreuzaufmerksamkeit durchgeführt wird. Es ist jedoch bekannt, dass zur Verbesserung der Effizienz von Aufmerksamkeitsmechanismen den Sequenzelementen Positionskodierungsmarken hinzugefügt werden müssen. Um diese Funktionalität zu erreichen, werden wir zwei trainierbare Schichten für die Positionskodierung einführen.
//--- Position Encoder if(!cStatePE.Init(0, 7, OpenCL, cStateMLP[1].Neurons(), optimization, iBatch)) return false; if(!cVariablesPE.Init(0, 8, OpenCL, cVariablesMLP[1].Neurons(), optimization, iBatch)) return false;
Und erst dann analysieren wir die Abhängigkeiten zwischen den einzelnen Zuständen im Selbstaufmerksamkeitsblock.
//--- Context if(!cStateToState.Init(0, 9, OpenCL, window_key, window_key, heads, heads / 2, units_count, 2, 1, optimization, iBatch)) return false;
Dann führen wir in den nächsten 2 Blöcken eine Analyse der gegenseitigen Abhängigkeiten durch.
if(!cStateToVariable.Init(0, 10, OpenCL, window_key, window_key, heads, window_key, heads / 2, units_count, window, 2, 1, optimization, iBatch)) return false; if(!cVariableToState.Init(0, 11, OpenCL, window_key, window_key, heads, window_key, heads / 2, window, units_count, 2, 1, optimization, iBatch)) return false;
Die angereicherten Darstellungen von Zuständen und Trajektorien werden zu einem einzigen Tensor verkettet.
if(!cContext.Init(0, 12, OpenCL, window_key * (units_count + window), optimization, iBatch)) return false;
Danach durchlaufen die Daten eine weitere MLP.
if(!cContextMLP[0].Init(0, 13, OpenCL, window_key, window_key, 4 * window_key, window + units_count, optimization, iBatch)) return false; cContextMLP[0].SetActivationFunction(LReLU); if(!cContextMLP[1].Init(0, 14, OpenCL, 4 * window_key, 4 * window_key, window_key, window + units_count, optimization, iBatch)) return false;
Als Nächstes folgt der Block für die Interaktionsmodellierung auf hoher Ebene. Hier verwenden die Autoren von Traj-LLM ein vortrainiertes Sprachmodell, das wir durch einen Transformer ersetzen werden.
if(!cHighLevelInteraction.Init(0, 15, OpenCL, window_key, window_key, heads, heads / 2, window + units_count, 4, 2, optimization, iBatch)) return false;
Als Nächstes folgt der kognitive Block, in dem die Wahrscheinlichkeiten der nachfolgenden Bewegungen unter Berücksichtigung der vorhandenen Fahrbahnen ermittelt werden. Hier verwenden wir 3 aufeinanderfolgende Mamba-Blöcke mit der gleichen Architektur.
for(int i = 0; i < int(caMamba.Size()); i++) { if(!caMamba[i].Init(0, 16 + i, OpenCL, window_key, 2 * window_key, window + units_count, optimization, iBatch)) return false; }
Die ermittelten Werte werden mit den historischen Flugfahrbahnen im Block der Kreuzaufmerksamkeit verglichen.
if(!cLaneAware.Init(0, 19, OpenCL, window_key, window_key, heads, window_key, heads / 2, window, window + units_count, 2, 1, optimization, iBatch)) return false;
Und schließlich verwenden wir MLP, um nachfolgende Trajektorien unabhängiger Datenkanäle vorherzusagen.
if(!caForecastMLP[0].Init(0, 20, OpenCL, window_key, window_key, 4 * forecast, window, optimization, iBatch)) return false; caForecastMLP[0].SetActivationFunction(LReLU); if(!caForecastMLP[1].Init(0, 21, OpenCL, 4 * forecast, 4 * forecast, forecast, window, optimization, iBatch)) return false; caForecastMLP[1].SetActivationFunction(TANH); if(!cTransposeOut.Init(0, 22, OpenCL, window, forecast, optimization, iBatch)) return false;
Beachten Sie, dass der vorhergesagte Trajektorientensor transponiert wird, um die Informationen in die Darstellung der Originaldaten zu bringen.
SetOutput(cTransposeOut.getOutput(), true); SetGradient(cTransposeOut.getGradient(), true); SetActivationFunction((ENUM_ACTIVATION)caForecastMLP[1].Activation()); //--- return true; }
Wir verwenden auch die Ersetzung von Datenpufferzeigern, um unnötige Kopiervorgänge zu vermeiden. Danach geben wir das logische Ergebnis der Methodenoperationen an das aufrufende Programm zurück.
Nachdem die Arbeit an der Klasseninitialisierungsmethode abgeschlossen ist, gehen wir zur Konstruktion des Algorithmus für den Vorwärtsdurchgang über, den wir in der Methode feedForward implementieren.
bool CNeuronTrajLLMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- State Encoder if(!cStateRNN.FeedForward(NeuronOCL)) return false; if(!cStateMLP[0].FeedForward(cStateRNN.AsObject())) return false; if(!cStateMLP[1].FeedForward(cStateMLP[0].AsObject())) return false;
In den Methodenparametern erhalten wir einen Zeiger auf ein Objekt mit den Anfangsdaten, die wir sofort durch den Zustandsgeberblock leiten.
Dann transponieren wir die ursprünglichen Daten und kodieren die historischen Trajektorien der analysierten Parameter, die den Zustand der Umwelt beschreiben.
//--- Variables Encoder if(!cTranspose.FeedForward(NeuronOCL)) return false; if(!cVariablesRNN.FeedForward(cTranspose.AsObject())) return false; if(!cVariablesMLP[0].FeedForward(cVariablesRNN.AsObject())) return false; if(!cVariablesMLP[1].FeedForward(cVariablesMLP[0].AsObject())) return false;
Wir fügen den erhaltenen Daten eine Positionskodierung hinzu.
//--- Position Encoder if(!cStatePE.FeedForward(cStateMLP[1].AsObject())) return false; if(!cVariablesPE.FeedForward(cVariablesMLP[1].AsObject())) return false;
Danach reichern wir die Daten mit dem Kontext der Interdependenzen an.
//--- Context if(!cStateToState.FeedForward(cStatePE.AsObject())) return false; if(!cStateToVariable.FeedForward(cStateToState.AsObject(), cVariablesPE.getOutput())) return false; if(!cVariableToState.FeedForward(cVariablesPE.AsObject(), cStateToVariable.getOutput())) return false;
Die angereicherten Daten werden zu einem einzigen Tensor verkettet.
if(!Concat(cStateToVariable.getOutput(), cVariableToState.getOutput(), cContext.getOutput(), cStateToVariable.Neurons(), cVariableToState.Neurons(), 1)) return false;
Und dann wird es von einer MLP verarbeitet.
if(!cContextMLP[0].FeedForward(cContext.AsObject())) return false; if(!cContextMLP[1].FeedForward(cContextMLP[0].AsObject())) return false;
Als Nächstes folgt der Block der Abhängigkeitsanalyse auf hoher Ebene.
//--- Lane aware if(!cHighLevelInteraction.FeedForward(cContextMLP[1].AsObject())) return false;
Und das Zustandsraummodell.
if(!caMamba[0].FeedForward(cHighLevelInteraction.AsObject())) return false; for(int i = 1; i < int(caMamba.Size()); i++) { if(!caMamba[i].FeedForward(caMamba[i - 1].AsObject())) return false; }
Anschließend vergleichen wir die historischen Entwicklungen mit den Ergebnissen unserer Analyse.
if(!cLaneAware.FeedForward(cVariablesPE.AsObject(), caMamba[caMamba.Size() - 1].getOutput())) return false;
Auf der Grundlage der gewonnenen Daten erstellen wir eine Vorhersage über die wahrscheinlichste bevorstehende Änderung der analysierten Parameter.
//--- Forecast if(!caForecastMLP[0].FeedForward(cLaneAware.AsObject())) return false; if(!caForecastMLP[1].FeedForward(caForecastMLP[0].AsObject())) return false;
Danach transponieren wir die vorhergesagten Werte in die Darstellung der Eingabedaten.
if(!cTransposeOut.FeedForward(caForecastMLP[1].AsObject())) return false; //--- return true; }
Schließlich gibt die Methode einen booleschen Wert an das aufrufende Programm zurück, der den Erfolg oder Misserfolg der durchgeführten Operationen angibt.
Der nächste Schritt unserer Arbeit ist die Entwicklung der Algorithmen für die Rückwärtsdurchgänge. Hier müssen wir die Verteilung der Fehlergradienten auf alle Objekte entsprechend ihres Einflusses auf die endgültige Ausgabe sowie die anschließende Anpassung der trainierbaren Parameter mit dem Ziel der Fehlerminimierung umsetzen.
Während die Aktualisierung der Parameter relativ einfach ist — da alle trainierbaren Parameter in den internen (verschachtelten) Objekten enthalten sind und es daher ausreicht, die Methoden zur Parameteraktualisierung dieser internen Objekte nacheinander aufzurufen — stellt die Verteilung der Fehlergradienten eine wesentlich komplexere und kompliziertere Herausforderung dar.
Die Verteilung der Fehlergradienten erfolgt in voller Übereinstimmung mit dem Algorithmus des Vorwärtsdurchgangs, jedoch in umgekehrter Reihenfolge. Und hier ist anzumerken, dass unser Vorwärtsdurchgang nicht so „vorwärts“ ist, wenn Sie das Wortspiel verzeihen. Im Vorwärtsdurchlauf lassen sich mehrere parallele Informationsströme erkennen. Und nun müssen wir die Fehlergradienten aus all diesen Fäden sammeln.
Der Algorithmus zur Verteilung der Fehlergradienten wird in der Methode calcInputGradients implementiert. Zu den Parametern dieser Methode gehört ein Zeiger auf das Objekt der vorhergehenden Schicht, in das wir den Fehlergradienten übergeben müssen, der entsprechend dem Einfluss der anfänglichen Eingabedaten auf die endgültige Modellausgabe verteilt wird. Gleich zu Beginn der Methode prüfen wir die Gültigkeit des empfangenen Zeigers, denn wenn der Zeiger nicht korrekt ist, wird der gesamte weitere Prozess sinnlos.
bool CNeuronTrajLLMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Es ist wichtig, sich daran zu erinnern, dass zu dem Zeitpunkt, an dem diese Methode aufgerufen wird, der Fehlergradient der aktuellen Schicht bereits in ihrem Gradientenpuffer gespeichert ist. Dieser Wert wurde bei der Ausführung der entsprechenden Methode in der nachfolgenden Schicht unseres Modells geschrieben. Dank des Mechanismus der Zeigersubstitution, den wir zuvor organisiert haben, ist derselbe Fehlergradient auch im Puffer unserer internen Schicht vorhanden, die die Vorhersageergebnisse umsetzt. Daher beginnen wir den Prozess der Gradientenverteilung, indem wir diesen Gradienten durch das MLP leiten, das für die Vorhersage der zukünftigen Bewegung zuständig ist.
//--- Forecast if(!caForecastMLP[1].calcHiddenGradients(cTransposeOut.AsObject())) return false; if(!caForecastMLP[0].calcHiddenGradients(caForecastMLP[1].AsObject())) return false;
Sobald dies abgeschlossen ist, wird der Fehlergradient an die Schicht weitergegeben, die die historischen Trajektorien der analysierten Parameter mit den Ergebnissen der kognitiven Analyse abgleicht.
//--- Lane aware if(!cLaneAware.calcHiddenGradients(caForecastMLP[0].AsObject())) return false;
In diesem Zusammenhang ist es wichtig zu wissen, dass der Kreuzaufmerksamkeitsblock Daten aus zwei verschiedenen Informationssträngen zusammenführt. Dementsprechend müssen wir den Fehlergradienten auf diese beiden Fäden aufteilen, und zwar proportional zu ihrem Einfluss auf die endgültige Modellausgabe.
if(!cVariablesPE.calcHiddenGradients(cLaneAware.AsObject(), caMamba[caMamba.Size() - 1].getOutput(), caMamba[caMamba.Size() - 1].getGradient(), (ENUM_ACTIVATION)caMamba[caMamba.Size() - 1].Activation())) return false;
Als Nächstes wird der Fehlergradient durch das Zustandsraummodell
for(int i = int(caMamba.Size()) - 2; i >= 0; i--) if(!caMamba[i].calcHiddenGradients(caMamba[i + 1].AsObject())) return false;
und einem Block zur Abhängigkeitsanalyse auf hoher Ebene geleitet.
if(!cHighLevelInteraction.calcHiddenGradients(caMamba[0].AsObject())) return false;
Mit dem Kontext von MLP schieben wir den Fehlergradienten eine Ebene tiefer - in den verketteten Datenpuffer von Zuständen und Trajektorien.
if(!cContextMLP[1].calcHiddenGradients(cHighLevelInteraction.AsObject())) return false; if(!cContextMLP[0].calcHiddenGradients(cContextMLP[1].AsObject())) return false; if(!cContext.calcHiddenGradients(cContextMLP[0].AsObject())) return false;
Und nun kommt der komplizierteste und wichtigste Teil. Hier ist äußerste Aufmerksamkeit gefragt, damit kein Detail übersehen wird.
An diesem Punkt müssen wir den Gradienten des verketteten Puffers in zwei separate Threads aufteilen. Es gibt nichts Kompliziertes daran. Wir können einfach die Methode, die eine Verkettung löst, ausführen und dabei die entsprechenden Datenpuffer angeben. In unserem Fall handelt es sich um die beiden Ebenen, auf denen sich die Aufmerksamkeit kreuzt: Trajektorien zu Zuständen und Zustände zu Trajektorien. Die Herausforderung liegt jedoch im nächsten Schritt. Sobald wir damit beginnen, den Fehlergradienten durch den Block für die Querbeobachtung von Trajektorien zu Zuständen zu leiten, erzeugt dieser Block ebenfalls einen Gradienten, der weiter an die Schicht für die Querbeobachtung von Zuständen zu Trajektorien geleitet werden muss. Um sicherzustellen, dass wir während dieses mehrstufigen Prozesses keinen Teil der Gradienteninformationen verlieren, müssen wir sie in einem temporären Puffer speichern. Aber innerhalb dieser Klasse haben wir auch ohne Hilfspuffer eine ganze Reihe von Objekten erstellt. Und unter diesen Objekten gibt es viele, die nur darauf warten, dass sie an die Reihe kommen. Wir sollten sie also für die vorübergehende Speicherung von Informationen verwenden. Verwenden wir die Positionskodierungsschicht, die mit dem Block für die Kreuzaufmerksamkeit von Zuständen zu Trajektorien verbunden ist, als temporären Halter für diesen partiellen Gradienten.
if(!DeConcat(cStatePE.getGradient(), cVariableToState.getGradient(), cContext.getGradient(), cStateToVariable.Neurons(), cVariableToState.Neurons(), 1)) return false;
Wir erinnern uns außerdem daran, dass der Gradientenpuffer der Positionskodierungsschicht für Trajektorien bereits nützliche Fehlergradienten enthält. Damit diese wertvollen Informationen nicht verloren gehen, übertragen wir sie vorübergehend in den Gradientenpuffer der MLP innerhalb des entsprechenden Encoders.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), 1, false)) return false;
Nachdem wir sichergestellt haben, dass alle notwendigen Gradienteninformationen erhalten bleiben, verteilen wir den Fehlergradienten durch den Kreuzaufmerksamkeitsblock, der die Trajektorien an die Zustände anpasst.
if(!cVariablesPE.calcHiddenGradients(cVariableToState.AsObject(), cStateToVariable.getOutput(), cStateToVariable.getGradient(), (ENUM_ACTIVATION)cStateToVariable.Activation())) return false;
Nun können wir die Fehlergradienten auf der Ebene des Blocks für die Ausrichtung von Zuständen an Trajektorien summieren, indem wir sie aus beiden Stämmen zusammenfassen.
if(!SumAndNormilize(cStateToVariable.getGradient(), cStatePE.getGradient(), cStateToVariable.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Im nächsten Schritt müssen wir jedoch den Fehlergradienten zum dritten Mal an die Schicht für die Positionskodierung der Trajektorien zurückgeben. Daher aggregieren wir zunächst die vorhandenen Fehlergradienten aus beiden Datenströmen.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), cVariablesMLP[1].getGradient(), 1, false, 0, 0, 0, 1)) return false;
Erst nach dieser Aggregation wenden wir die Gradientenverteilungsmethode des Kreuzaufmerksamkeitsblocks an, um die Zustände an die Trajektorien anzupassen.
if(!cStateToState.calcHiddenGradients(cStateToVariable.AsObject(), cVariablesPE.getOutput(), cVariablesPE.getGradient(), (ENUM_ACTIVATION)cVariablesPE.Activation())) return false;
An diesem Punkt können wir schließlich alle Fehlergradienten auf der Ebene der Positionskodierung für Trajektorien summieren, indem wir sie aus drei verschiedenen Quellen kombinieren.
if(!SumAndNormilize(cVariablesPE.getGradient(), cVariablesMLP[1].getGradient(), cVariablesPE.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Als Nächstes wird der Fehlergradient auf die Ebene der Positionskodierung für Zustände übertragen.
if(!cStatePE.calcHiddenGradients(cStateToState.AsObject())) return false;
Es ist erwähnenswert, dass die Positionskodierungsschichten in zwei unabhängigen, parallelen Datenströmen arbeiten, und wir müssen die jeweiligen Fehlergradienten an die entsprechenden Kodierer in jedem Strom weitergeben:
//--- Position Encoder if(!cStateMLP[1].calcHiddenGradients(cStatePE.AsObject())) return false; if(!cVariablesMLP[1].calcHiddenGradients(cVariablesPE.AsObject())) return false;
Als Nächstes werden die Fehlergradienten durch zwei parallele Encoder geleitet, die jeweils mit demselben Eingangstensor von Rohdaten arbeiten. Hier besteht die Notwendigkeit, die Fehlergradienten aus diesen beiden parallelen Strömen in einem einzigen Gradientenpuffer zusammenzuführen. Wir brauchen wieder einen Hilfsdatenpuffer, den wir nicht angelegt haben. Außerdem sind in diesem Stadium alle unsere internen Objekte bereits mit wichtigen Daten gefüllt, die wir nicht überschreiben können.
Es gibt jedoch eine subtile, aber entscheidende Nuance. Die Datentranspositionsschicht, mit der wir die rohen Eingabedaten vor der Trajektorienkodierung neu anordnen, enthält keine trainierbaren Parameter. Der Fehlergradientenpuffer wird nur für die Weitergabe von Daten an die vorherige Schicht verwendet. Außerdem entspricht die Größe dieses Puffers genau unseren Bedürfnissen, da es sich um dieselben Daten handelt, allerdings in einer anderen Reihenfolge. Wunderbar. Wir propagieren den Fehlergradienten durch den Trajektoriencodierungsblock.
//--- Variables Encoder if(!cVariablesMLP[0].calcHiddenGradients(cVariablesMLP[1].AsObject())) return false; if(!cVariablesRNN.calcHiddenGradients(cVariablesMLP[0].AsObject())) return false; if(!cTranspose.calcHiddenGradients(cVariablesRNN.AsObject())) return false; if(!NeuronOCL.FeedForward(cTranspose.AsObject())) return false;
Und wir übertragen den erhaltenen Fehlergradienten in den Puffer der Datenumsetzungsschicht.
if(!SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getGradient(), cTranspose.getGradient(), 1, false)) return false;
Auf ähnliche Weise leiten wir den Fehlergradienten durch den Zustandscodierer.
//--- State Encoder if(!cStateMLP[0].calcHiddenGradients(cStateMLP[1].AsObject())) return false; if(!cStateRNN.calcHiddenGradients(cStateMLP[0].AsObject())) return false; if(!NeuronOCL.calcHiddenGradients(cStateRNN.AsObject())) return false;
Anschließend summieren wir die Fehlergradienten aus beiden Strömen.
if(!SumAndNormilize(cTranspose.getGradient(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1)) return false; //--- return true; }
Schließlich geben wir das logische Ergebnis aller Operationen an das aufrufende Programm zurück, um den Erfolg oder Misserfolg anzuzeigen.
Damit ist die Beschreibung der Algorithmen der Klasse CNeuronTrajLLMOCL abgeschlossen. Den vollständigen Code dieser Klasse und alle ihre Methoden finden Sie im Anhang.
2.4 Modellarchitektur
Wir können diese Klasse nun nahtlos in unser Modell integrieren, um die praktische Effizienz des vorgeschlagenen Ansatzes anhand realer historischer Daten zu bewerten. Der Algorithmus Traj-LLM wurde speziell für die Vorhersage zukünftiger Trajektorien entwickelt. Wir verwenden ähnliche Methoden im Encoder des Umgebungszustand (Environmental State Encoder).
Bitte beachten Sie, dass unsere Interpretation der praktischen Anwendung von Traj-LLM in einem einheitlichen zusammengesetzten Block umgesetzt wurde. Auf diese Weise können wir eine saubere und unkomplizierte externe Modellstruktur beibehalten, ohne die Funktionalität zu beeinträchtigen.
Wie üblich werden rohe, unbearbeitete Daten, die die aktuelle Marktsituation beschreiben, in das Modell eingespeist.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Die primäre Datenverarbeitung erfolgt in der Batch-Normalisierungsschicht.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Danach werden die Daten sofort in unseren neuen Traj-LLM-Block übertragen. Es ist schwierig, eine derart komplexe architektonische Lösung als neuronale Schicht zu bezeichnen.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTrajLLMOCL; descr.window = BarDescr; //window descr.window_out = EmbeddingSize; //Inside Dimension descr.count = HistoryBars; //Units prev_count = descr.layers = NForecast; //Forecast descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Am Ausgang des Blocks liegen bereits vorhergesagte Werte vor, zu denen wir die statistischen Parameter der ursprünglichen Werte hinzufügen.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Dann gleichen wir die Ergebnisse im Frequenzbereich ab.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Die Architektur der anderen Modelle blieb unverändert. Sowie den Code aller verwendeten Programme. Sie können sie in dem unten beigefügten Code studieren. Wir gehen nun zur nächsten Phase unserer Arbeit über.
3. Tests
Wir haben umfangreiche Arbeiten zur Implementierung des Traj-LLM-Ansatzes in MQL5 durchgeführt. Und nun ist es an der Zeit, die praktischen Ergebnisse zu bewerten. Unser Ziel ist es, die Modelle auf realen historischen Daten zu trainieren und ihre Leistung auf bisher unbekannten Datensätzen zu bewerten.
Wie bereits erwähnt, hatten die Änderungen an der Architektur des Modells keine Auswirkungen auf die Struktur der Eingabedaten oder das Format der Ausgaben. Auf diese Weise können wir uns auf zuvor zusammengestellte Trainingsdatensätze für das Vortraining stützen.
In der ersten Phase trainieren wir den Encoder des Umgebungszustands, um kommende Preisbewegungen vorherzusagen. Das Training wird fortgesetzt, bis sich der Vorhersagefehler auf einem akzeptablen Niveau stabilisiert. In dieser Phase wird der Trainingsdatensatz weder aktualisiert noch verändert. In diesem Stadium zeigte das Modell vielversprechende Ergebnisse. Sie zeigte eine gute Fähigkeit, kommende Preistrends zu erkennen.
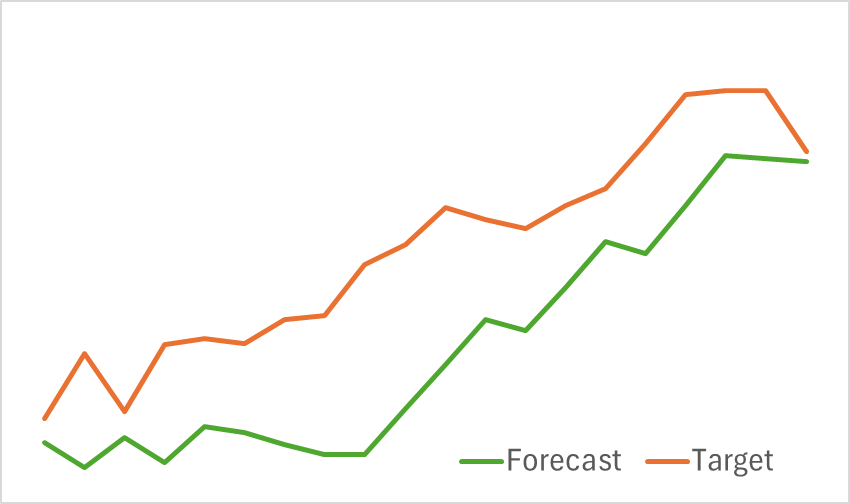
In der zweiten Phase führen wir ein iteratives Training der Verhaltenspolitik des Akteurs und der Belohnungsfunktion des Kritikers durch. Das Kritikermodell hat eine unterstützende Funktion. Es wurden Anpassungen an die Aktionen des Akteurs vorgenommen. Unser vorrangiges Ziel ist es jedoch, eine rentable Politik für den Akteur zu entwickeln. Um eine zuverlässige Bewertung der Handlungen der Akteure zu gewährleisten, wird der Trainingsdatensatz in dieser Phase regelmäßig aktualisiert. Nach mehreren Iterationen haben wir erfolgreich eine Strategie entwickelt, die auf dem Testdatensatz Gewinne erzielt.
Ich möchte Sie daran erinnern, dass alle Modelle mit historischen Daten von EURUSD für das Jahr 2023, Zeitrahmen H1, trainiert wurden. Die Tests werden mit Daten vom Januar 2024 durchgeführt, wobei alle anderen Parameter unverändert bleiben.
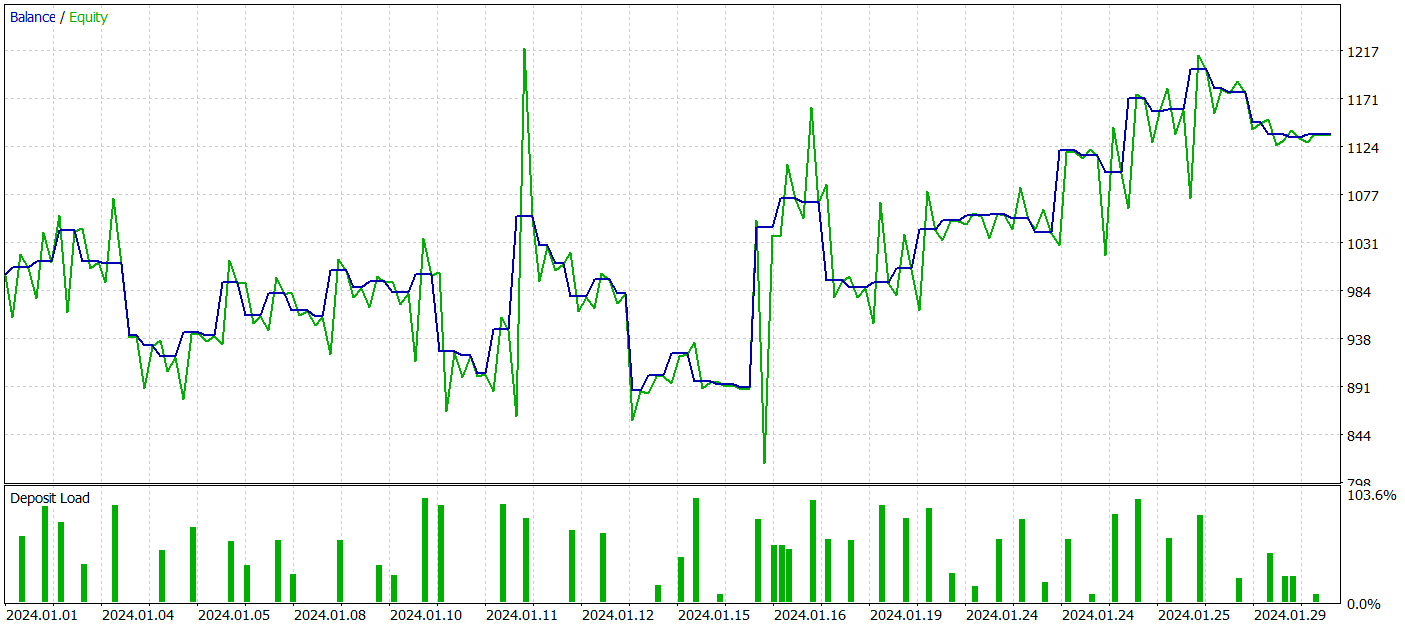
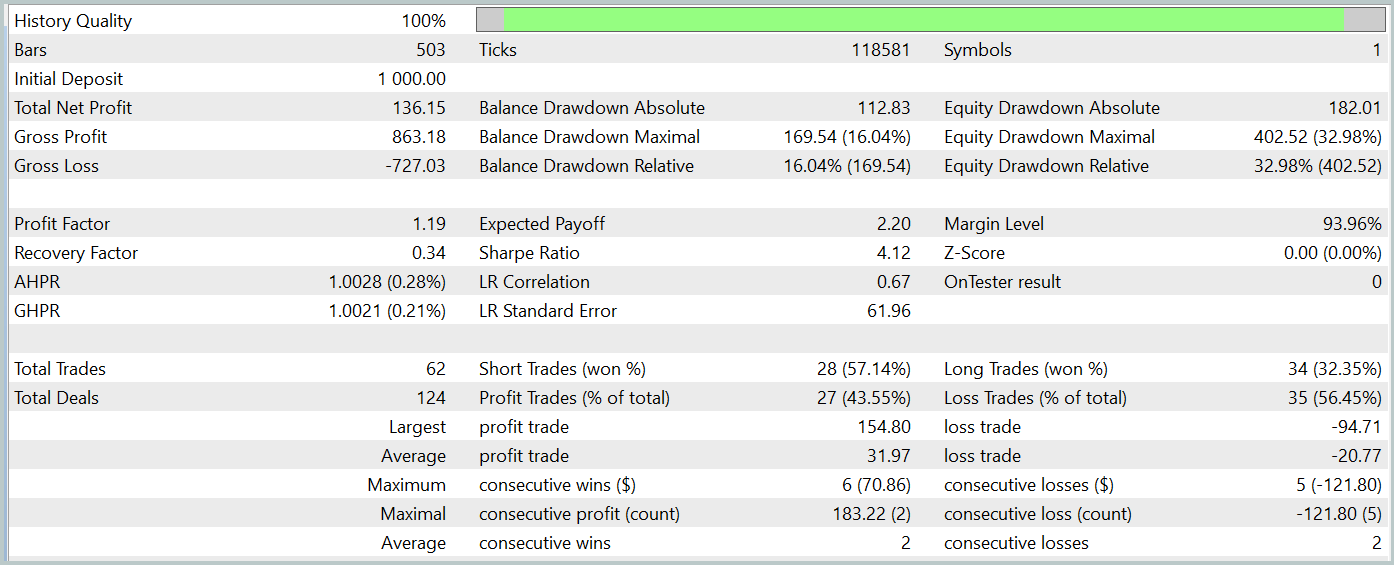
Während des Testzeitraums führte unser Modell 62 Handelsgeschäfte aus, von denen 27 (43,55 %) mit Gewinn abgeschlossen wurden. Da jedoch die maximalen und durchschnittlichen Gewinne mehr als die Hälfte der Variablen für die Verlustgeschäfte betragen, wurde während des Testzeitraums insgesamt ein Gewinn von 13,6 % erzielt. Und der Gewinnfaktor lag bei 1,19. Besonders besorgniserregend ist jedoch der Rückgang des Aktienkapitals, der fast 33 % erreicht hat. Es ist klar, dass das Modell in seiner derzeitigen Form noch nicht für den realen Handel geeignet ist und weitere Verbesserungen erfordert.
Schlussfolgerung
In diesem Artikel haben wir die neue Methode Traj-LLM untersucht, deren Autoren eine neue Perspektive für die Anwendung großer Sprachmodelle (LLMs) vorschlagen. Diese Methode zeigt, wie Fähigkeiten von LLM für die Vorhersage zukünftiger Werte verschiedener Zeitreihen angepasst werden können, wodurch genauere und adaptive Vorhersagen unter Bedingungen von Unsicherheit und Chaos möglich werden.
Im praktischen Teil haben wir unsere eigene Interpretation des vorgeschlagenen Ansatzes implementiert und ihn an realen historischen Daten getestet. Die Ergebnisse sind zwar noch nicht perfekt, aber sie sind vielversprechend und lassen auf weiteres Entwicklungspotenzial schließen.
Referenzen
- Traj-LLM: A New Exploration for Empowering Trajectory Prediction with Pre-trained Large Language Models
- Weitere Artikel aus dieser Serie
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA-Beispielsammlung |
| 2 | ResearchRealORL.mq5 | EA | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | EA | Trainings-EA des Modells |
| 4 | StudyEncoder.mq5 | EA | Trainings-EA des Encoders |
| 5 | Test.mq5 | EA | Modeltest-EA |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15595
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Generative Adversarial Networks (GANs) für synthetische Daten in der Finanzmodellierung (Teil 1): Einführung in GANs und synthetische Daten für die Finanzmodellierung
Generative Adversarial Networks (GANs) für synthetische Daten in der Finanzmodellierung (Teil 1): Einführung in GANs und synthetische Daten für die Finanzmodellierung
 Von der Grundstufe bis zur Mittelstufe: Übergabe als Wert oder Referenz
Von der Grundstufe bis zur Mittelstufe: Übergabe als Wert oder Referenz
 Erstellen von einem Trading Administrator Panel in MQL5 (Teil VI): Schnittstelle für mehrere Funktionen (I)
Erstellen von einem Trading Administrator Panel in MQL5 (Teil VI): Schnittstelle für mehrere Funktionen (I)
 Entwicklung eines Replay-Systems (Teil 60): Abspielen des Dienstes (I)
Entwicklung eines Replay-Systems (Teil 60): Abspielen des Dienstes (I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.