Chaostheorie im Handel (Teil 1): Einführung, Anwendung auf den Finanzmärkten und Lyapunov-Exponent

Einführung in die Chaostheorie und ihre Beziehung zu den Finanzmärkten

Was ist die Chaostheorie und wie lässt sie sich auf die Finanzmärkte anwenden? Wir werden uns in diesem Artikel mit diesem Thema befassen.

Ich werde eine Reihe von Artikeln schreiben, die die Fragen beantworten, was die Chaostheorie ist und wie sich das von Bill Williams vorgeschlagene Konzept des Marktchaos von der herkömmlichen, wissenschaftlich fundierten Theorie unterscheidet. Wie beschreibt die Theorie den Markt? Wie und in welchen Bereichen des Handels kann sie angewendet werden? 

Wir werden sowohl die theoretischen Grundlagen analysieren als auch eine Reihe von Tools entwickeln, die Händlern beim Handel helfen können.

Grundlegende Konzepte der Chaostheorie: Attraktoren, Fraktale und der Schmetterlingseffekt

Die Chaostheorie ist ein interessantes Gebiet der Mathematik und Physik, das uns hilft, komplexe Systeme, wie z. B. die Finanzmärkte, besser zu verstehen. Schauen wir uns die drei Hauptgedanken dieser Theorie an:

1. Attraktoren: Diese sind wie Magnete für die Zustände des Systems - das System wird mit der Zeit von ihnen angezogen. Auf den Finanzmärkten können dies bestimmte Preise oder sich wiederholende Muster sein, zu denen der Markt immer wieder zurückkehrt. Seltsame Attraktoren, die in chaotischen Systemen vorkommen, sind von besonderem Interesse. Sie sehen komplex aus und können eine versteckte Ordnung im zufälligen Verhalten des Marktes aufzeigen.

2. Fraktale: Das sind geometrische Formen, die bei jeder Vergrößerung gleich aussehen. Auf den Finanzmärkten sind Fraktale in Preisdiagrammen zu sehen - das gleiche Muster ist sowohl auf kurzen als auch auf langen Zeitskalen zu erkennen. Dadurch können dieselben Analysemethoden in verschiedenen Zeitintervallen angewendet werden, was die Analyse von Preisänderungen und die Bewertung von Risiken erleichtert.

3. Schmetterlingseffekt: Dieser Effekt zeigt, dass selbst kleinste Veränderungen am Anfang zu großen und unerwarteten Konsequenzen führen können. In der Finanzwelt bedeutet dies, dass kleine Änderungen in den Daten oder im Modell die Prognosen dramatisch verändern können. Dies macht langfristige Prognosen auf den Finanzmärkten schwierig und zeigt, wie wichtig es ist, unsere Modelle ständig zu aktualisieren und an neue Bedingungen anzupassen.

Das Verständnis dieser Ideen hilft Analysten und Händlern, die Märkte auf eine neue Art und Weise zu betrachten und verborgene Muster und mögliche Einstiegs- oder Ausstiegspunkte für Geschäfte zu entdecken. Die Chaostheorie eröffnet neue Wege der Analyse und Vorhersage, die über die herkömmlichen Modelle hinausgehen.

Chaotische Systeme im Kontext der Finanzmärkte

Die Finanzmärkte weisen die Merkmale chaotischer Systeme auf, was für ihre Analyse und Vorhersage wichtig ist.

• Nicht-Linearität: Kleine Änderungen verursachen unverhältnismäßige Schwankungen.
• Empfindlichkeit gegenüber Anfangsbedingungen: Kleine Ereignisse können zu großen Bewegungen führen.
• Selbst-Organisation: Bildung von Trends und Mustern ohne externe Kontrolle.
• Fraktale Struktur: Preisdiagramme weisen fraktale Eigenschaften auf.
• Begrenzte Vorhersehbarkeit: Die Vorhersagegenauigkeit nimmt mit zunehmendem Zeithorizont ab.
• Seltsame Attraktoren: Schwankungen um bestimmte Werte oder Zustände.
• Übergänge zwischen Staaten: Plötzliche Übergänge von Stabilität zu Volatilität.

Dieses Verständnis hilft bei der Entwicklung ausgefeilter Analysemethoden, Risikomanagement und Handelsalgorithmen.

Volatilität im Handel

Volatilität ist ein Schlüsselkonzept im Handel und im Finanzwesen, das mit der Chaostheorie zusammenhängt. Er misst, wie stark sich der Preis eines Vermögenswerts innerhalb eines bestimmten Zeitraums verändert. Im Handel hilft die Volatilität bei der Risikobewertung, der Bewertung von Optionen und der Entwicklung von Handelsstrategien.

Die Finanzmärkte verhalten sich oft wie chaotische Systeme. Sie können unerwartet auf kleine Veränderungen reagieren, ähnlich dem Schmetterlingseffekt. Die Märkte können sich auch selbst organisieren, indem sie Trends und Muster ohne Eingriffe von außen erzeugen, und die Preisdiagramme weisen Ähnlichkeiten zwischen verschiedenen Zeitrahmen auf, was als fraktale Eigenschaften bezeichnet wird.

Die Chaostheorie bietet einzigartige Instrumente für die Volatilitätsanalyse, wie z. B. die Rekonstruktion des Phasenraums und den Lyapunov-Exponenten, die helfen, verborgene Muster zu finden und die Vorhersagbarkeit zu bewerten. Diese chaotischen Modelle können traditionelle Methoden wie GARCH-Modelle ergänzen, insbesondere bei der Identifizierung von Marktregimen und der Vorhersage abrupter Veränderungen der Volatilität.

Das Verständnis der chaotischen Natur der Volatilität eröffnet neue Möglichkeiten für eine genauere Analyse und Vorhersage der Marktdynamik, was zur Entwicklung effizienter Handelsstrategien und Risikomanagementmethoden führt.

Herkömmliche Chaostheorie und der Ansatz von Bill Williams

Die herkömmliche Chaostheorie und das Konzept des „Chaos“ von Bill Williams sind sehr unterschiedlich. Erstere stützt sich auf strenge mathematische Grundsätze und verwendet hochentwickelte Instrumente zur Analyse von Systemen. Letztere hingegen verwenden einen intuitiven Ansatz und technische Indikatoren wie Alligator und Fraktale, die keinen direkten Bezug zur mathematischen Chaostheorie haben.

Die konventionelle Chaostheorie basiert auf strengen mathematischen Prinzipien und wissenschaftlichen Forschungen im Bereich der nichtlinearen Dynamik. Sie verwendet strenge mathematische Methoden und geht davon aus, dass Chaos ein deterministisches, aber unvorhersehbares Verhalten zeigt. Williams verwendet den Begriff „Chaos“ eher locker und bezieht sich auf die allgemeine Unvorhersehbarkeit der Märkte. Seine Methoden zielen eher auf die praktische Anwendung im Handel als auf eine tiefgehende Analyse der chaotischen Natur der Märkte.

Obwohl Williams einige Begriffe aus der Chaostheorie übernommen hat, basiert sein Ansatz eher auf der technischen Analyse und der persönlichen Interpretation der Marktbewegungen. Dies hat Kritik von Chaostheoretikern hervorgerufen, die die Verwendung des Begriffs „Chaos“ in diesem Zusammenhang für irreführend halten.

Chaostheorie in der Marktanalyse

Die Chaostheorie bietet eine neue Perspektive für die Analyse der Marktdynamik und trägt der Komplexität und Unvorhersehbarkeit der Finanzmärkte Rechnung. Im Gegensatz zu den traditionellen Methoden berücksichtigt die Chaostheorie die Nichtlinearität und Komplexität der Marktprozesse.

Dieser Ansatz hilft zu erklären, warum kleine Ereignisse zu großen Marktbewegungen führen können und warum langfristige Prognosen oft ungenau sind. Mit Hilfe der Chaostheorie können wir Phänomene wie Marktzusammenbrüche und Blasen analysieren und so neue Instrumente für eine genauere und anpassungsfähigere Marktanalyse bereitstellen.

Lyapunov-Exponent und seine Anwendung in der Finanzzeitreihenanalyse

Der Lyapunov-Exponent ist ein Werkzeug aus der Chaostheorie, das uns hilft zu verstehen, wie empfindlich ein System auf die Anfangsbedingungen reagiert. Auf den Finanzmärkten ist dies wichtig, weil man so abschätzen kann, wie stark sich die Preise bei kleinen Veränderungen der Marktbedingungen ändern werden.

Ist der Lyapunov-Exponent positiv, bedeutet dies, dass sich das System chaotisch verhält: Kleine Änderungen können in der Zukunft zu großen Schwankungen führen. Wenn der Exponent negativ ist, ist das System stabiler und die Preise ändern sich weniger.

Anhand dieses Exponenten können Sie feststellen, wann der Markt volatiler und berechenbarer wird. Hohe Werte können auf mögliche starke Preisänderungen hinweisen, was für die Risikobewertung und die Anpassung von Handelsstrategien nützlich ist.

Um den Lyapunov-Exponenten in Finanzdaten zu berechnen, muss ein Phasenraum erstellt werden, indem analysiert wird, wie nahe Punkte in diesem Raum divergieren. Dieser Prozess erfordert die Wahl der richtigen Parameter, wie z. B. Größe und Zeitverzögerung.

Ein wichtiger Aspekt bei der Verwendung des Lyapunov-Exponenten ist die Einschätzung, wie lange die Prognosen zutreffen werden. Je höher der Wert des Exponenten ist, desto kürzer ist der Zeitraum, in dem Prognosen zuverlässig bleiben. Dies ist besonders nützlich für den kurzfristigen Handel und das Risikomanagement.

Jetzt können wir mit der Implementierung des Lyapunov-Exponenten in MQL5 beginnen.

Implementierung des Lyapunov-Exponenten mit MQL5

Dieser Indikator implementiert die Berechnung des Lyapunov-Exponenten für die Analyse von Finanzzeitreihen. Sie ermöglicht es, den Grad des Marktchaos und die potenzielle Vorhersagbarkeit von Preisbewegungen zu beurteilen.

Eingaben:

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag - Zeitverzögerung für die Phasenraumrekonstruktion.
• InpEmbedDim - Einbettungsdimension für die Phasenraumrekonstruktion.
• InpDataLength - Anzahl der Kerzen, die zur Berechnung des Indikators verwendet werden.

Es gibt eine globale Variable:

double LyapunovBuffer[];

Initialisierung:

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

In der Funktion OnInit() konfigurieren wir den Indikatorpuffer, stellen die Anzeigegenauigkeit auf 5 Dezimalstellen ein und legen einen Kurznamen für den Indikator fest.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

Die Funktion OnCalculate() wird bei jedem Tick aufgerufen und führt die Berechnung des Lyapunov-Exponenten für jede Kerze ab der InpDataLength durch.

Berechnung des Lyapunov-Exponenten:

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

Die Funktion CalculateLyapunovExponent() implementiert den Algorithmus zur Berechnung des lokalen Lyapunov-Exponenten. Es verwendet die Methode der nächsten Nachbarn, um die Divergenz der Trajektorien im rekonstruierten Phasenraum zu schätzen.

Suche nach dem nächstgelegenen Nachbarn:

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

Die Funktion FindNearestNeighbor() findet den nächstgelegenen Punkt im rekonstruierten Phasenraum anhand des euklidischen Abstands.

Auswertung der Ergebnisse

• Positive Werte des Indikators zeigen das Vorhandensein eines chaotischen Marktverhaltens an.
• Negative Werte weisen auf eine stabilere und potenziell vorhersehbare Preisdynamik hin.
• Je höher der absolute Wert des Indikators, desto ausgeprägter ist das entsprechende Merkmal (chaotisch oder stabil).

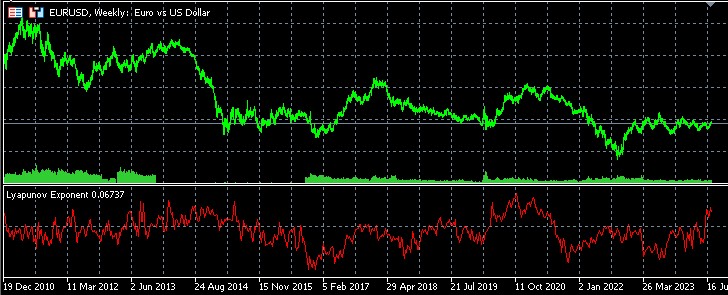
Statistische Analyse von Trendumkehrungen und -fortsetzungen mit Hilfe des Lyapunov-Exponenten

Ich habe ein spezielles Skript in der Sprache MQL5 entwickelt, um die Beziehung zwischen dem Lyapunov-Exponenten und der Dynamik der Finanzmärkte eingehend zu untersuchen. Dieses Tool ermöglicht eine detaillierte statistische Analyse von Trendumkehrungen und -fortsetzungen im Kontext der Lyapunov-Exponentenwerte und bietet Händlern und Analysten wertvolle Einblicke in das Marktverhalten.

Das Skript arbeitet mit historischen Daten des ausgewählten Finanzinstruments und analysiert eine bestimmte Anzahl von Balken. Für jeden Balken wird der lokale Lyapunov-Exponent mit Hilfe der Phasenraumrekonstruktion und der Methode der Suche nach dem nächsten Nachbarn berechnet. Dieser Ansatz ermöglicht es uns, den Grad des Chaos im System zu jedem spezifischen Zeitpunkt zu bewerten.

Gleichzeitig analysiert das Skript die Preisdynamik und identifiziert Umkehrungen und Trendfortsetzungen. Eine Umkehrung ist definiert als eine Situation, in der der aktuelle Schlusskurs höher ist als der vorherige und der nächste Kurs niedriger als der aktuelle (oder umgekehrt). Alle anderen Fälle werden als eine Fortsetzung des Trends betrachtet.

Das Hauptmerkmal des Skripts ist seine Fähigkeit, die Momente von Trendumkehrungen und -fortsetzungen mit den Werten des Lyapunov-Exponenten zu vergleichen. So können wir statistische Muster zwischen dem chaotischen Verhalten des Marktes und seiner Preisdynamik erkennen. Das Skript berechnet die Anzahl der Trendumkehrungen und -fortsetzungen, die bei positiven und negativen Werten des Lyapunov-Exponenten auftreten.

Nach Abschluss der Analyse zeigt das Skript detaillierte Statistiken an, einschließlich absoluter Werte und Prozentsätze von Trendumkehrungen und -fortsetzungen für positive und negative Werte des Lyapunov-Exponenten. Anhand dieser Informationen können Händler einschätzen, wie oft Trendumkehrungen mit Perioden erhöhter Marktvolatilität zusammenfallen und umgekehrt, wie oft Trendfortsetzungen mit stabileren Perioden korrespondieren.

Auswertung der Ergebnisse der statistischen Analyse

Die Ergebnisse der statistischen Analyse von Trendumkehrungen und -fortsetzungen unter Verwendung des Lyapunov-Exponenten liefern interessante Daten über die Dynamik des EURUSD-Marktes auf dem stündlichen Zeitrahmen.

Zunächst wird auf die nahezu gleichmäßige Verteilung der Ereignisse zwischen positiven und negativen Werten des Lyapunov-Exponenten hingewiesen. Sowohl Umkehrungen als auch Trendfortsetzungen werden in etwa der Hälfte der Fälle mit positiven und negativen Lyapunov-Exponenten beobachtet. Dies könnte darauf hinweisen, dass der EURUSD-Markt auf H1 ein Gleichgewicht zwischen Phasen relativer Stabilität und Chaos aufweist.

Positive Werte des Lyapunov-Exponenten, die typischerweise mit chaotischem, unvorhersehbarem Verhalten verbunden sind, werden in etwas mehr als der Hälfte aller Fälle beobachtet (50,61 % für Umkehrungen und 51,09 % für Fortsetzungen). Dies könnte auf ein leichtes Überwiegen von Zeiten erhöhter Volatilität oder Unsicherheit auf dem Markt hindeuten.

Negative Werte des Lyapunov-Exponenten, die in der Regel als Zeichen für ein geordneteres, weniger chaotisches Verhalten des Systems interpretiert werden, werden bei 49,39 % der Umkehrungen und 48,91 % der Trendfortsetzungen beobachtet. Diese Zeiträume können durch eine besser vorhersehbare, bestimmten Mustern folgende Kursentwicklung gekennzeichnet sein.

Interessanterweise ist der Prozentsatz der Trendumkehrungen und -fortsetzungen sowohl bei positiven als auch bei negativen Ljapunow-Werten fast identisch. Der Unterschied beträgt in beiden Fällen weniger als 0,5 %. Dies könnte darauf hindeuten, dass der Lyapunov-Exponent selbst kein entscheidender Faktor für die Vorhersage einer Trendumkehr oder -fortsetzung ist.

Diese gleichmäßige Verteilung von Ereignissen zwischen positiven und negativen Ljapunow-Werten könnte auf die komplexe Natur des EURUSD-Marktes hinweisen, auf dem sich Phasen der Stabilität und des Chaos mit ungefähr gleicher Häufigkeit abwechseln. 

Schlussfolgerung

Die Chaostheorie bietet einen innovativen Ansatz für die Analyse von Finanzmärkten und ermöglicht ein tieferes Verständnis ihrer komplexen und nichtlinearen Natur. In diesem Artikel haben wir uns mit den Schlüsselkonzepten der Chaostheorie (Attraktoren, Fraktale und der Schmetterlingseffekt) und ihrer Anwendung auf Finanzzeitreihen beschäftigt. Besonderes Augenmerk wurde auf den Lyapunov-Exponenten als Instrument zur Bewertung des Grades des Chaos in der Marktdynamik gelegt.