Datenwissenschaft und maschinelles Lernen (Teil 09): Der Algorithmus K-Nächste-Nachbarn (K-Nearest Neighbors, KNN)
412
0
Gleich und gleich gesellt sich gern - die Idee hinter dem KNN-Algorithmus.
Der Algorithmus K-Nächste-Nachbarn ist ein nicht-parametrischer überwachter Lernklassifikator, der die Nähe nutzt, um Klassifizierungen oder Vorhersagen über die Gruppierung eines einzelnen Datenpunktes zu treffen. Er wird häufig als Klassifizierungsalgorithmus verwendet, da er davon ausgeht, dass ähnliche Punkte im Datensatz nahe beieinander liegen. Der Algorithmus K-Nächste-Nachbarn ist einer der einfachsten Algorithmen des überwachten maschinellen Lernens. Wir werden unseren Algorithmus in diesem Artikel als Klassifikator aufbauen.
Bildquelle: skicit-learn.org
Ein paar Dinge zu beachten:
- Er wird häufig als Klassifikator verwendet, er kann aber auch für Regressionen eingesetzt werden.
- K-NN ist ein nichtparametrischer Algorithmus, d. h. er macht keine Annahmen über die zugrunde liegenden Daten.
- Der Algorithmus wird oft als "lernfaul" bezeichnet, weil er nicht aus dem Trainingsset lernt, sondern die Daten speichert und während der Zeit der Aktion verwendet.
- Der KNN-Algorithmus geht von der Ähnlichkeit zwischen den neuen Daten und dem vorhandenen Datensatz aus und ordnet die neuen Daten in die Kategorie ein, die den vorhandenen Kategorien am ähnlichsten ist.
Wie funktioniert KNN?
Bevor wir mit dem Schreiben von Code beginnen, sollten wir verstehen, wie der KNN-Algorithmus funktioniert;- Schritt 01: Auswahl der Anzahl k der Nachbarn
- Schritt 02: Berechnung des euklidischen Abstands eines Punktes zu allen Mitgliedern des Datensatzes
- Schritt 03: Auswahl der k nächsten Nachbarn entsprechend dem euklidischen Abstand
- Schritt 04: Zählen die Anzahl der Datenpunkte in jeder Kategorie unter diesen nächsten Nachbarn
- Schritt 05: Ordnen der neuen Datenpunkte der Kategorie zu, für die die Anzahl der Nachbarn am höchsten ist.
Schritt 01: Auswahl der Anzahl k der Nachbarn
Dies ist ein einfacher Schritt, alles was wir tun müssen, ist die Anzahl von k auszuwählen, die wir in unserer Klasse CKNNnearestNeighbors verwenden werden, dies wirft nun die Frage auf, wie wir k wählen werden.Wie können wir k beziffern?
k ist die Anzahl der nächsten Nachbarn, die zur Abstimmung darüber herangezogen werden, wo der gegebene Wert/Punkt hingehört. Die Wahl einer kleinen Anzahl k führt zu einer Menge Rauschen in den klassifizierten Datenpunkten, was zu einer höheren Anzahl von Verzerrungen führen kann. Eine größere Anzahl k macht den Algorithmus jedoch deutlich langsamer.
Dieser Fall tritt am häufigsten auf, wenn es 2 Kategorien zu klassifizieren gibt. Wir werden sehen, was wir tun können, wenn solche Situationen später auftreten, wenn es eine Menge Kategorien für die k Nachbarn gibt.
In unserer Clustering-Bibliothek erstellen wir eine Funktion, um die verfügbaren Klassen aus der Matrix der Datensätze zu erhalten und sie in einem globalen Klassenvektor namens m_classesVector zu speichern
vector CKNNNearestNeighbors::ClassVector() { vector t_vectors = Matrix.Col(m_cols-1); //target variables are found on the last column in the matrix vector temp_t = t_vectors, v = {t_vectors[0]}; for (ulong i=0, count =1; i<m_rows; i++) //counting the different neighbors { for (ulong j=0; j<m_rows; j++) { if (t_vectors[i] == temp_t[j] && temp_t[j] != -1000) { bool count_ready = false; for(ulong n=0;n<v.Size();n++) if (t_vectors[i] == v[n]) count_ready = true; if (!count_ready) { count++; v.Resize(count); v[count-1] = t_vectors[i]; temp_t[j] = -1000; //modify so that it can no more be counted } else break; //Print("t vectors vector ",t_vectors); } else continue; } } return(v); }
CKNNNearestNeighbors::CKNNNearestNeighbors(matrix<double> &Matrix_) { Matrix.Copy(Matrix_); k = (int)round(MathSqrt(Matrix.Rows())); k = k%2 ==0 ? k+1 : k; //make sure the value of k ia an odd number m_rows = Matrix.Rows(); m_cols = Matrix.Cols(); m_classesVector = ClassVector(); Print("classes vector | Neighbors ",m_classesVector); }
Ausgabe:
2022.10.31 05:40:33.825 TestScript classes vector | Neighbors [1,0]
Wenn Sie auf den Konstruktor geachtet haben, gibt es eine Zeile, die sicherstellt, dass der Wert von k eine ungerade Zahl ist, nachdem er standardmäßig als Quadratwurzel aus der Gesamtzahl der Zeilen im Datensatz/Anzahl der Datenpunkte generiert wurde; Es gibt einen anderen Konstruktor, der die Einstellung des Wertes von k ermöglicht, aber der Wert wird dann überprüft, um sicherzustellen, dass es sich um eine ungerade Zahl handelt; der Wert von k ist in diesem Fall 3, bei 9 Zeilen also √9 = 3 (ungerade Zahl)
CKNNNearestNeighbors:: CKNNNearestNeighbors(matrix<double> &Matrix_, uint k_) { k = k_; if (k %2 ==0) printf("K %d is an even number, It will be added by One so it becomes an odd Number %d",k,k=k+1); Matrix.Copy(Matrix_); m_rows = Matrix.Rows(); m_cols = Matrix.Cols(); m_classesVector = ClassVector(); Print("classes vector | Neighbors ",m_classesVector); }
Um die Bibliothek zu erstellen, werden wir den unten stehenden Datensatz verwenden. Danach werden wir sehen, wie wir Handelsinformationen verwenden können, um daraus etwas im MetaTrader zu machen.
Hier sehen Sie, wie diese Daten in MetaEditor aussehen;
matrix Matrix = {//weight(kg) | height(cm) | class {51, 167, 1}, //underweight {62, 182, 0}, //Normal {69, 176, 0}, //Normal {64, 173, 0}, //Normal {65, 172, 0}, //Normal {56, 174, 1}, //Underweight {58, 169, 0}, //Normal {57, 173, 0}, //Normal {55, 170, 0} //Normal };
Schritt 02: Berechnen des euklidischen Abstands eines Punktes zu allen Mitgliedern des Datensatzes
Angenommen, wir wissen nicht, wie man den Body-Mass-Index berechnet, aber wir wollen wissen, wo eine Person mit einem Gewicht von 57 kg und einer Größe von 170 cm zwischen den Kategorien normal- und untergewichtig liegt.
vector v = {57, 170}; nearest_neighbors = new CKNNNearestNeighbors(Matrix); //calling the constructor and passing it the matrix nearest_neighbors.KNNAlgorithm(v); //passing this new points to the algorithm
Die Funktion KNNAlgorithm ermittelt zunächst den euklidischen Abstand zwischen dem angegebenen Punkt und allen Punkten des Datensatzes.
vector vector_2; vector euc_dist; euc_dist.Resize(m_rows); matrix temp_matrix = Matrix; temp_matrix.Resize(Matrix.Rows(),Matrix.Cols()-1); //remove the last column of independent variables for (ulong i=0; i<m_rows; i++) { vector_2 = temp_matrix.Row(i); euc_dist[i] = Euclidean_distance(vector_,vector_2); }
Innerhalb der Funktion Euklidischer Abstand:
double CKNNNearestNeighbors:: Euclidean_distance(const vector &v1,const vector &v2) { double dist = 0; if (v1.Size() != v2.Size()) Print(__FUNCTION__," v1 and v2 not matching in size"); else { double c = 0; for (ulong i=0; i<v1.Size(); i++) c += MathPow(v1[i] - v2[i], 2); dist = MathSqrt(c); } return(dist); }
Ich habe den Euklidischen Abstand als Methode zur Messung des Abstands zwischen zwei Punkten in dieser Bibliothek gewählt, aber das ist nicht die einzige Methode. Sie können andere Methoden wie Rectilinear Abstand oder den Manhattan-Abstand verwenden, einige wurden in dem vorigen Artikel diskutiert.
Print("Euclidean distance vector\n",euc_dist); Output -----------> CS 0 19:29:09.057 TestScript Euclidean distance vector CS 0 19:29:09.057 TestScript [6.7082,13,13.41641,7.61577,8.24621,4.12311,1.41421,3,2]
Lassen Sie uns nun den euklidischen Abstand in die letzte Spalte der Matrix eintragen;
if (isdebug) { matrix dbgMatrix = Matrix; //temporary debug matrix dbgMatrix.Resize(dbgMatrix.Rows(),dbgMatrix.Cols()+1); dbgMatrix.Col(euc_dist,dbgMatrix.Cols()-1); Print("Matrix w Euclidean Distance\n",dbgMatrix); ZeroMemory(dbgMatrix); }
Ausgabe:
CS 0 19:33:48.862 TestScript Matrix w Euclidean Distance CS 0 19:33:48.862 TestScript [[51,167,1,6.7082] CS 0 19:33:48.862 TestScript [62,182,0,13] CS 0 19:33:48.862 TestScript [69,176,0,13.41641] CS 0 19:33:48.862 TestScript [64,173,0,7.61577] CS 0 19:33:48.862 TestScript [65,172,0,8.24621] CS 0 19:33:48.862 TestScript [56,174,1,4.12311] CS 0 19:33:48.862 TestScript [58,169,0,1.41421] CS 0 19:33:48.862 TestScript [57,173,0,3] CS 0 19:33:48.862 TestScript [55,170,0,2]]
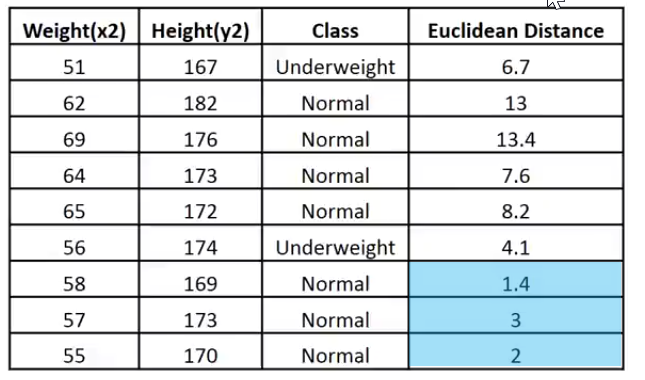
Ich möchte diese Daten zur leichteren Interpretation in ein Bild übertragen:
Da der Wert von k 3 ist, fallen die 3 nächsten Nachbarn alle in die Klasse Normal, so dass wir manuell wissen, dass der gegebene Punkt in die Kategorie Normal fällt.
Um die nächsten Nachbarn zu bestimmen und sie aufzuspüren, ist es sehr schwierig, mit Vektoren zu arbeiten, Arrays sind flexibel für die Aufteilung und Umformung, lassen Sie uns diesen Prozess mit ihnen abschließen
int size = (int)m_target.Size(); double tarArr[]; ArrayResize(tarArr, size); double eucArray[]; ArrayResize(eucArray, size); for(ulong i=0; i<m_target.Size(); i++) //convert the vectors to array { tarArr[i] = m_target[i]; eucArray[i] = euc_dist[i]; } double track[], NN[]; ArrayCopy(track, tarArr); int max; for(int i=0; i<(int)m_target.Size(); i++) { if(ArraySize(track) > (int)k) { max = ArrayMaximum(eucArray); ArrayRemove(eucArray, max, 1); ArrayRemove(track, max, 1); } } ArrayCopy(NN, eucArray); Print("NN "); ArrayPrint(NN); Print("Track "); ArrayPrint(track);
In dem obigen Codeblock werden die nächsten Nachbarn ermittelt und in einem NN-Array gespeichert, außerdem werden ihre Klassenwerte bzw. ihre Klassenzugehörigkeit im globalen Vektor der Zielwerte verfolgt. Darüber hinaus entfernen wir die Maximalwerte aus dem Array, bis wir mit einem k-großen Array kleinerer Werte dastehen (Nächste Nachbarn).
Nachfolgend finden Sie die Ausgabe:
CS 0 05:40:33.825 TestScript NN CS 0 05:40:33.825 TestScript 1.4 3.0 2.0 CS 0 05:40:33.825 TestScript Track CS 0 05:40:33.825 TestScript 0.0 0.0 0.0
Abstimmungsprozess (voting):
//--- Voting process vector votes(m_classesVector.Size()); for(ulong i=0; i<votes.Size(); i++) { int count = 0; for(ulong j=0; j<track.Size(); j++) { if(m_classesVector[i] == track[j]) count++; } votes[i] = (double)count; if(votes.Sum() == k) //all members have voted break; } Print("votes ", votes);
Ausgabe:
2022.10.31 05:40:33.825 TestScript votes [0,3]
Der Stimmenvektor ordnet die Stimmen auf der Grundlage des globalen Vektors der im Datensatz verfügbaren Klassen an, erinnern Sie sich?
2022.10.31 06:43:30.095 TestScript classes vector | Neighbors [1,0]
Dies sagt uns nun, dass von den 3 Nachbarn, die zur Stimmabgabe ausgewählt wurden, 3 dafür gestimmt haben, dass die gegebenen Daten zur Klasse der Nullen (0) gehören, und kein Mitglied hat für die Klasse der Einsen (1) gestimmt.
Schauen wir uns an, was passiert wäre, wenn 5 Nachbarn gewählt worden wären, d.h. wenn der Wert von k 5 gewesen wäre.
CS 0 06:43:30.095 TestScript NN CS 0 06:43:30.095 TestScript 6.7 4.1 1.4 3.0 2.0 CS 0 06:43:30.095 TestScript Track CS 0 06:43:30.095 TestScript 1.0 1.0 0.0 0.0 0.0 CS 0 06:43:30.095 TestScript votes [2,3]
Nun ist die endgültige Entscheidung leicht zu treffen: Die Klasse mit der höchsten Stimmenzahl hat die Entscheidung gewonnen. In diesem Fall gehört das angegebene Gewicht zur normalen Klasse, die mit 0 kodiert ist.
if(isdebug) Print(vector_, " belongs to class ", (int)m_classesVector[votes.ArgMax()]);
Ausgabe:
2022.10.31 06:43:30.095 TestScript [57,170] belongs to class 0
Großartig, jetzt funktioniert alles prima. Ändern wir den Typ von KNNAlgorithm von void auf int, damit er den Wert der Klasse zurückgibt, zu der der gegebene Wert gehört, das könnte sich im Live-Handel als nützlich erweisen, da wir die neuen Werte einfügen werden, von denen wir eine sofortige Ausgabe vom Algorithmus erwarten.
int KNNAlgorithm(vector &vector_);
Testen des Modells und Ermittlung seiner Genauigkeit.
Nun, da wir das Modell haben, müssen wir es wie jedes andere überwachte maschinelle Lernverfahren trainieren und mit Daten testen, die es vorher noch nicht gesehen hat. Der Testprozess hilft uns zu verstehen, wie unser Modell bei verschiedenen Datensätzen abschneiden kann.
float TrainTest(double train_size=0.7)
Standardmäßig werden 70 % des Datensatzes für das Training verwendet, während die restlichen 30 % für die Tests verwendet werden.
Wir müssen den Code für die Funktion zur Aufteilung des Datensatzes für die Trainings- und Testphase erstellen:
^//--- Split the matrix matrix default_Matrix = Matrix; int train = (int)MathCeil(m_rows*train_size), test = (int)MathFloor(m_rows*(1-train_size)); if (isdebug) printf("Train %d test %d",train,test); matrix TrainMatrix(train,m_cols), TestMatrix(test,m_cols); int train_index = 0, test_index =0; //--- for (ulong r=0; r<Matrix.Rows(); r++) { if ((int)r < train) { TrainMatrix.Row(Matrix.Row(r),train_index); train_index++; } else { TestMatrix.Row(Matrix.Row(r),test_index); test_index++; } } if (isdebug) Print("TrainMatrix\n",TrainMatrix,"\nTestMatrix\n",TestMatrix);
Ausgabe:
CS 0 09:51:45.136 TestScript TrainMatrix CS 0 09:51:45.136 TestScript [[51,167,1] CS 0 09:51:45.136 TestScript [62,182,0] CS 0 09:51:45.136 TestScript [69,176,0] CS 0 09:51:45.136 TestScript [64,173,0] CS 0 09:51:45.136 TestScript [65,172,0] CS 0 09:51:45.136 TestScript [56,174,1] CS 0 09:51:45.136 TestScript [58,169,0]] CS 0 09:51:45.136 TestScript TestMatrix CS 0 09:51:45.136 TestScript [[57,173,0] CS 0 09:51:45.136 TestScript [55,170,0]]
Das Training des des Algorithmus Nächster-Nachbar ist also sehr einfach. Man könnte meinen, dass es überhaupt kein Training gibt, denn wie bereits gesagt, versucht dieser Algorithmus nicht, die Muster im Datensatz zu verstehen, im Gegensatz zu Methoden wie der logistischen Regression oder SVM, sondern speichert die Daten nur während des Trainings, um die Daten dann für Testzwecke zu verwenden.
Training:
Matrix.Copy(TrainMatrix); //That's it ??? Tests:
//--- Testing the Algorithm vector TestPred(TestMatrix.Rows()); vector v_in = {}; for (ulong i=0; i<TestMatrix.Rows(); i++) { v_in = TestMatrix.Row(i); v_in.Resize(v_in.Size()-1); //Remove independent variable TestPred[i] = KNNAlgorithm(v_in); Print("v_in ",v_in," out ",TestPred[i]); }
Ausgabe:
CS 0 09:51:45.136 TestScript v_in [57,173] out 0.0 CS 0 09:51:45.136 TestScript v_in [55,170] out 0.0
Alle Tests wären umsonst, wenn wir nicht messen, wie genau unser Modell auf dem gegebenen Datensatz ist.
Die Konfusionsmatrix.
Dies wurde bereits im zweiten Artikel dieser Reihe erläutert.
matrix CKNNNearestNeighbors::ConfusionMatrix(vector &A,vector &P) { ulong size = m_classesVector.Size(); matrix mat_(size,size); if (A.Size() != P.Size()) Print("Cant create confusion matrix | A and P not having the same size "); else { int tn = 0,fn =0,fp =0, tp=0; for (ulong i = 0; i<A.Size(); i++) { if (A[i]== P[i] && P[i]==m_classesVector[0]) tp++; if (A[i]== P[i] && P[i]==m_classesVector[1]) tn++; if (P[i]==m_classesVector[0] && A[i]==m_classesVector[1]) fp++; if (P[i]==m_classesVector[1] && A[i]==m_classesVector[0]) fn++; } mat_[0][0] = tn; mat_[0][1] = fp; mat_[1][0] = fn; mat_[1][1] = tp; } return(mat_); }
Innerhalb von TrainTest() am Ende der Funktion habe ich den folgenden Code hinzugefügt, um die Funktion abzuschließen und die Genauigkeit zurückzugeben;
matrix cf_m = ConfusionMatrix(TargetPred,TestPred); vector diag = cf_m.Diag(); float acc = (float)(diag.Sum()/cf_m.Sum())*100; Print("Confusion Matrix\n",cf_m,"\nAccuracy ------> ",acc,"%"); return(acc);
Ausgabe:
CS 0 10:34:26.681 TestScript Confusion Matrix CS 0 10:34:26.681 TestScript [[2,0] CS 0 10:34:26.681 TestScript [0,0]] CS 0 10:34:26.681 TestScript Accuracy ------> 100.0%
Natürlich musste die Genauigkeit bei hundert Prozent liegen, das Modell erhielt nur zwei Datenpunkte zum Testen, die alle der Klasse Null (der Normalklasse) angehörten, was auch stimmt.
Bis zu diesem Punkt haben wir eine voll funktionsfähige Bibliothek für K-Nächste-Nachbarn. Schauen wir uns an, wie wir sie verwenden können, um den Preis verschiedener Deviseninstrumente und Aktien vorherzusagen.
Vorbereiten des Datensatzes.
Denken Sie daran, dass es sich hier um überwachtes Lernen handelt, was bedeutet, dass ein menschliches Eingreifen erforderlich ist, um die Daten zu erstellen und sie zu beschriften, damit die Modelle wissen, was ihre Ziele sind, damit sie die Beziehung zwischen unabhängigen und Zielvariablen verstehen können.
Die unabhängigen Variablen der Wahl sind die Messwerte der ATR und der Volumensindikator, während die Zielvariable auf 1 gesetzt wird, wenn der Markt gestiegen ist, und auf 0, wenn der Markt gesunken ist; dies wird dann das Kauf- bzw. Verkaufssignal beim Testen und Verwenden des Modells zum Handeln.
int OnInit() { //--- Preparing the dataset atr_handle = iATR(Symbol(),timeframe,period); volume_handle = iVolumes(Symbol(),timeframe,applied_vol); CopyBuffer(atr_handle,0,1,bars,atr_buffer); CopyBuffer(volume_handle,0,1,bars,volume_buffer); Matrix.Col(atr_buffer,0); //Independent var 1 Matrix.Col(volume_buffer,1); //Independent var 2 //--- Target variables vector Target_vector(bars); MqlRates rates[]; ArraySetAsSeries(rates,true); CopyRates(Symbol(),PERIOD_D1,1,bars,rates); for (ulong i=0; i<Target_vector.Size(); i++) //putting the labels { if (rates[i].close > rates[i].open) Target_vector[i] = 1; //bullish else Target_vector[i] = 0; } Matrix.Col(Target_vector,2); //---
Die Logik bei der Suche nach den unabhängigen Variablen besteht darin, dass wenn der Schlusskurs über dem Eröffnungskurs liegt, mit anderen Worten eine Aufwärtskerze, die Zielvariable für die unabhängigen Variablen 1 ist, andernfalls 0.
Denken Sie daran, wir arbeiten mit Tageskerzen, eine einzelne Kerze beinhaltet eine Menge von Preisbewegungen in diesen 24 Stunden, diese Logik kann keine gute sein, wenn Sie versuchen, zu scalpen oder etwas, das in kürzeren Zeiträumen handelt. Es gibt es auch einen kleinen Fehler in der Logik, weil, wenn der Schlusskurs größer ist als der Eröffnungskurs, der Zielvariablen 1 andernfalls 0 zugewiesen wird, aber könnte passieren, dass Eröffnungs- und Schlusskurs gleich sind? Ich verstehe, dass diese Situation bei höheren Zeitrahmen eher selten auftritt, also ist dies meine Art, dem Modell Raum für Fehler zu geben.
Dies ist übrigens keine Finanz- oder Handelsberatung.
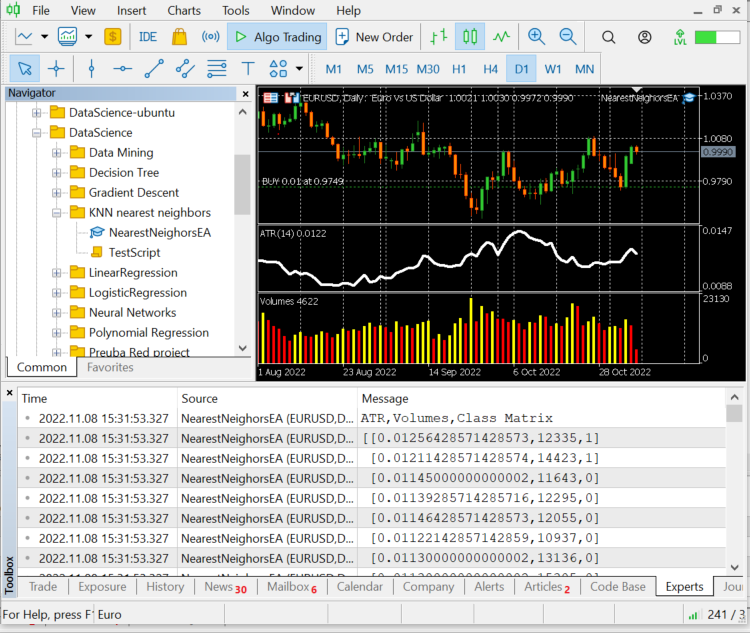
Drucken wir also die letzten 10 Werte der Kerzen, 10 Zeilen unserer Datenmatrix;
CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) ATR,Volumes,Class Matrix CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [[0.01139285714285716,12295,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01146428571428573,12055,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01122142857142859,10937,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01130000000000002,13136,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01130000000000002,15305,0] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01097857142857144,13762,1] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.0109357142857143,12545,1] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01116428571428572,18806,1] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01188571428571429,19595,1] CS 0 12:20:10.449 NearestNeighorsEA (EURUSD,D1) [0.01137142857142859,15128,1]]
Die Daten wurden anhand ihrer jeweiligen Kerzen und Indikatoren gut klassifiziert, jetzt können wir sie an den Algorithmus weitergeben.
nearest_neigbors = new CKNNNearestNeighbors(Matrix,k);
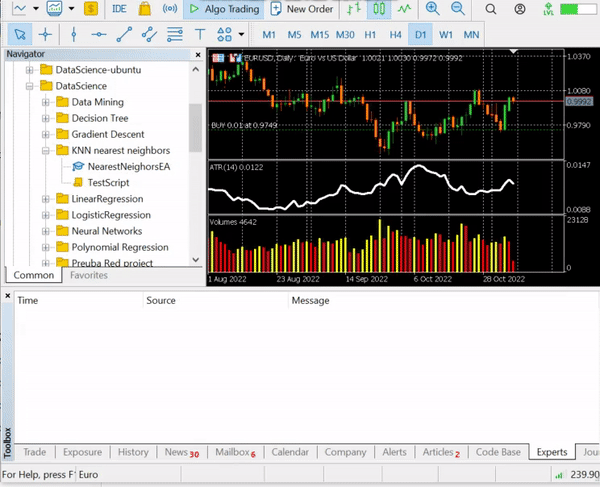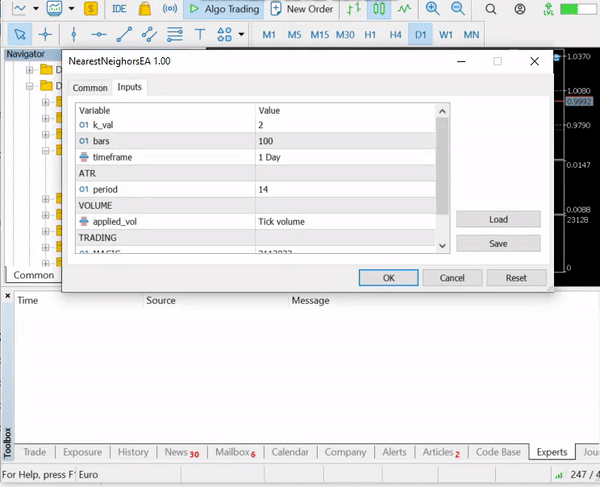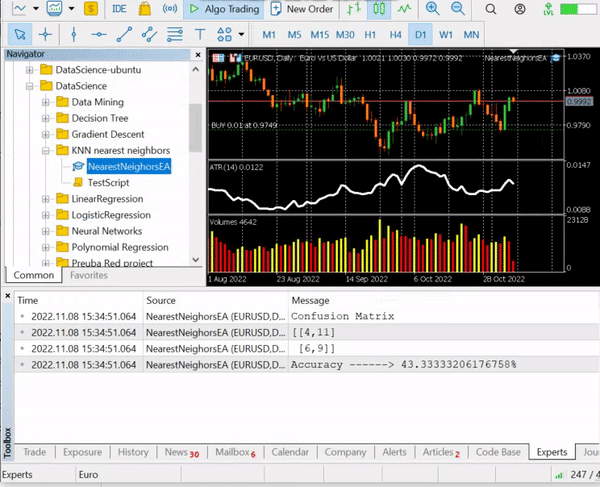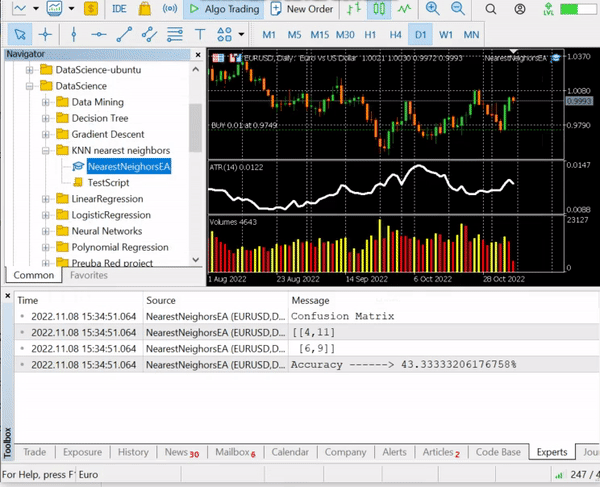
nearest_neigbors.TrainTest(); Ausgabe:
Wir haben eine Genauigkeit von ca. 43,33 %, was nicht schlecht ist, wenn man bedenkt, dass wir uns nicht die Mühe gemacht haben, den optimalen Wert von k zu finden. Wir sollten verschiedene Werte von k in einer Schleife ausprobieren und denjenigen auswählen, der eine bessere Genauigkeit bietet.
for(uint i=0; i<bars; i++) { printf("<<< k %d >>>",i); nearest_neigbors = new CKNNNearestNeighbors(Matrix,i); nearest_neigbors.TrainTest(); delete(nearest_neigbors); }
Ausgabe:
...... CS 0 16:22:28.013 NearestNeighorsEA (EURUSD,D1) <<< k 24 >>> CS 0 16:22:28.013 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 46.66666793823242% CS 0 16:22:28.014 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 46.66666793823242% CS 0 16:22:28.014 NearestNeighorsEA (EURUSD,D1) <<< k 26 >>> CS 0 16:22:28.014 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 40.0% CS 0 16:22:28.014 NearestNeighorsEA (EURUSD,D1) <<< k 27 >>> CS 0 16:22:28.015 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 40.0% CS 0 16:22:28.015 NearestNeighorsEA (EURUSD,D1) <<< k 28 >>> CS 0 16:22:28.015 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.016 NearestNeighorsEA (EURUSD,D1) <<< k 29 >>> CS 0 16:22:28.016 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.016 NearestNeighorsEA (EURUSD,D1) <<< k 30 >>> ..... ..... CS 0 16:22:28.017 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 60.000003814697266% CS 0 16:22:28.017 NearestNeighorsEA (EURUSD,D1) <<< k 31 >>> CS 0 16:22:28.017 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 60.000003814697266% CS 0 16:22:28.017 NearestNeighorsEA (EURUSD,D1) <<< k 32 >>> CS 0 16:22:28.018 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.018 NearestNeighorsEA (EURUSD,D1) <<< k 33 >>> CS 0 16:22:28.018 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.018 NearestNeighorsEA (EURUSD,D1) <<< k 34 >>> CS 0 16:22:28.019 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 50.0% CS 0 16:22:28.019 NearestNeighorsEA (EURUSD,D1) <<< k 35 >>> CS 0 16:22:28.019 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 50.0% CS 0 16:22:28.019 NearestNeighorsEA (EURUSD,D1) <<< k 36 >>> CS 0 16:22:28.020 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 53.333335876464844% CS 0 16:22:28.020 NearestNeighorsEA (EURUSD,D1) <<< k 37 >>> CS 0 16:22:28.020 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 53.333335876464844% CS 0 16:22:28.020 NearestNeighorsEA (EURUSD,D1) <<< k 38 >>> CS 0 16:22:28.021 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.021 NearestNeighorsEA (EURUSD,D1) <<< k 39 >>> CS 0 16:22:28.021 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.021 NearestNeighorsEA (EURUSD,D1) <<< k 40 >>> CS 0 16:22:28.022 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.022 NearestNeighorsEA (EURUSD,D1) <<< k 41 >>> ..... .... CS 0 16:22:28.023 NearestNeighorsEA (EURUSD,D1) <<< k 42 >>> CS 0 16:22:28.023 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 63.33333206176758% CS 0 16:22:28.023 NearestNeighorsEA (EURUSD,D1) <<< k 43 >>> CS 0 16:22:28.024 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 63.33333206176758% CS 0 16:22:28.024 NearestNeighorsEA (EURUSD,D1) <<< k 44 >>> CS 0 16:22:28.024 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 66.66667175292969% CS 0 16:22:28.024 NearestNeighorsEA (EURUSD,D1) <<< k 45 >>> CS 0 16:22:28.025 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 66.66667175292969% CS 0 16:22:28.025 NearestNeighorsEA (EURUSD,D1) <<< k 46 >>> CS 0 16:22:28.025 NearestNeighorsEA (EURUSD,D1) Accuracy ------> 56.66666793823242% CS 0 16:22:28.025 NearestNeighorsEA (EURUSD,D1) <<< k 47 >>> .... ....
Auch wenn diese Methode zur Bestimmung des Wertes von k nicht die beste ist, kann man mit der Loose-One-Out-Kreuzvalidierungsmethode die optimalen Werte von k finden. Es scheint, dass die Spitzenleistung erreicht wurde, als der Wert von k in den Vierzigern lag. Jetzt ist es an der Zeit, den Algorithmus in der Handelsumgebung einzusetzen.
void OnTick() { vector x_vars(2); //vector to store atr and volumes values double atr_val[], volume_val[]; CopyBuffer(atr_handle,0,0,1,atr_val); CopyBuffer(volume_handle,0,0,1,volume_val); x_vars[0] = atr_val[0]; x_vars[1] = volume_val[0]; //--- int signal = 0; double volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN); MqlTick ticks; SymbolInfoTick(Symbol(),ticks); double ask = ticks.ask, bid = ticks.bid; if (isNewBar() == true) //we are on the new candle { signal = nearest_neigbors.KNNAlgorithm(x_vars); //Calling the algorithm if (signal == 1) { if (!CheckPosionType(POSITION_TYPE_BUY)) { m_trade.Buy(volume,Symbol(),ask,0,0); if (ClosePosType(POSITION_TYPE_SELL)) printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_SELL),GetLastError()); } } else { if (!CheckPosionType(POSITION_TYPE_SELL)) { m_trade.Sell(volume,Symbol(),bid,0,0); if (ClosePosType(POSITION_TYPE_BUY)) printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_BUY),GetLastError()); } } } }
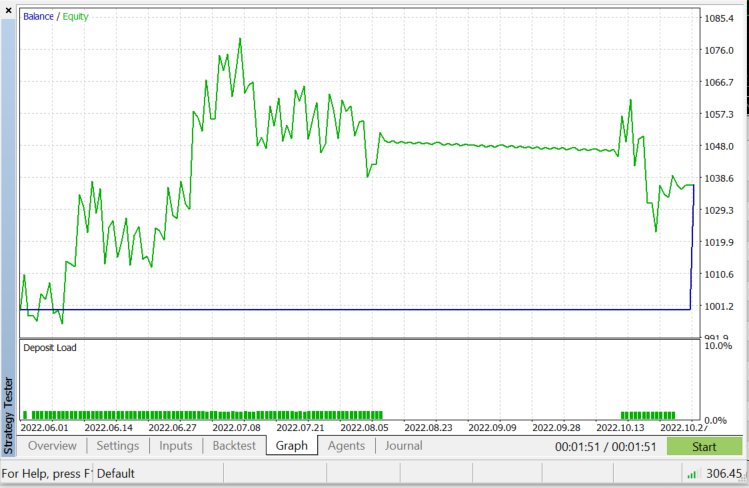
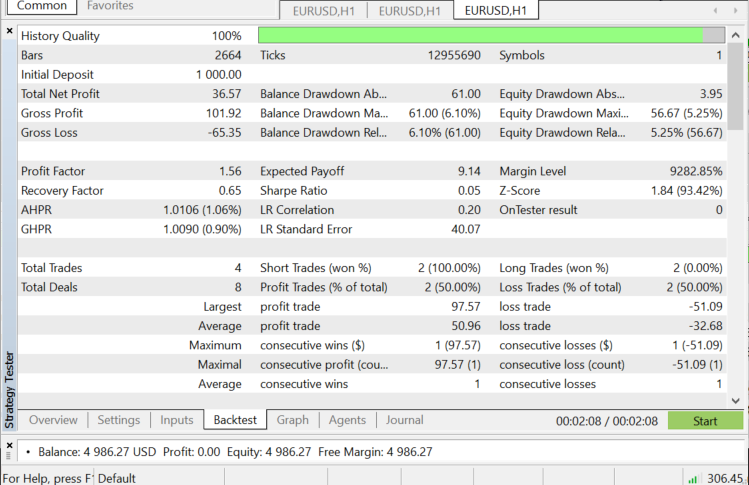
Nun, da unser EA in der Lage ist, Positionen zu öffnen und zu schließen, wollen wir es auf dem Strategie-Tester versuchen, aber vorher, Dies ist ein Überblick über den Aufruf des Algorithmus im gesamten Expert Advisor;
#include "KNN_nearest_neighbors.mqh"; CKNNNearestNeighbors *nearest_neigbors; matrix Matrix; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { // gathering data to Matrix has been ignored nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete(nearest_neigbors); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { vector x_vars(2); //vector to store atr and volumes values //adding live indicator values from the market has been ignored //--- int signal = 0; if (isNewBar() == true) //we are on the new candle { signal = nearest_neigbors.KNNAlgorithm(x_vars); //trading actions } }
Strategietester auf EURUSD: für 2022.06.01 bis 2022.11.03 (Jeder Tick):
Wann sollte KNN verwendet werden?
Es ist sehr wichtig zu wissen, wo dieser Algorithmus eingesetzt werden kann, da nicht jedes Problem mit ihm gelöst werden kann, genau wie jede andere maschinelle Lerntechnik.
- Wenn der Datensatz gekennzeichnet ist.
- Wenn der Datensatz rauschfrei ist.
- Wenn der Datensatz klein ist (dies ist auch aus Leistungsgründen hilfreich)
Vorteile:
- Es ist sehr einfach zu verstehen und umzusetzen
- Es basiert auf lokalen Datenpunkten, was bei Datensätzen mit vielen Gruppen mit lokalen Clustern von Vorteil sein kann.
Nachteile
Alle Trainingsdaten werden jedes Mal verwendet, wenn wir etwas vorhersagen müssen. Das bedeutet, dass alle Daten gespeichert werden müssen und jedes Mal verwendet werden können, wenn es einen neuen Punkt zu klassifizieren gibt.
Abschließende Überlegungen
Wie gesagt, dieser Algorithmus ist ein guter Klassifikator, aber nicht auf einem komplexen Datensatz, sodass ich denke, es könnte bessere Prognosen für Aktien und Indizes geben, aber ich überlasse es Ihnen, dass selbst zu erforschen. Eine Sache, die Sie sehen, wenn Sie diesen Algorithmus in einem Expert Advisor testen, ist, dass er Leistungsprobleme auf der Strategie-Tester verursacht, obwohl nur 50 Bars ausgewählt wurden und den Roboter nur bei einer neuen Bar agiert. Der Tester würde auf jeder Kerze für wie 20 bis 30 Sekunden stecken bleiben, nur um den Algorithmus den gesamten Prozess laufen zu lassen, obwohl der Prozess beim Live-Handel schneller ist, ist es das genaue Gegenteil im Tester, Es gibt immer Raum für Verbesserungen, vor allem unter den folgenden Zeilen des Codes, weil ich die Indikatorwerte in der Funktion OnInit() abrufen konnte, so musste ich sie abrufen, trainieren und verwenden, um den Markt vorherzusagen, alles an einem Ort.
if (isNewBar() == true) //we are on the new candle { if (MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_OPTIMIZATION)) { gather_data(); nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); signal = nearest_neigbors.KNNAlgorithm(x_vars); delete(nearest_neigbors); }
Danke fürs Lesen.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/11678
Neuronale Netze leicht gemacht (Teil 28): Gradientbasierte Optimierung
Algorithmen zur Populationsoptimierung Partikelschwarm (PSO)
DoEasy. Steuerung (Teil 21): SplitContainer-Steuerung. Paneel-Trennlinie
Lernen Sie, wie man ein Handelssystem mit den Fraktalen entwickelt
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.