MetaTrader 5 / 交易
English Русский Español Deutsch 日本語 Português
preview
数据科学与机器学习（第 09 部分）：K-最近邻算法（KNN）

数据科学与机器学习（第 09 部分）：K-最近邻算法（KNN）

MetaTrader 5 — 交易 |
1 101 2
Omega J Msigwa
Omega J Msigwa

物以类聚 — KNN算法背后的理念。

K-最近邻算法是一种非参数监督学习分类器，它运用邻近度对单个数据点的分组进行分类或预测。 虽然此算法主要用于分类问题，但它也可解决回归问题。 它通常作为分类算法，由于它假设数据集中的相似点可以在彼此的附近找到。 k-最近邻算法是监督机器学习中最简单的算法之一。 我们将在本文中构筑我们的算法作为分类器。


kNN 算法

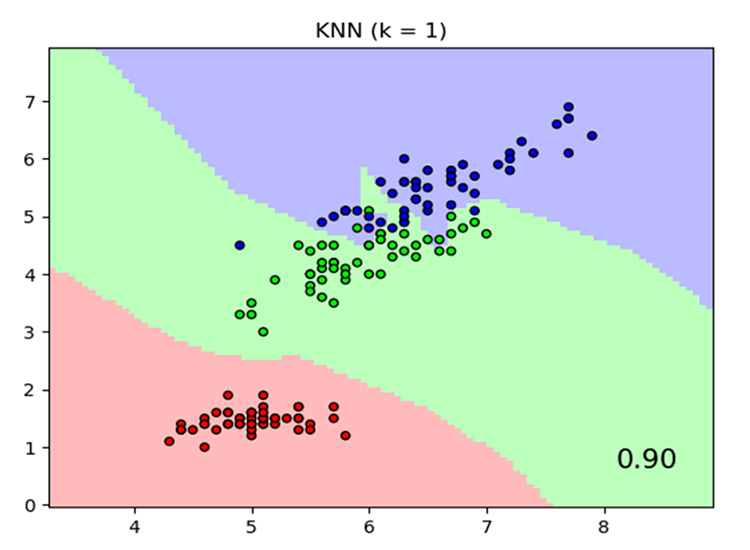
图源: skicit-learn.org

需要注意的几件事：

  1. 它通常用作分类器，但也可用于回归。
  2. K-NN 是一种非参数算法，这意味着它不会对底层数据做出任何假设。
  3. 它通常被称为惰性学习器算法，因为它不会基于训练集学习。 取而代之，它存储数据，并在操作期间使用它
  4. KNN 算法假定新数据和可用数据集之间存在相似度，并将新数据放入与可用类别最相似的类别之中。

KNN 如何运作？

在我们潜心编写代码之前，我们先了解一下 KNN 算法的工作原理：
  • 步骤 01:选择邻居的数量 k
  • 步骤 02: 计算点到数据集所有成员的欧氏距离
  • 步骤 03: 根据欧氏距离取 K 最近邻
  • 步骤 04: 在这些最近邻中，计算每个类别中的数据点数量
  • 步骤 05: 将新数据点分配给相邻要素数量最大的类别

步骤 01: 选择邻居的数量 k

这一步很简单，我们所要做的就是选择我们将在 CKNNnearestNeighbors 类中使用的 k 的数量，而这就提出了我们如何分解 k 的问题。

我们如何分解 K？

K 是针对给定值/点应属于的位置进行投票的最近邻居数量。 选择较低的 k 数值将导致分类数据点中存在大量噪声，故这可能导致较高的偏差数；而同时，较高的 k 数值会令算法明显变慢。 
k 值需要是一个奇数，从而避免卡在决策过程中，而这意味着什么呢？因为投票过程需要 k 个邻居，如果它设置为 4，然后 2 个成员投票给属于类别 A 的点，那么剩下的 2 票它属于类别 B？？ 那您如何判定哪一方赢得了决议？


当有 2 个类别需要分类时，这样的情况发生得最多，我们将看看以后当 k 个邻居有很多类别时，如果发生这样的情况，我们该怎么办。

在我们的聚类库内，我们创建一个函数从数据集矩阵中获取可用的类，并将它们存储在名为 m_classesVector 的类全局向量之中。

vector CKNNNearestNeighbors::ClassVector()
 {
   vector t_vectors = Matrix.Col(m_cols-1); //target variables are found on the last column in the matrix
   vector temp_t = t_vectors, v = {t_vectors[0]};
   
   for (ulong i=0, count =1; i<m_rows; i++) //counting the different neighbors
    {
      for (ulong j=0; j<m_rows; j++)
         {
            if (t_vectors[i] == temp_t[j] && temp_t[j] != -1000)
               {                   
                  bool count_ready = false;
                  
                  for(ulong n=0;n<v.Size();n++)
                      if (t_vectors[i] == v[n])
			 count_ready = true;
                    
                    if (!count_ready)
                      {
                        count++;
                        v.Resize(count);
                        
                        v[count-1] = t_vectors[i]; 
                        
                        temp_t[j] = -1000; //modify so that it can no more be counted
                      }
                    else 
			break;
                  //Print("t vectors vector ",t_vectors);
               }
             else
		 continue;
         }
    }
   
   return(v);
 } 

CKNNNearestNeighbors::CKNNNearestNeighbors(matrix<double> &Matrix_)
  {
    Matrix.Copy(Matrix_);

    k = (int)round(MathSqrt(Matrix.Rows())); 
    k = k%2 ==0 ? k+1 : k; //make sure the value of k ia an odd number    
    
    m_rows = Matrix.Rows();
    m_cols = Matrix.Cols();
    
   m_classesVector = ClassVector();
   Print("classes vector | Neighbors ",m_classesVector);
  }

输出:

2022.10.31 05:40:33.825 TestScript      classes vector | Neighbors [1,0]

如果您注意构造函数，这有一行可确保 k 值在默认情况下生成奇数，作为数据集中总行数/数据点数的平方根。 现在就是这种情况，当一个人决定不去干预 K 值时，换言之，他决定不调整算法。 还有另一个构造函数允许调整 k 值，但随后会检查该值，并确保它是一个奇数。 在这种情况下，K 值为 3，给定 9 行，因此 √9 = 3（奇数）

CKNNNearestNeighbors:: CKNNNearestNeighbors(matrix<double> &Matrix_, uint k_)
 {
   k = k_;
   
   if (k %2 ==0)
      printf("K %d is an even number, It will be added by One so it becomes an odd Number %d",k,k=k+1);
      
   Matrix.Copy(Matrix_);
   
   m_rows = Matrix.Rows();
   m_cols = Matrix.Cols();
   
   m_classesVector = ClassVector();
   Print("classes vector | Neighbors ",m_classesVector);
 }

为了构建函数库，我们将采用以下数据集，然后我们将看到如何利用交易信息在 MetaTrader 中挖取一些东西。

以下是此数据在 MetaEditor 中的样子：

    matrix Matrix = 
      {//weight(kg) | height(cm) | class
         {51, 167,   1}, //underweight
         {62, 182,   0}, //Normal
         {69, 176,   0}, //Normal
         {64, 173,   0}, //Normal
         {65, 172,   0}, //Normal
         {56, 174,   1}, //Underweight
         {58, 169,   0}, //Normal
         {57, 173,   0}, //Normal
         {55, 170,   0}  //Normal
      };    


步骤 02: 计算点到数据集所有成员的欧氏距离

假设我们不知道如何计算体重指数，我们想知道体重 57 公斤、身高 170 厘米的人，分别在体重不足类别、和正常类别之间处于什么位置。

    vector v = {57, 170};
    
    nearest_neighbors = new CKNNNearestNeighbors(Matrix); //calling the constructor and passing it the matrix
    nearest_neighbors.KNNAlgorithm(v);  //passing this new points to the algorithm

KNNAlgorithm 函数所做的第一件事就是找到给定点，和数据集中所有点之间的欧氏距离。

   vector vector_2;
   vector euc_dist;
   euc_dist.Resize(m_rows);
   
   matrix temp_matrix = Matrix;
   temp_matrix.Resize(Matrix.Rows(),Matrix.Cols()-1); //remove the last column of independent variables
   
   for (ulong i=0; i<m_rows; i++)
      {
         vector_2 = temp_matrix.Row(i);
         euc_dist[i] = Euclidean_distance(vector_,vector_2);
      }      

在欧几里得距离函数内部：

double CKNNNearestNeighbors:: Euclidean_distance(const vector &v1,const vector &v2)
 {
   double dist = 0;
   
   if (v1.Size() != v2.Size()) 
	Print(__FUNCTION__," v1 and v2 not matching in size");
   else
    {
       double c = 0;
         for (ulong i=0; i<v1.Size(); i++)
               c += MathPow(v1[i] - v2[i], 2); 

        dist = MathSqrt(c);
    } 
    
    return(dist);
 }

我选择欧氏距离作为测量本函数库中两点之间距离的方法，但这不是唯一的方法，您可以选用若干种方法，诸如直线距离和曼哈顿距离，在此之前的文章中曾讨论过一些。

Print("Euclidean distance vector\n",euc_dist);

输出  -----------> 

CS      0       19:29:09.057    TestScript   Euclidean distance vector
CS      0       19:29:09.057    TestScript   [6.7082,13,13.41641,7.61577,8.24621,4.12311,1.41421,3,2]

现在，我们将欧氏距离嵌入到矩阵的最后一列：

   if (isdebug)
      {  
         matrix dbgMatrix = Matrix; //temporary debug matrix
         dbgMatrix.Resize(dbgMatrix.Rows(),dbgMatrix.Cols()+1);
         dbgMatrix.Col(euc_dist,dbgMatrix.Cols()-1);
         
         Print("Matrix w Euclidean Distance\n",dbgMatrix);
         
         ZeroMemory(dbgMatrix);
      }

输出:

CS      0       19:33:48.862    TestScript   Matrix w Euclidean Distance
CS      0       19:33:48.862    TestScript   [[51,167,1,6.7082]
CS      0       19:33:48.862    TestScript    [62,182,0,13]
CS      0       19:33:48.862    TestScript    [69,176,0,13.41641]
CS      0       19:33:48.862    TestScript    [64,173,0,7.61577]
CS      0       19:33:48.862    TestScript    [65,172,0,8.24621]
CS      0       19:33:48.862    TestScript    [56,174,1,4.12311]
CS      0       19:33:48.862    TestScript    [58,169,0,1.41421]
CS      0       19:33:48.862    TestScript    [57,173,0,3]
CS      0       19:33:48.862    TestScript    [55,170,0,2]]

我把这个数据放在一个便于解释的图像：

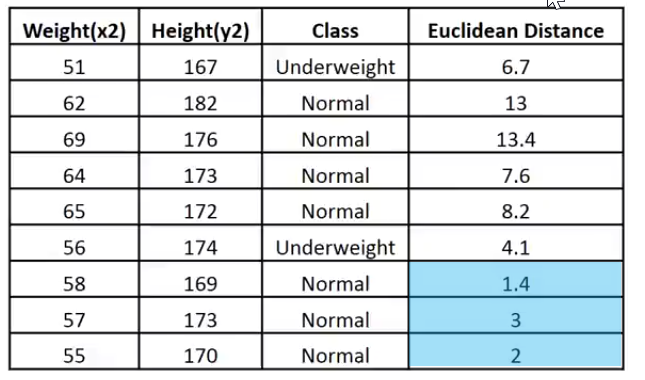
给定的 k 值为 3，3 个最近邻都属于 Normal 类，故此我们知道给定的点落在 Normal 类别，现在我们的代码能为此作出决策。 

为了能够判定最近邻，并追踪它们，使用矢量将非常困难。 数组可以更灵活地进行分片和重塑。 我们就用它们令该过程圆满完成。

   int size = (int)m_target.Size();

   double tarArr[];
   ArrayResize(tarArr, size);
   double eucArray[];
   ArrayResize(eucArray, size);

   for(ulong i=0; i<m_target.Size(); i++)  //convert the vectors to array
     {
      tarArr[i] = m_target[i];
      eucArray[i] = euc_dist[i];
     }

   double track[], NN[];
   ArrayCopy(track, tarArr);


   int max; 
   for(int i=0; i<(int)m_target.Size(); i++)
     {
      if(ArraySize(track) > (int)k)
        {
         max = ArrayMaximum(eucArray);
         ArrayRemove(eucArray, max, 1);
         ArrayRemove(track, max, 1);
        }
     }
   ArrayCopy(NN, eucArray);

   Print("NN ");
   ArrayPrint(NN);
   Print("Track ");
   ArrayPrint(track);

在上面的代码模块上，我们判定最近邻，并将它们存储在 NN 数组当中，我们还跟踪它们的类值/该类的目标值在全局向量中所处位置。 最重要的是，我们需删除数组中的最大值，最后我们只保留 k 的较小值数组（最近邻）。

下面是输出：

CS      0       05:40:33.825    TestScript    NN 
CS      0       05:40:33.825    TestScript    1.4 3.0 2.0
CS      0       05:40:33.825    TestScript    Track 
CS      0       05:40:33.825    TestScript    0.0 0.0 0.0

投票过程:

//--- Voting process

   vector votes(m_classesVector.Size());

   for(ulong i=0; i<votes.Size(); i++)
     {
      int count = 0;
      for(ulong j=0; j<track.Size(); j++)
        {
         if(m_classesVector[i] == track[j])
            count++;
        }

      votes[i] = (double)count;

      if(votes.Sum() == k)  //all members have voted
         break;
     }
   Print("votes ", votes);

输出:

2022.10.31 05:40:33.825 TestScript   votes [0,3]

投票向量根据数据集中可用类的全局向量排列投票，还记得吗？

2022.10.31 06:43:30.095 TestScript   classes vector | Neighbors [1,0]

现在，这告诉我们，在投票选出的 3 个邻居中，有 3 个投票认为给定的数据属于 zeros(0) 类，并且没有成员投票给 Ones(1) 类。

我们看看如果选择 5 个邻居投票会发生什么，即 K 值为 5。

CS      0       06:43:30.095    TestScript   NN 
CS      0       06:43:30.095    TestScript   6.7 4.1 1.4 3.0 2.0
CS      0       06:43:30.095    TestScript   Track 
CS      0       06:43:30.095    TestScript   1.0 1.0 0.0 0.0 0.0
CS      0       06:43:30.095    TestScript   votes [2,3]

现在最终的决定就很容易了，在这种情况下票数最高的类赢得决定，给定的权重属于编码为 0 的正常类。

   if(isdebug)
      Print(vector_, " belongs to class ", (int)m_classesVector[votes.ArgMax()]);

输出:

2022.10.31 06:43:30.095 TestScript      [57,170] belongs to class 0

很棒，现在一切工作正常，我们将 KNNAlgorithm 的类型从 void 更改为 int，令其返回给定值所属类的值，这可能会在实时交易中派上用场，因为我们将插入新值，期望算法立即将其输出。

   int               KNNAlgorithm(vector &vector_);


测试模型并判定其准确性。

现在我们已有了模型，就像任何其它监督机器学习技术一样，我们必须训练它，且测试过程需基于之前从未见过的数据上，这将有助于我们理解我们的模型在不同数据集上的表现。

float TrainTest(double train_size=0.7)

默认情况下，数据集的 70% 用来训练，而其余 30% 则用来测试。

我们需要为切分数据集的函数编码，从而能分阶段训练，以及分阶段测试：

^//--- Split the matrix
   
   matrix default_Matrix = Matrix; 
   
   int train = (int)MathCeil(m_rows*train_size),
       test  = (int)MathFloor(m_rows*(1-train_size));
   
   if (isdebug) printf("Train %d test %d",train,test);

   matrix TrainMatrix(train,m_cols), TestMatrix(test,m_cols);
   int train_index = 0, test_index =0;

//---
   
   for (ulong r=0; r<Matrix.Rows(); r++)
      {
         if ((int)r < train)
           {
             TrainMatrix.Row(Matrix.Row(r),train_index);
             train_index++;
           }
         else
           {
             TestMatrix.Row(Matrix.Row(r),test_index);
             test_index++;
           }     
      }

   if (isdebug) Print("TrainMatrix\n",TrainMatrix,"\nTestMatrix\n",TestMatrix);
  

输出:

CS      0       09:51:45.136    TestScript   TrainMatrix
CS      0       09:51:45.136    TestScript   [[51,167,1]
CS      0       09:51:45.136    TestScript    [62,182,0]
CS      0       09:51:45.136    TestScript    [69,176,0]
CS      0       09:51:45.136    TestScript    [64,173,0]
CS      0       09:51:45.136    TestScript    [65,172,0]
CS      0       09:51:45.136    TestScript    [56,174,1]
CS      0       09:51:45.136    TestScript    [58,169,0]]
CS      0       09:51:45.136    TestScript   TestMatrix
CS      0       09:51:45.136    TestScript   [[57,173,0]
CS      0       09:51:45.136    TestScript    [55,170,0]]

故此，最近邻算法的训练非常简单，您可能会认为根本未经训练，因为如早前所述，该算法本身不会尝试理解数据集中的形态，这与逻辑回归或 SVM 等方法不同，它只是在训练期间存储数据，然后取这些数据用于测试目的。

训练:

   Matrix.Copy(TrainMatrix); //That's it ???

测试:

//--- Testing the Algorithm
   
   vector TestPred(TestMatrix.Rows());
   vector v_in = {};
   
   for (ulong i=0; i<TestMatrix.Rows(); i++)
     {
        v_in = TestMatrix.Row(i);
        v_in.Resize(v_in.Size()-1); //Remove independent variable
        
        TestPred[i] = KNNAlgorithm(v_in);
        
        Print("v_in ",v_in," out ",TestPred[i]);
     }  

输出:

CS      0       09:51:45.136    TestScript   v_in [57,173] out 0.0
CS      0       09:51:45.136    TestScript   v_in [55,170] out 0.0

如果我们不基于给定数据集上衡量我们的模型准确度，那么所有的测试都将是徒劳的。

混淆矩阵。

在本系列早前的第二篇文章里曾予以解释。

matrix CKNNNearestNeighbors::ConfusionMatrix(vector &A,vector &P)
 {
   ulong size = m_classesVector.Size();
   matrix mat_(size,size);
   
   if (A.Size() != P.Size()) 
      Print("Cant create confusion matrix | A and P not having the same size ");
   else
     {
      
         int tn = 0,fn =0,fp =0, tp=0;
         for (ulong i = 0; i<A.Size(); i++)
            {              
               if (A[i]== P[i] && P[i]==m_classesVector[0])
                  tp++; 
               if (A[i]== P[i] && P[i]==m_classesVector[1])
                  tn++;
               if (P[i]==m_classesVector[0] && A[i]==m_classesVector[1])
                  fp++;
               if (P[i]==m_classesVector[1] && A[i]==m_classesVector[0])
                  fn++;
            }
            
       mat_[0][0] = tn; mat_[0][1] = fp;
       mat_[1][0] = fn; mat_[1][1] = tp;

    }
     
   return(mat_);    
 }

在函数末尾的 TrainTest() 中，我添加了以下代码来完成函数，并返回精确度;

   matrix cf_m = ConfusionMatrix(TargetPred,TestPred);
   vector diag = cf_m.Diag();
   float acc = (float)(diag.Sum()/cf_m.Sum())*100;
   
   Print("Confusion Matrix\n",cf_m,"\nAccuracy ------> ",acc,"%");
   
   return(acc);      

输出:

CS      0       10:34:26.681    TestScript   Confusion Matrix
CS      0       10:34:26.681    TestScript   [[2,0]
CS      0       10:34:26.681    TestScript    [0,0]]
CS      0       10:34:26.681    TestScript   Accuracy ------> 100.0%

当然，准确度必须是百分之百，模型只给出了两个用于测试的数据点，其中它们都属于 zero 类（正常类），这是真的。

至此，我们已拥有一个功能齐全的 K-最近邻函数库。 我们来看看如何利用它来预测不同的外汇产品和股票的价格。

准备数据集

请记住，这是监督学习，这意味着为了创建数据，并为其添加标签，必须存在人为干预，如此模型才会知道它们的目标是什么，以便它们能够理解自变量和目标变量之间的关系。

选取的自变量是来自 ATR 和交易量指标的读数，而如果市场上涨，目标变量将设置为 1，如果市场下跌，目标变量将设置为 0，然后在测试和利用模型进行交易时，它们分别变为买入信号和卖出信号。

int OnInit()
  {
//--- Preparing the dataset 

    atr_handle = iATR(Symbol(),timeframe,period);
    volume_handle = iVolumes(Symbol(),timeframe,applied_vol);
    
    CopyBuffer(atr_handle,0,1,bars,atr_buffer);
    CopyBuffer(volume_handle,0,1,bars,volume_buffer); 
    
    Matrix.Col(atr_buffer,0); //Independent var 1
    Matrix.Col(volume_buffer,1); //Independent var 2
    
//--- Target variables

    vector Target_vector(bars);
    
    MqlRates rates[];
    ArraySetAsSeries(rates,true);
    CopyRates(Symbol(),PERIOD_D1,1,bars,rates);
    
    for (ulong i=0; i<Target_vector.Size(); i++) //putting the labels
     {
       if (rates[i].close > rates[i].open)
          Target_vector[i] = 1; //bullish
       else
          Target_vector[i] = 0;
     }

   Matrix.Col(Target_vector,2);
        
//---

寻找自变量的逻辑是，如果蜡烛的收盘价高于其开盘，，换句话说，看涨蜡烛。 自变量的目标变量为 1，否则为 0。

现在请记住，我们在日线蜡烛上，一根蜡烛在这 24 小时内有很多次价格变动，当尝试进行剥头皮或短线交易时，这个逻辑也许不是很好，这里还有一个小缺陷，因为如果收盘价大于开盘价，我们将目标变量表示为 1，否则我们表示 0，但常常开盘价等于收盘价，对否？ 我明白，但这种情况很少发生在较高的时间帧内，所以这是我为模型提供容错空间的方式。 

顺便提一下，这不是财务要求或交易建议片言。

故此，我们打印数据集矩阵的最后 10 根柱线值，即 10 行：

CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)   ATR,Volumes,Class Matrix
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)   [[0.01139285714285716,12295,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01146428571428573,12055,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01122142857142859,10937,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01130000000000002,13136,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01130000000000002,15305,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01097857142857144,13762,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.0109357142857143,12545,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01116428571428572,18806,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01188571428571429,19595,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01137142857142859,15128,1]]


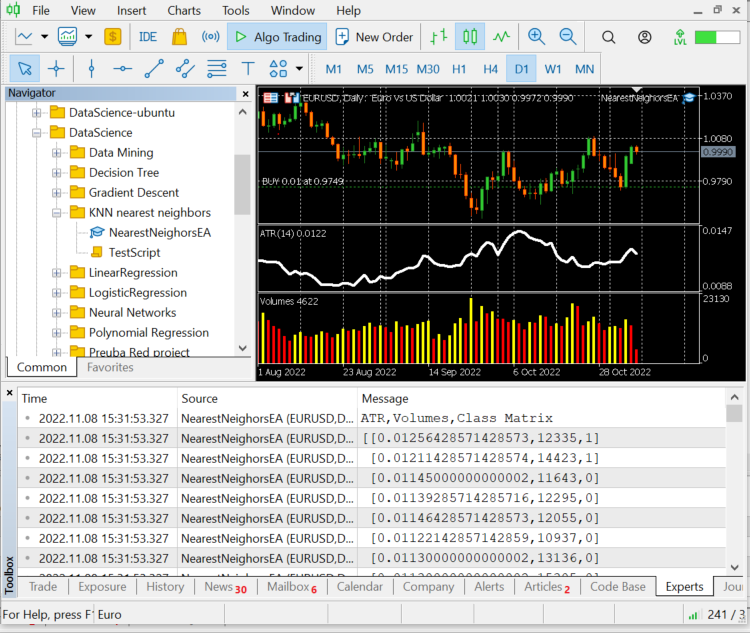
数据已从各自的蜡烛和指标中进行了很好的分类，现在我们将其传递给算法。

    nearest_neigbors = new CKNNNearestNeighbors(Matrix,k); 
    nearest_neigbors.TrainTest();

输出:


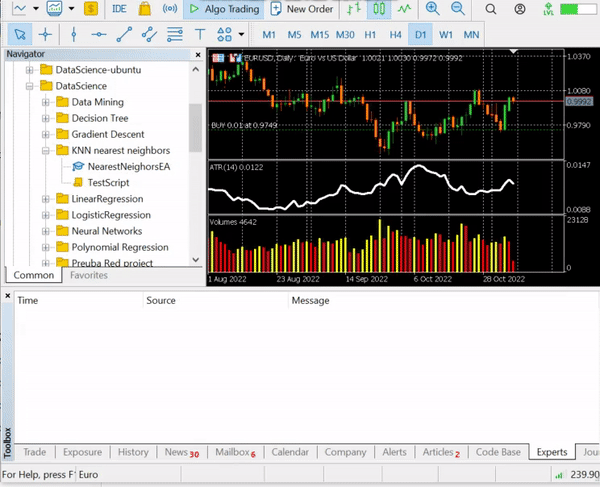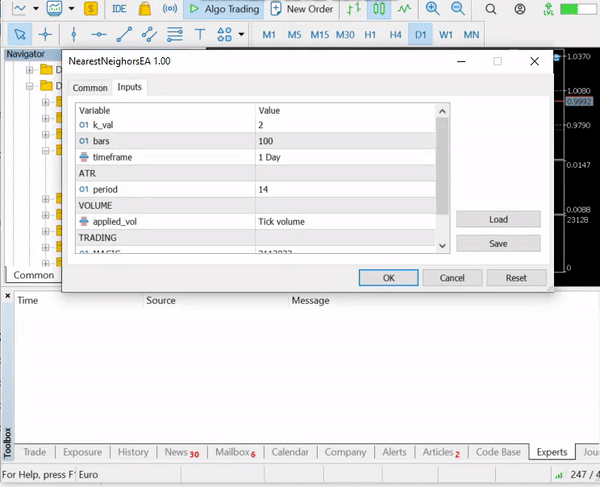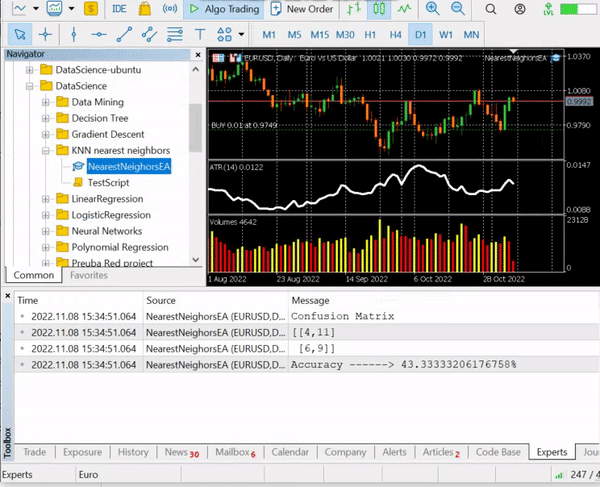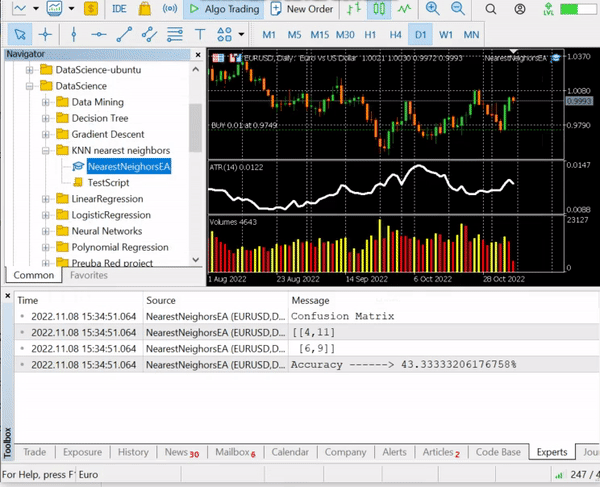
我们得到的准确度约为 43.33%，考虑到我们没有干预寻找 k 的最佳值，这还不错。 我们循环试验不同的 k 值，并选择提供更好精度的值。

    for(uint i=0; i<bars; i++)
      {
        printf("<<< k %d >>>",i);
        nearest_neigbors = new CKNNNearestNeighbors(Matrix,i); 
        nearest_neigbors.TrainTest(); 
        
        delete(nearest_neigbors);
      }

输出:

......
CS      0       16:22:28.013    NearestNeighorsEA (EURUSD,D1)   <<< k 24 >>>
CS      0       16:22:28.013    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 46.66666793823242%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 46.66666793823242%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   <<< k 26 >>>
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 40.0%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   <<< k 27 >>>
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 40.0%
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   <<< k 28 >>>
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   <<< k 29 >>>
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   <<< k 30 >>>
.....
.....
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 60.000003814697266%
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   <<< k 31 >>> 
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 60.000003814697266%
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   <<< k 32 >>> 
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   <<< k 33 >>> 
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   <<< k 34 >>> 
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 50.0%
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   <<< k 35 >>> 
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 50.0%
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   <<< k 36 >>> 
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 53.333335876464844%
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   <<< k 37 >>> 
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 53.333335876464844%
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   <<< k 38 >>> 
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   <<< k 39 >>> 
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   <<< k 40 >>> 
CS      0       16:22:28.022    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.022    NearestNeighorsEA (EURUSD,D1)   <<< k 41 >>>
.....
....
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   <<< k 42 >>>
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 63.33333206176758%
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   <<< k 43 >>>
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 63.33333206176758%
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   <<< k 44 >>>
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 66.66667175292969%
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   <<< k 45 >>>
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 66.66667175292969%
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   <<< k 46 >>>
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   <<< k 47 >>>
....
....

尽管这种判定 k 值的方法不是最佳方式，但可“省略一个交叉验证”方式来查找 k 的最佳值。 看起来，峰值性能是在 k 值处于四十附近。 现在是我们在交易环境中运用该算法的时候了。

void OnTick()
  {
  
    vector x_vars(2); //vector to store atr and volumes values
    double atr_val[], volume_val[];
    
    CopyBuffer(atr_handle,0,0,1,atr_val);
    CopyBuffer(volume_handle,0,0,1,volume_val);
    
    x_vars[0] = atr_val[0]; 
    x_vars[1] = volume_val[0];
    
//---
    int signal = 0;
    
    double volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN);
    
    MqlTick ticks;
    SymbolInfoTick(Symbol(),ticks);
    
    double ask = ticks.ask, bid = ticks.bid;
    
    
      if (isNewBar() == true) //we are on the new candle
         {
            signal = nearest_neigbors.KNNAlgorithm(x_vars); //Calling the algorithm
            
            if (signal == 1)
              {
                 if (!CheckPosionType(POSITION_TYPE_BUY))
                  {
                    m_trade.Buy(volume,Symbol(),ask,0,0);
                    if (ClosePosType(POSITION_TYPE_SELL))
                      printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_SELL),GetLastError());
                  }
              }
            else 
              {
                if (!CheckPosionType(POSITION_TYPE_SELL))
                  {
                    m_trade.Sell(volume,Symbol(),bid,0,0);
                    if (ClosePosType(POSITION_TYPE_BUY))
                      printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_BUY),GetLastError());
                  }
              }
         }
     
  }
  

现在我们的 EA 能够开仓和平仓，我们在策略测试器上尝试一下。 但在此之前，以下是在整个智能系统中调用算法的概览：

#include "KNN_nearest_neighbors.mqh";
CKNNNearestNeighbors *nearest_neigbors;

matrix Matrix;
//+------------------------------------------------------------------+
//| Expert initialization function                                     |
//+------------------------------------------------------------------+
int OnInit()
  { 
// gathering data to Matrix has been ignored
    
     nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); 
 
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- 

    delete(nearest_neigbors);
  }

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+

void OnTick()
  {
  
    vector x_vars(2); //vector to store atr and volumes values

//adding live indicator values from the market has been ignored 

//---
    int signal = 0;

      if (isNewBar() == true) //we are on the new candle
         {
            signal = nearest_neigbors.KNNAlgorithm(x_vars);
            //trading actions
         }
}

策略测试器基于 EURUSD: 从 2022.06.01 至 2022.11.03 (每次跳价):



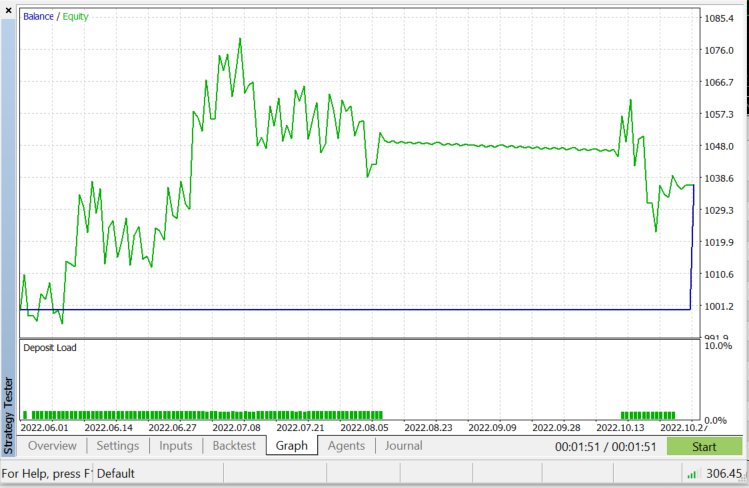
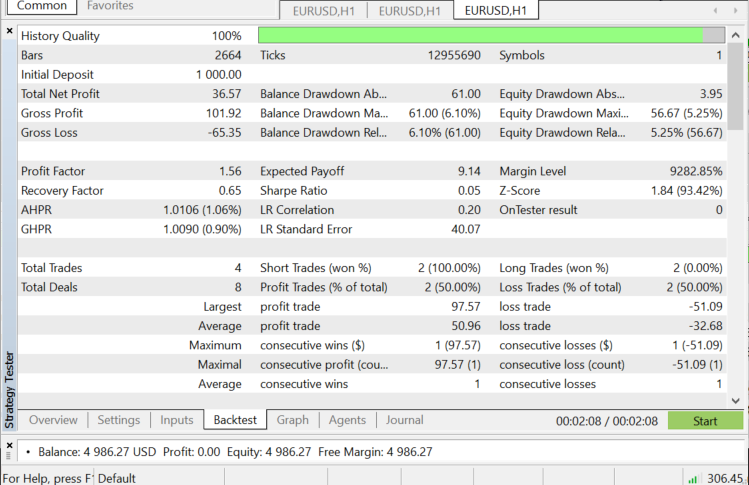
何时运用 KNN？

重要的是要知道在何处运用这种算法，因为不是每个问题都可以通过像各种机器学习技术来解决。

  • 当标记数据集时
  • 当数据集无噪声时
  • 当数据集规模较小时（这对于性能原因也很有帮助）

优势:

  • 它非常易于理解和实现 
  • 它基于局部数据点，这对于涉及具有局部聚集的许多群组的数据集可能有益

缺点

每次我们需要预测某件事时，都会用到所有训练数据，这意味着每次有新点需要分类时，都必须存储并准备所有数据供所用。


最后的随想

如前所述，该算法是一个很好的分类器，但并非针对复杂数据集，如此我认为它会在股票和指数中做出更好的预测，我把它留给您去探索。 在智能系统中测试此算法时，您将看到的一件事是，它会导致策略测试器的性能问题，即使我选择了 50 根柱线，并令机器人在新柱线开立时才行动。 测试器会在每根蜡烛上停顿 20 到 30 秒，只是为了等算法运行整个过程，即使该过程在实时交易中运行得更快，但在测试器上却完全相反。 总有改进的余地，尤其是在以下代码行下，因为我无法在 Init 函数上提取指标读数，故此我不得不在一个地方提取它们训练，并用它们来预测市场。

        if (isNewBar() == true) //we are on the new candle
         { 
           if (MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_OPTIMIZATION)) 
             {
               gather_data();      
               nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); 
               signal = nearest_neigbors.KNNAlgorithm(x_vars);
               
               delete(nearest_neigbors);
             }      

感谢您的阅读。

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/11678

附加的文件 |
下载ZIP
KNN_nearest_neighbors.zip (67.49 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

最近评论 | 前往讨论 (2)
Antonio valeriano costa
Antonio valeriano costa | 21 2月 2023 在 01:47
祝贺您的文章！我正在回顾更新。
wildyou
wildyou | 26 10月 2023 在 22:55
您好！

如果我的假设有误，请原谅，但我认为
void CKNNNearestNeighbors::VectorRemoveIndex(vector &v, ulong index)
 {
   vector new_v(v.Size()-1);
   
   for (ulong i=0, count = 0; i<v.Size(); i++)
      if (i == index)
        {
          new_v[count] = new_v[i];
          count++;
        }
 }
是无用的。代码取自 KNN_neareast_neighbors.mqh 文件。
我认为它应该删除具有特定索引的矢量元素，但它什么也没删除，因为原始矢量什么也没发生，函数什么也没返回。

我说错了吗？
您应该知道的 MQL5 向导技术（第 04 部分）：线性判别分析 您应该知道的 MQL5 向导技术（第 04 部分）：线性判别分析
今天的交易者都是哲学家，几乎总是在寻找新的想法，尝试提炼它们，选择修改或丢弃它们：一个探索性的过程，肯定会花费相当的勤奋程度。 这些系列文章将提出 MQL5 向导应该是交易者在此领域努力的中流砥柱。
DoEasy. 控件 (第 25 部分): Tooltip WinForms 对象 DoEasy. 控件 (第 25 部分): Tooltip WinForms 对象
在本文中，我将开始开发 Tooltip（工具提示）控件，以及函数库的新图形基元。 自然而然地，并非每个元素都有工具提示，但每个图形对象都有设置它的能力。
神经网络变得轻松（第三十二部分）：分布式 Q-学习 神经网络变得轻松（第三十二部分）：分布式 Q-学习
我们在本系列的早期文章中领略了 Q-学习方法。 此方法均化每次操作的奖励。 2017 年出现了两篇论文，在研究奖励分配函数时展现出了极大的成功。 我们来研究运用这种技术解决我们问题的可能性。
创建一个行情卷播面板：改进版 创建一个行情卷播面板：改进版
您如何看待复查我们的行情卷播面板基本版的主意？ 我们改进面板要做的第一件事就是能够添加图像，例如资产徽标或其它图像，从而用户可以迅速、轻松地识别所示品种。