Data Science and Machine Learning (Part 09): The K-Nearest Neighbors Algorithm (KNN)

MetaTrader 5 — Trading | 15 November 2022, 14:26

7 231

Omega J Msigwa

Birds of a feather flock together -- Idea behind KNN Algorithm.

K-Nearest Neighbors Algorithm is a non-parametric supervised learning classifier that uses proximity to make classifications or predictions about the grouping of an individual data point. While this algorithm is mostly used for classification problems, it can be used for solving a regression problem too. It is often used as a classification algorithm due to its assumption that similar points in the dataset can be found near one another. The k-nearest neighbors algorithm is one of the simplest algorithms in supervised machine learning. We will build our algorithm in this article as a classifier.

kNN algorithm

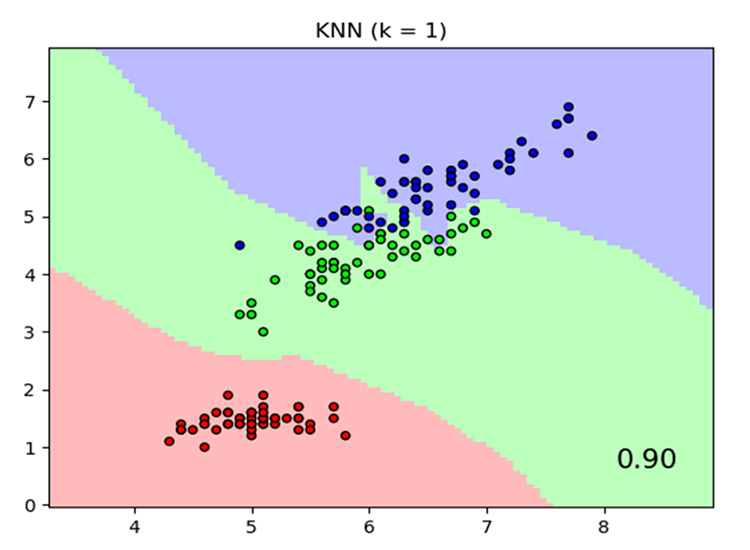
Image source: skicit-learn.org

Few things to note:

It is often used as a classifier but can be used for regression too.
K-NN is a non-parametric algorithm, which means it does not make any assumption on the underlying data.
It is often called a lazy learner algorithm because it does not learn from the training set. Instead, it stores the data and uses it during the time of action
The KNN algorithm assumes the similarity between the new data and the available dataset and put the new data into the category that is most similar to the available categories.

How do KNN works?

Before we dive into writing code let's understand how the KNN algorithm works:

Step 01: Selecting the number k of the neighbors
Step 02: Calculate the Euclidean distance of a point to all the members of the dataset
Step 03: Take the K nearest neighbors according to the Euclidean distance
Step 04: Among these nearest neighbors, count the number of data points in each category
Step 05: Assign the new data points to that category for which the number of neighbors is maximum

Step 01: Selecting the number k of the neighbors

This is a simple step, all we have to do is to select the number of k we are going to use in our CKNNnearestNeighbors class, this now raises a question of how we factor k.

How do we Factor K?

K is the number of nearest neighbors to use to cast a vote on where the given value/point should belong. Choosing the lower number of k will lead to a lot of noise in the classified data points which might lead to a higher number of bias, meanwhile, the higher number of k makes the algorithm significantly slower.

The k value needs to be an odd number to avoid getting stuck in the decision process, here is what this means because the voting process requires a k number of neighbors if it is set to like 4 then 2 members vote that the given point belongs to category A then the remaining 2 votes it belongs to category B?? how are you going to decide which side has won the decision?

This case happens the most when there are 2 categories to classify, we'll see what we can do if situations like this happen later on when there are a lot of categories for the k neighbors.

Inside our Clustering library, let us create the function to obtain the available classes from the matrix of datasets and store, them in a global vector of classes named m_classesVector

vector CKNNNearestNeighbors::ClassVector()
 {
   vector t_vectors = Matrix.Col(m_cols-1); //target variables are found on the last column in the matrix
   vector temp_t = t_vectors, v = {t_vectors[0]};
   
   for (ulong i=0, count =1; i<m_rows; i++) //counting the different neighbors
    {
      for (ulong j=0; j<m_rows; j++)
         {
            if (t_vectors[i] == temp_t[j] && temp_t[j] != -1000)
               {                   
                  bool count_ready = false;
                  
                  for(ulong n=0;n<v.Size();n++)
                      if (t_vectors[i] == v[n])
			 count_ready = true;
                    
                    if (!count_ready)
                      {
                        count++;
                        v.Resize(count);
                        
                        v[count-1] = t_vectors[i]; 
                        
                        temp_t[j] = -1000; //modify so that it can no more be counted
                      }
                    else 
			break;
                  //Print("t vectors vector ",t_vectors);
               }
             else
		 continue;
         }
    }
   
   return(v);
 }

CKNNNearestNeighbors::CKNNNearestNeighbors(matrix<double> &Matrix_)
  {
    Matrix.Copy(Matrix_);

    k = (int)round(MathSqrt(Matrix.Rows())); 
    k = k%2 ==0 ? k+1 : k; //make sure the value of k ia an odd number    
    
    m_rows = Matrix.Rows();
    m_cols = Matrix.Cols();
    
   m_classesVector = ClassVector();
   Print("classes vector | Neighbors ",m_classesVector);
  }

Output:

2022.10.31 05:40:33.825 TestScript      classes vector | Neighbors [1,0]

If you paid attention to the constructor there is a line that ensures the value of k is an odd number after it was generated by default as the square root of the total number of rows in the dataset/number of data points. Now this is the case when one decided not to bother with the value of K in other words he decided not to tune the algorithm. There is the other constructor that allows tuning for the value of k but the value then gets checked to ensure that it is an odd number. The value of K in this case is 3, given 9 rows so √9 = 3 (odd number)

CKNNNearestNeighbors:: CKNNNearestNeighbors(matrix<double> &Matrix_, uint k_)
 {
   k = k_;
   
   if (k %2 ==0)
      printf("K %d is an even number, It will be added by One so it becomes an odd Number %d",k,k=k+1);
      
   Matrix.Copy(Matrix_);
   
   m_rows = Matrix.Rows();
   m_cols = Matrix.Cols();
   
   m_classesVector = ClassVector();
   Print("classes vector | Neighbors ",m_classesVector);
 }

To build the library we are going to use the below dataset, then after we'll see how we can use trading information to make something out of this in MetaTrader.

Here is how this Data looks like in MetaEditor:

    matrix Matrix = 
      {//weight(kg) | height(cm) | class
         {51, 167,   1}, //underweight
         {62, 182,   0}, //Normal
         {69, 176,   0}, //Normal
         {64, 173,   0}, //Normal
         {65, 172,   0}, //Normal
         {56, 174,   1}, //Underweight
         {58, 169,   0}, //Normal
         {57, 173,   0}, //Normal
         {55, 170,   0}  //Normal
      };

Step 02: Calculate the Euclidean distance of a point to all the members of the dataset

Assuming that we don't know to calculate the Body mass index, we want to know the where the person with the weight of 57kg and height 170cm belongs between the underweight category and the Normal category.

    vector v = {57, 170};
    
    nearest_neighbors = new CKNNNearestNeighbors(Matrix); //calling the constructor and passing it the matrix
    nearest_neighbors.KNNAlgorithm(v);  //passing this new points to the algorithm

The first thing that the KNNAlgorithm function does is finding the Euclidean Distance between the given point and all the points in the dataset.

   vector vector_2;
   vector euc_dist;
   euc_dist.Resize(m_rows);
   
   matrix temp_matrix = Matrix;
   temp_matrix.Resize(Matrix.Rows(),Matrix.Cols()-1); //remove the last column of independent variables
   
   for (ulong i=0; i<m_rows; i++)
      {
         vector_2 = temp_matrix.Row(i);
         euc_dist[i] = Euclidean_distance(vector_,vector_2);
      }

Inside the Euclidean Distance function:

double CKNNNearestNeighbors:: Euclidean_distance(const vector &v1,const vector &v2)
 {
   double dist = 0;
   
   if (v1.Size() != v2.Size()) 
	Print(__FUNCTION__," v1 and v2 not matching in size");
   else
    {
       double c = 0;
         for (ulong i=0; i<v1.Size(); i++)
               c += MathPow(v1[i] - v2[i], 2); 

        dist = MathSqrt(c);
    } 
    
    return(dist);
 }

I have chosen the Euclidean distance as a method to measure distance between the two points in this library, but this isn't the only way, you can use several methods such as Rectilinear Distance and Manhattan distance, some were discussed in the article prior to this.

Print("Euclidean distance vector\n",euc_dist);

Output  -----------> 

CS      0       19:29:09.057    TestScript   Euclidean distance vector
CS      0       19:29:09.057    TestScript   [6.7082,13,13.41641,7.61577,8.24621,4.12311,1.41421,3,2]

Now, let's embed the Euclidean distance to the the last column of the Matrix:

   if (isdebug)
      {  
         matrix dbgMatrix = Matrix; //temporary debug matrix
         dbgMatrix.Resize(dbgMatrix.Rows(),dbgMatrix.Cols()+1);
         dbgMatrix.Col(euc_dist,dbgMatrix.Cols()-1);
         
         Print("Matrix w Euclidean Distance\n",dbgMatrix);
         
         ZeroMemory(dbgMatrix);
      }

Output:

CS      0       19:33:48.862    TestScript   Matrix w Euclidean Distance
CS      0       19:33:48.862    TestScript   [[51,167,1,6.7082]
CS      0       19:33:48.862    TestScript    [62,182,0,13]
CS      0       19:33:48.862    TestScript    [69,176,0,13.41641]
CS      0       19:33:48.862    TestScript    [64,173,0,7.61577]
CS      0       19:33:48.862    TestScript    [65,172,0,8.24621]
CS      0       19:33:48.862    TestScript    [56,174,1,4.12311]
CS      0       19:33:48.862    TestScript    [58,169,0,1.41421]
CS      0       19:33:48.862    TestScript    [57,173,0,3]
CS      0       19:33:48.862    TestScript    [55,170,0,2]]

Let me put this data is an image for easy interpretation:

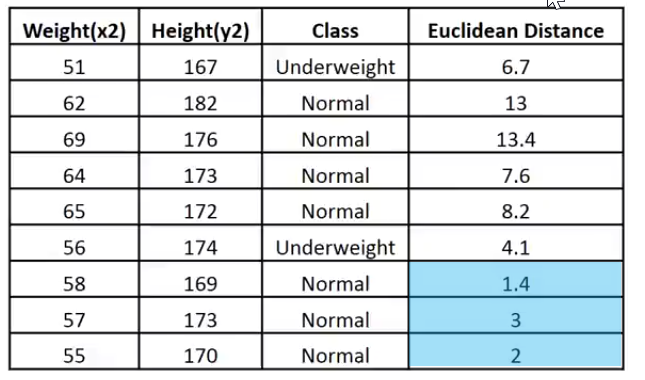
Given that the Value of k is 3, the 3 nearest neighbors all fall to the Normal class so we know manually that the given point falls under the Normal category, Now let's code for the making of this decision.

To be able to determine the Nearest Neighbors and to track them down it will be very difficult to do with vectors. Arrays are flexible for slicing and reshaping. Let's wrap up this process using them.

   int size = (int)m_target.Size();

   double tarArr[];
   ArrayResize(tarArr, size);
   double eucArray[];
   ArrayResize(eucArray, size);

   for(ulong i=0; i<m_target.Size(); i++)  //convert the vectors to array
     {
      tarArr[i] = m_target[i];
      eucArray[i] = euc_dist[i];
     }

   double track[], NN[];
   ArrayCopy(track, tarArr);


   int max; 
   for(int i=0; i<(int)m_target.Size(); i++)
     {
      if(ArraySize(track) > (int)k)
        {
         max = ArrayMaximum(eucArray);
         ArrayRemove(eucArray, max, 1);
         ArrayRemove(track, max, 1);
        }
     }
   ArrayCopy(NN, eucArray);

   Print("NN ");
   ArrayPrint(NN);
   Print("Track ");
   ArrayPrint(track);

On the above block of code we determine the nearest neighbors and store them in a NN Array, we also track their class values/which class they stand in the global vector of target values. On top of that we remove the maximum values in the array until we remain with the k sized array of smaller values (Nearest Neighbors).

Below is the output:

CS      0       05:40:33.825    TestScript    NN 
CS      0       05:40:33.825    TestScript    1.4 3.0 2.0
CS      0       05:40:33.825    TestScript    Track 
CS      0       05:40:33.825    TestScript    0.0 0.0 0.0

Voting Process:

//--- Voting process

   vector votes(m_classesVector.Size());

   for(ulong i=0; i<votes.Size(); i++)
     {
      int count = 0;
      for(ulong j=0; j<track.Size(); j++)
        {
         if(m_classesVector[i] == track[j])
            count++;
        }

      votes[i] = (double)count;

      if(votes.Sum() == k)  //all members have voted
         break;
     }
   Print("votes ", votes);

Output:

2022.10.31 05:40:33.825 TestScript   votes [0,3]

The votes vector arranges the votes based on the global vector of classes available in the dataset, remember?

2022.10.31 06:43:30.095 TestScript   classes vector | Neighbors [1,0]

This now tells us that out of 3 neighbors that were selected to cast a vote 3 of them voted that the given data belongs to the class of zeros(0), and No member voted for the class of Ones(1).

Let's see what could have happened if 5 neighbors were chosen to vote i.e. the value of K was 5.

CS      0       06:43:30.095    TestScript   NN 
CS      0       06:43:30.095    TestScript   6.7 4.1 1.4 3.0 2.0
CS      0       06:43:30.095    TestScript   Track 
CS      0       06:43:30.095    TestScript   1.0 1.0 0.0 0.0 0.0
CS      0       06:43:30.095    TestScript   votes [2,3]

Now the final decision is an easy one to make the class with the highest number of votes has won the decisionю In this case, the given weight belongs to the normal class encoded as 0.

   if(isdebug)
      Print(vector_, " belongs to class ", (int)m_classesVector[votes.ArgMax()]);

Output:

2022.10.31 06:43:30.095 TestScript      [57,170] belongs to class 0

Great, now everything works just fine let's change the type of KNNAlgorithm from void to int, to make it return the value of the class the given value belongs to, this might come in handy in live trading as we will be plugging the new values that we expect an immediate output from the algorithm.

   int               KNNAlgorithm(vector &vector_);

Testing the Model and finding it's accuracy.

Now that we have the model, just like any other supervised machine learning technique, we have to train it and test it on the data it hasn't seen before the testing process will help us understand how our model may even perform on different datasets.

float TrainTest(double train_size=0.7)

By default, 70% of the dataset will be used for training while the rest 30% will be used for testing.

We need to code for the function to Split the dataset for the training phase and the testing phase:

^//--- Split the matrix
   
   matrix default_Matrix = Matrix; 
   
   int train = (int)MathCeil(m_rows*train_size),
       test  = (int)MathFloor(m_rows*(1-train_size));
   
   if (isdebug) printf("Train %d test %d",train,test);

   matrix TrainMatrix(train,m_cols), TestMatrix(test,m_cols);
   int train_index = 0, test_index =0;

//---
   
   for (ulong r=0; r<Matrix.Rows(); r++)
      {
         if ((int)r < train)
           {
             TrainMatrix.Row(Matrix.Row(r),train_index);
             train_index++;
           }
         else
           {
             TestMatrix.Row(Matrix.Row(r),test_index);
             test_index++;
           }     
      }

   if (isdebug) Print("TrainMatrix\n",TrainMatrix,"\nTestMatrix\n",TestMatrix);

Output:

CS      0       09:51:45.136    TestScript   TrainMatrix
CS      0       09:51:45.136    TestScript   [[51,167,1]
CS      0       09:51:45.136    TestScript    [62,182,0]
CS      0       09:51:45.136    TestScript    [69,176,0]
CS      0       09:51:45.136    TestScript    [64,173,0]
CS      0       09:51:45.136    TestScript    [65,172,0]
CS      0       09:51:45.136    TestScript    [56,174,1]
CS      0       09:51:45.136    TestScript    [58,169,0]]
CS      0       09:51:45.136    TestScript   TestMatrix
CS      0       09:51:45.136    TestScript   [[57,173,0]
CS      0       09:51:45.136    TestScript    [55,170,0]]

So the training of the nearest neighbor algorithm is very simple you might consider that there is no training at all because as said earlier this algorithm itself does not try to understand the patterns in the dataset unlike methods such as logistic regression or SVM, it just stores the data during training, this data will then be used for testing purposes.

Training:

   Matrix.Copy(TrainMatrix); //That's it ???

Testing:

//--- Testing the Algorithm
   
   vector TestPred(TestMatrix.Rows());
   vector v_in = {};
   
   for (ulong i=0; i<TestMatrix.Rows(); i++)
     {
        v_in = TestMatrix.Row(i);
        v_in.Resize(v_in.Size()-1); //Remove independent variable
        
        TestPred[i] = KNNAlgorithm(v_in);
        
        Print("v_in ",v_in," out ",TestPred[i]);
     }

Output:

CS      0       09:51:45.136    TestScript   v_in [57,173] out 0.0
CS      0       09:51:45.136    TestScript   v_in [55,170] out 0.0

All the testing would be for nothing if we do not measure how accurate our model is on the given dataset.

Confusion Matrix.

Explained earlier in the second article of this series.

matrix CKNNNearestNeighbors::ConfusionMatrix(vector &A,vector &P)
 {
   ulong size = m_classesVector.Size();
   matrix mat_(size,size);
   
   if (A.Size() != P.Size()) 
      Print("Cant create confusion matrix | A and P not having the same size ");
   else
     {
      
         int tn = 0,fn =0,fp =0, tp=0;
         for (ulong i = 0; i<A.Size(); i++)
            {              
               if (A[i]== P[i] && P[i]==m_classesVector[0])
                  tp++; 
               if (A[i]== P[i] && P[i]==m_classesVector[1])
                  tn++;
               if (P[i]==m_classesVector[0] && A[i]==m_classesVector[1])
                  fp++;
               if (P[i]==m_classesVector[1] && A[i]==m_classesVector[0])
                  fn++;
            }
            
       mat_[0][0] = tn; mat_[0][1] = fp;
       mat_[1][0] = fn; mat_[1][1] = tp;

    }
     
   return(mat_);    
 }

Inside TrainTest() at the end of the function, I have added the following code to finalize the function and return the Accuracy;

   matrix cf_m = ConfusionMatrix(TargetPred,TestPred);
   vector diag = cf_m.Diag();
   float acc = (float)(diag.Sum()/cf_m.Sum())*100;
   
   Print("Confusion Matrix\n",cf_m,"\nAccuracy ------> ",acc,"%");
   
   return(acc);

Output:

CS      0       10:34:26.681    TestScript   Confusion Matrix
CS      0       10:34:26.681    TestScript   [[2,0]
CS      0       10:34:26.681    TestScript    [0,0]]
CS      0       10:34:26.681    TestScript   Accuracy ------> 100.0%

Of course, the accuracy had to be one hundred percent, the model was given only two data points for testing In which all of them belonged to the class of zero (the normal class), which is true.

To this point we have a fully function K-Nearest Neighbors library. Let's see how we can use it to predict the price of different forex instruments and Stocks.

Preparing the Dataset

Remember that this is supervised learning to mean that there must be human interference for the sake of creating the data and putting labels to it so that the models know what their goals are so they can understand the relationship between independent and target variables.

The independent variables of choice are the readings from the ATR and the Volumes indicator, while the target variable will be set to 1 if the market went up and 0 if the market went down, this will then become the buy signal and sell signal respectively when testing and using the model to trade.

int OnInit()
  {
//--- Preparing the dataset 

    atr_handle = iATR(Symbol(),timeframe,period);
    volume_handle = iVolumes(Symbol(),timeframe,applied_vol);
    
    CopyBuffer(atr_handle,0,1,bars,atr_buffer);
    CopyBuffer(volume_handle,0,1,bars,volume_buffer); 
    
    Matrix.Col(atr_buffer,0); //Independent var 1
    Matrix.Col(volume_buffer,1); //Independent var 2
    
//--- Target variables

    vector Target_vector(bars);
    
    MqlRates rates[];
    ArraySetAsSeries(rates,true);
    CopyRates(Symbol(),PERIOD_D1,1,bars,rates);
    
    for (ulong i=0; i<Target_vector.Size(); i++) //putting the labels
     {
       if (rates[i].close > rates[i].open)
          Target_vector[i] = 1; //bullish
       else
          Target_vector[i] = 0;
     }

   Matrix.Col(Target_vector,2);
        
//---

The logic of finding the independent variables is that if the closing of a candle was above its opening bullish candle in other words. The target variable for the independent variables is 1 otherwise 0.

Now remember we are on the daily candle a single candle has a lot of price movements in those 24 hours, this logic may not be a good one when trying to make a scalper or something that trades on shorter periods, there is also a minor flaw in the logic because if the closing price is greater than the open price we signify the target variable as 1 otherwise we signify 0 but there are often where the open price is equal to the close price right? I understand but this situation rarely happens on higher timeframes, so this is my way of giving the model room for errors.

This is not financial or a piece of trading advice by the way.

So let's print the last 10 bars values, 10 rows of our dataset matrix:

CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)   ATR,Volumes,Class Matrix
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)   [[0.01139285714285716,12295,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01146428571428573,12055,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01122142857142859,10937,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01130000000000002,13136,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01130000000000002,15305,0]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01097857142857144,13762,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.0109357142857143,12545,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01116428571428572,18806,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01188571428571429,19595,1]
CS      0       12:20:10.449    NearestNeighorsEA (EURUSD,D1)    [0.01137142857142859,15128,1]]

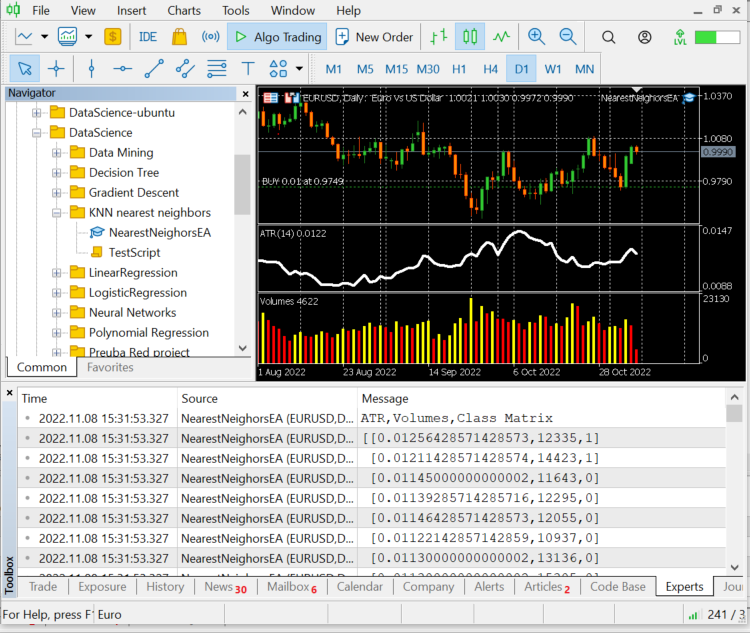
The data has been well classified from their respective candles and indicators, now let's pass it to the algorithm.

    nearest_neigbors = new CKNNNearestNeighbors(Matrix,k); 
    nearest_neigbors.TrainTest();

Output:

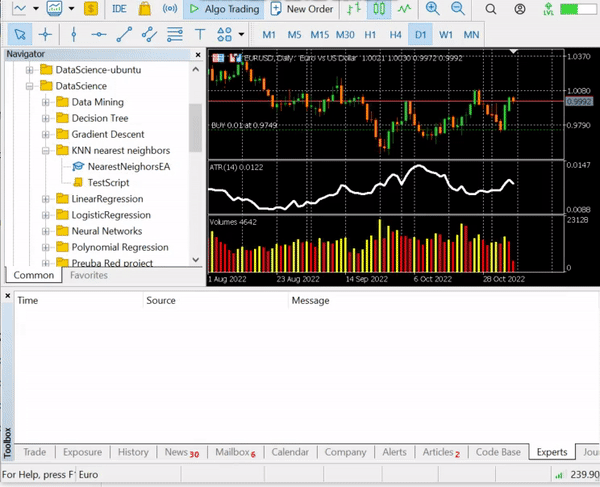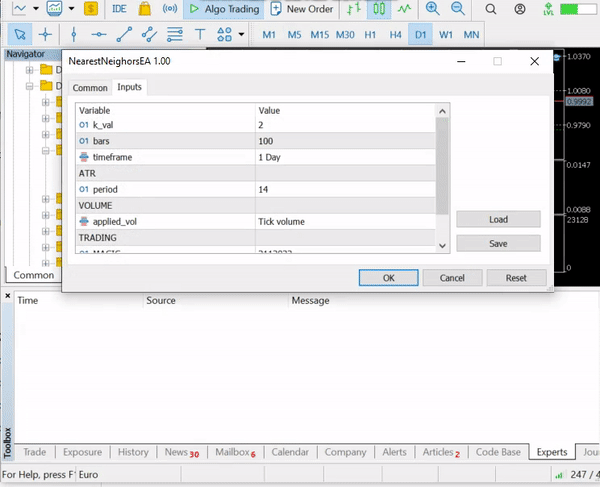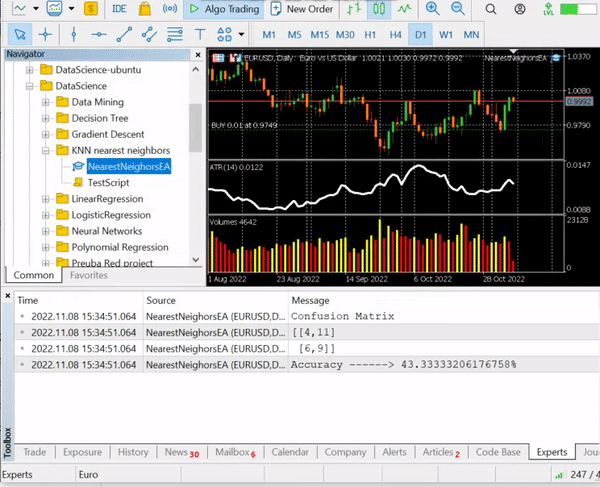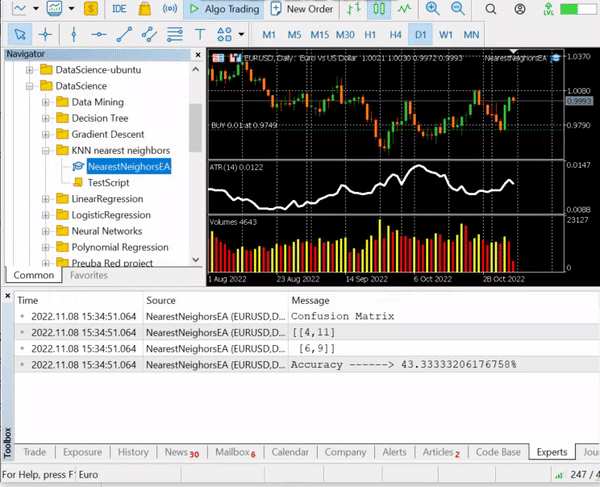
We have an accuracy of about 43.33%, not bad considering we did not bother to find the optimal value of k. Let's loop different values of k and choose the one that provides better accuracy.

    for(uint i=0; i<bars; i++)
      {
        printf("<<< k %d >>>",i);
        nearest_neigbors = new CKNNNearestNeighbors(Matrix,i); 
        nearest_neigbors.TrainTest(); 
        
        delete(nearest_neigbors);
      }

Output:

......
CS      0       16:22:28.013    NearestNeighorsEA (EURUSD,D1)   <<< k 24 >>>
CS      0       16:22:28.013    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 46.66666793823242%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 46.66666793823242%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   <<< k 26 >>>
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 40.0%
CS      0       16:22:28.014    NearestNeighorsEA (EURUSD,D1)   <<< k 27 >>>
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 40.0%
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   <<< k 28 >>>
CS      0       16:22:28.015    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   <<< k 29 >>>
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.016    NearestNeighorsEA (EURUSD,D1)   <<< k 30 >>>
.....
.....
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 60.000003814697266%
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   <<< k 31 >>> 
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 60.000003814697266%
CS      0       16:22:28.017    NearestNeighorsEA (EURUSD,D1)   <<< k 32 >>> 
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   <<< k 33 >>> 
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.018    NearestNeighorsEA (EURUSD,D1)   <<< k 34 >>> 
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 50.0%
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   <<< k 35 >>> 
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 50.0%
CS      0       16:22:28.019    NearestNeighorsEA (EURUSD,D1)   <<< k 36 >>> 
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 53.333335876464844%
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   <<< k 37 >>> 
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 53.333335876464844%
CS      0       16:22:28.020    NearestNeighorsEA (EURUSD,D1)   <<< k 38 >>> 
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   <<< k 39 >>> 
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.021    NearestNeighorsEA (EURUSD,D1)   <<< k 40 >>> 
CS      0       16:22:28.022    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.022    NearestNeighorsEA (EURUSD,D1)   <<< k 41 >>>
.....
....
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   <<< k 42 >>>
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 63.33333206176758%
CS      0       16:22:28.023    NearestNeighorsEA (EURUSD,D1)   <<< k 43 >>>
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 63.33333206176758%
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   <<< k 44 >>>
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 66.66667175292969%
CS      0       16:22:28.024    NearestNeighorsEA (EURUSD,D1)   <<< k 45 >>>
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 66.66667175292969%
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   <<< k 46 >>>
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   Accuracy ------> 56.66666793823242%
CS      0       16:22:28.025    NearestNeighorsEA (EURUSD,D1)   <<< k 47 >>>
....
....

Even though this method for determining the value of k is not the best way, one can use Leave One Out Cross-Validation method to find the optimal values of k. It appears, the peak performance was when the value of k was in the Forty's. Now it's the time we use the Algorithm in the trading environment.

void OnTick()
  {
  
    vector x_vars(2); //vector to store atr and volumes values
    double atr_val[], volume_val[];
    
    CopyBuffer(atr_handle,0,0,1,atr_val);
    CopyBuffer(volume_handle,0,0,1,volume_val);
    
    x_vars[0] = atr_val[0]; 
    x_vars[1] = volume_val[0];
    
//---
    int signal = 0;
    
    double volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN);
    
    MqlTick ticks;
    SymbolInfoTick(Symbol(),ticks);
    
    double ask = ticks.ask, bid = ticks.bid;
    
    
      if (isNewBar() == true) //we are on the new candle
         {
            signal = nearest_neigbors.KNNAlgorithm(x_vars); //Calling the algorithm
            
            if (signal == 1)
              {
                 if (!CheckPosionType(POSITION_TYPE_BUY))
                  {
                    m_trade.Buy(volume,Symbol(),ask,0,0);
                    if (ClosePosType(POSITION_TYPE_SELL))
                      printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_SELL),GetLastError());
                  }
              }
            else 
              {
                if (!CheckPosionType(POSITION_TYPE_SELL))
                  {
                    m_trade.Sell(volume,Symbol(),bid,0,0);
                    if (ClosePosType(POSITION_TYPE_BUY))
                      printf("Failed to close %s Err = %d",EnumToString(POSITION_TYPE_BUY),GetLastError());
                  }
              }
         }
     
  }

Now that our EA is capable of opening trades and closing them, let's try it on the strategy tester. But before that, this is an overview on calling the algorithm in the entire Expert Advisor:

#include "KNN_nearest_neighbors.mqh";
CKNNNearestNeighbors *nearest_neigbors;

matrix Matrix;
//+------------------------------------------------------------------+
//| Expert initialization function                                     |
//+------------------------------------------------------------------+
int OnInit()
  { 
// gathering data to Matrix has been ignored
    
     nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); 
 
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- 

    delete(nearest_neigbors);
  }

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+

void OnTick()
  {
  
    vector x_vars(2); //vector to store atr and volumes values

//adding live indicator values from the market has been ignored 

//---
    int signal = 0;

      if (isNewBar() == true) //we are on the new candle
         {
            signal = nearest_neigbors.KNNAlgorithm(x_vars);
            //trading actions
         }
}

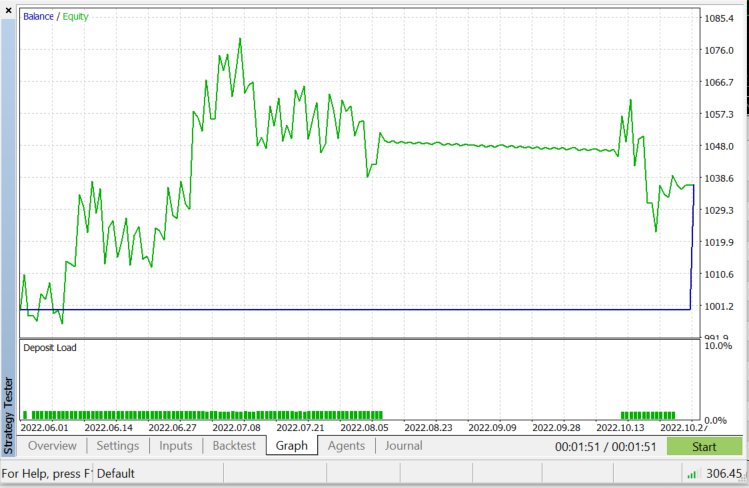
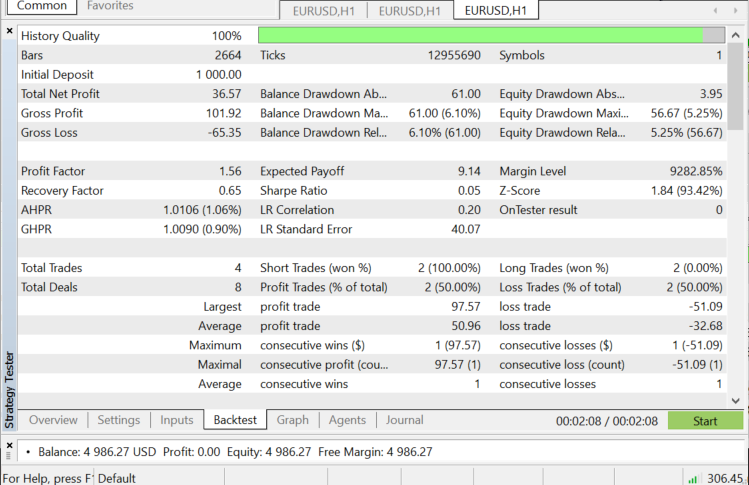
Strategy tester on EURUSD: for 2022.06.01 to 2022.11.03 (Every tick):

When to use KNN?

It is very crucial to know where to use this algorithm because not every problem can be tackled by it just like every machine-learning technique

When the dataset is labeled
When the dataset is noise-free
When the dataset is small (this is helpful for performance reasons too)

Advantages:

It is very easy to understand and implement
It is based on local data points which might be beneficial for datasets involving many groups with local clusters

Disadvantages

All training data is used every time we need to predict something, this means that all the data must be stored and ready to be used every time there is a new point to classify.

Final thoughts

As said earlier this algorithm is a good classifier but not on a complex dataset, so I think it would make better predictors in stocks and indices, I leave that for you to explore. One thing that you will see when testing this algorithm in an Expert advisor is that it causes performance issues on the strategy tester, even though I chose 50 bars and made the robot kick into action on a new bar. The tester would get stuck on every candle for like 20 to 30 seconds just to let the algorithm run the entire process even though the process goes faster on live trading it is the exact opposite on the tester. There is always room for improvement, especially under the following lines of code because I couldn't extract the indicator readings on the Init function so I had to extract them train and use them to predict the market, all in one place.

        if (isNewBar() == true) //we are on the new candle
         { 
           if (MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_OPTIMIZATION)) 
             {
               gather_data();      
               nearest_neigbors = new CKNNNearestNeighbors(Matrix,_k); 
               signal = nearest_neigbors.KNNAlgorithm(x_vars);
               
               delete(nearest_neigbors);
             }

Thanks for reading.

Attached files |

Download ZIP

KNN_nearest_neighbors.zip (67.49 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

Few things to note:

How do KNN works?

Step 01: Selecting the number k of the neighbors

Step 02: Calculate the Euclidean distance of a point to all the members of the dataset

Testing the Model and finding it's accuracy.

Confusion Matrix.

Preparing the Dataset

When to use KNN?

Disadvantages

Final thoughts

Other articles by this author