Data Science et Machine Learning - Réseaux neuronaux (Partie 01) : Le Réseau Neuronal à Propagation Avant, ou à Action Directe, Feed Forward Neural Network en anglais, démystifié
"...lassés d'en savoir trop et d'en comprendre trop peu."
- Jan Karon, Home to Holly Springs
Introduction
Les réseaux neuronaux ont l'air d'être cette nouvelle chose fantaisiste qui semble être la voie à suivre pour construire des systèmes de trading sacrés. De nombreux traders sont stupéfaits par les programmes constitués de réseaux neuronaux, car ils semblent être capables de prédire les mouvements du marché. En fait, ils sont bons pour n'importe quelle tâche. Je pense moi aussi qu'ils ont un potentiel énorme lorsqu'il s'agit de prédire ou de classer sur la base de données non formées/jamais vues.
Aussi bons soient-ils, ils doivent être construits par quelqu'un qui s'y connaît, et doivent parfois être optimisés pour s'assurer que non seulement le perceptron multicouche est dans la bonne architecture, mais aussi que le type de problème est celui qui nécessite un réseau neuronal plutôt qu'un simple modèle de régression linéaire ou logistique, ou toute autre technique d'apprentissage automatique.
Les réseaux neuronaux sont un sujet plus vaste, tout comme l'apprentissage automatique en général. C'est pourquoi j'ai décidé d'ajouter une sous-rubrique pour les réseaux neuronaux, car j'aborderai d'autres aspects de l'apprentissage automatique dans l'autre sous-rubrique de la série.
Dans cet article, nous allons voir les bases d'un réseau neuronal et répondre à certaines des questions fondamentales que je pense être importantes pour un enthousiaste du ML afin de maîtriser ce sujet.
Qu'est-ce qu'un Réseau Neuronal Artificiel ?
Les Réseaux Neuronaux Artificiels (RNA), ou Artificial Neural Network en anglais (ANN), généralement appelés réseaux neuronaux, sont des systèmes informatiques inspirés des réseaux neuronaux biologiques qui constituent le cerveau des animaux.
Perceptron Multicouche vs. Réseau Neuronal Profond
Lorsque l'on parle de réseaux neuronaux, on entend souvent le terme de Perceptron Multicouche (ou Multi-Layer Perceptron en anglais, MLP). Il s'agit du type de réseau neuronal le plus courant. Un MLP est un réseau composé d'une couche d'entrée, d'une couche cachée et d'une couche de sortie. En raison de leur simplicité, ils nécessitent des temps d'apprentissage courts pour apprendre les présentations dans les données et produire un résultat.
Applications :
Les MLP sont généralement utilisés pour les données qui ne sont pas linéairement séparables, comme l'analyse de régression. En raison de leur simplicité, ils sont particulièrement adaptés aux tâches de classification complexes et à la modélisation prédictive. Ils ont été utilisés pour la traduction automatique, les prévisions météorologiques, la détection des fraudes, les prévisions boursières, les prévisions de notation de crédit et bien d'autres aspects auxquels vous pouvez penser.
Les Réseaux Neuronaux Profonds, quant à eux, ont une structure commune, mais la seule différence est qu'ils comportent un trop grand nombre de couches cachées. Si votre réseau comporte plus de 3 couches cachées, on considère qu'il s'agit d'un réseau neuronal profond. En raison de leur complexité, ils nécessitent de longues périodes pour former le réseau sur les données d'entrée. Ils requièrent aussi des ordinateurs puissants dotés d'unités de traitement spécialisées telles que les Unités de Traitement de Tenseur, ou Tensor Processing Unit en anglais (TPU), et les Accélérateurs d’Intelligence Artificielle, ou Neural Processing Units en anglais (NPU).
Applications :
Les DNN sont des algorithmes puissants en raison de leurs couches profondes. Ils sont donc généralement utilisés pour traiter des tâches informatiques complexes, la vision par ordinateur étant l'une de ces tâches.
Tableau des différences :
| MLP | DNN |
|---|---|
| Petit nombre de couches cachées | Nombre élevé de couches cachées |
| Périodes de formation courtes | Des heures de formation plus longues |
| Un appareil équipé d'un GPU est suffisant | Le dispositif de validation de la TPU est suffisant |
Voyons maintenant les types de réseaux neuronaux.
Il existe de nombreux types de réseaux neuronaux, mais ils se répartissent grosso modo en 3 catégories principales :
- Les réseaux neuronaux à propagation avant
- Les réseaux neuronaux convolutifs
- Les réseaux neuronaux récurrents
1 - Réseau neuronal à propagation avant (Feedforward Neural Network)
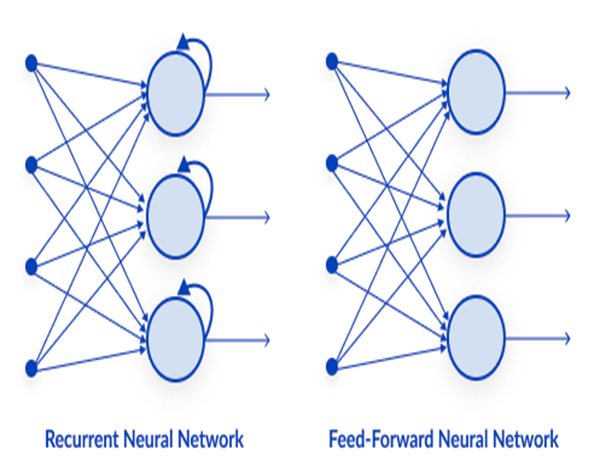
Il s'agit de l'un des types de réseaux neuronaux les plus simples. Dans un réseau neuronal de type feed-forward, les données passent par les différents nœuds d'entrée jusqu'à ce qu'elles atteignent un nœud de sortie. Contrairement à la rétro-propagation, les données se déplacent ici dans une seule direction.
Simplement, la rétro-propagation effectue les mêmes processus dans le réseau neuronal que la rétro-action où les données sont transmises de la couche d'entrée à la couche de sortie. Sauf que dans la rétro-propagation, une fois que la sortie du réseau atteint la couche de sortie, elle voit la valeur réelle d'une classe et la compare à la valeur qu'elle a prédite, le modèle voit s'il a fait des prédictions correctes ou erronées. S'il a fait une prédiction erronée, il transmet les données au réseau et met à jour ses paramètres pour qu'il prédise correctement la prochaine fois. Il s'agit d'un algorithme de type autodidacte.
2 - Réseau Neuronal Récurrent
Un réseau neuronal récurrent est un type de réseau neuronal artificiel dans lequel la sortie d'une couche particulière est enregistrée et renvoyée à la couche d'entrée. Cela permet de prédire le résultat de la couche.
Les réseaux neuronaux récurrents sont utilisés pour résoudre des problèmes liés aux données
- De séries temporelles
- Textuelles
- Audio
L'utilisation la plus courante des données textuelles est la recommandation des prochains mots à prononcer par une IA, par exemple : Comment + allez + vous + ?
03 : Réseau Neuronal à Convolution (CNN)
Les CNN font fureur dans la communauté de l'apprentissage profond. Ils prévalent dans les projets de traitement d'images et de vidéos.
Par exemple, les IA de détection et de classification d'images sont composées de réseaux neuronaux à convolution.
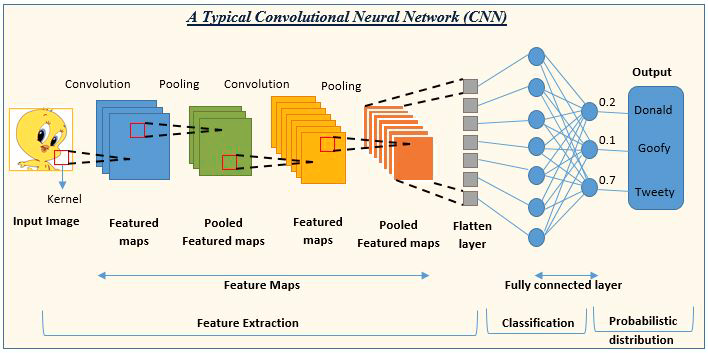
Source de l'image : analyticsvidhya.com
Maintenant que nous avons vu les types de réseaux neuronaux, nous allons nous concentrer sur le sujet principal de cet article, à savoir les réseaux neuronaux de type Feed Forward (à Propagation Avant).
Réseaux Neuronaux à Propagation Avant
Contrairement à d'autres types de réseaux neuronaux plus complexes, il n'y a pas de rétro-propagation, ce qui signifie que les données circulent dans une seule direction dans ce type de réseau neuronal. Un réseau neuronal feed-forward peut avoir une ou plusieurs couches cachées.
Voyons ce qui caractérise ce réseau.
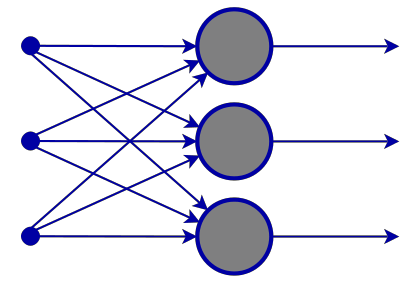
Couche d'entrée
D'après les images d'un réseau neuronal, il semble qu'il y ait une couche d'entrée, mais au fond, la couche d'entrée n'est qu'une présentation. Aucun calcul n'est effectué dans la couche d'entrée.
Couche cachée
C'est dans la couche cachée que s'effectue la majeure partie du travail dans le réseau.
Pour clarifier les choses, décortiquons le nœud de la deuxième couche cachée.
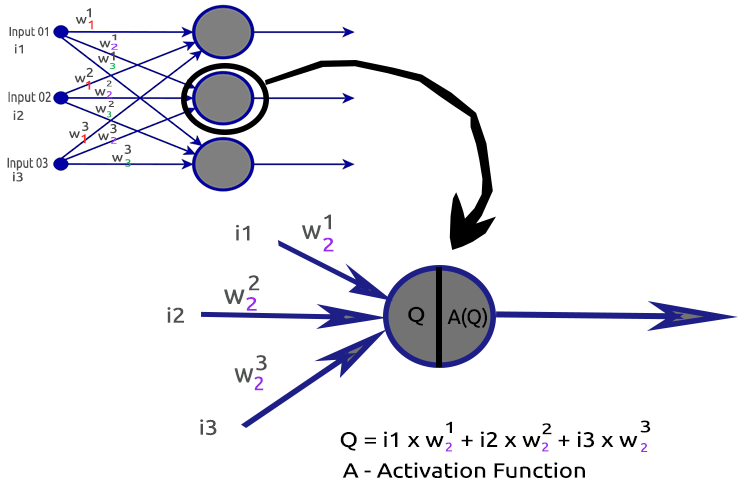
Processus concernés :
- Trouver le produit scalaire des entrées et de leurs poids respectifs
- Ajout du produit scalaire obtenu au biais
- Le résultat de la deuxième procédure est transmis à la fonction d'activation
Qu'est-ce qu'un biais ?
Le biais permet de déplacer la régression linéaire vers le haut ou vers le bas afin de mieux adapter la ligne de prédiction aux données. C'est la même chose que l'ordonnée à l'origine dans une ligne de régression linéaire.
Vous comprendrez bien ce paramètre dans la section Le MLP avec un seul nœud dans une couche cachée est un modèle de régression linéaire.
L'importance de la partialité est bien expliquée dans ces réponses sur StackOverflow.
Que sont les poids ?
Les poids reflètent l'importance de l'entrée, ce sont les coefficients de l'équation que vous essayez de résoudre. Les poids négatifs réduisent la valeur de la sortie et vice versa. Lorsqu'un réseau neuronal est formé sur un ensemble de données d'apprentissage, il est initialisé avec un ensemble de poids. Ces poids sont ensuite optimisés pendant la période de formation et la valeur optimale des poids est produite.
Qu'est-ce qu'une fonction d'activation ?
Une fonction d'activation n'est rien d'autre qu'une fonction mathématique qui prend une entrée et produit une sortie.
Types de fonctions d'activation
Il existe de nombreuses fonctions d'activation et leurs variantes, mais voici les plus couramment utilisées :
- Relu
- Sigmoid
- TanH
- Softmax
Il est très important de savoir quelle fonction d'activation utiliser et à quel endroit. Je ne saurais vous dire combien de fois j'ai vu des articles en ligne suggérant d'utiliser une fonction d'activation à un endroit où elle n'était pas pertinente. Voyons cela en détail.
1 - RELU
RELU signifie Rectified Linear Activation Function (fonction d'activation linéaire rectifiée).
Il s'agit de la fonction d'activation la plus utilisée dans les réseaux neuronaux. C'est la plus simple de toutes, facile à coder et facile à interpréter, c'est pourquoi elle est si populaire. Cette fonction affiche directement l'entrée si celle-ci est un nombre positif ; sinon, elle affiche zéro.
Voici la logique
if x < 0 : return 0
else return x
Cette fonction peut être utilisée pour résoudre des problèmes de régression.
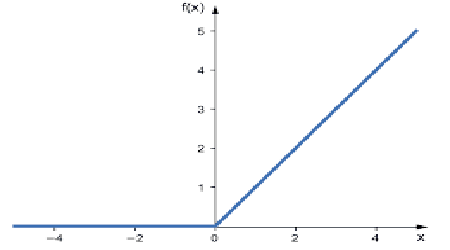
Sa sortie va de 0 à l'infini positif.
Son code MQL5 est le suivant :
double CNeuralNets::Relu(double z) { if (z < 0) return(0); else return(z); }
RELU résout le problème de la disparition du gradient dont souffrent la sigmoïde et le TanH (nous verrons de quoi il s'agit dans l'article sur la rétro-propagation).
2 - Sigmoid
Cela vous semble familier, n'est-ce pas ? Souvenez-vous de la régression logistique.
Sa formule est la suivante :
![]()
Cette fonction est mieux adaptée aux problèmes de classification, en particulier à la classification d'une ou deux classes seulement.
Son résultat est compris entre 0 et 1 (termes de probabilité).
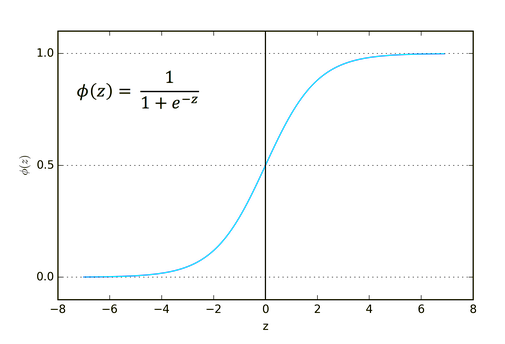
Par exemple, votre réseau comporte deux nœuds en sortie. Le premier nœud correspond à un chat et l'autre à un chien. Vous pourriez choisir la sortie si la sortie du premier nœud est supérieure à 0,5 pour indiquer qu'il s'agit d'un chat et la même chose mais à l'opposé pour un chien.
Son code MQL5 est le suivant :
double CNeuralNets::Sigmoid(double z) { return(1.0/(1.0+MathPow(e,-z))); }
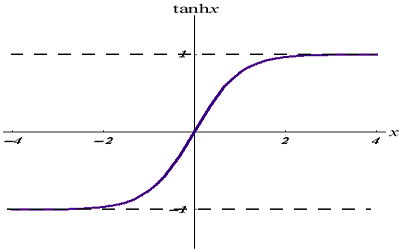
03 : TanH
La fonction tangente hyperbolique.
Elle est donnée par la formule :
Son graphique se présente comme suit :
Cette fonction d'activation est similaire à la sigmoïde mais plus performante.
Sa valeur de sortie est comprise entre -1 et 1.
Cette fonction est mieux utilisée dans les réseaux neuronaux de classification multi-classes.
Son code MQL5 est indiqué ci-dessous :
double CNeuralNets::tanh(double z) { return((MathPow(e,z) - MathPow(e,-z))/(MathPow(e,z) + MathPow(e,-z))); }
4 - SoftMax
Quelqu'un a demandé pourquoi il n'y avait pas de graphique pour la fonction SoftMax. Contrairement à d'autres fonctions d'activation, SoftMax n'est pas utilisée dans les couches cachées mais uniquement dans la couche de sortie et ne doit être utilisée que lorsque vous souhaitez convertir la sortie d'un réseau neuronal multi-classes en termes de probabilité.
SoftMax prédit une distribution de probabilité multinomiale.
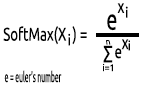
Par exemple, les sorties d'un réseau neuronal de régression sont [1,3,2]. Si nous appliquons la fonction SoftMax à cette sortie, celle-ci devient [0,09003, 0,665240, 0,244728].
La sortie de cette fonction est comprise entre 0 et 1.
Son code MQL5 sera :
void CNeuralNets::SoftMax(double &Nodes[]) { double TempArr[]; ArrayCopy(TempArr,Nodes); ArrayFree(Nodes); double proba = 0, sum=0; for (int j=0; j<ArraySize(TempArr); j++) sum += MathPow(e,TempArr[j]); for (int i=0; i<ArraySize(TempArr); i++) { proba = MathPow(e,TempArr[i])/sum; Nodes[i] = proba; } ArrayFree(TempArr); }
Maintenant que nous savons de quoi est constitué un neurone unique d'une couche cachée, codons-le.
void CNeuralNets::Neuron(int HLnodes, double bias, double &Weights[], double &Inputs[], double &Outputs[] ) { ArrayResize(Outputs,HLnodes); for (int i=0, w=0; i<HLnodes; i++) { double dot_prod = 0; for(int j=0; j<ArraySize(Inputs); j++, w++) { if (m_debug) printf("i %d w %d = input %.2f x weight %.2f",i,w,Inputs[j],Weights[w]); dot_prod += Inputs[j]*Weights[w]; } Outputs[i] = ActivationFx(dot_prod+bias); } }
Dans ActivationFx(), la fonction d'activation choisie lors de l'appel du constructeur de NeuralNets peut être sélectionnée.
double CNeuralNets::ActivationFx(double Q) { switch(A_fx) { case SIGMOID: return(Sigmoid(Q)); break; case TANH: return(tanh(Q)); break; case RELU: return(Relu(Q)); break; default: Print("Unknown Activation Function"); break; } return(0); }
Plus d'explications sur le code :
La fonction Neuron() n'est pas un simple nœud à l'intérieur de la couche cachée, mais toutes les opérations d'une couche cachée sont effectuées à l'intérieur de cette seule fonction. Les nœuds de toutes les couches cachées auront la même taille que le nœud d'entrée jusqu'au nœud de sortie final. J'ai choisi cette structure parce que je suis sur le point d'effectuer une classification à l'aide de ce réseau neuronal sur un ensemble de données généré de manière aléatoire.
La fonction FeedForwardMLP() ci-dessous est une structure NxN, ce qui signifie que si vous avez 3 nœuds d'entrée et que vous choisissez d'avoir 3 couches cachées, vous aurez 3 nœuds cachés sur chaque couche cachée (voir l'image).
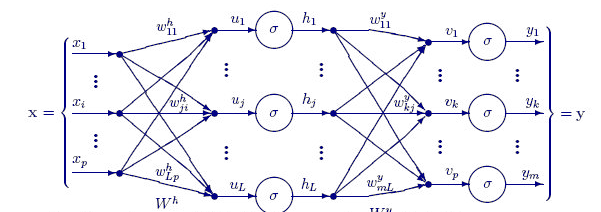
Voici la fonction FeedForwardMLP() :
void CNeuralNets::FeedForwardMLP(int HiddenLayers, double &MLPInputs[], double &MLPWeights[], double &bias[], double &MLPOutput[]) { double L_weights[], L_inputs[], L_Out[]; ArrayCopy(L_inputs,MLPInputs); int HLnodes = ArraySize(MLPInputs); int no_weights = HLnodes*ArraySize(L_inputs); int weight_start = 0; for (int i=0; i<HiddenLayers; i++) { if (m_debug) printf("<< Hidden Layer %d >>",i+1); ArrayCopy(L_weights,MLPWeights,0,weight_start,no_weights); Neuron(HLnodes,bias[i],L_weights,L_inputs,L_Out); ArrayCopy(L_inputs,L_Out); ArrayFree(L_Out); ArrayFree(L_weights); weight_start += no_weights; } if (use_softmax) SoftMax(L_inputs); ArrayCopy(MLPOutput,L_inputs); if (m_debug) { Print("\nFinal MLP output(s)"); ArrayPrint(MLPOutput,5); } }
Les opérations permettant de trouver le produit scalaire dans un réseau neuronal pourraient être traitées par des opérations matricielles. Mais pour que les choses restent claires et faciles à comprendre pour tout le monde dans ce premier article, j'ai choisi la méthode de la boucle ; nous utiliserons la multiplication matricielle la prochaine fois.
Vous avez maintenant vu l'architecture que j'ai choisie par défaut pour la construction de la bibliothèque. Cela soulève une question sur l'architecture des réseaux neuronaux.
Si vous allez sur Google et cherchez les images d'un réseau neuronal, vous serez bombardé par des milliers, voire des dizaines de milliers d'images avec différentes structures de réseaux neuronaux, comme celles-ci par exemple :
La question à un million de dollars est la suivante : quelle est la meilleure architecture de réseau neuronal ?
"Personne ne se trompe autant que l'homme qui connaît toutes les réponses" -- Thomas Merton.
Décortiquons les choses pour comprendre ce qui est nécessaire et ce qui ne l'est pas.
La couche d'entréeLe nombre d'entrées composant cette couche doit être égal au nombre de caractéristiques (colonnes de l'ensemble de données).
La couche de sortie
La taille (le nombre de neurones) est déterminée par les classes de votre ensemble de données pour un réseau neuronal de classification. Pour un problème de type régression, le nombre de neurones est déterminé par la configuration du modèle choisi. Une couche de sortie pour un régresseur est souvent plus que suffisante.
Couches cachées
Si votre problème n'est pas assez complexe, une ou deux couches cachées suffisent amplement. En fait, deux couches cachées suffisent pour la grande majorité des problèmes. Mais, de combien de nœuds a-t-on besoin dans chaque couche cachée ? Je n'en suis pas sûr, mais je pense que cela dépend de la performance. En tant que développeur, vous devez explorer et essayer différents nœuds pour voir ce qui fonctionne le mieux pour un type de problème particulier.
Il existe un excellent sujet sur stats.stackexchange.com à ce sujet, dont le lien est ici.
Je pense que le fait d'avoir le même nombre de nœuds que la couche d'entrée pour toutes les couches cachées est idéal pour un réseau neuronal feed-forward, et c'est la configuration que j'utilise la plupart du temps.
Le MLP avec un seul nœud et une seule couche cachée est un modèle linéaire.
Si vous prêtez attention aux opérations effectuées à l'intérieur d'un seul nœud d'une couche cachée d'un réseau neuronal, vous remarquerez ceci :
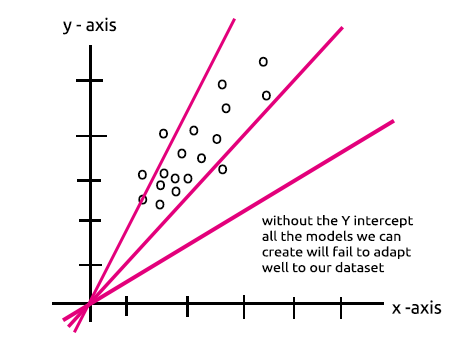
Q = wi * Ii + b
En attendant, l'équation de régression linéaire est la suivante ;
Y = mi * xi + c
Vous remarquez des similitudes ? C'est la même chose en théorie. Cette opération est le régresseur linéaire, ce qui nous ramène à l'importance du biais d'une couche cachée. Le biais est une constante pour le modèle linéaire dont le rôle est d'ajouter la flexibilité de notre modèle pour s'adapter à l'ensemble de données donné. Sans lui, tous les modèles passeront entre l'axe x et l'axe y à 0.
Lors de la formation du réseau neuronal, les poids et les biais seront mis à jour. Les paramètres qui produisent le moins d'erreurs pour notre modèle seront conservés et mémorisés dans l'ensemble de données de test.
Pour clarifier les choses, je vais maintenant construire un MLP pour une classification en deux classes. Avant cela, permettez-moi de générer un ensemble de données aléatoires avec des échantillons étiquetés que nous allons voir à travers notre réseau neuronal. La fonction ci-dessous crée un ensemble de données aléatoires, le deuxième échantillon étant multiplié par 5 et le premier par 2 afin d'obtenir des données à différentes échelles.
void MakeBlobs(int size=10) { ArrayResize(data_blobs,size); for (int i=0; i<size; i++) { data_blobs[i].sample_1 = (i+1)*(2); data_blobs[i].sample_2 = (i+1)*(5); data_blobs[i].class_ = (int)round(nn.MathRandom(0,1)); } }
Lorsque j'imprime le jeu de données, voici le résultat :
QK 0 18:27:57.298 TestScript (EURUSD,M1) CNeural Nets Initialized activation = SIGMOID UseSoftMax = No IR 0 18:27:57.298 TestScript (EURUSD,M1) [sample_1] [sample_2] [class_] LH 0 18:27:57.298 TestScript (EURUSD,M1) [0] 2.0000 5.0000 0 GG 0 18:27:57.298 TestScript (EURUSD,M1) [1] 4.0000 10.0000 0 NL 0 18:27:57.298 TestScript (EURUSD,M1) [2] 6.0000 15.0000 1 HJ 0 18:27:57.298 TestScript (EURUSD,M1) [3] 8.0000 20.0000 0 HQ 0 18:27:57.298 TestScript (EURUSD,M1) [4] 10.0000 25.0000 1 OH 0 18:27:57.298 TestScript (EURUSD,M1) [5] 12.0000 30.0000 1 JF 0 18:27:57.298 TestScript (EURUSD,M1) [6] 14.0000 35.0000 0 DL 0 18:27:57.298 TestScript (EURUSD,M1) [7] 16.0000 40.0000 1 QK 0 18:27:57.298 TestScript (EURUSD,M1) [8] 18.0000 45.0000 0 QQ 0 18:27:57.298 TestScript (EURUSD,M1) [9] 20.0000 50.0000 0
L'étape suivante consiste à générer des valeurs de poids aléatoires et le biais :
generate_weights(weights,ArraySize(Inputs));
generate_bias(biases); Voici le résultat :
RG 0 18:27:57.298 TestScript (EURUSD,M1) weights QS 0 18:27:57.298 TestScript (EURUSD,M1) 0.7084 -0.3984 0.6182 0.6655 -0.3276 0.8846 0.5137 0.9371 NL 0 18:27:57.298 TestScript (EURUSD,M1) biases DD 0 18:27:57.298 TestScript (EURUSD,M1) -0.5902 0.7384
Voyons maintenant l'ensemble des opérations dans la fonction principale de notre script :
#include "NeuralNets.mqh"; CNeuralNets *nn; input int batch_size =10; input int hidden_layers =2; data data_blobs[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- nn = new CNeuralNets(SIGMOID); MakeBlobs(batch_size); ArrayPrint(data_blobs); double Inputs[],OutPuts[]; ArrayResize(Inputs,2); ArrayResize(OutPuts,2); double weights[], biases[]; generate_weights(weights,ArraySize(Inputs)); generate_bias(biases); Print("weights"); ArrayPrint(weights); Print("biases"); ArrayPrint(biases); for (int i=0; i<batch_size; i++) { Print("Dataset Iteration ",i); Inputs[0] = data_blobs[i].sample_1; Inputs[1]= data_blobs[i].sample_2; nn.FeedForwardMLP(hidden_layers,Inputs,weights,biases,OutPuts); } delete(nn); }
A noter :
- Le nombre de biais est le même que le nombre de couches cachées.
- Nombre total de poids = nombre d'entrées au carré multiplié par le nombre de couches cachées. Cela a été rendu possible par le fait que notre réseau a le même nombre de nœuds que la couche d'entrée/couche précédente du réseau (toutes les couches ont le même nombre de nœuds de l'entrée à la sortie).
- Le même principe sera suivi : disons que si vous avez 3 nœuds d'entrée, toutes les couches cachées auront 3 nœuds, à l'exception de la dernière couche où nous allons voir comment la traiter.
En regardant l'ensemble de données généré aléatoirement, vous remarquerez deux caractéristiques / colonnes en entrée dans l'ensemble de données. J'ai choisi d'avoir 2 couches cachées. Voici un bref aperçu dans nos journaux de la façon dont notre modèle va effectuer les calculs(éviter ces journaux en réglant le mode de débogage sur false dans le code).
NL 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 0 EJ 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> GO 0 18:27:57.298 TestScript (EURUSD,M1) NS 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 EI 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 2.00000 x weight 0.70837 FQ 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 5.00000 x weight -0.39838 QP 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -0.57513 + bias -0.590 = -1.16534 RH 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.23770 CQ 0 18:27:57.298 TestScript (EURUSD,M1) OE 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 CO 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 2.00000 x weight 0.61823 FI 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 5.00000 x weight 0.66553 PN 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 4.56409 + bias -0.590 = 3.97388 GM 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.98155 DI 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> GL 0 18:27:57.298 TestScript (EURUSD,M1) NF 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 FH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.23770 x weight -0.32764 ID 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.98155 x weight 0.88464 QO 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.79044 + bias 0.738 = 1.52884 RK 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82184 QG 0 18:27:57.298 TestScript (EURUSD,M1) IH 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 DQ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.23770 x weight 0.51367 CJ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.98155 x weight 0.93713 QJ 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.04194 + bias 0.738 = 1.78034 JP 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85574 EI 0 18:27:57.298 TestScript (EURUSD,M1) GS 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) OF 0 18:27:57.298 TestScript (EURUSD,M1) 0.82184 0.85574 CN 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 1 KH 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> EM 0 18:27:57.298 TestScript (EURUSD,M1) DQ 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 QH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 4.00000 x weight 0.70837 PD 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 10.00000 x weight -0.39838 HR 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -1.15027 + bias -0.590 = -1.74048 DJ 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.14925 OP 0 18:27:57.298 TestScript (EURUSD,M1) CK 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 MN 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 4.00000 x weight 0.61823 NH 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 10.00000 x weight 0.66553 HI 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 9.12817 + bias -0.590 = 8.53796 FO 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.99980 RG 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> IR 0 18:27:57.298 TestScript (EURUSD,M1) PD 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 RN 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.14925 x weight -0.32764 HF 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.99980 x weight 0.88464 EM 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.83557 + bias 0.738 = 1.57397 EL 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82835 KE 0 18:27:57.298 TestScript (EURUSD,M1) GN 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 LS 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.14925 x weight 0.51367 FL 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.99980 x weight 0.93713 KH 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.01362 + bias 0.738 = 1.75202 IR 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85221 OH 0 18:27:57.298 TestScript (EURUSD,M1) IM 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) MH 0 18:27:57.298 TestScript (EURUSD,M1) 0.82835 0.85221
Observez maintenant les sorties finales du MLP pour toutes les itérations. Vous remarquerez un comportement étrange : les sorties ont tendance à avoir les mêmes valeurs. Ce problème a plusieurs causes, comme indiqué ici, l'une d'entre elles étant l'utilisation d'une mauvaise fonction d'activation dans la couche de sortie. C'est ici que la fonction d'activation SoftMax entre en jeu.
D'après ce que j'ai compris, la fonction sigmoïde ne renvoie des probabilités que lorsqu'il n'y a qu'un seul nœud dans la couche de sortie, qui doit classer une seule classe. Dans ce cas, vous auriez besoin de la sortie de la fonction sigmoïde pour vous dire si quelque chose appartient à une certaine classe ou non, mais c'est une autre histoire en cas de classes multiples. Si nous additionnons les sorties de nos nœuds finaux, la valeur dépasse 1 la plupart du temps. Vous savez donc maintenant qu'il ne s'agit pas de probabilités, car une probabilité ne peut pas dépasser la valeur de 1.
Si nous appliquons SoftMax à la dernière couche, les résultats seront les suivants :
Résultats de la première itération [0,4915 0,5085], Résultats de la deuxième itération [0,4940 0,5060].
Vous pouvez interpréter les résultats comme[Probabilité d'appartenir à la classe 0 Probabilité d'appartenir à la classe 1] dans ce cas
Au moins, nous disposons maintenant de probabilités sur lesquelles nous pouvons nous appuyer pour interpréter quelque chose de significatif à partir de notre réseau.
Dernières réflexions
Nous n'avons pas terminé avec le réseau neuronal feed-forward. Mais au moins pour l'instant, vous avez compris la théorie et les éléments les plus importants qui vous aideront à maîtriser les réseaux neuronaux dans MQL5. Le réseau neuronal Feedforward conçu est destiné à la classification, ce qui signifie que les fonctions d'activation appropriées sont sigmoïde et tanh, en fonction des échantillons et des classes que vous souhaitez classer dans votre ensemble de données. Nous ne pouvions pas modifier la couche de sortie pour qu'elle renvoie ce que nous voulions, pas plus que les nœuds des couches cachées. L'introduction des matrices permettra de rendre toutes ces opérations dynamiques, ce qui nous permettra de construire un réseau neuronal très standard pour n'importe quelle tâche, ce qui est l'objectif de cette série d'articles.
Il est également important de savoir quand utiliser le réseau neuronal, car toutes les tâches ne doivent pas être résolues par des réseaux neuronaux. Si une tâche peut être résolue par régression linéaire, un modèle linéaire peut être plus performant que le réseau neuronal. C'est l'une des choses à garder à l'esprit.
Repo GitHub https://github.com/MegaJoctan/NeuralNetworks-MQL5
Lecture complémentaire | Livres | Références
-
Networks for Pattern Recognition (Advanced Texts in Econometrics)
-
Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
Références d’articles :
-
Science des données et apprentissage automatique (partie 01) : Régression linéaire
-
Science des données et apprentissage automatique (partie 02) : Régression logistique
-
Science des données et apprentissage automatique (partie 03) : Régressions matricielles
-
Science des données et apprentissage automatique (partie 06) : Descente en gradient
Traduit de l’anglais par MetaQuotes Ltd.
Article original : https://www.mql5.com/en/articles/11275
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.
Cet article a été rédigé par un utilisateur du site et reflète ses opinions personnelles. MetaQuotes Ltd n'est pas responsable de l'exactitude des informations présentées, ni des conséquences découlant de l'utilisation des solutions, stratégies ou recommandations décrites.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation

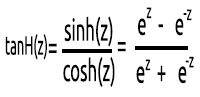
...
Pouvez-vous l'expliquer ? Ou donner des exemples ?
La différence entre l'optimisation sur le testeur de stratégie et l'optimisation des paramètres du réseau neuronal est l'objectif. Sur le testeur de stratégie, nous avons tendance à nous concentrer sur les paramètres qui fournissent les sorties les plus rentables ou au moins les résultats commerciaux que nous souhaitons, ce qui ne signifie pas nécessairement que le réseau neuronal dispose d'un bon modèle qui a conduit à ce type de résultats.
certains préfèrent placer les poids et le biais comme paramètres d'entrée des systèmes basés sur les réseaux neuronaux(Feed forward en gros), mais je pense que l'optimisation à l'aide du testeur de stratégie consiste essentiellement à trouver les valeurs aléatoires des meilleurs résultats(trouver les valeurs optimales semble dépendre de la chance), alors que si nous devions optimiser à l'aide de la descente de gradient stochastique, nous nous dirigeons vers le modèle présentant le moins d'erreurs dans les prédictions à chaque étape.
la différence entre l'optimisation sur le testeur de stratégie et l'optimisation des paramètres du réseau neuronal est l'objectif, sur le testeur de stratégie nous avons tendance à nous concentrer sur les paramètres qui fournissent les résultats les plus rentables ou au moins les résultats commerciaux que nous souhaitons, ce qui ne signifie pas nécessairement que le réseau neuronal a un bon modèle qui a conduit à ce type de résultats.
certains préfèrent placer les poids et le biais comme paramètres d'entrée des systèmes basés sur les réseaux neuronaux(Feed forward en gros), mais je pense que l'optimisation à l'aide du testeur de stratégie consiste essentiellement à trouver les valeurs aléatoires des meilleurs résultats(trouver les valeurs optimales semble dépendre de la chance), alors que si nous devions optimiser à l'aide de la descente de gradient stochastique, nous nous dirigeons vers le modèle présentant le moins d'erreurs dans les prédictions à chaque étape.
Je vous remercie pour votre réponse.
J'ai compris votre point de vue.
Pourquoi avez-vous commencé par la première partie ?
ancien article :
SCIENCE DES DONNÉES ET APPRENTISSAGE AUTOMATIQUE (PARTIE 01) : RÉGRESSION LINÉAIRE
https://www.mql5.com/fr/articles/10459
Pourquoi avez-vous commencé par la première partie ?
ancien article :
SCIENCE DES DONNÉES ET APPRENTISSAGE AUTOMATIQUE (PARTIE 01) : RÉGRESSION LINÉAIRE
https://www.mql5.com/fr/articles/10459
que voulez-vous dire ?
Pourquoi avez-vous commencé par la première partie ?
ancien article :
SCIENCE DES DONNÉES ET APPRENTISSAGE AUTOMATIQUE (PARTIE 01) : RÉGRESSION LINÉAIRE
https://www.mql5.com/fr/articles/10459