Veri Bilimi ve Makine Öğrenimi - Sinir Ağları (Bölüm 01): İleri Beslemeli Sinir Ağları
“...çok fazla şey bilmekten ve çok az şey anlamaktan yoruldum.”
- Jan Karon, Home to Holly Springs
Giriş
Sinir ağları, alım-satımın kutsal kasesine yaklaşmanın bir yolunu sunan yeni popüler şey gibi görünüyor. Birçok yatırımcı, piyasa hareketlerini tahmin etmede ve genel olarak eldeki herhangi bir görev için iyi bir iş çıkardıkları için sinir ağı tabanlı programlar karşısında şaşkınlığa uğruyor. Ben de eğitimsiz/görülmemiş yeni verilere dayalı tahmin veya sınıflandırma söz konusu olduğunda muazzam bir potansiyele sahip olduklarını düşünüyorum.
Ne kadar iyi olurlarsa olsunlar, bilgili insanlar tarafından tasarlanmalı ve optimize edilmelidirler. Sadece çok katmanlı algılayıcının doğru mimariye sahip olması değil, aynı zamanda çözülecek problemin türünün de sadece lineer veya lojistik regresyon modeli ya da başka bir makine öğrenimi tekniği değil, sinir ağlarının kullanımını içermesi gerektiğinin farkına varılmalıdır.
Sinir ağları, genel olarak makine öğrenimi gibi çok geniş bir konudur, bu nedenle ayrı bir alt seri başlatmaya karar verdim. Makine öğreniminin diğer yönlerini serinin diğer dalında ele almaya devam edeceğiz.
Bu makalede, sinir ağlarının temellerine göz atacağız ve makine öğrenimi meraklılarının bu alanda uzmanlaşmak için anlamalarının önemli olduğunu düşündüğüm bazı ana konuları inceleyeceğiz.
Yapay sinir ağı nedir?
Genellikle “sinir ağları” olarak adlandırılan yapay sinir ağları (Artificial Neural Networks, ANN), canlıların beyinlerini oluşturan biyolojik sinir ağlarından esinlenen hesaplama sistemleridir.
Çok katmanlı algılayıcı ve derin sinir ağı
Sinir ağlarını tartışırken, insanların çok katmanlı algılayıcı (Multi-Layer Perceptron, MLP) terimini sık sık kullandığını duyarsınız. Bu, en yaygın sinir ağı türüdür. MLP, bir girdi katmanı, bir gizli katman ve bir çıktı katmanından oluşan bir ağdır. Basitlikleri nedeniyle, verilerdeki sunumları öğrenmek ve bir çıktı üretmek için kısa eğitim sürelerine ihtiyaç duyarlar.
Uygulama alanları:
MLP’ler genellikle regresyon analizi gibi doğrusal olarak ayrılamayan veriler için kullanılır. Basitlikleri, onları karmaşık sınıflandırma ve tahmine dayalı modelleme görevleri için en uygun hale getirir. Makine çevirisi, hava durumu tahmini, dolandırıcılık tespiti, borsa tahmini, kredi notu tahmini ve aklınıza gelebilecek diğer birçok konuda kullanılırlar.
Derin sinir ağları (Deep Neural Networks, DNN) da ortak bir yapıya sahiptir ancak burada çok fazla gizli katman bulunmaktadır. Ağınızda 3’ten fazla gizli katman varsa, bunu bir derin sinir ağı olarak kabul edin. Karmaşık yapıları nedeniyle, ağın girdi verileri üzerinde uzun süre eğitilmesini gerektirirler ve ayrıca tensör işlem birimleri (Tensor Processing Units, TPU) ve nöral işlem birimleri (Neural Processing Units, NPU) gibi özel işlem birimlerine sahip güçlü bilgisayarlar gerektirirler.
Uygulama alanları:
DNN’ler, derin katmanları nedeniyle güçlü algoritmalardır, bu nedenle genellikle karmaşık hesaplama problemlerini çözmek için kullanılırlar. Bilgisayarlı görme bu görevlerden biridir.
Farklılıklar tablosu:
| MLP | DNN |
|---|---|
| Az sayıda gizli katman | Çok sayıda gizli katman |
| Kısa eğitim süresi | Uzun eğitim süresi |
| GPU donanımı gerektirir | TPU donanımı gerektirir |
Şimdi, sinir ağlarının türlerine bakalım.
Birçok sinir ağı türü vardır, ancak kabaca üç ana sınıfa ayrılırlar:
- İleri beslemeli sinir ağları
- Tekrarlayan sinir ağları
- Konvolüsyonel sinir ağları
01: İleri beslemeli sinir ağları
Bu, en basit sinir ağı türlerinden biridir. Burada veriler çıktı düğümüne ulaşana kadar çeşitli girdi düğümlerinden geçer. Geri yayılımın aksine, burada veriler yalnızca tek bir yönde hareket eder.
Basitçe söylemek gerekirse, geri yayılım, bir sinir ağında veriler girdi katmanından çıktı katmanına iletildiği şekilde ileri beslemeyle aynı işlemleri gerçekleştirir, ancak geri yayılımda, ağın çıktısı çıktı katmanına ulaştığında, gerçek sınıf değerini alır. Model, bunu tahmin edilen değerle karşılaştırarak yaptığı tahminin ne kadar yanlış ya da doğru olduğunu görür. Tahmin yanlışsa, veriler ağa geri gönderilir ve parametreler tahmini düzeltmek için güncellenir. Bu bir kendi kendine öğrenme algoritmasıdır.
02: Tekrarlayan sinir ağları
Tekrarlayan sinir ağı, belirli bir katmanın çıktısının depolandığı ve girdi katmanına geri gönderildiği bir yapay sinir ağı türüdür. Bu, katmanın sonucunun tahmin edilmesine yardımcı olur.
Tekrarlayan sinir ağları aşağıdakilerle ilgili problemleri çözmek için kullanılır:
- Zaman serisi verileri
- Metin verileri
- Ses verileri
Metin verilerinin en yaygın kullanımı, yapay zekanın konuşması için kelimeler sunmaktır, örn: How + are + you + ?
03: Konvolüsyonel sinir ağları (CNN)
CNN’ler çok sık kullanılmaktadır. Görüntü ve video işleme projelerinde baskındırlar.
Örneğin, görüntü algılama ve sınıflandırma yapay zekası konvolüsyonel sinir ağlarından oluşur.
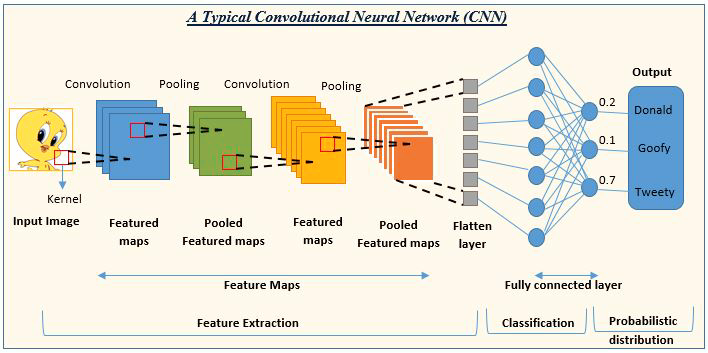
Görüntü kaynağı: analyticsvidhya.com
Sinir ağı türlerine baktık, şimdi bu makalenin ana konusu olan ileri beslemeli sinir ağlarına odaklanalım.
İleri beslemeli sinir ağları
Diğer daha karmaşık sinir ağı türlerinden farklı olarak, geri yayılım yoktur, yani bu tür sinir ağlarında veriler yalnızca tek yönde iletilir. İleri beslemeli bir sinir ağı bir veya birkaç gizli katmana sahip olabilir.
Aşağıdaki diyagram bu sinir ağının nasıl çalıştığını göstermektedir.
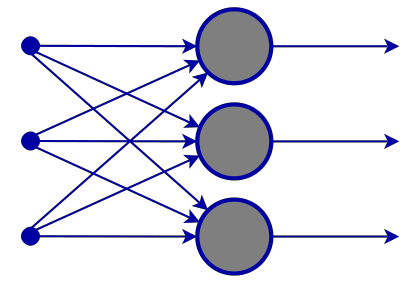
Girdi katmanı
Sinir ağı diyagramından bir girdi katmanına sahip olduğunu görebilirsiniz. Özünde, girdi katmanı sadece verilerin bir temsilidir. Girdi katmanında herhangi bir hesaplama yapılmaz.
Gizli katman
Gizli katman, sinir ağının çalışmalarının çoğunun yapıldığı yerdir.
Çalışma prensibini daha iyi anlamak için ikinci gizli katman düğümünü analiz edelim.
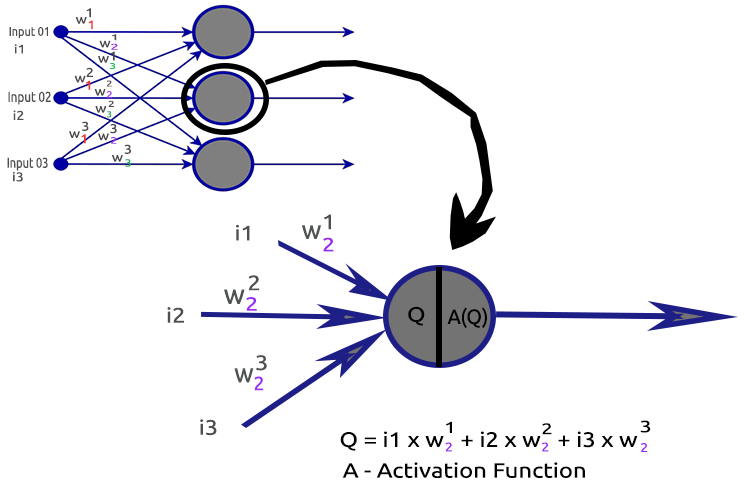
İlgili süreçler:
- Girdilerin ve ilgili ağırlıklarının nokta çarpımını bulma
- Elde edilen nokta çarpımının yanlılığa eklenmesi
- İkinci prosedürün sonucunun aktivasyon fonksiyonuna aktarılması
Yanlılık nedir?
Yanlılık, tahmin çizgisini verilere daha iyi uydurmak için lineer regresyonu yukarı ve aşağı kaydırmanıza olanak tanır. Bu, lineer regresyondaki Kesişim ile aynıdır.
Bu parametre, gizli katmanda tek düğümlü MLP - lineer regresyon modeli bölümünde daha iyi açıklanacaktır.
Ayrıca yanlılığın önemi de bu Stack başlığında iyi bir şekilde açıklanmıştır.
Ağırlıklar nedir?
Ağırlıklar, girdi verilerinin ne kadar önemli olduğunu yansıtır. Çözmeye çalıştığınız denklemin katsayıları gibi davranırlar. Negatif ağırlıklar çıktı verilerinin önemini azaltır ve bunun tersi de geçerlidir. Bir sinir ağı bir eğitim veri kümesi üzerinde eğitildiğinde, bir dizi ağırlık ile başlatılır. Bu ağırlıklar daha sonra eğitim süresi boyunca optimize edilir ve ağırlıkların optimum değeri elde edilir.
Aktivasyon fonksiyonu nedir?
Bir aktivasyon fonksiyonu, girdi verilerini alan ve bir çıktı sinyali üreten matematiksel bir fonksiyondan başka bir şey değildir.
Aktivasyon fonksiyonu çeşitleri
Varyantlarıyla birlikte birçok aktivasyon fonksiyonu vardır, ancak burada en yaygın kullanılanlar verilmiştir:
- ReLU
- Sigmoid
- TanH
- Softmax
Hangi aktivasyon fonksiyonunun nerede kullanılacağını bilmek çok önemlidir. Ancak, internette aktivasyon fonksiyonunun uygun olmadığı yerlerde kullanılmasını öneren makalelere pek çok kez rastladım. Şimdi bu türlere daha detaylı bakalım.
01: ReLU
Düzeltilmiş lineer birim (Rectified Linear Unit, ReLU) anlamına gelir.
Sinir ağlarında en yaygın kullanılan aktivasyon fonksiyonudur. Diğerlerinden daha basittir, kodlaması kolaydır ve çıktıyı yorumlaması kolaydır, bu yüzden bu kadar popülerdir. Bu fonksiyon, girdi pozitif bir sayı ise doğrudan çıktıyı verir; aksi takdirde sıfır çıktısı verir.
Mantık şu şekildedir:
if x < 0 : return 0
else return x
Bu fonksiyon regresyon problemlerinin çözümünde daha iyi kullanılır.
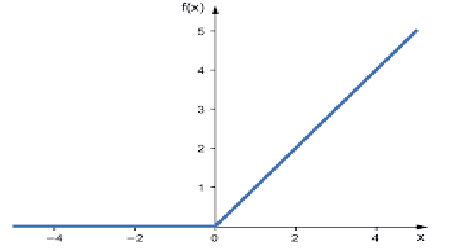
Çıktı değerleri sıfır ile pozitif sonsuz arasında değişir.
MQL5'te kodu aşağıdaki gibi olacaktır:
double CNeuralNets::Relu(double z) { if (z < 0) return(0); else return(z); }
ReLU, sigmoid ve TanH’nin muzdarip olduğu kaybolan gradyan sorununu çözer (geri yayılma ile ilgili makalede bunun hakkında daha fazla bilgi edineceğiz).
02: Sigmoid
Tanıdık geliyor değil mi? Lojistik regresyondan hatırlayın.
Formülü aşağıdaki gibidir:
![]()
Bu fonksiyon, özellikle yalnızca bir veya iki sınıfı sınıflandırırken sınıflandırma problemlerinde kullanım için daha uygundur.
Çıktı değerleri sıfır ile bir (olasılık terimleri) arasında değişir.
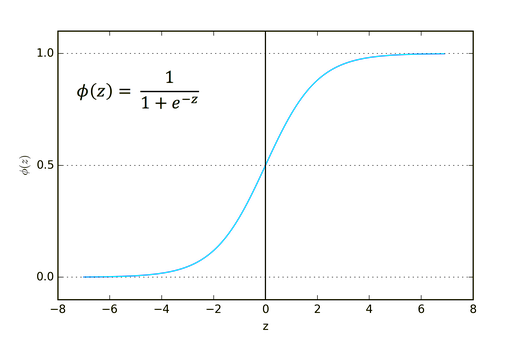
Örneğin, ağınızda iki çıktı düğümü var. İlk düğüm bir kedi için, ikinci düğüm ise bir köpek için. İlk düğümün çıktısı 0.5'ten büyükse, bu kedi anlamına gelecektir. Ve köpek için tam tersidir.
MQL5'te kodu aşağıdaki gibi olacaktır:
double CNeuralNets::Sigmoid(double z) { return(1.0/(1.0+MathPow(e,-z))); }
03: TanH
Hiperbolik tanjant fonksiyonu.
Formülü şu şekildedir:
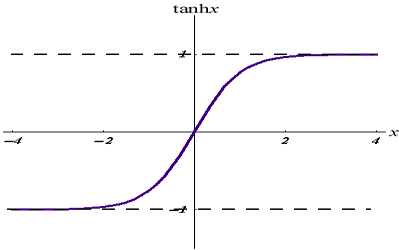
Grafiği aşağıdaki gibidir:
Bu aktivasyon fonksiyonu sigmoid fonksiyonuna benzer ancak daha iyidir.
Çıkış değerleri -1 ile 1 arasında değişir.
Bu fonksiyon, çok sınıflı sınıflandırma sinir ağlarında kullanım için uygundur.
MQL5 kodu aşağıda verilmiştir:
double CNeuralNets::tanh(double z) { return((MathPow(e,z) - MathPow(e,-z))/(MathPow(e,z) + MathPow(e,-z))); }
04: SoftMax
Birisi bir keresinde SoftMax fonksiyonunun grafiğinin neden olmadığını sormuştu. Diğer aktivasyon fonksiyonlarının aksine SoftMax gizli katmanlarda kullanılmaz, sadece çıktı katmanında kullanılır ve sadece çok sınıflı bir sinir ağının çıktısını olasılık terimlerine dönüştürmek istediğinizde kullanılmalıdır.
SoftMax çok terimli olasılık dağılımını tahmin eder.
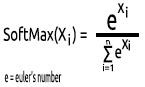
Örneğin, bir regresyon sinir ağının çıktısı [1,3,2] olsun. Eğer bu çıktıya SoftMax fonksiyonunu uygularsak, çıktı artık [0.09003, 0.665240, 0.244728] olur.
Bu fonksiyonun çıktı değerleri 0 ila 1 aralığındadır.
MQL5'te kodu aşağıdaki gibidir:
void CNeuralNets::SoftMax(double &Nodes[]) { double TempArr[]; ArrayCopy(TempArr,Nodes); ArrayFree(Nodes); double proba = 0, sum=0; for (int j=0; j<ArraySize(TempArr); j++) sum += MathPow(e,TempArr[j]); for (int i=0; i<ArraySize(TempArr); i++) { proba = MathPow(e,TempArr[i])/sum; Nodes[i] = proba; } ArrayFree(TempArr); }
Artık tek bir gizli katman nöronunun nelerden oluştuğunu anladığımıza göre, kodunu yazalım.
void CNeuralNets::Neuron(int HLnodes, double bias, double &Weights[], double &Inputs[], double &Outputs[] ) { ArrayResize(Outputs,HLnodes); for (int i=0, w=0; i<HLnodes; i++) { double dot_prod = 0; for(int j=0; j<ArraySize(Inputs); j++, w++) { if (m_debug) printf("i %d w %d = input %.2f x weight %.2f",i,w,Inputs[j],Weights[w]); dot_prod += Inputs[j]*Weights[w]; } Outputs[i] = ActivationFx(dot_prod+bias); } }
ActivationFx() içinde, NeuralNets yapıcısı çağrıldığında hangi aktivasyon fonksiyonunun seçileceğini belirleyebilirsiniz.
double CNeuralNets::ActivationFx(double Q) { switch(A_fx) { case SIGMOID: return(Sigmoid(Q)); break; case TANH: return(tanh(Q)); break; case RELU: return(Relu(Q)); break; default: Print("Unknown Activation Function"); break; } return(0); }
Kod hakkında daha fazla açıklama:
Neuron() fonksiyonu sadece gizli katman içindeki tek bir düğüm değildir, gizli katmanın tüm işlemleri bu fonksiyon içinde gerçekleştirilir. Tüm gizli katmanlardaki düğümler, son çıktı düğümüne kadar girdi düğümü ile aynı büyüklükte olacaktır. Bu yapıyı seçtim çünkü bu sinir ağını kullanarak rastgele oluşturulmuş bir veri kümesi üzerinde sınıflandırma yapacağım.
Aşağıdaki FeedForwardMLP() fonksiyonu bir NxN yapısıdır, yani üç girdi düğümünüz varsa ve üç gizli katman seçerseniz, her gizli katmanda üç gizli düğüm olacaktır. Şekle bakın:
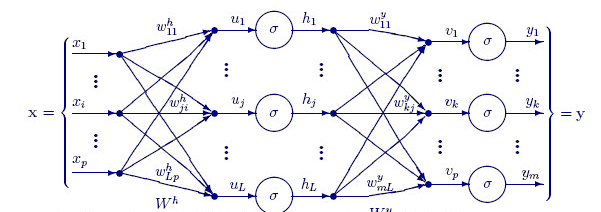
FeedForwardMLP() fonksiyonu:
void CNeuralNets::FeedForwardMLP(int HiddenLayers, double &MLPInputs[], double &MLPWeights[], double &bias[], double &MLPOutput[]) { double L_weights[], L_inputs[], L_Out[]; ArrayCopy(L_inputs,MLPInputs); int HLnodes = ArraySize(MLPInputs); int no_weights = HLnodes*ArraySize(L_inputs); int weight_start = 0; for (int i=0; i<HiddenLayers; i++) { if (m_debug) printf("<< Hidden Layer %d >>",i+1); ArrayCopy(L_weights,MLPWeights,0,weight_start,no_weights); Neuron(HLnodes,bias[i],L_weights,L_inputs,L_Out); ArrayCopy(L_inputs,L_Out); ArrayFree(L_Out); ArrayFree(L_weights); weight_start += no_weights; } if (use_softmax) SoftMax(L_inputs); ArrayCopy(MLPOutput,L_inputs); if (m_debug) { Print("\nFinal MLP output(s)"); ArrayPrint(MLPOutput,5); } }
Bir sinir ağında nokta çarpımı bulma işlemleri matris işlemleri kullanılarak gerçekleştirilebilirdi. Ancak bu ilk makalede her şeyi herkese açık hale getirmek için döngü yöntemini seçtim. Bir dahaki sefere matris çarpımını kullanacağız.
Kütüphaneyi oluşturmak için seçtiğim varsayılan mimari hakkında bilgi edindik. Şimdi sinir ağı mimarileri konusu ortaya çıkıyor.
Google'ı açıp sinir ağı görsellerini aratırsanız, şunlar gibi farklı sinir ağı yapılarına sahip binlerce, hatta on binlerce görsel önerilecektir:
Milyon dolarlık soru: En iyi sinir ağı mimarisi nedir?
“Hiç kimse tüm cevapları bilen bir kişi kadar yanılgı içinde değildir” - Thomas Merton.
Şimdi bu konuyu parçalara ayıralım ve neyin gerekli olup neyin olmadığını anlayalım.
Girdi katmanıBu katmanı oluşturan girdilerin sayısı, özelliklerin (veri kümesindeki sütunlar) sayısına eşit olmalıdır.
Çıktı katmanı
Büyüklük (nöron sayısı), sınıflandırma sinir ağı için veri kümesindeki sınıflar tarafından belirlenir. Regresyon tipi görevler için nöron sayısı seçilen model konfigürasyonuna göre belirlenir. Bir regresör için bir çıktı katmanı genellikle fazlasıyla yeterli olur.
Gizli katmanlar
Eğer problem çok karmaşık değilse, bir veya iki gizli katman fazlasıyla yeterlidir. Aslında, problemlerin büyük çoğunluğu için iki gizli katman yeterlidir. Ancak her gizli katmanda kaç düğüm olmalıdır? Bu konuda emin değilim, ancak bunun performansa bağlı olduğunu düşünüyorum. Belirli bir problem türü için neyin en iyi sonucu verdiğini görmek için farklı düğümleri keşfetmek ve denemek geliştiriciye kalmıştır. Düğümlerle denemeler yapmadan önce, daha önce tartıştığımız diğer sinir ağı türlerini anlamanız gerekir.
Bu konuyla ilgili stats.stackexchange.com'da harika bir başlık var (buraya bir link ekliyorum).
Bence tüm gizli katmanlar için girdi katmanıyla aynı sayıda düğüm, ileri beslemeli bir sinir ağı için idealdir. Ben çoğu zaman bu yapılandırmayı kullanıyorum.
Gizli katmanda tek düğümlü MLP - lineer regresyon modeli
Sinir ağının gizli katmanının bir düğümünde gerçekleştirilen işlemlere dikkat ederseniz, aşağıdakileri fark edeceksiniz:
Q = wi*Ii + b
Bu arada, lineer regresyon denklemi şöyledir:
Y = mi*xi + c
Benzerliği fark ettiniz mi? Teorik olarak aynı şeylerdir, bu işlem lineer regresyondur, bu da bizi gizli katman yanlılığının önemine geri getirir. Yanlılık, lineer bir model için bir sabittir ve belirli bir veri kümesine uyması için modelimize esneklik katar. Bu olmadan, tüm modeller x ve y eksenleri arasından sıfırdan geçecektir.
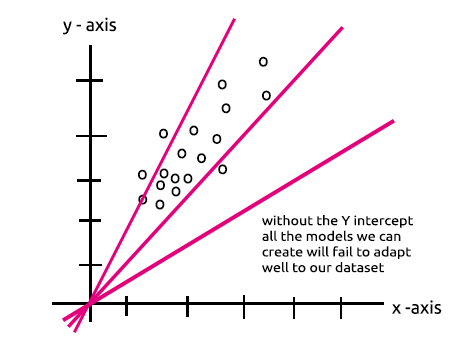
Sinir ağı eğitildikçe ağırlıklar ve yanlılıklar güncellenecektir. Modelimiz için daha az hata veren parametreler saklanacak ve test için veri kümesinde hatırlanacaktır.
Şimdi iki sınıfı sınıflandırmak için bir MLP oluşturalım. Bu, kullanımın daha iyi anlaşılmasına yardımcı olacaktır. Ancak bundan önce, sinir ağımızın birlikte çalışacağı etiketli rastgele bir veri kümesi oluşturalım. Aşağıdaki fonksiyon rastgele bir veri kümesi oluşturur: farklı ölçeklerde veri elde etmek için ilk örneklem 2 ile ve ikinci örneklem 5 ile çarpılır.
void MakeBlobs(int size=10) { ArrayResize(data_blobs,size); for (int i=0; i<size; i++) { data_blobs[i].sample_1 = (i+1)*(2); data_blobs[i].sample_2 = (i+1)*(5); data_blobs[i].class_ = (int)round(nn.MathRandom(0,1)); } }
Veri kümesini yazdırdığımda çıkan sonuç:
QK 0 18:27:57.298 TestScript (EURUSD,M1) CNeural Nets Initialized activation = SIGMOID UseSoftMax = No IR 0 18:27:57.298 TestScript (EURUSD,M1) [sample_1] [sample_2] [class_] LH 0 18:27:57.298 TestScript (EURUSD,M1) [0] 2.0000 5.0000 0 GG 0 18:27:57.298 TestScript (EURUSD,M1) [1] 4.0000 10.0000 0 NL 0 18:27:57.298 TestScript (EURUSD,M1) [2] 6.0000 15.0000 1 HJ 0 18:27:57.298 TestScript (EURUSD,M1) [3] 8.0000 20.0000 0 HQ 0 18:27:57.298 TestScript (EURUSD,M1) [4] 10.0000 25.0000 1 OH 0 18:27:57.298 TestScript (EURUSD,M1) [5] 12.0000 30.0000 1 JF 0 18:27:57.298 TestScript (EURUSD,M1) [6] 14.0000 35.0000 0 DL 0 18:27:57.298 TestScript (EURUSD,M1) [7] 16.0000 40.0000 1 QK 0 18:27:57.298 TestScript (EURUSD,M1) [8] 18.0000 45.0000 0 QQ 0 18:27:57.298 TestScript (EURUSD,M1) [9] 20.0000 50.0000 0
Bir sonraki kısım rastgele ağırlık ve yanlılık değerleri üretmektir.
generate_weights(weights,ArraySize(Inputs));
generate_bias(biases); Sonuç:
RG 0 18:27:57.298 TestScript (EURUSD,M1) weights QS 0 18:27:57.298 TestScript (EURUSD,M1) 0.7084 -0.3984 0.6182 0.6655 -0.3276 0.8846 0.5137 0.9371 NL 0 18:27:57.298 TestScript (EURUSD,M1) biases DD 0 18:27:57.298 TestScript (EURUSD,M1) -0.5902 0.7384
Şimdi kodumuzun ana fonksiyonundaki tüm işlemlere bakalım:
#include "NeuralNets.mqh"; CNeuralNets *nn; input int batch_size =10; input int hidden_layers =2; data data_blobs[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- nn = new CNeuralNets(SIGMOID); MakeBlobs(batch_size); ArrayPrint(data_blobs); double Inputs[],OutPuts[]; ArrayResize(Inputs,2); ArrayResize(OutPuts,2); double weights[], biases[]; generate_weights(weights,ArraySize(Inputs)); generate_bias(biases); Print("weights"); ArrayPrint(weights); Print("biases"); ArrayPrint(biases); for (int i=0; i<batch_size; i++) { Print("Dataset Iteration ",i); Inputs[0] = data_blobs[i].sample_1; Inputs[1]= data_blobs[i].sample_2; nn.FeedForwardMLP(hidden_layers,Inputs,weights,biases,OutPuts); } delete(nn); }
Dikkat edilmesi gereken şeyler:
- Yanlılık sayısı gizli katman sayısı ile aynıdır.
- Toplam ağırlık sayısı = girdi sayısının karesi ile gizli katman sayısının çarpımı. Bu mümkündür çünkü ağımız, ağın girdi katmanı/önceki katmanı ile aynı sayıda düğüme sahiptir (tüm katmanlar girdiden çıktıya kadar aynı sayıda düğüme sahiptir).
- Aynı prensibi izleyerek, diyelim ki 3 girdi düğümünüz varsa, son katman hariç tüm gizli katmanlar 3 düğüme sahip olacaktır. Bu son katmana ne olacağını görelim.
Rastgele oluşturulmuş veri kümesine baktığınızda, veri kümesinde iki girdi özelliği/sütunu göreceksiniz. Bu yüzden iki gizli katman eklemeye karar verdim. İşte modelimizin hesaplamaları nasıl yapacağına dair günlüğe kısa bir genel bakış (bu tür günlük kayıtlarını almak istemiyorsanız, kodda hata ayıklama modunu false olarak ayarlayın).
NL 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 0 EJ 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> GO 0 18:27:57.298 TestScript (EURUSD,M1) NS 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 EI 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 2.00000 x weight 0.70837 FQ 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 5.00000 x weight -0.39838 QP 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -0.57513 + bias -0.590 = -1.16534 RH 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.23770 CQ 0 18:27:57.298 TestScript (EURUSD,M1) OE 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 CO 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 2.00000 x weight 0.61823 FI 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 5.00000 x weight 0.66553 PN 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 4.56409 + bias -0.590 = 3.97388 GM 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.98155 DI 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> GL 0 18:27:57.298 TestScript (EURUSD,M1) NF 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 FH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.23770 x weight -0.32764 ID 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.98155 x weight 0.88464 QO 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.79044 + bias 0.738 = 1.52884 RK 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82184 QG 0 18:27:57.298 TestScript (EURUSD,M1) IH 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 DQ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.23770 x weight 0.51367 CJ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.98155 x weight 0.93713 QJ 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.04194 + bias 0.738 = 1.78034 JP 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85574 EI 0 18:27:57.298 TestScript (EURUSD,M1) GS 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) OF 0 18:27:57.298 TestScript (EURUSD,M1) 0.82184 0.85574 CN 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 1 KH 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> EM 0 18:27:57.298 TestScript (EURUSD,M1) DQ 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 QH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 4.00000 x weight 0.70837 PD 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 10.00000 x weight -0.39838 HR 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -1.15027 + bias -0.590 = -1.74048 DJ 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.14925 OP 0 18:27:57.298 TestScript (EURUSD,M1) CK 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 MN 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 4.00000 x weight 0.61823 NH 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 10.00000 x weight 0.66553 HI 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 9.12817 + bias -0.590 = 8.53796 FO 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.99980 RG 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> IR 0 18:27:57.298 TestScript (EURUSD,M1) PD 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 RN 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.14925 x weight -0.32764 HF 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.99980 x weight 0.88464 EM 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.83557 + bias 0.738 = 1.57397 EL 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82835 KE 0 18:27:57.298 TestScript (EURUSD,M1) GN 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 LS 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.14925 x weight 0.51367 FL 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.99980 x weight 0.93713 KH 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.01362 + bias 0.738 = 1.75202 IR 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85221 OH 0 18:27:57.298 TestScript (EURUSD,M1) IM 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) MH 0 18:27:57.298 TestScript (EURUSD,M1) 0.82835 0.85221
Şimdi tüm yinelemeler için nihai MLP çıktılarına dikkat edin. Çıktıların düzgün bir şekilde aynı değerlere sahip olma eğiliminde olduğu garip bir davranış fark edeceksiniz. Bu sorunun birkaç nedeni vardır. Bu Stack başlığına bakılırsa, bunlardan biri çıktı katmanında yanlış aktivasyon fonksiyonunun kullanılmasıdır. İşte bu noktada SoftMax aktivasyon fonksiyonu imdada yetişiyor.
Anladığım kadarıyla, sigmoid fonksiyonu yalnızca çıktı katmanında tek bir sınıfı sınıflandırması gereken tek bir düğüm olduğunda olasılıkları geri döndürüyor. Bu durumda, bir şeyin belirli bir sınıfa ait olup olmadığını söylemek için sigmoid fonksiyonunun çıktısına ihtiyacımız olacaktır. Ama bu başka bir hikaye. Son düğümlerin çıktılarını toplarsak, değer çoğu zaman 1 değerini aşar. Yani, bunların olasılık olmadığı açıktır, çünkü olasılık 1 değerini aşamaz.
SoftMax fonksiyonunu son katmana uygularsak çıktılar aşağıdaki gibi olur:
Birinci yineleme çıktıları: [0.4915 0.5085]. İkinci yineleme çıktıları: [0.4940 0.5060].
Bu durumda çıktılar [Sınıf 0'a ait olma olasılığı Sınıf 1'e ait olma olasılığı] olarak yorumlanabilir.
En azından şimdi ağımızdan anlamlı bir şey yorumlarken güvenebileceğimiz olasılıklarımız var.
Son düşünceler
İleri beslemeli sinir ağı ile çalışmayı henüz bitirmedik, ancak en azından şimdilik teoriyi ve MQL5'te sinir ağlarında ustalaşmanıza yardımcı olacak en önemli şeyleri anladınız. Tasarlanan ileri beslemeli sinir ağı sınıflandırma amaçlıdır, bu nedenle uygun aktivasyon fonksiyonları veri kümenizde sınıflandırmak istediğiniz örneklemlere ve sınıflara bağlı olarak sigmoid ve TanH'dir. Tıpkı gizli katmanlardaki düğümler gibi, üzerinde oynanacak bir şey geri döndürmek için çıktı katmanını değiştiremeyiz. Matris kullanımı, tüm bu işlemleri dinamik hale getirmeye yardımcı olacaktır, böylece herhangi bir görev için standart bir sinir ağı oluşturabileceğiz. Bu makale serisinin amacı budur, bu nedenle daha fazlası için takip etmeye devam edin.
Bir sinir ağını ne zaman kullanacağınızı bilmek de önemlidir çünkü tüm görevlerin sinir ağları ile çözülmesi gerekmez. Eğer bir görev lineer regresyon ile çözülebiliyorsa, lineer bir model sinir ağından daha iyi performans gösterebilir. Bu da akılda tutulması gereken noktalardan biridir.
GitHub deposu: https://github.com/MegaJoctan/NeuralNetworks-MQL5
Daha Fazla Kaynak | Kitaplar | Referanslar
-
Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
-
Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
-
Deep Learning (Adaptive Computation and Machine Learning series)
Makale referansları:
-
Veri Bilimi ve Makine Öğrenimi (Bölüm 02): Lojistik Regresyon
-
Veri Bilimi ve Makine Öğrenimi (Bölüm 03): Matris Regresyonları
MetaQuotes Ltd tarafından İngilizceden çevrilmiştir.
Orijinal makale: https://www.mql5.com/en/articles/11275
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.
Bu makale sitenin bir kullanıcısı tarafından yazılmıştır ve kendi kişisel görüşlerini yansıtmaktadır. MetaQuotes Ltd, sunulan bilgilerin doğruluğundan veya açıklanan çözümlerin, stratejilerin veya tavsiyelerin kullanımından kaynaklanan herhangi bir sonuçtan sorumlu değildir.
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz


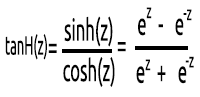
...
Bunu açıklayabilir misiniz? Ya da bazı örnekler verebilir misiniz?
strateji test cihazında optimizasyon ile sinir ağı parametrelerini optimize etmek arasındaki fark hedeftir, strateji test cihazında en karlı çıktıları veya en azından istediğimiz ticaret sonuçlarını sağlayan parametrelere odaklanma eğilimindeyiz, bu mutlaka sinir ağının bu tür sonuçlara yol açan iyi bir modele sahip olduğu anlamına gelmez
Bazı insanlar ağırlıkları ve önyargıyı sinir ağı tabanlı sistemlerin giriş parametreleri olarak koymayı tercih ediyor(kabaca ileri besleme), ancak strateji test cihazını kullanarak optimize etmenin temelde en iyi sonuçların rastgele değerlerini bulmak olduğunu düşünüyorum (en uygun olanları bulmak şansa bağlı gibi geliyor), stokastik gradyan inişi kullanarak optimize edersek, her adımda tahminlerde en az hataya sahip modele doğru ilerliyoruz.
strateji test cihazında optimizasyon ile sinir ağı parametrelerini optimize etmek arasındaki fark hedeftir, strateji test cihazında en karlı çıktıları veya en azından istediğimiz ticaret sonuçlarını sağlayan parametrelere odaklanma eğilimindeyiz, bu mutlaka sinir ağının bu tür sonuçlara yol açan iyi bir modele sahip olduğu anlamına gelmez
Bazı insanlar ağırlıkları ve önyargıyı sinir ağı tabanlı sistemlerin giriş parametreleri olarak koymayı tercih ediyor(kabaca ileri besleme), ancak strateji test cihazını kullanarak optimize etmenin temelde en iyi sonuçların rastgele değerlerini bulmak olduğunu düşünüyorum (en uygun olanları bulmak şansa bağlı gibi geliyor), stokastik gradyan inişi kullanarak optimize edersek, her adımda tahminlerde en az hataya sahip modele doğru ilerliyoruz.
Cevabınız için teşekkür ederim.
Demek istediğinizi anladım.
Neden ilk bölümden başladınız?
eski makale:
VERİ BİLİMİ VE MAKİNE ÖĞRENMESİ (BÖLÜM 01): DOĞRUSAL REGRESYON
https://www.mql5.com/tr/articles/10459
Neden ilk bölümden başladınız?
Eski makale:
VERİ BİLİMİ VE MAKİNE ÖĞRENMESİ (BÖLÜM 01): DOĞRUSAL REGRESYON
https://www.mql5.com/tr/articles/10459
Ne demek istiyorsun?
Neden ilk bölümden başladınız?
Eski makale:
VERİ BİLİMİ VE MAKİNE ÖĞRENMESİ (BÖLÜM 01): DOĞRUSAL REGRESYON
https://www.mql5.com/tr/articles/10459