데이터 과학 및 머신 러닝 - 신경망(1부): 피드 포워드 신경망에 대한 이해
"...너무 많이 알면서 너무 적게 이해하는 것에 지쳤습니다."
- 얀 카론, 홀리 스프링스의 고향
소개
신경망은 성배 거래 시스템을 구축하기 위한 방법으로 보이기도 하며 멋진 새로운 것처럼 들리기도 합니다. 많은 트레이더들은 신경망으로 만든 프로그램이 기본적으로 시장의 움직임을 예측하는 데 능숙하고 모든 작업에 능숙하기 때문에 신경망으로 만든 프로그램에 놀라움을 금치 못합니다. 저 역시 이러한 시스템들은 학습되지 않았거나 본 적 없는 데이터를 기반으로 예측하거나 분류하는 데 있어 엄청난 잠재력이 있다고 생각합니다.
이들 시스템들은 다층 퍼셉트론이 올바른 아키텍처에 있는지 문제 유형이 선형 또는 로지스틱 회귀 모델이나 다른 머신러닝 기법이 아닌 신경망이 필요한 문제인지 등을 잘 알고 있는 사람이 구축해야 하고 최적화해야 합니다.
신경망은 더 광범위한 주제이며 일반적으로 머신 러닝도 마찬가지입니다. 저는 시리즈의 다른 소제목에서 ML의 또 다른 측면을 진행할 것입니다. 그래서 신경망에 대한 소제목을 추가하기로 결정했습니다.
이 글에서는 신경망의 기본을 살펴보고 머신러닝 애호가들이 이 주제를 마스터하기 위해서 이해해야 하는 몇 가지 기본적인 질문에 답해 보겠습니다.
인공 신경망이란 무엇인가요?
일반적으로 신경망이라고 불리는 인공 신경망(ANN;Artificial Neural Networks)은 동물의 두뇌를 구성하는 생물학적 신경망에서 영감을 얻은 컴퓨팅 시스템입니다.
다층 퍼셉트론 대 심층 신경망
신경망에 대해 논의할 때 여러분은 다층 퍼셉트론(MLP)이라는 용어를 자주 듣게 될 것입니다. 이것은 가장 일반적인 유형의 신경망에 불과합니다. MLP는 입력 계층, 숨겨진 계층, 출력 계층으로 구성된 네트워크입니다. 단순하기 때문에 데이터의 프레젠테이션을 학습하고 결과물을 생성하는 데 짧은 교육 시간이 필요합니다.
애플리케이션:
MLP는 일반적으로 회귀 분석과 같이 선형적으로 분리할 수 없는 데이터에 사용되고 단순하기 때문에 복잡한 분류 작업과 예측 모델링에 가장 적합하며 기계 번역, 일기 예보, 사기 탐지, 주식 시장 예측, 신용 등급 예측 등 여러분이 생각할 수 있는 다양한 분야에서 활용되고 있습니다.
반면 심층 신경망은 일반적인 구조를 가지고 있지만 숨겨진 계층이 너무 많다는 점이 유일한 차이점입니다. 만약 네트워크에 숨겨진 레이어가 3개(3) 이상이면 심층 신경망으로 간주합니다. 복잡한 특성상 입력 데이터에 대한 네트워크 학습에 오랜 시간이 추가로 필요하기 때문에 텐서 처리 장치(TPU) 및 신경망 처리 장치(NPU)와 같은 특수한 처리 장치를 갖춘 강력한 컴퓨터가 필요합니다.
애플리케이션:
DNN은 심층 계층으로 인해 강력한 알고리즘이므로 일반적으로 복잡한 계산 작업을 처리하는 데 사용되며 컴퓨터 비전도 이러한 작업 중 하나입니다.
차이점:
| MLP | DNN |
|---|---|
| 적은 수의 숨겨진 레이어 | 많은 수의 숨겨진 레이어 |
| 짧은 교육 기간 | 더 긴 교육 시간 |
| GPU 지원 장치로 충분 | TPU 지원 장치로 충분 |
이제 신경망의 종류에 대해 알아보겠습니다.
신경망에는 여러 종류가 있지만 크게 세 가지로 분류할 수 있습니다;
- 피드 포워드 신경망
- 컨볼루션 신경망
- 순환 신경망
01: 피드 포워드 신경망
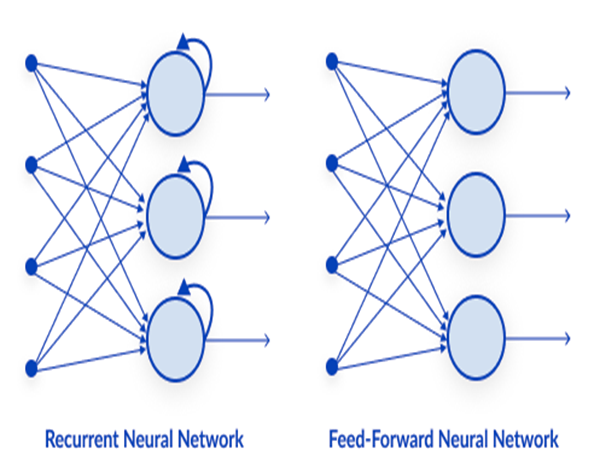
이것은 가장 간단한 유형의 신경망 중 하나입니다. 피드 포워드 신경망에서 데이터는 출력 노드에 도달할 때까지 여러 입력 노드를 통과합니다. 역전파와 달리 여기서는 데이터가 한 방향으로만 이동합니다.
간단히 말해 역전파는 신경망에서 데이터가 입력 계층에서 출력 계층으로 전달되는 피드 포워드와 동일한 프로세스를 수행하지만 역전파에서는 네트워크의 출력이 출력 계층에 도달한 후 클래스의 실제 값을 확인하고 예측한 값과 비교하여 모델이 얼마나 잘못 예측했는지 또는 예측이 올바른지 확인합니다. 만약 잘못된 예측을 한 경우에는 데이터를 네트워크에 역전파하고 다음 번에 올바른 예측을 할 수 있도록 매개변수를 업데이트합니다. 이것은 스스로 학습하는 알고리즘 유형입니다.
02: 순환 신경망
순환 신경망은 특정 계층의 출력이 저장되고 다시 입력 계층으로 피드백 되는 인공 신경망의 한 유형입니다. 이는 레이어의 결과를 예측하는 데 도움이 됩니다.
순환 신경망은 다음과 관련된 문제를 해결하는 데 사용됩니다.
- 시계열 데이터
- 텍스트 데이터
- 오디오 데이터
텍스트 데이터의 가장 일반적인 용도는 인공지능이 말할 다음 단어를 추천하는 것입니다 가령 다음과 같습니다: How + are + you +?
03: 컨볼루션 신경망(CNN;Convolution Neural Network)
CNN은 딥러닝 커뮤니티에서 큰 인기를 끌고 있습니다. 이 신경망은 이미지 및 비디오 처리 프로젝트에서 널리 사용됩니다.
예를 들어 이미지 감지 및 분류 AI는 컨볼루션 신경망으로 구성됩니다.
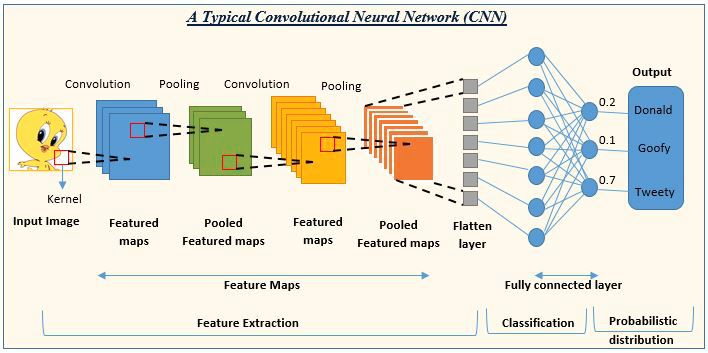
이미지 출처: analyticsvidhya.com
이제 신경망의 유형을 살펴봤으니 이 글의 주요 주제인 피드 포워드 신경망으로 초점을 옮겨보겠습니다.
피드 포워드 신경망
다른 복잡한 유형의 신경망과 달리 역전파가 없으므로 이 유형의 신경망에서는 데이터가 한 방향으로만 흐르며 하나의 숨겨진 레이어 또는 여러 개의 숨겨진 레이어를 가질 수 있습니다.
이 네트워크의 작동 원리를 살펴보겠습니다.
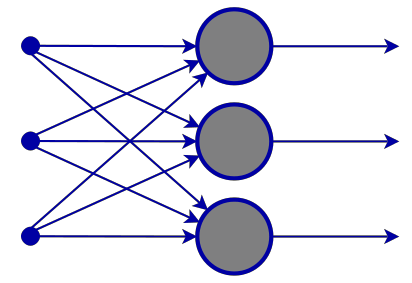
입력 레이어
신경망의 이미지를 보면 입력 계층이 있는 것처럼 보이지만 내부를 들여다보면 입력 레이어는 단지 하나의 표현일 뿐이며 계산이 수행되지 않습니다.
숨겨진 레이어
숨겨진 레이어는 네트워크에서 대부분의 작업이 이루어지는 곳입니다.
좀더 확실히 하기 위해 두 번째 숨겨진 레이어 노드를 자세히 살펴봅시다.
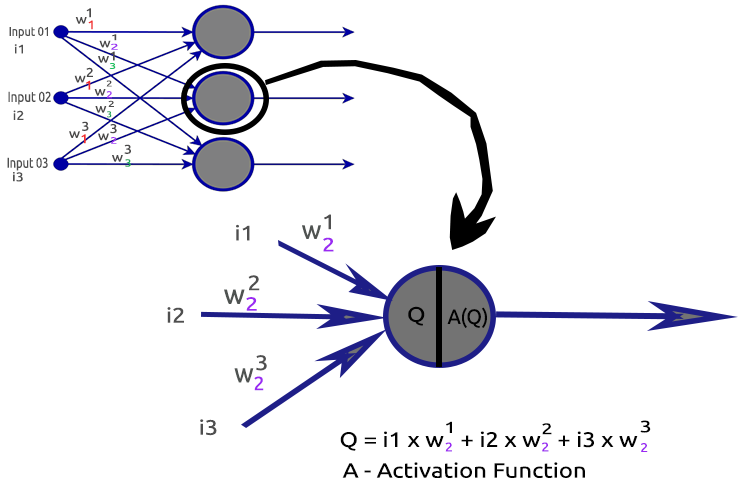
관련 프로세스:
- 입력과 각각의 가중치의 내적 구하기
- 편향성에 얻은 내적 더하기
- 두 번째 절차의 결과는 활성화 함수에 전달됩니다.
편향성(Bias)이란 무엇인가요?
편향성을 사용하면 선형 회귀를 위아래로 이동하여 예측 라인을 데이터에 더 잘 맞출 수 있습니다. 이는 선형 회귀선의 절편과 동일합니다.
이 매개변수는 숨겨진 레이어에 단일 노드가 있는 MLP는 선형 회귀 모델라는 섹션을 통해 잘 이해할 수 있을 것입니다.
편향성의 중요성은 여기 Stack에 잘 설명되어 있습니다.
가중치(Weight)란 무엇인가요?
가중치는 해결하려는 방정식의 계수인 입력이 얼마나 중요한지를 반영합니다. 가중치가 음수이면 출력 값이 감소하고 그 반대의 경우도 마찬가지입니다. 학습 데이터 세트에 대해 신경망이 학습될 때 가중치 세트로 초기화됩니다. 그런 다음 훈련 기간 동안 이러한 가중치를 최적화하여 최적의 가중치 값을 생성합니다.
활성화 함수란 무엇인가요?
활성화 함수는 입력을 받아 출력을 생성하는 수학적 함수일 뿐입니다.
활성화 함수의 종류
다양한 활성화 함수가 그 변형과 함께 존재하지만 가장 일반적으로 사용되는 활성화 함수는 다음과 같습니다:
- Relu
- Sigmoid
- TanH
- Softmax
어떤 활성화 함수를 어디에 사용해야 하는지 알고 있다는 것은 매우 중요한데 저는 온라인에서 활성화 함수를 관련 없는 곳에서 사용하라는 글을 몇 번이나 보았는지 모릅니다. 자세히 살펴보겠습니다.
01: RELU
RELU는 정류된 선형 활성화 함수의 약자로
신경망에서 가장 많이 사용되는 활성화 함수입니다. 가장 간단하고 코딩하기 쉬우며 결과물을 해석하기 쉽기 때문에 인기가 높습니다. 이 함수는 입력이 양수인 경우 입력값을 바로 출력하고 그렇지 않으면 0을 출력합니다.
로직은 다음과 같습니다.
if x < 0 : return 0
else return x
이 함수는 회귀 문제를 해결하는데에 잘 사용됩니다.
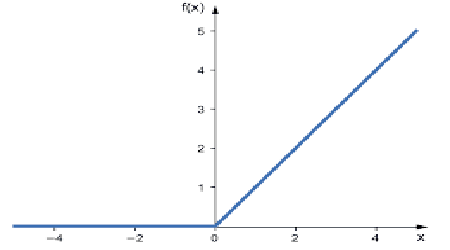
출력 범위는 0에서 양의 무한대까지 입니다.
MQL5 코드는 다음과 같습니다:
double CNeuralNets::Relu(double z) { if (z < 0) return(0); else return(z); }
RELU는 sigmoid와 TanH가 겪는 소실 경사 문제를 해결합니다(자세한 내용은 역전파에 관한 글에서 확인할 수 있습니다).
02: Sigmoid
익숙하게 들리시죠? 로지스틱 회귀를 기억하시나요
그 공식은 다음과 같습니다.
![]()
이 함수는 분류 문제, 특히 한 클래스 또는 두 클래스만 분류할 때 사용하는 것이 좋습니다.
출력 범위는 0에서 1까지입니다(확률 용어).
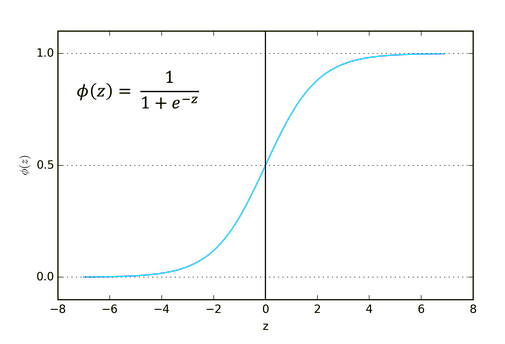
예를 들어 여러분의 네트워크가 출력에 두 개의 노드가 있습니다. 첫 번째 노드는 고양이용이고 다른 노드는 강아지 용입니다. 여러분은 첫 번째 노드의 출력이 0.5보다 크면 고양이이고 같지만 그 반대이면 강아지라는 것을 나타내는 출력을 선택할 수 있습니다.
MQL5 코드는 다음과 같습니다:
double CNeuralNets::Sigmoid(double z) { return(1.0/(1.0+MathPow(e,-z))); }
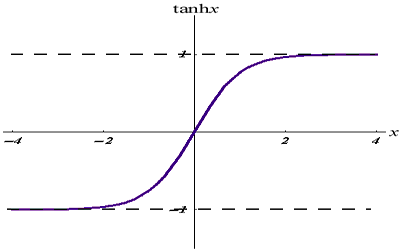
03: TanH
쌍곡선 탄젠트 함수입니다.
공식에 의해 주어집니다:
그래프는 아래와 같습니다:
이 활성화 함수는 sigmoid와 비슷하지만 더 나은 함수입니다.
출력 범위는 -1에서 1까지입니다.
이 함수는 멀티클래스 분류 신경망에서 더 잘 사용됩니다.
MQL5 코드는 아래와 같습니다:
double CNeuralNets::tanh(double z) { return((MathPow(e,z) - MathPow(e,-z))/(MathPow(e,z) + MathPow(e,-z))); }
04: SoftMax
누군가 SoftMax 함수에 대한 그래프가 없는 이유를 물어본 적이 있습니다. 다른 활성화 함수와 달리 SoftMax는 숨겨진 레이어에서 사용되지 않고 출력 레이어에서만 사용되며 멀티클래스 신경망의 출력을 확률 용어로 변환하려는 경우에만 사용해야 합니다.
SoftMax는 다항식 확률 분포를 예측합니다.
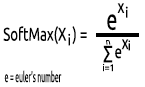
예를 들어 회귀 신경망의 출력은 [1,3,2] 인데 이 출력에 SoftMax 함수를 적용하면 이제 출력은 [0.09003, 0.665240, 0.244728]이 됩니다.
이 함수의 출력 범위는 0에서 1 사이입니다.
MQL5 코드는 다음과 같습니다:
void CNeuralNets::SoftMax(double &Nodes[]) { double TempArr[]; ArrayCopy(TempArr,Nodes); ArrayFree(Nodes); double proba = 0, sum=0; for (int j=0; j<ArraySize(TempArr); j++) sum += MathPow(e,TempArr[j]); for (int i=0; i<ArraySize(TempArr); i++) { proba = MathPow(e,TempArr[i])/sum; Nodes[i] = proba; } ArrayFree(TempArr); }
이제 숨겨진 레이어의 단일 뉴런이 무엇으로 구성되는지 이해했으니 이를 코딩해 보겠습니다.
void CNeuralNets::Neuron(int HLnodes, double bias, double &Weights[], double &Inputs[], double &Outputs[] ) { ArrayResize(Outputs,HLnodes); for (int i=0, w=0; i<HLnodes; i++) { double dot_prod = 0; for(int j=0; j<ArraySize(Inputs); j++, w++) { if (m_debug) printf("i %d w %d = input %.2f x weight %.2f",i,w,Inputs[j],Weights[w]); dot_prod += Inputs[j]*Weights[w]; } Outputs[i] = ActivationFx(dot_prod+bias); } }
ActivationFx() 내부에서 우리는 NeuralNets 생성자를 호출할 때 어떤 활성화 함수를 사용할지 선택할 수 있습니다.
double CNeuralNets::ActivationFx(double Q) { switch(A_fx) { case SIGMOID: return(Sigmoid(Q)); break; case TANH: return(tanh(Q)); break; case RELU: return(Relu(Q)); break; default: Print("Unknown Activation Function"); break; } return(0); }
코드에 대한 자세한 설명입니다:
Neuron() 함수는 숨겨진 레이어 내부의 단일 노드일 뿐만 아니라 숨겨진 레이어의 모든 연산이 이 하나의 함수 안에서 수행되기도 합니다. 모든 숨겨진 레이어의 노드는 최종 출력 노드까지 입력 노드와 동일한 크기를 갖습니다. 제가 이 구조를 선택한 이유는 무작위로 생성된 데이터 세트에서 이 신경망을 사용하여 분류를 수행하려고 하기 때문입니다.
아래 함수 FeedForwardMLP()는 NxN 구조입니다. 이는 다시 말해 만약 여러분이 3개의 입력 노드가 있고 3개의 숨겨진 레이어를 선택했다면 각 숨겨진 레이어에 3개의 숨겨진 노드가 이미지를 보게 되는 것입니다 .
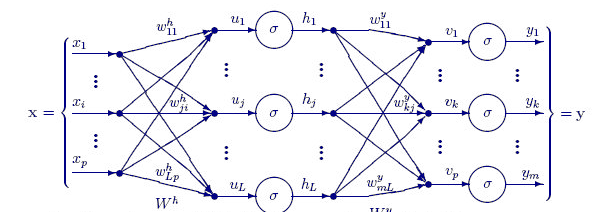
FeedForwardMLP() 함수는 다음과 같습니다:
void CNeuralNets::FeedForwardMLP(int HiddenLayers, double &MLPInputs[], double &MLPWeights[], double &bias[], double &MLPOutput[]) { double L_weights[], L_inputs[], L_Out[]; ArrayCopy(L_inputs,MLPInputs); int HLnodes = ArraySize(MLPInputs); int no_weights = HLnodes*ArraySize(L_inputs); int weight_start = 0; for (int i=0; i<HiddenLayers; i++) { if (m_debug) printf("<< Hidden Layer %d >>",i+1); ArrayCopy(L_weights,MLPWeights,0,weight_start,no_weights); Neuron(HLnodes,bias[i],L_weights,L_inputs,L_Out); ArrayCopy(L_inputs,L_Out); ArrayFree(L_Out); ArrayFree(L_weights); weight_start += no_weights; } if (use_softmax) SoftMax(L_inputs); ArrayCopy(MLPOutput,L_inputs); if (m_debug) { Print("\nFinal MLP output(s)"); ArrayPrint(MLPOutput,5); } }
신경망에서 내적을 구하는 연산은 행렬 연산으로 처리할 수도 있지만 이 첫 번째 기사에서는 누구나 이해하기 쉽도록 하기 위해 행렬 곱셈을 사용하는 루프 방식을 선택했습니다.
이제 여러분은 라이브러리 구축을 위해 기본적으로 선택한 아키텍처를 보셨을 것입니다. 그러면 이제 신경망 아키텍처에 대한 의문이 생깁니다.
구글에 가서 신경망 이미지를 검색하면 예를 들어 이와 같이 서로 다른 신경망 구조를 가진 수천, 아니 수만 개의 이미지가 쏟아져 나옵니다:
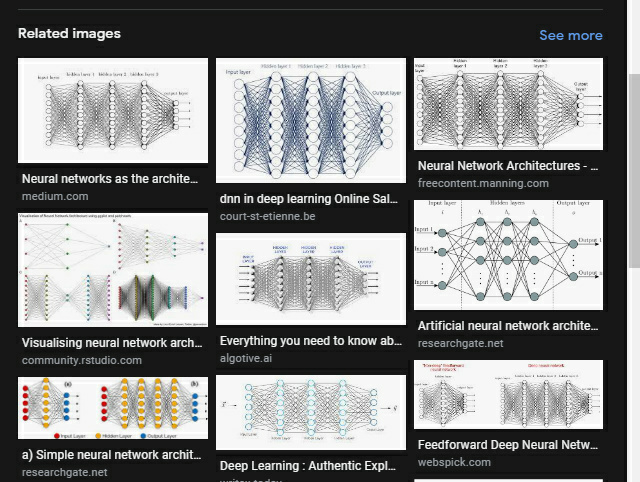
백만 달러짜리 질문은 아마도 최고의 신경망 아키텍처는 무엇일까요? 일 것입니다
"모든것에 대해 답을 아는 사람만큼 틀리는 사람은 없다." - 토마스 머튼.
이제 무엇이 필요하고 무엇이 필요하지 않은지 이해하기 위해 세분화해 보겠습니다.
입력 레이어이 계층을 구성하는 입력의 수는 피처(데이터 세트의 열)의 수와 같아야 합니다.
출력 레이어
크기(뉴런 수)를 결정하는 것은 분류 신경망의 경우 데이터 세트의 클래스에 따라 결정되며 회귀 유형의 문제의 경우 뉴런의 수는 선택한 모델 구성에 따라 결정됩니다. 회귀분석을 위한 출력 레이어 하나면 충분할 때가 많습니다.
숨겨진 레이어
문제가 많이 복잡하지 않다면 한두 개의 숨겨진 레이어만으로도 충분합니다. 사실 대부분의 문제는 숨겨진 레이어 두 개면 충분하기 때문입니다. 하지만 각각의 숨겨진 레이어에는 몇 개의 노드가 필요할까요? 저 생각으로는 성능에 따라 다를 것입니다. 이는 개발자가 다양한 노드를 탐색하고 시도하여 특정 종류의 문제에 가장 적합한 것이 무엇인지 확인하기 위해서 이고 여러분은 이 작업을 시작하기 전에 앞서 설명한 다른 유형의 신경망에 대해 알아 두어야 합니다.
이 주제에 대한 훌륭한 주제가 stats.stackexchange.com에 여기에 링크되어 있습니다.
저는 모든 숨겨진 레이어에 대해 입력 레이어와 동일한 수의 노드를 갖는 것이 피드 포워드 신경망에 이상적이라고 생각합니다. 저는 그렇게 대부분의 구성을 합니다.
단일 노드와 단일 숨겨진 레이어가 있는 MLP는 선형 모델입니다.
이는 신경망의 숨겨진 계층의 단일 노드 내부에서 수행되는 연산에 주의를 기울이면 이를 알 수 있습니다:
Q = wi * Ii + b
반면 선형 회귀 방정식은 다음과 같습니다;
Y = mi * xi + c
비슷한 점이 있나요? 이 연산은 이론적으로 동일한 선형 회귀 분석으로 숨겨진 레이어의 편향성의 중요성에 대해 다시 한 번 생각하게 해줍니다. 평향성은 주어진 데이터 세트에 맞게 모델의 유연성을 더하는 역할을 하는 선형 모델의 상수로 이 편향성이 없으면 모든 모델이 0(0)에서 X축과 Y축 사이를 통과하게 됩니다.
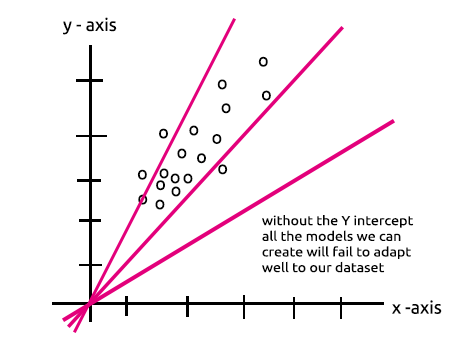
신경망을 훈련할 때는 가중치와 편향성이 업데이트됩니다. 모델에서 오류가 적은 매개변수들은 테스트 데이터 세트에 보관되어 기억됩니다.
이제 두 가지 클래스 분류를 위한 MLP를 구축하여 요점을 명확히 해보겠습니다. 그 전에 우리가 신경망을 통해 볼 레이블이 지정된 샘플로 무작위 데이터 세트를 생성해 보겠습니다. 아래 함수는 무작위 데이터 집합을 만들고 두 번째 샘플에 5를 곱하고 첫 번째 샘플에 2를 곱하여 다른 스케일의 데이터를 얻습니다.
void MakeBlobs(int size=10) { ArrayResize(data_blobs,size); for (int i=0; i<size; i++) { data_blobs[i].sample_1 = (i+1)*(2); data_blobs[i].sample_2 = (i+1)*(5); data_blobs[i].class_ = (int)round(nn.MathRandom(0,1)); } }
데이터 집합을 인쇄하면 다음과 같은 출력이 나옵니다:
QK 0 18:27:57.298 TestScript (EURUSD,M1) CNeural Nets Initialized activation = SIGMOID UseSoftMax = No IR 0 18:27:57.298 TestScript (EURUSD,M1) [sample_1] [sample_2] [class_] LH 0 18:27:57.298 TestScript (EURUSD,M1) [0] 2.0000 5.0000 0 GG 0 18:27:57.298 TestScript (EURUSD,M1) [1] 4.0000 10.0000 0 NL 0 18:27:57.298 TestScript (EURUSD,M1) [2] 6.0000 15.0000 1 HJ 0 18:27:57.298 TestScript (EURUSD,M1) [3] 8.0000 20.0000 0 HQ 0 18:27:57.298 TestScript (EURUSD,M1) [4] 10.0000 25.0000 1 OH 0 18:27:57.298 TestScript (EURUSD,M1) [5] 12.0000 30.0000 1 JF 0 18:27:57.298 TestScript (EURUSD,M1) [6] 14.0000 35.0000 0 DL 0 18:27:57.298 TestScript (EURUSD,M1) [7] 16.0000 40.0000 1 QK 0 18:27:57.298 TestScript (EURUSD,M1) [8] 18.0000 45.0000 0 QQ 0 18:27:57.298 TestScript (EURUSD,M1) [9] 20.0000 50.0000 0
다음 단계는 무작위 가중치 값과 편향성을 생성하는 것입니다,
generate_weights(weights,ArraySize(Inputs));
generate_bias(biases); 출력은 다음과 같습니다:
RG 0 18:27:57.298 TestScript (EURUSD,M1) weights QS 0 18:27:57.298 TestScript (EURUSD,M1) 0.7084 -0.3984 0.6182 0.6655 -0.3276 0.8846 0.5137 0.9371 NL 0 18:27:57.298 TestScript (EURUSD,M1) biases DD 0 18:27:57.298 TestScript (EURUSD,M1) -0.5902 0.7384
이제 스크립트의 메인 함수에서 전체 연산을 살펴보겠습니다:
#include "NeuralNets.mqh"; CNeuralNets *nn; input int batch_size =10; input int hidden_layers =2; data data_blobs[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- nn = new CNeuralNets(SIGMOID); MakeBlobs(batch_size); ArrayPrint(data_blobs); double Inputs[],OutPuts[]; ArrayResize(Inputs,2); ArrayResize(OutPuts,2); double weights[], biases[]; generate_weights(weights,ArraySize(Inputs)); generate_bias(biases); Print("weights"); ArrayPrint(weights); Print("biases"); ArrayPrint(biases); for (int i=0; i<batch_size; i++) { Print("Dataset Iteration ",i); Inputs[0] = data_blobs[i].sample_1; Inputs[1]= data_blobs[i].sample_2; nn.FeedForwardMLP(hidden_layers,Inputs,weights,biases,OutPuts); } delete(nn); }
주의해야 할 사항:
- 편향성의 수는 숨겨진 레이어의 수와 동일합니다.
- 총 가중치 수 = 입력의 제곱에 숨겨진 레이어의 수를 곱한 값입니다. 이는 우리의 네트워크가 입력 레이어/이전 레이어와 동일한 수의 노드를 가지고 있기 때문에 가능합니다 (모든 레이어는 입력에서 출력까지 동일한 수의 노드를 가짐).
- 입력 노드가 3개인 경우와 같이 처리 방법을 살펴볼 마지막 레이어를 제외한 모든 숨겨진 레이어에 3개의 노드가 있는 것과 같은 원리를 따릅니다.
무작위로 생성된 데이터 세트를 보면 데이터 세트에 두 개의 입력 기능/열을 볼 수 있습니다. 저는 2개의 숨겨진 레이어를 선택했습니다. 다음은 모델이 계산을 수행하는 방법에 대한 로그의 간략한 개요입니다(코드에서 디버그 모드를 false로 설정하여 이러한 로그를 방지합니다).
NL 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 0 EJ 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> GO 0 18:27:57.298 TestScript (EURUSD,M1) NS 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 EI 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 2.00000 x weight 0.70837 FQ 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 5.00000 x weight -0.39838 QP 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -0.57513 + bias -0.590 = -1.16534 RH 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.23770 CQ 0 18:27:57.298 TestScript (EURUSD,M1) OE 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 CO 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 2.00000 x weight 0.61823 FI 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 5.00000 x weight 0.66553 PN 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 4.56409 + bias -0.590 = 3.97388 GM 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.98155 DI 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> GL 0 18:27:57.298 TestScript (EURUSD,M1) NF 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 FH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.23770 x weight -0.32764 ID 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.98155 x weight 0.88464 QO 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.79044 + bias 0.738 = 1.52884 RK 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82184 QG 0 18:27:57.298 TestScript (EURUSD,M1) IH 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 DQ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.23770 x weight 0.51367 CJ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.98155 x weight 0.93713 QJ 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.04194 + bias 0.738 = 1.78034 JP 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85574 EI 0 18:27:57.298 TestScript (EURUSD,M1) GS 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) OF 0 18:27:57.298 TestScript (EURUSD,M1) 0.82184 0.85574 CN 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 1 KH 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> EM 0 18:27:57.298 TestScript (EURUSD,M1) DQ 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 QH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 4.00000 x weight 0.70837 PD 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 10.00000 x weight -0.39838 HR 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -1.15027 + bias -0.590 = -1.74048 DJ 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.14925 OP 0 18:27:57.298 TestScript (EURUSD,M1) CK 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 MN 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 4.00000 x weight 0.61823 NH 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 10.00000 x weight 0.66553 HI 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 9.12817 + bias -0.590 = 8.53796 FO 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.99980 RG 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> IR 0 18:27:57.298 TestScript (EURUSD,M1) PD 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 RN 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.14925 x weight -0.32764 HF 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.99980 x weight 0.88464 EM 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.83557 + bias 0.738 = 1.57397 EL 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82835 KE 0 18:27:57.298 TestScript (EURUSD,M1) GN 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 LS 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.14925 x weight 0.51367 FL 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.99980 x weight 0.93713 KH 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.01362 + bias 0.738 = 1.75202 IR 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85221 OH 0 18:27:57.298 TestScript (EURUSD,M1) IM 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) MH 0 18:27:57.298 TestScript (EURUSD,M1) 0.82835 0.85221
이제 모든 반복에 대한 최종 MLP 출력을 살펴보면 출력 값이 깔끔하게 동일한 경향이 있는 이상한 곳을 발견할 수 있습니다. 그 이유는 Stack에서 설명한 것처럼 여러 가지 원인이 있으며 그 중 하나는 출력 레이어에서 잘못된 활성화 함수를 사용하기 때문입니다. 바로 이 부분에서 SoftMax 활성화 함수가 빛을 발합니다.
제가 알기로 sigmoid 함수는 하나의 클래스를 분류해야 하는 출력 레이어에 단일 노드가 있을 때만 확률을 반환하는데 이 경우 어떤 것이 특정 클래스에 속하는지 여부를 알려면 sigmoid의 출력이 필요합니다. 그러나 멀티클래스에서는 또 다른 이야기가 되어 버립니다. 최종 노드의 출력값을 합하면 대부분 1(1)을 초과합니다. 그러나 확률은 1의 값을 초과할 수 없습니다. 그러므로 이제 여러분은 이것이 확률이 아니라는 것을 알 수 있습니다.
마지막 레이어에 SoftMax를 적용하면 출력은 다음과 같습니다.
첫 번째 반복 출력 [0.4915 0. 5085], 두 번째 반복 출력 [0.4940 0. 5060]
이 경우 출력을 [클래스 0에 속할 확률 클래스 1에 속할 확률]로 해석할 수 있습니다.
적어도 이제 우리는 네트워크에서 의미 있는 것을 해석하는 데 신뢰할 수 있는 확률을 갖게 되었습니다.
최종 리뷰
피드 포워드 신경망에 대한 설명은 아직 끝나지 않았지만 여러분은 적어도 MQL5에서 신경망을 마스터하는 데 도움이 될 이론과 가장 중요한 내용을 이해했을 것입니다. 피드포워드 신경망은 분류를 목적으로 설계된 것이므로 데이터 세트에서 분류하려는 샘플과 클래스에 따라 적합한 활성화 함수가 sigmoid와 tanh이라는 뜻입니다. 우리는 원하는 것을 반환하기위해 출력 레이어를 변경하여 할 수 없으며 숨겨진 레이어의 노드도 마찬가지입니다. 행렬을 도입하면 이 모든 작업이 동적이 되어 모든 작업에 대해 매우 표준적인 신경망을 구축할 수 있습니다. 이와 관련한 이 기사 시리즈를 계속 지켜봐 주시기 바랍니다.
모든 작업을 신경망으로 해결할 필요는 없으며 선형 회귀로 해결할 수 있는 작업의 경우 선형 모델이 신경망보다 성능이 우수할 수 있습니다. 그러므로 신경망을 사용할 시기를 아는 것도 중요한 일입니다. 이 점을 염두에 두어야 합니다.
더 읽어보기 | 서적 | 참고 자료
-
Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
-
Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
-
Deep Learning (Adaptive Computation and Machine Learning series)
문서 참조:
MetaQuotes 소프트웨어 사를 통해 영어가 번역됨
원본 기고글: https://www.mql5.com/en/articles/11275
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.
이 글은 사이트 사용자가 작성했으며 개인의 견해를 반영합니다. Metaquotes Ltd는 제시된 정보의 정확성 또는 설명 된 솔루션, 전략 또는 권장 사항의 사용으로 인한 결과에 대해 책임을 지지 않습니다.

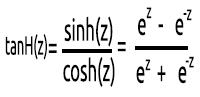
...
설명해 주시겠어요? 아니면 몇 가지 예를 들어주시겠어요?
전략 테스터에서 최적화와 신경망 매개 변수 최적화의 차이점은 전략 테스터에서 가장 수익성있는 결과 또는 적어도 우리가 원하는 거래 결과를 제공하는 매개 변수에 초점을 맞추는 경향이 있으며, 이것이 반드시 신경망에 그러한 종류의 결과를 가져온 좋은 모델이 있다는 것을 의미하지는 않습니다.
어떤 사람들은 신경망 기반 시스템의 입력 매개 변수로 가중치와 바이어스를 선호하지만(대략적으로 말하면 피드 포워드) 전략 테스터를 사용하여 최적화하는 것은 기본적으로 최상의 결과의 임의 값을 찾는 것이라고 생각합니다(최적의 결과를 찾는 것은 운에 의존하는 것처럼 들립니다) 확률 적 기울기 하강을 사용하여 최적화하는 경우 모든 단계에서 예측 오류가 가장 적은 모델로 이동하는 것입니다.
전략 테스터에서 최적화와 신경망 매개 변수를 최적화하는 것의 차이점은 전략 테스터에서 우리는 가장 수익성이 높은 결과 또는 적어도 우리가 원하는 거래 결과를 제공하는 매개 변수에 집중하는 경향이 있으며, 이것이 반드시 신경망에 그러한 종류의 결과를 가져온 좋은 모델이 있다는 것을 의미하지는 않습니다.
어떤 사람들은 신경망 기반 시스템의 입력 매개 변수로 가중치와 편향을 선호하지만(대략적으로 말하면 피드 포워드) 전략 테스터를 사용하여 최적화하는 것은 기본적으로 최상의 결과의 임의 값을 찾는 것이라고 생각합니다(최적의 결과를 찾는 것은 운에 의존하는 것처럼 들립니다) 확률 적 기울기 하강을 사용하여 최적화하는 경우 모든 단계에서 예측 오류가 가장 적은 모델을 향해 나아가고 있습니다.
답변 주셔서 감사합니다.
무슨 말씀인지 알겠습니다.
왜 첫 번째 파트부터 시작하셨나요?
이전 문서
데이터 과학과 머신 러닝(1부): 선형 회귀
https://www.mql5.com/ko/articles/10459
첫 번째 파트부터 시작하게 된 이유는 무엇인가요?
이전 기사:
데이터 과학과 머신 러닝(1부): 선형 회귀
https://www.mql5.com/ko/articles/10459
무슨 뜻인가요?
첫 번째 파트부터 시작하게 된 이유는 무엇인가요?
이전 기사:
데이터 과학과 머신 러닝(1부): 선형 회귀
https://www.mql5.com/ko/articles/10459