因果推理中的倾向性评分

概述

我们继续深入研究因果推理及其现代工具的世界。当然，任务要更广泛一些 - 在交易中使用因果推理方法。我们已经开始研究基础知识，甚至编写了我们的第一个元学习器，顺便说一句，它被证明是相当强大的。或者更确切地说，在它们的帮助下获得的模型被证明是稳健的。值得一提的是，它们是第一批仅供读者阅读的作品，因为它们只是作者的另一个实验。因此，没有回头路，我们必须走到最后，直到涵盖了交易中因果推理的整个主题。毕竟，因果推理的方法可能不同，我想尽可能广泛地涵盖这个有趣的话题。

在本文中，我将介绍上 一篇文章中简要提到的匹配主题，或者更确切地说是它的一个变体 - 倾向性评分匹配。 

这很重要，因为我们有一组异构的标记数据。例如，在外汇市场中，每个单独的训练示例可能属于高波动性或低波动性区域。此外，有些示例在样本中出现的频率可能较高，而有些示例出现的频率则较低。当尝试确定此类样本中的平均因果效应 (ATE) 时，如果我们假设样本中的所有示例都具有相同的产生处理的倾向，我们将不可避免地遇到有偏差的估计。当试图获得条件平均处理效应（CATE）时，我们可能会遇到一个称为“维数灾难”的问题。

匹配是通过匹配处理组和对照组中的相似观察结果（或单位）来估计因果效应的一系列方法。匹配的目的是对相似的单位进行比较，以尽可能准确地估计真实的因果关系。

因果推理文献的一些作者建议，匹配应被视为数据预处理步骤，在此基础上可以使用任何估计器（例如元学习器）。如果我们有足够的数据来丢弃一些观察结果，那么使用匹配作为预处理步骤通常是有用的。 

假设您有一组需要分析的数据集，该数据包含 1000 个观测值。如果数据集中有18个变量，那么每行至少找到一个完全匹配的机会有多大？答案显然取决于许多因素。有多少个变量是二元的？其中有多少个是连续的？其中有多少是分类变量？分类变量有多少个级别？变量之间是独立的还是相互相关的？

Aleksander Molak 在他的书“Python 中的因果推理和发现”中给出了一个很好的可视示例。

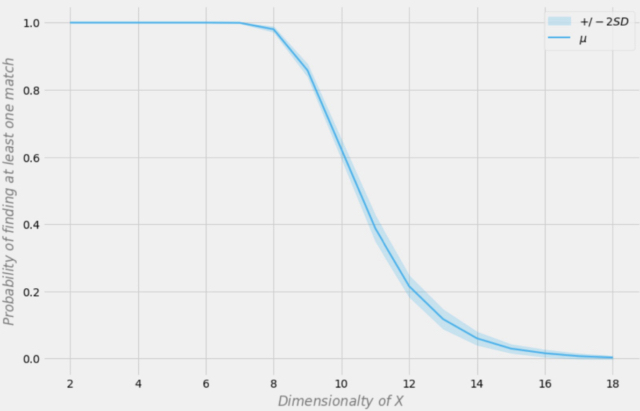
找到精确匹配的概率取决于数据集的维度

假设我们的样本有 1000 个观测值。在上图中，X 轴表示数据集的维度（数据集中的变量数量），Y 轴表示在每一行中找到至少一个完全匹配的概率。

蓝线代表平均概率，阴影区域代表 +/- 两个标准差。该数据集是使用 p = 0.5 的独立伯努利分布生成的。因此，每个变量都是二元且独立的。 

我决定测试一下书中的这个说法，并编写了一个计算这个概率的 Python 脚本。

import numpy as np
import matplotlib.pyplot as plt

def calculate_exact_match_probability(dimensions):
    num_samples = 1000
    num_trials = 1000
    match_count = 0

    for _ in range(num_trials):
        dataset = np.random.randint(2, size=(num_samples, dimensions))
        row_sums = np.sum(dataset, axis=1)
        if any(row_sums == dimensions):
            match_count += 1

    return match_count / num_trials

def plot_probability_curve(max_dimensions):
    dimensions_range = list(range(1, max_dimensions + 1))
    probabilities = [calculate_exact_match_probability(dim) for dim in dimensions_range]

    mean_probability = np.mean(probabilities)
    std_dev = np.std(probabilities)

    plt.plot(dimensions_range, probabilities, label='Exact Match Probability')
    plt.axhline(mean_probability, color='blue', linestyle='--', label='Mean Probability')

    plt.xlabel('Number of Variables')
    plt.ylabel('Probability')
    plt.title('Exact Match Probability in Binary Dataset')
    plt.legend()
    plt.show()

事实上，对于 1000 次观察来说，概率是一致的。作为一项实验，您可以自己计算数据集的维度。对于我们进一步的工作，只要理解到，如果数据中的特征（协变量）相对于训练示例的数量来说太多，那么通过分类器概括此类数据的能力就会受到限制。数据量越大，统计估计就越准确。

*在实际情况下，情况并非总是如此，因为应该满足 iid（独立且相同分布）条件。

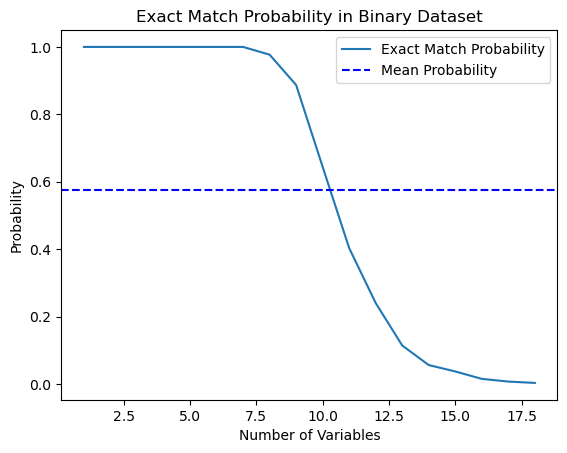
如您所见，在 18 维二分随机数据集中找到完全匹配的概率基本上为零。在现实世界中，我们很少处理纯二分数据集，而对于连续数据，多维映射变得更加困难。即使在近似情况下，这也给匹配带来了严重的问题。我们怎样才能解决这个问题？

使用倾向性评分降低数据维数

我们可以使用倾向性评分来解决维数灾难问题。倾向性评分是根据某个单位的特征，对该单位被分配到实验组的概率的估计。根据倾向性评分定理（Rosenbaum and Rubin，1983），如果我们有X特征的未混淆数据，那么在假设为阳性的情况下，给定倾向性评分我们也将得到不混淆的数据。阳性意味着处理过的和未处理的分布应该重叠。这就是因果推理的阳性假设。这也是符合直觉的。如果测试组和对照组不重叠，则意味着它们非常不同，我们无法将一个组的影响推断到另一个组。这种推断并非不可能（回归使得不可能），但它非常危险。这类似于在实验中测试一种新药，该实验仅对男性进行治疗，然后假设女性对该药的反应同样良好。

倾向性评分的形式如下：

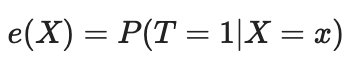
在完美的世界中，我们会有一个真实的倾向性评分。然而，在实践中，分配处理的机制尚不清楚，我们需要用对处理的评估或期望来取代真实的倾向。一种常见的方法是使用逻辑回归，但也可以使用其他机器学习技术，如梯度增强（尽管这需要一些额外的步骤来避免过度拟合）。

我们可以利用这个方程来解决多维问题。倾向性评分是单变量的，因此我们现在只能匹配两个值而不是多变量向量。

因此，如果我们有条件地将潜在结果与处理分开，

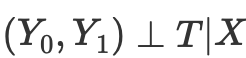
然后我们可以计算在没有倾向性评分匹配的情况下连续和离散情况的平均因果效应：

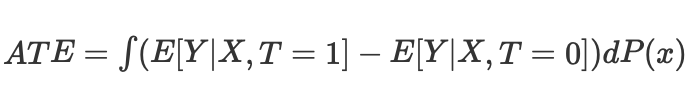
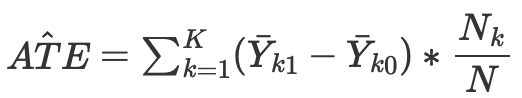
其中 Nk 是每个单元格中的观测值数量。每个单元是通过某些接近度度量匹配的观察子组。

然而，倾向性评分源于这样的认识：我们不需要直接控制X混杂因素来实现条件独立性

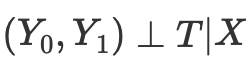
相反，控制平衡指标就足够了

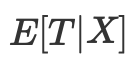
倾向性评分允许一个个体独立于 X 整体，以确保潜在结果与处理无关。以此单一变量为条件就足够了，该变量是一个倾向性评分：

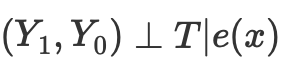
因果推理的来源描述了这种方法的一些问题：

• 首先，倾向性评分降低了我们数据的维度，并且根据定义，迫使我们抛弃一些信息。

• 其次，原始特征空间中两个非常不同的观察结果可能具有相同的倾向性评分。这可能导致非常不同的观察结果匹配，从而使结果产生偏差。

• 第三，PSM（倾向性评分模型）导致了悖论。在二元情况下，最佳倾向性评分为 0.5。在所有观察结果的最佳倾向性评分都为 0.5 的完美情况下会发生什么？倾向性评分空间中每个观察的位置变得与其他每个观察的位置相同。这有时被称为 PSM 悖论。 

倾向性评分匹配及相关方法

有许多基于倾向性评分匹配单位的方法。主要方法被认为是最近邻方法，该方法将实验组中的每个单元 i 与对照组中的单元 j 进行匹配，其倾向性评分之间的绝对距离最近，表示为

d(i, j) = minj{|e(Xi) – e(Xj)|}。

或者，阈值匹配将处理组中的每个单元 i 与对照组中的单元 j 在预先指定的 b 范围内进行匹配；阈值为

d(i, j) = minj{|e(Xi) – e(Xj)| <b}。

建议b预定阈值小于或等于倾向性评分的0.25个标准差。其他研究人员认为倾向性评分标准差b = 0.20是最佳的。 

阈值匹配的另一种选择是半径匹配，它是一对多匹配，将处理组中的每个单元 i 与 b 预定义范围内的对照组中的几个单元进行匹配；即

d（i，j）= {|e（Xi）-e（Xj）| \ <b \}。

其他倾向性评分匹配方法包括 Mahalanobis 度量。在使用 Mahalanobis 距离进行匹配时，实验组中的每个单元 i 与对照组中的单元 j 进行匹配，并根据变量的接近度计算最近的 Mahalanobis 距离。

目前讨论的倾向性评分匹配方法可以使用贪婪匹配算法或最佳匹配算法来实现。

• 在贪婪匹配中，一旦匹配完成，匹配的单位就不能改变。每对匹配的单元都是当前可用的最佳对。 

• 通过最佳匹配，可以在执行当前匹配之前修改先前匹配的单元，以实现总体最小或最佳距离。 

• 当控制组规模较大时，两种匹配算法通常都会产生相同的匹配数据。然而，最佳匹配会导致匹配单元内的整体距离较小。因此，如果目标只是找到匹配良好的群体，贪婪匹配可能就足够了。如果目标是找到匹配度较高的配对，那么最佳匹配可能更为可取。

存在与倾向性评分匹配相关的方法，这些方法并不严格匹配单个采样单元。例如，子分类（或分层）将整个样本中的所有单位根据相应的倾向性评分百分位数分为几个层，并按层匹配单位。据观察，五层可消除高达 90％ 的选择偏差。

一种特殊类型的子分类是完全匹配，其中子类以最佳方式创建。完全匹配样本由匹配的子集组成，其中每个匹配集包含一个实验单元和一个或多个控制单元，或一个控制单元和一个或多个实验单元。从最小化每个子类中每个处理对象和每个对照对象之间的估计距离测量的加权平均值的角度来看，完全匹配是最佳的。

与倾向性评分匹配相关的另一种方法是核匹配（或局部线性匹配），它将匹配和结果分析结合在一个过程中，进行一对多匹配。

尽管提出的比较方法多种多样，但它们的应用效率更多地取决于问题的正确表述，而不是特定的方法。

强忽视假设

“强忽视”（Strong neglect）是倾向性评分构建中的一个关键假设，旨在估计处理分配随机的观察中的因果效应。本质上，这意味着处理分配与观察到的基线协变量（特征）的潜在结果无关。 

让我们仔细看看：

• 处理分布：这指的是一个单位是否接受处理（例如服用新药物或参加某个项目）。

• 可能的结果：这些是一个单位在处理和控制条件下都会经历的结果，但我们只能观察到每个单位的一个结果。

• 基线协变量：这些是在分配处理之前测量的单位特征，可能会影响接受治疗的可能性和结果。

“强忽略”假设指出：

• 无未测量的混杂因素：不存在影响处理分配或结果的未观察到的变量。这很重要，因为未观察到的混杂因素可能会影响估计的处理效果。

• 积极性：考虑到观察到的协变量，每个单位都有非零的接受处理和控制的概率。这确保了所比较的组中有足够的单元来进行有意义的比较。

如果满足这些条件，那么根据倾向性评分（给定协变量接受处理的估计概率）进行条件分析就会产生平均处理效果（ATE）的无偏估计。ATE 表示处理组和对照组之间的结果平均差异，就好像处理是随机分配的。

逆概率加权

逆概率加权是消除噪音或混杂因素的方法之一，它通过尝试根据治疗分配概率的倒数重新加权数据集中的观测值来消除噪音或混杂因素。这样做的目的是对那些被认为不太可能通过处理得到处理的观察结果给予更多的权重，使其更能代表总体人群。

• 首先，估计倾向性评分，即在观察到的协变量的情况下接受处理的概率。

• 针对每个观察结果计算一个逆倾向得分。

• 然后将每个观察值乘以其相应的权重。这意味着接受观察到的处理的概率较低的观察结果将被赋予更大的权重。

• 然后使用加权数据集进行分析。对处理组和对照组都应用权重，以调整观察到的协变量的潜在影响。

逆概率加权可以帮助平衡处理组和对照组之间的协变量分布，减少估计因果关系的偏差。然而，它基于这样的假设：所有相关的混杂变量都已被测量并包含在用于估计倾向得分的模型中。此外，与任何统计方法一样，IPW 的成功取决于用于估计倾向得分的模型的质量。

逆倾向得分方程如下：

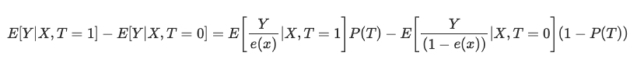
无需详细分析，您可比较一下等式的两个项。左边是处理组，右边是对照组。该等式表明，简单的平均值比较等同于倒数加权平均值的比较。这样就创建了一个与原始群体大小相同的群体，但其中左侧的每个个体都会接受处理。出于同样的原因，正确的方法会考虑未经处理的样本，并高度重视那些看起来像已处理过的样本。

匹配后的结果评估

在因果推断中，估计值被构建为 ATE 或 CATE，即已处理和未处理的目标值的加权平均值（根据倾向得分进行调整）的差异。 

一旦我们获得了倾向得分 e(x)，我们就可以使用这些值来训练另一个分类器，而不是 X 特征的原始值。我们还可以根据倾向性评分比较样本，以将它们划分为不同的层。另一种选择是在训练最终评估器时将 e(x) 添加为单独的特征，当样本中的不同示例根据倾向得分具有不同的估计时，这将有助于消除由于混淆而产生的偏差估计。

我们感兴趣的是找到对处理反应良好或较差的亚群（模型训练），然后仅在可以训练良好（分类错误最小）的数据上训练最终的分类器。然后，我们应该将分类不佳的数据放入第二个子组中，并训练第二个分类器来区分这两个子组，即将好的数据与坏的数据分开，或者识别最适合处理的子组。因此，我们现在不会采用整个倾向性评分方法，而是根据训练好的分类器得到的概率来匹配样本，而整体的ATE（平均处理效果）评估对我们来说并不那么重要。

换句话说，我们将根据未参与训练的新数据运行的算法结果来进行评估。此外，我们仍然对在随机数据上训练的一组模型的平均速度感兴趣。独立模型的平均得分越高，我们对每个特定模型的信心就越大。

继续实验

当开始写这篇文章时，我意识到对于许多交易者来说，特别是那些不熟悉机器学习的交易者，这种深入的材料可能看起来非常违反直觉。回想起我第一次接触因果推理时，最初的误解严重伤害了我的自尊，所以我忍不住要深入研究细节。此外，我甚至无法想象我会擅自采用因果推理技术来对时间序列进行分类。

• propensity without matching.py 文件

让我们首先将倾向性评分直接纳入我们的估计器或元学习器中。为此，我们需要训练两个模型。首先，PSM（倾向性评分模型）本身，它将使我们能够获得将训练示例分配给处理组或测试组的概率。我们将把获得的概率与特征（协变量）一起作为输入提供给第二个模型，该模型将预测结果（买入或卖出）。

这种方法的直觉是，元学习者现在将能够根据样本的处理倾向来区分样本子组。这将为我们提供更准确的结果加权预测。之后，我们将把数据集分为可预测性好和可预测性差的情况，就像之前的文章中提到的那样。在这种情况下，我们不需要明确的样本匹配，因为元学习器会自动将倾向得分考虑在其估计中。这种方法对我来说似乎非常方便，因为机器学习为我们完成了所有工作。

首先，让我们创建“train”和“val”子样本来训练元模型。由于元学习器将在训练子样本上进行训练，我们将创建一对目标 y_T1、y_T0，并用 1 和 0 填充它们。这将对应于单位是否接受处理（模型训练）。然后我们重新洗牌以处理为目标变量的子选择。

        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # randomly assign treated and control
        y_T1 = pd.DataFrame(y_train)
        y_T1['T'] = 1
        y_T1 = y_T1.drop(['labels'], axis=1)

        y_T0 = pd.DataFrame(y_val)
        y_T0['T'] = 0
        y_T0 = y_T0.drop(['labels'], axis=1)

        y_TT = pd.concat([y_T1, y_T0])
        y_TT = y_TT.sort_index()

        X_trainT, X_valT, y_trainT, y_valT = train_test_split(
            X, y_TT, train_size = 0.5, test_size = 0.5, shuffle = True)

下一步是训练 PSM 模型来预测样本是属于处理子样本还是控制子样本。

        # fit propensity model
        PSM = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                use_best_model=True,
                                early_stopping_rounds=15,
                                verbose = False).fit(X_trainT, y_trainT, eval_set = (X_valT, y_valT), plot = False)

然后我们需要得到属于处理组和对照组的预测，并将它们添加到元学习器的特征中，然后对其进行训练。

        # predict probabilities
        train_proba = PSM.predict_proba(X_train)[:, 1]
        val_proba = PSM.predict_proba(X_val)[:, 1]

        # fit meta-learner
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True,
                                early_stopping_rounds=15).fit(X_train.assign(T=train_proba), y_train, 
				eval_set = (X_val.assign(T=val_proba), y_val), plot = False)
        

在最后阶段，我们将获得元学习者的预测，将预测的标签与实际标签进行比较，并填写不佳例子的记录。

        # create daatset with predicted values
        predicted_PSM = PSM.predict_proba(X)[:,1]
        X_psm = X.assign(T=predicted_PSM)
        coreset = X.assign(T=predicted_PSM)
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X_psm)[:,1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)

        # add bad samples of this iteration (bad labels indices)
        coreset_b = coreset[coreset['labels']==0]
        coreset_s = coreset[coreset['labels']==1]

        diff_negatives_b = coreset_b['labels'] != coreset_b['labels_pred']
        diff_negatives_s = coreset_s['labels'] != coreset_s['labels_pred']
        BAD_BUY = BAD_BUY.append(diff_negatives_b[diff_negatives_b == True].index)
        BAD_SELL = BAD_SELL.append(diff_negatives_s[diff_negatives_s == True].index)

现在让我们尝试训练 25 个模型并查看最佳和平均结果。

options = []
best_res = 0.0
for i in range(25):
    print('Learn ' + str(i) + ' model')
    options.append(learn_final_models(meta_learners(models_number=5, 
                                                    iterations=25, 
                                                    depth=2,
                                                    bad_samples_fraction=0.5)))
    if options[-1][0] > best_res:
        best_res = options[-1][0]
    print("BEST: " + str(best_res))

options.sort(key=lambda x: x[0])
test_model(options[-1][1:], plt=True)
test_all_models(options)

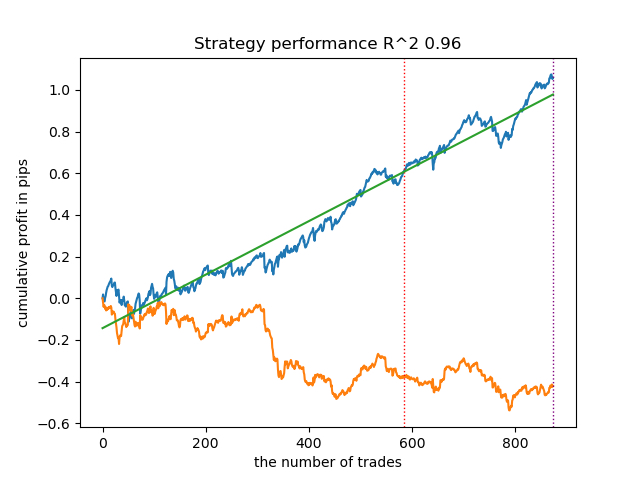
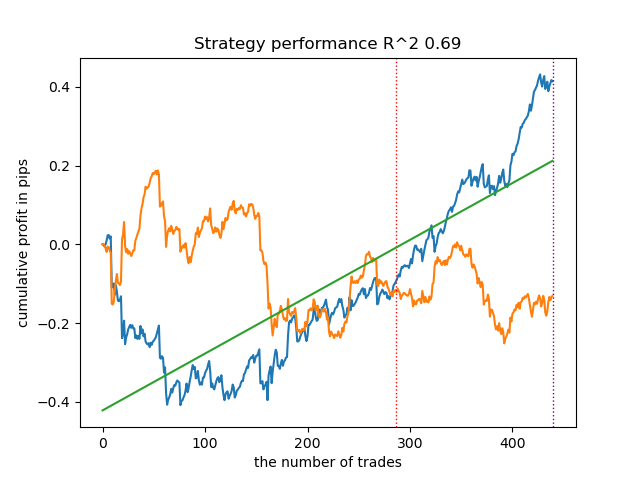
我进行了一系列这样的训练，并得出结论，这种方法在模型质量上与我上一篇文章中描述的方法几乎没有区别。这两种选项都能够生成通过 OOS 的良好模型。这并不奇怪，因为我们使用 e(x) 作为附加特征，而算法的其余部分保持不变。

• propensity matching naive.py 文件

在考虑实现方法时，我们永远无法提前知道哪种方法效果更好。作为一项实验，我决定不根据分配处理的倾向来进行匹配，而是根据预测目标标签的倾向来进行匹配。对于读者来说这应该更加直观。这里的主要区别是我们只训练一个（传统命名的）PSM 模型。接下来，预测概率，并根据我们想要将获得的概率划分到的层数创建一个箱列表。对于每个层，都会计算正确/错误猜测结果的数量，之后对于错误猜测（乘以比率）的示例数量超过正确猜测的示例数量的层，将触发将不佳示例添加到不佳示例记录中的条件。

        bins = np.linspace(lower_bound, upper_bound, num=bins_number)
        coreset['bin'] = pd.cut(coreset['propensity'], bins)
        

        for val in range(len(coreset['bin'].unique())):
            values = coreset.loc[coreset['bin'] == coreset['bin'].unique()[val]]
            diff_negatives = values['labels'] != values['labels_pred']
            if len(diff_negatives[diff_negatives == False]) < (len(diff_negatives[diff_negatives == True]) * coefficient):
                B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index)

这种方法有附加参数：

• bins_number - 箱子数量
• lower_bound - 计算级数的下限概率
• upper_bound - 概率上限，级数计算到该上限

由于我们使用的元学习器深度较小，因此概率通常聚集在 0.5 左右，很少达到极限。因此，我们可以通过设置上限和下限来丢弃不具有参考价值的极端值。

让我们训练25个模型并看看结果。我想指出的是，所有模型都是在相同的数据集上训练的，因此它们的比较是相当正确的。

options = []
best_res = 0.0
for i in range(25):
    print('Learn ' + str(i) + ' model')
    options.append(learn_final_models(meta_learners(models_number=5, 
                                                    iterations=25, 
                                                    depth=2,
                                                    bad_samples_fraction=0.5,
                                                    bins_number=25,
                                                    lower_bound=0.3,
                                                    upper_bound=0.7,
                                                    coefficient=1.0)))
    if options[-1][0] > best_res:
        best_res = options[-1][0]
    print("BEST: " + str(best_res))

options.sort(key=lambda x: x[0])
test_model(options[-1][1:], plt=True)

令人惊讶的是，这种自发的实施在新数据上表现相当良好。下面是最佳模型和所有 25 个模型的交易图表。

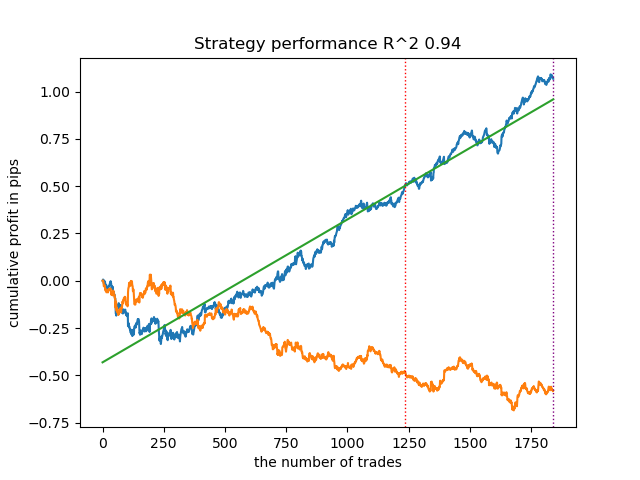
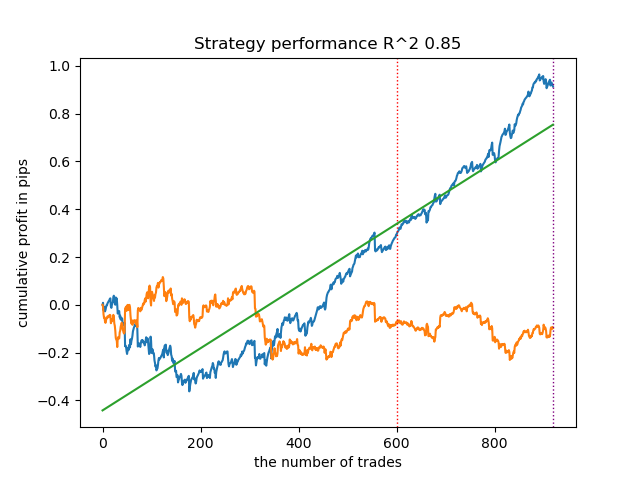
• propensity matching original.py 文件

我们继续实现最接近理论的例子，其中强忽视（强可忽略）的假设得到满足。让我提醒你，“强可忽略”是指处理的分配不以任何方式依赖于潜在结果，这意味着它是完全随机的并且没有影响偏见的未考虑的变量。为此，我们将随机分配一种处理方法并训练 PSM 模型。然后我们训练元估计器来预测交易结果（类别标签）。此后，我们根据倾向得分对样本进行分层，并仅将来自那些不成功预测的数量超过成功预测的数量（考虑到比率）的箱中的样本添加到不佳样本记录中。

我还添加了使用理论部分中描述的IPW（逆概率加权）的能力。

训练完两个分类器后，执行下面的代码。

        # create daatset with predicted values
        coreset = X.copy()
        coreset['labels'] = y
        coreset['propensity'] = PSM.predict_proba(X)[:, 1]
        if Use_IPW:
            coreset['propensity'] = coreset['propensity'].apply(lambda x: 1 / x if x > 0.5 else 1 / (1 - x))

        coreset['propensity'] = coreset['propensity'].round(3)
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)

        bins = np.linspace(lower_bound, upper_bound, num=bins_number)
        coreset['bin'] = pd.cut(coreset['propensity'], bins)        

        for val in range(len(coreset['bin'].unique())):
            values = coreset.loc[coreset['bin'] == coreset['bin'].unique()[val]]
            diff_negatives = values['labels'] != values['labels_pred']
            if len(diff_negatives[diff_negatives == False]) < (len(diff_negatives[diff_negatives == True]) * coefficient):
                B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index)

让我们在不使用 IPW 的情况下训练 25 个模型，并查看最佳余额图和所有模型的平均余额图，使用以下设置：

options = []
best_res = 0.0
for i in range(25):
    print('Learn ' + str(i) + ' model')
    options.append(learn_final_models(meta_learners(models_number=5, 
                                                    iterations=25, 
                                                    depth=2,
                                                    bad_samples_fraction=0.5,
                                                    bins_number=25,
                                                    lower_bound=0.3,
                                                    upper_bound=0.7,
                                                    coefficient=1.5,
                                                    Use_IPW=False)))
    if options[-1][0] > best_res:
        best_res = options[-1][0]
    print("BEST: " + str(best_res))

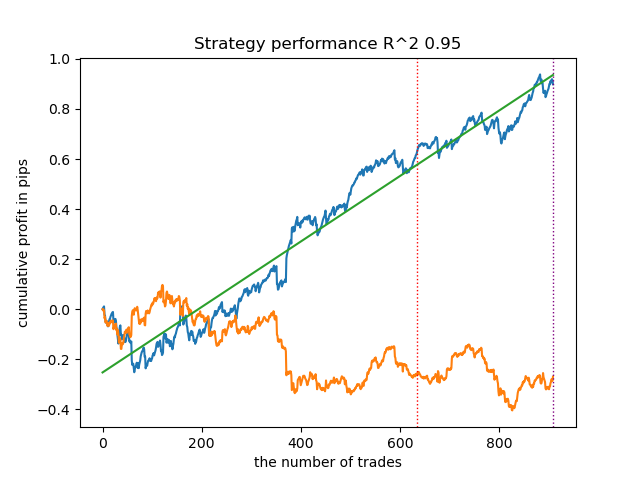
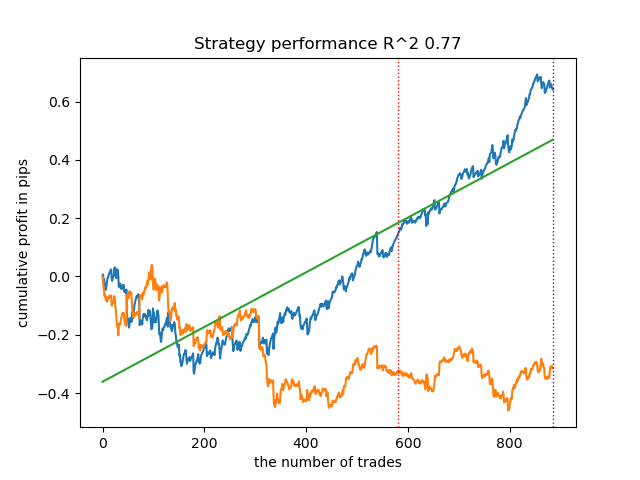
总体而言，结果与之前的实现结果相当。现在让我们启用 IPW 执行相同的操作。

options = []
best_res = 0.0
for i in range(25):
    print('Learn ' + str(i) + ' model')
    options.append(learn_final_models(meta_learners(models_number=5, 
                                                    iterations=25, 
                                                    depth=2,
                                                    bad_samples_fraction=0.5,
                                                    bins_number=25,
                                                    lower_bound=0.1,
                                                    upper_bound=10.0,
                                                    coefficient=1.5,
                                                    Use_IPW=True)))
    if options[-1][0] > best_res:
        best_res = options[-1][0]
    print("BEST: " + str(best_res))

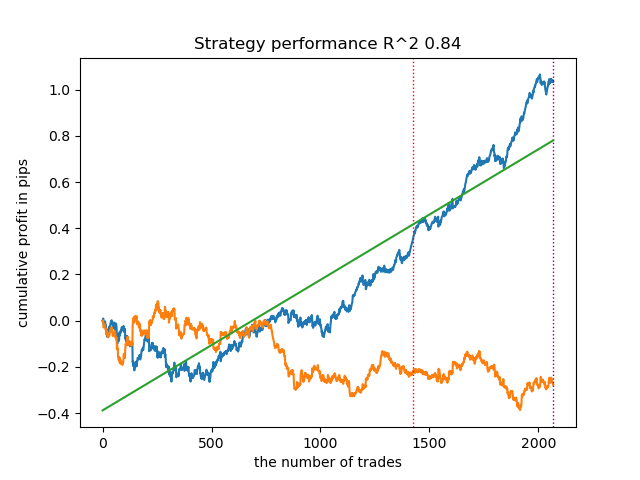
事实证明，结果是最好的。当然，为了进行更加详细的比较，需要对不同的交易品种进行多次测试，但这会增加本来就很大的文章的体积。所得结果表格如下。

算法	最佳结果	平均结果（25 个模型）
propensity without matching.py	0.96	0.69
propensity matching naive.py	0.94	0.85
propensity matching original.py	0.95	0.77
propensity matching original.py IPW	0.97	0.84

结论

我们考虑了使用倾向性评分来解决金融时间序列分类问题的可能性。该方法在因果推理领域有很好的理论依据，但也有其缺点。总的来说，它使我们能够获得在新数据上保留其特征的模型。