CatBoost 模型中的交叉验证和因果推理基础及导出为 ONNX 格式

概述

在之前的文章中，我描述了使用机器学习算法创建交易系统的各种方法。其中一些非常成功，而其他一些（大部分来自早期发表的文章）则训练过度。因此，我文章的顺序恰好反映了理解的演化：机器学习实际上能够做什么。当然，我们讨论的是时间序列的分类。

例如，前一篇文章“机器学习中的元模型”探讨了通过两个分类器的交互来寻找模式的算法。选择这种非凡方法的原因在于，机器学习算法能够很好地概括和预测，但在寻找因果关系方面却很“懒惰”。换句话说，它们概括的训练样例中，可能已经建立了因果关系，并且该关系会随着新数据的出现而持续存在，但这种关系也可能只是联想性的，即暂时的和不可靠的。 

该模型不了解它正在处理什么连接。它只知将所有训练数据视为训练数据。对于初学者来说，如何教会它使用新数据也能进行盈利交易是一个大问题。因此，在上一篇文章中，我们尝试教会算法来分析自身的错误，以便将具有统计意义的预测与随机预测区分开来。

本文是前一个主题的拓展，也是创建能够在数据中寻找模式，同时最大限度地减少过度拟合的自训练算法的下一步。毕竟，我们希望从机器学习的使用中获得真正的效果，以便它不仅可以概括训练示例，还可以判断其中是否存在因果关系。

阴（理论）

本节将包含一定程度的主观推理，这些推理基于在外汇交易中尝试创建“人工智能”所获得的一些经验。因为它还不算是爱情，但它仍然是一种经历。 

正如我们的结论经常是错误的并且需要验证一样，机器学习模型的预测结果也应该经过仔细检查。如果我们将反复检查的过程转向我们自己，我们就能获得自制力。机器学习模型的自我控制归结为在不同但相似的情况下多次检查其预测的错误。如果模型平均犯的错误很少，则意味着它没有过度训练，但如果它经常犯错误，那么它就有问题了。

如果我们在选定的数据上只是对模型进行一次训练，那么它无法进行自我控制。如果我们在随机子样本上多次训练模型，然后检查每个子样本的预测质量并将所有错误加起来，我们就会得到一个相对可靠的图像，其中显示了模型实际错误的情况和经常正确的情况。这些情况可以分为两组，彼此之间相互独立。这类似于进行前向验证或交叉验证，但包含附加元素。这是实现自我控制并获得更为鲁棒的模型的唯一方法。

因此，有必要对训练数据集进行交叉验证，将模型的预测与训练标签进行比较，并对所有结果取平均值。那些平均预测错误的例子应该作为错误的例子从最终训练集中删除。我们还应该对所有数据训练第二个模型，该模型可以区分可预测性高的情况和可预测性低的情况，从而让我们能够更全面地涵盖所有可能的结果。 

当删除不良训练样本后，主模型将具有较小的分类误差，但在预测被删除的案例时表现会很差。它的准确率较高，但召回率较低。如果我们现在添加第二个分类器，并且教它让第一个模型仅在已经学会很好分类的情况下进行交易，那么它应该会改善整个交易系统的结果，因为它的准确率较低但召回率较高。

事实证明，第一个模型的错误被转移到了第二个分类器，但并没有消失，所以现在它会更频繁地做出错误的预测。但由于它并不直接预测交易的走向，且数据覆盖范围较大，因此这样的预测仍然很有价值。

我们将假设两个模型足以用它们的正面结果来弥补训练中的错误。

因此，通过消除不好的训练示例，我们将寻找平均而言能够带来利润的情况。并且我们会尽量不在平均情况下会造成亏损的地方进行交易。

算法核心

“meta_learner”函数是该算法的核心，完成上述所有操作，因此应该对其进行更详细的分析。其余函数都是辅助的。

def meta_learner(folds_number: int, iter: int, depth: int, l_rate: float) -> pd.DataFrame:
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()

    X = data[data.columns[1:-2]]
    y = data['labels']

    B_S_B = pd.DatetimeIndex([])

    # learn meta model with CV method
    meta_model = CatBoostClassifier(iterations = iter,
                                max_depth = depth,
                                learning_rate=l_rate,
                                verbose = False)
    
    predicted = cross_val_predict(meta_model, X, y, method='predict_proba', cv=folds_number)
    
    coreset = X.copy()
    coreset['labels'] = y
    coreset['labels_pred'] = [x[0] < 0.5 for x in predicted]
    coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
    
    # select bad samples (bad labels indices)
    diff_negatives = coreset['labels'] != coreset['labels_pred']
    B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index)
    to_mark = B_S_B.value_counts()
    marked_idx = to_mark.index
    data.loc[data.index.isin(marked_idx), 'meta_labels'] = 0.0
    return data[data.columns[1:]]

它接受的参数：

• 用于交叉验证的折叠次数
• 用于基础学习者的训练迭代次数
• 基础学习树的深度
• 梯度步数

这些参数会影响最终结果，应根据经验或使用网格进行选择。 

scikit learn 包的 cross_val_predict 函数返回每个训练示例的交叉验证分数，然后将这些分数与原始标签进行比较。如果预测不正确，则将其输入到错误例子集中，然后在此基础上为第二个分类器生成“元标签（meta labels）”。

该函数返回传递给它的数据帧以及附加的“元标签”。然后使用该数据帧来训练最终模型，如代码所示。

# features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[:-2]]
    X = X[X.columns[:-2]]
    
    # labels for model\meta models
    y, y_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[-1]]
    y = y[y.columns[-2]]

上面的代码中注意到，第一个模型只对元标签与 1 对应的那些行进行训练，也就是说，它们被标记为好的训练示例。第二个分类器在整个数据集上进行训练。

然后对两个分类器进行简单的训练。一个预测买卖的概率，而第二个确定是否值得交易。

这里，每个模型也有自己的训练参数，这些参数不包含在超参数中。这些可以单独配置，但我故意选择了等于 100 的小迭代次数，以便模型在这个最后阶段不会过度训练。我们可以改变训练和测试样本的相对大小，这也会稍微影响到最终结果。一般来说，第一个模型相当容易训练，因为它只对分类良好的样本进行训练，模型不需要太复杂。第二个模型的任务更复杂，因此可能会增加模型的复杂性。

# train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.5, test_size=0.5, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.5, test_size=0.5, shuffle=True)

    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=100,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU')
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=15, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=100,
                                    custom_loss=['Accuracy'],
                                    eval_metric='Accuracy',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU')
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=15, plot=False)

算法超参数

在开始训练之前，我们应该正确配置所有输入参数，这也会影响到最终结果。

export_path = '/Users/dmitrievsky/Library/Application Support/MetaTrader 5/\
Bottles/metatrader5/drive_c/Program Files/MetaTrader 5/MQL5/Include/'

# GLOBALS
SYMBOL = 'EURUSD'
MARKUP = 0.00015
PERIODS = [i for i in range(10, 50, 10)]
BACKWARD = datetime(2015, 1, 1)
FORWARD = datetime(2022, 1, 1)

• 用于保存训练模型的终端 Include 文件夹的路径。
• 交易品种代码。
• 平均点数，包括点差、佣金和滑点。
• 用于计算价格增量的移动平均周期数，这些是用于训练模型的属性。
• 训练的日期范围。该范围的左边和右边是对新数据进行测试的未经训练的历史记录（OOS）。

def get_labels(dataset, min= 3, max= 25) -> pd.DataFrame:

此函数具有“min”和“max”参数，用于随机抽样交易。每笔新交易的持续时间都是随机的。如果我们设置相同的值，那么所有交易都会有固定的持续时间。 

辅助函数和库

在开始之前，请确保所有必需的包都已安装并导入。

import numpy as np
import pandas as pd
import random
import math
from datetime import datetime
import matplotlib.pyplot as put
from catboost import CatBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_predict

接下来，我们应该从 MetaTrader 5 终端导出报价。选择所需的交易品种、时间范围和历史深度，并将它们保存到 Python 项目的 /files 子目录中。

def get_prices() -> pd.DataFrame:
    p = pd.read_csv('files/EURUSD_H1.csv', delim_whitespace=True)
    pFixed = pd.DataFrame(columns=['time', 'close'])
    pFixed['time'] = p['<DATE>'] + ' ' + p['<TIME>']
    pFixed['time'] = pd.to_datetime(pFixed['time'], format='mixed')
    pFixed['close'] = p['<CLOSE>']
    pFixed.set_index('time', inplace=True)
    pFixed.index = pd.to_datetime(pFixed.index, unit='s')
    pFixed = pFixed.dropna()
    pFixedC = pFixed.copy()

    count = 0
    for i in PERIODS:
        pFixed[str(count)] = pFixedC.rolling(i).mean() - pFixedC
        count += 1

    return pFixed.dropna()

突出显示的代码显示了机器人从哪里获取报价以及它如何创建属性 - 通过从 PERIODS 列表中指定为超参数的移动平均线中减去收盘价。

之后，生成的数据集被传递给下一个函数以标记标签（或目标）。

def get_labels(dataset, min= 3, max= 25) -> pd.DataFrame:
    labels = []
    meta_labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]

        if future_pr < curr_pr:
            labels.append(1.0)
            if future_pr + MARKUP < curr_pr:
                meta_labels.append(1.0)
            else:
                meta_labels.append(0.0)
        elif future_pr > curr_pr:
            labels.append(0.0)
            if future_pr - MARKUP > curr_pr:
                meta_labels.append(1.0)
            else:
                meta_labels.append(0.0)
        else:
            labels.append(2.0)
            meta_labels.append(0.0)
        
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset['meta_labels'] = meta_labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2.0].index)
    
    return dataset

此函数返回相同的数据帧，但带有附加的“labels”和“meta labels”列。

tester 函数已显著加速。现在我们可以加载大型数据集，而不必担心测试程序运行得太慢：

def tester(dataset: pd.DataFrame, plot= False):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    chart = [0.0]
    line = 0
    line2 = 0

    indexes = pd.DatetimeIndex(dataset.index)
    labels = dataset['labels'].to_numpy()
    metalabels = dataset['meta_labels'].to_numpy()
    close = dataset['close'].to_numpy()

    for i in range(dataset.shape[0]):
        if indexes[i] <= FORWARD:
            line = len(report)
        if indexes[i] <= BACKWARD:
            line2 = len(report)

        pred = labels[i]
        pr = close[i]
        pred_meta = metalabels[i] # 1 = allow trades

        if last_deal == 2 and pred_meta==1:
            last_price = pr
            last_deal = 0 if pred <= 0.5 else 1
            continue

        if last_deal == 0 and pred > 0.5 and pred_meta == 1:
            last_deal = 2
            report.append(report[-1] - MARKUP + (pr - last_price))
            chart.append(chart[-1] + (pr - last_price))
            continue

        if last_deal == 1 and pred < 0.5 and pred_meta==1:
            last_deal = 2
            report.append(report[-1] - MARKUP + (last_price - pr))
            chart.append(chart[-1] + (pr - last_price))

    y = np.array(report).reshape(-1, 1)
    X = np.arange(len(report)).reshape(-1, 1)
    lr = LinearRegression()
    lr.fit(X, y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.plot(chart)
        plt.axvline(x = line, color='purple', ls=':', lw=1, label='OOS')
        plt.axvline(x = line2, color='red', ls=':', lw=1, label='OOS2')
        plt.plot(lr.predict(X))
        plt.title("Strategy performance R^2 " + str(format(lr.score(X, y) * l,".2f")))
        plt.xlabel("the number of trades")
        plt.ylabel("cumulative profit in pips")
        plt.show()

    return lr.score(X, y) * l

用于测试已训练模型的辅助函数现在具有更简洁的外观。它将模型列表作为输入，计算类概率并将其传递给 tester 函数，就像它是一个具有特征和标签的现成数据帧一样，可供测试。这样，tester 本身既可以使用原始训练数据帧，也可以使用从已训练模型接收预测后生成的数据帧。

def test_model(result: list, plt= False):
    pr_tst = get_prices()
    X = pr_tst[pr_tst.columns[1:]]
    pr_tst['labels'] = result[0].predict_proba(X)[:,1]
    pr_tst['meta_labels'] = result[1].predict_proba(X)[:,1]
    pr_tst['labels'] = pr_tst['labels'].apply(lambda x: 0.0 if x < 0.5 else 1.0)
    pr_tst['meta_labels'] = pr_tst['meta_labels'].apply(lambda x: 0.0 if x < 0.5 else 1.0)

    return tester(pr_tst, plot=plt)

阳 (实践)

设置好超参数后，我们直接进行模型训练，这是一个循环的过程。

options = []
for i in range(25):
    print('Learn ' + str(i) + ' model')
    options.append(learn_final_models(meta_learner(folds_number= 5, iter= 150, depth= 5, l_rate= 0.01)))

options.sort(key=lambda x: x[0])
test_model(options[-1][1:], plt=True)

在这里我们将训练 25 个模型，之后我们将对它们进行测试并将它们导出到 MetaTrader 5 终端。

训练结果受所选参数、训练和测试的日期范围以及交易持续时间的影响最大。我们应该使用这些设置做实验。

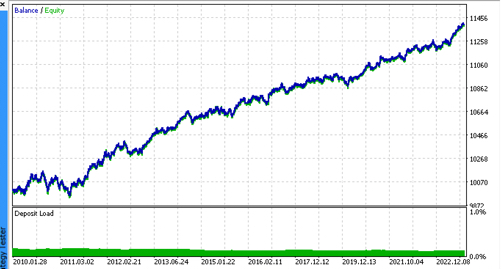
让我们根据 R^2 的原则来选择 5 个最佳模型，用于测试新数据。图中的水平线显示左侧和右侧的 OOS。

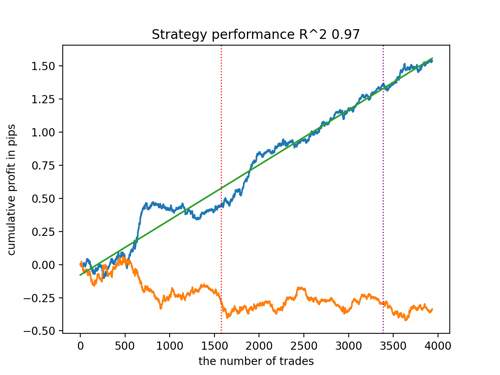
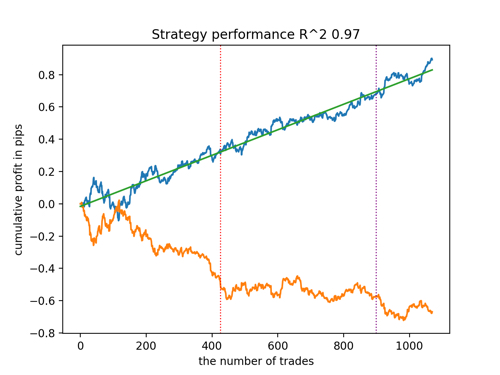
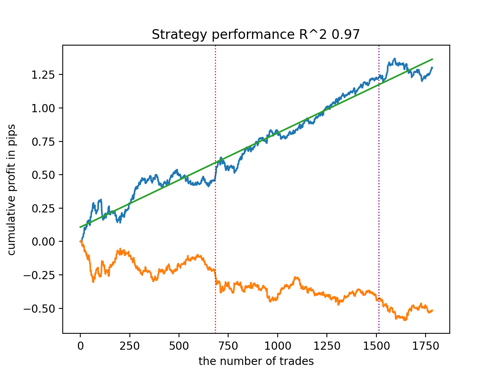
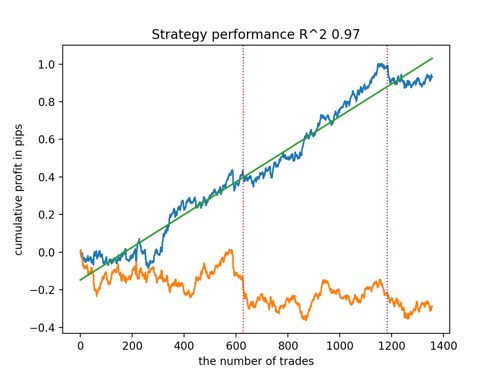
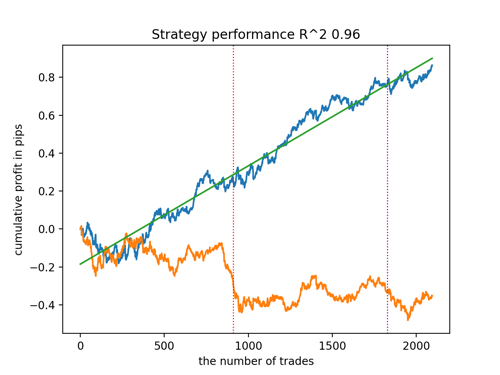
余额图以蓝色显示，报价图以橙色显示。我们可以看到所有模型都是不同的。这是由于交易的随机抽样以及每个模型内置的随机化。然而，这些模型不再像测试圣杯，并且在 OOS 中相当自由地工作。此外，我们还可以比较交易数量、利润点数以及曲线的总体外观。当然，第一种和第二种模型相比更有优势，所以我们就把它们输出到终端。

应该记住，通过改变训练参数并进行几次重启，我们将获得独特的行为。图表几乎永远不会完全相同，但其中很大一部分（这很重要）会在 OOS 上显示不错的结果。

将模型以 ONNX 格式导出

在之前的文章中，我使用了从 cpp 到 MQL 来解析模型。目前 MetaTrader 5 终端支持将模型导入ONNX格式。这非常方便，因为您可以编写更少的代码并转移几乎任何用 Python 训练的模型。

CatBoost 算法有自己的方法，用于以 ONNX 格式导出模型。让我们更详细地了解一下导出过程。

在输出处，我们有两个 CatBoost 模型和一个以增量形式生成特征的函数。由于该函数非常简单，我们将简单地将其转移到机器人代码中，同时将模型导出到 ONNX 文件中。

def export_model_to_ONNX(model, model_number):
    model[1].save_model(
    export_path +'catmodel' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'test model for BinaryClassification',
        'onnx_graph_name': 'CatBoostModel_for_BinaryClassification'
    },
    pool=None)

    model[2].save_model(
    export_path + 'catmodel_m' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'test model for BinaryClassification',
        'onnx_graph_name': 'CatBoostModel_for_BinaryClassification'
    },
    pool=None)
    
    code = '#include <Math\Stat\Math.mqh>'
    code += '\n'
    code += '#resource "catmodel'+str(model_number)+'.onnx" as uchar ExtModel[]'
    code += '\n'
    code += '#resource "catmodel_m'+str(model_number)+'.onnx" as uchar ExtModel2[]'
    code += '\n'
    code += 'int Periods' + '[' + str(len(PERIODS)) + \
        '] = {' + ','.join(map(str, PERIODS)) + '};'
    code += '\n\n'

    # get features
    code += 'void fill_arays' + '( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(Periods'')-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_H1,1,Periods''[i],pr);\n'
    code += '       ret[0] = MathMean(pr) - pr[Periods[i]-1];\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    file = open(export_path + str(SYMBOL) + ' ONNX include' + str(model_number) + '.mqh', "w")
    file.write(code)

    file.close()
    print('The file ' + 'ONNX include' + '.mqh ' + 'has been written to disk')

导出函数接收模型列表。它们每个都以 ONNX 格式存储，并带有可选的导出参数。所有这些代码会将模型保存到终端的 Include 文件夹中，并生成一个如下所示的 .mqh 文件：

#resource "catmodel.onnx" as uchar ExtModel[]
#resource "catmodel_m.onnx" as uchar ExtModel2[]

#include <Math\Stat\Math.mqh>
int Periods[4] = {10,20,30,40};

void fill_arays( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(Periods)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_H1,1,Periods[i],pr);
       ret[0] = MathMean(pr) - pr[Periods[i]-1];
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

接下来，我们需要将它连接到机器人。每个文件都有一个唯一的名称，通过交易品种代码和末尾的模型序列号指定。因此，我们可以将此类训练模型的集合存储在磁盘上，或者一次将多个模型连接到机器人。为了演示目的，我将做一个文件的限制。

#include <EURUSD ONNX include1.mqh>

在函数中，我们需要正确初始化模型，如下所示。 最重要的是正确设置输入和输出数据的维度。我们的模型具有可变长度的特征向量，其长度取决于 PERIODS 列表或导出数组中指定的特征数量，因此我们定义输入向量的维度，如下所示。两种模型都采用相同数量的特征作为输入。

输出向量的维度可能会引起一些混乱。 

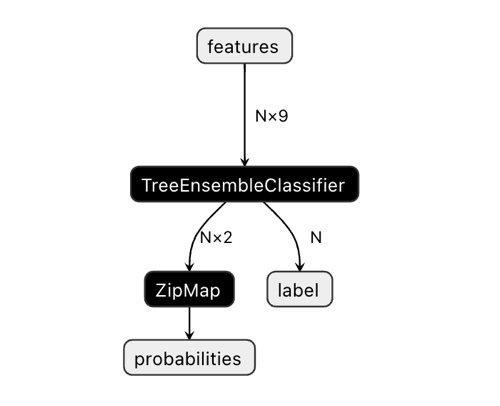
在 Netron 应用程序中，我们可以看到该模型有两个输出。第一个是单位张量，其类标签在代码中稍后定义为零输出或零索引输出。但它不能用于进行预测，因为 CatBoost 文档中描述了已知问题：

“对于二元分类，该标签推断不正确。这是 onnxruntime 实现中的一个已知错误。如果是二元分类则忽略此参数的值。”

因此，我们应该使用第二个“probabilities（概率）”输出，但我无法在 MQL 代码中正确设置它，所以我根本没有定义它。然而，它是自行定义了，并且一切正常。我不知道为什么。

因此，第二个输出用于获取机器人中的类概率。

const long  ExtInputShape [] = {1, ArraySize(Periods)};

int OnInit() {
   ExtHandle = OnnxCreateFromBuffer(ExtModel, ONNX_DEFAULT);
   ExtHandle2 = OnnxCreateFromBuffer(ExtModel2, ONNX_DEFAULT);

   if(ExtHandle == INVALID_HANDLE || ExtHandle2 == INVALID_HANDLE) {
      Print("OnnxCreateFromBuffer error ", GetLastError());
      return(INIT_FAILED);
   }

   if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape)) {
      Print("OnnxSetInputShape failed, error ", GetLastError());
      OnnxRelease(ExtHandle);
      return(-1);
   }

   if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape)) {
      Print("OnnxSetInputShape failed, error ", GetLastError());
      OnnxRelease(ExtHandle2);
      return(-1);
   }

   const long output_shape[] = {1};
   if(!OnnxSetOutputShape(ExtHandle, 0, output_shape)) {
      Print("OnnxSetOutputShape error ", GetLastError());
      return(INIT_FAILED);
   }
   if(!OnnxSetOutputShape(ExtHandle2, 0, output_shape)) {
      Print("OnnxSetOutputShape error ", GetLastError());
      return(INIT_FAILED);
   }

   return(INIT_SUCCEEDED);
}

接收模型信号就是这样实现的。这里我们声明一个特征数组，并通过位于导出的 .mqh 文件中的 fill_arrays() 函数填充它。

接下来，我声明另一个数组 f 来反转特征数组值的顺序，并将其提交给 Onnx Runtime 执行。第一个输出参数作为向量只需要传入，但我们不会使用它。结构数组作为第二个输出参数传递。

模型（主模型和元模型）被执行并将预测值返回到 tensor 数组。我从中得出第二类概率。

void OnTick() {
   if(!isNewBar())
      return;

   double features[];
   fill_arays(features);

   double f[ArraySize(Periods)];

   int k = ArraySize(Periods) - 1;
   for(int i = 0; i < ArraySize(Periods); i++) {
      f[i] = features[i];
      k--;
   }

   static vector out(1), out_meta(1);

   struct output {
      long           label[];
      float          tensor[];
   };

   output out2[], out2_meta[];

   OnnxRun(ExtHandle, ONNX_DEBUG_LOGS, f, out, out2);
   OnnxRun(ExtHandle2, ONNX_DEBUG_LOGS, f, out_meta, out2_meta);

   double sig = out2[0].tensor[1];
   double meta_sig = out2_meta[0].tensor[1];

您应该已经从上一篇文章中熟悉了机器人代码的其余部分。我们检查 meta_sig 来启用信号。如果它大于 0.5，则允许根据第一个模型的 sig 信号指定的方向进行开仓和平仓。

if(meta_sig > 0.5)
      if(count_market_orders(0) || count_market_orders(1))
         for(int b = OrdersTotal() - 1; b >= 0; b--)
            if(OrderSelect(b, SELECT_BY_POS) == true) {
               if(OrderType() == 0 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig > 0.5)
                  if(SymbolInfoInteger(_Symbol, SYMBOL_TRADE_FREEZE_LEVEL) < MathAbs(Bid - OrderOpenPrice())) {
                     int res = -1;
                     do {
                        res = OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red);
                        Sleep(50);
                     } while (res == -1);
                  }
               if(OrderType() == 1 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig < 0.5)
                  if(SymbolInfoInteger(_Symbol, SYMBOL_TRADE_FREEZE_LEVEL) < MathAbs(Bid - OrderOpenPrice())) {
                     int res = -1;
                     do {
                        res = OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red);
                        Sleep(50);
                     } while (res == -1);
                  }
            }


   if(meta_sig > 0.5)
      if(countOrders() < max_orders && CheckMoneyForTrade(_Symbol, LotsOptimized(meta_sig), ORDER_TYPE_BUY)) {
         double l = LotsOptimized(meta_sig);
         if(sig < 0.5) {
            int res = -1;
            do {
               double stop = Bid - stoploss * _Point;
               double take = Ask + takeprofit * _Point;
               res = OrderSend(Symbol(), OP_BUY, l, Ask, 0, stop, take, comment, OrderMagic);
               Sleep(50);
            } while (res == -1);
         } else {
            if(sig > 0.5) {
               int res = -1;
               do {
                  double stop = Ask + stoploss * _Point;
                  double take = Bid - takeprofit * _Point;
                  res = OrderSend(Symbol(), OP_SELL, l, Bid, 0, stop, take, comment, OrderMagic);
                  Sleep(50);
               } while (res == -1);
            }
         }
      }

最终测试

让我们依次将 2 个文件与我们喜欢的模型连接起来，并确保自定义测试器的结果与 MetaTrader 5 测试器的结果完全一致。

此外，我们可以在真实的报价上测试机器人，优化止损和止盈，选择手数并在 MetaTrader 5 优化器中添加更多交易。

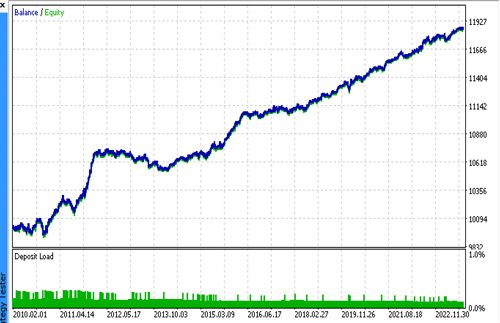
最后的话

我不知道这种对交易任务的时间序列进行分类的方法是否有科学依据。它是通过反复试验发明出来的，对我来说相当有趣和有前景。

通过这项小研究，我想强调的是，有时机器学习模型应该以不同于显而易见的方式进行训练。除了特定的架构之外，这些模型的应用方式也非常重要。与此同时，分析训练结果的统计方法也开始崭露头角，无论是本文介绍的全自动“交易员和研究人员（trader and researcher）”方法，还是需要“老师（Teacher）”这样的专家干预的更简单的算法。