机器学习和交易中的元模型：交易订单的原始时序

概述

一些交易系统的一个显著特征是选择性交易，这意味着它们不会持续停留在市场中。 在大多数情况下，这是由于在某些时间点存在形态，而在其它时间，形态不存在或未定义。

在前面的文章中，我详细讲述了机器学习模型应用于时间序列分类任务的各种方法。 所有这些模型都在训练集合上“按原样”训练，并在训练后编译到机器人。 标记训练数据集合和选择最佳模型的过程理应尽可能自动化，几乎完全消除了人为因素。 尽管提出的方式非常雅致，但这些模型有两个缺点，如果不引入额外的功能，则难以修复。

我开始扩展该方法，覆盖模型能够做到的情况：

1. 适配训练数据集合，选择最佳训练示例
2. 厘清时间序列中难以分类的部分，并在训练和交易期间跳过它们

如此归纳令我重新考虑了部分训练方式。 结果表明，仅用一个分类器不能满足新的需求。 它在训练时无法自我校正。 因此，我决定修改上述案例的功能。

新方式的理论层面

首先，我需要画个小重点。 由于研究人员在开发交易系统（包括应用机器学习的系统）时所作所为的不确定性，因此不可能严格正规化搜索对象。 它可以定义为多维空间中的一些或多或少稳定的依赖关系，这些依赖关系很难用人类甚或数学语言来解释。 我们从高度参数化的自我训练系统中，很难进行详细的分析。 这种算法需要交易者基于回测的结果给予一定程度的信任，但它们并没有阐明所发现形态的精髓，甚至是本质。

我打算编写一个算法，能够自行分析和校正错误，迭代改进结果。 为此，我提议采用一组两个分类器，并按照下图所示顺序对它们进行训练。 下面提供了该思路的详细描述。

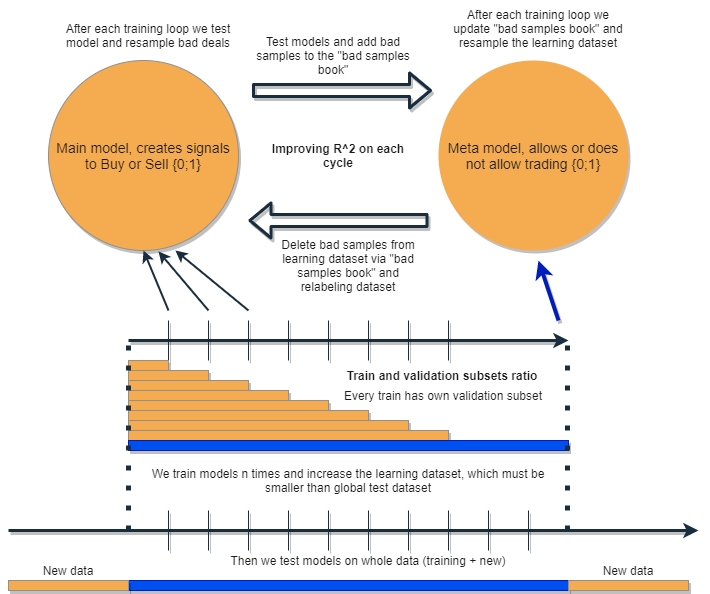
每个分类器都基于自己的数据集合训练，数据集合有自己的大小。 蓝色水平线表示元模型的条件历史深度，橙色线代表基准模型。 换句话说，元模型的历史深度始终大于基准模型，并且等于评估（测试）时间间隔，在该时间间隔上测试这些模型的组合。

该组模型曾被重新训练若干次，而基准模型的训练数据集合可以逐渐增加（在每次新迭代时增加橙色列的长度），但其长度不应超过蓝色列的长度。 在每次迭代之后，从基准模型的训练样本中移除被元模型分类为假（或零）的所有样本。 依序，元模型继续基于所有样本进行训练。

隐藏在这种方式背后的直觉是，根据混淆矩阵的术语，亏损交易是我把底层模型进行了错误的I分类。 换言之，这些都是它的分类为假阳性的情况。 元模型过滤掉了这些情况，并为真阳性给出了 1 分，其它所有情况则给了 0 分。 经由元模型整理训练基准模型的数据集合，我们提升高了其精度，即正确触发买入和卖出的次数。 与此同时，元模型能够尽可能多的带来不同结果的分类，从而提升其召回率（完整性）。 

精度越高，模型越精确。 但在真实状况中，一个指标的改善会导致同一分类器中另一指标的恶化，如此这般使用一组两个分类器看起来是似乎一个有趣的想法，或可两个指标一同得到改善。 

其思路在于，两个模型基于相同的属性进行训练，故此具有额外的交叠。 由于对元模型的选择增加（蓝色水平列与橙色水平列相比），它保留了优良的交易状况，如同基于新数据理清基准模型的错误一样。 通过彼此间相互交互，由于重新标记，模型迭代改进，且基于验证集合上的R ^ 2 得分持续增加。 但是元模型可以在其自身属性上作为基准模型的过滤器进行训练。 这种联系不完全符合所拟议方式的框架，因此在此不予考虑。

由于元模型的持续“维护”，基准模型应该工作得更好，但元模型本身有可能是错误的。 例如，第一次迭代揭示了不适合交易的案例。 在第二次迭代中，在重新训练基准模型，并调整元模型的示例之后，不良示例可能与上一次迭代中的不同。 因此，元模型可能会不断地重新标记不同迭代的示例。 这种行为也许永远不会达到平衡。 为了解决这个缺陷，我们创建“不良样本簿”表格，该表格将用以前所有迭代中的示例进行更新。 更具体地说，它将存储所有先前训练迭代中被标记为交易不良时刻的特征值。 这将允许在每次重新训练之前更新元模型的数据集合，令之前迭代的所有不成功时刻也能被标记为不良（零）。

“不良样本簿”也有其缺陷，因为太多的迭代会增加太多的零（不良交易）。 对于每次新的训练迭代，样本的数量将显著减少。 因此，有必要在迭代次数和添加到不良样本簿中的样本数量之间寻找平衡。 依据不良样本发生的时间计算其平均值，且仅整理最常见的样本，如此可部分解决这种状况。 在这种情况下，元模型数据集合不会退化（将保持 0 和 1 之间的平衡）。 如果该例被证明高度不平衡，则最好采用过度样本。

经过若干次迭代后，这组模型将在训练和验证数据上展现出完美的结果。 更有甚者，结果将随着迭代而不断改进。 训练之后，应基于全新数据测试一组模型，这些数据的定位比训练子样本更早或更晚均可。 没有一种理论可以毫不含糊地表明，应该选择哪一部分历史来测试非稳态金融时间序列。 尽管如此，我期望依据新数据所提方式的性能会有所改善，而真实的实践会展现其余内容。

那么，我们训练单一模型，用另一个模型基于新数据校正其错误，并重复这个过程若干次。 为什么这会增加分类器对新数据的稳固性？ 这个问题没有单一的答案。 有一种假设，我们正在处理某种形态。 如果它存在，它就会被发现，无形态的状况就会被整理出来。 如果形态稳定，则模型将基于新数据上操作。

理论上，这种方式应该能够一石两鸟：

• 提供高利润交易预期
• 交易系统自动“时分”，仅在某些高效时间点进行交易

既然我们谈论的是交易系统的时分，我们应该再谈谈一个有趣的问题。 现在，减少了对模型属性（特征）选择的依赖。

基本方式和监督标记意味着谨慎选择预测因子和目标。 而事实上，这正是该方式的主要问题。 数据准备和分析始终是重中之重，而模型的品质直接取决于特定领域分析师的专业水准（在我们的案例中，是外汇）。

所提议方式应自动查找相关的时序、预测器和标记事件，并采用自动发现的形态。 预测器的选择和成交的标记也是自动发生。 它仍然需要遵守一定数量的条件：例如，属性应该是固定的，并且至少与金融产品有间接关系。 但在我们不知道真实形态的情行下，没有地方可以获得信息，那么这种方式看起来就是合理的。

当然，如果我们使用与交易没有因果关系的“垃圾”属性，算法则会随机工作。 然而，这已经是一个存在/不存在因果关系的问题。 本文有意不考虑增量（移动平均线和价格之间的差异）以外的特性构建，因为这是一个单独且庞大的主题，也许会在其它文章中加以研究。 此处假设针对信息特征选择的分析方式应能显著提高算法在新数据上的稳定性。

实施提议方式的实现

和往常一样，理论上一切看起来都很完美。 现在，我们来检查一下从两个分类器中获得的实际效果。 为此，我们需要再次重写代码。

成交自动标记的函数

我已做了一些改动。 现在可以根据元模型标签重新标记基准模型的标签：

def labelling_relabeling(dataset, min=15, max=15, relabeling=False) -> pd.DataFrame:
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]

        if relabeling:
            m_labels  = dataset['meta_labels'][i:rand+1].values
        
        if relabeling and 0.0 in m_labels:
            labels.append(2.0)
        else:
            if future_pr + MARKUP < curr_pr:
                labels.append(1.0)
            elif future_pr - MARKUP > curr_pr:
                labels.append(0.0)
            else:
                labels.append(2.0)
        
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2].index)

    return dataset

高亮显示的代码检查是否存在重新标记标志。 如果它为真，并且当前交易水平线元标记包含零，则元模型拒绝在该部分进行交易。 相应地，此类成交被标记为 2.0，并从数据集合中删除。 因此，我们能够从基准模型的训练样本中迭代去除不必要的样本，从而减少其训练的误差。

自定义测试器函数

现在有一个扩展功能，允许我们同时测试两个模型（基准模型和元模型）。 此外，定制测试器现在能够重新标记元模型的标签，以便在下一次迭代中改进它。

def tester(dataset: pd.DataFrame, markup=0.0, use_meta=False, plot=False):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    meta_labels = dataset['labels'].copy()

    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        meta_labels[i] = np.nan
        if use_meta:
            pred_meta = dataset['meta_labels'][i] # 1 = allow trades

        if last_deal == 2 and ((use_meta and pred_meta==1) or not use_meta):
            last_price = dataset['close'][i]
            last_deal = 0 if pred <= 0.5 else 1
            continue

        if last_deal == 0 and pred > 0.5 and ((use_meta and pred_meta==1) or not use_meta):
            last_deal = 2
            report.append(report[-1] - markup +
                          (dataset['close'][i] - last_price))
            if report[-1] > report[-2]:
                meta_labels[i] = 1
            else:
                meta_labels[i] = 0
            continue

        if last_deal == 1 and pred < 0.5 and ((use_meta and pred_meta==1) or not use_meta):
            last_deal = 2
            report.append(report[-1] - markup +
                          (last_price - dataset['close'][i]))
            if report[-1] > report[-2]:
                meta_labels[i] = 1
            else:
                meta_labels[i] = 0

    y = np.array(report).reshape(-1, 1)
    X = np.arange(len(report)).reshape(-1, 1)
    lr = LinearRegression()
    lr.fit(X, y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.plot(lr.predict(X))
        plt.title("Strategy performance R^2 " + str(format(lr.score(X, y) * l,".2f")))
        plt.xlabel("the number of trades")
        plt.ylabel("cumulative profit in pips")
        plt.show()

    return lr.score(X, y) * l, meta_labels.fillna(method='backfill')

测试器的工作原理如下。

测试期间如果设置了参考元模型的标志，则检查其信号（1）存在的条件。 如果信号存在，则允许基准模型开仓和平仓，否则不进行交易。 浅绿色标记高亮显示根据已完成成交的结果为元模型添加新标签。 如果结果为正面，则添加一个。 否则，成交标记为 0（不成功）。

蛮力函数 

最大的变化发生在这里。 我将在清单中用不同的颜色标记它们，并对它们进行讲解，以便能更好地理解。

def brute_force(dataset, bad_samples_fraction=0.5):
    # features for model\meta models. We learn main model only on filtered labels 
    X = dataset[dataset['meta_labels']==1]
    X = dataset[dataset.columns[:-2]]
    X = X[X.index >= START_DATE]
    X = X[X.index <= STOP_DATE]

    X_meta = dataset[dataset.columns[:-2]]
    X_meta = X_meta[X_meta.index >= TSTART_DATE]
    X_meta = X_meta[X_meta.index <= STOP_DATE]

    # labels for model\meta models
    y = dataset[dataset['meta_labels']==1]
    y = dataset[dataset.columns[-2]]
    y = y[y.index >= START_DATE]
    y = y[y.index <= STOP_DATE]

    y_meta = dataset[dataset.columns[-1]]
    y_meta = y_meta[y_meta.index >= TSTART_DATE]
    y_meta = y_meta[y_meta.index <= STOP_DATE]

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.5, test_size=0.5, shuffle=True,)

    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=1000,
                               depth=6,
                               learning_rate=0.1,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU',
                               random_seed=13)
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=50, plot=False)

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X_meta, y_meta, train_size=0.5, test_size=0.5, shuffle=True)

    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=1000,
                                    depth=6,
                                    learning_rate=0.1,
                                    custom_loss=['Accuracy'],
                                    eval_metric='Accuracy',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU',
                                    random_seed=13)
    meta_model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=50, plot=False)

    # predict on new data (validation plus learning)
    pr_tst = get_prices()
    X = pr_tst[pr_tst.columns[1:]]
    X.columns = [''] * len(X.columns)
    X_meta = X.copy()

    # predict the learned models (base and meta)
    p = model.predict_proba(X)
    p_meta = meta_model.predict_proba(X_meta)

    p2 = [x[0] < 0.5 for x in p]
    p2_meta = [x[0] < 0.5 for x in p_meta]
    pr2 = pr_tst.iloc[:len(p2)].copy()
    pr2['labels'] = p2
    pr2['meta_labels'] = p2_meta
    pr2['labels'] = pr2['labels'].astype(float)
    pr2['meta_labels'] = pr2['meta_labels'].astype(float)
    full_pr = pr2.copy()
    pr2 = pr2[pr2.index >= TSTART_DATE]
    pr2 = pr2[pr2.index <= STOP_DATE]

    # add bad samples of this iteratin (bad meta labels)
    global BAD_SAMPLES_BOOK
    BAD_SAMPLES_BOOK = BAD_SAMPLES_BOOK.append(pr2[pr2['meta_labels']==0.0].index)
    
    # test mdels and resample meta labels
    R2, meta_labels = tester(pr2, MARKUP, use_meta=True, plot=False)
    pr2['meta_labels'] = meta_labels

    # resample labels based on meta labels
    pr2 = labelling_relabeling(pr2, relabeling=True)
    pr2['labels'] = pr2['labels'].astype(float)
    pr2['meta_labels'] = pr2['meta_labels'].astype(float)

    # mark bad labels from bad_samples_book
    if BAD_SAMPLES_BOOK.value_counts().max() > 1:
        to_mark = BAD_SAMPLES_BOOK.value_counts()
        mean = to_mark.mean()
        marked_idx = to_mark[to_mark > mean*bad_samples_fraction].index
        pr2.loc[pr2.index.isin(marked_idx), 'meta_labels'] = 0.0
    else:
        pr2.loc[pr2.index.isin(BAD_SAMPLES_BOOK), 'meta_labels'] = 0.0

    R2, _ = tester(full_pr, MARKUP, use_meta=True, plot=False)

    return [R2, model, meta_model, pr2]

BAD_SAMPLES_BOOK 和其余用相应标记高亮显示的代码负责实现不良样本簿。 在重新训练两个模型的每一次新迭代中，都会补充先前模型在训练后开立的不成功交易的新示例。 使用测试器进行验证。

最后一个高亮显示的模块可以灵活配置，这取决于在下一次重新训练时不成功示例的哪个部分会被标记为 0。 默认情况下，针对工作簿中包含的每个日期，计算 其所有重复项的平均值。

marked_idx = to_mark[to_mark > mean*bad_samples_fraction].index

这样做的目的是，并非所有的不良日期都可以被排除，而是只有模型中那些经历了所有训练迭代后犯了最多错误的日期可以被删除。 bad_samples_fraction 参数值越大，删除的错误日期越少，反之亦然。

蓝色表示数据集合从 START_DATE 开始的缩减部分用于基准模型。 早期数据不参与其训练。 然而，它参与元模型的训练。 此外，该颜色表示正在训练两种不同的模型 — 基准模型和元模型。

粉红色高亮显示的部分抽取的是两个模型的预测部分。 在这些预测的帮助下形成了一个新的数据集。 数据集会由代码进一步推送。 其中的不良元模型标签也会被添加到不良样本簿里。 

之后，两个模型都在自定义测试器中进行测试，该测试器还为下一次训练迭代重新标记（调整）元模型标签。 在校正的数据集上对基础模型执行进一步的重新标记。

在最后阶段，使用不良样本簿对数据集进行额外调整，并由函数返回用于下一次训练迭代。

尽管 Python 代码很丰富，但由于缺少嵌套循环，且执行过优化，它工作起来很快。 训练 CatBoost 分类器需要花费大部分时间。 训练时间随着属性数量和数据集长度的增加而增加。

模型重训练迭代

这些就是新方法的主要细节。 现在是时候进入模型训练循环了。 我们看看每个阶段将要发生的一切。

# make dataset
pr = get_prices()
pr = labelling_relabeling(pr, relabeling=False)
a, b = tester(pr, MARKUP, use_meta=False, plot=False)
pr['meta_labels'] = b
pr = pr.dropna()
pr = labelling_relabeling(pr, relabeling=True)


# iterative learning
res = []
BAD_SAMPLES_BOOK = pd.DatetimeIndex([])
for i in range(25):
    res.append(brute_force(pr[pr.columns[1:]], bad_samples_fraction=0.7))

    print('Iteration: {}, R^2: {}'.format(i, res[-1][0]))
    pr = res[-1][3] 

前两段代码简单地创建训练数据集合，就像前文中的示例一样。

>>> pr = get_prices(START_DATE, STOP_DATE)
>>> pr = labelling_relabeling(pr, relabeling=False)
>>> pr
                       close         0         1         2         3         4         5         6  labels       
time
2020-05-06 20:00:00  1.08086  0.000258 -0.000572 -0.001667 -0.002396 -0.004554 -0.007759 -0.009549     1.0       
2020-05-06 21:00:00  1.08032 -0.000106 -0.000903 -0.002042 -0.002664 -0.004900 -0.008039 -0.009938     1.0       
2020-05-06 22:00:00  1.07934 -0.001020 -0.001568 -0.002788 -0.003494 -0.005663 -0.008761 -0.010778     1.0       
2020-05-06 23:00:00  1.07929 -0.000814 -0.001319 -0.002624 -0.003380 -0.005485 -0.008559 -0.010684     1.0       
2020-05-07 00:00:00  1.07968 -0.000218 -0.000689 -0.002065 -0.002873 -0.004894 -0.007929 -0.010144     1.0       
...                      ...       ...       ...       ...       ...       ...       ...       ...     ...       
2021-04-13 23:00:00  1.19474  0.000154  0.002590  0.003375  0.003498  0.004095  0.004273  0.004888     0.0       
2021-04-14 00:00:00  1.19492  0.000108  0.002337  0.003398  0.003565  0.004183  0.004410  0.005001     0.0       
2021-04-14 01:00:00  1.19491 -0.000038  0.002023  0.003238  0.003433  0.004076  0.004353  0.004908     0.0       
2021-04-14 02:00:00  1.19537  0.000278  0.002129  0.003534  0.003780  0.004422  0.004758  0.005286     0.0       
2021-04-14 03:00:00  1.19543  0.000356  0.001783  0.003423  0.003700  0.004370  0.004765  0.005259     0.0       

[5670 rows x 9 columns]

现在我们需要为元模型添加标签。 您可能还记得，tester() 函数返回 R^2 得分和一个带有标记成交的帧。 因此，我们运行测试器并将结果帧添加到原始数据之中。

>>> a, b = tester(pr, MARKUP, use_meta=False, plot=False)
>>> pr['meta_labels'] = b
>>> pr = pr.dropna()
>>> pr
                       close         0         1         2  ...         5         6  labels  meta_labels
time                                                        ...
2020-05-06 20:00:00  1.08086  0.000258 -0.000572 -0.001667  ... -0.007759 -0.009549     1.0          1.0
2020-05-06 21:00:00  1.08032 -0.000106 -0.000903 -0.002042  ... -0.008039 -0.009938     1.0          1.0
2020-05-06 22:00:00  1.07934 -0.001020 -0.001568 -0.002788  ... -0.008761 -0.010778     1.0          1.0
2020-05-06 23:00:00  1.07929 -0.000814 -0.001319 -0.002624  ... -0.008559 -0.010684     1.0          1.0
2020-05-07 00:00:00  1.07968 -0.000218 -0.000689 -0.002065  ... -0.007929 -0.010144     1.0          1.0
...                      ...       ...       ...       ...  ...       ...       ...     ...          ...
2021-04-13 18:00:00  1.19385  0.001442  0.003437  0.003198  ...  0.003637  0.004279     0.0          1.0
2021-04-13 19:00:00  1.19379  0.000546  0.003121  0.003015  ...  0.003522  0.004166     0.0          1.0
2021-04-13 20:00:00  1.19423  0.000622  0.003269  0.003349  ...  0.003904  0.004555     0.0          1.0
2021-04-13 21:00:00  1.19465  0.000820  0.003315  0.003640  ...  0.004267  0.004929     0.0          1.0
2021-04-13 22:00:00  1.19552  0.001112  0.003733  0.004311  ...  0.005092  0.005733     1.0          1.0

[5665 rows x 10 columns]

训练数据现在已准备就绪。 我们可以根据第二个标签（“meta_labels”）对主标签（“labels”）进行额外的重新标记。 换言之，我们可以从数据集合中删除所有被证明无利可图的成交。

pr = labelling_relabeling(pr, relabeling=True)

数据准备好了，现在我们看看两个模型的训练循环。

# iterative learning
res = []
BAD_SAMPLES_BOOK = pd.DatetimeIndex([])
for i in range(25):
    res.append(brute_force(pr[pr.columns[1:]], bad_samples_fraction=0.7))

    print('Iteration: {}, R^2: {}'.format(i, res[-1][0]))
    pr = res[-1][3] 

首先，如果在之前的训练后还剩下一些东西，我们就需要重新设置不良成交簿。 接下来，在循环中设置所需的迭代次数。 在每次迭代中，含有所保存模型的嵌套列表（以及 brute_force() 函数返回的所有其它内容）被写入 res[] 列表。 例如，我们还可以在每次迭代时打印模型的主要参量。

pr 变量包含转换和返回的数据集合，其将用于下一次迭代的训练。 

正如理论层面所建议的，它可以增加基准模型的训练区间。 为了达成这一点，训练的开始日期将按照指定的天数变更。 与此同时，其大小不应超过元模型所训练的 TSTART_DATE 间隔的大小。

启动训练后，您可以看到类似于下图的内容：

Iteration: 0, R^2: 0.30121038659012245
Iteration: 1, R^2: 0.7400055934041012
Iteration: 2, R^2: 0.6221261327516192
Iteration: 3, R^2: 0.8892813889403367
Iteration: 4, R^2: 0.787251984980149
Iteration: 5, R^2: 0.794241109825588
Iteration: 6, R^2: 0.9167876214355855
Iteration: 7, R^2: 0.903399695678254
Iteration: 8, R^2: 0.8273236332747745
Iteration: 9, R^2: 0.8646088124681762
Iteration: 10, R^2: 0.8614746864767437
Iteration: 11, R^2: 0.7900599001415054
Iteration: 12, R^2: 0.8837049280116869
Iteration: 13, R^2: 0.784793801426211
Iteration: 14, R^2: 0.941340102099874
Iteration: 15, R^2: 0.8715065229034792
Iteration: 16, R^2: 0.8104990158946458
Iteration: 17, R^2: 0.8542444489379808
Iteration: 18, R^2: 0.8307365677342298
Iteration: 19, R^2: 0.9092509787525882

第一次运行通常不会有好结果。 然后，模型尝试经由每次新演算来自我提升。 然后，模型按 R^2 升序排序，并可以根据新数据进行测试。 我们可以先看看模型的演变，好过立即进行排序。 这一演变的一个特征符号是测试模型时成交数量减少。

例如，我所测试的最后一个训练模型，得到了以下结果（所有结果都基于新数据）：

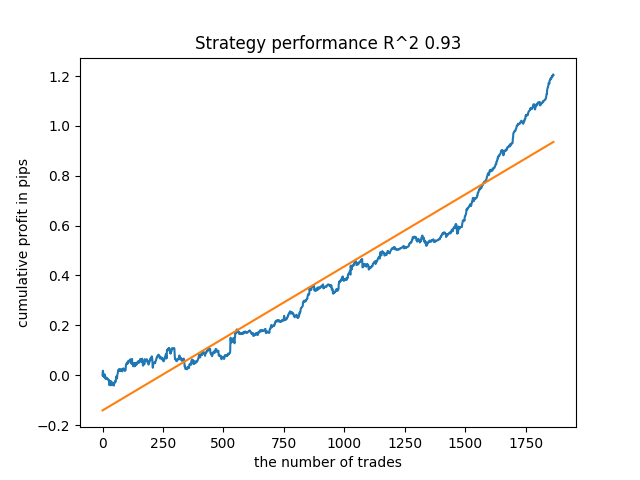
来自最后的第五种模型将有更多的成交，以此类推：

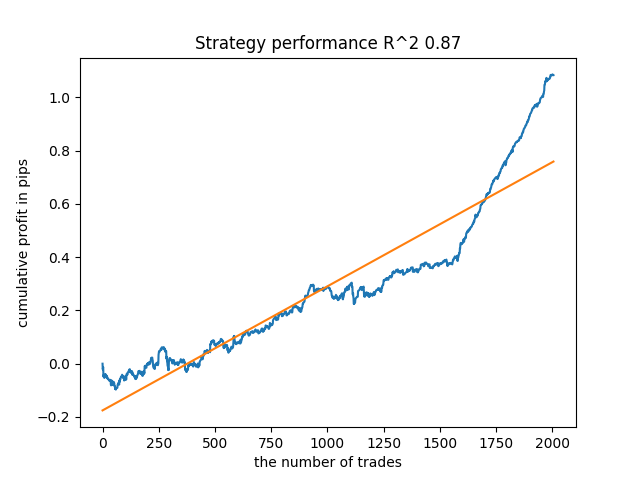
根据迭代次数和 bad_samples_fraction 参数，以及训练和测试样本的大小，我们可以得到基于新数据的稳定模型。 通常来说，这个思路证明是可行的，尽管很难理解和实施。 若启用 use_GMM_resampling 参数，情况大致相同，成交数量直接取决于迭代次数，但也可能有例外。 我从函数库中删除了重新采样，因为它花费了太多的训练时间，并且即使应用该方法，结果并无太多改善。

例如，我喜欢靠后的第五个结果：

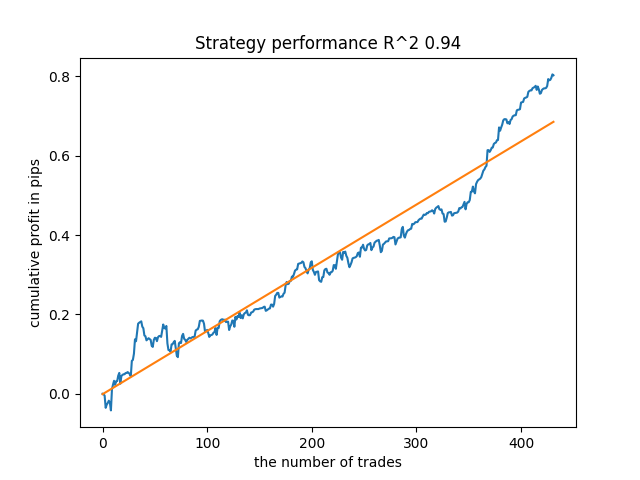
但从成交数量来看，第七个结果更为可取，其后果有两倍多。 以点数计算的总利润也增加了：

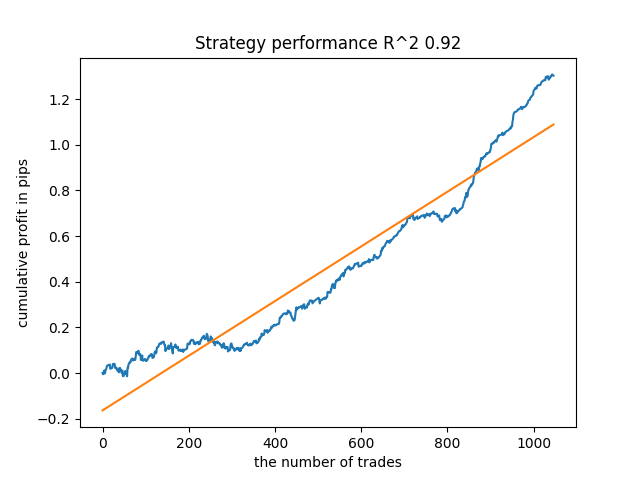
将模型导出为 MQL5 格式，并编译交易 EA

现在要保存两个模型：基准模型和元模型。 如前所述，基准模型控制买入和卖出信号，而元模型禁止或启用在特定时间点进行交易。

# add CatBosst base model
    code += 'double catboost_model' + '(const double &features[]) { \n'
    code += '    '
    with open('catmodel.h', 'r') as file:
        data = file.read()
        code += data[data.find("unsigned int TreeDepth")
                               :data.find("double Scale = 1;")]
    code += '\n\n'
    code += 'return ' + \
        'ApplyCatboostModel(features, TreeDepth, TreeSplits , BorderCounts, Borders, LeafValues); } \n\n'

    # add CatBosst meta model
    code += 'double catboost_meta_model' + '(const double &features[]) { \n'
    code += '    '
    with open('meta_catmodel.h', 'r') as file:
        data = file.read()
        code += data[data.find("unsigned int TreeDepth")
                               :data.find("double Scale = 1;")]
    code += '\n\n'
    code += 'return ' + \
        'ApplyCatboostModel(features, TreeDepth, TreeSplits , BorderCounts, Borders, LeafValues); } \n\n'

交易 EA 略有变化。 调用 catboost_meta_model() 函数生成信号。 如果超过 0.5，则允许交易。

void OnTick() {
//---
   if(!isNewBar()) return;
   TimeToStruct(TimeCurrent(), hours);
   double features[];

   fill_arays(features);
   if(ArraySize(features) !=ArraySize(MAs)) {
      Print("No history availible, will try again on next signal!");
      return;
   }
   double sig = catboost_model(features);
   double meta_sig = catboost_meta_model(features);

// close positions by an opposite signal
   if(meta_sig > 0.5)
      if(count_market_orders(0) || count_market_orders(1))
         for(int b = OrdersTotal() - 1; b >= 0; b--)
            if(OrderSelect(b, SELECT_BY_POS) == true) {
               if(OrderType() == 0 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig > 0.5)
                  if(OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red)) {
                  }
               if(OrderType() == 1 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig < 0.5)
                  if(OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red)) {
                  }
            }


// open positions and pending orders by signals
   if(meta_sig > 0.5)
      if(countOrders() == 0 && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY)) {
         double l = LotsOptimized();

         if(sig < 0.5) {
            OrderSend(Symbol(),OP_BUY,l, Ask, 0, Bid-stoploss*_Point, Ask+takeprofit*_Point, NULL, OrderMagic);

         } else {
            OrderSend(Symbol(),OP_SELL,l, Bid, 0, Ask+stoploss*_Point, Bid-takeprofit*_Point, NULL, OrderMagic);

         }
      }
}

附言

对于 MAC 和 Linux 用户，加载报价的终端 API 不可用。 我建议使用另一个函数，接收从 MetaTrader 5 终端加载到文件中的报价。 文件应保存到工作目录。

def get_prices() -> pd.DataFrame:
    p = pd.read_csv('EURUSDMT5.csv', delim_whitespace=True)
    pFixed = pd.DataFrame(columns=['time', 'close'])
    pFixed['time'] = p['<DATE>'] + ' ' + p['<TIME>']
    pFixed['time'] = pd.to_datetime(pFixed['time'], infer_datetime_format=True)
    pFixed['close'] = p['<CLOSE>']
    pFixed.set_index('time', inplace=True)
    pFixed.index = pd.to_datetime(pFixed.index, unit='s')
    pFixed = pFixed.dropna()
    pFixedC = pFixed.copy()

    count = 0
    for i in MA_PERIODS:
        pFixed[str(count)] = pFixedC - pFixedC.rolling(i).mean()
        count += 1
    return pFixed.dropna()

现在使用三个日期。 因此，现在可以通过回测和前向验证测试对模型进行整理。 前向验证的开始由 STOP_DATE 全局变量设置。 此日期之后的数据将不用于训练。 取而代之的是，它在测试中会被用到。 类似地，TSTART_DATE 之前的所有内容都是回测。

START_DATE = datetime(2021, 1, 1)
TSTART_DATE = datetime(2017, 1, 1)
STOP_DATE = datetime(2022, 1, 1)

请记住，基准模型是介于 START_DATE - STOP_DATE 区间进行训练的，而元模型是针对 TSTART_DATE - STOP_DATE 数据进行训练的。 文件中剩余的所有其它数据仅参与回测和前向验证测试。

更多的测试

我决定在一些交叉外汇对上测试所提议的训练方法，例如 GBPJPY H1。 从终端下载了 2010 年的报价。 训练的属性数量和周期如下：

MA_PERIODS = [i for i in range(15, 500, 15)]
MARKUP = 0.00002
START_DATE = datetime(2021, 1, 1)
TSTART_DATE = datetime(2018, 1, 1)
STOP_DATE = datetime(2022, 1, 1)

基准模型从 2021 到 2022 年初进行训练，而元模型从 2018 年到 2022 年进行训练。 所有其它数据用于测试新数据，即 2010 年至 2022 年 6 月 15 日。

在 15-35 范围内选择交易采样的随机持续时间。

def labelling_relabeling(dataset, min=15, max=35, relabeling=False):

选择了 25 作为训练迭代。 样本簿中不良示例的乘数等于 0.5：

# iterative learning
res = []
BAD_SAMPLES_BOOK = pd.DatetimeIndex([])
for i in range(25):
    res.append(brute_force(pr[pr.columns[1:]], bad_samples_fraction=0.5))

    print('Iteration: {}, R^2: {}'.format(i, res[-1][0]))
    pr = res[-1][3] 

# test best model
res.sort()
p = test_model(res[-1])

在训练期间，自 2010 年以来，整个数据集获得了以下 R^2 得分：

Iteration: 0, R^2: 0.8364212812476872
Iteration: 1, R^2: 0.8265960950867208
Iteration: 2, R^2: 0.8710535097094494
Iteration: 3, R^2: 0.820894300254345
Iteration: 4, R^2: 0.7271704621597865
Iteration: 5, R^2: 0.8746302835797399
Iteration: 6, R^2: 0.7746283871087961
Iteration: 7, R^2: 0.870806543378866
Iteration: 8, R^2: 0.8651222653557956
Iteration: 9, R^2: 0.9452164577256995
Iteration: 10, R^2: 0.867541289963404
Iteration: 11, R^2: 0.9759544230548619
Iteration: 12, R^2: 0.9063804006221455
Iteration: 13, R^2: 0.9609701853129079
Iteration: 14, R^2: 0.9666262255426672
Iteration: 15, R^2: 0.7046628448822643
Iteration: 16, R^2: 0.7750941894554821
Iteration: 17, R^2: 0.9436968900331276
Iteration: 18, R^2: 0.8961403809578388
Iteration: 19, R^2: 0.9627553719743711
Iteration: 20, R^2: 0.9559809326980575
Iteration: 21, R^2: 0.9578579606050637
Iteration: 22, R^2: 0.8095556721129047
Iteration: 23, R^2: 0.654147043077418
Iteration: 24, R^2: 0.7538928969905255

接下来，模型按最高 R^2 排序。 以下是它们中最好的，按得分降序排列。

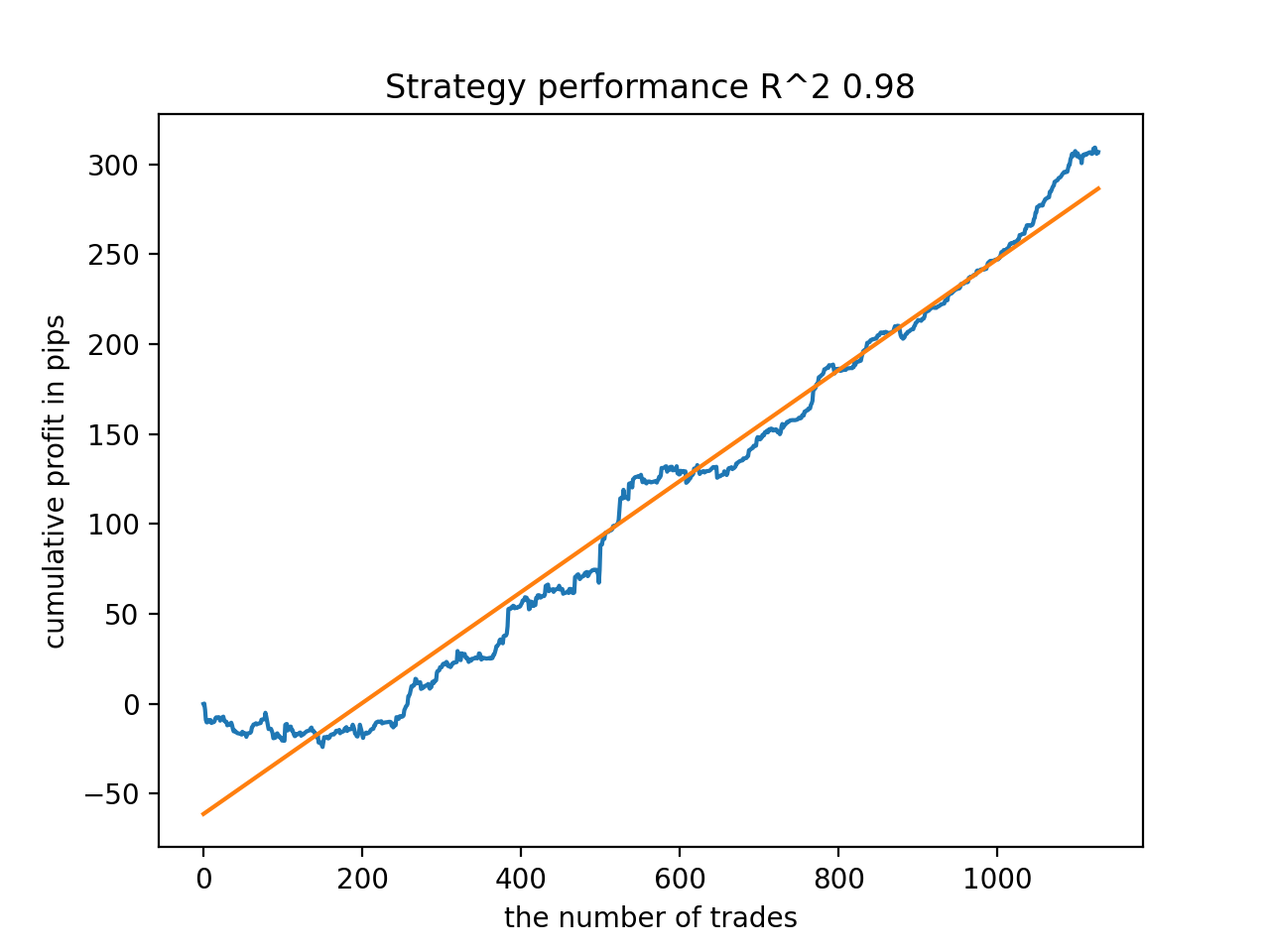
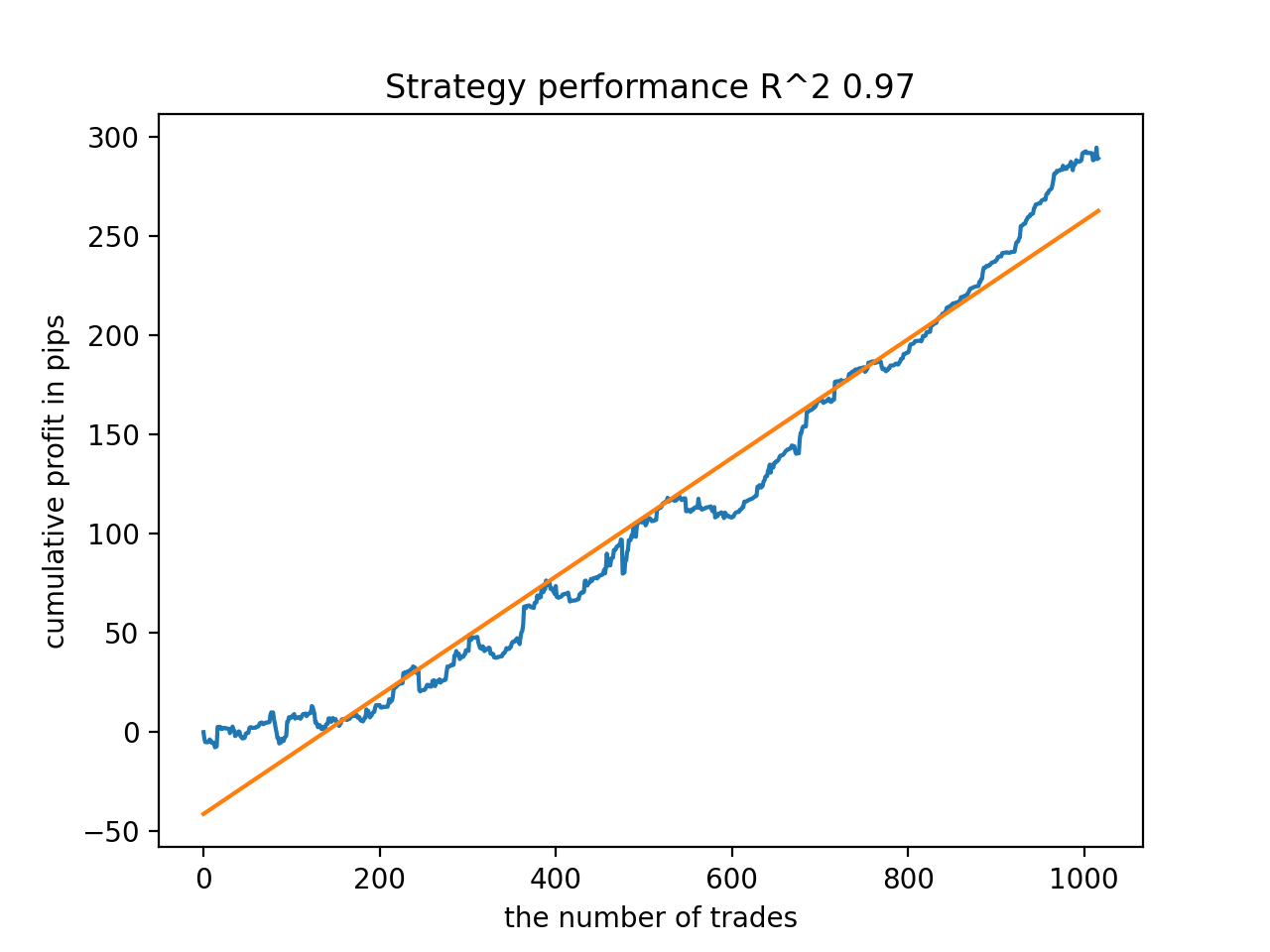
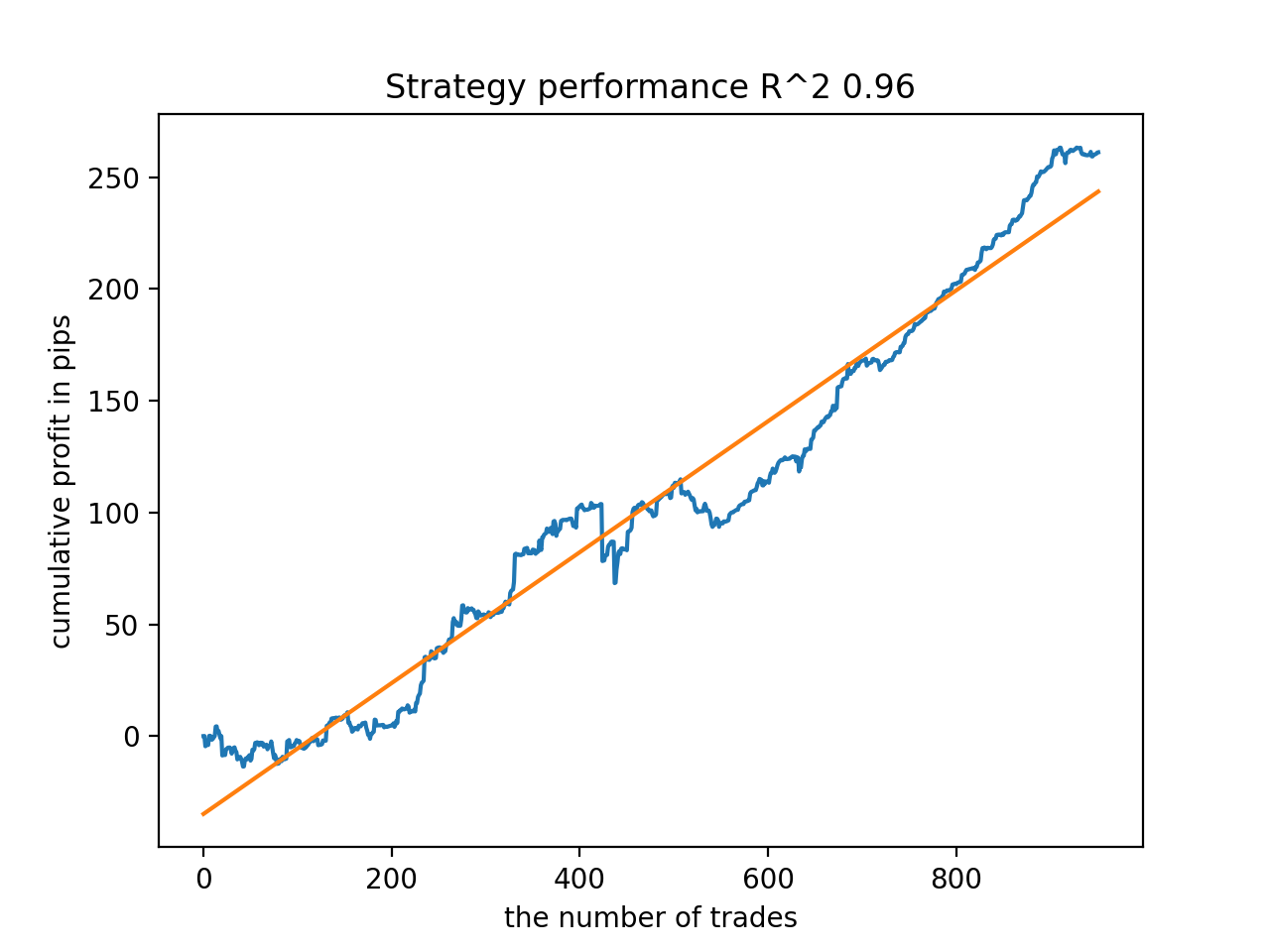
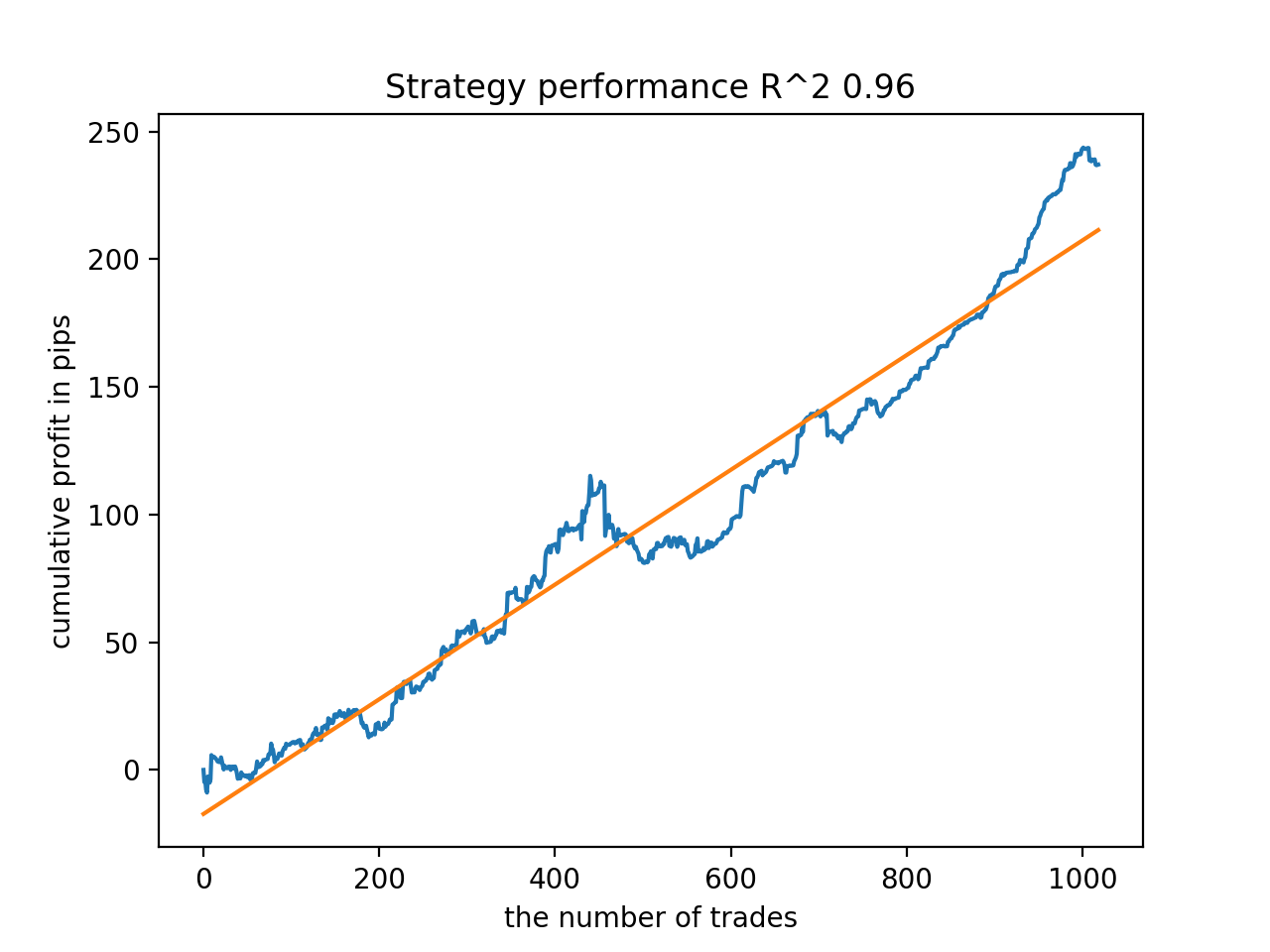
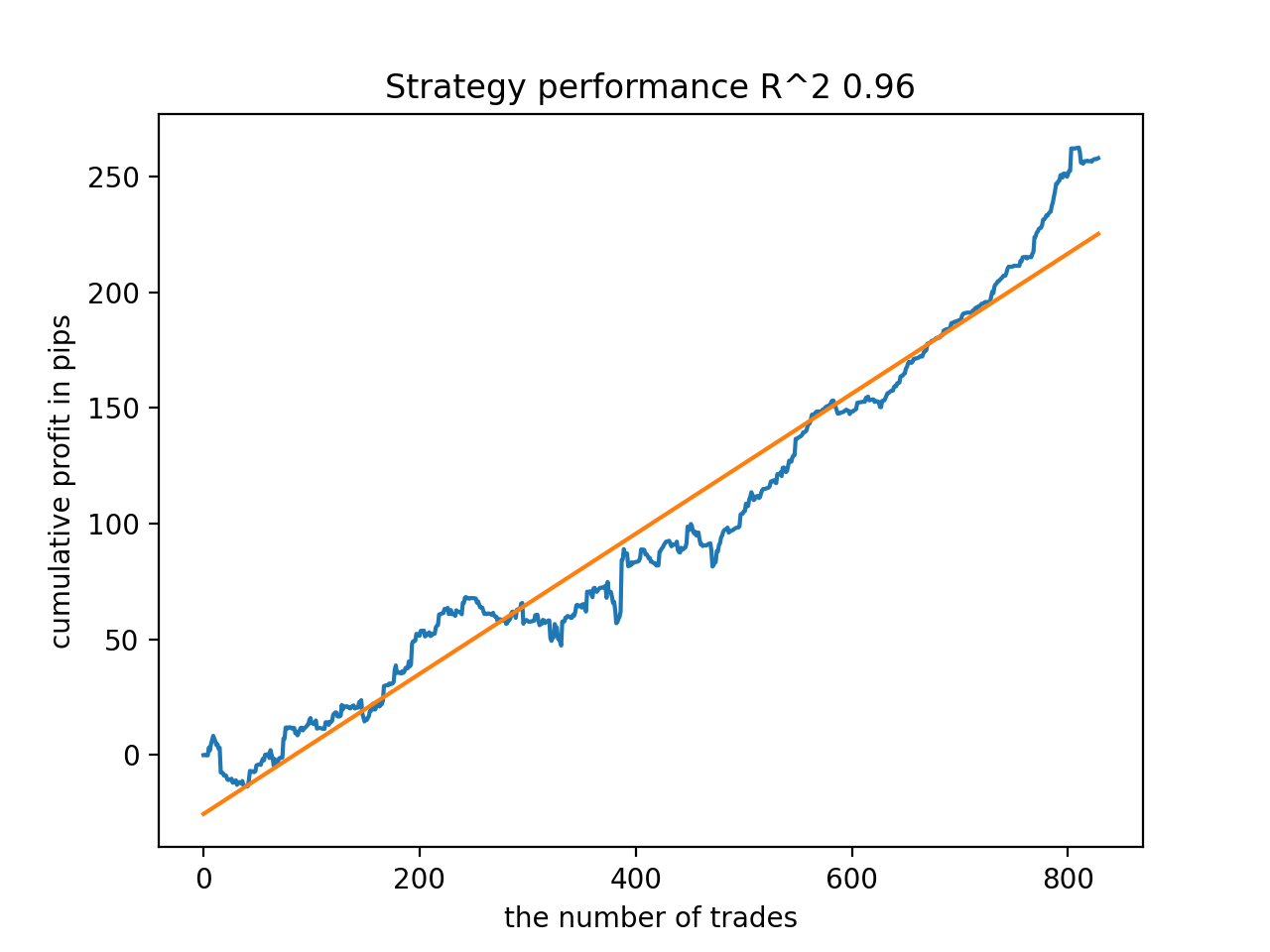
自 2010 年以来，所有形态总体上相当稳定，尽管图形呈现的曲线并不完美。

在最后阶段，我们将感兴趣的模型导出到 MetaTrader 5，以便进行其它测试、或用于交易。 导出函数取模型作为输入（在本例中，是从末尾开始的最佳模型），以及模型编号来更改文件名，如此您就可以同时记录多个模型。

export_model_to_MQL_code(res[-1], str(1))

编译机器人，并在 MetaTrader 5 策略测试器中验证它。

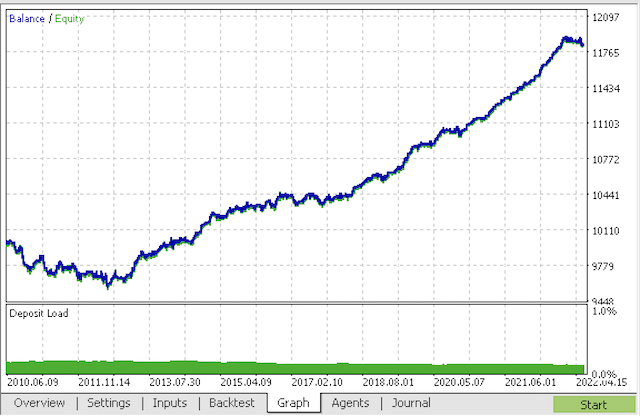
在最后阶段，您可以在熟悉的 MetaTrader 5 终端中使用模型。

结束语

本文的演示，可能是我实现过的最复杂和最深奥的时间序列分类模型。 有趣的一点是利用元模型自动丢弃难以分类的历史片段的能力。 这样的模型有时甚至比季节性模型表现得更好，季节性模型经训练后会在一天中的特定时间、或一周中的某一天进行交易，并具有明显的季节性周期。 在此，整理是自动执行的，无需人工干预。