因果推断中的时间序列聚类

简介

• 什么是聚类
• 在因果推断中使用聚类
• 使用聚类进行匹配
• 确定异质效应的影响
• 定义市场模式

波动性聚类：

• 代码
• 算法的评级
• 模型输入参数

使用聚类算法进行交易匹配：

• 代码
• 算法
• 考虑数据异质性
• 结果
• 结论

简介

聚类是一种机器学习技术，它能够将数据集划分为多个对象组（即聚类），使得同一聚类内的对象彼此相似，而不同聚类的对象则各不相同。聚类有助于揭示数据结构，识别隐藏的模式，并根据对象的相似性进行分组。

聚类可以用于因果推断。在这种背景下应用聚类的一种方法是识别出与特定原因相关联的相似对象或事件组。一旦数据被聚类，就可以分析聚类与原因之间的关系，以确定潜在的因果关系。

此外，聚类还可以帮助识别可能受到相同影响或具有共同原因的对象组，这对于分析因果关系也非常有用。

在因果推断中使用聚类对于分析数据和识别潜在的因果关系尤其有用。在本文中，我们将探讨如何在这种情况下利用聚类算法：

1. 识别相似对象组：聚类可以帮助识别具有相似特征或行为的对象组。然后，可以分析这些组，寻找可能与它们相关的共同原因或因素。
2. 确定因果关系：一旦数据被划分为聚类，就可以探索聚类之间的关系，并确定潜在的因果关系。例如，如果某个对象聚类表现出某种行为或特征，就可以进行分析，找出可能导致这种行为或特征的因素。
3. 发现隐藏模式：聚类有助于揭示数据中可能与因果关系相关的隐藏模式。通过分析聚类的结构并识别其中的共同对象特征，可以发现可能在某些现象发生中起关键作用的因素。
4. 预测未来事件：一旦确定了聚类和因果关系，就可以利用获得的知识来预测未来事件或趋势。基于数据分析和已识别的模式，可以假设哪些因素可能影响未来事件，以及可以采取哪些措施来管理这些事件。

聚类可用于因果推断中的匹配。匹配是根据相似性或符合某些标准将不同数据集的对象进行配对的过程。在因果推断的背景下，匹配可用于建立原因和结果之间的关系，并识别可能导致某些现象的共同特征或因素。

在匹配中，聚类可以用于以下方面：

1. 对象分组：聚类可以将数据集划分为具有相似特征或行为的对象组。 之后，可以在每个聚类内部进行匹配，找到对象之间的匹配项并建立它们之间的联系。
2. 相似性识别：一旦对象被分类，就可以检查每类内对象之间的相似性，并将其用于匹配。例如，如果某个聚类中的对象表现出相似的行为或特征，就可以进行匹配，找出可能与这些对象相关的共同因素。
3. 减少噪声：聚类有助于减少数据中的噪声数据，并突出主要对象组，从而使匹配过程更容易。通过将数据划分为不同的类，可以关注最重要和最相似的对象，从而提高匹配的质量，并允许识别更清晰的因果关系。

因此，时间序列聚类有助于识别异质处理效应，即算法在不同时间序列组中的差异。进行时间序列分析的分类或预测时，异质处理效应意味着时间序列的行为可能根据其特征或其他因素而有所不同。

因此，通过聚类时间序列，可以实现以下效果：

1. 时间序列分组：聚类可以根据时间序列的特征、趋势或其他因素将其划分为组。然后，可以分别检查每个组的表现，以确定不同时间序列聚类之间在预测或分类上是否存在差异。
2. 识别具有不同效应的子组：通过聚类时间序列，可以识别出具有不同行为或变化轨迹的子组。这允许研究人员确定哪些特征或因素可能影响分类或预测结果，并识别可能需要不同分析方法来处理的时间序列子集。
3. 模型个性化：利用聚类结果和识别出的具有不同行为的时间序列子组，可以对分类或预测模型进行个性化，并为每个组选择最佳策略。这可以提高预测和分类的准确性，并使模型适应不同类型的时间序列。

聚类同样可以用于识别市场状态，例如基于波动率的市场状态。

对于投资者和交易者来说，市场波动率分析是一个关键工具，因为它能帮助他们了解当前的市场状况，并根据预期的价格变动做出明智的决策。在金融分析的背景下，基于波动率的聚类算法有助于突出显示不同的市场“状态”，这些状态可能代表不同的趋势、震荡状态或方向极为不确定的时期。

基于波动率确定市场状态的聚类算法如何工作：

• 数据准备：对资产的原始价格波动率时间序列进行预处理，这包括根据价格的标准差或价格分布的变动来计算波动率。
• 应用聚类算法：接着，将聚类算法应用于波动率数据，以识别市场的隐含状态结构和状态。可以使用多种方法作为聚类算法，例如K-均值（K-Means）、基于密度的噪声应用空间聚类方法（DBSCAN），或专门为时间序列分析设计的算法，如考虑时间依赖性的算法。
• 对结果的说明：所得的聚类代表了不同的市场状态，这些状态可以为交易策略所用。例如，低波动率的聚类可能对应于横向趋势，而高波动率的聚类可能表明市场出现尖峰或趋势的变化。

基于波动率确定市场状态问题中聚类算法的优势：

• 确定市场结构： 聚类算法能够突出市场结构并识别隐藏模式，这有助于投资者和交易者理解当前的市场状况。
• 分析自动化：聚类算法的应用能够自动化分析市场波动率和识别不同模式的过程，从而节省时间并降低人为出错的可能性。
• 决策支持：基于波动率识别市场模式有助于预测未来的价格走势，并为交易和投资决策提供信息支持。

基于波动率确定市场状态问题中聚类算法的劣势：

• 参数选择的敏感性：聚类结果可能依赖于算法参数的选择，如聚类数量或距离度量，这需要仔细调整。
• 算法的局限性：在处理大量数据时，一些聚类算法可能不够高效，或者可能未考虑时间依赖性。

聚类算法的种类

我们可以使用不同的聚类算法。主要的聚类类型都已作为现成的库在Python中实现了。因此，开始尝试聚类算法测试的最佳方式是使用这些库，因为您无需从头开始实现每个算法。这大大加快了配置和进行实验的过程。

接下来，我们将简要了解可能对我们有用的主要聚类算法，并将它们应用到我们的任务中。

• K-Means算法以其简单性和高效性而著称，但其存在局限性，如依赖于初始条件以及需要事先知道聚类数量。
• Affinity Propagation（邻近传播）算法无需预先确定聚类数量，并且能很好地处理各种形状的数据，但其计算复杂度可能较高。
• Mean Shift（均值漂移）算法能够检测任意形状的聚类，并且无需指定聚类数量。然而，当处理大量数据时，其计算成本可能较高。
• Spectral Clustering（谱聚类）算法适用于具有非线性结构的数据，并且具有通用性。但是，其参数调整可能较为困难，且计算成本较高。
• Agglomerative Clustering（层次聚类）算法能够创建层次聚类，并且适用于处理未知数量的聚类。
• GMM（高斯混合模型）提供了一种概率聚类方法，能够模拟不同形状和密度的聚类。
• HDBSCAN和BIRCH算法都提供了高效处理大量数据以及自动确定聚类数量的功能，但它们也存在一些缺点，如计算复杂度和对参数的敏感性。

时间序列聚类（波动率聚类）的实现

我们对金融时间序列的聚类感兴趣，这既可以作为确定市场状态的手段，也可以作为匹配和确定异质处理效果的手段。我们首先从尝试聚类市场状态开始。

以下代码首先训练了一个元学习模型，然后基于聚类结果（该聚类基于金融数据的波动率）来训练最终模型和元模型。

def meta_learner(models_number: int, 
                 iterations: int, 
                 depth: int, 
                 bad_samples_fraction: float, 
                 n_clusters: int, 
                 algorithm: int) -> pd.DataFrame:
    
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()
    X = data[data.columns[1:-2]]
    X = X.loc[:, ~X.columns.str.contains('std')]
    meta_X = data.loc[:, data.columns.str.contains('std')]
    y = data['labels']

    B_S_B = pd.DatetimeIndex([])
    for i in range(models_number):
        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # learn debias model with train and validation subsets
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True)
        
        meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False)
        
        coreset = X.copy()
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
        
        # add bad samples of this iteration (bad labels indices)
        diff_negatives = coreset['labels'] != coreset['labels_pred']
        B_S_B = B_S_B.append(diff_negatives[diff_negatives == True].index)

    to_mark = B_S_B.value_counts()
    marked_idx = to_mark[to_mark > to_mark.mean() * bad_samples_fraction].index
    data.loc[data.index.isin(marked_idx), 'meta_labels'] = 0.0


    if algorithm==0:
        data['clusters'] = KMeans(n_clusters=n_clusters).fit(meta_X).labels_
    elif algorithm==1:
        data['clusters'] = AffinityPropagation().fit(meta_X).predict(meta_X)
    elif algorithm==2:
        data['clusters'] = SpectralClustering(n_clusters=n_clusters, assign_labels='discretize', random_state=0).fit_predict(meta_X)
    elif algorithm==3:
        data['clusters'] = MeanShift().fit_predict(meta_X)
    elif algorithm==4:
        data['clusters'] = AgglomerativeClustering(n_clusters=n_clusters).fit_predict(meta_X)
    elif algorithm==5:
        data['clusters'] = mixture.GaussianMixture(n_components=n_clusters, covariance_type='full').fit(meta_X).predict(meta_X)
    elif algorithm==6:
        data['clusters'] = HDBSCAN(min_cluster_size=150).fit_predict(meta_X)
    elif algorithm==7:
        data['clusters'] = Birch(threshold=0.01, n_clusters=n_clusters).fit_predict(meta_X)
    return data[data.columns[1:]]

函数说明：

meta_learner函数旨在通过训练一个分类模型来识别和纠正数据集中的错误标签样本。它使用CatBoostClassifier模型的集合来识别这些样本，并应用聚类算法对数据进行进一步处理。以下是该算法的更详细描述：

1. 数据准备：函数首先获取一个按时间戳过滤的数据集（排除某些时间段的数据）。然后，将数据分为特征（X）、基于标准差的元特征（meta_X）和目标标签（y）。

2. 变量初始化：创建一个空的日期索引B_S_B，用于存储错误标签样本的索引。

3. 训练模型和识别错误标签：对于models_number指定的每个模型，将数据分为训练集和验证集。然后，使用给定的参数训练CatBoostClassifier模型。一旦训练完成，模型将用于预测整个特征集X的标签。通过比较预测标签和原始标签，函数可以识别出错误标签的样本，并将其索引添加到B_S_B中。

4. 标记错误样本：训练完所有模型后，函数分析存储在B_S_B中的错误样本索引，并标记那些出现频率超过bad_samples_fraction所确定值的样本，在源数据的meta_labels列中将其标记为0.0。

5. 聚类：根据“algorithm”参数的值，函数将元特征（meta_X）应用于其中一个聚类算法，并将生成的聚类标签添加到源数据中。

6. 返回结果：函数返回一个更新后的数据集，其中包含标签和分配的聚类。

这种方法不仅可以识别和纠正数据标签中的错误，还可以对数据进行分组以供进一步分析或模型训练，这在存在大量错误标签样本的问题中尤其有用。

最终模型的训练函数如下：

def fit_final_models(dataset) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[:-3]]
    X = X[X.columns[:-3]]
    X = X.loc[:, ~X.columns.str.contains('std')]
    X_meta = X_meta.loc[:, X_meta.columns.str.contains('std')]
    
    # labels for model\meta models
    y, y_meta = dataset[dataset['meta_labels']==1], dataset[dataset.columns[-1]]
    y = y[y.columns[-3]]
    
    y = y.astype('int16')
    y_meta = y_meta.astype('int16')

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.8, test_size=0.2, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.8, test_size=0.2, shuffle=True)

    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=200,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU')
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=25, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=100,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU')
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=15, plot=False)
    
    R2 = test_model([model, meta_model])
    if math.isnan(R2):
        R2 = -1.0
        print('R2 is fixed to -1.0')
    print('R2: ' + str(R2))
    return [R2, model, meta_model]

fit_final_models 函数旨在使用提供的数据集来训练主要模型和元模型。以下是详细说明：

1. 准备数据

• 函数会从数据集中选择meta_labels等于1的行来训练主要模型（X, y）。
• 数据集中的所有行（X_meta, y_meta）都会用于训练元模型。
• 在训练主要模型的特征中，会排除名称中包含“std”的列以及最后三列。
• 对于元模型，该函数仅使用名称中包含“std”的特征。
• 主要模型的目标变量（y）取自倒数第三列，并将其类型转换为int16。
• 元模型的目标变量（y_meta）取自最后一列，也将其类型转换为int16。

2. 将数据划为训练集和测试集：

• 对于主要模型和元模型，数据按照80%到20%的比例被划分为训练集和测试集。

3. 基础模型训练：

• 我们使用CatBoostClassifier分类器，设置迭代次数为200，损失函数和评估指标均为“Accuracy”（准确率）。训练过程中不输出进度信息，选择最佳模型，并将任务类型设置为“CPU”。
• 模型在训练数据集上进行训练。如果评估指标在25轮迭代后没有提升，则进行提前停止。

4. 元模型训练：

• 与主要模型类似，但迭代次数为100，损失函数和评估指标均为“F1”。如果评估指标在15轮后没有提升，则进行提前停止。

5. 测试模型

• 使用test_model函数对训练好的模型进行测试，该函数返回R2指标的值。
• 如果得到的R2值为NaN，则将其替换为-1.0，并打印相应的消息。

6. 返回值：

• 函数返回一个列表，包含R2值、主模型和元模型。

这个特性是机器学习流程中的一部分，其中主要模型是在经过筛选的数据（假设其标签已经过验证或调整）上进行训练的，而元模型则用于预测选定的波动性集群。

整个算法是在一个循环中进行训练的：

该函数基于输入数据集，训练一个主模型和元模型。然后，它返回一个列表，该列表中包含R2值、主要模型和元模型。

# LEARNING LOOP
models = []
for i in range(1):
    data = meta_learner(5, 25, 2, 0.9, n_clusters=N_CLUSTERS, algorithm=6)
    for clust in data['clusters'].unique():
        print(f'Iteration: {i}, Cluster: {clust}')
        filtered_data = data.copy()
        filtered_data['clusters'] = filtered_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(filtered_data))

这段代码是一个循环训练，它使用meta_learner函数来对模型进行元训练（meta-train），然后根据得到的集群来训练最终的模型。以下是该算法的更详细描述：

1. 初始化模型列表：创建一个空的列表“models”，用于存储训练好的最终模型。

2. 运行循环训练程序：配置了一个for循环，其迭代次数为1（range(1)），这意味着整个过程将只执行一次。这通常是为了演示或测试目的而设置的，因为在实际应用中，由于学习算法的随机性，这些循环通常会使用更多的迭代次数。

3. 使用meta_learner进行元学习：调用meta_learner函数，并传入给定的参数：

• models_number=5: we use 5 basic models to meta-learning.
• iterations=25: each base model is trained with 25 iterations.
• depth=2: classifier tree depth for base models is set to 2.
• bad_samples_fraction=0.9: the fraction of wrongly flagged samples is 90%.
• n_clusters=N_CLUSTERS: the number of clusters for the clustering algorithm, where N_CLUSTERS must be defined in advance.
• algorithm=6: HDBSCAN clustering algorithm is used.

meta_learner函数返回一个更新后的数据集，该数据集包含了标签和已分配的集群。

4. 对唯一集群进行遍历：对于数据集中的每一个唯一集群，都会显示一条包含迭代次数和集群编号的消息。然后，对数据进行过滤，使得当前集群的所有记录都被标记为1，而其他所有记录都被标记为0。这为每个集群创建了一个二分类问题。

5. 训练最终模型：对于每个集群，都会调用fit_final_models函数，该函数基于过滤后的数据训练并返回一个模型。训练好的模型会被添加到models列表中。

这种方法允许你训练多个专业化的模型，每个模型都专注于一个特定的数据集群，这样便可以通过精确考虑不同数据组的特性来提高整体建模性能。

所有提出的聚类算法都是为了分析和确定市场状态。一些算法表现良好，而另一些则表现不佳。

下面是使用不同聚类算法得到的训练结果：

首先，我感兴趣的是聚类算法运行速度。经过测试，发现近邻传播（Affinity Propagation）、谱聚类（Spectral Clustering）、凝聚聚类（Agglomerative Clustering）和均值漂移（Mean Shift）算法的速度都非常慢，因此它们在排名中垫底。由于使用标准设置无法获得这些算法的聚类结果，所以这里并未展示它们的结果。

我在这个网站上找到了确认信息：

为了测试结果的信息量更丰富，我对整个训练过程进行了10次迭代，因为由于算法内部的随机性，不同训练迭代的结果会有所不同。

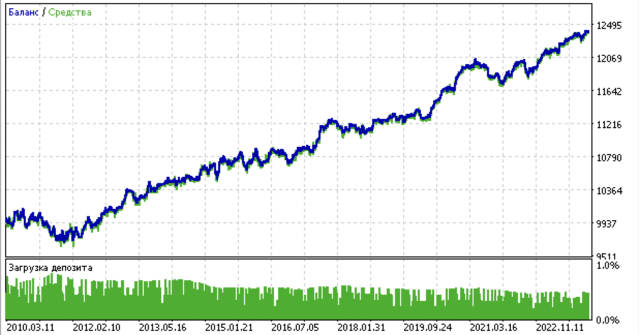
• 蓝色线条显示收益情况。
• 橙色线条是金融标的的图表（这里为 EURUSD）

1. 在剩下的四种算法中，我决定将HDBSCAN置于评级之首。它能够很好地分离数据，并且无需设置集群的数量。

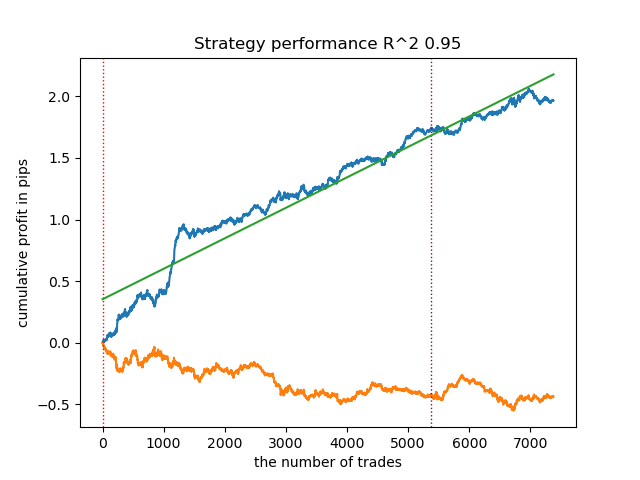
2. K-means算法表现良好，测试结果也相当不错。但缺点是它对聚类数量的敏感度高，在这个例子中，聚类数量被设定为十个。

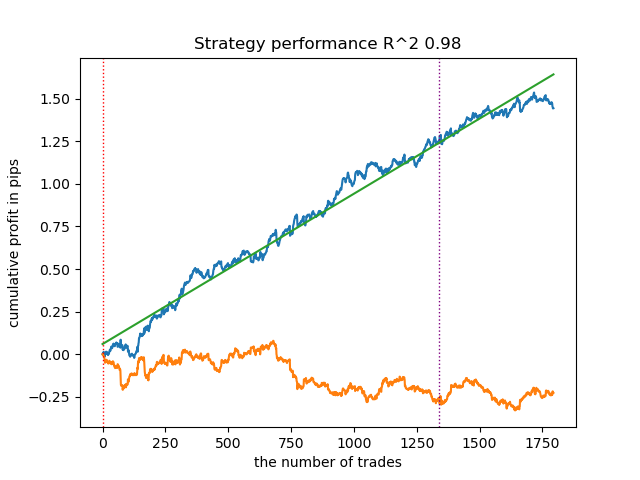
3. BIRCH算法表现良好，但其计算速度略慢于之前的算法。此外，它也不需要预先设定聚类数量。

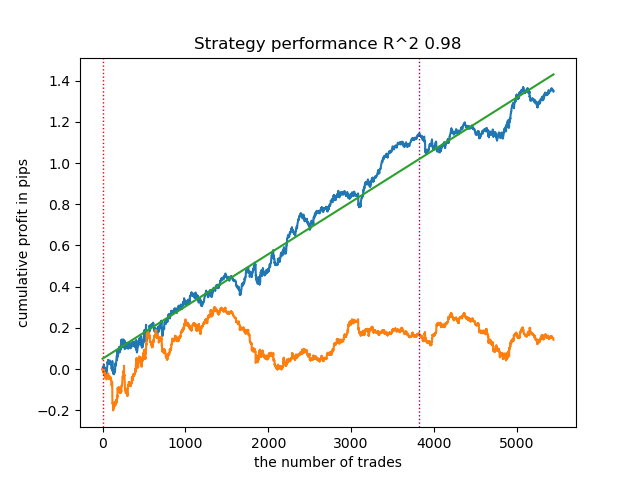
4. 高斯混合模型（Gaussian Mixture Model）完成了这次测试。在我看来，其测试结果似乎比其他聚类算法差。从视觉上看，这体现在一个“更嘈杂”的利润图上。与K-means算法一样，我们也定义了10个聚类。

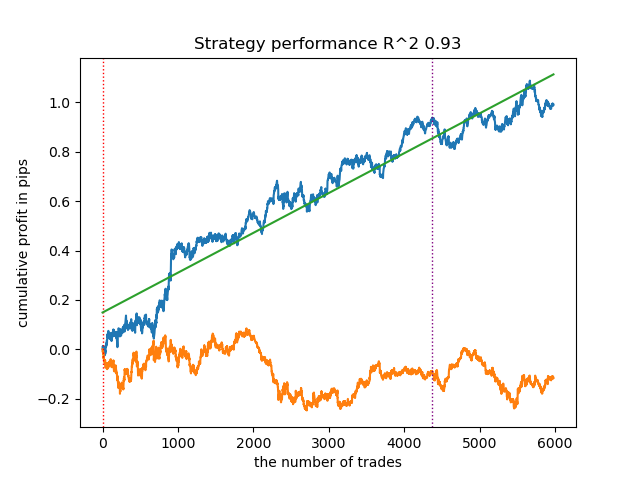
因此，根据所选的市场形态，我们可以得到不同的交易系统。在训练过程中，基于指定数量的聚类，每个市场形态都会显示模型测试结果。

聚类的质量受到输入参数集的影响。下面是我们使用的参数：

• 货币对。
• 时间框架
• 训练的起始和结束时间
• 主模型特征数量
• 元模型（波动性）的特征数量
• 聚类数量 n_clusters
• get_labels(min, max) 函数的 “min”和 “max” 参数

例如，这是使用以下参数得到的另一组聚类结果：

SYMBOL = 'EURUSD'
MARKUP = 0.00010
PERIODS = [i for i in range(10, 100, 10)]
PERIODS_META = [20]
BACKWARD = datetime(2019, 1, 1)
FORWARD = datetime(2023, 1, 1)
n_clusters = 40

def get_labels(dataset, min = 5, max = 5)

Timeframe = H1

由于聚类搜索算法也是随机的，因此多尝试运行几次。

使用聚类算法进行交易匹配：

我们进入最后一部分，这实际上是文章的主要内容。我想通过加入聚类元素来加深对因果推断的理解。这篇文章解释了什么是因果推断，而另一篇文章则讲述了通过倾向评分进行匹配。现在，让我们用我们自己的方法，即通过聚类进行匹配，来替代通过倾向评分进行匹配。为此，我们将使用第一篇文章中的算法并对其进行修改。

def meta_learners(models_number: int, iterations: int, depth: int, bad_samples_fraction: float, n_clusters: int):
    dataset = get_labels(get_prices())
    data = dataset[(dataset.index < FORWARD) & (dataset.index > BACKWARD)].copy()

    X = data[data.columns[1:-2]]
    y = data['labels']
    clusters = KMeans(n_clusters=n_clusters).fit(X[X.columns[0:1]]).labels_

    BAD_CLUSTERS = []
    for _ in range(n_clusters):
        sublist =  [pd.DatetimeIndex([]), pd.DatetimeIndex([])]
        BAD_CLUSTERS.append(sublist)

    for i in range(models_number):
        X_train, X_val, y_train, y_val = train_test_split(
            X, y, train_size = 0.5, test_size = 0.5, shuffle = True)
        
        # learn debias model with train and validation subsets
        meta_m = CatBoostClassifier(iterations = iterations,
                                depth = depth,
                                custom_loss = ['Accuracy'],
                                eval_metric = 'Accuracy',
                                verbose = False,
                                use_best_model = True)
        
        meta_m.fit(X_train, y_train, eval_set = (X_val, y_val), plot = False)
        
        coreset = X.copy()
        coreset['labels'] = y
        coreset['labels_pred'] = meta_m.predict_proba(X)[:, 1]
        coreset['labels_pred'] = coreset['labels_pred'].apply(lambda x: 0 if x < 0.5 else 1)
        coreset['clusters'] = clusters
        
        # add bad samples of this iteration (bad labels indices)
        coreset_b = coreset[coreset['labels']==0]
        coreset_s = coreset[coreset['labels']==1]

        for clust in range(n_clusters):
            diff_negatives_b = (coreset_b['labels'] != coreset_b['labels_pred']) & (coreset['clusters'] == clust)
            diff_negatives_s = (coreset_s['labels'] != coreset_s['labels_pred']) & (coreset['clusters'] == clust)
            BAD_CLUSTERS[clust][0] = BAD_CLUSTERS[clust][0].append(diff_negatives_b[diff_negatives_b == True].index)
            BAD_CLUSTERS[clust][1] = BAD_CLUSTERS[clust][
        1].append(diff_negatives_s[diff_negatives_s == True].index)

    for clust in range(n_clusters):
        to_mark_b = BAD_CLUSTERS[clust][0].value_counts()
        to_mark_s = BAD_CLUSTERS[clust][1].value_counts()
        marked_idx_b = to_mark_b[to_mark_b > to_mark_b.mean() * bad_samples_fraction].index
        marked_idx_s = to_mark_s[to_mark_s > to_mark_s.mean() * bad_samples_fraction].index
        data.loc[data.index.isin(marked_idx_b), 'meta_labels'] = 0.0
        data.loc[data.index.isin(marked_idx_s), 'meta_labels'] = 0.0

    return data[data.columns[1:]]

对于那些还没有读过我之前文章的读者，我将对该算法进行简要描述：

• 数据处理：
• 一开始，我们使用 get_prices() 和 get_labels() 函数获取数据集。上述函数分别返回价格信息和类标签。
• get_labels() 函数将价格数据与标签相关联，这是在处理与金融数据相关的机器学习任务中常见的操作。
• 然后，数据会被由FORWARD 和 BACKWARD常量定义的时间间隔过滤。
• 准备数据：
• 数据被分为特征(X)和标签(y)。
• 然后我们使用KMeans聚类算法来创建数据聚类。
• 模型训练：
• 在一个for循环中，我们用models_number定义模型数量。在每次迭代中，模型会在数据集的一半上进行训练（train_size = 0.5），并在另一半上进行验证（验证集）。
• 我们使用了带有特定参数的CatBoostClassifier模型。这种梯度提升方法专门设计用于处理分类特征。
• 请注意，该算法使用了自定义的损失函数“Accuracy”（准确率）和评估指标“Accuracy”（准确率）。这表明我们关注预测的准确性。
• 然后，我们应用元模型来评估和调整主模型的预测。这使我们能够考虑到主模型中可能存在的偏差或错误。
• 识别不良样本：
• 该算法创建了BAD_CLUSTERS列表，其中包含了每个聚类中不良样本数据的相关信息。不良样本被定义为模型对其做出大量错误的样本。
• 在每次训练迭代中，算法会识别出不良样本，并将其索引保存在相应的列表中。
• 元分析与校正：
• 上一步中识别出的不良样本的索引会被汇总，然后用于在主数据中标记对应的样本。
• 这有助于通过消除或校正不良样本来提高模型训练的质量。
• 返回数据：
• 该函数会返回处理后的数据，但不包括包含时间戳的第一列。

该算法旨在通过检测和校正不良样本，并使用元模型来考虑主模型中的错误，从而提高机器学习模型的质量。它较为复杂，需要仔细调整参数才能有效运行。

在提供的代码中，聚类算法以多种方式解释数据中的异质性：

• 识别数据聚类：
• 使用KMeans聚类算法可以将数据分成具有相似对象的组。每个聚类包含具有相似特征的数据。这在处理异质数据时特别有用，因为对象可能属于不同的类别或具有不同的结构。
• 分别分析和处理聚类：
• 每个聚类都与其他聚类分开处理，这使得我们可以考虑每个组内数据的特性和结构。这有助于理解数据的异质性，并使学习算法能够适应每个聚类中的特定条件。
• 聚类内的误差校正：
• 在训练模型后，会循环分析每个聚类中的不良样本。这些样本是模型对其做出大量错误的样本。这使得我们可以定位并专注于每个聚类内的误差校正，这比将整个数据应用相同的校正更为有效。
• 在元模型训练中考虑数据特征：
• 在训练元模型时，聚类算法也被用来识别聚类之间的差异。这使得元模型能够更好地适应数据的异质性，通过纳入每个聚类内数据结构的信息。

因此，聚类在解释数据异质性方面发挥着关键作用，使算法能够更有效地适应对象和数据结构的多样性。

模型训练结果如下。您可以看到，随着新数据的加入，模型变得更加稳定。

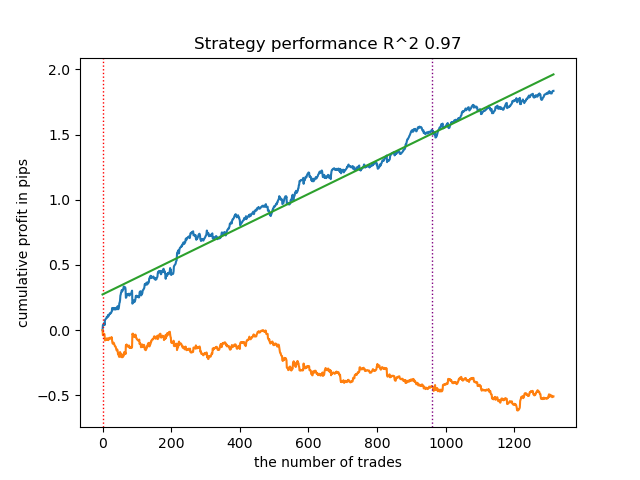
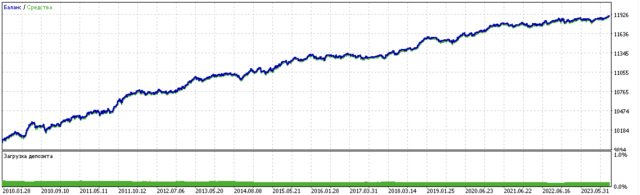
该模型可以导出为ONNX格式，并且与ONNX TraderEA完全兼容。

结论

在这篇文章中，我们讨论了关于时间序列聚类方法的原创思路。我测试了多种通过波动性聚类市场状态的算法。我发现，复杂的算法并不总是符合预期：有时，像K均值（K-means）这样简单且快速的聚类算法反而效果更好。同时，我也非常喜欢HDBSCAN算法。

在第二部分中，我们利用聚类算法来确定异质数据的处理效果。实验表明，将不良交易考虑在内，聚类算法可以降低波动（利润曲线变得更加平滑），并提高模型对新数据进行预测的能力。总的来说，这是一个相当复杂且深奥的课题，需要对众多参数进行配置来对算法进行微调。