利用箱形图（Boxplot）探索金融时间序列的季节性形态

尝试驳斥有效市场假说，并证明市场周期的存在

2013 年，尤金·法玛（Eugene Fama）开发了有效市场假设，并获得了诺贝尔经济学奖。 根据他的假设，资产价格能够完全反映所有重要信息。 这意味着没有任何一个市场参与者会比其人更具有优势。 

不过，假设本身有一些保留，而有效性可以具有以下三个程度：

• 如果市场资产价格充分反映了有关该资产的过去信息，则偏弱
• 当价格不仅反映过去，而且反映了当前公开信息，则较为平均
• 当它还反映了非公开的内部信息时，则偏强

取决于有效性程度，市场的可预测性也可拥有不同程度。 对于技术分析师而言，这意味着市场中可能存在不同的季节性周期成分。

例如，市场活动可能年年有别，月月有别，季季有别，时时有别，等等。 甚而，这些周期可以表现出某些可预测的顺序，在其内间或之间，交易者可以找到自己的出发点。 周期可以重叠，并创建不同的合成形态，这些都可以进一步探索。 

在价格增幅中搜索季节性形态

我们可以巡复合期研究常规周期。 我们来观察一个金融产品每月波动的研究示例。 为此目的，我们将 IPython 语言和 MetaTrader 5 终端结合利用。

为了从终端直接导入报价更加容易，我们会用到以下代码：

from MetaTrader5 import *
from datetime import datetime
import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt 
%matplotlib inline
import seaborn; seaborn.set()
# Initializing MT5 connection 
MT5Initialize("C:\\Program Files\\MetaTrader 5\\terminal64.exe")
MT5WaitForTerminal()

print(MT5TerminalInfo())
print(MT5Version())

指定您的终端路径，该路径可能与我的不同。

加入更多行来开始分析：

rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_D1, datetime(2010, 1, 1), datetime(2020, 1, 1)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)

# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
returns.head(5)

Monthly_Returns = returns.groupby([returns.index.year.rename('year'), returns.index.month.rename('month')]).mean()
Monthly_Returns.boxplot(column='close', by='month', figsize=(15, 8))

变量 rates 接收含有指定时间间隔（例如，在本示例中为 10 年）内的价格数据帧。 假设我们只对收盘价感兴趣（以此简化往后的解释）。 我们利用 rates.drop() 方法删除不必要的数据列。

随时间和形势趋势变化，价格距均值会有偏移，因此统计分析不适用于此类原始序列。 百分比计量价格变化（价格增幅）通常在计量经济学中使用，以确保它们都位于相同的数值范围内。 可以利用 pd.DataFrame(rates['close'].pct_change(1)) 方法接收百分比变化。

我们需要平均每月价格范围。 我们来安排表格，以便接收按年增幅的月度平均值，并将其显示在箱形图中。

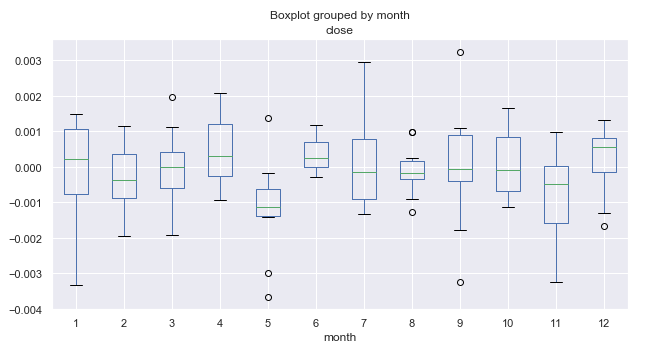
图例 1. 月度平均价格增幅，覆盖 10 年。

什么是箱形图，以及如何解释它们？

我们需要访问选定区间内的价格数据的波动性或其分布数据。 每个单独的箱形图（或箱须图）都能直观地展现数值如何沿数据集的分布。 不要把箱形图与烛条图混淆，尽管它们在外观上可能相似。 与烛条图不同，箱形图基于五种读数提供了一种显示数据分布的标准化方法。

1. 中位数，Q2 或第 50 的百分数显示数据集的平均值。 该值在图例中的箱内以绿色水平线示意。
2. 第一个四分位数，Q1（或第 25 的百分数）代表 Q2 和样本中最小值之间的中位数，该中位数落在 99％ 置信区间内。 它在图中显示为箱子的“实体”下边缘。
3. 第三个四分位数，Q3（或第 75 的百分数）是 Q2 和最大值之间的中位数，显示为箱子的“实体”上边缘。
4. 箱子的实体形成了四分位间距（介于 25％ 和 75％ 之间），也称为 IQR。
5. 箱子的须则充实了分布。 它们覆盖了整个样本的 99％，上方和下方的点表示超出 99％ 范围的数值。

该数据足以评估波动范围，和内部范围内的数值离散度。

进一步分析季节性形态

我们更详尽地研究图例 1。 我们可以看到，第五个月（五月份）的增幅中位数偏移到零轴下方，且其异常值显见高于零轴。 通常，从十年的统计数据里可以看出，五月份的市场相对于三月份有所下跌。 只有一个年份，五月份市场上涨。 这是一个有趣的思路，很符合交易者的格言“在五月份卖掉，并离开！”。

我们看一下五月份之后的六月份。 相对于五月份，六月份市场几乎总是（排除一年以外）在增长，这种情况每年都在重复。 六月份的波动范围很小，没有异常值（与五月份不同），这表明良好的季节性稳定。

请注意第 11 个月（十一月份）。 在此期间市场下跌的概率很高。 之后，在十二月份，市场通常会再度上行。 一月份（第一个月）的波动性很高，且相对于十二月份有所下跌。

所获得的数据可为交易决策提供很有用的基础条件概览。 而且，概率可以集成到交易系统当中。 例如，可以在某些月份执行更多的买卖操作。

月度周期数据非常有趣，但在较短的日线周期中能更深入地研究其可能性。

我们利用相同的 10 年度观察一周中每个单独交易日的价格增幅分布：

Daily_Returns = returns.groupby([returns.index.week.rename('week'), returns.index.dayofweek.rename('day')]).mean()

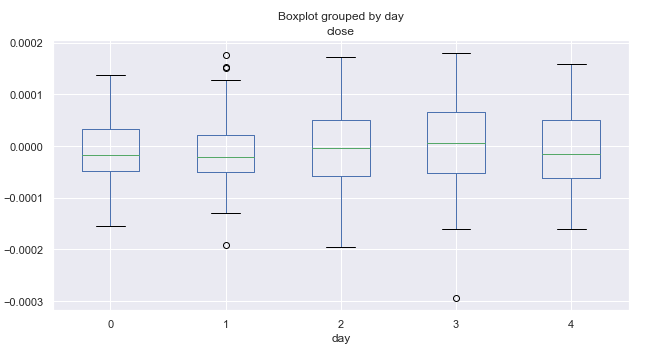
图例 2. 按交易日计的平均价格增幅，覆盖 10 年。

此处零对应于星期一，四则对应于星期五。 根据价格范围，按日波动率几乎保持不变。 然而不能据此得出结论，即在一周中的某个特定日期交易更为密集。 平均来说，市场在星期一和星期五时更倾向于下行非上行。 也许在一些单独的月份中，按日分布的样子会有所不同。 我们来执行附加分析。

# leave only one month "returns.index[~returns.index.month.isin([1])"
returns = returns.drop(returns.index[~returns.index.month.isin([1])])

在上面的代码中，1 表示一月份。 通过修改此值，我们可以从 10 年度里获得任意月份的统计信息。

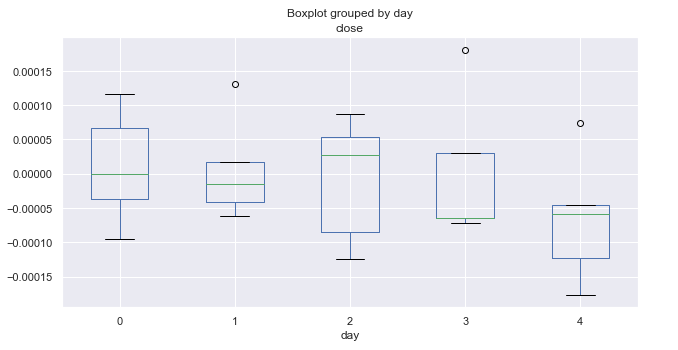
图例 3. 按交易日的平均价格增幅，覆盖 10 年（一月份）。

上图展示了一月份按日的增幅分布。 与所有月份的摘要统计相比，该图现在提供了更多有用的详细信息。 它清晰地表明，周五市场趋于下跌。 只有 EURUSD 货币对没有下跌（所示异常值高于零轴）。

此处是三月份的类似统计信息：

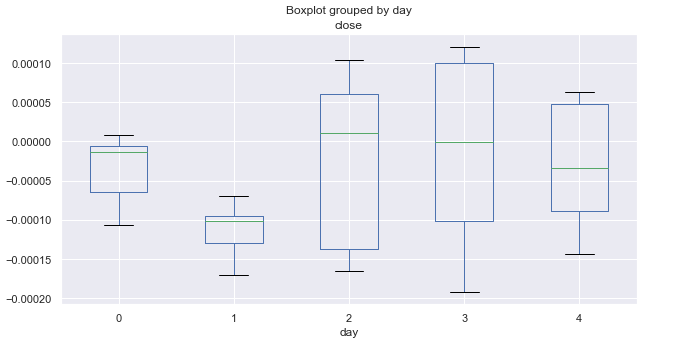
 图例 4. 按交易日的平均价格增幅，覆盖 10 年（三月份）。

三月份的统计数据与一月份的统计数据完全不同。 周一和周二（尤其是周二）表现出看跌趋势。 所有周二的收盘价都大幅下降，而其余的几天则在零轴附近波动（平均）。 

我们来看看十月份：

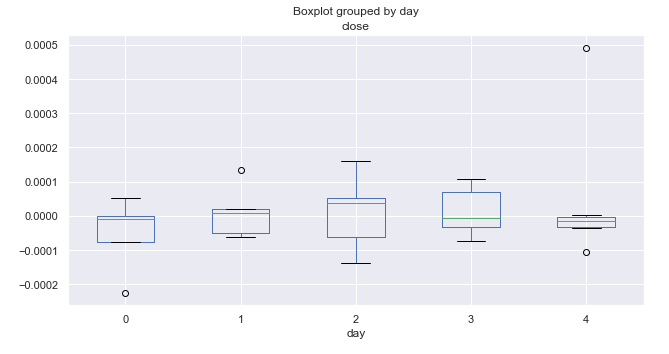
图例 5. 按交易日的平均价格增幅，覆盖 10 年（十月份）。

分析按星期的增幅分布没有发现任何突出的形态。 我们只能单挑出周三，这天的价格走势范围和潜力最大。 所有其他日子上行和下行走势的概率表现都相同，且有一些异常值。

季节性分析日内形态

在创建交易系统时，通常要考虑日内的分布，例如，除了日线和月线的分布，还要用到小时线数据。 这轻易就可做到。

研究每小时的价格增幅分布：

rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)

# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]

Hourly_Returns = returns.groupby([returns.index.day.rename('day'), returns.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(10, 5))

这些是 10 年度的 15 分钟时间帧报价。 另一个区别是，将数据按日和小时分组，以便得到子样本中所有交易日的小时统计中值。

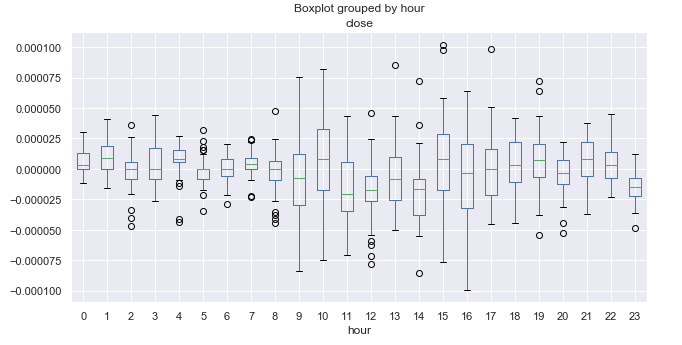
图例 6. 按小时计平均价格增幅，覆盖 10 年。

此处有必要知道终端的时区。 以我为例，其为 +2。 作为参考，我们的主要外汇交易时段的开盘和收盘时间写为 UTC+2。

时段	开盘价	收盘价
太平洋区	21.00	08.00
亚洲区	01.00	11.00
欧洲区	08.00	18.00
美洲区	14.00	00.00

太平洋时段的交易通常较平静。 如果观察箱子的大小，您会很容易注意到，在 21.00-08.00 之间范围最小，这与平静的交易相呼应。 在欧洲时段美洲时段开盘后，范围扩大，然后逐渐递减。 似乎没有明显的周期性形态，而这种形态在日线时间帧内却很明显。 平均增幅在零轴附近波动，且没有清晰的上行或下行的小时线。

一个有趣的区间是 23.00（每周时段收盘），在此区间价格通常相对于 22.00 降低。 这可以表示为交易时段收盘时的修正。 在 00.00 点时价格相对于 23.00 有所增长，因此可以将其视为规律性。 很难检测到更明显的周期，但是我们对价格范围有完整的全景，并且知道该时段的期望值。

用单个滞后造成增幅去趋势化，可以掩盖一些形态。 因此，按任意周期的移动均线来观察去趋势化数据是合理的。

按均线（MA）搜索去趋势化季节性形态

正确检测趋势分量非常棘手。 有时，时间序列可能会太平滑。 在这种情况下，交易信号极少。 如果缩短平滑周期，那么高频成交可能无法负担点差和佣金。 我们编辑代码，以便利用移动平均线进行去趋势化：

rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
rates = rates.set_index('time')
# set the moving average period
window = 25
# detrend tome series by MA
ratesM = rates.rolling(window).mean()
ratesD = rates[window:] - ratesM[window:]

plt.figure(figsize=(10, 5))
plt.plot(rates)
plt.plot(ratesM)

移动平均周期设置为 25。 所需参数作为收盘价的时间周期，参数值可更改。 我使用 15 分钟时间帧。 结果就是，我们得到了小时收盘价与 15 分钟移动平均线之间的平均偏差。 这是结果时间序列：

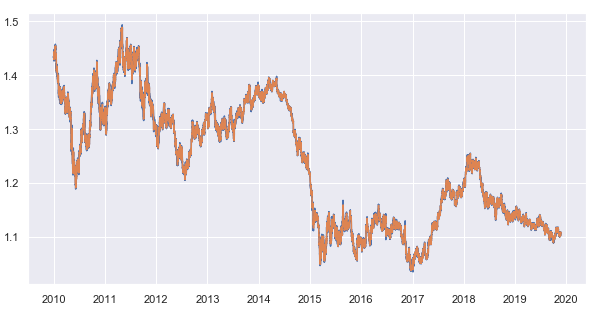
图例 7. 15 分钟时间帧的收盘价和 25 周期的移动平均线

从收盘价中减去移动平均线值，得到一个去趋势化的时间序列（余数）：

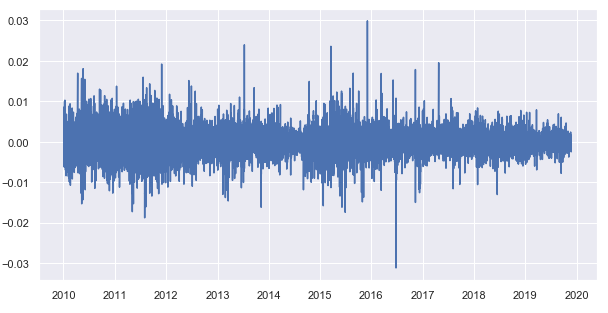
图例 8. 自收盘价减去移动平均数的余数

现在，我们得到每个交易小时的余数分布小时统计信息：

Hourly_Returns = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(15, 8))

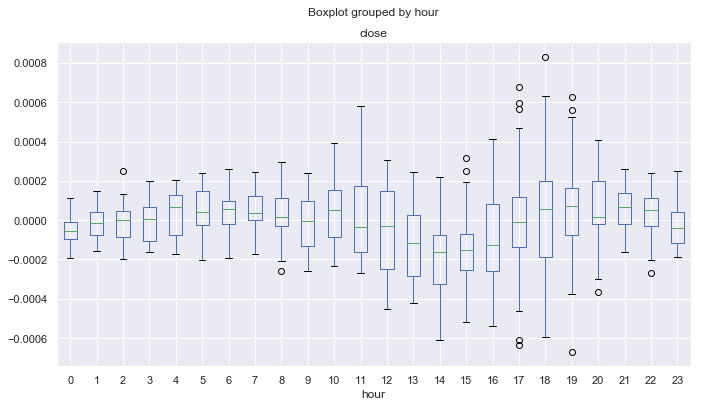
图例 9. 按小时计平均价格增幅，覆盖 10 年，按 25 周期均线去趋势化。

与图例 6 不同，创建的价格增幅有单次滞后，该图例展示的异常值更少，并揭示出更多的周期形态。 例如，您可以看到从 0.00 点到 08.00 点（太平洋时段），价格通常相对于移动平均线平稳上涨。 而在 12.00 点至 14.00 点，可定义为下降趋势。 此后，在美洲时段，价格高于均线上涨。 太平洋时段开盘后，价格自 21.00 点开始持续下跌 4 个小时。

下一个合乎逻辑的步骤是仔细检查分布矩，以便获得更准确的统计评估。 例如，以箱形图的形式计算得到的去趋势化序列的标准差：

Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).std()

                                                                                       

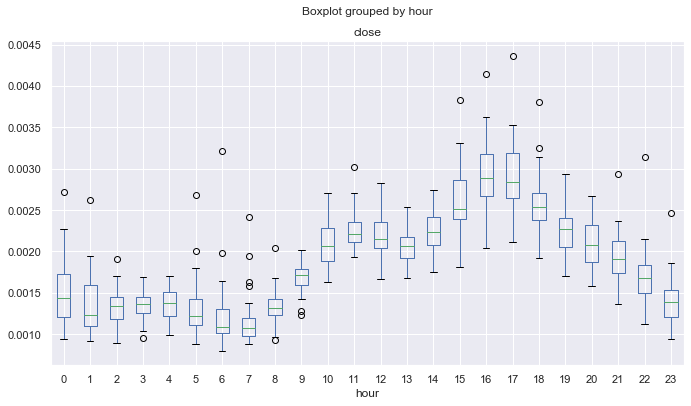
图例 10. 按小时计价格增幅的平均标准偏差，覆盖 10 年，按 25 周期均线去趋势化。

从图例 10 展示出的距数学期望的标准差来看，小时线有最稳定的价格行为。 例如，在所有交易日中，于 4 点、13 点、14 点、19 点都有稳定的分散，这对均值回归策略可能很有吸引力。 其他时间可能会有异常值和较长的胡须，这表明在不同交易日里波动性更大。

另一个有趣的点是不对称系数。 我们计算一下：

Hourly_skew = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).skew()

 

图例 11. 按小时数计价格增幅的平均不对称系数，覆盖 10 年，按 25 周期均线去趋势化。

接近零周和较小的分散度表示增幅分布更“标准”。 此处的图表形式变为凹形。 例如，尽管欧美时段的波动较大（图例 9），但它们的小时分布更稳定且偏差较小，这与太平洋时段和亚洲时段不同。 这也许是由于过去的两个交易日内活动大幅波动所致，当突然的波动取代了几乎为零的交易活动之时，会很大程度上造成分布偏差。

超量的统计数据显示类似的结果：

Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).apply(pd.DataFrame.kurt)

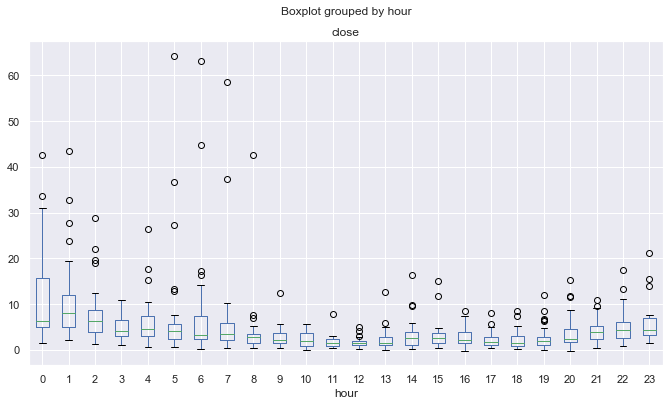
图例 12. 按小时计价格增幅的平均超量系数，覆盖 10 年，按 25 周期均线去趋势化。

由于上述可能的影响，对于波动性较大的交易时段，分布的峰值较少，“常规”更多；而对于平静的交易时段则是“非常规”。 这有点自相矛盾。

搜索特定月份或一周中某天的季节性形态，按均线去趋势化

我们可以观察到每个单独月份的去趋势化小时线价格分布，以及一周中的每一天。 完整的代码可在下面的附件中找到。 在此，我仅提供三月份和十一月份之间的比较。

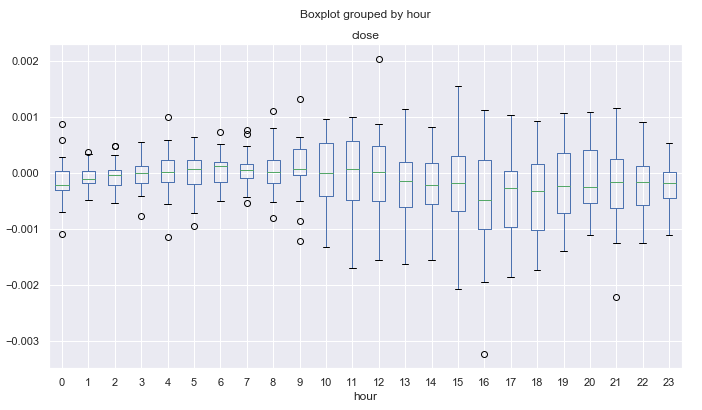
图例 13. 按小时计三月份平均价格增幅，覆盖 10 年，按 25 周期的移动平均去趋势化。

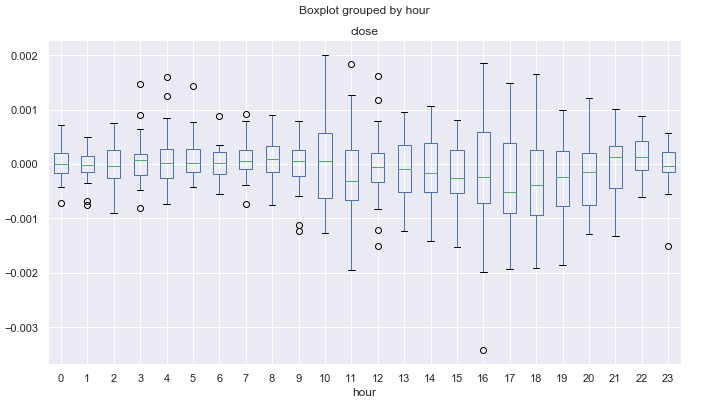
图例 14. 十一月份按小时计平均价格增幅，覆盖 10 年，按 25 周期的移动平均去趋势化。

搜索更小的日内周期也是可能的，包括即时报价数据，但是在这里，我们仅处理基本的季节性形态，根据交易员的观点，这些季节性形态也许存在于金融时间序列中。 考虑到金融产品的季节性特征，您也许可利用此数据开发自己的交易系统。  

利用交易逻辑检查形态

我们创建一个简单的智能交易系统，该工具将采用图例 9 中所示的形态。 它展示自 0.00 点到 04.00 点（GMT+2）四个小时内，EURUSD 价格相对于其平均价格的上涨。

//+------------------------------------------------------------------+
//|                                              Seasonal trader.mq5 |
//|                                  Copyright 2020, Max Dmitrievsky |
//|                        https://www.mql5.com/en/users/dmitrievsky |
//+------------------------------------------------------------------+
#property copyright "Copyright 2020, Max Dmitrievsky"
#property link      "https://www.mql5.com/en/users/dmitrievsky"
#property version   "1.00"

#include <MT4Orders.mqh>
#include <Trade\AccountInfo.mqh>
#include <Math\Stat\Math.mqh>

input int OrderMagic = 666;
input double   MaximumRisk=0.01;
input double   CustomLot=0;

int hnd = iMA(NULL, 0, 25, 0, MODE_SMA, PRICE_CLOSE);
MqlDateTime hours;
double maArr[], prArr[];

void OnTick()
  {
//---
      CopyBuffer(hnd, 0, 0, 1, maArr);
      CopyClose(NULL, 0, 0, 1, prArr);
      double pr = prArr[0] - maArr[0];
      
      TimeToStruct(TimeCurrent(), hours);
      if(hours.hour >=0 && hours.hour <=4)
         if(countOrders(0)==0 && countOrders(1)==0)
            if(pr < -0.0002) OrderSend(Symbol(),OP_BUY,0.01,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN);
            
      if(countOrders(0)!=0 && pr >=0)
         for(int b=OrdersTotal()-1; b>=0; b--)
            if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) {
               if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
            }
         
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int countOrders(int a) {
   int result=0;
   for(int k=0; k<OrdersTotal(); k++) {
      if(OrderSelect(k,SELECT_BY_POS,MODE_TRADES)==true)
         if(OrderType()==a && OrderMagicNumber()==OrderMagic && OrderSymbol() == _Symbol) result++;
   }
   return(result);
}

移动平均线的运用与统计评估相同。 其周期也为 25。 从最近的已知价格中减去平均值，然后检查当前交易时间是否在 0:00 点到 4:00 点之间。 从图例 9 中可见，此期间收盘价和移动平均线之间的最大偏差等于 -0.0002，且均线高于零轴。 相应地，我们的交易逻辑是在达到此差值时开立多头成交，并在其收敛至零轴时平仓。 测试机器人没有任何停止订单或其他检查，仅用于测试找到的形态。 在 2015 年到 2019 年区间进行测试，15 分钟时间帧（我们的研究中也均线也在此时间帧里创建），每次即时报价模式：

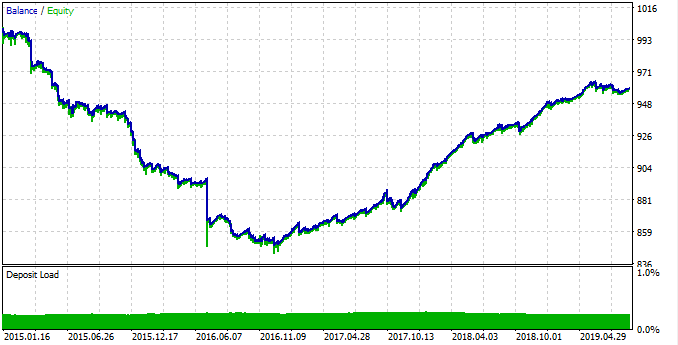
图例 15. 测试找到的形态。

从 2015 年到 2017 年，该形态效果不佳，图表也是下行。 然后，从 2017 年到 2019 年表现出稳定的增长。 因何如此？ 为了理解它，我们来分别观察每个时间间隔的统计信息。

首先，是获利的交易间隔：

rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2017, 1, 1), datetime(2019, 11, 25)), 
                     columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])

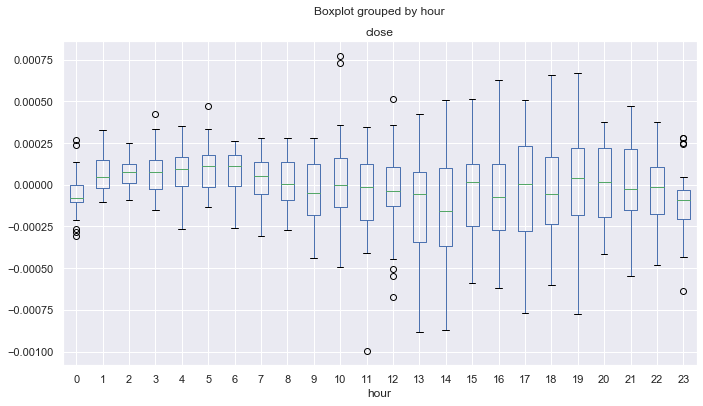
图例 16. 2017-2019 的统计。

可以看出，相对于移动平均线，所有小时的中位数（零除外）均大于零轴。 统计原点在我们的交易系统一侧，并且该系统平均保持利润。 现在，这是 2015-2017 年的分布。

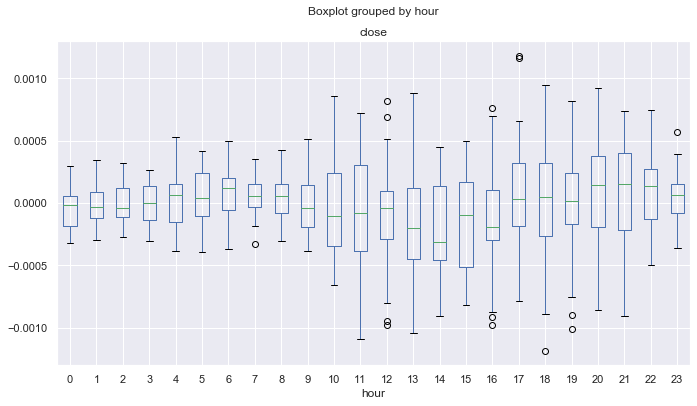
图例 17. 2015-2017 的统计。

在此，除第四小时外，所有的小时分布中值均小于或等于零，这意味着获利可能性较小。 另外，同其他时间间隔相比，盒子的平均范围明显更大，其最小值不小低于 -0.00025。 在此，它几乎为 -0.0005。 另一个缺点是仅以收盘价评估分布，因此未考虑价格尖峰。 这可通过分析即时报价数据来修复，但这不在本文的讨论范围之内。 差异很明显，因此您可以尝试对系统进行微调，以便令所有年份的结果保持平衡。

我们只允许在 0-1 点的时间开放交易。 因此，我们假设在接下来的几个小时内该交易会以盈利平仓，因为平均偏差趋向于朝正方向迈进。 另外，将成交平仓阈值从 0.0 提高到 0.0003，因此机器人可以赚取更多潜在利润。 修改展示在以下代码中：

TimeToStruct(TimeCurrent(), hours);
      if(hours.hour >=0 && hours.hour <=1)
         if(countOrders(0)==0 && countOrders(1)==0)
            if(pr < -0.0004) OrderSend(Symbol(),OP_BUY,LotsOptimized(), SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN);
            
      if(countOrders(0)!=0 && pr >= 0.0003)
         for(int b=OrdersTotal()-1; b>=0; b--)
            if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) {
               if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {};
            }

我们测试一下机器人，得出最终结论：

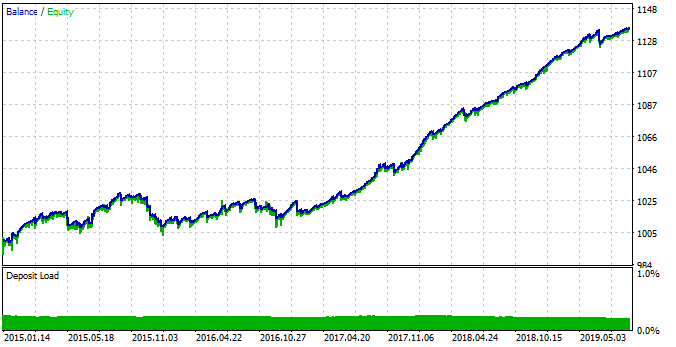
图例 18. 按照更改的 EA 参数测试检测到的形态。

这次系统在 2015 年至 2017 年的时间间隔内更加稳定。 然而，由于季节性形态的变化，该区间的有效性不如 2017 年至 2019 年。 此行为与市场的根本变化有关，这些也可利用箱形图轻松描述。

当然，仍然有许多未探索的形态，但是这个基本示例说明了，运用这种技术能开创新奇有趣的可能性。

结束语

本文介绍了检测金融时间序列中季节性形态的建议统计方法。 市场可能会有月度季节性周期，以及依据月份的日内周期。 小时分析显示，按照某些平滑周期（例如，移动平均线），您可以在交易时段内，以及从一个交易时段转移到另一个时搜索到某些周期性。

该方法的优点之一是可以运用特定的市场形态，并且不存在过度优化（参数过度拟合）的情况，因此交易系统高度稳定。

至于说缺点，季节性形态挖掘过程并不轻松，并且涉及各种组合和周期的操作。

针对 EURUSD 货币对执行分析，时间间隔为 10 年。 Python 源代码附在本文的末尾，格式为 .ipynb （Jupyter notebook）。 您可以利用随附的函数库这对任何所需的金融产品进行同样的研究，然后将获得的结果应用于创建自己的交易系统，或改善现有交易系统。