网格和马丁格尔交易系统中的机器学习。 您敢为其打赌吗？

概述

我们曾努力研究各种运用机器学习的方式，旨在发现外汇市场中的形态。 您已经知道如何训练模型并实现它们。 但还有很多交易方式，几乎每种方法都可以通过运用现代机器学习算法进行改进。 其中最流行的算法之一就是网格和/或马丁格尔。 在撰写本文之前，我做了一些探索性分析，在互联网上搜索相关信息。 令人惊讶的是，这种方法在全球网络中难觅踪迹。 我在社区成员中发起了一次有关此解决方案前景的调查，大多数人回答说他们甚至不知道如何入手该主题，但是这个想法听起来很有趣。 虽然，这个思路本身似乎很简单。

我们抱着两个目的来进行一系列实验。 首先，我们将尝试证明它并不像乍看起来那样困难。 其次，我们将尝试找出这种方式是否实用和有效。 

成交贴标签

主要任务是正确地为成交贴标签。 我们还记得以前文章中如何处理单一仓位的。 我们设置了随机或确定性的成交边际，例如，15 根柱线。 如果行情在这 15 根柱线上都在上涨，则该成交被贴上标签“买入”，否则被贴上标签“卖出”。 类似的逻辑也运用在订单网格，但是此处必须考虑一组持仓的总盈利/亏损。 这可以用一个简单的例子来阐述。 作者会尽力描绘蓝图。

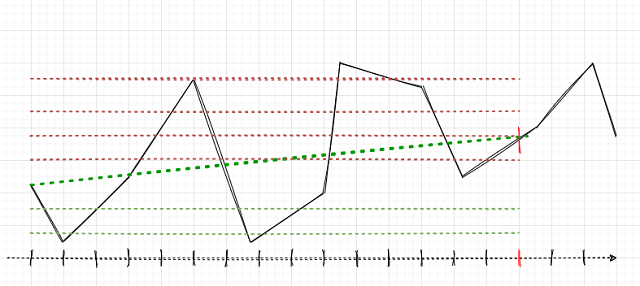
假设交易边际是15（十五）根柱线（在传统时间标尺上以垂直线标记的红色笔划）。 如果只有一笔持仓，由于行情已从一个点位上涨到另一个点位，故它将被贴上标签“买入”（绿色点划斜线）。 行情在此处显示为黑色折线。

有了这样的标签，过渡行情的波动即被忽略了。 如果我们运用订单网格（红色和绿色水平线），则必须计算所有已触发挂单的总利润，包括自最初开始的订单（您可在同一方向上开仓布局网格；或者选择放置挂单网格，无需即刻开仓）。 针对学习历史的整个深度，在滑动窗口中持续如此贴标签。 ML（机器学习）的任务是归纳各种状况，并基于新数据有效地预测（如果可能）。

在这种情况下，也许会有若干个选项用于选择交易方向，并为数据贴标签。 如何选择在此即是哲学也是实验任务。

• 依据最大总利润进行选择。 如果“卖出”网格产生更多的利润，则为该网格贴标签。
• 在持单数量和总利润之间进行加权选择。 如果网格中每笔持单的平均利润高于逆向的平均利润，则选择该边。
• 依据已触发订单的最大数量进行选择。 由于所期望的机器人应遵照网格交易，该选项看起来很合理。 如果已触发订单数量最大，且总仓位处于获利状态，则选择此侧。 这一侧代表网格的方向（卖出或买入）。

这三条准测对于开始似乎已经足够了。 我们来详细研究第一个，因为它是最简单的一个，旨在获得最大的利润。

在代码中为成交贴标签

现在我们回想一下以前文章中如何为成交贴标签。

def add_labels(dataset, min, max):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]
        
        if future_pr + MARKUP < curr_pr:
            labels.append(1.0)
        elif future_pr - MARKUP > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2].index).reset_index(drop=True)
    return dataset

该代码需要针对常规网格和马丁格尔网格进行归纳。 另一个令人兴奋的功能是，您可以浏览含有不同数量订单的网格，订单之间的距离不同，甚至可以运用马丁格尔（手数递增）。

为此，我们添加全局变量，以后可用它来优化。

GRID_SIZE = 10
GRID_DISTANCES = np.full(GRID_SIZE, 0.00200)
GRID_COEFFICIENTS = np.linspace(1, 3, num= GRID_SIZE)

GRID_SIZE 变量里包含双向订单的数量。

GRID_DISTANCES 设置订单之间的距离。 距离可以是固定的，亦或可变的（对于所有订单而言各有不同）。 这将有助于提升交易系统的灵活性。

GRID_COEFFICIENTS 变量包含每笔订单的手数乘数。 如果它们是常数，则系统将创建规则的网格。 如果手数不同，那么它会是马丁格尔或逆马丁格尔，或任何其他运用不同手数乘数的网格名称。

对于那些刚接触 numpy 函数库的人：

• np.full 用指定数量的相同值填充数组
• np.linspace 用指定数量的值填充数组，其值均匀地分布在两个实数之间。 在上面的示例中，GRID_COEFFICIENTS 将包含以下内容。

array([1.        , 1.22222222, 1.44444444, 1.66666667, 1.88888889,
       2.11111111, 2.33333333, 2.55555556, 2.77777778, 3.        ])

相应地，第一个手数乘数将等于 1，因此该手数将等于交易系统参数中指定的基本手数。 在以后的网格里订单手数乘数连续从 1 到 3。 若在网格里的所有订单采用固定乘数，则需调用 np.full。 

统计已触发和未触发订单可能有些棘手，故此我们需要创建某种数据结构。 我决定创建一本字典来保存每个特定案例（样本）的订单和仓位记录。 取而代之，我们可以利用数据类对象，熊猫数据框架或 numpy 结构化数组。 最后的解决方案，很可能是最快的，但在此它并不要紧。

每次迭代将样本添加到训练集合当中，并创建有关的订单网格信息，保存在字典里。 这可能需要一些解释。 grid_stats 字典包含有关当前订单网格从打开到平仓的所有必需信息。 

def add_labels(dataset, min, max, distances, coefficients):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        all_pr = dataset['close'][i:i + rand + 1]

        grid_stats = {'up_range': all_pr[0] - all_pr.min(),
                      'dwn_range': all_pr.max() - all_pr[0],
                      'up_state': 0,
                      'dwn_state': 0,
                      'up_orders': 0,
                      'dwn_orders': 0,
                      'up_profit': all_pr[-1] - all_pr[0] - MARKUP,
                      'dwn_profit': all_pr[0] - all_pr[-1] - MARKUP
                      }

        for i in np.nditer(distances):
            if grid_stats['up_state'] + i <= grid_stats['up_range']:
                grid_stats['up_state'] += i
                grid_stats['up_orders'] += 1
                grid_stats['up_profit'] += (all_pr[-1] - all_pr[0] + grid_stats['up_state']) \
                * coefficients[int(grid_stats['up_orders']-1)]
                grid_stats['up_profit'] -= MARKUP * coefficients[int(grid_stats['up_orders']-1)]

            if grid_stats['dwn_state'] + i <= grid_stats['dwn_range']:
                grid_stats['dwn_state'] += i
                grid_stats['dwn_orders'] += 1
                grid_stats['dwn_profit'] += (all_pr[0] - all_pr[-1] + grid_stats['dwn_state']) \
                * coefficients[int(grid_stats['dwn_orders']-1)]
                grid_stats['dwn_profit'] -= MARKUP * coefficients[int(grid_stats['dwn_orders']-1)]
        
        if grid_stats['up_profit'] > grid_stats['dwn_profit'] and grid_stats['up_profit'] > 0:
            labels.append(0.0)
            continue
        elif grid_stats['dwn_profit'] > 0:
            labels.append(1.0)
            continue
        
        labels.append(2.0)

    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2].index).reset_index(drop=True)
    return dataset

all_pr 变量包含从当前到未来的价格。 需要计算网格本身。 为了构建网格，我们想知道从第一根到最后一根柱线的价格范围。 这些值包含在 “up_range” 和 “dwn_range” 字典条目当中。 变量 “up_profit” 和 “dwn_profit” 将包含当前历史片段中的 “买入” 或 “卖出” 网格所获得的最终利润。 这些数值的初始值，来自最初开仓的一笔成交中获得的利润。 然后，如果网格挂单被触发，所有开单成交均会汇总。

现在，我们需要遍历所有 GRID_DISTANCES，并检查是否触发了挂单。 如果订单处于 up_range 或 dwn_range 范围内，则该订单已被触发。 在这种情况下，我们增加相应的 up_state 和 dwn_state 计数器，这些计数器存储最后一次激活订单的级别。 在下一次迭代中，网格中距新订单的距离会被添加到该级别 - 如果该订单在价格范围内，则它也已被触发。

所有已触发的订单均要编写附加信息。 例如，挂单的利润被添加到总数值之中。 对于买入仓位，此利润采用以下公式计算。 此处，用仓位的最后价格（应该是该仓位的平仓价）减去开仓价格，加上与系列中所选挂单的距离，并将结果乘以网格中该订单的手数乘数。 卖出订单则是逆计算。 累积的标记则会另外计算。 

grid_stats['up_profit'] += (all_pr[-1] - all_pr[0] + grid_stats['up_state']) \
                * coefficients[int(grid_stats['up_orders']-1)]
grid_stats['up_profit'] -= MARKUP * coefficients[int(grid_stats['up_orders']-1)]

下一个代码模块检查买入和卖出网格的利润。 参考累计的标记，若利润大于零，且是最大值，则将相应的样本添加到训练集合当中。 如果不满足任何条件，则添加 2.0 标记 - 带有该标记的样本将从训练数据集合中删除，因为这代表它们是无用的。 这些条件可以以后更改，取决于所期望网格的构建选项。

升级测试器以便能操控订单网格 

为了正确地计算来自网格交易中获得的利润，我们需要修改策略测试器。 我决定令其类似于 MetaTrader 5 测试器，如此它即可顺序地遍历报价历史，并像真实交易一样开仓和平仓。 这样可以提升对代码的理解，并避免以后有所遗漏。 我将重点介绍代码的要点。 我不会在这里提供测试器旧版，但是您可以在我以前的文章中找到它。 我猜测有些读者可能不理解下面的代码，因为他们想快点拿到圣杯，不想啰嗦。 然而，关键点应予以澄清。

def tester(dataset, markup, distances, coefficients, plot=False):
    last_deal = int(2)
    all_pr = np.array([])
    report = [0.0]
    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        all_pr = np.append(all_pr, dataset['close'][i])

        if last_deal == 2:
            last_deal = 0 if pred <= 0.5 else 1
            continue

        if last_deal == 0 and pred > 0.5:
            last_deal = 1
            up_range = all_pr[0] - all_pr.min()
            up_state = 0
            up_orders = 0
            up_profit = (all_pr[-1] - all_pr[0]) - markup
            report.append(report[-1] + up_profit)
            up_profit = 0
            for d in np.nditer(distances):
                if up_state + d <= up_range:
                    up_state += d
                    up_orders += 1
                    up_profit += (all_pr[-1] - all_pr[0] + up_state) \
                    * coefficients[int(up_orders-1)]
                    up_profit -= markup * coefficients[int(up_orders-1)]    
                    report.append(report[-1] + up_profit)
                    up_profit = 0
            all_pr = np.array([dataset['close'][i]])
            continue

        if last_deal == 1 and pred < 0.5:
            last_deal = 0
            dwn_range = all_pr.max() - all_pr[0]
            dwn_state = 0
            dwn_orders = 0
            dwn_profit = (all_pr[0] - all_pr[-1]) - markup
            report.append(report[-1] + dwn_profit)
            dwn_profit = 0
            for d in np.nditer(distances):
                if dwn_state + d <= dwn_range:
                    dwn_state += d
                    dwn_orders += 1
                    dwn_profit += (all_pr[0] + dwn_state - all_pr[-1]) \
                    * coefficients[int(dwn_orders-1)]
                    dwn_profit -= markup * coefficients[int(dwn_orders-1)] 
                    report.append(report[-1] + dwn_profit)
                    dwn_profit = 0
            all_pr = np.array([dataset['close'][i]])   
            continue

    y = np.array(report).reshape(-1, 1)
    X = np.arange(len(report)).reshape(-1, 1)
    lr = LinearRegression()
    lr.fit(X, y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.figure(figsize=(12,7))
        plt.plot(report)
        plt.plot(lr.predict(X))
        plt.title("Strategy performance")
        plt.xlabel("the number of trades")
        plt.ylabel("cumulative profit in pips")
        plt.show()

    return lr.score(X, y) * l

纵观历史，网格交易者仅对余额曲线感兴趣，而往往忽视净值曲线。 因此，我们将坚持这一传统，且不会令我们复杂的测试仪变得过于复杂。 我们将仅显示余额图形。 进而，净值曲线可始终在 MetaTrader 5 终端中查看。 

我们循环遍历所有价格，并将它们添加到数组 all_pr。 此外，上面标记了三个选项。 由于以前的文章中已经讨论过该测试器，因此，我仅解释出现相反信号时网格平单的选项。 就像在为成交贴标签时一样，up_range 变量存储按平仓时间的价格范围。 接下来，计算第一笔仓位（按市价开仓）的利润。 然后，循环检查是否存在已触发挂单。 如果有，则将其结果添加到余额图形中。 卖出订单/仓位也需执行相同的操作。 因此，余额图形反映的是所有已平仓位，而不是一组的总利润。 

测试操控订单网格的新方法

我们已经很熟悉如何为机器学习准备数据。 首先获取价格和一套功能，然后为数据贴标签（创建“买入”和“卖出”标签），然后在自定义测试器中检查标签。

# Get prices and labels and test it

pr = get_prices(START_DATE, END_DATE)
pr = add_labels(pr, 15, 15, GRID_DISTANCES, GRID_COEFFICIENTS)
tester(pr, MARKUP, GRID_DISTANCES, GRID_COEFFICIENTS, plot=True)

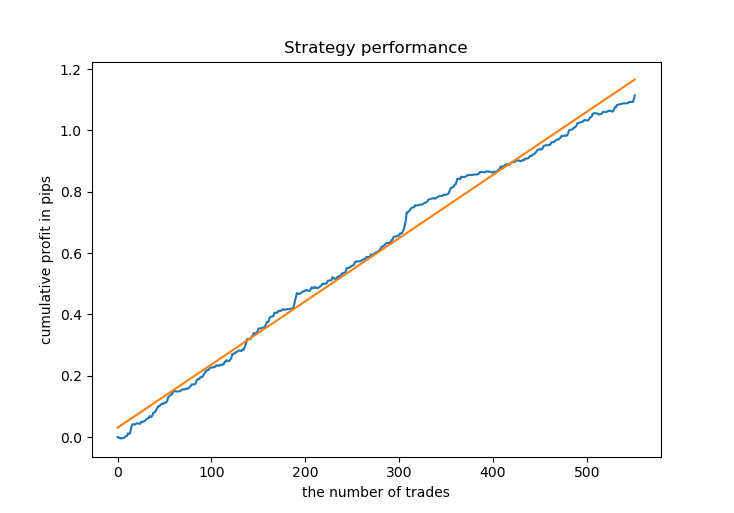
现在，我们需要训练 CatBoost 模型，并依据新数据对其进行测试。 由于其效果良好，我决定再次依据高斯混合模型生成的合成数据进行训练。

# Learn and test CatBoost model

gmm = mixture.GaussianMixture(
    n_components=N_COMPONENTS, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])
res = []
for i in range(10):
    res.append(brute_force(10000))
    print('Iteration: ', i, 'R^2: ', res[-1][0])
res.sort()
test_model(res[-1])

在此示例中，我们将依据 10,000 个生成的样本上训练 10 个模型，并通过 R^2 分数选择最佳的一个模型。 学习过程如下。

Iteration:  0 R^2:  0.8719436661855786
Iteration:  1 R^2:  0.912006346274096
Iteration:  2 R^2:  0.9532278725035132
Iteration:  3 R^2:  0.900845571741786
Iteration:  4 R^2:  0.9651728908727953
Iteration:  5 R^2:  0.966531822300101
Iteration:  6 R^2:  0.9688263099200539
Iteration:  7 R^2:  0.8789927823514787
Iteration:  8 R^2:  0.6084261786804662
Iteration:  9 R^2:  0.884741078512629

大多数模型在新数据上的 R^2 分数都很高，这表明该模型具有很高的稳定性。 这是训练数据和训练外数据的余额图结果。

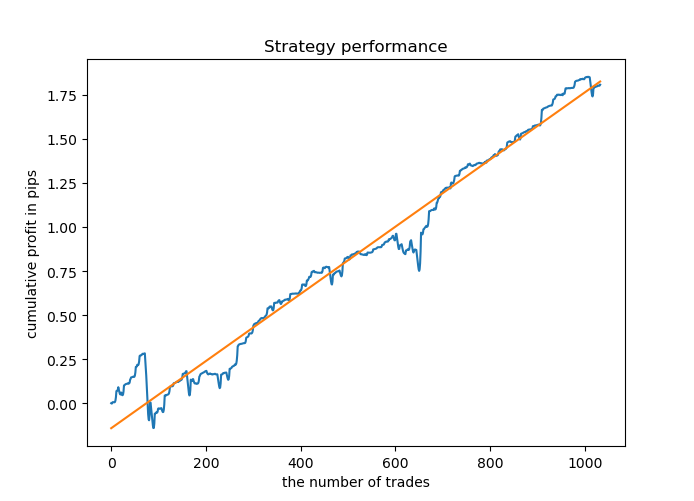
看起来不错。 现在，我们可以导出经过 MetaTrader 5 训练的模型，并在终端测试器中检查其结果。 在测试之前，有必要准备智能交易系统，并包含文件。 每个训练过的模型都有其自己的文件，因此可以轻松存储和更改它们。

把 CatBoost 模型导出到 MQL5

调用以下函数来导出模型。

export_model_to_MQL_code(res[-1][1])

该函数已稍作修改。 针对修改的解释如下。

def export_model_to_MQL_code(model):
    model.save_model('catmodel.h',
                     format="cpp",
                     export_parameters=None,
                     pool=None)

    # add variables
    code = '#include <Math\Stat\Math.mqh>'
    code += '\n'
    code += 'int MAs[' + str(len(MA_PERIODS)) + \
        '] = {' + ','.join(map(str, MA_PERIODS)) + '};'
    code += '\n'
    code += 'int grid_size = ' + str(GRID_SIZE) + ';'
    code += '\n'
    code += 'double grid_distances[' + str(len(GRID_DISTANCES)) + \
        '] = {' + ','.join(map(str, GRID_DISTANCES)) + '};'
    code += '\n'
    code += 'double grid_coefficients[' + str(len(GRID_COEFFICIENTS)) + \
        '] = {' + ','.join(map(str, GRID_COEFFICIENTS)) + '};'
    code += '\n'

    # get features
    code += 'void fill_arays( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(MAs)-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_CURRENT,1,MAs[i],pr);\n'
    code += '       double mean = MathMean(pr);\n'
    code += '       ret[0] = pr[MAs[i]-1] - mean;\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    # add CatBosst
    code += 'double catboost_model' + '(const double &features[]) { \n'
    code += '    '
    with open('catmodel.h', 'r') as file:
        data = file.read()
        code += data[data.find("unsigned int TreeDepth")
                               :data.find("double Scale = 1;")]
    code += '\n\n'
    code += 'return ' + \
        'ApplyCatboostModel(features, TreeDepth, TreeSplits , BorderCounts, Borders, LeafValues); } \n\n'

    code += 'double ApplyCatboostModel(const double &features[],uint &TreeDepth_[],uint &TreeSplits_[],uint &BorderCounts_[],float &Borders_[],double &LeafValues_[]) {\n\
    uint FloatFeatureCount=ArrayRange(BorderCounts_,0);\n\
    uint BinaryFeatureCount=ArrayRange(Borders_,0);\n\
    uint TreeCount=ArrayRange(TreeDepth_,0);\n\
    bool     binaryFeatures[];\n\
    ArrayResize(binaryFeatures,BinaryFeatureCount);\n\
    uint binFeatureIndex=0;\n\
    for(uint i=0; i<FloatFeatureCount; i++) {\n\
       for(uint j=0; j<BorderCounts_[i]; j++) {\n\
          binaryFeatures[binFeatureIndex]=features[i]>Borders_[binFeatureIndex];\n\
          binFeatureIndex++;\n\
       }\n\
    }\n\
    double result=0.0;\n\
    uint treeSplitsPtr=0;\n\
    uint leafValuesForCurrentTreePtr=0;\n\
    for(uint treeId=0; treeId<TreeCount; treeId++) {\n\
       uint currentTreeDepth=TreeDepth_[treeId];\n\
       uint index=0;\n\
       for(uint depth=0; depth<currentTreeDepth; depth++) {\n\
          index|=(binaryFeatures[TreeSplits_[treeSplitsPtr+depth]]<<depth);\n\
       }\n\
       result+=LeafValues_[leafValuesForCurrentTreePtr+index];\n\
       treeSplitsPtr+=currentTreeDepth;\n\
       leafValuesForCurrentTreePtr+=(1<<currentTreeDepth);\n\
    }\n\
    return 1.0/(1.0+MathPow(M_E,-result));\n\
    }'

    file = open('C:/Users/dmitrievsky/AppData/Roaming/MetaQuotes/Terminal/D0E8209F77C8CF37AD8BF550E51FF075/MQL5/Include/' +
                str(SYMBOL) + '_cat_model_martin' + '.mqh', "w")
    file.write(code)
    file.close()
    print('The file ' + 'cat_model' + '.mqh ' + 'has been written to disc')

现在可以保存训练中所用的网格设置。 它们将会在交易时用到。 

来自标准终端发布包的移动平均线和指标缓冲区，已不再使用。 取而代之，所有功能都在函数主体中计算。 添加原始功能时，也应在导出的函数里添加这些功能。

绿色高亮示意终端的 “Include” 文件夹的路径。 它允许保存 .mqh 文件，并将其连接到智能交易系统。

我们来查看 .mqh 文件本身（此处省略了 CatBoost 模型）

#include <Math\Stat\Math.mqh>
int MAs[14] = {5,25,55,75,100,125,150,200,250,300,350,400,450,500};
int grid_size = 10;
double grid_distances[10] = {0.003,0.0035555555555555557,0.004111111111111111,0.004666666666666666,0.005222222222222222,
			     0.0057777777777777775,0.006333333333333333,0.006888888888888889,0.0074444444444444445,0.008};
double grid_coefficients[10] = {1.0,1.4444444444444444,1.8888888888888888,2.333333333333333,
				2.7777777777777777,3.2222222222222223,3.6666666666666665,4.111111111111111,4.555555555555555,5.0};
void fill_arays( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(MAs)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_CURRENT,1,MAs[i],pr);
       double mean = MathMean(pr);
       ret[0] = pr[MAs[i]-1] - mean;
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

如您所见，所有网格设置均已保存，模型已准备就绪。 您仅需将其连接到智能交易系统即可。

#include <EURUSD_cat_model_martin.mqh>

现在，我要解释智能交易系统处理信号所依据的逻辑。 以 OnTick() 函数为例。 该机器人用到了 MT4Orders 函数库，该函数库需另行下载。

void OnTick() {
//---
   if(!isNewBar()) return;
   TimeToStruct(TimeCurrent(), hours);
   double features[];

   fill_arays(features);
   if(ArraySize(features) !=ArraySize(MAs)) {
      Print("No history available, will try again on next signal!");
      return;
   }
   double sig = catboost_model(features);

// Close positions by an opposite signal
   if(count_market_orders(0) || count_market_orders(1))
      for(int b = OrdersTotal() - 1; b >= 0; b--)
         if(OrderSelect(b, SELECT_BY_POS) == true) {
            if(OrderType() == 0 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig > 0.5)
               if(OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red)) {
               }
            if(OrderType() == 1 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic && sig < 0.5)
               if(OrderClose(OrderTicket(), OrderLots(), OrderClosePrice(), 0, Red)) {
               }
         }

// Delete all pending orders if there are no pending orders
   if(!count_market_orders(0) && !count_market_orders(1)) {

      for(int b = OrdersTotal() - 1; b >= 0; b--)
         if(OrderSelect(b, SELECT_BY_POS) == true) {

            if(OrderType() == 2 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic )
               if(OrderDelete(OrderTicket())) {
               }

            if(OrderType() == 3 && OrderSymbol() == _Symbol && OrderMagicNumber() == OrderMagic )
               if(OrderDelete(OrderTicket())) {
               }
         }
   }

// Open positions and pending orders by signals
   if(countOrders() == 0 && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY)) {
      double l = LotsOptimized();

      if(sig < 0.5) {
         OrderSend(Symbol(),OP_BUY,l, Ask, 0, Bid-stoploss*_Point, Ask+takeprofit*_Point, NULL, OrderMagic);
         double p = Ask;
         for(int i=0; i<grid_size; i++) {
            p = NormalizeDouble(p - grid_distances[i], _Digits);
            double gl = NormalizeDouble(l * grid_coefficients[i], 2);
            OrderSend(Symbol(),OP_BUYLIMIT,gl, p, 0, p-stoploss*_Point, p+takeprofit*_Point, NULL, OrderMagic);
         }
      }
      else {
         OrderSend(Symbol(),OP_SELL,l, Bid, 0, Ask+stoploss*_Point, Bid-takeprofit*_Point, NULL, OrderMagic);
         double p = Ask;
         for(int i=0; i<grid_size; i++) {
            p = NormalizeDouble(p + grid_distances[i], _Digits);
            double gl = NormalizeDouble(l * grid_coefficients[i], 2);
            OrderSend(Symbol(),OP_SELLLIMIT,gl, p, 0, p+stoploss*_Point, p-takeprofit*_Point, NULL, OrderMagic);
         }
      }
   }
}

fill_arrays 函数为 CatBoost 模型提供填充 features 数组的功能。 然后将此数组传递给 catboost_model() 函数，该函数返回 0;1 范围的信号。

如您从买入订单示例中所见，这里用到了 grid_size 变量。 它示意了挂单的数量，这些订单位于 grid_distances 的距离上。 标准手数乘以 grid_coefficients 数组中的系数，该系数与订单号相对应。

机器人经编译之后，我们就可进行测试了。

在 MetaTrader 5 测试器中检查机器人

测试应在机器人所训练的时间帧内进行。 在这种情况下，它是 H1。 可以采用开盘价对其进行测试，因为该机器人对于柱线开盘拥有明确的控制权。 不过，由于运用的是网格，因此可以选择 M1 OHLC 来获得更高的精度。

该特定的机器人已在以下周期内经历了训练：

START_DATE = datetime(2020, 5, 1)
TSTART_DATE = datetime(2019, 1, 1)
FULL_DATE = datetime(2018, 1, 1)
END_DATE = datetime(2022, 1, 1)

• 从 2020 年第五个月到今天的间隔是一个训练期，将 50/50 分为训练和验证子样本。 
• 从 2019 年 1 月起，根据 R^2 对模型进行评估，然后选择最佳模型。
• 从 2018 年第一个月起，该模型在自定义测试器中进行了测试。
• 综合数据用于训练（由高斯混合模型生成）
• CatBoost 模型拥有强大的正则化功能，有助于避免基于训练样本进行过度拟合。

所有这些因素表明（并经自定义测试器确认）我们在从 2018 年到今天的区间中找到了某种形态。

我们来看看在 MetaTrader 5 策略测试器中它的样子。

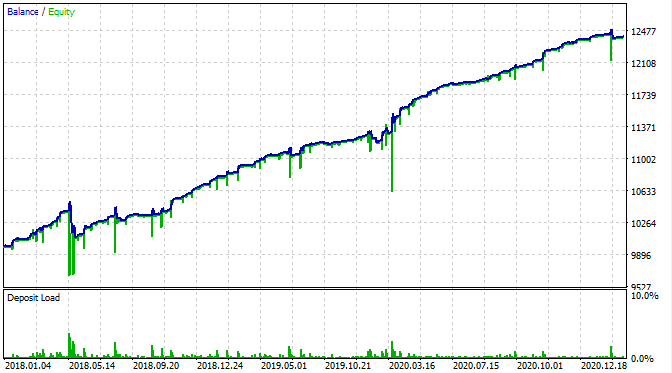
除了我们现在可以看到净值回撤以外，余额图的图表与我的自定义测试器相同。 这是个好消息。 我们来确保该机器人正在遵照网格正确交易，且无其他干扰。

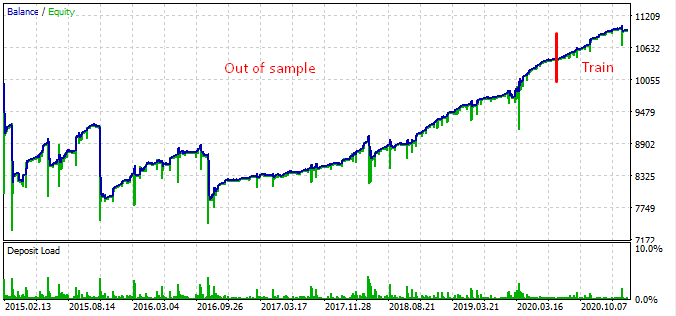
这是从 2015 年开始的测试结果。

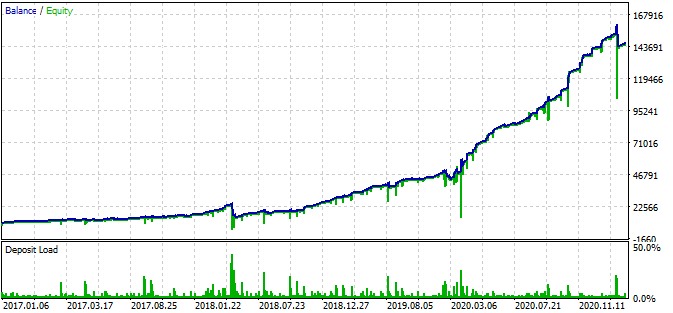
根据该图形，找到的形态从 2016 年底到今天有效，而在其余时间区间则失效。 在这种情况下，初始手数很少，这有助于该机器人得以生存。 至少我们知道该机器人自 2017 年初以来一直有效。 有基于此，我们可以增加风险，以期提高盈利效果。 该机器人展现出令人印象深刻的结果：3 年内达到 1600％，回撤 40％，有亏损全部本金的风险。

此外，机器人在每笔持仓里使用了止损和止盈。 使用 SL 和 TP 会牺牲性，但同时能限制风险。 

请注意，我采用了非常激进的网格。

GRID_COEFFICIENTS = np.linspace(1, 5, num= GRID_SIZE)

array([1.        , 1.44444444, 1.88888889, 2.33333333, 2.77777778,
       3.22222222, 3.66666667, 4.11111111, 4.55555556, 5.        ])

最后的乘数等于 5。 这意味着该系列中最后一笔订单的手数比初始手数高五倍，这带来了额外的风险。 您可以选择更多稳妥的模式。

为什么该机器人在 2016 年或更早的时间内会停止工作？ 对于这个问题，我没有任何有意义的答案。 似乎在外汇市场上有很长的七年周期，或者较短周期，它们彼此的形态毫无关联。 这是一个单独的主题，需要进行更详细的研究。

结束语

在本文中，我尝试讲述可用于训练模型或神经网络，提升其马丁格尔交易能力的技术。 本文介绍了一种现成的解决方案，您可参考它来创建自己的交易机器人。