您应该知道的 MQL5 向导技术（第 03 部分）：香农（Shannon）熵
933
2
1.0 概述
克劳德·香农（Claude Shannon）在 1948 年发表了他的论文通信的数学理论，该论文具有信息熵的新理年。 熵是物理学中的一个概念。 它是物体内粒子活跃程度的量度。 如果我们考虑水的 3 种状态，例如冰固态、水液态和蒸汽态，我们可以看到，粒子动能在蒸汽态中最高，在冰固态中最小。 同样的概念应用于数学中既是概率。 考虑以下三个集合。
集合 1:
集合 2:
集合 3:
如果您要猜测这些集合中哪一个的熵最高？ 如果您选择了最后一组，那么您是对的，但是我们如何验证这个答案？ 回答这个问题的最简单方式是取您重新组织每个集合的方式数量作为熵估算，同时忽略同色拉伸。 因此，对于第一个集合，只有一种方式可以“重新排列”它，然而当我们仔细查看这些集合，显然，从颜色的角度排列数量显著增加，所以您可以认定最后一个集合具有最高的熵。
有一种基于信息确定熵的更精确的方式。 如果您从第一个集合中任意选择一个球，在您选择这个球之前，您应当知道什么？ 好吧，因为该集合只包含蓝色球，所以您可以确定它一定是一个蓝色球。 故此，您可以说我掌握了关于从集合 1 中选择内容的完整信息。 当我们考虑集合 2 和 3 时，我们的信息分别变得越来越不完整。 因此，在数学中，熵与信息成反比。 熵越高，未知就越多。
那么我们如何推导出计算熵的公式呢？ 如果我们再次研究集合，集合中球的类型越多样，熵就越高。 在选择球之前衡量我们掌握的有关球的信息时，最敏感的因素可能是在一个集合中每个球被选择的概率。 那好，如果我们要整体考虑每个集合，并找到选择 8 个球的可能性，每种颜色的选择频率与它在其集合中出现的频率一样多，因为选择每个球都是一个独立事件；那么每个集合的概率（当然“信息已知”）是每个球的独立独自概率的乘积。
集合 1:
(1.0 x 1.0 x 1.0 x 1.0 x 1.0 x 1.0 x 1.0 x 1.0) = 1.0
集合 2:
(0.625 x 0.625 x 0.625 x 0.625 x 0.625 x 0.375 x 0.375 x 0.375) ~ 0.0050
集合 3:
(0.375 x 0.375 x 0.375 x 0.25 x 0.25 x 0.25 x 0.25 x 0.125) ~ 0.000025
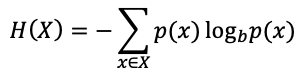
集合 1:
-(8 x 0.125 x log2(1.0)) = 0.0
集合 2:
(-(0.625 x log2(0.625)) - (0.375 x log2(0.375))) ~ 0.9544
集合 3:
(- (0.375 x log2(0.375)) - (2 x 0.25 x log2(0.25)) - (0.125 x log2(0.125))) ~ 1.906
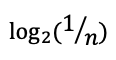
2.0 创建类
在本文中，我们将使用来自 MQL5 函数库的决策森林（Decision Forest）类。 具体来说，我们将随机森林的抽象思维来探索香农（Shannon）熵信号的有效性。 这篇文章不是关于随机森林，而是关于香农熵。
我们重新审视决策森林类，因为它是随机森林模型的基础。 这是一件好事，决策森林是与生俱来的。 我们都在某个时候用过决策树，无论有意与否，因此这个概念并不稀奇。
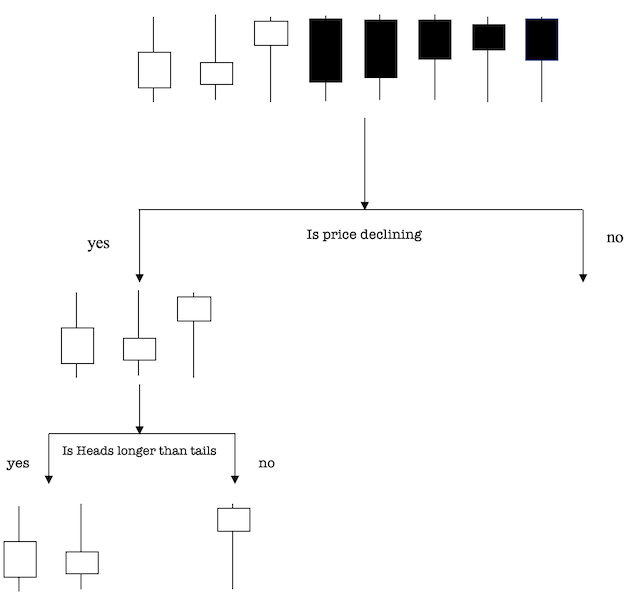
我们看一个能更好描绘如何工作的示例。
假设我们的数据集合由上述价格柱线组成。 我们已有三根下跌蜡烛和五根上涨蜡烛（取看跌行情和看涨行情作为我们的类），并希望按照它们的属性来区分类。 属性是价格方向和头尾长度的比较，因为这些可能是方向变化的前兆。 那么我们该如何做呢？
价格方向似乎是一个可以直接作为区分的属性，因为白色代表看跌蜡烛，蓝色代表看涨。 那么，我们可用这个问题，“价格会暴跌吗？”来区分第一个分叉点。 树中的分叉点，作为枝杈一分为二的点 — 满足选择“是”和“否”分支的准则。
No 分支（上涨蜡烛）的尾巴都比头部长，所以我们可据此完成，但在 Yes 分支上并非如此，因此还有更多的工作要做。 在使用第二个属性时，我们问，“头比尾长吗？”进行第二次切分。
两个头部较长的下跌蜡烛位于 Yes 子分支下，一个具有较长尾部的下跌蜡烛被归类在右侧子分支下。 此决策树能够利用这两个属性根据我们的准则完美地划分数据。
在真实交易系统中，跳价交易量、一天中的时间和许多其它交易指标都可用来构建更全面的决策树。 尽管如此，节点上每个问题的中心前提是找到一个属性，将上面的数据拆分（或分类）至两个不同的集合，每个集合的创建成员都是相似的。
进入随机森林，顾名思义，由大量独立决策树组成，可作为一个群组操作。 对于随机森林中的每棵树，都会进行类预测，并且选择得票最多的类作为模型的预测。随机森林背后的主要概念很容易被忽视，但它非常有潜力 — 大众的智慧。 进行预测时，不相关的树都优于独立树，无论独体基于多少数据进行了训练。 低相关性是症结所在。 这样做的原因是，根据 Ton 的说法，树可以相互保护，免受各自误差的影响（只要它们不在同一个方向上持续犯错）。 为了令随机森林发挥作用，尽管预测信号需要优于平均值，并且每棵树的毁灭/误差需要彼此之间具有低相关性。
举个例子，如果您有两个交易系统，第一个系统一年内最多可以下达一千笔保证金为一美元的订单，另一个您只能下达一笔保证金为一千美元的订单，假设类似的预期，您更喜欢哪一个？ 对于大多数人来说，会选择第一个系统，因为它给予交易者“更多的控制”。
那么，随机森林算法如何确保每棵树的特征与森林中任何其它树木的特征不太相关呢？ 它可以归结为两个特征：
2.0.1 打包
决策树对训练数据非常敏感，微小的变化就可能会导致森林显著不同。随机森林以每棵树在替换数据集时随机采样数据集合这种方式来使用它，成果是生成不同的树。 此过程已知作为引导聚合的打包缩写。
请注意，经由打包，我们不会将训练数据替换为较小的集合，但取代原始训练数据，我们随机抽取大小为 N 的样本，并会有一些替换。 保持初始集合大小 N。 例如，如果我们的训练数据是 [U, V, W, X, Y, Z]，那么我们可以给我们的一棵树以下列表 [U, U, V, X, X, Z]。 在这两个列表中，大小N（六）保持不变，并且 “U” 和 “X” 都在随机选择的数据中重复。
2.0.2 特征随机性
通常在决策树中，拆分节点涉及参考每个可能的特征，并在最终左节点与最终右节点中的观察值之间对比，选择能产生最大区别的那个。 另一方面，在随机森林中，每棵树只能从随机特征子集中进行选择。 这往往会迫使森林内产生更多的变化，并最终导致树木之间的相关性降低，和更多的多样化。
我们来看一个直观的示例 — 在上图中，传统的决策树（蓝色）在决定如何拆分节点时可以从所有四个特征中进行选择。 它决定前往特征 1（黑色带下划线），因为它尽可能地把数据拆分为分离的群组。
现在，我们来看看我们的随机森林。 在此示例中，我们只检查森林中的两棵树。 当我们查看随机森林树 1 时，我们发现它只能参考特征 2 和 3（随机选择）作为其节点拆分决策。 我们从传统的决策树（蓝色）中知道，特征 1 是拆分的最佳特征，但树 1 看不到特征 1，因此它被迫采用特征 2（黑色带下划线）。 另一方面，树 2 只能看到特征 1 和 3，因此它能够选择特征 1。
因此，在随机森林中，树木不仅在数据集上训练（由于打包），而且还在决策中采用各种特征。
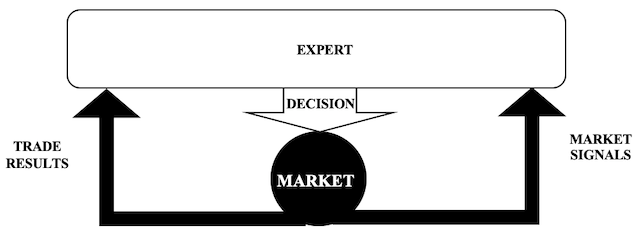
在运用随机森林时，我们的智能系统处理过去的交易结果和行情信号，从而制定买入或卖出的决策。 在从熵中获取信号而不仅仅是筛选器时，我们将分别参考最近一个集合中价格阳线的熵和价格阴线的熵。
随机森林的构建和训练仅在用单线程进行优化时采用。
2.1 智能系统信号类
// wizard description start //+------------------------------------------------------------------+ //| Description of the class | //| Title=Signals of'Shannon Entropy' | //| Type=SignalAdvanced | //| Name=Shannon Entropy | //| ShortName=SE | //| Class=CSignalSE | //| Page=signal_se | //| Parameter=Reset,bool,false,Reset Training | //| Parameter=Trees,int,50,Trees number | //| Parameter=Regularization,double,0.15,Regularization Threshold | //| Parameter=Trainings,int,21,Trainings number | //+------------------------------------------------------------------+ // wizard description end //+------------------------------------------------------------------+ //| Class CSignalSE. | //| Purpose: Class of generator of trade signals based on | //| the 'Shannon Entropy' signals. | //| Is derived from the CExpertSignal class. | //+------------------------------------------------------------------+ class CSignalSE : public CExpertSignal { public: //Decision Forest objects. CDecisionForest DF; //Decision Forest CMatrixDouble DF_SIGNAL; //Decision Forest Matrix for inputs and output CDFReport DF_REPORT; //Decision Forest Report for results int DF_INFO; //Decision Forest feedback double m_out_calculations[2], m_in_calculations[__INPUTS]; //Decision Forest calculation arrays //--- adjusted parameters bool m_reset; int m_trees; double m_regularization; int m_trainings; //--- methods of setting adjustable parameters void Reset(bool value){ m_reset=value; } void Trees(int value){ m_trees=value; } void Regularization(double value){ m_regularization=value; } void Trainings(int value){ m_trainings=value; } //Decision Forest FUZZY system objects CMamdaniFuzzySystem *m_fuzzy; CFuzzyVariable *m_in_variables[__INPUTS]; CFuzzyVariable *m_out_variable; CDictionary_Obj_Double *m_in_text[__INPUTS]; CDictionary_Obj_Double *m_out_text; CMamdaniFuzzyRule *m_rule[__RULES]; CList *m_in_list; double m_signals[][__INPUTS]; CNormalMembershipFunction *m_update; datetime m_last_time; double m_last_signal; double m_last_condition; CSignalSE(void); ~CSignalSE(void); //--- method of verification of settings virtual bool ValidationSettings(void); //--- method of creating the indicator and timeseries virtual bool InitIndicators(CIndicators *indicators); //--- methods of checking if the market models are formed virtual int LongCondition(void); virtual int ShortCondition(void); bool m_random; bool m_read_forest; int m_samples; //--- method of initialization of the oscillator bool InitSE(CIndicators *indicators); double Data(int Index){ return(Close(StartIndex()+Index)-Close(StartIndex()+Index+1)); } void ReadForest(); void WriteForest(); void SignalUpdate(double Signal); void ResultUpdate(double Result); double Signal(void); double Result(void); bool IsNewBar(void); };
2.1.1 信号
该熵将按新近度指数加权。
if(_data>0.0) { _long_entropy-=((1.0/__SIGNALS[i])*((__SIGNALS[i]-s)/__SIGNALS[i])*(fabs(_data)/_range)*(log10(1.0/__SIGNALS[i])/log10(2.0))); } else if(_data<0.0) { _short_entropy-=((1.0/__SIGNALS[i])*((__SIGNALS[i]-s)/__SIGNALS[i])*(fabs(_data)/_range)*(log10(1.0/__SIGNALS[i])/log10(2.0))); }
且它还将根据价格柱线的体量进行加权。
if(_data>0.0) { _long_entropy-=((1.0/__SIGNALS[i])*((__SIGNALS[i]-s)/__SIGNALS[i])*(fabs(_data)/_range)*(log10(1.0/__SIGNALS[i])/log10(2.0))); } else if(_data<0.0) { _short_entropy-=((1.0/__SIGNALS[i])*((__SIGNALS[i]-s)/__SIGNALS[i])*(fabs(_data)/_range)*(log10(1.0/__SIGNALS[i])/log10(2.0))); }
生成的信号将是阴线熵减去阳线熵。 此处的推理是，如果阴线熵超过阳线熵，那么我们关于阴线的信息更少，因此空头仓位比阳线的信息少，阳线同样意味着多头仓位。 从表面上看，它体现出将是一个“危险”的趋势跟随系统！ 然而，由于上面在计算熵时附加的权重，也许情况并非如此。
当多头或空头条件超过开仓阈值时，信号将更新，因为这意味着开仓。 这将在计时器上发生，因此我们将修改向导装配智能系统，以满足这种情况。
//+------------------------------------------------------------------+ //| "Timer" event handler function | //+------------------------------------------------------------------+ void OnTimer() { if(PositionSelect(Symbol()) && Signal_ThresholdClose<=fabs(filter0.m_last_condition)) { filter0.ResultUpdate(filter0.Result()); } // if(!PositionSelect(Symbol()) && Signal_ThresholdOpen<=fabs(filter0.m_last_condition)) { filter0.SignalUpdate(filter0.m_last_signal); } ExtExpert.OnTimer(); }
如前所述，类中的源函数只会在优化时运行。
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalSE::SignalUpdate(double Signal) { if(MQLInfoInteger(MQL_OPTIMIZATION)) { m_samples++; DF_SIGNAL.Resize(m_samples,__INPUTS+2); for(int i=0;i<__INPUTS;i++) { DF_SIGNAL[m_samples-1].Set(i,m_signals[0][i]); } // DF_SIGNAL[m_samples-1].Set(__INPUTS,Signal); DF_SIGNAL[m_samples-1].Set(__INPUTS+1,1-Signal); } }
2.1.2 结果
结果将基于最后平仓的利润。
if(HistorySelect(0,m_symbol.Time())) { int _deals=HistoryDealsTotal(); for(int d=_deals-1;d>=0;d--) { ulong _deal_ticket=HistoryDealGetTicket(d); if(HistoryDealSelect(_deal_ticket)) { if(HistoryDealGetInteger(_deal_ticket,DEAL_ENTRY)==DEAL_ENTRY_OUT) { _result=HistoryDealGetDouble(_deal_ticket,DEAL_PROFIT); break; } } } } return(_result);
当多头或空头条件超过平仓阈值时，它们将被更新，因为这意味着持仓将被平仓。 如上所述，这也将在计时器上发生，类函数仅在优化时更新决策林文件。
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalSE::ResultUpdate(double Result) { if(MQLInfoInteger(MQL_OPTIMIZATION)) { int _err; if(Result<0.0) { double _odds = MathRandomUniform(0,1,_err); // DF_SIGNAL[m_samples-1].Set(__INPUTS,_odds); DF_SIGNAL[m_samples-1].Set(__INPUTS+1,1-_odds); } } }
2.1.3 森林写入
在每次跳价时，读取之前森林将被写入，因此我们修改了向导装配智能系统，以便适应这种情况。
//+------------------------------------------------------------------+ //| "Tick" event handler function | //+------------------------------------------------------------------+ void OnTick() { if(!signal_se.m_read_forest) signal_se.WriteForest(); ExtExpert.OnTick(); }
2.1.4 森林读取
在测试器验算结束时，将在测试器上读取森林，因此我们修改向导装配智能系统，以便适应这种情况。
//+------------------------------------------------------------------+ //| "Tester" event handler function | //+------------------------------------------------------------------+ double OnTester() { signal_se.ReadForest(); return(0.0); }
2.2 智能系统资金管理类
在本文中，我们还将探索利用向导创建一个自定义仓位调整类。 我们将利用 “Money Size Optimized” 类，并对其进行修改，以便根据香农熵规范化仓位规模。 我们的新接口将如下所示：
// wizard description start //+------------------------------------------------------------------+ //| Description of the class | //| Title=Trading with 'Shannon Entropy' optimized trade volume | //| Type=Money | //| Name=SE | //| Class=CMoneySE | //| Page=money_se | //| Parameter=ScaleFactor,int,3,Scale factor | //| Parameter=Percent,double,10.0,Percent | //+------------------------------------------------------------------+ // wizard description end //+------------------------------------------------------------------+ //| Class CMoneySE. | //| Purpose: Class of money management with 'Shannon Entropy' optimized volume. | //| Derives from class CExpertMoney. | //+------------------------------------------------------------------+ class CMoneySE : public CExpertMoney { protected: int m_scale_factor; public: double m_absolute_condition; CMoneySE(void); ~CMoneySE(void); //--- void ScaleFactor(int scale_factor) { m_scale_factor=scale_factor; } void AbsoluteCondition(double absolute_condition) { m_absolute_condition=absolute_condition; } virtual bool ValidationSettings(void); //--- virtual double CheckOpenLong(double price,double sl); virtual double CheckOpenShort(double price,double sl); protected: double Optimize(double lots); };
变量 “m_absolute_condition” 将是 “LongCondition”和“ShortCondition” 函数返回的整数型绝对值。 由于它是一个常规化值，我们可用其大小与我们的仓位规模的比例。 此变量将通过信号类经由修改的向导装配智能系统传递到资金管理类。
//+------------------------------------------------------------------+ //| Global expert object | //+------------------------------------------------------------------+ CExpert ExtExpert; CSignalSE *signal_se; CMoneySE *money_se;
并在跳价函数上
//+------------------------------------------------------------------+ //| "Tick" event handler function | //+------------------------------------------------------------------+ void OnTick() { if(!signal_se.m_read_forest) signal_se.WriteForest(); money_se.AbsoluteCondition(fabs(signal_se.m_last_condition)); ExtExpert.OnTick(); }
主要修改是在下面的 “Optimize” 函数当中：
//+------------------------------------------------------------------+ //| Optimizing lot size for open. | //+------------------------------------------------------------------+ double CMoneySE::Optimize(double lots) { double lot=lots; //--- normalize lot size based on magnitude of condition lot*=(20*m_scale_factor/fmax(20.0,((100.0-m_absolute_condition)/100.0)*20.0*m_scale_factor*m_scale_factor)); //--- reduce lot based on number of losses orders without a break if(m_scale_factor>0) { //--- select history for access HistorySelect(0,TimeCurrent()); //--- int orders=HistoryDealsTotal(); // total history deals int losses=0; // number of consequent losing orders CDealInfo deal; //--- for(int i=orders-1;i>=0;i--) { deal.Ticket(HistoryDealGetTicket(i)); if(deal.Ticket()==0) { Print("CMoneySE::Optimize: HistoryDealGetTicket failed, no trade history"); break; } //--- check symbol if(deal.Symbol()!=m_symbol.Name()) continue; //--- check profit double profit=deal.Profit(); if(profit>0.0) break; if(profit<0.0) losses++; } //--- if(losses>1){ lot*=m_scale_factor; lot/=(losses+m_scale_factor); lot=NormalizeDouble(lot,2);} } //--- normalize and check limits double stepvol=m_symbol.LotsStep(); lot=stepvol*NormalizeDouble(lot/stepvol,0); //--- double minvol=m_symbol.LotsMin(); if(lot<minvol){ lot=minvol; } //--- double maxvol=m_symbol.LotsMax(); if(lot>maxvol){ lot=maxvol; } //--- return(lot); }
3.0 MQL5 向导
我们将装配两个智能系统，一个只有我们创建的信号类，再加上以最低交易量交易的资金管理，第二个包含我们创建的信号和资金管理类。
4.0 策略测试器
运行第一个智能系统优化给出的盈利因子为 2.89，锋锐比率为 4.87，而优化第二个智能系统的盈利因子为 3.65，锋锐比率为 5.79。
第一个报告
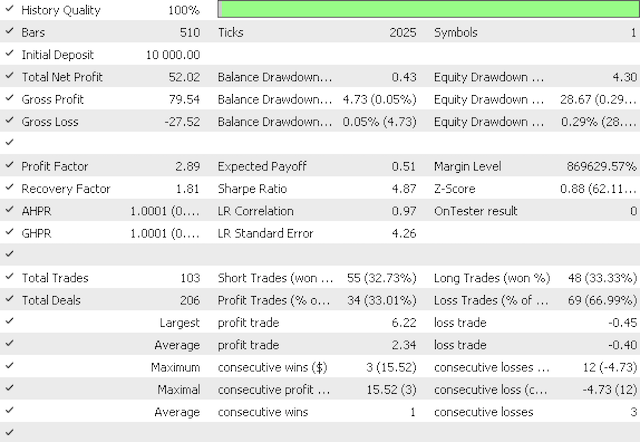
第一个净值曲线
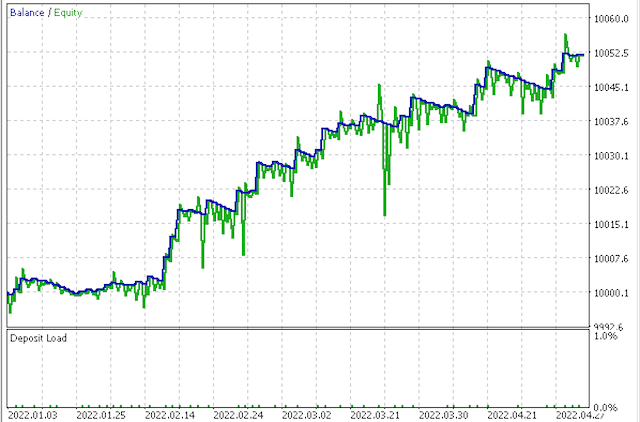
第二个报告
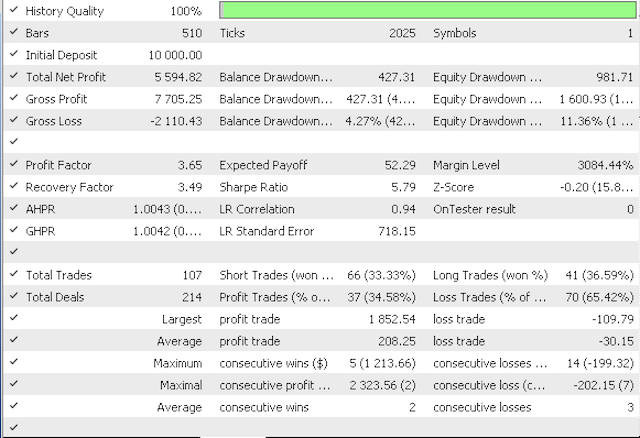
第二个净值曲线
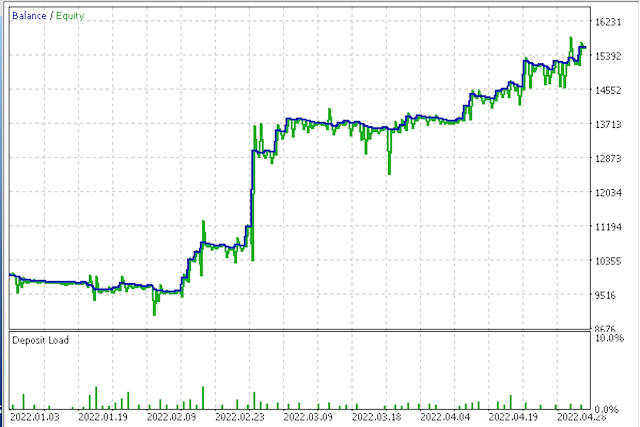
5.0 结束语
所附 EA 基于 4 小时时间帧的开盘价上进行了优化，以获得理想的止盈和止损水平。这意味着您无法在实盘账户上复制这些结果，甚至在策略测试器中每次跳价模式下也是如此。 这并非本文的重点。 与其试图遇到一个圣杯，不如每个人都复制这些系列文章揭示的独特想法，它们可以进一步定制，如此每名交易者都能达至自己的边锋。 总体而言，行情相关性仍然过重，这就是为什么寻找边锋可以在高波动中为您提供良好的助力。 感谢阅读！
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/11487
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
利用智能系统进行风险和资本管理
学习如何基于加速（Accelerator）振荡器设计交易系统
数据科学与机器学习（第 07 部分）：多项式回归
DoEasy. 控件 (第 20 部分): SplitContainer WinForms 对象
我读了这篇文章，但不是很理解：
1.随机森林 的输入是什么？
2.如何根据森林的分类历史计算熵？
不幸的是，这篇文章的翻译质量不高，导致我很难理解。
有时，文章中似乎没有足够的插图，尽管文中提到了这些插图：
"
让我们来看一个说明性的例子--在上图中，传统的决策树（蓝色 表示） 在决定如何分割一个节点时，可以从所有四个属性中进行选择。它决定使用属性 1（下划线为黑色），因为这可以将数据最大限度地分割成不同的组。
"
这个信号发生器有问题，代码本身没有意义。
我是在第 158 行出现错误时开始注意到问题的。 你创建了 __INPUTS 规则数，而它应该是
规则。
我知道决策森林是在优化过程中使用的，但在非优化运行中不读取它时，又有什么意义呢？
决策森林似乎是用来验证什么的，但对信号决策毫无帮助。
而且，如果要使用决策森林，也没有解释其用法（或需要事先了解）。这里 ：
你正在改变中性集的轮廓。这确实会对信号产生影响，但能否请您解释一下如何影响以及为什么会影响。
其他方面都很好。