
Брутфорс-подход к поиску закономерностей (Часть IV): Минимальная функциональность
- Изменения в новой версии
- Первая демонстрация работы и новая концепция
- Новый полином на основе видоизмененных рядов Фурье
- Немного о реализации софта изнутри
- Новый механизм подавления спредовых шумов и учета спреда
- Вариация лота на коротких участках
- Рабочие варианты на глобальной истории
- Математика брутфорса
- Немного о прибивке к истории и переобучении
- Рекомендации к использованию
- Заключение
- Ссылки на предыдущие статьи цикла
Изменения в новой версии
Как и в предыдущей статье, программа довольно сильно изменилась в лучшую сторону в плане функциональности и, самое главное, удобства использования. Предыдущие версии были очень неудобны, имели кучу косяков, багов и недоработок. В данной версии этих изменений максимум. Проведена большая работа по модернизации как шаблонов советников, так и самого софта. Список изменений:
- Переработан интерфейс
- Добавлен другой полином для брутфорса (за основу взят переработанный ряд Фурье)
- Расширен механизм генерации случайных чисел
- Расширена концепция метода в сторону удобства и простоты использования
- Добавлены механизмы вариации лота для сверхкоротких участков
- Добавлен механизм учета спреда
- Добавлен механизм, отсекающий спредовые шумы
- Исправлено множество ошибок
Многие из запланированных модификаций были реализованы. Правки алгоритмов будут в будущем, но уже не такие глобальные.
Первая демонстрация работы и новая концепция
В процессе создания советников я понял, что не всегда хочется придумывать названия и, кроме того, не всегда хочется каждый раз ковыряться в терминалах и чистить настройки роботов. Ведь может быть так, что у нас уже был робот с таким же названием и от него остались настройки где-то в глубине терминала, и как-то не очень хочется каждый раз их вычищать,. Решением данной проблемы стал советник-приемник настроек. Иначе говоря, программа генерирует файл настройки в обычном txt-формате, а советник просто ее читает. Подобный подход как ускоряет работу с данным решением, так и делает ее более простой и понятной. Схема решения теперь выглядит так:
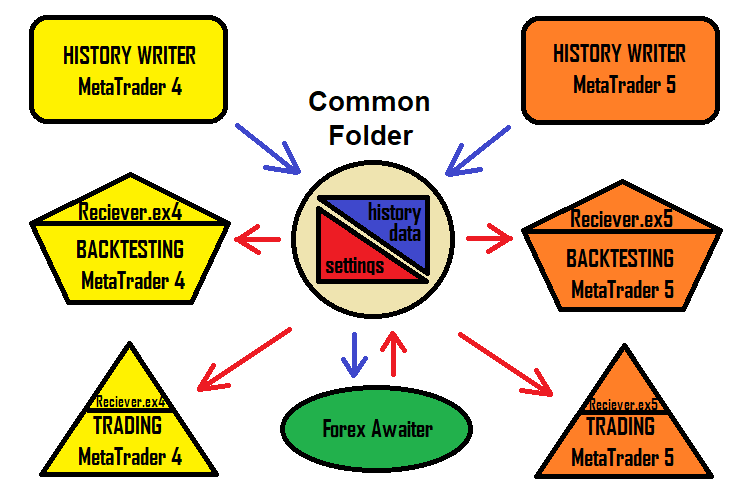
Конечно, версия программы, которая генерирует роботов, осталась, но специально для того, чтобы приблизить данный метод к обычному пользователю, была придумана новая концепция специально для терминалов MetaTrader 4 и MetaTrader 5, которая позволяет максимально просто и быстро использовать данное решение. Самым удобным в данном решении, как мне кажется, является то, что настройка одинаково работает как на MetaTrader 4, так и на MetaTrader 5.
Новый интерфейс я покажу частично, в виду того что он довольно большой и будет занимать слишком много места в статье. Я покажу только первую вкладку.
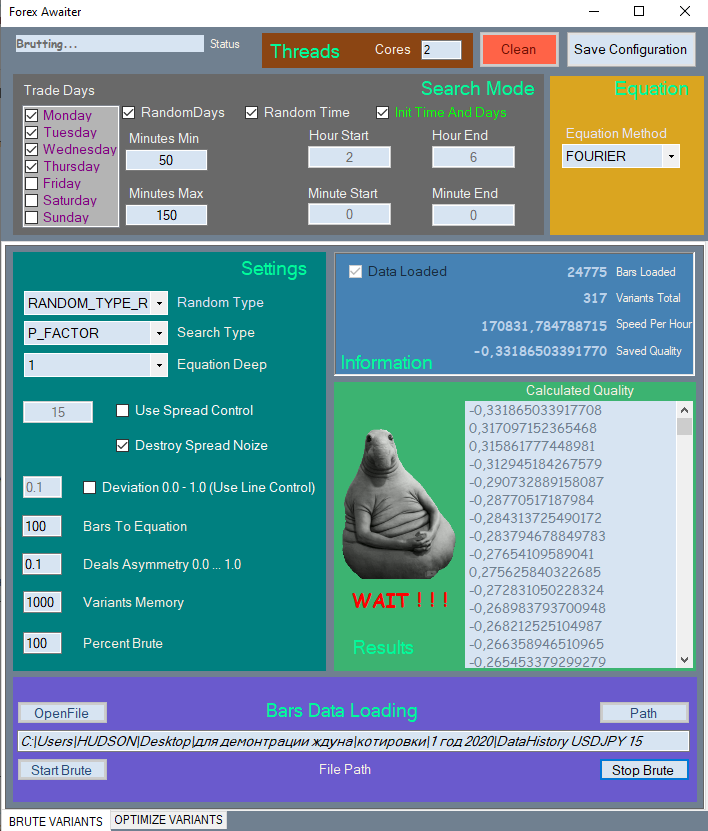
Все элементы распределены по соответствующим секциям для удобства восприятия, все неиспользуемые элементы блокируются, если их использование бессмысленно.
Также я создал специально для статьи видео , где демонстрирую работу программы.
Почему бы не сделать передачу настроек через старые добрые set-файлы? Все очень просто, set-файлы не могут в себе содержать массивы, а в данном методе в качестве входных настроек присутствуют массивы, кроме того у них плавающая длина. В данном случае более удобно будет использовать обычные текстовые файлы.
Новый полином на основе видоизмененных рядов Фурье
Многие люди, знакомые с машинным обучением, активно используют ряд Фурье для своих алгоритмов, находят ему самое разнообразное применение. Изначально ряд Фурье был придуман для разложения функций на промежутке [-π;π]. При этом нужно еще знать, как раскладывать функцию в этот ряд и вообще для чего и нужно ли нам вообще это разложение? Кроме того нужно знать нюансы метода замены переменной, ведь нам может понадобиться разложение на совсем ином промежутке чем [-π;π]. Все это требует хорошей математической подготовки и знания тонкостей, а также понимания, есть ли в этом какой-то смысл для торговли? Общий вид ряда Фурье выглядит так:
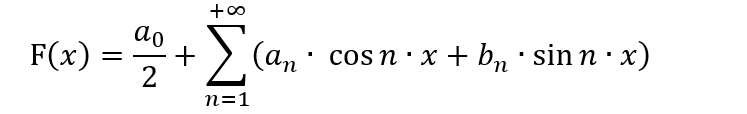
В таком виде данный полином может сгодиться разве что для представления торговых паттернов в более удобном виде, а также для попытки предсказать движение цены, предполагая что цена есть процесс волновой. Скорее всего, данное предположение имеет под собой силу, но в таком виде он неприменим для брутфорса, ведь для этого пришлось бы кардинально поменять всю концепцию метода. Вместо этого можно подумать, как преобразовать данный полином так, чтобы он был пригоден для данного метода. В целом вариаций может быть очень много, но если мы хотим оставить формулу максимально похожей на ряд Фурье и в то же время не использовать формулу по прямому назначению, то можно, на мой взгляд, поступить вот так:
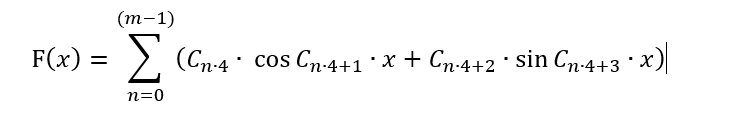
Здесь ничего не поменялось, разве что ряд обрел большую свободу, и теперь его период плавает как в плюс так и в минус. Ну разве что слагаемых стало конечное число. Это связано с тем, что массив C[] — это наши коэффициенты, которые мы будем комбинировать для того, чтобы найти подходящую формулу, а их число ограничено. Мы не можем писать этот ряд до бесконечности, а будем вынуждены ограничиться лишь "m" барами. Кроме всего прочего я убрал первое слагаемое для пущей симметрии, чтобы значения формулы выдавали максимально симметричные сигналы как в "+" так и в "-" диапазонах. Но так мы сможем подбирать лишь функцию, зависящую от 1 бара! А нам нужно сделать так, чтобы значения всех баров присутствовали в формуле, кроме того у бара не 1 параметр, а 6. Эти 6 параметров я приводил в статье №2 данного цикла. Понятно, что придется пожертвовать точностью обработки данных 1 бара для того, чтобы иметь возможность учесть все остальные. В идеале нужно будет эту сумму обернуть в еще одну. Но я не хочу усложнять полином и ограничусь пока что самой простой версией:
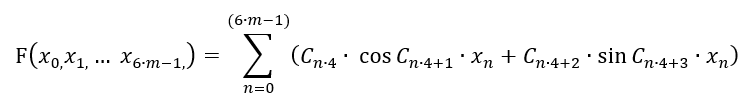
По сути, функция из одномерной превратилась в многомерную, но это не значит, что этот полином способен описать любую многомерную функцию в выбранном многомерном гиперкубе. Но все равно эта формула подарит нам еще одно семейство многомерных функций, которые смогут описать те закономерности, которые ряду Тейлора будут не под силу либо там, где этот ряд не может достаточно качественно описать искомую функцию. Просто у нас так будет больше шансов найти более лучшую закономерность на одной и той же выборке данных.
В коде данная функция будет выглядеть вот так:
if ( Method == "FOURIER" ) { for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*MathSin(C1[iterator+1]*(Close[i+1]-Open[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Close[i+1]-Open[i+1])/_Point); iterator+=4; } for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*MathSin(C1[iterator+1]*(High[i+1]-Open[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(High[i+1]-Open[i+1])/_Point); iterator+=4; } for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*MathSin(C1[iterator+1]*(Open[i+1]-Low[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Open[i+1]-Low[i+1])/_Point); iterator+=4; } for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*MathSin(C1[iterator+1]*(High[i+1]-Close[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(High[i+1]-Close[i+1])/_Point); iterator+=4; } for ( int i=0; i<CNum; i++ ) { Val+=C1[iterator]*MathSin(C1[iterator+1]*(Close[i+1]-Low[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Close[i+1]-Low[i+1])/_Point); iterator+=4; } return Val; }
Здесь не вся функция, а только та часть, что реализует данный полином, но в целом этого достаточно для понимания. Несмотря на простоту конструкции, даже такие формулы способны адаптироваться к рынку.
Я провел максимально быстрый брутфорс по последнему году истории, используя данный метод, просто чтобы показать, что данная формула работает. Хуже или лучше, не знаю. Нужно выяснять. Строго говоря, мне пока не удалось найти что-то реально рабочее данной формулой, но я думаю, это из-за того, что у меня не было толком ни времени ни вычислительных мощностей. Все время ушло на исследование первоначального варианта. Вот то, что мне удалось получить на валютной паре USDJPY M15 по последнему году истории:
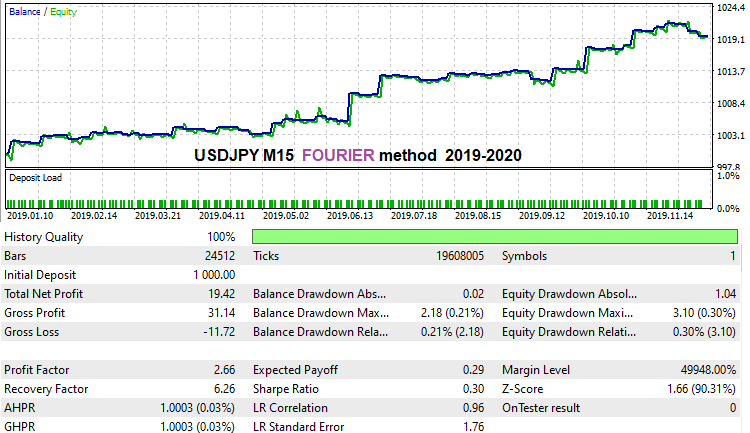
Единственное, что мне не понравилось в этой формуле, она очень неустойчива относительно механизма подавления спредовых шумов, видимо, таковы особенности применения гармонических функций в рамках данного метода. Возможно, я не совсем правильно составил формулу, но мне так почему-то не кажется. В данном методе нужно обязательно включать галку "Spread Control" на второй вкладке, тогда механизм подавления спредовых шумов отключается при оптимизации и выдает довольно хорошие варианты. Я думаю, что все в порядке, просто эта формула получилась очень "нежной". Тем не менее, как видно, она тоже способна находить довольно хорошие варианты.
Немного о реализации софта изнутри
Этого вопроса я мало касался в прошлых статьях цикла и решил немного приоткрыть завесу тайны, как же все это устроено изнутри. Наиболее интересная и простая часть — это генерация коэффициентов для формулы. Данная часть, в первую очередь, должна быть освещена по той причине, что так будет понятнее, как происходит генерация коэффициентов:
public void GenerateC(Tester CoreWorker) { double RX; TYPE_RANDOM RT; RX = RandomX.NextDouble(); if (RandomType == TYPE_RANDOM.RANDOM_TYPE_R) RT = (TYPE_RANDOM)RandomX.Next(0, Enum.GetValues(typeof(TYPE_RANDOM)).Length-1); else RT = RandomType; for (int i = 0; i < CoreWorker.Variant.ANum; i++) { if (RT == TYPE_RANDOM.RANDOM_TYPE_0) { if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i-1]*RandomX.NextDouble(); else CoreWorker.Variant.Ci[0]=1.0; } if (RT == TYPE_RANDOM.RANDOM_TYPE_5) { if (RandomX.NextDouble() >= 0.5) { if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i - 1] * RandomX.NextDouble(); else CoreWorker.Variant.Ci[0] = 1.0; } else { if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i - 1] * (-RandomX.NextDouble()); else CoreWorker.Variant.Ci[0] = -1.0; } } if (RT == TYPE_RANDOM.RANDOM_TYPE_1) CoreWorker.Variant.Ci[i] = RandomX.NextDouble(); if (RT == TYPE_RANDOM.RANDOM_TYPE_2) { if (RandomX.NextDouble() >= 0.5) CoreWorker.Variant.Ci[i] = RandomX.NextDouble(); else CoreWorker.Variant.Ci[i] = -RandomX.NextDouble(); } if (RT == TYPE_RANDOM.RANDOM_TYPE_3) { if (RandomX.NextDouble() >= RX) { if (RandomX.NextDouble() >= RX + (1.0 - RX) / 2.0) CoreWorker.Variant.Ci[i] = RandomX.NextDouble(); else CoreWorker.Variant.Ci[i] = -RandomX.NextDouble(); } else CoreWorker.Variant.Ci[i] = 0.0; } if (RT == TYPE_RANDOM.RANDOM_TYPE_4) { if (RandomX.NextDouble() >= RX) CoreWorker.Variant.Ci[i] = RandomX.NextDouble(); else CoreWorker.Variant.Ci[i] = 0.0; } } }
Все довольно просто, есть несколько фиксированных типов генерации случайных чисел и есть некий общий тип, который реализует все сразу. Каждый из типов генерации был проверен на практике и оказалось, что общий тип генерации "RANDOM_TYPE_R" работает максимально эффективно. Фиксированные типы не всегда дают результат, так как характер котировок на разных инструментах и таймфреймах практически везде разный. Визуально в большинстве случаев эти отличия увидеть невозможно, но машина видит все. Хотя некоторые фиксированные типы на некоторых таймфреймах способны дать больше сигналов с максимальными показателями качества. Так я заметил, что, например, на паре NZDUSD H1 наблюдается резкий скачок в качестве результатов, если использовать RANDOM_TYPE_4, который означает "только нули и положительные числа", что может быть явным намеком на скрытые волновые процессы, недоступные глазу. Очень хотелось бы исследовать разные инструменты более глубоко, но, к сожалению, в одиночку это невозможно.
Новый механизм подавления спредовых шумов и учета спреда
Как было замечено в предыдущей статье, спред искажает ценовые данные так, что большинство из найденных закономерностей преимущественно лежит внутри спреда. На самом деле спред — это злейший враг любой стратегии по той лишь причине, что вопреки нашим ожиданиям большинство стратегий неспособно обеспечить достаточное математическое ожидание для того, чтобы преодолеть спред. В данном случае не стоит обманываться бектестом или положительной статистикой торговли на реальном счете в течение месяца или даже года, потому что это слишком маленькая выборка данных для оценки будущей работоспособности. Так существует целый класс стратегий и автоматических торговых систем, называемых ночными скальперами. Данные роботы берут небольшую прибыль за очень ограниченный промежуток времени. С такими системами активно борются брокеры путем расширения спредов после полуночи. Спред просто выставляют на таком уровне, чтобы большинство стратегий были убыточными и ваши деньги благополучно отправлялись к брокеру.
Есть одна величина, которая практически неизменна у большинства брокеров:
- Spread = (Ask - Bid) / _Point
- MidPrice = ( Ask + Bid ) / 2
Данная цена выделена зеленым. Это не что иное, как середина стакана. Стакан, как правило, выстраивается относительно данной цены, и все это происходит так, что обе цены находятся на равном удалении от данной цены. На самом деле, если использовать классическое определение стакана, эта цена не имеет никакого смысла, поскольку там отсутствуют торговые заявки, но если предположить, что спреды у всех брокеров свои, то можно сделать вывод, что вот эта цена которая не имеет никакого смысла и у всех практически идентична. Нарисую это:
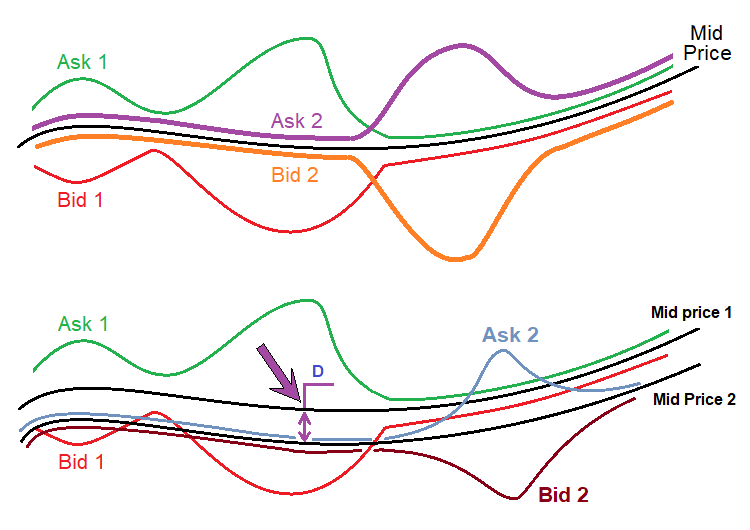
На верхнем рисунке изображен ценовой ряд двух произвольно взятых брокеров. Всегда есть цена "Ask" и цена "Bid", которые символизируют цены для покупки или продажи. А вот черная линия — общая для обеих ценовых рядов. Считается эта величина очень просто, как я показал выше. Самое главное, что эта величина практически не зависит от расширения или сужения спредов конкретного брокера, так как сужение или расширение стакана происходят практически равномерно относительно данной цены.
На нижнем рисунке нарисована реальная ситуация которая в действительности случается с котировками разных брокеров. Все дело в том, что даже эта средняя цена бывает разная в разных потоках. Причины лично мне неизвестны, да и не интересны, поскольку вряд ли из этой информации можно извлечь что-то полезное для торговли. Данный факт я обнаружил, когда занимался арбитражной торговлей, потому что все эти нюансы крайне там важны. Применительно к нашему методу важно только что:
- MidPrice1=f(t)
- MidPrice2=MidPrice1-D
- MidPrice1 '(t) = MidPrice2 '(t)
Иначе говоря, средняя цена обоих ценовых рядов, если представить их в виде временных функций, имеет одинаковую производную, поскольку отличаются эти функции только константой "D". А поскольку наш полином использует не столько сами цены, сколько их разницу, то все данные величины будут являться функционалами от производной этих функций средней цены. А поскольку эти производные равны у всех брокеров, то это дает нам, помимо абстрагирования от скачков спред,а еще и уверенность в том, что на другом брокере наши настройки будут так же эффективны. В случае альтернативы наши настройки, которые мы найдем, будут иметь крайне низкий шанс пройти бектест на реальных тиках, и, соответственно, еще более низкий шанс, что наши настройки будут применимы к другому брокеру. Если использовать данную концепцию, то все эти проблемы исчезают, что уже было мной проверено на практике.
Для того чтобы реализовать данный механизм, мне пришлось внести соответствующие модификации во все элементы решения. Во-первых, для того чтобы реализовать подобный подход, нужно дополнительно записывать спреды на всех важных точках бара при записи файла котировки, таких как Open[], Close[], High[], Low[], чтобы в дальнейшем скорректировать эти значения используя тот самый спред, который, по сути, дает нам цену "Ask" благодаря тому, что бары строятся по ценам "Bid". Советники для записи котировок превратились при этом из побаровых в потиковые. Функция для записи данных баров стала такой:
void WriteBar() { FileWriteString(Handle0x,"\r\n"); FileWriteString(Handle0x,DoubleToString(Close[1],8)+"\r\n"); FileWriteString(Handle0x,DoubleToString(Open[1],8)+"\r\n"); FileWriteString(Handle0x,DoubleToString(High[1],8)+"\r\n"); FileWriteString(Handle0x,DoubleToString(Low[1],8)+"\r\n"); FileWriteString(Handle0x,IntegerToString(int(Time[1]))+"\r\n"); FileWriteString(Handle0x,IntegerToString(PrevSpread)+"\r\n"); FileWriteString(Handle0x,IntegerToString(CurrentSpread)+"\r\n"); FileWriteString(Handle0x,IntegerToString(PrevHighSpread)+"\r\n"); FileWriteString(Handle0x,IntegerToString(PrevLowSpread)+"\r\n"); MqlDateTime T; TimeToStruct(Time[1],T); FileWriteString(Handle0x,IntegerToString(int(T.hour))+"\r\n"); FileWriteString(Handle0x,IntegerToString(int(T.min))+"\r\n"); FileWriteString(Handle0x,IntegerToString(int(T.day_of_week))+"\r\n"); }
Зеленым цветом выделены 4 строчки, которые производят запись спреда на всех четырех точках бара, по которым он строится. В предыдущей версии данные величины не записывались и не учитывались при расчетах. Записать эти данные не проблема, как и получить их. Для того чтобы получить спред на "High" и "Low", была введена вот такая простенькая функция, которая работает по тикам:
void RecalcHighLowSpreads() { if ( Close[0] > LastHigh ) { LastHigh=Close[0]; HighSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD)); } if ( Close[0] < LastLow ) { LastLow=Close[0]; LowSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD)); } }
Эта функция лишь определяет спред на высшей и низшей точке бара, пока текущий бар формируется. При появлении нового бара текущий бар считается полностью сформированным и его данные записываются в файл. Одной этой функции недостаточно, работает она в тандеме с побаровой:
bool bNewBar() { ArraySetAsSeries(Close,false); ArraySetAsSeries(Open,false); ArraySetAsSeries(High,false); ArraySetAsSeries(Low,false); CopyOpen(_Symbol,_Period,0,2,Open); CopyClose(_Symbol,_Period,0,2,Close); CopyHigh(_Symbol,_Period,0,2,High); CopyLow(_Symbol,_Period,0,2,Low); ArraySetAsSeries(Close,true); ArraySetAsSeries(Open,true); ArraySetAsSeries(High,true); ArraySetAsSeries(Low,true); if ( Time0 < Time[1] ) { if (Time0 != 0) { Time0=Time[1]; PrevHighSpread=HighSpread; PrevLowSpread=LowSpread; PrevSpread=CurrentSpread; CurrentSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD)); HighSpread=CurrentSpread; LowSpread=CurrentSpread; return true; } else { Time0=Time[1]; return false; } } else return false; }
Функция является одновременно и предикатом и важным элементом логики, в котором окончательно определяются все 4 спреда на всех важных точках баров. Схожим образом все это реализовано и внутри программы. В обработчике OnTick это работает все очень просто:
RecalcHighLowSpreads();
if ( bNewBar()) WriteBar();
В файле с котировкой это все теперь будет выглядеть так:
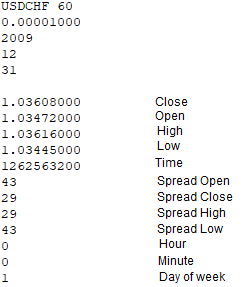
Внутри программы массив со средними ценами реализован абсолютно идентично:
OpenX[1]=Open[1]+(double(PrevSpread)/2.0)*_Point; CloseX[1]=Close[1]+(double(Spread)/2.0)*_Point; HighX[1]=High[1]+(double(PrevHighSpread)/2.0)*_Point; LowX[1]=Low[1]+(double(PrevLowSpread)/2.0)*_Point;
Касаемо реализации всего этого подхода в советниках, на первый взгляд кажется, что можно идентичным образом реализовать подавление спредовых шумов, но проблема в том, что для этого необходимо собрать определенное количество тиков, и чем больше таймфрейм, тем больше тиков нужно собрать на один бар, а чем больше тиков, тем больше времени нужно на то, чтобы их собрать. Если бы в барах сохранялись еще и цены "Ask" или хотя бы спреды, то это было бы легко сделать, но в данном случае проще считать по ценам "Bid".
Как дополнительная опция был добавлен механизм учета спреда при оптимизации результатов. Этот механизм совсем необязателен, как показали тесты, но при наличии достаточных вычислительных мощностей он может дать достаточно неплохие результаты. Суть в том, чтобы потребовать от алгоритма, чтобы ордеры могли открываться и закрываться, только если спред не превышает требуемое значение. Благодаря тому, что текущая версия решения пишет в данные баров еще и спреды, то мы вполне можем контролировать данную величину и считать истинные показатели теста за вычетом спреда.
Вариация лота на коротких участках
На самом деле вариацию лота можно использовать не только на очень коротких участках, но и на длинных, но только одну из разновидностей. Существует всего 2 механизма управления рисками или лотами, кому как угодно.
- Увеличение лотов
- Уменьшение лотов
Первый механизм стоит использовать при инвертированной торговле, когда мы ставим на то, что сигнал в скором времени инвертируется. Второй вариант работает только, если известно, что сигнал стабилен и продержится долго. Управляющие функции можно выбрать самые разнообразные. Я взял самые простые — линейные. Иначе говоря лоты, изменяются в зависимости от времени. Сейчас я покажу, как работают данные механизмы на практике.
Для этих целей я взял M15 котировку пары USDJPY. В данном случае я выбрал MQL4 версию робота для демонстрации, поскольку бектесты на реальных тиках этот робот не проходит, потому что он торгует в точках повышенного спреда. Мне хотелось доказать, что достаточно качественный брутфорс на низких таймфреймах способен обеспечить хороший форвард-период размером с областью, на которой производился брутфорс, и выше. В виду того, что мощности мои сейчас крайне ограничены, этому вопросу пришлось уделить минимум времени. Но данного результата вполне хватит для того, чтобы и продемонстрировать достаточно длительный рабочий форвард-период и два механизма работы с лотами на данных форвард участках. Начнем с демонстрации найденного варианта на участке, где производиля поиск. Размер участка — один год:
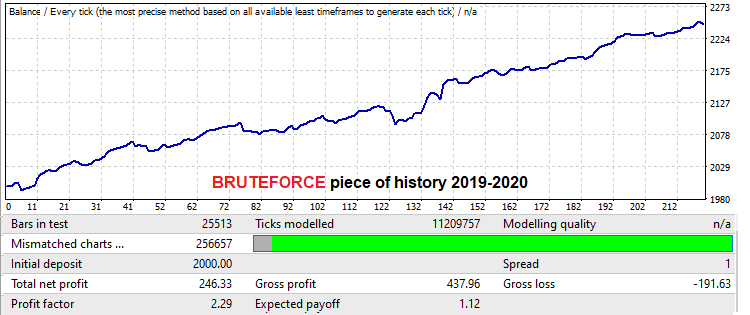
Математическое ожидание здесь чуть больше 12 пунктов, если не учитывать спред, но нам оно особо неинтересно, раз мы абстрагируемся от спреда. Будем смотреть на профит-фактор. Тест на год в будущее выглядит вот так:
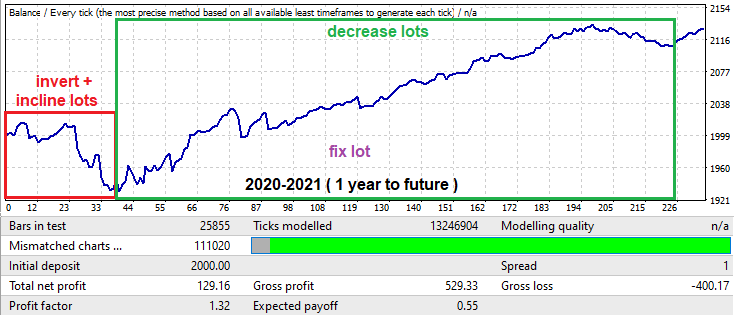
Очень интересно, что несмотря на то, что поиск производился всего по одному году, продолжительность работы закономерности составила по крайней мере 1 год, что очень неплохо. Это означает на практике, что при наличии хорошего железа можно за недельку-другую произвести анализ всех основных валютных пар с низкими спредами, после чего выбрать самые хорошие варианты и, по крайней мере, еще год эксплуатировать закономерность. Конечно при условии, что она выдержала бектест на реальных тиках в MetaTrader 5. Конечно, чтобы железно подтвердить данное предположение, нужно гораздо больше времени и наличие большого количества хороших серверов и усердие, но данный анализ возможно провести силами нескольких человек при желании, при этом не нужно будет прикладывать каких-то титанических усилий, ведь всю работу делает машина, а наша задача — только сбор результатов и составление статистики.
Теперь посмотрим на бектест из будущего, там в начале есть очень большая просадка, которая обычно очень часто встречается, когда мы ищем закономерности на небольших участках типа года, тем не менее можно и эту просадку использовать в своих целях. На бектесте по году этот участок выделен красной рамкой. Я ограничил время работы советника в настройках чтобы он торговал ровно 50 торговых дней (суббота и воскресенье не считаются), а так же инвертировал сигнал, чтобы просадка стала прибылью. Сделал я это для того, чтобы отсечь ту часть графика которая начинает идти в плюс после данной просадки, поскольку она превратится в отрицательную при инверте. В итоге бектест станет вот таким:
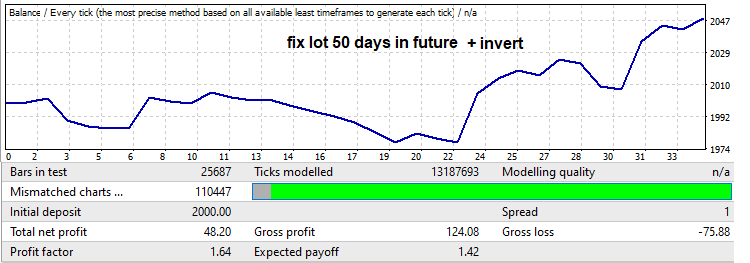
Обратите внимание на профит-фактор. Его мы собираемся увеличивать. На самом деле никогда не угадаешь, будет ли разворот и насколько далеко этот разворот уйдет, но обычно он откатывает достаточно большую часть движения, которое произошло на участке брутфорса. Если применить линейное усиление лота от минимального к максимальному, то мы получим вот такой бектест и усиление профит-фактора:
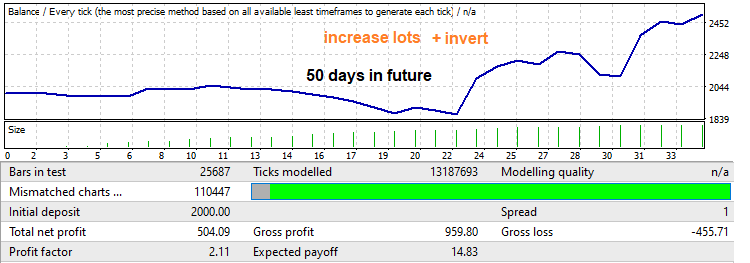
Теперь продемонстрирую обратный механизм, на бектесте за 1 год в будущее он выделен зеленым. На этом участке как раз есть довольно большой возрастающий участок и в конце — разворот закономерности. Данную ситуацию мы и будем исправлять при помощи затухающих лотов. Я выставил настройки робота так, чтобы торговля шла как раз до края данного участка. Сначала протестируем его с фиксированным лотом, чтобы было с чем сравнивать наш результирующий профит-фактор, который мы получим после того, как применим наш второй механизм:
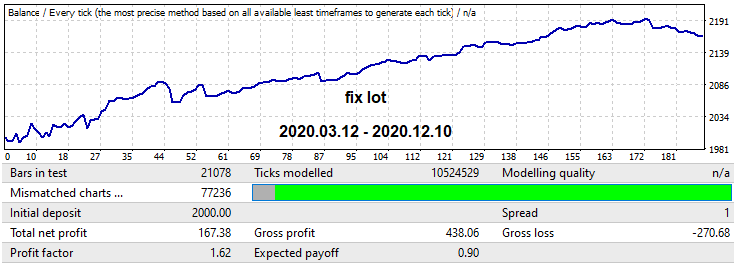
Теперь я включаю механизм, который реализует уменьшение лотов со временем, и мы так же получаем усиление профит-фактора, только график становится гораздо более приятнее и глаже, кроме того мы избавились от просадки в конце:
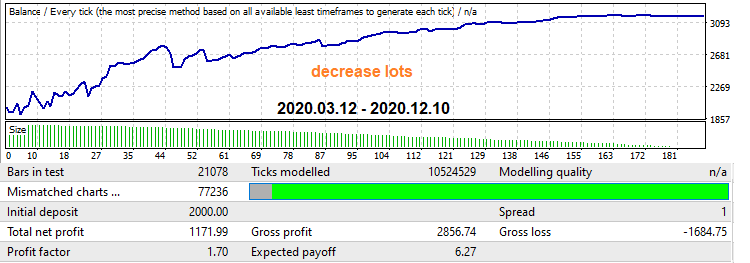
Данные приемы я видел в роботах у многих продавцов. Если применять их в нужное время и нужном месте, то можно как усилить показатели прибыльности, так и сократить убытки. В теории, конечно, все красиво, но на практике же все намного сложнее, тем не менее данные механизмы теперь присутствуют в советниках, которые генерирует моя программа, и их можно включать и выключать ситуативно.
Рабочие варианты на глобальной истории
Я думаю, многим было бы интересно увидеть своими глазами и пощупать хоть какие-то варианты рабочих настроек, которые способны проходить глобальные бектесты по реальной тиковой истории. Такие настройки были мной найдены. По причине ограниченных вычислительных мощностей и в виду того, что я произвожу брутфорс в одиночку, данные поиски заняли достаточно продолжительное время, но тем не менее несколько вариантов мне уже удалось найти, вот они:
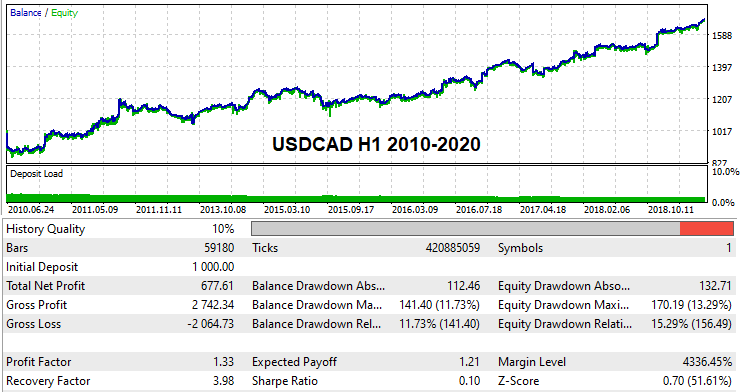
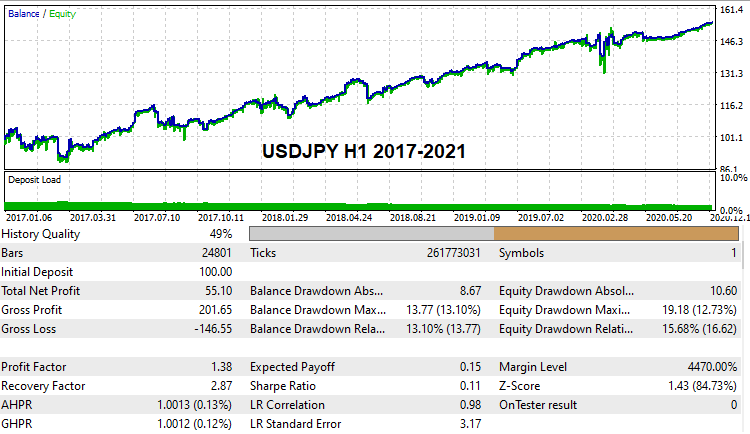
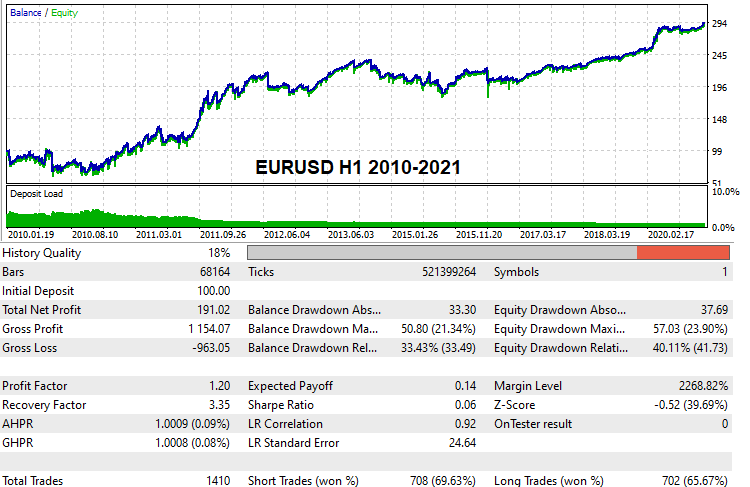
Данные настройки будут приложены к статье и каждый желающий сможет самостоятельно протестировать их при желании. Ну и, конечно, никто не мешает искать свои настройки и проверять бектестами на демо счетах. В целом, начиная с этой версии решения, любой желающий может попробовать данный метод.
Математика брутфорса
Данный раздел стоит осветить максимально подробно, чтобы у любого пользователя осталось минимум вопросов касаемо данного метода. Начнем с того, как работает первая вкладка программы и как стоит интерпретировать ее результаты.
Брутфорс на первой вкладке
На самом деле все, что происходит в любом брутфорс алгоритме, всегда подчиняется теории вероятностей — всё потому, что у нас всегда есть какая-то модель и всегда есть итерация, одна итерация. Под итерацией понимается полный цикл анализа текущего варианта стратегии. Полный цикл может состоять как из одного теста, так и из десяти, все зависит от конкретного подхода. Не так важно сколько тестов и прочих манипуляций с вариантом производит алгоритм метода, все это можно классифицировать как одну итерацию. Итерацию можно считать успешной или неуспешной в зависимости от предъявляемых требований к результату. Критериями хорошего результата могут служить самые различные количественные показатели, все зависит опять же от того, каков метод анализа.
На выходе алгоритма всегда один или несколько вариантов, подходящих под наши требования. В наших силах только сказать алгоритму, сколько данных результатов хранить в памяти. Все остальные результаты, которые попадают под требования, но которым не хватило места в хранилище, неизбежно будут выброшены. Независимо от того, сколько ступеней в нашем брутфорсе, данный процесс всегда будет иметь место просто потому, что данный процесс неизбежен. В альтернативном случае мы сталкиваемся с ситуацией, когда мы рискуем потратить время на обработку заведомо низкокачественных данных. Так мы не потеряем ни одного варианта, но это может на порядок снизить скорость поиска. Какой подход использовать, в конечном итоге решать вам.
Теперь перейду прямо к делу. Любой процесс поиска результатов в конечном итоге сводится к процессу независимых испытаний по схеме Бернулли, конечно же, если алгоритм фиксирован. Все зависит от вероятности выпадения хорошего варианта. Данная вероятность всегда фиксирована для фиксированного алгоритма. В нашем случае эта вероятность зависит от следующих величин:
- Размер выборки
- Вариативность алгоритма
- Близость к основе
- Жесткость требований к конечному результату
Количество и качество полученных результатов, конечно же, в связи с этим растет с количеством итераций, ровно по формуле Бернулли. Но стоит помнить, что это процесс чисто вероятностный! То есть нельзя со стопроцентной вероятностью спрогнозировать, какой набор результатов мы получим, а можно лишь посчитать вероятность того, что желаемый результат будет найден:
- Pk - вероятность, что из итерации получится рабочий вариант c заданными требованиями (в зависимости от требований данная вероятность сильно скачет)
- C(n,m) - количество сочетаний из "n" по "m"
- Pa=Сумм(m0...m...n)[C(n,m)*Pow(Pk ,m)*Pow(1-Pk ,n-m)] - вероятность того, что по истечении "n" итераций мы получим хотя бы "m0" первичных вариантов, которые удовлетворяют нашим требованиям
- m0 - минимальное количество удовлетворительных прототипов
- Pa — вероятность того, что в результате разработки мы получим хотя-бы "m0" или больше из "n" итераций внутри софта.
- n — максимально доступное количество циклов поиска рабочих прототипов (сколько мы готовы ждать результатов)
Количество циклов можно также выразить через время, если взять скорость брутфорса со счетчика на первой вкладке и время, которое мы готовы потратить на обработку текущих данных:
- Sh - скорость итераций в час
- T - время в часах которое мы готовы ждать
- n = Sh*T
Примерно похоже можно вычислить вероятность нахождения вариантов при условии требований к качеству. Наверху были формулы для простого нахождения вариантов, которые попадают под фильтр "Deviation", это требование к линейности результата. Если этот фильтр не включать, то каждая итерация будет удачной и всегда будет найден какой-либо вариант, независимо от того, какой показатель найден. Варианты будут сортироваться по показателю качества. При условии требований качеству величина "Ps" будет функцией от величины качества взятой по модулю. Чем больше качество, которое нам требуется, тем меньше величина данной функции:
- Ps - вероятность выпадения результата с определенными дополнительными требованиями качества
- q - требуемое качество, которое мы хотим получить
- qMax - максимально доступное качество
- Ps = Ps(|q|) = K * Px(|q|) , q <= qMax
- K = Pk - данный коэффициент учитывает вероятность выпадения какого-либо произвольного варианта (а уже из них отбираются варианты по качеству)
- Ps ' (|q|) < 0
- Lim (q-->qMax) [ Ps(|q|) ] = 0
Первая производная данной функции отрицательна, символизируя, что с возрастанием требований вероятность их выполнения стремится к нулю. При стремлении "q" к максимально доступному значению величина данной функции стремится к "0", поскольку это вероятность. При "q" большей, чем максимальное значение, данная функция не имеет смысла, поскольку более высокое качество недостижимо для выбранного алгоритма. Данная функция является следствием функции плотности распределения вероятности случайной величины "q". Ps(q) и плотность вероятности случайной величины P(q) изображены ниже, как и дополнительные важные для понимания величины:
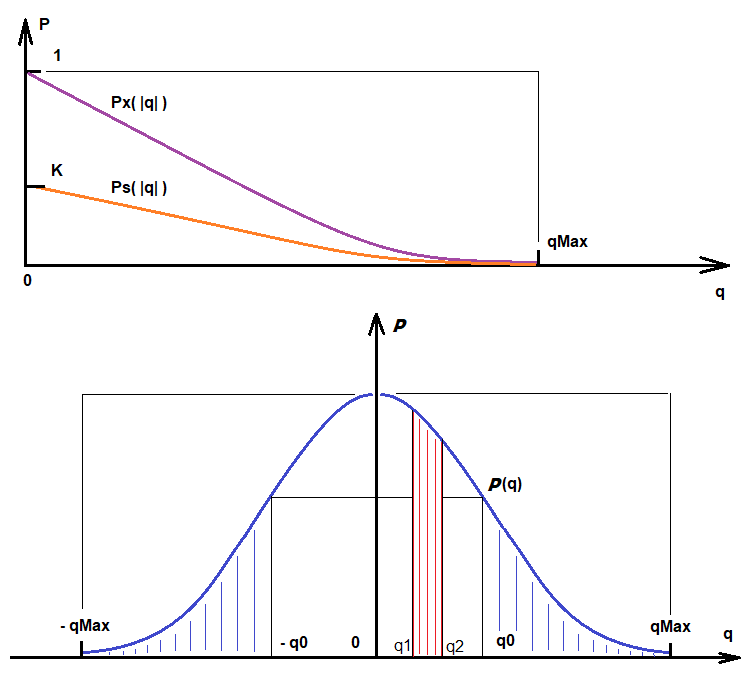
Исходя из данных иллюстраций можно записать:
- Integral(q0,qMax) [P(q)] = Integral(-qMax,-q0) [P(q)] = K*Px(|q|) = Ps(|q|) - вероятность того, что при текущей итерации выпадет вариант с |q| от q0 до qMax .
- Integral(q1,q2) [P(q)] - вероятность того, что в результате итерации выпадет значение качества в диапазоне от q1 до q2 (просто для примера как интерпретировать показания функции распределения случайной величины)
Видно, что чем больше качества мы хотим, тем больше времени мы должны потратить и тем меньше таких вариантов будет найдено в зависимости от наших аппетитов. Кроме того, у любого метода есть верхнее ограничение величины качества, которое зависит как от данных, которые мы анализируем, так и от совершенства нашего метода.
Оптимизация на второй вкладке
Процесс оптимизации на второй вкладке немного отличается от процесса первичного поиска, но в целом за основу взята все та же итерация и вероятность выпадения варианта, удовлетворяющего нашим требованиям. Фильтров здесь гораздо больше и, соответственно, вероятность выпадения хороших результатов тоже ниже. Но, так как на второй вкладке улучшаются уже обработанные варианты, то чем лучше и красивее варианты на первой, тем лучшие показатели мы получим на второй вкладке с более высокой вероятностью. Процесс улучшения конкретного варианта уже не опишешь так просто уравнением Бернулли, но тем не менее итоговая формула будет похожа на него чем-то. Нас будет интересовать вероятность выпадения хотя бы одного варианта, который попадает под наши фильтры. Распишу все это:
- Py = Сумм(1...m...n)[ Сумм(0... i ... C(n,m)-1) { Произведение(0 .. j .. i-1 )[Pk[j]) * Произведение(i .. j .. m) [1 - Pk[j]] } ] - вероятность выпадения хотя бы одного удовлетворительного варианта, отвечающего требованиям фильтров
- Pk[i] - вероятность выпадения варианта, удовлетворяющего требованиям фильтров второй вкладки
- n - разбиение интервала оптимизации (Interval Points значение на 2 вкладке)
Оптимизация происходит точно так же, как и в оптимизаторах терминалов MetaTrader 4 и MetaTrader 5, за тем лишь отличием, что оптимизируется всего один параметр, который и является нашим сигналом на покупку или продажу. Шаг оптимизации вычисляется автоматически, исходя из того, на сколько частей мы дробим интервал оптимизации (Interval Points). Верхнее значение числа, которое мы оптимизируем, вычисляется в процессе поиска на первой вкладке. После того, как процесс на первой вкладке прошел, нам становится известен диапазон колебания значений оптимизируемого числа, и на второй вкладке нам остается только задать точность сетки для дробления этого интервала. В результате оптимизации данный вариант как занимал 1 слот вариантов, так и занимает на второй вкладке, просто он будет обновляться по мере получения более лучшего качества.
Точно так же, как и на первой вкладке, вероятность получения какого-то варианта с требованиями к качеству будет точно так же иметь некую функцию распределения, похожую на ту, которая была выше. Соответственно, это означает, что можно к этому процессу применить те же формулы, за небольшим отличием:
- Integral(q0,qMax) [P(q)] = Integral(-qMax,-q0) [P(q)] = K*Px(|q|) = Pz(|q|) - вероятность того, что при текущей итерации выпадет вариант с |q| от q0 до qMax .
- K = Py
Отличие тут только в коэффициенте "K", который равен уже новой вероятности, которую мы получили чуть выше. Вероятность выпадения требуемого качества из одного варианта ничтожно мала, но ведь на первой вкладке у нас очень много таких вариантов, и чем их больше, тем для нас лучше. Из этого даже на интуитивном уровне следует, что чем больше первичных вариантов, то тем больше и лучше варианты появятся на второй вкладке. Считается все это аналогично. К сожалению, формула Бернулли тут неприменима, но применима предыдущая конструкция, которая встала на ее замену. Тут мы уже интерпретируем оптимизацию одного варианта как отдельную итерацию. Количество итераций, значит, будет в точности равно этому числу. Нам необходим хотя бы один вариант, который удовлетворяет нашим требованиям, поэтому прошлая формула идеально нам подходит, только, конечно, нужно заменить величину Pk на Pz, которая будет определяться уже семейством функций Pz[j](|q|), так как для каждого варианта оптимизации существует своя такая функция в силу того, что варианты разные.
- Pb = Сумм(1...m...n)[ Сумм(0... i ... C(n,m)-1) { Произведение(0.. j .. i-1 )[Pz[j]) * Произведение(i.. j .. m) [1 - Pz[j]] } ]
- n - количество найденных вариантов на первой вкладке
Итог таков, что чем больше брутим, тем большее качество получаем, конечно при этом не забываем что абсолютно каждый параметр влияет как на вероятности, так и на результат. Настройки стоит выставлять с умом и не переводить зря вычислительные ресурсы. Современные машины очень сильны, но не стоит забывать про то, что грамотная настройка и знание деталей повысит эффективность ваших машин в разы, а в некоторых случаях в десятки раз.
Немного о прибивке к истории и переобучении
Так называемая "прибивка к истории или "переобучение'' — это беда очень большого числа автоматических торговых систем. На самом деле понятия разные, но на деле означают одно и то же. Можно создать такую торговую систему, которая будет показывать невероятные показатели, вплоть до 1000 процентов в месяц. На самом деле такие системы в реальности никогда не будут работать. Часть пользователей выиграет и будет несказанно рада, а вторая часть будет неистово ругать торговую систему. Я никогда не удивлялся данному факту. Поведение людей, в особенности покупателя, поддается статистическому анализу и очень классно вписывается в теорию вероятности.
Теперь ближе к делу. Чем больше входных параметров у торговой системы и чем больше вариативность логики советника, тем лучше такой советник прибивается в историю. Все дело в том, что мы имеем очень простой процесс преобразования котировки в другой формат данных. Всегда есть прямая и обратная функции преобразования, которые могут обеспечить как прямой, так и обратный процесс преобразования данных. Это можно сравнить с шифрованием и дешифрованием. Например архив WinRar — типичный пример шифрования, если установить пароль. У него есть и сжатие, но это мы опустим. В контексте нашей задачи алгоритмом шифрования является комбинация процесса оптимизации и наличия торговой логики. Достаточное количество бектестов в оптимизаторе и определенная гибкая логика способны сотворить чудо — тестерный Грааль. Сама же торговая логика и является тем же дешифратором, который дешифрует будущие цены исходя из показаний прошлого.
К сожалению, тестерным граалем являются в какой-то степени все советники, разница только в степени их прибивки к истории. Но раз есть прибивочная часть логики, то есть и та часть, которая должна сохранить часть работоспособности в будущем. На деле такой алгоритм крайне трудно получить. Сложность состоит в том, что мы не знаем, каковы максимальные возможности "честного предсказания" конкретного алгоритма, и мы в итоге из-за этого не можем определить границы переобучения. Для того чтобы максимально абстрагироваться от этого негативного процесса, мы должны обеспечить такой алгоритм, который сможет с наибольшей вероятностью предсказать движение следующей свечи, при этом чем сильнее степень сжатия ценовых данных, тем больше доверия к этому алгоритму. Например, возьмем какую-нибудь функцию типа sin(w*t) , мы знаем что этой функции соответствует бесконечное число точек [X[i],Y[i]] — это массив данных бесконечной длинны, который сжимается в одну коротенькую запись функции синуса. В данном случае мы имеем идеальное сжатие данных. На деле такое сжатие невозможно и у нас всегда есть какой-то коэффициент сжатия данных. Чем больше этот коэфициент, тем более качественно определена формула рынка.
В моем методе количество варьируемых данных фиксирована, но тем не менее, как и в любом другом методе, прибивка к истории возможна. Единственным способом борьбы с прибивкой к истории является увеличение коэффициента сжатия данных. Реализуеется это только через увеличение размеров анализируемого участка истории. Есть и второй путь — уменьшение количества анализируемых баров в формуле (Bars To Equation). В реальности же лучше прибегать к первому методу, потому что уменьшая количество баров в формуле, мы заведомо снижаем верхнюю границу "qMax", а нам бы желательно ее увеличивать. Подводя итоги, лучше всего брать как больше размер выборки для обучения, так не скупиться и на "Bars To Equation", но при этом нужно помнить, что чрезмерное повышение данной величины как уменьшает скорость нашего брутфорса, так и неизбежно создает риски более высокого показателя прибивки к истории.
Рекомендации к использованию
В процессе тестирования решения были определены некоторые важные тонкости по настройке основной программы Awaiter.exe. Сейчас я постараюсь перечислить самые важные из этих тонкостей ниже:
- Когда вы выставили настройки на всех вкладках так, как вам хочется, то обязательно сохраняем их (кнопка Save Settings)
- На второй вкладке можно включать Spread Control
- При генерации котировок советником HistoryWriter использовать как можно больше выборку (минимум 10 лет истории)
- На первой вкладке можно сохранять побольше вариантов, 1000 вполне достаточно ( Variants Memory )
- На вкладке оптимизации не выставляйте слишком много Interval Points (20-100 вполне достаточно)
- Если хотим получить более менее нормальные настройки, у которых есть шанс пройти бектест по реальным тикам, то не стоит требовать от оптимизатора большого количества ордеров в вариантах (Min Orders)
- Необходимо контролировать скорость поиска вариантов (если вы уже очень долго брутите и варианты вообще не находятся, значит, стоит подумать о том, чтобы поменять настройки)
- Для получения максимально стабильных результатов выставляйте Deviation в диапазоне "0.1 - 0.2", лучше если 0.1
- При использовании уравнения "FOURIER" на вкладке оптимизации используйте галку "Spread Control" (формула очень нежная и крайне чувствительна к спредовым шумам)
Заключение
В заключение скажу, конечно же, не стоит интерпретировать данное решение как Грааль. В действительности это лишь инструмент. Довольно трудно реализовать достаточно эффективное и в то же время удобное для любого пользователя решение, при этом еще избавляя его от программирования и процесса оптимизации в терминалах MetaTrader 4 и MetaTrader 5. Но я считаю, что задача минимум все-таки выполнена и решение готово к общему использованию. Конечно, у меня есть сомнения насчет того, что оно кому-то приглянется, но в целом это не так важно.
Я думаю, что найдутся люди, которым данный метод будет полезен. Конечно, простора для улучшений еще очень много, как и несовершенств и багов, но в целом уже есть рабочий инструмент как для изучения рынка, так и для торговли. Но радует то, что теперь в большей степени все зависит от вычислительных мощностей, а не от улучшений. Несмотря на готовность, все еще очень сыро конечно, но я надеюсь что в будущем все удастся исправить.
Есть еще идеи касаемо проекта, надеюсь постепенно все реализовать по мере появления свободного времени. Одной из таких идей является построение логического полинома на основе самых знаменитых как осцилляторных индикаторов, так и ценовых, на подобие полос Боллинджера или Moving Average. Но данную концепцию нужно сначала тщательно обмозговать. Мне бы не хотелось опускаться до уровня "индикаторы пересеклись — торганул", но все же можно грамотно применять сигналы индикаторов, кое-какие идеи имеются. Так же надеюсь, что смог привнести что-то новое и какую-то общую полезную информацию для людей, которая была бы полезна если не в практическом плане, то хотя бы в теоретическом.
Ссылки на предыдущие статьи цикла
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети — это просто (Часть 13): Пакетная нормализация (Batch Normalization)
Нейросети — это просто (Часть 13): Пакетная нормализация (Batch Normalization)
 Многослойный перцептрон и алгоритм обратного распространения ошибки
Многослойный перцептрон и алгоритм обратного распространения ошибки
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Не понятно, зачем все это? За десять лет прогона в тестере на фунте получить 107 фунтов прибыли? А может выйти на площадь и попросит подаяния?
Интересно вы считаете, не проценты годовых а просто фунты, да еще только одну валютную пару. Про прогнозы работы в будущем я вообще молчу. Вам дается инструмент для исследования рынка, для создания и поиска прибыльных торговых систем без участия человека, а вам не то чтобы лень на кнопку просто нажать, а лень даже вникнуть. Подозреваю что если я начну новый цикл статей по нейросетям, то суть ваших реплик не изменится. Теперь я вас спрошу вы на какие проценты годовых рассчитываете при торговле или использовании автоматической торговой системы ?
Я скачал вложения к статье. Я научился использовать "Forex Awaiter" для поиска методом грубой силы, посмотрев видео Ютобура. В итоге "Awaiter" сгенерировал документ "GBPUSD 5 MATH_WAITING OPTIMIZED.txt", но как мне использовать этот документ? Или как можно превратить этот документ в конфигурационный файл типа *.set?
И еще, этот документ создается для бэктестинга через "Reciever" или "Sacred fruit"? И все тот же вопрос, как преобразовать сгенерированный результат в соответствующий файл настроек советника?
Большое спасибо, что поделились, спасибо!
Я скачал вложения к статье. Я научился использовать "Forex Awaiter" для поиска методом грубой силы, посмотрев видео Ютобура. В итоге "Awaiter" сгенерировал документ "GBPUSD 5 MATH_WAITING OPTIMIZED.txt", но как мне использовать этот документ? Или как превратить этот документ в конфигурационный файл типа *.set?
И еще, этот документ создается для бэктестинга через "Reciever" или "Sacred fruit"? И все тот же вопрос, как преобразовать сгенерированный результат в соответствующий файл настроек советника?
Большое спасибо, что поделились, спасибо!
Thank you very much for your work!
Unfortunately, I do not understand exactly how I convert the data from the awaiter into an MT5 EA
If I understand everything correctly, I have to upload the data from the awaiter (see below) to the Reciever.ex5, right?
Additionally, If you could upload the Reciever.ex5 as .mql5 file, I would be more likely to understand how the Reciever accesses the file from the Awaiter.
Большое спасибо за вашу работу! К сожалению, я точно не понимаю, как я преобразую данные от Anciter в MT5 EA Если я все правильно понимаю, я должен загрузить данные от avaiter reciever.ex5, верно?
Если вы можете загрузить файл Reciever.ex5 в качестве файла .mql5, я был бы, скорее всего, поймете, как присоединяется к файлу от avaiter.Большое спасибо! :)