Математика в трейдинге: Коэффициенты Шарпа и Сортино

MetaTrader 5 — Трейдинг | 11 марта 2022, 09:51

6 250

Доходность является самым очевидным показателем, который используют инвесторы и начинающие трейдеры для анализа эффективности торговли. Профессиональные трейдеры пользуются более надежными инструментами для анализа стратегии, среди них — коэффициенты Шарпа и Сортино. В этой статье мы расскажем на простых примерах, как они считаются. Тема оценки торговых стратегий уже рассматривалась в предыдущей статье "Математика в трейдинге. Оценка результатов торговых сделок". Рекомендуем почитать эту статью, чтобы освежить знания или узнать что-то новое для себя.

Коэффициент Шарпа

Опытные инвесторы и трейдеры знают, что для получения стабильных результатов необходимо торговать несколькими стратегиями или инвестировать в несколько разных ценных бумаг. Это одна из концепций разумного инвестирования, которая предполагает создание инвестиционного портфеля. Каждый портфель бумаг/стратегий будет иметь свои параметры риска и доходности, поэтому требуется как-то сравнивать их между собой.

Один из первых инструментов такого сравнения — коэффициент Шарпа — был разработан в 1966 году будущим нобелевским лауреатом Уильямом Шарпом. Основные показатели, используемые этим инструментом, — это средняя доходность, стандартное отклонение доходности и безрисковая доходность.

Недостаток коэффициента Шарпа в том, что исходные данные для его анализа должны быть нормально распределены. Иными словами, график распределения доходностей должен быть симметричным и не должен иметь резких пиков или падений.

Расчёт коэффициента Шарпа производится по следующей формуле:

Sharpe Ratio = (Return - RiskFree)/Std

где:

Return — среднее значение дохода за некий период. Например, за месяц, квартал, год и т.д.
RiskFree — значение безрискового дохода за тот же промежуток времени. Это может быть процент на депозит в банке, облигации и другие финансовые инструменты с минимальным риском и 100-процентной надежностью.
Std — стандартное отклонение доходностей за этот же период. Чем сильнее разброс доходностей, тем выше риск и выше волатильность испытывает счет трейдера/активы портфеля/средства под управлением фонда.

Доходность

Доходность вычисляется как изменение стоимости активов за какой-то интервал. Значения доходностей берутся за тот период времени, на который рассчитывается коэффициент Шарпа. Как правило, рассматривают значение коэффициента Шарпа за год, но можно рассчитывать квартальные, месячные и даже дневные значения. Доходности рассчитываются по формуле:

Return[i] = (Close[i]-Close[i-1])/Close[i-1]

где:

Return[i] — доходность за интервала с индексом i;
Close[i] — стоимость активов на конец i-го интервала;
Close[i-1] — стоимость активов на конец предыдущего интервала.

Другими словами, доходность можно записать как относительное изменение стоимости активов за интервал:

Return[i] = Delta[i]/Previous

где:

Delta[i] = (Close[i]-Close[i-1]) — абсолютное изменение стоимости активов за интервал;
Previous = Close[i-1] — стоимость активов на конец предыдущего интервала.

Для того чтобы посчитать коэффициент Шарпа на дневных значениях за год, нам нужно взять значения доходностей за каждый день в течение этого года и вычислить среднюю дневную доходность как сумму доходностей, поделенную на количество дней, которые попали в расчет.

Return = Sum(Return[i])/N

где N — количество дней.

Безрисковый доход

Понятие безрискового дохода условно, так как риск есть всегда. Кроме того, так как коэффициент Шарпа используют для сравнения различных стратегий/портфелей на одинаковом интервале времени, то проще всего принять безрисковый доход равным нулю. То есть

RiskFree = 0

Стандартное отклонение доходностей

Стандартное отклонение показывает разброс случайной величины вокруг среднего значения. Сначала вычисляется среднее значение доходности, затем складываются квадраты отклонений доходностей от среднего значения. Полученную сумму делится на количество доходностей — это дисперсия. Квадратный корень из дисперсии — это и есть стандартное отклонение доходностей.

D = Sum((Return - Return[i])^2 )/N

STD = SQRT(D)

Пример расчета стандартного отклонения дается в упомянутой ранее статье.

Расчет коэффициента Шарпа на любом таймфрейме и приведение его к годовому значению

Расчет коэффициента Шарпа не изменился с 1966 года, а современное название этот показатель получил после всемирного признания его методики. В то время оценку фондов и портфелей делали на основании доходов, полученных за несколько лет. Позже стали делать расчеты на месячных данных и переводить полученный коэффициент Шарпа в годовое значение. Таким образом можно сравнивать два фонда/портфеля/стратегии.

Коэффициент Шарпа легко масштабируется на разных интервалах и таймфреймах к годовому значению. Для этого нужно полученное значение умножить на корень квадратный из отношения годового интервала к текущему. Покажем на простом примере.

Пусть мы рассчитали коэффициент Шарпа на дневных значениях доходности — SharpeDaily. Теперь нам нужно полученный показатель привести к годовому значению SharpeAnnual. Годовой коэффициент пропорционален квадратному корню соотношения периодов — проще говоря, сколько интервалов укладывается в год. Так как в году 252 рабочих дня, то коэффициент Шарпа, полученный на дневных доходностях, нужно умножить на корень квадратный из 252. Это и будет годовое значение коэффициента Шарпа:

SharpeAnnual = SQRT(252)*SharpeDaily // в году 252 рабочих дня

Если считать на таймфрейме H1, то принцип остается тот же — сначала приводим SharpeHourly к SharpeDaily, а затем получаем годовой коэффициент Шарпа. Один бар на таймфрейме D1 содержит в себе 24 бара H1, поэтому формула будет такой:

SharpeDaily = SQRT(24)*SharpeHourly   // в D1 входит 24 часа

Хотя не все финансовые инструменты торгуются 24 часа в сутки, но для целей оценки торговых стратегий в тестере на одном и том же инструменте это не имеет значения, так как сравнение стратегий происходит на одном и том же периоде тестирования и таймфрейме.

Оценка стратегий с помощью коэффициента Шарпа

В зависимости от показателей стратегии/портфеля Sharpe Ratio может принимать любые значения, в том числе и отрицательные. Приведение коэффициента Шарпа к годовому значению позволяет трактовать его классическим образом:

Значение	Оценка	Описание
Sharpe Ratio < 0	Плохо	Стратегия убыточна, не годится
0 < Sharpe Ratio < 1.0	Неопределенно	Риск не окупается. Такие стратегии могут браться в работу, если нет альтернатив
Sharpe Ratio ≥ 1.0	Хорошо	Если коэффициент Шарпа превышает единицу, это означает, что риск окупается, портфель/стратегия работает
Sharpe Ratio ≥ 3.0	Очень хорошо	Высокий показатель говорит о том, что вероятность получить убыток в каждой конкретной сделке очень мала

Нужно помнить, что коэффициент Шарпа — обычный статистический показатель. Это просто доходность отнесенная к риску. Поэтому при анализе портфелей и стратегий важно соотносить Sharpe Ratio с рекомендованными значениями и/или между собой.

Расчет коэффициента Шарпа на EURUSD за 2020 год

Коэффициент Шарпа изначально разрабатывался для оценки портфелей, которые всегда имеют в своем составе множество акций. Стоимость акций изменяется каждый день, соответственно изменяется и стоимость портфеля. Таким образом, снимать изменение стоимости и доходности можно на любом таймфрейме. Мы проведем вычисления на валютной паре EURUSD.

Расчеты сделаем на таймфреймах H1 и D1, затем приведем к годовому значению и сравним, чтобы понять — есть ли разница и почему. Вычисления будем делать по ценам закрытия баров в течение 2020 года.

Код на MQL5

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   double H1_close[],D1_close[];
   double h1_returns[],d1_returns[];
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nВычислим среднее и среднеквадратичное отклонение доходностей на барах H1");
      Print("H1 bars=",ArraySize(H1_close));
      GetReturns(H1_close,h1_returns);
      double average = ArrayMean(h1_returns);
      PrintFormat("H1 average=%G",average);
      double std = ArrayStd(h1_returns);
      PrintFormat("H1 std=%G",std);
      double sharpe_H1 = average / std;
      PrintFormat("H1 Sharpe=%G",sharpe_H1);
      double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_H1);
     }

   bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nВычислим среднее и среднеквадратичное отклонение доходностей на барах D1");     
      Print("D1 bars=",ArraySize(D1_close));
      GetReturns(D1_close,d1_returns);
      double average = ArrayMean(d1_returns);
      PrintFormat("D1 average=%G",average);
      double std = ArrayStd(d1_returns);
      PrintFormat("D1 std=%G",std);
      double sharpe_D1 = average / std;
      double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_D1);
     }
  }

//+------------------------------------------------------------------+
//|  Заполняет массив доходностей returns[]                          |
//+------------------------------------------------------------------+
void GetReturns(const double & values[], double & returns[])
  {
   int size = ArraySize(values);
//--- если меньше 2-х значений, то возвращаем пустой массив доходностей
   if(size < 2)
     {
      ArrayResize(returns,0);
      PrintFormat("%s: Error. ArraySize(values)=%d",size);
      return;
     }
   else
     {
      //--- заполним в цикле доходности
      ArrayResize(returns, size - 1);
      double delta;
      for(int i = 1; i < size; i++)
        {
         returns[i - 1] = 0;
         if(values[i - 1] != 0)
           {
            delta = values[i] - values[i - 1];
            returns[i - 1] = delta / values[i - 1];
           }
        }
     }
//---
  }
//+------------------------------------------------------------------+
//|  Вычисляет среднее значение элементов массива                    |
//+------------------------------------------------------------------+
double ArrayMean(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += array[i];
   mean /= size;
   return(mean);
  }
//+------------------------------------------------------------------+
//|  Вычисляет стандартное отклонение элементов массива              |
//+------------------------------------------------------------------+
double ArrayStd(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = ArrayMean(array);
   double std = 0;
   for(int i = 0; i < size; i++)
      std += (array[i] - mean) * (array[i] - mean);
   std /= size;
   std = MathSqrt(std);
   return(std);
  }  
//+------------------------------------------------------------------+

/*
Результат

Вычислим среднее и среднеквадратичное отклонение доходностей на барах H1
H1 bars:6226
H1 average=1.44468E-05
H1 std=0.00101979
H1 Sharpe=0.0141664
Sharpe_annual(H1)=1.117708053392263

Вычислим среднее и среднеквадратичное отклонение доходностей на барах D1
D1 bars:260
D1 average=0.000355823
D1 std=0.00470188
Sharpe_annual(H1)=1.2179005039019222

*/

Код на Python для вычисления с помощью библиотеки MetaTrader 5

import math
from datetime import datetime
import MetaTrader5 as mt5

# выведем данные о пакете MetaTrader5
print("MetaTrader5 package author: ", mt5.__author__)
print("MetaTrader5 package version: ", mt5.__version__)

# импортируем модуль pandas для вывода полученных данных в табличной форме
import pandas as pd

pd.set_option('display.max_columns', 50)  # сколько столбцов показываем
pd.set_option('display.width', 1500)  # макс. ширина таблицы для показа
# импортируем модуль pytz для работы с таймзоной
import pytz

# установим подключение к терминалу MetaTrader 5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# установим таймзону в UTC
timezone = pytz.timezone("Etc/UTC")
# создадим объекты datetime в таймзоне UTC, чтобы не применялось смещение локальной таймзоны
utc_from = datetime(2020, 1, 1, tzinfo=timezone)
utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone)
# получим бары с EURUSD H1 в интервале 2020.01.01 00:00 - 2020.31.12 13:00 в таймзоне UTC
rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to)
# получим также бары с D1 в интервале 2020.01.01 00:00 - 2020.31.12 13:00 в таймзоне UTC
rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to)
# завершим подключение к терминалу MetaTrader 5 и продолжим обработку полученных баров
mt5.shutdown()

# создадим из полученных данных DataFrame
rates_frame = pd.DataFrame(rates_H1)

# добавим столбец"Доходность"
rates_frame['return'] = 0.0
# теперь вычислим доходности как return[i] = (close[i] - close[i-1])/close[i-1]
prev_close = 0.0
for i, row in rates_frame.iterrows():
    close = row['close']
    rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0
    prev_close = close

print("\nВычислим среднее и среднеквадратичное отклонение доходностей на H1 барах")
print('H1 rates:', rates_frame.shape[0])
ret_average = rates_frame[1:]['return'].mean()  # не берем первую строку с нулевой доходностью
print('H1 return average=', ret_average)
ret_std = rates_frame[1:]['return'].std(ddof=0) # не берем первую строку с нулевой доходностью
print('H1 return std =', ret_std)
sharpe_H1 = ret_average / ret_std
print('H1 Sharpe = Average/STD = ', sharpe_H1)

sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1)
print('Sharpe_annual(H1) =', sharpe_annual_H1)

# теперь вычислим коэффициент Шарпа на таймфрейме D1
rates_daily = pd.DataFrame(rates_D1)

# добавим столбец "Доходность"
rates_daily['return'] = 0.0
# теперь вычислим доходности
prev_return = 0.0
for i, row in rates_daily.iterrows():
    close = row['close']
    rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0
    prev_return = close

print("\nВычислим среднее и среднеквадратичное отклонение доходностей на D1 барах")
print('D1 rates:', rates_daily.shape[0])
daily_average = rates_daily[1:]['return'].mean()
print('D1 return average=', daily_average)
daily_std = rates_daily[1:]['return'].std(ddof=0)
print('D1 return std =', daily_std)
sharpe_daily = daily_average / daily_std
print('D1 Sharpe =', sharpe_daily)

sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1)
print('Sharpe_annual(D1) =', sharpe_annual_D1)

Результат
Вычислим среднее и среднеквадратичное отклонение доходностей на H1 барах

H1 rates: 6226
H1 return average= 1.4446773215242986e-05
H1 return std = 0.0010197932969323495
H1 Sharpe = Average/STD = 0.014166373968823358
Sharpe_annual(H1) = 1.117708053392236

Вычислим среднее и среднеквадратичное отклонение доходностей на D1 барах
D1 rates: 260
D1 return average= 0.0003558228355051694
D1 return std = 0.004701883757646081
D1 Sharpe = 0.07567665511222807
Sharpe_annual(D1) = 1.2179005039019217

Видно, что результаты вычислений на MQL5 и Python совпадают. Исходные коды приложены к статье (CalculateSharpe_2TF).

При этом годовое значение коэффициента Шарпа, полученного на барах H1 и D1, отличаются между собой — 1.117708 против 1.217900. Изучим этот вопрос более детально.

Вычисление годового коэффициента Шарпа на EURUSD за 2020 год на всех таймфреймах

Вычислим таким же способом годовой коэффициент Шарпа на всех таймфреймах. Для этого полученные данные соберем в таблицу:

TF — таймфрейм
Minutes — сколько минут в таймфрейме
Rates — количество баров за год на данном таймфрейме
Avg — средняя доходность на таймфрейме за бар в процентах (средний процент изменения цены за бар)
Std — стандартное отклонение на таймфрейме за бар в процентах (волатильность цены в процентах на данном таймфрейме)
SharpeTF — коэффициент Шарпа, рассчитанный на данном таймфрейме
SharpeAnnual — годовой коэффициент Шарпа, который вычисляется на основании Шарпа на данном таймфрейме

Приведем блок кода для вычисления. Полный код — в приложенном файле CalculateSharpe_All_TF.mq5.

//--- структура для вывода статистики в лог
struct Stats
  {
   string            TF;
   int               Minutes;
   int               Rates;
   double            Avg;
   double            Std;
   double            SharpeTF;
   double            SharpeAnnual;
  };
//--- массив статистики по таймфреймам
Stats stats[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---массивы для цен закрытия
   double H1_close[],D1_close[];
//--- массивы доходностей
   double h1_returns[],d1_returns[];
//--- массив таймфреймов, на которых будем считать коэффициент Шарпа
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,
                                   PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1
                                  };

   ArrayResize(stats,ArraySize(timeframes));
//--- параметры запроса таймсерии
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print(symbol);
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- получим массив доходностей на указанном таймфрейме
      double returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      //--- вычислим статистику
      GetStats(returns,avr,std,sharpe);
      double sharpe_annual = sharpe * MathSqrt(ArraySize(returns));
      PrintFormat("%s  aver=%G%%   std=%G%%  sharpe=%G  sharpe_annual=%G",
                  EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual);
      //--- заполним структуру статистики
      Stats row;
      string tf_str = EnumToString(timeframes[i]);
      StringReplace(tf_str,"PERIOD_","");
      row.TF = tf_str;
      row.Minutes = PeriodSeconds(timeframes[i]) / 60;
      row.Rates = ArraySize(returns);
      row.Avg = avr;
      row.Std = std;
      row.SharpeTF = sharpe;
      row.SharpeAnnual = sharpe_annual;
      //--- добавим строку статистики для таймфрема
      stats[i] = row;
     }
//--- выведем в журнал статистику по всем таймфреймам
   ArrayPrint(stats,8);
  }

/*
Результат

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeTF] [SharpeAnnual]
[ 0] "M1"          1  373023 0.00000024 0.00168942 0.00168942     1.03182116
[ 1] "M2"          2  186573 0.00000048 0.00239916 0.00239916     1.03629642
[ 2] "M3"          3  124419 0.00000072 0.00296516 0.00296516     1.04590258
[ 3] "M4"          4   93302 0.00000096 0.00341717 0.00341717     1.04378592
[ 4] "M5"          5   74637 0.00000120 0.00379747 0.00379747     1.03746116
[ 5] "M6"          6   62248 0.00000143 0.00420265 0.00420265     1.04854166
[ 6] "M10"        10   37349 0.00000239 0.00542100 0.00542100     1.04765562
[ 7] "M12"        12   31124 0.00000286 0.00601079 0.00601079     1.06042363
[ 8] "M15"        15   24900 0.00000358 0.00671964 0.00671964     1.06034161
[ 9] "M20"        20   18675 0.00000477 0.00778573 0.00778573     1.06397070
[10] "M30"        30   12450 0.00000716 0.00966963 0.00966963     1.07893298
[11] "H1"         60    6225 0.00001445 0.01416637 0.01416637     1.11770805
[12] "H2"        120    3115 0.00002880 0.01978455 0.01978455     1.10421905
[13] "H3"        180    2076 0.00004305 0.02463458 0.02463458     1.12242890
[14] "H4"        240    1558 0.00005746 0.02871564 0.02871564     1.13344977
[15] "H6"        360    1038 0.00008643 0.03496339 0.03496339     1.12645075
[16] "H8"        480     779 0.00011508 0.03992838 0.03992838     1.11442404
[17] "H12"       720     519 0.00017188 0.05364323 0.05364323     1.22207717
[18] "D1"       1440     259 0.00035582 0.07567666 0.07567666     1.21790050
[19] "W1"      10080      51 0.00193306 0.14317328 0.14317328     1.02246174
[20] "MN1"     43200      12 0.00765726 0.43113365 0.43113365     1.49349076

*/

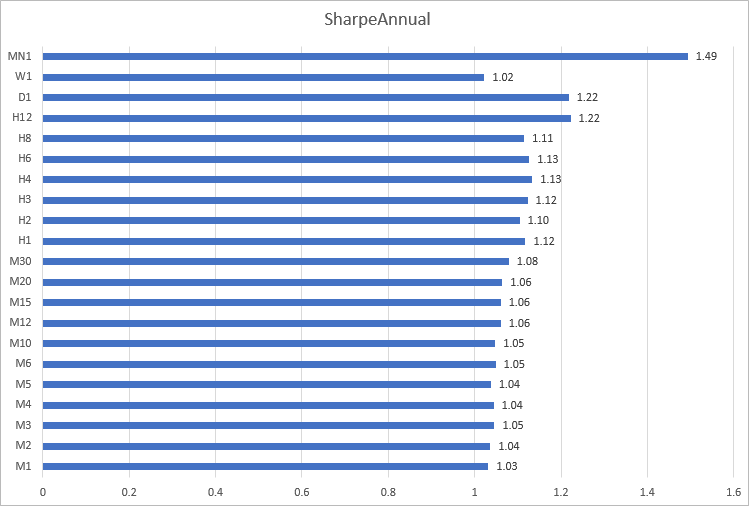
Построим гистограмму коэффициента Шарпа EURUSD за 2020 год по таймфреймам. Видно, что на минутных таймфреймах от M1 до M30 вычисления дают близкий результат от 1.03 до 1.08. Самые нестабильные результаты на таймфреймах от H12 до MN1.

Расчет годового коэффициента Шарпа на EURUSD за 2020 год по таймфреймам

Расчет коэффициента Шарпа за 2020 год на GBPUSD, USDJPY и USDCHF

Сделаем такие же расчеты еще на трех основных валютных парах.

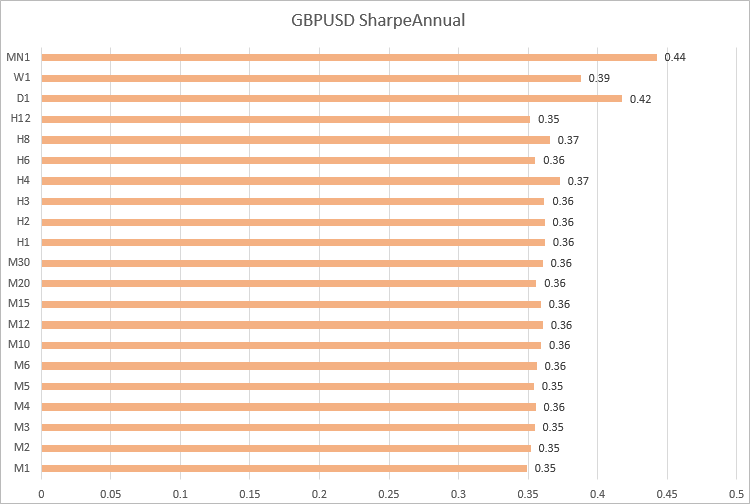
GBPUSD, значения коэффициента Шарпа получились близкими на таймфреймах от M1 до H12.

Расчет годового коэффициента Шарпа на GBPUSD за 2020 год по таймфреймам

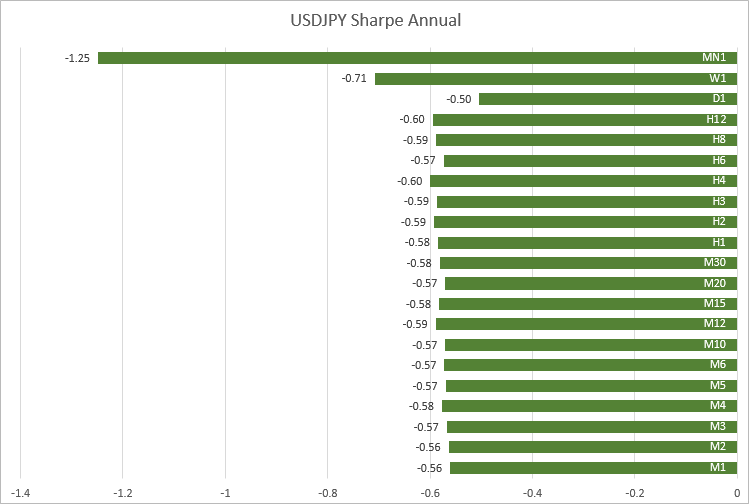
USDJPY, значения также получились близкими на таймфреймах от M1 до H12 — от -0.56 до -0.60.

Расчет годового коэффициента Шарпа на USDJPY за 2020 год по таймфреймам

USDCHF, близкие значения на таймфреймах от M1 до M30. С ростом таймфрейма коэффициент Шарпа испытывает колебания.

Расчет годового коэффициента Шарпа на USDCHF за 2020 год по таймфреймам

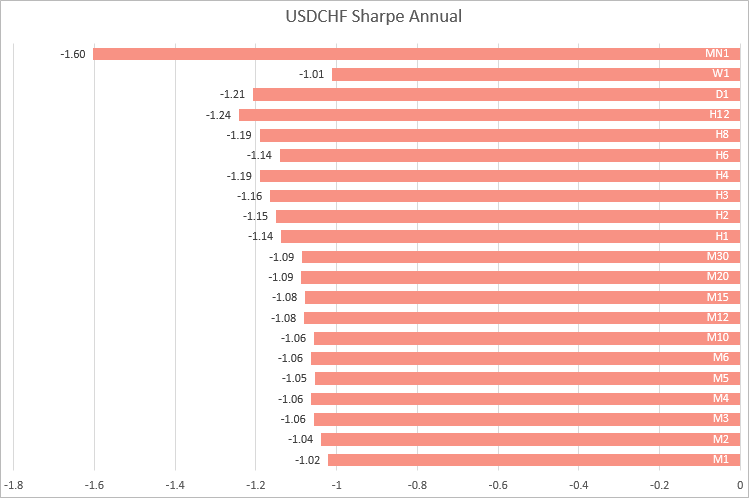
Таким образом, на примере 4-х основных валютных пар можно сделать вывод, что наиболее стабильные вычисления коэффициента Шарпа получаются на таймфреймах от M1 до M30. То есть для расчетов лучше брать значения доходности именно на мелких таймфреймах, если нужно сравнивать между собой стратегии, работающие на разных символах.

Вычисление годового коэффициента Шарпа на EURUSD за 2020 год по каждому месяцу

Возьмем доходности внутри каждого месяца за 2020 год и посчитаем годовое значение Sharpe Ratio на таймфреймах от M1 до H1. Полный код скрипта CalculateSharpe_Months.mq5 приложен к статье.

//--- структура для хранения доходности
struct Return
  {
   double            ret;   // доходность
   datetime          time;  // дата
   int               month; // месяц
  };
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   SharpeMonths sharpe_by_months[];
//--- массив таймфреймов, на которых будем считать коэффициент Шарпа
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1
                                  };
   ArrayResize(sharpe_by_months,ArraySize(timeframes));
//--- параметры запроса таймсерии
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print("Calculate Sharpe Annual on ",symbol, " for 2020 year");
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- получим массив доходностей на указанном таймфрейме
      Return returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      double avr,std,sharpe;
      //--- вычислим статистику за год
      GetStats(returns,avr,std,sharpe);
      string tf_str = EnumToString(timeframes[i]);
      //--- посчитаем годовое значение Sharpe Ratio на каждом месяце
      SharpeMonths sharpe_months_on_tf;
      sharpe_months_on_tf.SetTimeFrame(tf_str);
      //--- выберем доходности за месяц i
      for(int m = 1; m <= 12; m++)
        {
         Return month_returns[];
         GetReturnsByMonth(returns,m,month_returns);
         //--- вычислим статистику за год
         double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns);
         sharpe_months_on_tf.Sharpe(m,sharpe_annual);
        }
      //--- добавим значения коэффициента Шарпа для 12 месяцев на таймфрейме i
      sharpe_by_months[i] = sharpe_months_on_tf;
     }
//--- выведем таблицу годовых значений Шарпа помесячно на всех таймфреймах
   ArrayPrint(sharpe_by_months,3);
  }

/*
Результат

Calculate Sharpe Annual on EURUSD for 2020 year
             [TF]  [Jan]  [Feb] [Marc]  [Apr] [May] [June] [July] [Aug] [Sept]  [Oct] [Nov] [Dec]
[ 0] "PERIOD_M1"  -2.856 -1.340  0.120 -0.929 2.276  1.534  6.836 2.154 -2.697 -1.194 3.891 4.140
[ 1] "PERIOD_M2"  -2.919 -1.348  0.119 -0.931 2.265  1.528  6.854 2.136 -2.717 -1.213 3.845 4.125
[ 2] "PERIOD_M3"  -2.965 -1.340  0.118 -0.937 2.276  1.543  6.920 2.159 -2.745 -1.212 3.912 4.121
[ 3] "PERIOD_M4"  -2.980 -1.341  0.119 -0.937 2.330  1.548  6.830 2.103 -2.765 -1.219 3.937 4.110
[ 4] "PERIOD_M5"  -2.929 -1.312  0.120 -0.935 2.322  1.550  6.860 2.123 -2.729 -1.239 3.971 4.076
[ 5] "PERIOD_M6"  -2.945 -1.364  0.119 -0.945 2.273  1.573  6.953 2.144 -2.768 -1.239 3.979 4.082
[ 6] "PERIOD_M10" -3.033 -1.364  0.119 -0.934 2.361  1.584  6.789 2.063 -2.817 -1.249 4.087 4.065
[ 7] "PERIOD_M12" -2.952 -1.358  0.118 -0.956 2.317  1.609  6.996 2.070 -2.933 -1.271 4.115 4.014
[ 8] "PERIOD_M15" -3.053 -1.367  0.118 -0.945 2.377  1.581  7.132 2.078 -2.992 -1.274 4.029 4.047
[ 9] "PERIOD_M20" -2.998 -1.394  0.117 -0.920 2.394  1.532  6.884 2.065 -3.010 -1.326 4.074 4.040
[10] "PERIOD_M30" -3.008 -1.359  0.116 -0.957 2.379  1.585  7.346 2.084 -2.934 -1.323 4.139 4.034
[11] "PERIOD_H1"  -2.815 -1.373  0.116 -0.966 2.398  1.601  7.311 2.221 -3.136 -1.374 4.309 4.284

*/

Видно, что значения годового коэффициента для каждого месяца очень близки на всех таймфреймах, на которых проведены вычисления. Для лучшего представления полученные результаты изобразим в виде 3D-поверхности с помощью диаграммы в Excel.

3-D график годового коэффициента Шарпа на EURUSD за 2020 год по месяцам и таймфреймам

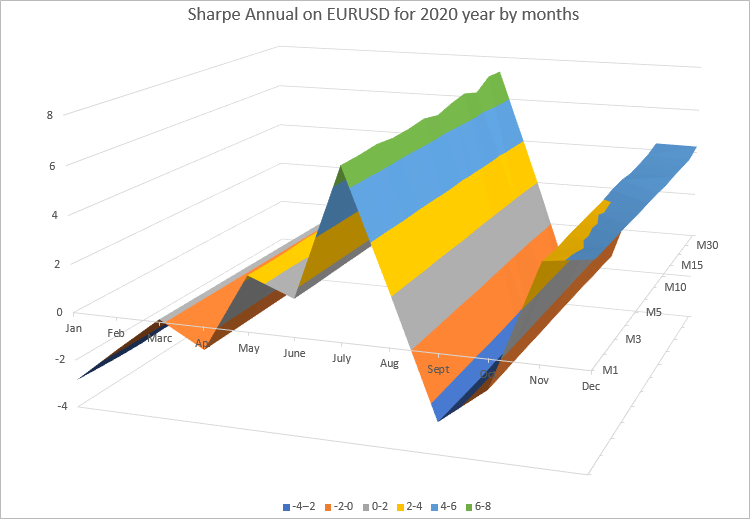
На графике хорошо видно, что значения годового коэффициента Шарпа на каждом месяце меняются. Это зависит от того, как изменялся график EURUSD в этом месяце. Но при этом значение годового коэффициента Шарпа для каждого месяца на всех таймфреймах почти не меняется.

Таким образом, годовой Sharpe Ratio мы можем вычислять на любом таймфрейме, при этом полученное значение также не зависит от количества баров, на которых были получены доходности. Это значит, что приведенный алгоритм вычисления можно использовать при тестировании, оптимизации и во время мониторинга в режиме реального времени. Главное, чтобы массив доходностей не был слишком мал по размеру.

Коэффицент Сортино

При расчете коэффициента Шарпа в качестве риска принимается полная волатильность котировок, как в сторону повышения, так и понижения активов. Но повышение стоимости портфеля является выгодным для инвестора, а убыток может причинить только их снижение. Поэтому действительный риск в коэффициенте оказывается завышенным. Коэффициент Сортино, разработанный в начале 90-х годов прошлого века Фрэнком Сортино, позволяет решить эту проблему.

Как и его предшественники, Ф. Сортино рассматривает будущую доходность в качестве случайной величины, равной ее математическому ожиданию, а риск — как дисперсию. Доходность и риск определяются на основе исторических значений котировок за определенный период. Как в расчете коэффициента Шарпа, доходность делится на риск.

Сортино обратил внимание на то, что риск, определенный как общий разброс доходностей (или, по-другому, полная волатильность) зависит как от положительных, так и от отрицательных изменений. Сортино заменил общую дисперсию полудисперсией, которая учитывает только падения активов. Полудисперсию в различных публикациях называют "волатильностью вниз", отрицательной дисперсией, нижней дисперсией или стандартным отклонением убытков.

Коэффициент Сортино считается фактически так же, как и показатель Шарпа, только из расчета волатильности исключаются положительные доходности. Это позволяет уменьшить меру риска и увеличить значение коэффициента.

Положительные и отрицательные доходности

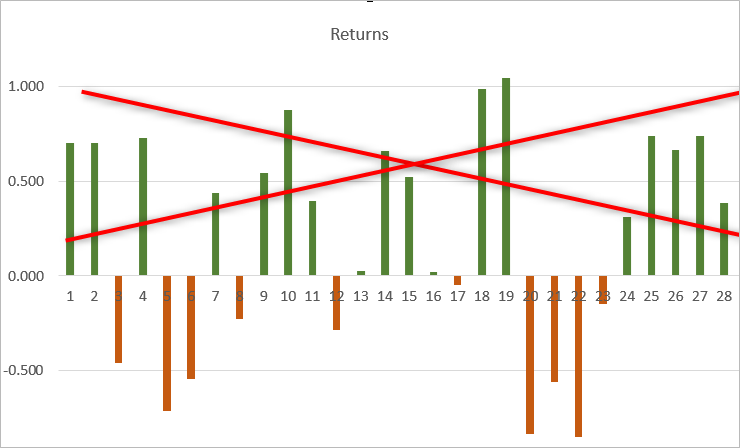
Пример кода для расчета коэффициента Сортино на основе расчета коэффициента Шарпа. Для вычисления "полудисперсии" берутся только отрицательные доходности.

//+------------------------------------------------------------------+
//|  Вычисляет коэффициенты Шарпа и Сортино                          |
//+------------------------------------------------------------------+
void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino)
  {
   avr = ArrayMean(returns);
   std = ArrayStd(returns);
   sharpe = (std == 0) ? 0 : avr / std;
//--- теперь уберем положительные доходности и посчитаем Sortino
   double negative_only[];
   int size = ArraySize(returns);
   ArrayResize(negative_only,size);
   ZeroMemory(negative_only);
//--- скопируем только отрицательные доходности
   for(int i = 0; i < size; i++)
      negative_only[i] = (returns[i] > 0) ? 0 : returns[i];
   double semistd = ArrayStd(negative_only);
   sortino = avr / semistd;   
   return;
  }

Приложенный к статье скрипт CalculateSortino_All_TF.mq5 дает такие результаты на EURUSD за 2020 год:

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeAnnual] [SortinoAnnual]    [Ratio]
[ 0] "M1"          1  373023 0.00000024 0.00014182     1.01769617      1.61605380 1.58795310
[ 1] "M2"          2  186573 0.00000048 0.00019956     1.02194170      1.62401856 1.58914991
[ 2] "M3"          3  124419 0.00000072 0.00024193     1.03126142      1.64332243 1.59350714
[ 3] "M4"          4   93302 0.00000096 0.00028000     1.02924195      1.62618200 1.57998030
[ 4] "M5"          5   74637 0.00000120 0.00031514     1.02303684      1.62286584 1.58632199
[ 5] "M6"          6   62248 0.00000143 0.00034122     1.03354379      1.63789024 1.58473231
[ 6] "M10"        10   37349 0.00000239 0.00044072     1.03266766      1.63461839 1.58290848
[ 7] "M12"        12   31124 0.00000286 0.00047632     1.04525580      1.65215986 1.58062730
[ 8] "M15"        15   24900 0.00000358 0.00053223     1.04515816      1.65256608 1.58116364
[ 9] "M20"        20   18675 0.00000477 0.00061229     1.04873529      1.66191269 1.58468272
[10] "M30"        30   12450 0.00000716 0.00074023     1.06348332      1.68543441 1.58482449
[11] "H1"         60    6225 0.00001445 0.00101979     1.10170316      1.75890688 1.59653431
[12] "H2"        120    3115 0.00002880 0.00145565     1.08797046      1.73062372 1.59068999
[13] "H3"        180    2076 0.00004305 0.00174762     1.10608991      1.77619289 1.60583048
[14] "H4"        240    1558 0.00005746 0.00200116     1.11659184      1.83085734 1.63968362
[15] "H6"        360    1038 0.00008643 0.00247188     1.11005321      1.79507001 1.61710267
[16] "H8"        480     779 0.00011508 0.00288226     1.09784908      1.74255746 1.58724682
[17] "H12"       720     519 0.00017188 0.00320405     1.20428761      2.11045830 1.75245371
[18] "D1"       1440     259 0.00035582 0.00470188     1.20132966      2.04624198 1.70331429
[19] "W1"      10080      51 0.00193306 0.01350157     1.03243721      1.80369984 1.74703102
[20] "MN1"     43200      12 0.00765726 0.01776075     1.49349076      5.00964481 3.35431926

Видно, что практические на всех таймфреймах годовое значение Сортино в 1.60 раз больше, чем коэффициент Шарпа. Но при расчетах на торговых результатах такой четкой закономерности, конечно, не будет. Поэтому имеет смысл сравнивать стратегии/портфели с помощью обоих показателей.

Коэффициент Шарпа и Сортино на EURUSD за 2020 год по таймфреймам

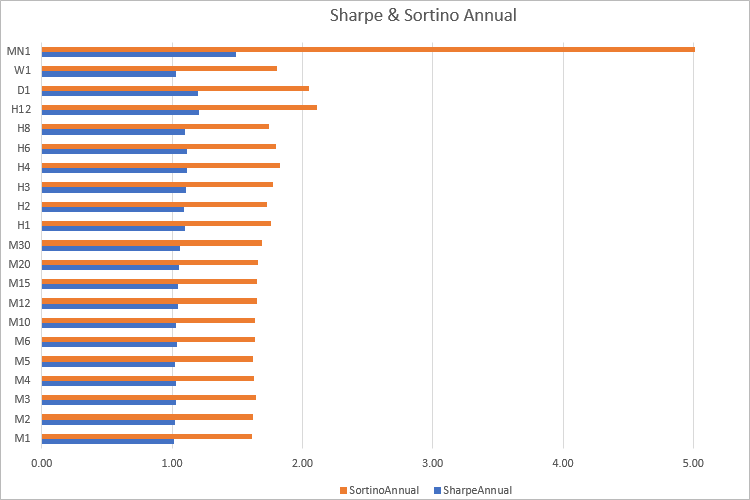
Разница между этими двумя показателями заключается в том, что коэффициент Шарпа показывает в первую очередь волатильность, а коэффициент Сортино действительно показывает уровень дохода на единицу риска. Но не стоит забывать и то, что все эти вычисления делаются на истории, и хорошие значения показателей не дают гарантии прибыли в будущем.

Пример вычисления коэффициента Шарпа в тестере стратегий MetaTrader 5

Коэффициент Шарпа был разработан для оценки портфелей, имеющих в своем составе акции. Цена акций меняется каждый день, следовательно, размер активов также изменяется каждый день. Торговые стратегии по умолчанию не подразумевают наличие открытых позиций, поэтому часть времени состояние торгового счета будет оставаться неизменным. Это означает, что при отсутствии открытых позиций мы будем получать нулевые значения доходности, и вычисление коэффициента Шарпа на таких данных будет недостоверным. Поэтому в расчет нужно брать только бары, на которых состояние торгового счета изменилось. Наиболее подходящим вариантом будет снимать значения эквити на каждом последнем тике бара. Это позволит вычислять коэффициент Шарпа при любом режиме генерации тиков в тестере стратегий MetaTrader 5.

Второй момент, который необходимо учесть — приращение цен в процентах, которое обычно считается как Return[i]=(CloseCurrent-ClosePrevious)/ClosePrevious, имеет определенный недостаток при расчетах. А именно: если цена уменьшилась на 5%, а затем увеличилась на 5%, то мы не получим первоначальное значение. Поэтому вместо обычного относительного приращения цен в статистических исследованиях обычно используют логарифм приращения цен. Логарифмическая доходность (или просто логдоходность) лишена этого недостатка линейной доходности. Она рассчитывается по формуле:

Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)

Логарифмические доходности удобны тем, что их можно складывать, так как сумма логарифмов эквивалентна произведению относительных доходностей.

Таким образом, алгоритм вычисления коэффициента Шарпа меняется минимально.

//--- вычислим логарифмы приращений из массива эквити
   for(int i = 1; i < m_bars_counter; i++)
     {
      //--- добавляем только если эквити изменилось
      if(m_equities[i] != prev_equity)
        {
         log_return = MathLog(m_equities[i] / prev_equity); // логарифм приращения
         aver += log_return;            // средний логарифм приращений
         AddReturn(log_return);         // заполняем массив логарифмов от приращений
         counter++;                     // счетчик доходностей
        }
      prev_equity = m_equities[i];
     }
//--- если значений не хватает для расчета коэффициента Шарпа, вернем 0
   if(counter <= 1)
      return(0);
//--- среднее значение логарифма приращения
   aver /= counter;
//--- вычислим стандартное отклонение
   for(int i = 0; i < counter; i++)
      std += (m_returns[i] - aver) * (m_returns[i] - aver);
   std /= counter;
   std = MathSqrt(std);
//--- коэффициент Шарпа на текущем таймфрейме
   double sharpe = aver / std;

Полный код вычисления реализован в виде включаемого файла Sharpe.mqh, приложенного к статье. Для вычисления коэффициента Шарпа в виде пользовательского критерия оптимизации подключите данный файл к своему советнику и добавьте несколько строк кода. Покажем, как это сделать, на примере советника "MACD Sample.mq5" из стандартной поставки MetaTrader 5.

#define MACD_MAGIC 1234502
//---
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\PositionInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include "Sharpe.mqh"
//---
input double InpLots          = 0.1;// Lots
input int    InpTakeProfit    = 50; // Take Profit (in pips)
input int    InpTrailingStop  = 30; // Trailing Stop Level (in pips)
input int    InpMACDOpenLevel = 3;  // MACD open level (in pips)
input int    InpMACDCloseLevel = 2; // MACD close level (in pips)
input int    InpMATrendPeriod = 26; // MA trend period
//---
int ExtTimeOut = 10; // time out in seconds between trade operations
CReturns   returns;
....
//+------------------------------------------------------------------+
//| Expert new tick handling function                                |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   static datetime limit_time = 0; // last trade processing time + timeout
//--- добавляем текущее эквити в массив для вычисления коэффициента Шарпа
   MqlTick tick;
   SymbolInfoTick(_Symbol, tick);
   returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY));
//--- don't process if timeout
   if(TimeCurrent() >= limit_time)
     {
      //--- check for data
      if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod)
        {
         //--- change limit time by timeout in seconds if processed
         if(ExtExpert.Processing())
            limit_time = TimeCurrent() + ExtTimeOut;
        }
     }
  }
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester(void)
  {
//--- вычислим коэффициент Шарпа
   double sharpe = returns.OnTester();
   return(sharpe);
  }
//+------------------------------------------------------------------+

Получившийся код сохраним с новым именем "MACD Sample Sharpe.mq5", он также приложен к статье.

Запустим генетическую оптимизацию на EURUSD M10 за 2020 год, выбрав пользовательский критерий оптимизации.

Настройки тестера для генетической оптимизации советника по пользовательнскому критерию

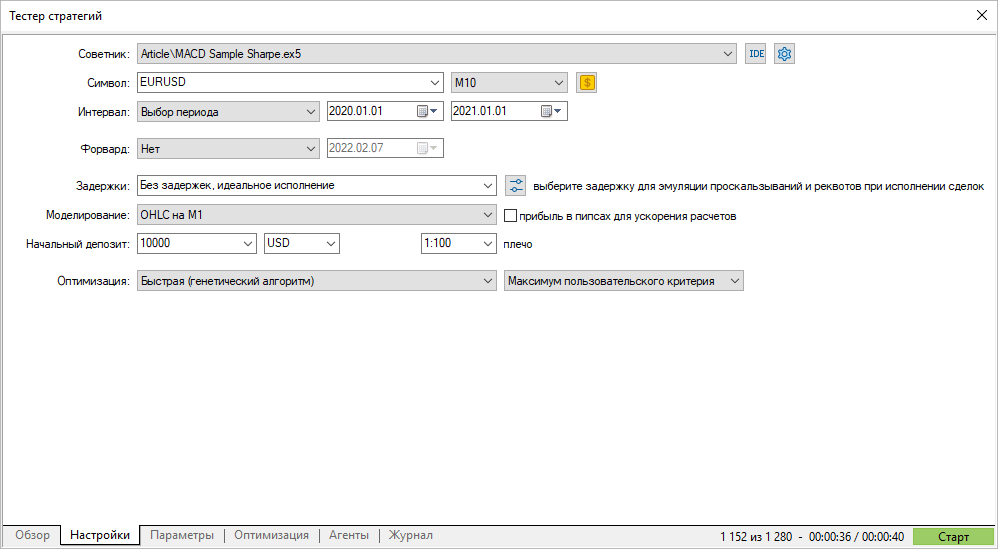
Полученные значения пользовательского критерия совпадают с коэффициентом Шарпа, который посчитал тестер стратегий. Теперь вы знаете механизм расчета и как трактовать полученные значения.

Результаты генетической оптимизации советника по пользовательнскому критерию

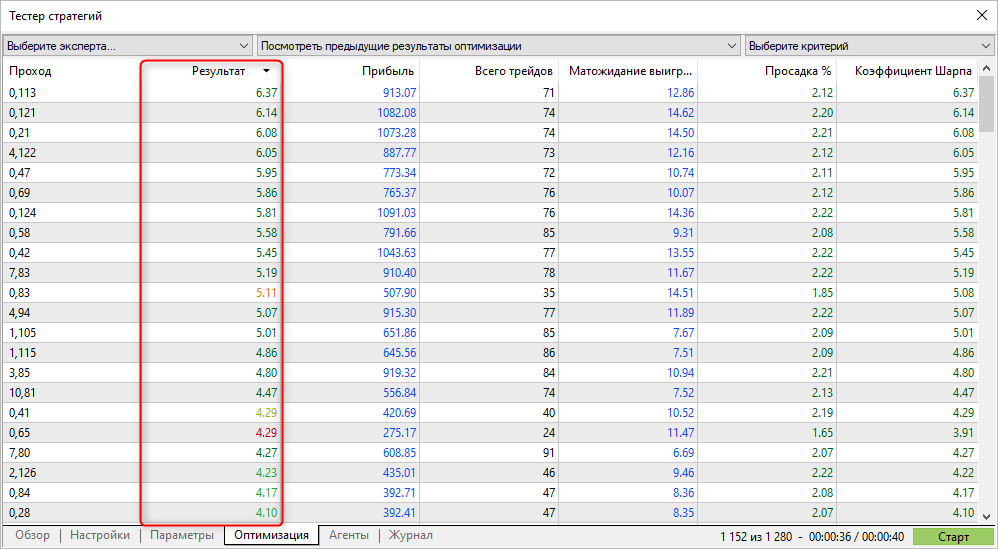
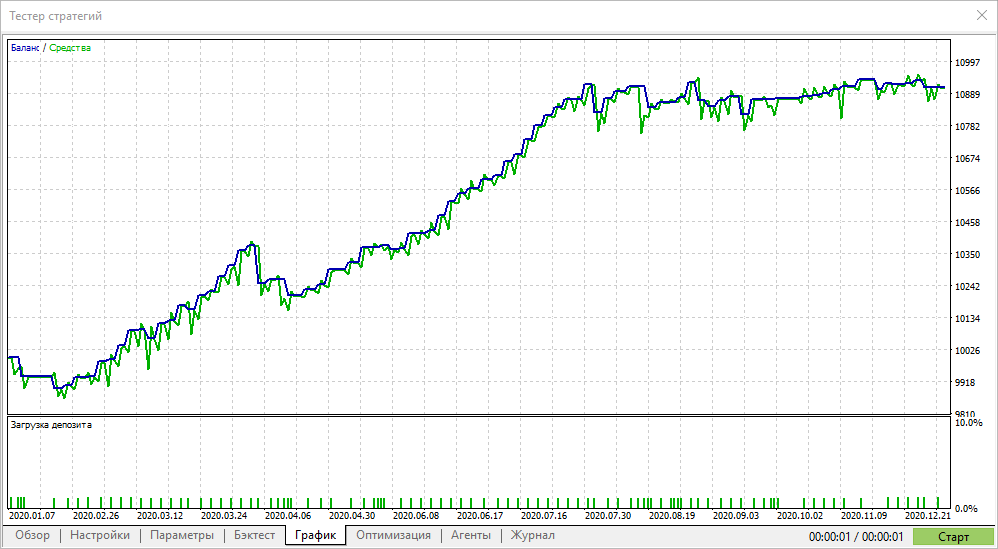
Проходы с максимальным коэффициентом Шарпа не всегда показывают самую большую прибыль в тестере, но зато позволяют найти параметры с плавным графиком эквити. На таких графиках, как правило, нет резкого роста, но нет и больших провалов и просадок по эквити.

Таким образом, оптимизация по коэффициенту Шарпа действительно позволяет искать более стабильные параметры по сравнению с другими критериями оптимизации.

График тестирования советника с коэффицентом Шарпа равным 6.14 >

Достоинства и недостатки

Коэффициенты Шарпа и Сортино позволяют определить, компенсирует ли полученная прибыль риск, связанный с его получением или нет. Другим преимуществом по сравнению с альтернативными измерителями риска является то, что их можно применять к активам всех типов. Например, можно сравнить золото с серебром, используя коэффициент Шарпа, потому что он не требует конкретный внешний ориентир для оценки. Таким образом, их можно применять как к отдельным стратегиям или ценным бумагам, так и к портфелям на объединенных фондах.

Недостатком этих инструментов является то, что расчет подразумевает нормальное распределение доходностей. В реальности это требование, как правило, не выполняется, но тем не менее, коэффициенты Шарпа и Сортино являются наиболее простыми и понятными для сравнения разных стратегий и портфелей.

Прикрепленные файлы |

Загрузить ZIP

CalculateSharpe_2TF.mq5 (9.58 KB)

CalculateSharpe_2TF.py (4.06 KB)

CalculateSharpe_Months.mq5 (21.93 KB)

CalculateSharpe_All_TF.mq5 (14.9 KB)

CalculateSortino_All_TF.mq5 (21.57 KB)

Sharpe.mqh (10.21 KB)

MACD_Sample_Sharpe.mq5 (37.13 KB)

MQL5.zip (20.95 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (18)

Kristian Kafarov | 23 окт. 2024 в 18:40

Кроме того, шарп на логарифмах существенно зависит от размера начального депозита. В приведенном выше примере (эквити 1) при исходном депо 4000 он дает 2.08. При депо 400000 он дает 3.83. Хотя форма эквити никоим образом не изменилась (торговля фикс.лотом).

Kristian Kafarov | 23 окт. 2024 в 18:44

Шарп на логарифмах не зависит от размера депо только в случае, если идет торговля с реинвестом.

Но в этом случае и шарп на простых приращениях не зависит от размера депо.

Следовательно, пока не понимаю, зачем использовать шарп на логарифмах.

Rashid Umarov | 24 окт. 2024 в 08:19

Почитайте логарифм цены

Другие упоминания сами найдете

Kristian Kafarov | 29 окт. 2024 в 14:52

Rashid Umarov #:

Почитайте логарифм цены

Другие упоминания сами найдете

Еще один крайне важный нюанс состоит в том, что в этом скрипте в расчете шарпа учитываются только те бары, на которых было изменение эквити:

     
      //--- add only if equity has changed
      if(m_equities[i] != prev_equity)
        {  
         log_return = MathLog(m_equities[i] / prev_equity); // increment logarithm
         aver += log_return;            // average logarithm of increments
         AddReturn(log_return);         // fill the array of increment logarithms
         counter++;                     // counter of returns
        }
      prev_equity = m_equities[i];

Затем среднее изменение находится делением на число таких баров:

//--- average value of the increment logarithm
   aver /= counter;

Однако переход к годовому шарпу происходит на основе отношения таймфреймов, как если бы в расчете учитывались все бары текущего тф:

//--- recalculate the Sharpe ratio to annual value in all other cases
//--- how many periods of the current timeframe fit into D1
   double factor = double(PeriodSeconds(PERIOD_D1)) / PeriodSeconds(timeframe);
   sharpe = sharpe * MathSqrt(factor);     // recalculate to daily value
   sharpe = sharpe * MathSqrt(252);        // obtain annual from daily

Т.е., еще раз: скрипт находит усредненный шарп на 1 бар с изменением эквити, а затем, чтобы найти годовой, умножает его не на число таких баров в году, а на общее число баров этого тф в году (его корень, естественно). Что ошибочно и завышает итоговый показатель.

Видимо в тестере шарп считается так же?

Ivan Titov | 29 окт. 2024 в 15:17

Kristian Kafarov #:
скрипт находит усредненный шарп на 1 бар с изменением эквити, а затем, чтобы найти годовой, умножает его не на число таких баров в году, а на общее число баров этого тф в году (его корень, естественно). Что ошибочно и завышает итоговый показатель

Тоже заметил. Поэтому в своей версии добавил опцию учета нулевых баров.

Что можно сделать с помощью скользящих средних

В данной статье мне захотелось собрать некоторые способы применения индикатора "Скользящая средняя". Практически к каждому способу, если требуется анализ кривых, сделаны индикаторы, визуализирующие полезную идею. В большинстве случаев идеи подсмотрены у других авторов, однако, собранные все вместе, они помогут точнее видеть основные направления и — надеюсь — принимать более правильные торговые решения. Уровень знания языка MQL5 — начальный.

Графика в библиотеке DoEasy (Часть 98): Перемещаем опорные точки расширенных стандартных графических объектов

В статье продолжим развитие расширенных стандартных графических объектов, и создадим функционал перемещения опорных точек составных графических объектов при помощи контрольных точек управления координатами опорных точек графического объекта.

Как и зачем разрабатывать собственную систему для алгоритмической торговли

В этой статье мы рассмотрим основы языка программирования MQL. Цель статьи — помочь начинающим программистам разработать собственную систему алгоритмической торговли (торгового советника).

Советы профессионального программиста (Часть III): Логирование. Подключение к системе сбора и анализа логов Seq

Реализация класса Logger для унификации (структурирования) сообщений, выводимых в журнал эксперта. Подключение к системе сбора и анализа логов Seq. Наблюдение за сообщениями в онлайн режиме.