交易中的数学:夏普(Sharpe)和索蒂诺(Sortino)比率
投资回报率是投资者和萌新交易员用来分析交易绩效的最明显指标。 专业交易者会采用更可靠的工具来分析策略,比如夏普(Sharpe)比率和索蒂诺(Sortino)比率等。 在这篇文章中,我们研究简单的例子来理解这些比率是如何计算的。 交易策略的评估细节在前文中曾进行了讨论“交易中的数学: 如何评估交易结果"。 建议您阅读这篇文章,从而刷新认知、或学习新知识。
夏普比率
经验丰富的投资者和交易者经常运用多种策略进行交易,投资不同的资产,以此获得持久的结果。 这是智能投资的概念之一,意味着创建投资组合。 每个证券/策略组合都有自己的风险和回报参数,能以某种方式进行比较。
进行这种比较的最具参考价值的工具之一就是夏普比率,它是由诺贝尔奖获得者威廉·F·夏普于 1966 年开发的。 该比率的计算采用基本绩效指标,包括平均回报率、回报标准差和无风险回报。
夏普比率的缺点是,用于分析的源数据必须呈正态分布。 换言之,收益分布图应该是对称的,不应该有尖峰或陡坑。
夏普比率使用以下公式计算:
Sharpe Ratio = (Return - RiskFree)/Std
其中:
- Return — 某一时段的平均回报率。 例如,月度、季度、年度、等等。
- RiskFree — 同期无风险回报率。 传统上,这些资产包括银行存款、债券和其它 100% 可靠的最低风险资产。
- Std — 同期投资组合回报的标准偏差。 收益偏离预期值越大,交易员账户或投资组合资产的风险和波动性就越高。
回报
回报率是依据一定时段内资产价值的变化来计算的。 返回值用于计算夏普比率的同一时间段。 一般来讲,会考虑年度夏普比率,但计算也可以依据季度、月度、甚至每日的数值。 回报率由以下公式计算:
Return[i] = (Close[i]-Close[i-1])/Close[i-1]
其中:
- Return[i] — 间隔 i 的回报;
- Close[i] — 第 i 个区间结束时的资产价值;
- Close[i-1] — 上一个间隔结束时的资产价值。
换言之,回报可以写为所选期间资产价值的相对变化:
Return[i] = Delta[i]/Previous
其中:
- Delta[i] = (Close[i]-Close[i-1]) — 所选期间资产价值的绝对变化;
- Previous = Close[i-1] — 上一个间隔结束时的资产价值。
若要依据日线数值计算年度的夏普比率,我们应该采用年内每天的回报值,并取回报累积除以天数计算平均日回报。
Return = Sum(Return[i])/N
其中 N 是天数。
无风险回报
无风险回报的概念是有条件的,因为风险总会存在。 由于夏普比率用于比较相同时间间隔内的不同策略/投资组合,因此可以在公式中选取零无风险回报。 就是,
RiskFree = 0
标准偏差或回报率
标准偏差表示随机变量如何偏离平均值。 首先,计算平均回报值,然后累计距均值的回报偏差。 结果之和除以回报数字以便获得离散度。 离散度的平方根是标准偏差。
D = Sum((Return - Return[i])^2 )/N
STD = SQRT(D)
前面提及的文章中提供了计算标准偏差的示例。
计算任何时间段的夏普比率,并将其转换为年度值
自 1966 年以来,夏普比率的计算方法一直不曾改变。 这种计算方法被广泛认可后,该变量改为更现代的名称。 在那时,资金和投资组合绩效评估是基于若干年来赚取的回报。 此后,依据月度数据进行计算,而由此产生的夏普比率会被映射到年度值。 这种方法可以比较两种资金、投资组合或策略。
夏普比率能够轻易地从不同时期和时间帧扩展到年度值。 这是依据将结果值乘以年度间隔与当前间隔之比的平方根来实现的。 我们来研究下面的例子。
假设我们采用每日回报值计算夏普比率 — SharpeDaily。 结果应转换为年度值 SharpeAnnual。 年度比率与周期比率的平方根成正比,即一年当中相应的每日间隔数量。 鉴于一年当中有 252 个交易日,基于每日回报的夏普比率应乘以 252 的平方根。 这将得到年度夏普比率:
SharpeAnnual = SQRT(252)*SharpeDaily // 252 working days in a year
如果该值是基于 H1 时间帧计算的,我们要采用相同的原则 — 首先将 SharpeHourly 转换为 SharpeDaily,然后计算年度 Sharpe 比率。 一根 D1 柱线包括 24 根 H1 柱线,因此公式如下:
SharpeDaily = SQRT(24)*SharpeHourly // 24 hours fit into D1
并非所有金融产品都是 24 小时交易的。 但在测试人员对同一金融产品的交易策略进行评估时,这一点并不重要,因为比较是针对相同的测试间隔和时间帧进行的。
依据夏普比率评估策略
依据策略/投资组合的绩效,夏普比率可得到不分数值,甚至是负值。 将夏普比率转换为年度值可由经典方式进行解释: | 分值 | 含义 | 说明 |
|---|---|---|
| 夏普比率 < 0 | 糟糕 | 这样的策略无利可图 |
| 0 < 夏普比率 < 1.0 | 未定义 | 风险没有得到足够回报。 在没有其它选择的情况下,可以考虑这种策略 |
| 夏普比率 ≥ 1.0 | 良好 | 如果夏普比率大于 1,可能意味着风险得到了足够回报,投资组合/策略可以显示出正面的结果 |
| 夏普比率 ≥ 3.0 | 优秀 | 高分值表示在每笔特定成交中遭遇亏损的概率非常低 |
不要忘记夏普系数是一个常规的统计变量。 它反映了回报和风险之间的比率。 因此,在分析不同的投资组合和策略时,重要的是将夏普比率与建议值相关联,或与相关值进行比较。
针对 EURUSD,2020 年度的夏普比率计算
夏普比率最初用来评估通常由许多股票组成的投资组合。 股票的价值每天都在变化,投资组合的价值也随之变化。 价值和回报的变化可以在任何时间帧内进行衡量。 我们来观察 EURUSD 计算结果。
计算是在两个时间帧 H1 和 D1 上进行的。 然后,我们将结果转换为年度值,并进行比较,看看是否存在差异。 我们将选用 2020 年的柱线收盘价进行计算。
MQL5 的代码
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- double H1_close[],D1_close[]; double h1_returns[],d1_returns[]; datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close); if(bars == -1) Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError()); else { Print("\nCalculate the mean and standard deviation of returns on H1 bars"); Print("H1 bars=",ArraySize(H1_close)); GetReturns(H1_close,h1_returns); double average = ArrayMean(h1_returns); PrintFormat("H1 average=%G",average); double std = ArrayStd(h1_returns); PrintFormat("H1 std=%G",std); double sharpe_H1 = average / std; PrintFormat("H1 Sharpe=%G",sharpe_H1); double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_H1); } bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close); if(bars == -1) Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError()); else { Print("\nCalculate the mean and standard deviation of returns on D1 bars"); Print("D1 bars=",ArraySize(D1_close)); GetReturns(D1_close,d1_returns); double average = ArrayMean(d1_returns); PrintFormat("D1 average=%G",average); double std = ArrayStd(d1_returns); PrintFormat("D1 std=%G",std); double sharpe_D1 = average / std; double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_D1); } } //+------------------------------------------------------------------+ //| Fills the returns[] array of returns | //+------------------------------------------------------------------+ void GetReturns(const double & values[], double & returns[]) { int size = ArraySize(values); //--- if less than 2 values, return an empty array of returns if(size < 2) { ArrayResize(returns,0); PrintFormat("%s: Error. ArraySize(values)=%d",size); return; } else { //--- fill returns in a loop ArrayResize(returns, size - 1); double delta; for(int i = 1; i < size; i++) { returns[i - 1] = 0; if(values[i - 1] != 0) { delta = values[i] - values[i - 1]; returns[i - 1] = delta / values[i - 1]; } } } //--- } //+------------------------------------------------------------------+ //| Calculates the average number of array elements | //+------------------------------------------------------------------+ double ArrayMean(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Error, array is empty",__FUNCTION__); return(0); } double mean = 0; for(int i = 0; i < size; i++) mean += array[i]; mean /= size; return(mean); } //+------------------------------------------------------------------+ //| Calculates the standard deviation of array elements | //+------------------------------------------------------------------+ double ArrayStd(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Error, array is empty",__FUNCTION__); return(0); } double mean = ArrayMean(array); double std = 0; for(int i = 0; i < size; i++) std += (array[i] - mean) * (array[i] - mean); std /= size; std = MathSqrt(std); return(std); } //+------------------------------------------------------------------+ /* Result Calculate the mean and standard deviation of returns on H1 bars H1 bars:6226 H1 average=1.44468E-05 H1 std=0.00101979 H1 Sharpe=0.0141664 Sharpe_annual(H1)=1.117708053392263 Calculate the mean and standard deviation of returns on D1 bars D1 bars:260 D1 average=0.000355823 D1 std=0.00470188 Sharpe_annual(H1)=1.2179005039019222 */
使用 MetaTrader 5 函数库 计算的 Python 代码
import math from datetime import datetime import MetaTrader5 as mt5 # display data on the MetaTrader 5 package print("MetaTrader5 package author: ", mt5.__author__) print("MetaTrader5 package version: ", mt5.__version__) # import the 'pandas' module for displaying data obtained in the tabular form import pandas as pd pd.set_option('display.max_columns', 50) # how many columns to show pd.set_option('display.width', 1500) # max width of the table to show # import pytz module for working with the time zone import pytz # establish connection to the MetaTrader 5 terminal if not mt5.initialize(): print("initialize() failed") mt5.shutdown() # set time zone to UTC timezone = pytz.timezone("Etc/UTC") # create datetime objects in the UTC timezone to avoid the local time zone offset utc_from = datetime(2020, 1, 1, tzinfo=timezone) utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone) # get EURUSD H1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to) # also get D1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to) # shut down connection to the MetaTrader 5 terminal and continue processing obtained bars mt5.shutdown() # create DataFrame out of the obtained data rates_frame = pd.DataFrame(rates_H1) # add the "Return" column rates_frame['return'] = 0.0 # now calculate the returns as return[i] = (close[i] - close[i-1])/close[i-1] prev_close = 0.0 for i, row in rates_frame.iterrows(): close = row['close'] rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0 prev_close = close print("\nCalculate the mean and standard deviation of returns on H1 bars") print('H1 rates:', rates_frame.shape[0]) ret_average = rates_frame[1:]['return'].mean() # skip the first row with zero return print('H1 return average=', ret_average) ret_std = rates_frame[1:]['return'].std(ddof=0) # skip the first row with zero return print('H1 return std =', ret_std) sharpe_H1 = ret_average / ret_std print('H1 Sharpe = Average/STD = ', sharpe_H1) sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1) print('Sharpe_annual(H1) =', sharpe_annual_H1) # now calculate the Sharpe ratio on the D1 timeframe rates_daily = pd.DataFrame(rates_D1) # add the "Return" column rates_daily['return'] = 0.0 # calculate returns prev_return = 0.0 for i, row in rates_daily.iterrows(): close = row['close'] rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0 prev_return = close print("\nCalculate the mean and standard deviation of returns on D1 bars") print('D1 rates:', rates_daily.shape[0]) daily_average = rates_daily[1:]['return'].mean() print('D1 return average=', daily_average) daily_std = rates_daily[1:]['return'].std(ddof=0) print('D1 return std =', daily_std) sharpe_daily = daily_average / daily_std print('D1 Sharpe =', sharpe_daily) sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1) print('Sharpe_annual(D1) =', sharpe_annual_D1) Result Calculate the mean and standard deviation of returns on H1 bars H1 rates: 6226 H1 return average= 1.4446773215242986e-05 H1 return std = 0.0010197932969323495 H1 Sharpe = Average/STD = 0.014166373968823358 Sharpe_annual(H1) = 1.117708053392236 Calculate the mean and standard deviation of returns on D1 bars D1 rates: 260 D1 return average= 0.0003558228355051694 D1 return std = 0.004701883757646081 D1 Sharpe = 0.07567665511222807 Sharpe_annual(D1) = 1.2179005039019217
如您所见,MQL5 和 Python 的计算结果是相同的。 源代码附在下面(CalculateSharpe_2TF)。
依据 H1 和 D1 柱线计算的年度夏普比率的差别:分别对应 1.117708 和 1.217900。 我们来尝试找出原因。
计算所有时间帧 2020 年 EURUSD 的年度夏普比率
现在,我们来计算所有时间帧的年度夏普比率。 为此,我们在表格中收集获得的数据:
- TF — 时间帧
- Minutes — 时间帧内含的分钟数量
- Rates — 每年内此时间帧的柱线数量
- Avg — 该时间帧内,每根柱线的平均回报率(每根柱线的平均价格变化百分比)
- Std — 时间帧内每根柱线的标准偏差百分比(该时间帧内的价格波动百分比)
- SharpeTF — 依据给定时间帧计算的夏普比率
- SharpeAnnual — 依据该时间帧夏普比率计算的年度夏普比率
以下是计算代码模块。 完整代码可在附于文后的 CalculateSharpe_All_TF.mq5 文件中找到。
//--- structure to print statistics to log struct Stats { string TF; int Minutes; int Rates; double Avg; double Std; double SharpeTF; double SharpeAnnual; }; //--- array of statistics by timeframes Stats stats[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- arrays for close prices double H1_close[],D1_close[]; //--- arrays of returns double h1_returns[],d1_returns[]; //--- arrays of timeframes on which the Sharpe coefficient will be calculated ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4, PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1 }; ArrayResize(stats,ArraySize(timeframes)); //--- timeseries request parameters string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print(symbol); for(int i = 0; i < ArraySize(timeframes); i++) { //--- get the array of returns on the specified timeframe double returns[]; GetReturns(symbol,timeframes[i],from,to,returns); //--- calculate statistics GetStats(returns,avr,std,sharpe); double sharpe_annual = sharpe * MathSqrt(ArraySize(returns)); PrintFormat("%s aver=%G%% std=%G%% sharpe=%G sharpe_annual=%G", EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual); //--- fill the statistics structure Stats row; string tf_str = EnumToString(timeframes[i]); StringReplace(tf_str,"PERIOD_",""); row.TF = tf_str; row.Minutes = PeriodSeconds(timeframes[i]) / 60; row.Rates = ArraySize(returns); row.Avg = avr; row.Std = std; row.SharpeTF = sharpe; row.SharpeAnnual = sharpe_annual; //--- add a row for the timeframe statistics stats[i] = row; } //--- print statistics on all timeframes to log ArrayPrint(stats,8); } /* Result [TF] [Minutes] [Rates] [Avg] [Std] [SharpeTF] [SharpeAnnual] [ 0] "M1" 1 373023 0.00000024 0.00168942 0.00168942 1.03182116 [ 1] "M2" 2 186573 0.00000048 0.00239916 0.00239916 1.03629642 [ 2] "M3" 3 124419 0.00000072 0.00296516 0.00296516 1.04590258 [ 3] "M4" 4 93302 0.00000096 0.00341717 0.00341717 1.04378592 [ 4] "M5" 5 74637 0.00000120 0.00379747 0.00379747 1.03746116 [ 5] "M6" 6 62248 0.00000143 0.00420265 0.00420265 1.04854166 [ 6] "M10" 10 37349 0.00000239 0.00542100 0.00542100 1.04765562 [ 7] "M12" 12 31124 0.00000286 0.00601079 0.00601079 1.06042363 [ 8] "M15" 15 24900 0.00000358 0.00671964 0.00671964 1.06034161 [ 9] "M20" 20 18675 0.00000477 0.00778573 0.00778573 1.06397070 [10] "M30" 30 12450 0.00000716 0.00966963 0.00966963 1.07893298 [11] "H1" 60 6225 0.00001445 0.01416637 0.01416637 1.11770805 [12] "H2" 120 3115 0.00002880 0.01978455 0.01978455 1.10421905 [13] "H3" 180 2076 0.00004305 0.02463458 0.02463458 1.12242890 [14] "H4" 240 1558 0.00005746 0.02871564 0.02871564 1.13344977 [15] "H6" 360 1038 0.00008643 0.03496339 0.03496339 1.12645075 [16] "H8" 480 779 0.00011508 0.03992838 0.03992838 1.11442404 [17] "H12" 720 519 0.00017188 0.05364323 0.05364323 1.22207717 [18] "D1" 1440 259 0.00035582 0.07567666 0.07567666 1.21790050 [19] "W1" 10080 51 0.00193306 0.14317328 0.14317328 1.02246174 [20] "MN1" 43200 12 0.00765726 0.43113365 0.43113365 1.49349076 */
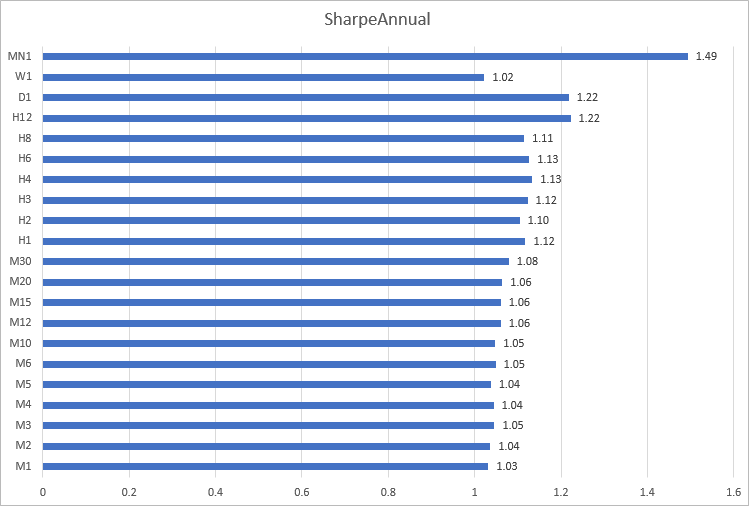
我们来依据一个不同的时间帧,构建 2020 年 EURUSD 夏普比率的柱状图。 从中可以看出,依据 M1 到 M30 分钟时间帧计算得出的结果非常接近:从 1.03 到 1.08。 而在 H12 至 MN1 的时间帧内得到的结果最不一致。
2020 年 GBPUSD、USDJPY 和 USDCHF 计算出的夏普比率
我们针对另外三对货币进行类似的计算。
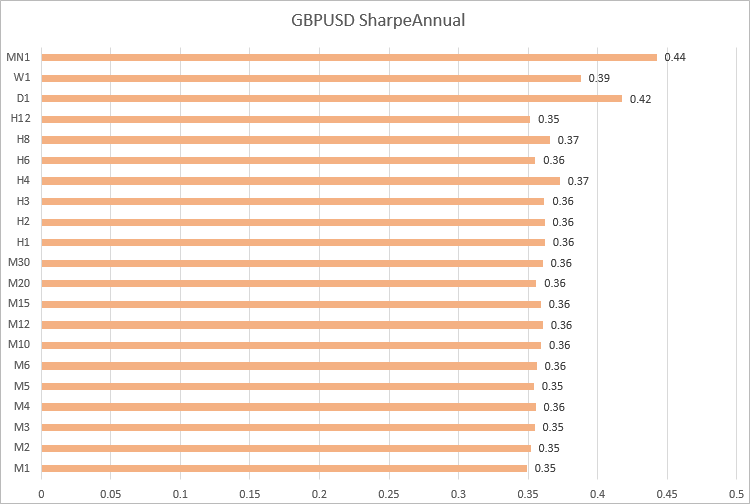
GBPUSD,夏普比率值在 M1 至 H12 的时间帧内近似。
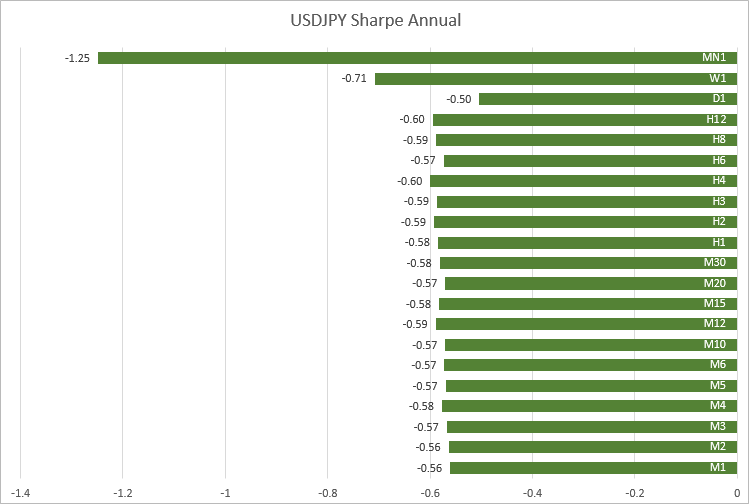
USDJPY,M1 至 H12 的时间帧数值也近似:-0.56 至 -0.60。
USDCHF,在 M1 至 M30 的时间帧内获得了类似的值。 随着时间的增加,夏普比率随之波动。
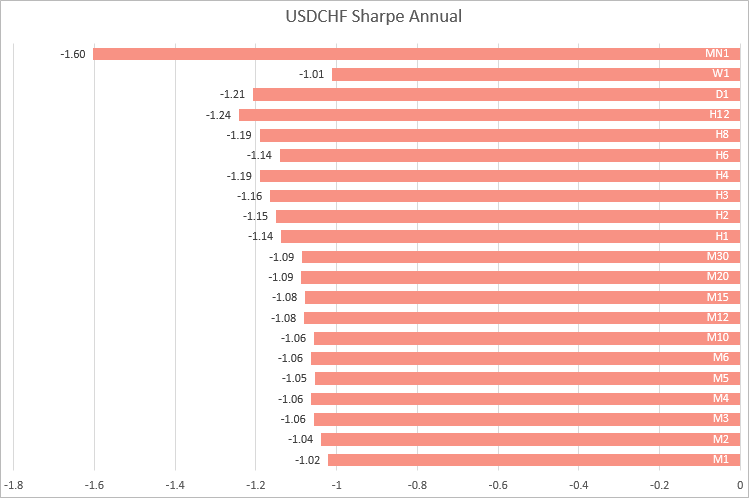
因此,基于四种主要货币对的例子,我们可以得出结论,最稳定的夏普比率计算是在 M1 至 M30 的时间帧内获得的。 这意味着,当您想要比较不同品种的策略时,最好选用较低时间帧的回报来计算比率。
按月度计算 2020 年 EURUSD 的年度夏普比率
我们取用 2020 年每个月的月回报率,计算 M1 至 H1 时间帧的年度夏普比率。 CalculateSharpe_Months.mq5 脚本的完整代码附于文后。
//--- structure to store returns struct Return { double ret; // return datetime time; // date int month; // month }; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { SharpeMonths sharpe_by_months[]; //--- arrays of timeframes on which the Sharpe coefficient will be calculated ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1 }; ArrayResize(sharpe_by_months,ArraySize(timeframes)); //--- timeseries request parameters string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print("Calculate Sharpe Annual on ",symbol, " for 2020 year"); for(int i = 0; i < ArraySize(timeframes); i++) { //--- get the array of returns on the specified timeframe Return returns[]; GetReturns(symbol,timeframes[i],from,to,returns); double avr,std,sharpe; //--- Calculate statistics for the year GetStats(returns,avr,std,sharpe); string tf_str = EnumToString(timeframes[i]); //--- calculate the annual Sharpe ratio for each month SharpeMonths sharpe_months_on_tf; sharpe_months_on_tf.SetTimeFrame(tf_str); //--- select returns for i-th month for(int m = 1; m <= 12; m++) { Return month_returns[]; GetReturnsByMonth(returns,m,month_returns); //--- Calculate statistics for the year double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns); sharpe_months_on_tf.Sharpe(m,sharpe_annual); } //--- add Sharpe ratio for 12 months on timeframe i sharpe_by_months[i] = sharpe_months_on_tf; } //--- display the table of annual Sharpe values by months on all timeframes ArrayPrint(sharpe_by_months,3); } /* Result Calculate Sharpe Annual on EURUSD for 2020 year [TF] [Jan] [Feb] [Marc] [Apr] [May] [June] [July] [Aug] [Sept] [Oct] [Nov] [Dec] [ 0] "PERIOD_M1" -2.856 -1.340 0.120 -0.929 2.276 1.534 6.836 2.154 -2.697 -1.194 3.891 4.140 [ 1] "PERIOD_M2" -2.919 -1.348 0.119 -0.931 2.265 1.528 6.854 2.136 -2.717 -1.213 3.845 4.125 [ 2] "PERIOD_M3" -2.965 -1.340 0.118 -0.937 2.276 1.543 6.920 2.159 -2.745 -1.212 3.912 4.121 [ 3] "PERIOD_M4" -2.980 -1.341 0.119 -0.937 2.330 1.548 6.830 2.103 -2.765 -1.219 3.937 4.110 [ 4] "PERIOD_M5" -2.929 -1.312 0.120 -0.935 2.322 1.550 6.860 2.123 -2.729 -1.239 3.971 4.076 [ 5] "PERIOD_M6" -2.945 -1.364 0.119 -0.945 2.273 1.573 6.953 2.144 -2.768 -1.239 3.979 4.082 [ 6] "PERIOD_M10" -3.033 -1.364 0.119 -0.934 2.361 1.584 6.789 2.063 -2.817 -1.249 4.087 4.065 [ 7] "PERIOD_M12" -2.952 -1.358 0.118 -0.956 2.317 1.609 6.996 2.070 -2.933 -1.271 4.115 4.014 [ 8] "PERIOD_M15" -3.053 -1.367 0.118 -0.945 2.377 1.581 7.132 2.078 -2.992 -1.274 4.029 4.047 [ 9] "PERIOD_M20" -2.998 -1.394 0.117 -0.920 2.394 1.532 6.884 2.065 -3.010 -1.326 4.074 4.040 [10] "PERIOD_M30" -3.008 -1.359 0.116 -0.957 2.379 1.585 7.346 2.084 -2.934 -1.323 4.139 4.034 [11] "PERIOD_H1" -2.815 -1.373 0.116 -0.966 2.398 1.601 7.311 2.221 -3.136 -1.374 4.309 4.284 */
可以看出,在所有时间帧内,我们依据每个月度计算出的年度比率值都非常接近。 为了更好地演示,我们利用 Excel 图表将结果渲染为 3D 示意图。
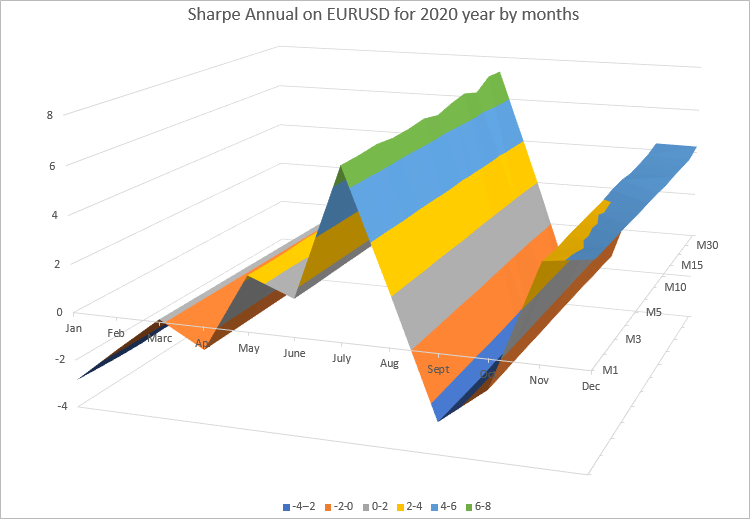
示意图清楚地表明,年度夏普比率的值每个月都在变化。 这取决于 EURUSD 本月的变化。 另一方面,在所有时间帧内,每个月的年度夏普比率几乎没有变化。
因此,年度夏普比率可以在任何时间帧内计算,而结果值也取决于获得回报的柱线数量。 这意味着该算法可以用于实时测试、优化和监控。 唯一的先决条件是拥有足够大的回报数组。
索提诺(Sortino)比率
在夏普比率计算中,风险来自报价的全部波动性,包括资产的增加和减少。 但投资组合价值的增加对投资者有利,而损失只与投资组合价值的减少有关。 因此,比率中的实际风险被夸大了。 弗兰克·索蒂诺在 20 世纪 90 年代初提出的索蒂诺比率解决了这个问题。
与他的前任一样,索蒂诺 将未来回报视为一个随机变量,等于其数学预期,而风险则视为一个方差。 回报和风险依据一定时期的历史报价来判定。 在夏普比率计算中,回报除以风险。
索蒂诺指出,把风险应定义为回报总方差(或完全波动率),应取决于正、负两方面的变化。 索蒂诺将总体波动率替换为仅由资产减少导致的半波动率。 半波动率也称为有害波动率、下行风险、下行偏差、负波动率、或下行标准差。
索蒂诺比率的计算与夏普的计算类似,唯一的区别是正回报被排除在波动率计算之外。 这降低了风险度量,并增加了比率权重。
基于夏普比率计算索蒂诺比率的代码示例。 半离散度仅采用负回报计算。
//+------------------------------------------------------------------+ //| Calculates Sharpe and Sortino ratios | //+------------------------------------------------------------------+ void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino) { avr = ArrayMean(returns); std = ArrayStd(returns); sharpe = (std == 0) ? 0 : avr / std; //--- now, remove negative returns and calculate the Sortino ratio double negative_only[]; int size = ArraySize(returns); ArrayResize(negative_only,size); ZeroMemory(negative_only); //--- copy only negative returns for(int i = 0; i < size; i++) negative_only[i] = (returns[i] > 0) ? 0 : returns[i]; double semistd = ArrayStd(negative_only); sortino = avr / semistd; return; }
附于文后的脚本 CalculateSortino_All_TF.mq5 生成了 2020 年 EURUSD 的以下结果:
[TF] [Minutes] [Rates] [Avg] [Std] [SharpeAnnual] [SortinoAnnual] [Ratio] [ 0] "M1" 1 373023 0.00000024 0.00014182 1.01769617 1.61605380 1.58795310 [ 1] "M2" 2 186573 0.00000048 0.00019956 1.02194170 1.62401856 1.58914991 [ 2] "M3" 3 124419 0.00000072 0.00024193 1.03126142 1.64332243 1.59350714 [ 3] "M4" 4 93302 0.00000096 0.00028000 1.02924195 1.62618200 1.57998030 [ 4] "M5" 5 74637 0.00000120 0.00031514 1.02303684 1.62286584 1.58632199 [ 5] "M6" 6 62248 0.00000143 0.00034122 1.03354379 1.63789024 1.58473231 [ 6] "M10" 10 37349 0.00000239 0.00044072 1.03266766 1.63461839 1.58290848 [ 7] "M12" 12 31124 0.00000286 0.00047632 1.04525580 1.65215986 1.58062730 [ 8] "M15" 15 24900 0.00000358 0.00053223 1.04515816 1.65256608 1.58116364 [ 9] "M20" 20 18675 0.00000477 0.00061229 1.04873529 1.66191269 1.58468272 [10] "M30" 30 12450 0.00000716 0.00074023 1.06348332 1.68543441 1.58482449 [11] "H1" 60 6225 0.00001445 0.00101979 1.10170316 1.75890688 1.59653431 [12] "H2" 120 3115 0.00002880 0.00145565 1.08797046 1.73062372 1.59068999 [13] "H3" 180 2076 0.00004305 0.00174762 1.10608991 1.77619289 1.60583048 [14] "H4" 240 1558 0.00005746 0.00200116 1.11659184 1.83085734 1.63968362 [15] "H6" 360 1038 0.00008643 0.00247188 1.11005321 1.79507001 1.61710267 [16] "H8" 480 779 0.00011508 0.00288226 1.09784908 1.74255746 1.58724682 [17] "H12" 720 519 0.00017188 0.00320405 1.20428761 2.11045830 1.75245371 [18] "D1" 1440 259 0.00035582 0.00470188 1.20132966 2.04624198 1.70331429 [19] "W1" 10080 51 0.00193306 0.01350157 1.03243721 1.80369984 1.74703102 [20] "MN1" 43200 12 0.00765726 0.01776075 1.49349076 5.00964481 3.35431926
可以看出,在几乎所有的时间帧内,索蒂诺值都是夏普比率的 1.60 倍。 当然,在根据交易结果计算比率时,不会有如此明显的相关性。 因此,使用这两个比率来比较策略/投资组合是有意义的。
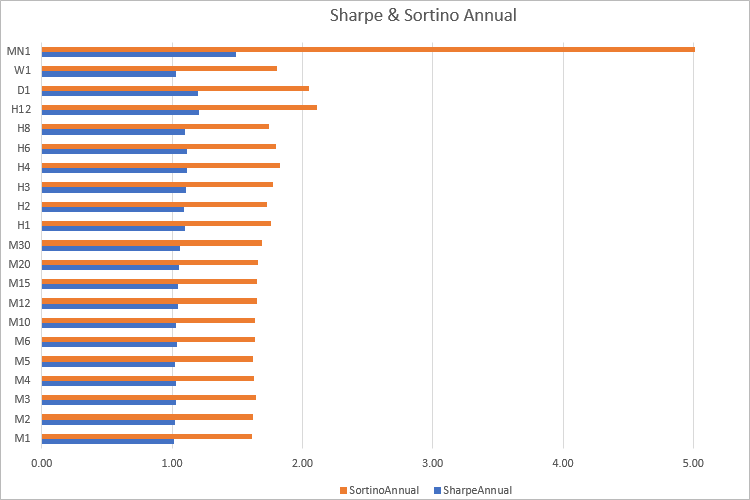
这两个指标之间的区别在于,夏普比率主要反映波动性,而索蒂诺比率真正反映的是每单位风险的比率或回报。 但不要忘记,计算是基于历史的,所以即使看上去不错的结果也不能保证未来盈利。
MetaTrader 5 策略测试器中夏普比率计算示例
夏普比率最初用来评估包含股票的投资组合。 股票价格每天都在变化,因此资产的价值也每天都在变化。 默认情况下,交易策略并不意味着存在持仓,故此交易账户的状态在一定时间内保持不变。 这意味着,当没有持仓时,我们就得到零回报值,因此针对这种情况计算夏普比率就是错误的。 因此,计算应只运用在交易账户状态有所变化的柱线。 最合适的选择是在每根柱线的最后一次即时报价上分析股票价值。 这将允许在 MetaTrader 5 策略测试器中采用任何即时报价生成模式计算夏普比率。
另一需要考虑的重点是,通常计算为 Return[i]=(CloseCurrent-ClosePrevious)/ClosePrevious,而价格增量百分比在计算中有一定的缺点。 它如下所示:如果价格下降 5%,后又增长 5%,我们将不会得到初始值。 这就是为什么统计研究通常使用价格增量对数,而不是通常的相对价格增量。 对数回报没有线性回报的缺点。 该值的计算如下:
Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)
对数回报很方便,因为它们可以相加,因为对数之和等于相对回报的乘积。
因此,夏普比率计算算法需要少量的调整。
//--- calculate the logarithms of increments using the equity array for(int i = 1; i < m_bars_counter; i++) { //--- only add if equity has changed if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // increment logarithm aver += log_return; // average logarithm of increments AddReturn(log_return); // fill the array of increment logarithms counter++; // counter of returns } prev_equity = m_equities[i]; } //--- if values are not enough for Sharpe calculation, return 0 if(counter <= 1) return(0); //--- average value of the increment logarithm aver /= counter; //--- calculate standard deviation for(int i = 0; i < counter; i++) std += (m_returns[i] - aver) * (m_returns[i] - aver); std /= counter; std = MathSqrt(std); //--- Sharpe ratio on the current timeframe double sharpe = aver / std;
完整的计算代码作为包含文件 Sharpe.mqh,附在文后。 为了将夏普比率计算为自定义优化准则,请将此文件连接到智能交易系统,并添加几行代码。 我们看看如何利用来自标准 MetaTrader 5 发行包中的 MACD Sample.mq5 EA 示例来实现它。
#define MACD_MAGIC 1234502 //--- #include <Trade\Trade.mqh> #include <Trade\SymbolInfo.mqh> #include <Trade\PositionInfo.mqh> #include <Trade\AccountInfo.mqh> #include "Sharpe.mqh" //--- input double InpLots = 0.1;// Lots input int InpTakeProfit = 50; // Take Profit (in pips) input int InpTrailingStop = 30; // Trailing Stop Level (in pips) input int InpMACDOpenLevel = 3; // MACD open level (in pips) input int InpMACDCloseLevel = 2; // MACD close level (in pips) input int InpMATrendPeriod = 26; // MA trend period //--- int ExtTimeOut = 10; // time out in seconds between trade operations CReturns returns; .... //+------------------------------------------------------------------+ //| Expert new tick handling function | //+------------------------------------------------------------------+ void OnTick(void) { static datetime limit_time = 0; // last trade processing time + timeout //--- add current equity to the array to calculate the Sharpe ratio MqlTick tick; SymbolInfoTick(_Symbol, tick); returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY)); //--- don't process if timeout if(TimeCurrent() >= limit_time) { //--- check for data if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod) { //--- change limit time by timeout in seconds if processed if(ExtExpert.Processing()) limit_time = TimeCurrent() + ExtTimeOut; } } } //+------------------------------------------------------------------+ //| Tester function | //+------------------------------------------------------------------+ double OnTester(void) { //--- calculate Sharpe ratio double sharpe = returns.OnTester(); return(sharpe); } //+------------------------------------------------------------------+
将生成的代码另存为 “MACD Sample Sharpe.mq5” — 相关文件也附在下面。
我们针对 EURUSD M10 2020 运行一个遗传优化,选择一个自定义优化准则。
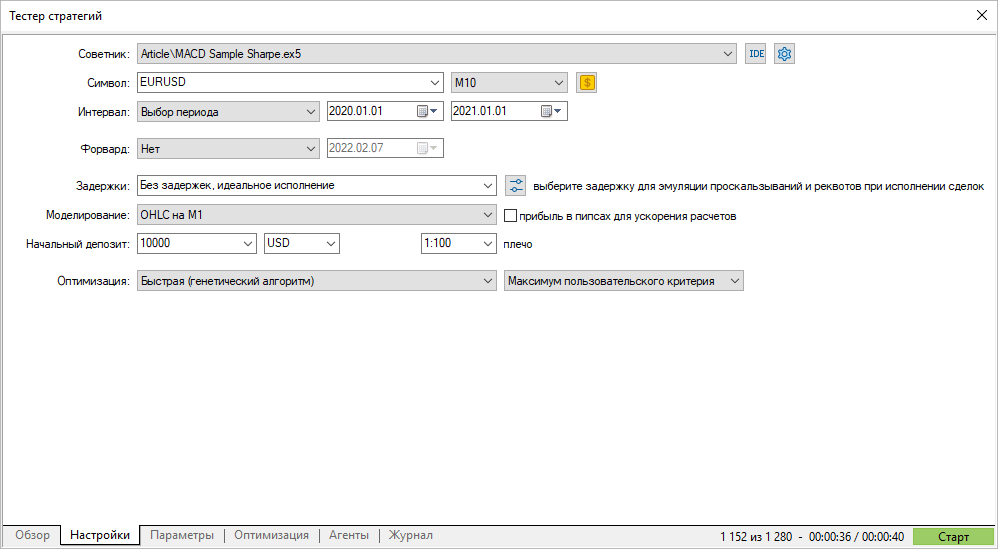
得到的自定义准则值与策略测试器计算的夏普比率一致。 现在您知道了计算机制,以及如何解释得到的结果。
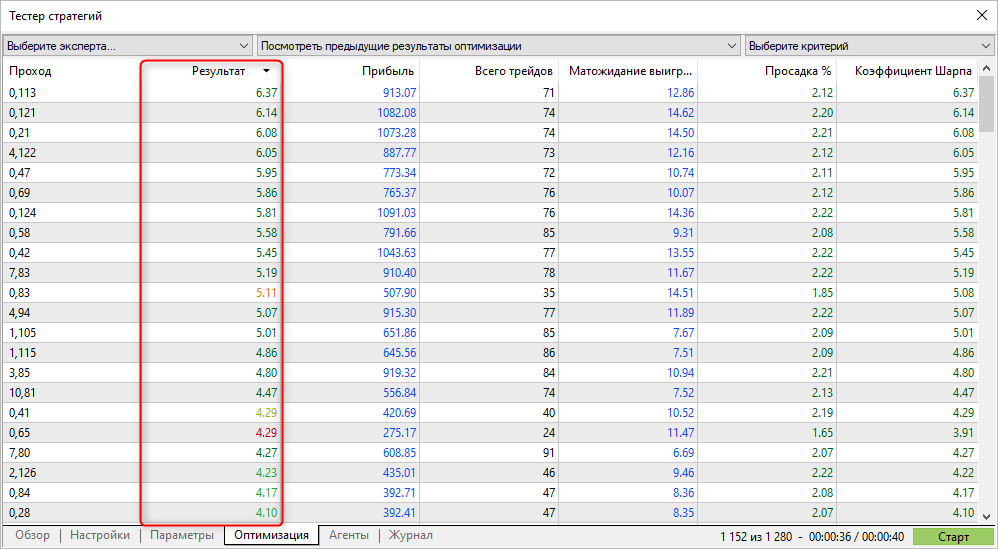
夏普比率最高的通测结果并不总是在测试中显示最高的利润,但它们能够依据平滑的净值图形来发现参数。 这样的图形通常不会显示出大幅增长,但也不会出现大幅下跌和净值回撤。
这意味着,与其它优化准则相比,采用夏普比率优化,可以找到更稳定的参数。
 >
>
优点与缺点
夏普和索蒂诺比率能够判定赚取的利润是否能涵盖相关风险。 与其它风险度量相比的另一个优势是,该计算可以应用于所有类型的资产。 例如,您可以采用夏普比率来比较黄金和白银,因为它不依靠特定的外部基准来评估。 因此,这些比率可以应用于单个策略或证券,以及资产或策略组合。
这些工具的缺点是,计算时需假设回报为正态分布。 而实际上,这一需求很难得到满足。 无论如何,夏普比率和索蒂诺比率是最简单、最容易理解的工具,可以用来比较不同的策略和投资组合。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/9171
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

只有在进行再投资交易时,对数的夏普才不取决于存款额。
但在这种情况下,简单增量的夏普并不取决于存款规模。
因此,我不明白为什么要使用对数夏普。
读取价格的对数
您还可以找到其他参考文献
读取价格的对数
您还可以找到其他参考文献
另一个极其重要的细微差别是,在本脚本中,计算夏普时只考虑股本发生变化的条形图:
//--- add only if equity has changed if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // 递增对数 aver += log_return; // 增量的平均对数 AddReturn(log_return); // 填充递增对数数组 counter++; // 返回计数器 } prev_equity = m_equities[i];然后用平均变化除以这些 柱状图的数量:
然而,向年度夏普的过渡是基于时间框架比率,就好像当前 tf的所有条形图 都被计算在内:
也就是说,脚本又一次找到了每一栏股票变化 的平均利差,然后,为了找到年度利差,不是将其乘以一年中的此类栏数,而是乘以一年中该 tf 的总栏数(当然是其根数)。这是错误的,会高估最终的数字。
显然,夏普在测试仪中也是以同样的方式计算的?
该脚本会找出每 1 条股票变动 条形图的平均夏普值,然后,为了找出年度夏普值,它不是乘以一年中此类条形图的数量,而是乘以一年中该 tf 条形图的总数(当然是其根)。这样做是错误的,会高估最终数字。
我也注意到了。因此,我在自己的版本中增加了一个选项,将零条计算在内。