트레이딩에서의 수학: 샤프 및 소르티노 비율

투자에 따른 수익은 투자자와 초보 트레이더가 거래의 효율성을 분석하기 위해 사용하는 가장 확실한 지표입니다. 전문적인 트레이더는 샤프 및 소르티노 비율과 같은 전략을 분석하기 위해 보다 안정적인 도구를 사용합니다. 이 기사에서는 이러한 비율을 계산하는 방법을 이해하기 위한 간단한 예를 살펴볼 것입니다. 거래 전략에 대한 평가와 관련한 세부 사항은 다음의 기사에서 확인할 수 있습니다. "트레이딩에서의 수학. 거래 결과를 측정하는 방법". 귀하가 가진 지식을 다시 확인해 보기 위해 혹은 새롭게 배우기 위해 기사를 읽어 보시기 바랍니다.

샤프 비율

경험이 많은 투자자와 트레이더들은 지속적인 결과를 얻기 위해 여러가지 전략으로 거래하고 다양한 자산에 투자합니다. 이것은 스마트 투자의 개념 중 하나로서 투자 포트폴리오를 만드는 것을 의미합니다. 증권/전략 등 각각의 포트폴리오에는 고유한 위험 및 수익 매개변수가 있으므로 서로 비교해야 봐야 합니다.

이러한 비교를 위해 가장 많이 사용되는 도구 중 하나가 1966년 노벨상 수상자 William F. Sharpe가 개발한 샤프 비율입니다. 비율의 계산은 평균 수익률, 수익의 표준 편차 및 무위험 수익률을 포함한 기본 성과 지표를 사용합니다.

샤프 비율의 단점은 분석에 사용된 소스 데이터가 정규 분포를 따라야 한다는 것입니다. 즉, 수익률 분포 그래프는 대칭이어야 하며 급격한 고점이나 저점이 없어야 합니다.

샤프 비율은 다음 공식을 사용하여 계산됩니다:

Sharpe Ratio = (Return - RiskFree)/Std

설명:

• Return — 특정 기간 동안의 평균 수익률. 예를 들어, 월, 분기, 연도 등
  
• RiskFree — 같은 기간 동안의 무위험 수익률. 전통적으로 여기에는 100% 신뢰성을 가진 은행 예금, 채권 및 기타의 최소 위험 자산이 포함됩니다.
  
• Std — 같은 기간 동안의 포트폴리오 수익의 표준 편차. 수익이 기대 가치에서 크게 벗어날수록 트레이더의 계정 또는 포트폴리오 자산의 위험과 변동성이 커집니다.
  

수익

수익은 특정 기간 동안의 자산 가치의 변화로 계산됩니다. 수익의 값은 샤프 비율이 계산되는 동일한 기간 동안 사용됩니다. 일반적으로 년간 샤프 비율이 사용되지만 분기별, 월별 또는 일일의 값도 계산할 수 있습니다. 수익은 다음 공식으로 계산됩니다.

Return[i] = (Close[i]-Close[i-1])/Close[i-1]

설명:

• Return[i] — i 구간의 수익;
• Close[i] — i 번째 구간이 끝날 때 자산의 값.
• Close[i-1] — 이전 간격의 종료 시의 자산 가치.

즉, 수익은 선택한 기간 동안의 자산 가치의 상대적인 변화로 기록될 수 있습니다.

Return[i] = Delta[i]/Previous

설명:

• Delta[i] = (Close[i]-Close[i-1]) — 선택한 기간 동안의 자산 가치의 절대적인 변화;
• Previous = Close[i-1] — 이전 간격의 종료 시점의 자산의 가치.
  

일별 값을 사용하여 1년 동안의 샤프 비율을 계산하려면 해당 연도의 각 날짜의 수익 값을 사용하고 계산의 일수로 나눈 수익의 합계로 평균 일일 수익을 계산해야 합니다. 

Return = Sum(Return[i])/N

N은 일수.

Risk-free return

무위험 수익의 개념은 항상 위험이 있기 때문에 조건부입니다. 샤프 비율은 동일한 시간 간격에서 다른 전략/포트폴리오를 비교하는 데 사용되므로 공식에는 무위험 수익률이 사용될 수 있습니다. 다시 말해,

RiskFree = 0

표준편차 혹은 수익

표준 편차는 확률 변수가 평균 값에서 얼마나 벗어나 있는지를 보여줍니다. 먼저 평균 수익 값을 계산한 다음 평균 값에서 수익의 제곱 편차를 합산합니다. 결과로 나온 합계를 수익률로 나누어 분산을 얻습니다. 분산의 제곱근은 표준 편차입니다.

D = Sum((Return - Return[i])^2 )/N

STD = SQRT(D)

표준 편차 계산의 예는 이전 기사에서 찾아 볼수 있습니다.

모든 시간대의 샤프 비율을 계산하고 연간 가치로 변환하기

샤프 비율 계산 방법은 1966년 이후로 변경되지 않았습니다. 이 변수는 이 계산 방법이 널리 인식된 후 현대적인 이름을 얻었습니다. 당시에는 펀드 및 포트폴리오의 성과를 평가하는 것은 수년간의 수익을 기반으로 했습니다. 이후에 월별 데이터에 대한 계산이 이루어지며 샤프 비율은 연간 값으로 매핑 되었습니다. 이 방법을 사용하면 두개의 펀드, 포트폴리오 또는 전략을 비교할 수 있습니다.

샤프 비율은 다양한 기간과 시간에서 연간 값으로 쉽게 확장될 수 있습니다. 이것은 결과 값에 현재 간격에 대한 연간 간격의 비율의 제곱근을 곱하여 수행됩니다. 다음과 같은 예를 살펴보겠습니다.

일일 반환 값인 SharpeDaily를 사용하여 샤프 비율을 계산했다고 가정합니다. 결과는 연간 값 SharpeAnnual로 변환되어야 합니다. 연간 비율은 기간 비율의 제곱근 - 즉 1년에 얼마나 많은 일일 간격이 들어가 있는지에 비례합니다. 1년간 거래일이 252일이므로 일일 수익률 기준 샤프 비율에 252의 제곱근을 곱해야 합니다. 이것이 연간 샤프 비율이 됩니다:

SharpeAnnual = SQRT(252)*SharpeDaily // 252 거래일수

값이 H1 기간을 기준으로 계산되는 경우 동일한 원칙을 사용합니다. - 먼저 SharpeHourly를 SharpeDaily로 변환한 다음 연간 Sharpe 비율을 계산합니다. 하나의 D1 바에는 24개의 H1 바가 포함되어 있으므로 공식은 다음과 같습니다.

SharpeDaily = SQRT(24)*SharpeHourly   // 24 시간은 D1에 해당

모든 금융 상품이 하루 24시간 거래되는 것은 아닙니다. 그러나 테스터에서 동일한 금융 상품에 대해 거래 전략을 평가할 때는 동일한 테스트 간격 및 동일한 기간에 대해 비교가 수행되기 때문에 중요하지 않습니다.

샤프 비율을 이용한 전략 평가

전략/포트폴리오의 성과에 따라 샤프 비율은 음수 값을 포함한 다른 값을 가질 수 있습니다. 샤프 비율을 연간 값으로 변환하면 고전적인 방식으로 해석할 수 있습니다.

값	의미는	설명
샤프 비율 < 0	나쁨	전략이 수익적이지 않습니다
0 < 샤프 비율  < 1.0	비정의	위험이 보상을 가져오지 못했습니다. 이러한 전략은 대안이 없을 때 고려할 수 있습니다.
샤프 비율 ≥ 1.0	좋음	샤프 비율이 1보다 크면 위험이 보상되고 포트폴리오/전략이 긍정적인 결과를 나타낼 수 있음을 의미할 수 있습니다.
샤프 비율 ≥ 3.0	매우 좋음	높은 값은 각각의 거래에서 손실을 얻을 확률이 매우 낮다는 것을 나타냅니다.

샤프 계수는 일반 통계 변수라는 것을 잊지 마십시오. 샤프 계수는 수익률과 위험의 비율을 반영합니다. 따라서 서로 다른 포트폴리오나 전략을 분석할 때 샤프 비율을 권장 값과 연관시키거나 관련 값과 비교하는 것이 중요합니다.

EURUSD, 2020에 대한 샤프 비율 계산

샤프 비율은 원래는 많은 주식으로 구성된 포트폴리오를 평가하기 위해 개발되었습니다. 주식의 가치는 매일 변하고 그에 따라 포트폴리오의 가치도 변합니다. 가치와 수익의 변화는 어느 시간대로도 측정할 수 있습니다. EURUSD에 대한 계산을 살펴보겠습니다.

계산은 H1과 D1의 두 기간에 대해 수행됩니다. 그런 다음 결과를 연간 값으로 변환하고 비교하여 차이가 있는지 확인합니다. 계산에는 2020년의 바의 종가를 사용합니다.

MQL5 코드

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   double H1_close[],D1_close[];
   double h1_returns[],d1_returns[];
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nCalculate the mean and standard deviation of returns on H1 bars");
      Print("H1 bars=",ArraySize(H1_close));
      GetReturns(H1_close,h1_returns);
      double average = ArrayMean(h1_returns);
      PrintFormat("H1 average=%G",average);
      double std = ArrayStd(h1_returns);
      PrintFormat("H1 std=%G",std);
      double sharpe_H1 = average / std;
      PrintFormat("H1 Sharpe=%G",sharpe_H1);
      double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_H1);
     }

   bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nCalculate the mean and standard deviation of returns on D1 bars");     
      Print("D1 bars=",ArraySize(D1_close));
      GetReturns(D1_close,d1_returns);
      double average = ArrayMean(d1_returns);
      PrintFormat("D1 average=%G",average);
      double std = ArrayStd(d1_returns);
      PrintFormat("D1 std=%G",std);
      double sharpe_D1 = average / std;
      double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_D1);
     }
  }

//+------------------------------------------------------------------+
//|  Fills the returns[] array of returns                            |
//+------------------------------------------------------------------+
void GetReturns(const double & values[], double & returns[])
  {
   int size = ArraySize(values);
//--- if less than 2 values, return an empty array of returns
   if(size < 2)
     {
      ArrayResize(returns,0);
      PrintFormat("%s: Error. ArraySize(values)=%d",size);
      return;
     }
   else
     {
      //--- fill returns in a loop
      ArrayResize(returns, size - 1);
      double delta;
      for(int i = 1; i < size; i++)
        {
         returns[i - 1] = 0;
         if(values[i - 1] != 0)
           {
            delta = values[i] - values[i - 1];
            returns[i - 1] = delta / values[i - 1];
           }
        }
     }
//---
  }
//+------------------------------------------------------------------+
//|  Calculates the average number of array elements                 |
//+------------------------------------------------------------------+
double ArrayMean(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += array[i];
   mean /= size;
   return(mean);
  }
//+------------------------------------------------------------------+
//|  Calculates the standard deviation of array elements             |
//+------------------------------------------------------------------+
double ArrayStd(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = ArrayMean(array);
   double std = 0;
   for(int i = 0; i < size; i++)
      std += (array[i] - mean) * (array[i] - mean);
   std /= size;
   std = MathSqrt(std);
   return(std);
  }  
//+------------------------------------------------------------------+

/*
결과

H1 바의 평균과 표준편차 계산
H1 bars:6226
H1 average=1.44468E-05
H1 std=0.00101979
H1 Sharpe=0.0141664
Sharpe_annual(H1)=1.117708053392263

D1 바의 평균과 표준편차 계산
D1 bars:260
D1 average=0.000355823
D1 std=0.00470188
Sharpe_annual(H1)=1.2179005039019222

*/

메타 트레이더 5 라이브러리를 사용하여 계산하기 위한 Python 코드

import math
from datetime import datetime
import MetaTrader5 as mt5

# display data on the MetaTrader 5 package
print("MetaTrader5 package author: ", mt5.__author__)
print("MetaTrader5 package version: ", mt5.__version__)

# import the 'pandas' module for displaying data obtained in the tabular form
import pandas as pd

pd.set_option('display.max_columns', 50)  # how many columns to show
pd.set_option('display.width', 1500)  # max width of the table to show
# import pytz module for working with the time zone
import pytz

# establish connection to the MetaTrader 5 terminal
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# set time zone to UTC
timezone = pytz.timezone("Etc/UTC")
# create datetime objects in the UTC timezone to avoid the local time zone offset
utc_from = datetime(2020, 1, 1, tzinfo=timezone)
utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone)
# get EURUSD H1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone
rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to)
# also get D1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone
rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to)
# shut down connection to the MetaTrader 5 terminal and continue processing obtained bars
mt5.shutdown()

# create DataFrame out of the obtained data
rates_frame = pd.DataFrame(rates_H1)

# add the "Return" column
rates_frame['return'] = 0.0
# now calculate the returns as return[i] = (close[i] - close[i-1])/close[i-1]
prev_close = 0.0
for i, row in rates_frame.iterrows():
    close = row['close']
    rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0
    prev_close = close

print("\nCalculate the mean and standard deviation of returns on H1 bars")
print('H1 rates:', rates_frame.shape[0])
ret_average = rates_frame[1:]['return'].mean()  # skip the first row with zero return
print('H1 return average=', ret_average)
ret_std = rates_frame[1:]['return'].std(ddof=0) # skip the first row with zero return
print('H1 return std =', ret_std)
sharpe_H1 = ret_average / ret_std
print('H1 Sharpe = Average/STD = ', sharpe_H1)

sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1)
print('Sharpe_annual(H1) =', sharpe_annual_H1)

# now calculate the Sharpe ratio on the D1 timeframe
rates_daily = pd.DataFrame(rates_D1)

# add the "Return" column
rates_daily['return'] = 0.0
# calculate returns
prev_return = 0.0
for i, row in rates_daily.iterrows():
    close = row['close']
    rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0
    prev_return = close

print("\nCalculate the mean and standard deviation of returns on D1 bars")
print('D1 rates:', rates_daily.shape[0])
daily_average = rates_daily[1:]['return'].mean()
print('D1 return average=', daily_average)
daily_std = rates_daily[1:]['return'].std(ddof=0)
print('D1 return std =', daily_std)
sharpe_daily = daily_average / daily_std
print('D1 Sharpe =', sharpe_daily)

sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1)
print('Sharpe_annual(D1) =', sharpe_annual_D1)

결과
H1 바의 평균과 표준편차 계산 

H1 rates: 6226
H1 return average= 1.4446773215242986e-05
H1 return std = 0.0010197932969323495
H1 Sharpe = Average/STD = 0.014166373968823358
Sharpe_annual(H1) = 1.117708053392236

D1 바의 평균과 표준편차 계산
D1 rates: 260
D1 return average= 0.0003558228355051694
D1 return std = 0.004701883757646081
D1 Sharpe = 0.07567665511222807
Sharpe_annual(D1) = 1.2179005039019217 

상기와 같이 MQL5와 Python 계산 결과는 동일합니다. 소스 코드는 아래에 첨부되어 있습니다(CalculateSharpe_2TF).

H1과 D1 막대에서 계산된 연간 샤프 비율은 각각 1.117708 및 1.217900으로 다릅니다. 그 이유를 알아보도록 하겠습니다.

모든 시간대에서 2020년 EURUSD에 대한 연간 샤프 비율 계산

이제 모든 기간에 대한 연간 샤프 비율을 계산해 보겠습니다. 이를 위해 데이터를 테이블에 수집합니다.

• TF — 기간
• Minutes — 기간에서 분의 개수
• Rates — 이 기간에서 연간 바의 개수
• Avg — 기간의 바별 평균 수익률(%)(바별 평균 가격 변화 백분율)
• Std — 기간의 바별 표준 편차(%)(이 시간대의 가격 변동성 백분율)
• SharpeTF — 주어진 기간에서 계산된 샤프 비율
• SharpeAnnual — 이 기간을 기반으로 계산된 샤프 비율의 연간 샤프 비율

아래는 계산과 관련한 코드 블록입니다. 전체 코드는 기사에 첨부된 CalculateSharpe_All_TF.mq5 파일에 있습니다.

//--- structure to print statistics to log
struct Stats
  {
   string            TF;
   int               Minutes;
   int               Rates;
   double            Avg;
   double            Std;
   double            SharpeTF;
   double            SharpeAnnual;
  };
//--- array of statistics by timeframes
Stats stats[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- arrays for close prices
   double H1_close[],D1_close[];
//--- arrays of returns
   double h1_returns[],d1_returns[];
//--- arrays of timeframes on which the Sharpe coefficient will be calculated
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,
                                   PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1
                                  };

   ArrayResize(stats,ArraySize(timeframes));
//--- timeseries request parameters
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print(symbol);
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- get the array of returns on the specified timeframe
      double returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      //--- calculate statistics
      GetStats(returns,avr,std,sharpe);
      double sharpe_annual = sharpe * MathSqrt(ArraySize(returns));
      PrintFormat("%s  aver=%G%%   std=%G%%  sharpe=%G  sharpe_annual=%G",
                  EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual);
      //--- fill the statistics structure
      Stats row;
      string tf_str = EnumToString(timeframes[i]);
      StringReplace(tf_str,"PERIOD_","");
      row.TF = tf_str;
      row.Minutes = PeriodSeconds(timeframes[i]) / 60;
      row.Rates = ArraySize(returns);
      row.Avg = avr;
      row.Std = std;
      row.SharpeTF = sharpe;
      row.SharpeAnnual = sharpe_annual;
      //--- add a row for the timeframe statistics
      stats[i] = row;
     }
//--- print statistics on all timeframes to log
   ArrayPrint(stats,8);
  }

/*
Result

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeTF] [SharpeAnnual]
[ 0] "M1"          1  373023 0.00000024 0.00168942 0.00168942     1.03182116
[ 1] "M2"          2  186573 0.00000048 0.00239916 0.00239916     1.03629642
[ 2] "M3"          3  124419 0.00000072 0.00296516 0.00296516     1.04590258
[ 3] "M4"          4   93302 0.00000096 0.00341717 0.00341717     1.04378592
[ 4] "M5"          5   74637 0.00000120 0.00379747 0.00379747     1.03746116
[ 5] "M6"          6   62248 0.00000143 0.00420265 0.00420265     1.04854166
[ 6] "M10"        10   37349 0.00000239 0.00542100 0.00542100     1.04765562
[ 7] "M12"        12   31124 0.00000286 0.00601079 0.00601079     1.06042363
[ 8] "M15"        15   24900 0.00000358 0.00671964 0.00671964     1.06034161
[ 9] "M20"        20   18675 0.00000477 0.00778573 0.00778573     1.06397070
[10] "M30"        30   12450 0.00000716 0.00966963 0.00966963     1.07893298
[11] "H1"         60    6225 0.00001445 0.01416637 0.01416637     1.11770805
[12] "H2"        120    3115 0.00002880 0.01978455 0.01978455     1.10421905
[13] "H3"        180    2076 0.00004305 0.02463458 0.02463458     1.12242890
[14] "H4"        240    1558 0.00005746 0.02871564 0.02871564     1.13344977
[15] "H6"        360    1038 0.00008643 0.03496339 0.03496339     1.12645075
[16] "H8"        480     779 0.00011508 0.03992838 0.03992838     1.11442404
[17] "H12"       720     519 0.00017188 0.05364323 0.05364323     1.22207717
[18] "D1"       1440     259 0.00035582 0.07567666 0.07567666     1.21790050
[19] "W1"      10080      51 0.00193306 0.14317328 0.14317328     1.02246174
[20] "MN1"     43200      12 0.00765726 0.43113365 0.43113365     1.49349076

*/

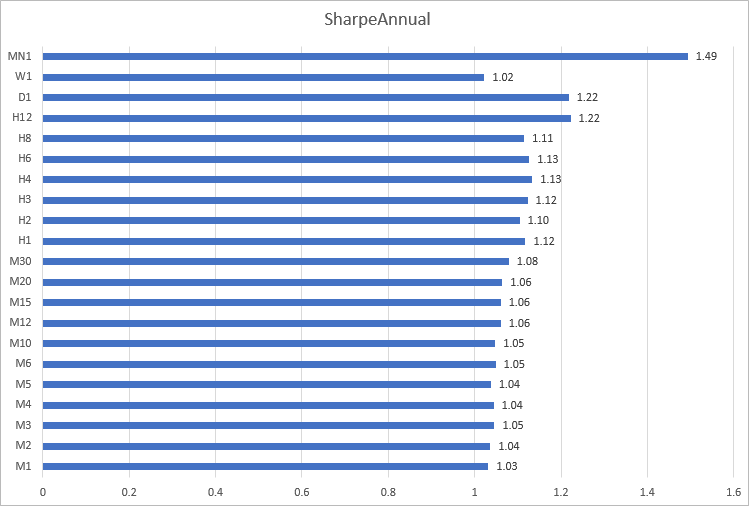
다양한 시간대에서 2020년 EURUSD에 대한 샤프 비율의 히스토그램을 구성해 보겠습니다. 여기에서 M1에서 M30까지의 기간에 대한 계산이 1.03에서 1.08까의 결과로 나온다는 것을 알 수 있습니다. H12에서 MN1까지의 시간대에서 가장 일관성이 없는 결과가 얻어졌습니다.

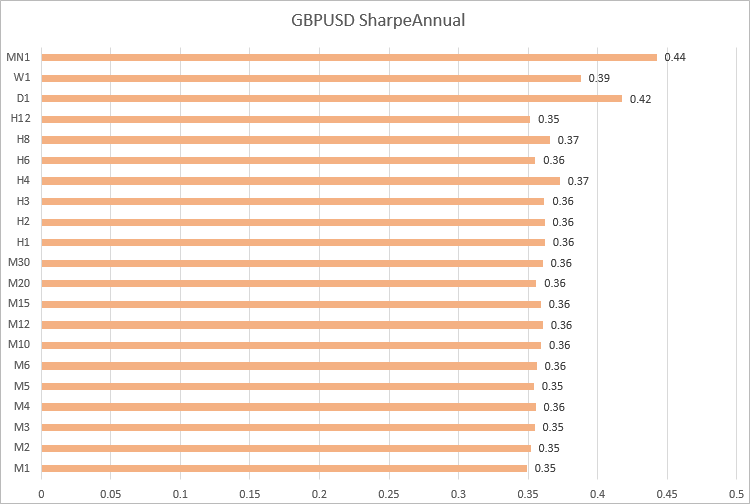
2020년 GBPUSD, USDJPY와 USDCHF에 대한 샤프 비율 계산

세 개의 통화 쌍에 대해 유사한 계산을 수행해 보겠습니다.

GBPUSD, 샤프 비율 값은 M1에서 H12까지의 기간에서 유사합니다.

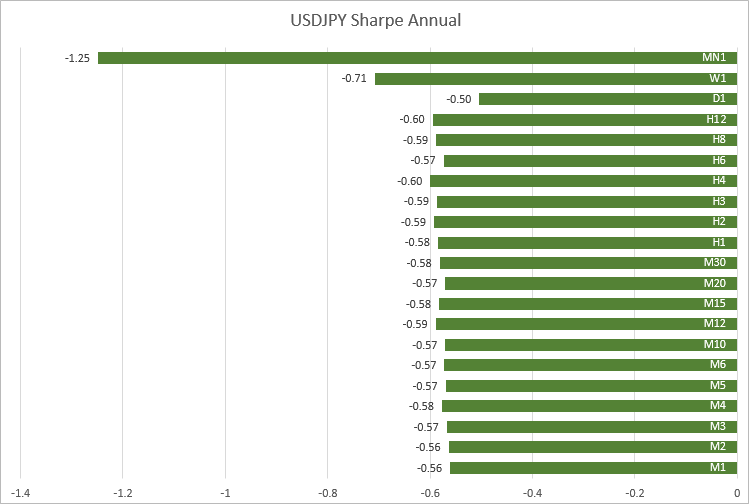
USDJPY, 값도 M1에서 H12까지의 기간에 가깝습니다: -0.56에서 -0.60.

USDCHF, 유사한 값이 M1에서 M30까지의 기간에서 획득되었습니다. 기간이 증가함에 따라 샤프 비율이 변동합니다.

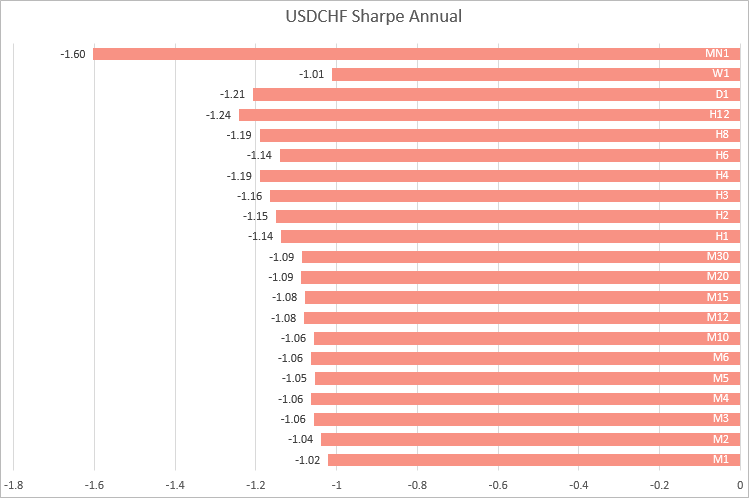
따라서 4개의 주요 통화 쌍의 예를 기반으로 M1에서 M30까지의 기간 동안에 샤프 비율의 가장 안정적인 계산을 얻을 수 있다는 결론을 내릴 수 있습니다. 이는 다른 심볼에서 작동하는 전략을 비교하려는 경우 더 낮은 기간의 수익률을 사용하여 비율을 계산하는 것이 더 낫다는 것을 의미합니다.

2020년 EURUSD에 대한 연간 샤프 비율 계산

2020년 월별 수익률을 사용하고 M1에서 H1까지의 기간에 대한 연간 샤프 비율을 계산해 보겠습니다. CalculateSharpe_Months.mq5 스크립트의 전체 코드는 기사에 첨부되어 있습니다.

//--- structure to store returns
struct Return
  {
   double            ret;   // return
   datetime          time;  // date
   int               month; // month
  };
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   SharpeMonths sharpe_by_months[];
//--- arrays of timeframes on which the Sharpe coefficient will be calculated
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1
                                  };
   ArrayResize(sharpe_by_months,ArraySize(timeframes));
//--- timeseries request parameters
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print("Calculate Sharpe Annual on ",symbol, " for 2020 year");
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- get the array of returns on the specified timeframe
      Return returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      double avr,std,sharpe;
      //--- Calculate statistics for the year
      GetStats(returns,avr,std,sharpe);
      string tf_str = EnumToString(timeframes[i]);
      //--- calculate the annual Sharpe ratio for each month
      SharpeMonths sharpe_months_on_tf;
      sharpe_months_on_tf.SetTimeFrame(tf_str);
      //--- select returns for i-th month
      for(int m = 1; m <= 12; m++)
        {
         Return month_returns[];
         GetReturnsByMonth(returns,m,month_returns);
         //--- Calculate statistics for the year
         double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns);
         sharpe_months_on_tf.Sharpe(m,sharpe_annual);
        }
      //--- add Sharpe ratio for 12 months on timeframe i
      sharpe_by_months[i] = sharpe_months_on_tf;
     }
//--- display the table of annual Sharpe values by months on all timeframes
   ArrayPrint(sharpe_by_months,3);
  }

/*
결과

2020년 EURUSD에서 연간 샤프 계산
             [TF]  [Jan]  [Feb] [Marc]  [Apr] [May] [June] [July] [Aug] [Sept]  [Oct] [Nov] [Dec]
[ 0] "PERIOD_M1"  -2.856 -1.340  0.120 -0.929 2.276  1.534  6.836 2.154 -2.697 -1.194 3.891 4.140
[ 1] "PERIOD_M2"  -2.919 -1.348  0.119 -0.931 2.265  1.528  6.854 2.136 -2.717 -1.213 3.845 4.125
[ 2] "PERIOD_M3"  -2.965 -1.340  0.118 -0.937 2.276  1.543  6.920 2.159 -2.745 -1.212 3.912 4.121
[ 3] "PERIOD_M4"  -2.980 -1.341  0.119 -0.937 2.330  1.548  6.830 2.103 -2.765 -1.219 3.937 4.110
[ 4] "PERIOD_M5"  -2.929 -1.312  0.120 -0.935 2.322  1.550  6.860 2.123 -2.729 -1.239 3.971 4.076
[ 5] "PERIOD_M6"  -2.945 -1.364  0.119 -0.945 2.273  1.573  6.953 2.144 -2.768 -1.239 3.979 4.082
[ 6] "PERIOD_M10" -3.033 -1.364  0.119 -0.934 2.361  1.584  6.789 2.063 -2.817 -1.249 4.087 4.065
[ 7] "PERIOD_M12" -2.952 -1.358  0.118 -0.956 2.317  1.609  6.996 2.070 -2.933 -1.271 4.115 4.014
[ 8] "PERIOD_M15" -3.053 -1.367  0.118 -0.945 2.377  1.581  7.132 2.078 -2.992 -1.274 4.029 4.047
[ 9] "PERIOD_M20" -2.998 -1.394  0.117 -0.920 2.394  1.532  6.884 2.065 -3.010 -1.326 4.074 4.040
[10] "PERIOD_M30" -3.008 -1.359  0.116 -0.957 2.379  1.585  7.346 2.084 -2.934 -1.323 4.139 4.034
[11] "PERIOD_H1"  -2.815 -1.373  0.116 -0.966 2.398  1.601  7.311 2.221 -3.136 -1.374 4.309 4.284

*/

월별 연간 비율의 값은 우리가 계산을 수행한 모든 기간에서 매우 가깝다는 것을 알 수 있습니다. 더 나은 프레젠테이션을 위해 Excel 다이어그램을 사용하여 결과를 3D로 렌더링해 보겠습니다.

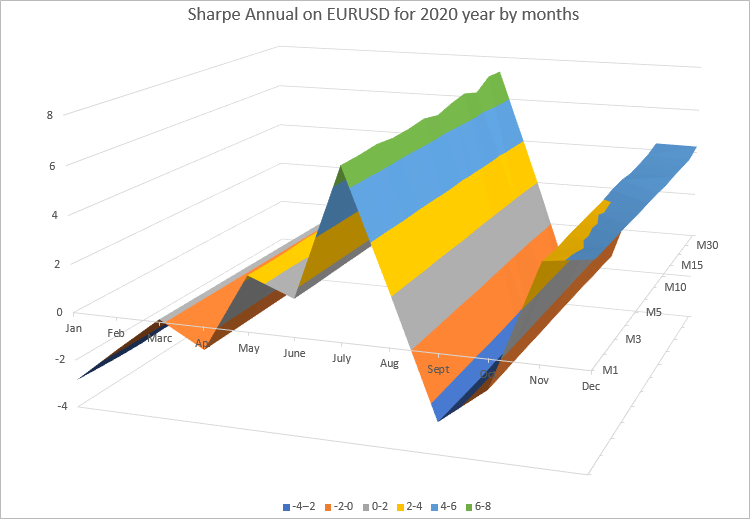
다이어그램은 연간 샤프 비율의 값이 매월 변경됨을 명확하게 보여줍니다. 이는 이번 달 EURUSD가 어떻게 변했는지에 따라 다릅니다. 반면 모든 기간의 월별 연간 샤프 비율은 거의 변하지 않습니다.

따라서 연간 샤프 비율은 모든 기간에서 계산할 수 있으며 결과 값은 수익을 얻은 바의 수에 따라 달라집니다. 이는 이 계산 알고리즘을 실시간으로 테스트하고 최적화하고 모니터링에 사용할 수 있음을 의미합니다. 유일한 전제 조건은 충분히 큰 수익 배열을 갖는 것입니다.

소르티노 비율

샤프 비율의 계산에서 위험은 자산의 증가 및 감소 모두를 포함하는 시세의 전체 변동성입니다. 그러나 포트폴리오 가치의 증가는 투자자에게 좋은 반면 손실은 가치의 감소와 관련이 있습니다. 따라서 비율의 실제 위험은 과장되어 있습니다. Frank Sortino가 1990년대 초에 개발한 소르티노 비율은 이 문제를 해결합니다.

그의 전임자들과 마찬가지로 F. Sortino도 미래 수익을 수학적 기대치와 동일한 확률 변수로 간주하고 위험은 분산으로 간주합니다. 수익과 위험은 특정 기간의 역사적 호가를 기반으로 결정됩니다. 샤프 비율 계산에서와 같이 수익을 위험으로 나눕니다.

Sortino는 수익의 총 분산(또는 전체 변동성)으로 정의된 위험이 긍정적인 변화와 부정적인 변화 모두로부터 영향을 받는다고 봤습니다. Sortino는 전체의 변동성을 자산 감소만 고려하는 반 변동성으로 대체했습니다. 반 변동성은 유해한 변동성, 하방 위험, 하방 편차, 음의 변동성 또는 하방 표준 편차라고도 합니다.

소르티노 비율 계산은 샤프 계산과 유사하지만 양수의 수익률은 변동성 계산에서 제외된다는 점만 다릅니다. 이것은 위험 측정을 줄이고 비율 가중치를 증가시킵니다.

샤프 비율을 기반으로 소르티노 비율을 계산하는 코드의 예제입니다. 반분산은 마이너스 수익만을 사용하여 계산됩니다.

//+------------------------------------------------------------------+
//|  Calculates Sharpe and Sortino ratios                            |
//+------------------------------------------------------------------+
void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino)
  {
   avr = ArrayMean(returns);
   std = ArrayStd(returns);
   sharpe = (std == 0) ? 0 : avr / std;
//--- now, remove negative returns and calculate the Sortino ratio
   double negative_only[];
   int size = ArraySize(returns);
   ArrayResize(negative_only,size);
   ZeroMemory(negative_only);
//--- copy only negative returns
   for(int i = 0; i < size; i++)
      negative_only[i] = (returns[i] > 0) ? 0 : returns[i];
   double semistd = ArrayStd(negative_only);
   sortino = avr / semistd;   
   return;
  }

이 기사에 첨부된 CalculateSortino_All_TF.mq5 스크립트는 2020년 EURUSD에 대해 다음과 같은 결과를 보여줍니다.

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeAnnual] [SortinoAnnual]    [Ratio]
[ 0] "M1"          1  373023 0.00000024 0.00014182     1.01769617      1.61605380 1.58795310
[ 1] "M2"          2  186573 0.00000048 0.00019956     1.02194170      1.62401856 1.58914991
[ 2] "M3"          3  124419 0.00000072 0.00024193     1.03126142      1.64332243 1.59350714
[ 3] "M4"          4   93302 0.00000096 0.00028000     1.02924195      1.62618200 1.57998030
[ 4] "M5"          5   74637 0.00000120 0.00031514     1.02303684      1.62286584 1.58632199
[ 5] "M6"          6   62248 0.00000143 0.00034122     1.03354379      1.63789024 1.58473231
[ 6] "M10"        10   37349 0.00000239 0.00044072     1.03266766      1.63461839 1.58290848
[ 7] "M12"        12   31124 0.00000286 0.00047632     1.04525580      1.65215986 1.58062730
[ 8] "M15"        15   24900 0.00000358 0.00053223     1.04515816      1.65256608 1.58116364
[ 9] "M20"        20   18675 0.00000477 0.00061229     1.04873529      1.66191269 1.58468272
[10] "M30"        30   12450 0.00000716 0.00074023     1.06348332      1.68543441 1.58482449
[11] "H1"         60    6225 0.00001445 0.00101979     1.10170316      1.75890688 1.59653431
[12] "H2"        120    3115 0.00002880 0.00145565     1.08797046      1.73062372 1.59068999
[13] "H3"        180    2076 0.00004305 0.00174762     1.10608991      1.77619289 1.60583048
[14] "H4"        240    1558 0.00005746 0.00200116     1.11659184      1.83085734 1.63968362
[15] "H6"        360    1038 0.00008643 0.00247188     1.11005321      1.79507001 1.61710267
[16] "H8"        480     779 0.00011508 0.00288226     1.09784908      1.74255746 1.58724682
[17] "H12"       720     519 0.00017188 0.00320405     1.20428761      2.11045830 1.75245371
[18] "D1"       1440     259 0.00035582 0.00470188     1.20132966      2.04624198 1.70331429
[19] "W1"      10080      51 0.00193306 0.01350157     1.03243721      1.80369984 1.74703102
[20] "MN1"     43200      12 0.00765726 0.01776075     1.49349076      5.00964481 3.35431926

거의 모든 시간 프레임에서 소르티노 값이 샤프 비율의 1.60배임을 알 수 있습니다. 물론 거래 결과를 기반으로 비율을 계산할 때는 그러한 명확한 의존성은 없을 것입니다. 따라서 두 비율을 모두 사용하여 전략/포트폴리오를 비교하는 것이 합리적입니다.

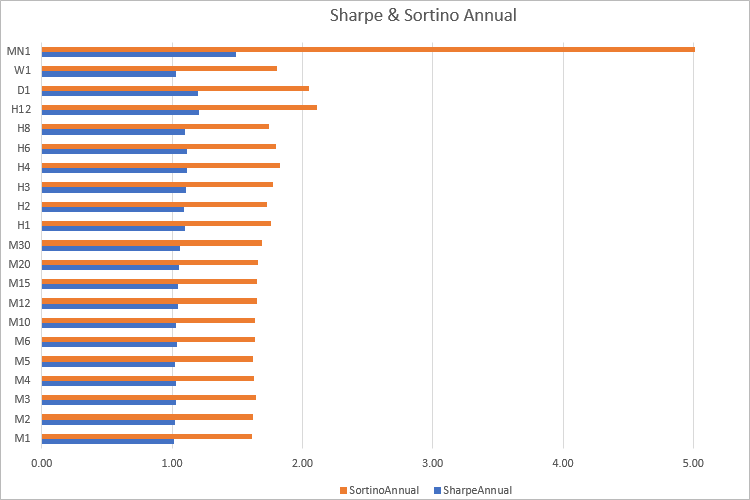
이 두 지표의 차이점은 샤프 비율은 주로 변동성을 반영하는 반면 소르티노 비율은 위험 단위당 비율 또는 수익을 보여줍니다. 그러나 계산은 히스토리를 기반으로 하므로 좋은 결과가 미래의 이익을 보장할 수 없다는 것을 잊지 마십시오.

MetaTrader 5 전략 테스터에서 샤프 비율 계산의 예

샤프 비율은 원래는 주식이 포함된 포트폴리오를 평가하기 위해 개발되었습니다. 주가는 매일 변하므로 자산의 가치도 매일 변합니다. 기본적으로 거래 전략은 오픈 포지션의 존재를 의미하지 않으므로 일정 시간 동안의 거래 계정의 상태는 변경되지 않은 상태로 유지됩니다. 즉, 진입한 포지션이 없을 때는 반환 값이 0이므로 샤프 계산은 틀리게 됩니다. 따라서 계산은 거래 계정의 상태가 변경된 바만을 사용합니다. 가장 적합한 옵션은 각 바의 마지막 틱에서 자기자본 가치를 분석하는 것입니다. 이렇게 하면 MetaTrader 5 전략 테스터의 틱 생성 모드에서 모든 샤프 비율을 계산할 수 있습니다.

고려해야 할 또 다른 점은 일반적으로 Return[i]=(CloseCurrent-ClosePrevious)/ClosePrevious로 계산되는 백분율 가격 증분은 계산시 특징적인 단점이 존재 한다는 것입니다. 가령 가격이 5% 하락한 다음 5% 상승하면 초기 값을 얻지 못합니다. 그렇기 때문에 통계 연구는 일반적인 상대 가격 증분 대신 가격 증분 로그를 사용합니다. 로그 반환(대수 반환)에는 선형 반환의 이러한 단점이 없습니다. 값은 다음과 같이 계산됩니다:

Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)

로그 수익은 로그의 합이 상대 수익의 곱과 같기 때문에 함께 더할 수 있으므로 편리합니다.

따라서 샤프 비율의 계산 알고리즘에는 최소한의 조정이 필요합니다.

//--- calculate the logarithms of increments using the equity array
   for(int i = 1; i < m_bars_counter; i++)
     {
      //--- only add if equity has changed
      if(m_equities[i] != prev_equity)
        {
         log_return = MathLog(m_equities[i] / prev_equity); // increment logarithm
         aver += log_return;            // average logarithm of increments
         AddReturn(log_return);         // fill the array of increment logarithms
         counter++;                     // counter of returns
        }
      prev_equity = m_equities[i];
     }
//--- if values are not enough for Sharpe calculation, return 0
   if(counter <= 1)
      return(0);
//--- average value of the increment logarithm
   aver /= counter;
//--- calculate standard deviation
   for(int i = 0; i < counter; i++)
      std += (m_returns[i] - aver) * (m_returns[i] - aver);
   std /= counter;
   std = MathSqrt(std);
//--- Sharpe ratio on the current timeframe
   double sharpe = aver / std;

전체 계산 코드는 기사에 첨부된 파일 Sharpe.mqh로 구현됩니다. 샤프 비율을 맞춤 최적화 기준과 같이 계산하려면 이 파일을 Expert Advisor에 연결하고 몇 줄의 코드를 추가하십시오. 표준 MetaTrader 5 팩의 MACD Sample.mq5 EA를 예로 하여 수행하는 방법을 살펴보겠습니다.

#define MACD_MAGIC 1234502
//---
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\PositionInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include "Sharpe.mqh"
//---
input double InpLots          = 0.1;// Lots
input int    InpTakeProfit    = 50; // Take Profit (in pips)
input int    InpTrailingStop  = 30; // Trailing Stop Level (in pips)
input int    InpMACDOpenLevel = 3;  // MACD open level (in pips)
input int    InpMACDCloseLevel = 2; // MACD close level (in pips)
input int    InpMATrendPeriod = 26; // MA trend period
//---
int ExtTimeOut = 10; // time out in seconds between trade operations
CReturns   returns;
....
//+------------------------------------------------------------------+
//| Expert new tick handling function                                |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   static datetime limit_time = 0; // last trade processing time + timeout
//--- add current equity to the array to calculate the Sharpe ratio
   MqlTick tick;
   SymbolInfoTick(_Symbol, tick);
   returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY));
//--- don't process if timeout
   if(TimeCurrent() >= limit_time)
     {
      //--- check for data
      if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod)
        {
         //--- change limit time by timeout in seconds if processed
         if(ExtExpert.Processing())
            limit_time = TimeCurrent() + ExtTimeOut;
        }
     }
  }
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester(void)
  {
//--- calculate Sharpe ratio
   double sharpe = returns.OnTester();
   return(sharpe);
  }
//+------------------------------------------------------------------+

결과 코드를 "MACD Sample Sharpe.mq5"로 저장하십시오 - 관련 파일도 아래에 첨부되어 있습니다.

맞춤형 최적화 기준을 선택하여 EURUSD M10 2020에 대한 제네릭 최적화를 실행해 보겠습니다.

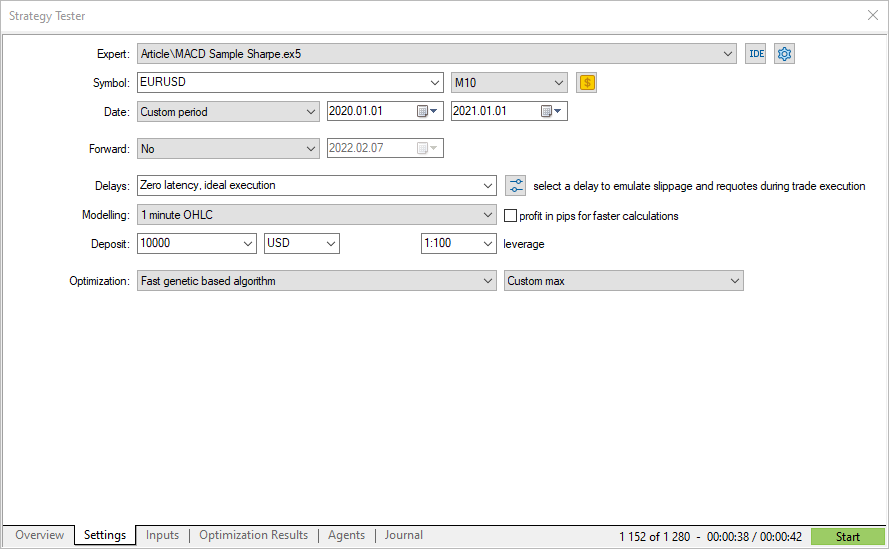
획득한 맞춤형 기준의 값은 전략 테스터가 계산한 샤프 비율과 일치합니다. 이제 계산 메커니즘과 얻은 결과를 해석하는 방법을 알게 되었을 것입니다.

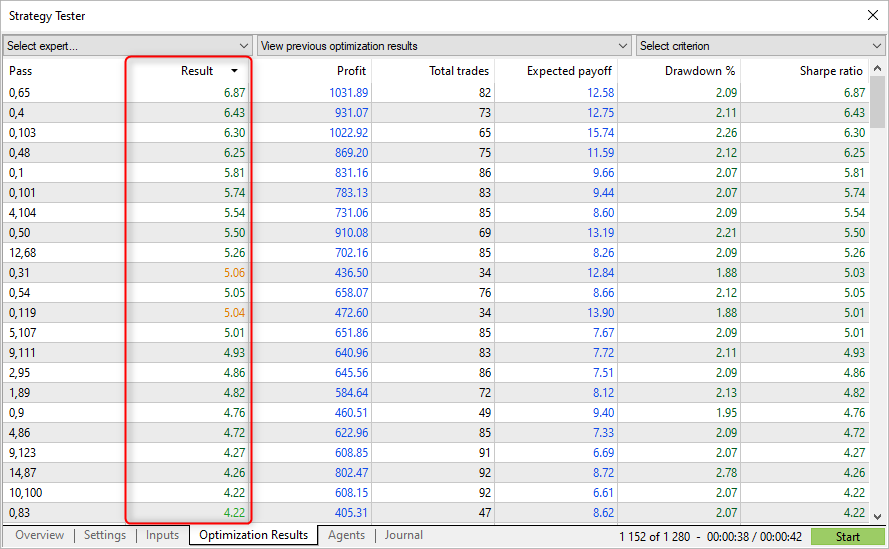
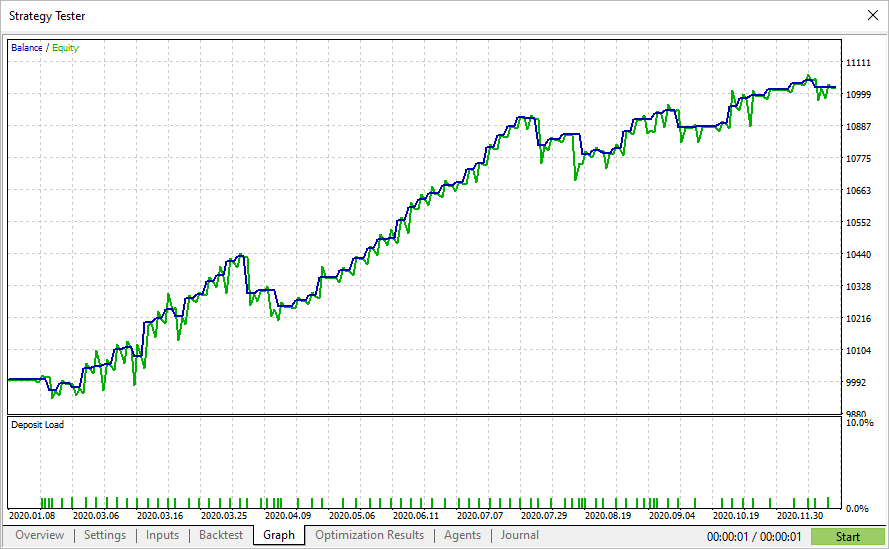
샤프 비율이 가장 높은 값들이 테스터에서 항상 가장 높은 수익을 나타내는 것은 아니지만 부드러운 자산 그래프의 매개변수를 찾을 수 있습니다. 이러한 그래프는 일반적으로 급격한 성장을 보이지는 않지만 큰 하락과 자본 손실도 없습니다.

이는 샤프 비율을 사용한 최적화를 이용하면 다른 최적화 기준에 비해 보다 안정적인 파라미터를 찾을 수 있음을 의미한다.

장점과 단점

샤프 비율과 소르티노 비율은 수익이 관련 위험 보다 많은지 여부를 결정할 수 있게 합니다. 다른 위험 측정 방식과 비교한 또 다른 이점은 모든 유형의 자산에 적용할 수 있다는 것입니다. 예를 들어 샤프 비율을 사용하여 금과 은을 비교할 수 있습니다. 평가를 위해 특정한 외부의 벤치마크가 필요하지 않기 때문입니다. 따라서 비율은 개별 전략이나 증권뿐만 아니라 자산 또는 전략 포트폴리오에도 적용될 수 있습니다.

이러한 툴의 단점은 계산이 수익의 정규 분포를 가정한다는 것입니다. 그러나 실제로는 이러한 요구 사항은 거의 충족되지 않습니다. 그럼에도 불구하고 샤프 및 소르티노 비율은 다양한 전략과 포트폴리오를 비교할 수 있는 가장 간단하고 이해하기 쉬운 도구입니다.