Matemática na negociação: indices de Sharpe e de Sortino
A rentabilidade é a medida mais óbvia que investidores e operadores novatos utilizam para analisar o desempenho da negociação. Já os traders profissionais empregam ferramentas mais robustas para analisar estratégias, entre elas os índices de Sharpe e de Sortino. Este artigo explicará com exemplos simples como são calculados. Já tratamos o tema da avaliação das estratégias de negociação no artigo "Matemática na negociação. Como estimar resultados de trading". Recomendamos que leia este artigo para refrescar seus conhecimentos ou aprender algo novo.
Índice de Sharpe
Investidores e traders experientes sabem que, para obter resultados consistentes, precisam negociar com várias estratégias ou investir em diferentes títulos. Este é um dos conceitos de investimento inteligente, e envolve a criação de uma carteira de investimentos. Como cada carteira de títulos/estratégias terá seus próprios parâmetros de risco e retorno, precisamos de alguma forma compará-los.
Uma das primeiras ferramentas que permitem realizar uma comparação desse tipo é o índice de Sharpe, que foi desenvolvido em 1966 por William Sharpe, ganhador do prêmio Nobel. Os principais indicadores utilizados por esta ferramenta são o rendimento médio, o desvio padrão do rendimento e o rendimento sem risco.
A desvantagem do índice de Sharpe é que os dados brutos para sua análise devem ser normalmente distribuídos. Em outras palavras, o gráfico de distribuição de rendimentos deve ser simétrico e não deve ter picos ou quedas acentuadas.
O índice de Sharpe é calculado usando a seguinte fórmula:
Sharpe Ratio = (Return - RiskFree)/Std
Onde:
- Return — rendimento médio durante um determinado período. Por exemplo, mensal, trimestral, anual, etc.
- RiskFree — rendimento sem risco durante o mesmo período de tempo. Isso pode ser juros sobre um depósito bancário, títulos e outros instrumentos financeiros com risco mínimo e 100% de confiabilidade.
- Std — desvio padrão do rendimento durante o mesmo período. Quanto maior a dispersão dos retornos, maior o risco e a volatilidade experimentados pela conta/ativos da carteira/fundos sob gestão do trader.
Rentabilidade
A rentabilidade é calculada como uma mudança no valor dos ativos ao longo de um determinado intervalo. O valor da rentabilidade é tomado durante o período para o qual se calcula o índice de Sharpe. Normalmente, o índice de Sharpe é considerado um valor anual, mas podem ser calculados valores trimestrais, mensais e até mesmo diários. A rentabilidade é calculada de acordo com a fórmula:
Return[i] = (Close[i]-Close[i-1])/Close[i-1]
Onde:
- Return[i] — rendimento para o intervalo com índice i;
- Close[i] — valor do ativo no final do i-ésimo intervalo;
- Close[i-1] — valor do ativo no final do intervalo anterior.
Em outras palavras, a rentabilidade pode ser escrita como a mudança relativa no valor dos ativos ao longo de um intervalo:
Return[i] = Delta[i]/Previous
Onde:
- Delta[i] = (Close[i]-Close[i-1]) — mudança absoluta no valor dos ativos ao longo do intervalo;
- Previous = Close[i-1] — valor do ativo no final do intervalo anterior.
Para calcular o índice de Sharpe em valores diários durante um ano, precisamos tomar os rendimentos diários durante o ano em questão e calcular o rendimento médio diário como a soma dos rendimentos dividido pelo número de dias que entram no cálculo.
Return = Sum(Return[i])/N
onde N é o número de dias.
Rendimento sem risco
O conceito de rendimento sem risco é condicional, pois sempre existe um risco. Além disso, como o índice de Sharpe é usado para comparar diferentes estratégias/carteiras no mesmo horizonte temporal, é mais fácil assumir um rendimento sem riscos igual a zero. Quer dizer
RiskFree = 0
Desvio padrão dos rendimentos
O desvio padrão mostra a dispersão de uma variável aleatória em torno do valor médio. Primeiro, calcula-se o rendimento médio, depois somam-se os quadrados dos desvios dos rendimentos em relação à média. O valor resultante é dividido pelo número de rendimentos, e esta é a dispersão. A raiz quadrada da dispersão é o desvio padrão dos rendimentos.
D = Sum((Return - Return[i])^2 )/N
STD = SQRT(D)
No artigo mencionado anteriormente, é apresentado um exemplo de como calcular o desvio padrão.
Cálculo do índice de Sharpe em qualquer timeframe e seu valor anual
O cálculo do índice de Sharpe não mudou desde 1966, e recebeu seu nome após o reconhecimento mundial de sua metodologia. Naquela época, a avaliação dos fundos e carteiras era feita com base nos rendimentos recebidos ao longo de vários anos. Mais tarde, começaram a efetuar cálculos com dados mensais e apresentar o índice de Sharpe resultante como um valor anual. Desta forma, é possível comparar dois fundos/carteiras/estratégias.
O índice de Sharpe é facilmente escalonável em diferentes intervalos e timeframes para o valor anual. Para fazer isso, basta multiplicar o valor obtido pela raiz quadrada da razão entre o intervalo anual e o intervalo atual. Vamos dar um exemplo simples.
Imaginemos que calculamos o índice Sharpe sobre os rendimentos diários - SharpeDaily. Agora precisamos apresentar o indicador resultante como um valor anual, SharpeAnnual. O índice anual é proporcional à raiz quadrada da proporção de períodos, em outras palavras, quantos intervalos cabem em um ano. Como no ano existem 252 dias úteis, o índice de Sharpe derivado dos rendimentos diários deve ser multiplicado pela raiz quadrada de 252. Este será o valor anual do índice de Sharpe:
SharpeAnnual = SQRT(252)*SharpeDaily // há 252 dias úteis em um ano
Se calcularmos no timeframe H1, o princípio permanece o mesmo, primeiro convertemos o SharpeHourly no SharpeDaily e, em seguida, obtemos o índice de Sharpe anual. Visto que um barra no timeframe D1 contém 24 barras H1, a fórmula será a seguinte:
SharpeDaily = SQRT(24)*SharpeHourly // D1 tem 24 horas
Embora nem todos os instrumentos financeiros sejam negociados 24 horas por dia, isto não importa para efeitos de avaliação de estratégias de negociação no testador sobre o mesmo instrumento, pois a comparação de estratégias ocorre no mesmo período de teste e no mesmo timeframe.
Avaliando estratégias usando a índice de Sharpe
Dependendo do desempenho da estratégia/carteira, o índice de Sharpe pode assumir qualquer valor, inclusive valores negativos. A conversão do índice de Sharpe em um valor anual nos permite interpretá-lo de maneira clássica: | Valor | Avaliação | Descrição |
|---|---|---|
| Sharpe Ratio < 0 | Ruim | Estratégia não lucrativa, não é boa. |
| 0 < Sharpe Ratio < 1.0 | indefinidamente | Risco não compensa. Tais estratégias podem ser tomadas para operar se não houver alternativas. |
| Sharpe Ratio ≥ 1.0 | Bom | Caso o índice de Sharpe seja maior que um, o risco está compensando, a carteira/estratégia está funcionando. |
| Sharpe Ratio ≥ 3.0 | Muito bom | Um número alto indica que a probabilidade de ocorrência de uma perda em qualquer negócio em particular é muito baixa. |
É preciso lembrar que o índice de Sharpe é uma estatística comum. É simplesmente o rendimento atribuível ao risco. Por isso, ao analisar as carteiras e estratégias, é importante correlacionar o índice de Sharpe com os valores recomendados e/ou uns aos outros.
Cálculo do índice de Sharpe em EURUSD para 2020
O Índice Sharpe foi originalmente desenvolvido para avaliar portfólios que sempre contêm muitas ações. O valor das ações muda todos os dias, assim como o valor da carteira. Assim, é possível remover a mudança de valor e de rendimento em qualquer timeframe. Faremos cálculos sobre o par de moedas EURUSD.
Faremos cálculos nos timeframes H1 e D1, depois converteremos no valor anual e compararemos se há diferença e veremos o porquê. Calcularemos com base nos preços de fechamento das barras durante 2020.
Código em MQL5
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- double H1_close[],D1_close[]; double h1_returns[],d1_returns[]; datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close); if(bars == -1) Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError()); else { Print("\nCalculamos a média e o desvio padrão dos rendimentos das barras H1"); Print("H1 bars=",ArraySize(H1_close)); GetReturns(H1_close,h1_returns); double average = ArrayMean(h1_returns); PrintFormat("H1 average=%G",average); double std = ArrayStd(h1_returns); PrintFormat("H1 std=%G",std); double sharpe_H1 = average / std; PrintFormat("H1 Sharpe=%G",sharpe_H1); double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_H1); } bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close); if(bars == -1) Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError()); else { Print("\nCalculamos a média e o desvio padrão dos rendimentos nas barras D1"); Print("D1 bars=",ArraySize(D1_close)); GetReturns(D1_close,d1_returns); double average = ArrayMean(d1_returns); PrintFormat("D1 average=%G",average); double std = ArrayStd(d1_returns); PrintFormat("D1 std=%G",std); double sharpe_D1 = average / std; double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_D1); } } //+------------------------------------------------------------------+ //| Preenche a matriz de rendimentos returns[] | //+------------------------------------------------------------------+ void GetReturns(const double & values[], double & returns[]) { int size = ArraySize(values); //--- se menos de 2 valores, devolvemos um conjunto vazio de rendimentos if(size < 2) { ArrayResize(returns,0); PrintFormat("%s: Error. ArraySize(values)=%d",size); return; } else { //--- preenchemos no loop de rendimento ArrayResize(returns, size - 1); double delta; for(int i = 1; i < size; i++) { returns[i - 1] = 0; if(values[i - 1] != 0) { delta = values[i] - values[i - 1]; returns[i - 1] = delta / values[i - 1]; } } } //--- } //+------------------------------------------------------------------+ //| Calcula o valor médio dos elementos da matriz | //+------------------------------------------------------------------+ double ArrayMean(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Error, array is empty",__FUNCTION__); return(0); } double mean = 0; for(int i = 0; i < size; i++) mean += array[i]; mean /= size; return(mean); } //+------------------------------------------------------------------+ //| Calcula o desvio padrão dos elementos da matriz | //+------------------------------------------------------------------+ double ArrayStd(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Error, array is empty",__FUNCTION__); return(0); } double mean = ArrayMean(array); double std = 0; for(int i = 0; i < size; i++) std += (array[i] - mean) * (array[i] - mean); std /= size; std = MathSqrt(std); return(std); } //+------------------------------------------------------------------+ /* Resultado Calculamos a média e o desvio padrão dos rendimentos nas barras H1 H1 bars:6226 H1 average=1.44468E-05 H1 std=0.00101979 H1 Sharpe=0.0141664 Sharpe_annual(H1)=1.117708053392263 Calculamos a média e o desvio padrão dos rendimentos nas barras D1 D1 bars:260 D1 average=0.000355823 D1 std=0.00470188 Sharpe_annual(H1)=1.2179005039019222 */
Código em Python para calcular usando a biblioteca MetaTrader5
import math from datetime import datetime import MetaTrader5 as mt5 # exibimos os dados para o pacote MetaTrader5 print("MetaTrader5 package author: ", mt5.__author__) print("MetaTrader5 package version: ", mt5.__version__) # importamos o módulo pandas para exibir os dados recebidos em forma de tabela import pandas as pd pd.set_option('display.max_columns', 50) # número de colunas a serem mostradas pd.set_option('display.width', 1500) # largura máxima da tabela a ser exibida # importam o módulo pytz para trabalhar com o fuso horário import pytz # estabelecemos a conexão com o terminal MetaTrader 5 if not mt5.initialize(): print("initialize() failed") mt5.shutdown() # definimos o fuso horário como UTC timezone = pytz.timezone("Etc/UTC") # criamos o objeto datetime no fuso horário UTC, para que não se aplique a diferença de fuso horário local utc_from = datetime(2020, 1, 1, tzinfo=timezone) utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone) # obtemos as barras de EURUSD H1 no intervalo 2020.01.01 00:00 - 2020.31.12 13:00 no fuso horário UTC rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to) # obtemos também as barras D1 no intervalo 2020.01.01 00:00 - 2020.31.12 13:00 no fuso horário UTC rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to) # concluímos a conexão com o terminal MetaTrader 5 e continuamos a processar as barras obtidas mt5.shutdown() # criamos DataFrame a partir dos dados recebidos rates_frame = pd.DataFrame(rates_H1) # adicionamos a coluna "Rendimento" rates_frame['return'] = 0.0 # agora calculamos os rendimentos como return[i] = (close[i] - close[i-1])/close[i-1] prev_close = 0.0 for i, row in rates_frame.iterrows(): close = row['close'] rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0 prev_close = close print("\nCalculamos a média e o desvio padrão dos rendimentos nas barras D1") print('H1 rates:', rates_frame.shape[0]) ret_average = rates_frame[1:]['return'].mean() # não tomamos a primeira linha com rendimento zero print('H1 return average=', ret_average) ret_std = rates_frame[1:]['return'].std(ddof=0) # não tomamos a primeira linha com rendimento zero print('H1 return std =', ret_std) sharpe_H1 = ret_average / ret_std print('H1 Sharpe = Average/STD = ', sharpe_H1) sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1) print('Sharpe_annual(H1) =', sharpe_annual_H1) # agora calculamos o índice de Sharpe no timeframe D1 rates_daily = pd.DataFrame(rates_D1) # adicionamos a coluna "Rendimento" rates_daily['return'] = 0.0 # agora calculamos a rentabilidade prev_return = 0.0 for i, row in rates_daily.iterrows(): close = row['close'] rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0 prev_return = close print("\nCalculamos a média e o desvio padrão dos rendimentos nas barras D1") print('D1 rates:', rates_daily.shape[0]) daily_average = rates_daily[1:]['return'].mean() print('D1 return average=', daily_average) daily_std = rates_daily[1:]['return'].std(ddof=0) print('D1 return std =', daily_std) sharpe_daily = daily_average / daily_std print('D1 Sharpe =', sharpe_daily) sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1) print('Sharpe_annual(D1) =', sharpe_annual_D1) Resultado Calculamos a média e o desvio padrão dos rendimentos nas barras H1 H1 rates: 6226 H1 return average= 1.4446773215242986e-05 H1 return std = 0.0010197932969323495 H1 Sharpe = Average/STD = 0.014166373968823358 Sharpe_annual(H1) = 1.117708053392236 Calculamos a média e o desvio padrão dos rendimentos nas barras D1 D1 rates: 260 D1 return average= 0.0003558228355051694 D1 return std = 0.004701883757646081 D1 Sharpe = 0.07567665511222807 Sharpe_annual(D1) = 1.2179005039019217
Pode-se ver que os resultados dos cálculos em MQL5 e Python são os mesmos. Os códigos-fonte estão anexados ao artigo (CalculateSharpe_2TF).
Além disso, o valor anual do índice de Sharpe obtido nas barras H1 e D1 difere entre si: 1,117708 versus 1,217900. Vamos estudar essa questão com mais detalhes.
Cálculo do índice de Sharpe anual sobre EURUSD para 2020 em todos os timeframes
Vamos calcular o índice de Sharpe anual em todos os timeframes da mesma maneira. Para fazer isso, coletamos os dados obtidos em uma tabela:
- TF — timeframe
- Minutes — quantidade de minutos no timeframe
- Rates — quantidade de barras por ano em dado timeframe
- Avg — rendimento médio no timeframe por barra em porcentagem (variação percentual média no preço por barra)
- Std — desvio padrão no timeframe por barra como porcentagem (volatilidade do preço como uma porcentagem de dado timeframe)
- SharpeTF — índice de Sharpe calculado para dado timeframe
- SharpeAnnual — índice de Sharpe anual, que é calculado com base no Sharpe em dado timeframe
Criamos o bloco de código para cálculo. Código completo está no arquivo anexo CalculateSharpe_All_TF.mq5.
//--- estrutura para impressão de estatísticas no log struct Stats { string TF; int Minutes; int Rates; double Avg; double Std; double SharpeTF; double SharpeAnnual; }; //--- matriz de estatísticas por timeframe Stats stats[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- matrizes para preços de fechamento double H1_close[],D1_close[]; //--- matrizes de rendimentos double h1_returns[],d1_returns[]; //--- matrizes de timeframes para calcular o índice de Sharpe ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4, PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1 }; ArrayResize(stats,ArraySize(timeframes)); //--- parâmetros de consulta da série temporal string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print(symbol); for(int i = 0; i < ArraySize(timeframes); i++) { //--- obtemos a matriz de rendimentos no timeframe especificado double returns[]; GetReturns(symbol,timeframes[i],from,to,returns); //--- calculamos a estatística GetStats(returns,avr,std,sharpe); double sharpe_annual = sharpe * MathSqrt(ArraySize(returns)); PrintFormat("%s aver=%G%% std=%G%% sharpe=%G sharpe_annual=%G", EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual); //--- preenchemos a estrutura da estatística Stats row; string tf_str = EnumToString(timeframes[i]); StringReplace(tf_str,"PERIOD_",""); row.TF = tf_str; row.Minutes = PeriodSeconds(timeframes[i]) / 60; row.Rates = ArraySize(returns); row.Avg = avr; row.Std = std; row.SharpeTF = sharpe; row.SharpeAnnual = sharpe_annual; //--- adicionamos a linha de estatística para o timeframe stats[i] = row; } //--- exibimos estatísticas no log para todos os timeframes ArrayPrint(stats,8); } /* Resultado [TF] [Minutes] [Rates] [Avg] [Std] [SharpeTF] [SharpeAnnual] [ 0] "M1" 1 373023 0.00000024 0.00168942 0.00168942 1.03182116 [ 1] "M2" 2 186573 0.00000048 0.00239916 0.00239916 1.03629642 [ 2] "M3" 3 124419 0.00000072 0.00296516 0.00296516 1.04590258 [ 3] "M4" 4 93302 0.00000096 0.00341717 0.00341717 1.04378592 [ 4] "M5" 5 74637 0.00000120 0.00379747 0.00379747 1.03746116 [ 5] "M6" 6 62248 0.00000143 0.00420265 0.00420265 1.04854166 [ 6] "M10" 10 37349 0.00000239 0.00542100 0.00542100 1.04765562 [ 7] "M12" 12 31124 0.00000286 0.00601079 0.00601079 1.06042363 [ 8] "M15" 15 24900 0.00000358 0.00671964 0.00671964 1.06034161 [ 9] "M20" 20 18675 0.00000477 0.00778573 0.00778573 1.06397070 [10] "M30" 30 12450 0.00000716 0.00966963 0.00966963 1.07893298 [11] "H1" 60 6225 0.00001445 0.01416637 0.01416637 1.11770805 [12] "H2" 120 3115 0.00002880 0.01978455 0.01978455 1.10421905 [13] "H3" 180 2076 0.00004305 0.02463458 0.02463458 1.12242890 [14] "H4" 240 1558 0.00005746 0.02871564 0.02871564 1.13344977 [15] "H6" 360 1038 0.00008643 0.03496339 0.03496339 1.12645075 [16] "H8" 480 779 0.00011508 0.03992838 0.03992838 1.11442404 [17] "H12" 720 519 0.00017188 0.05364323 0.05364323 1.22207717 [18] "D1" 1440 259 0.00035582 0.07567666 0.07567666 1.21790050 [19] "W1" 10080 51 0.00193306 0.14317328 0.14317328 1.02246174 [20] "MN1" 43200 12 0.00765726 0.43113365 0.43113365 1.49349076 */
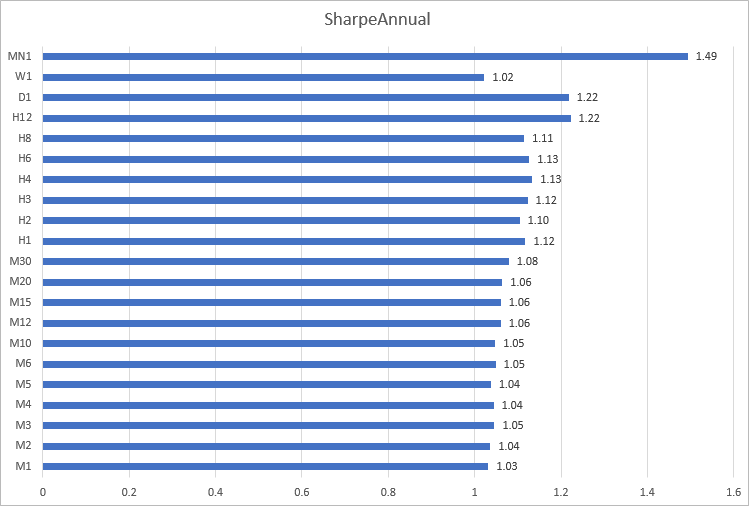
Desenhemos um histograma do índice de Sharpe do EURUSD para 2020 com base nos timeframes. Pode-se ver que, nos timeframes de M1 a M30, os cálculos dão um resultado próximo de 1,03 a 1,08. Os resultados mais instáveis se dão nos timeframes de H12 a MN1.
Cálculo do índice Sharpe do GBPUSD, do USDJPY e do USDCHF para 2020
Vamos fazer os mesmos cálculos para mais três pares de moedas importantes.
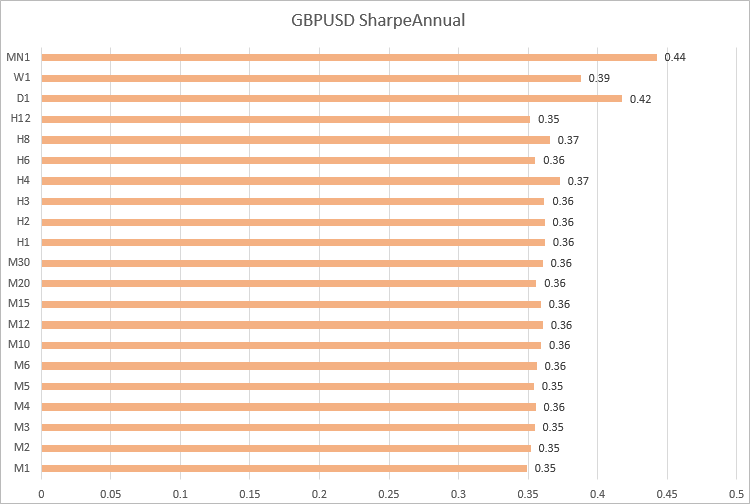
GBPUSD, os valores do índice de Sharpe foram próximos nos timeframes de M1 a H12.
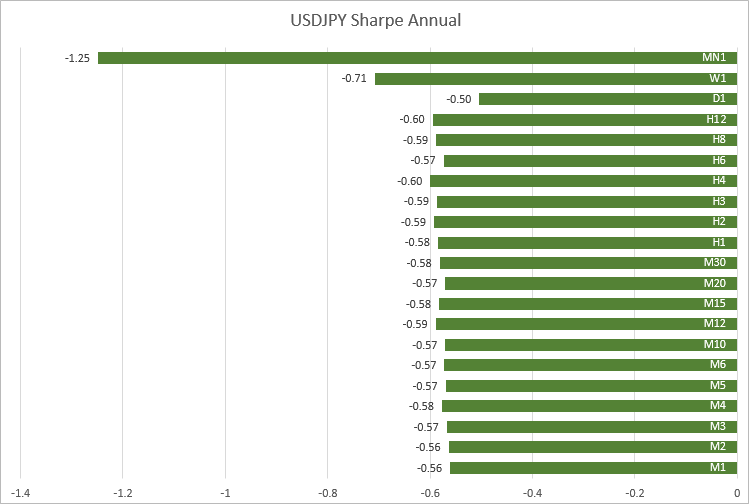
USDJPY, os valores também foram próximos nos timeframes de M1 a H12 - -0,56 a -0,60.
USDCHF, valores próximos nos timeframes de M1 a M30. À medida que o timeframe aumenta, o índice de Sharpe flutua.
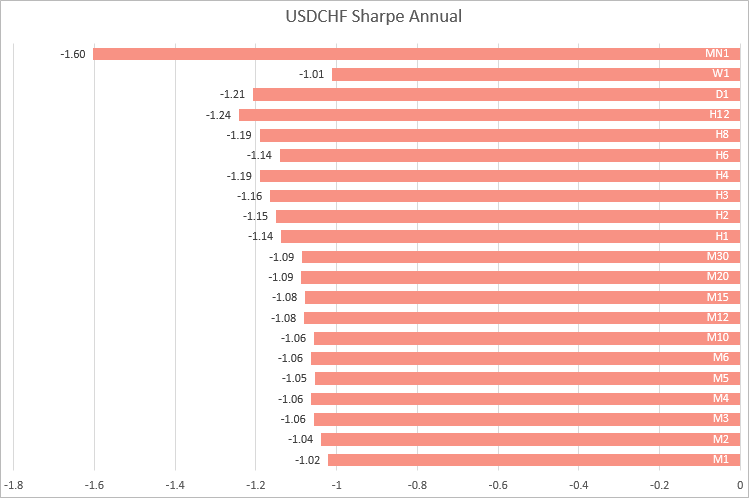
Assim, com o exemplo de 4 pares de moedas, podemos concluir que os cálculos mais estáveis do índice Sharpe são obtidos nos timeframes de M1 a M30. Ou seja, caso precisemos comparar estratégias que funcionem em símbolos diferentes, é melhor tirar os valores de rendimentos dos timeframes pequenos.
Cálculo do índice de Sharpe anual do EURUSD para cada mês do 2020
Pegamos os rendimentos de cada mês do 2020 e calculamos o valor anual do Índice de Sharpe nos timeframes de M1 a H1. O código completo do script CalculateSharpe_Months.mq5 está anexado ao artigo.
//--- estrutura para armazenamento do rendimento struct Return { double ret; // rendimento datetime time; // data int month; // mês }; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { SharpeMonths sharpe_by_months[]; //--- matrizes de timeframes para calcular o índice de Sharpe ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1 }; ArrayResize(sharpe_by_months,ArraySize(timeframes)); //--- parâmetros de consulta da série temporal string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print("Calculate Sharpe Annual on ",symbol, " for 2020 year"); for(int i = 0; i < ArraySize(timeframes); i++) { //--- obtemos a matriz de rendimentos no timeframe especificado Return returns[]; GetReturns(symbol,timeframes[i],from,to,returns); double avr,std,sharpe; //--- calculamos as estatísticas anuais GetStats(returns,avr,std,sharpe); string tf_str = EnumToString(timeframes[i]); //--- calculamos o valor do índice de Sharpe anual para cada mês SharpeMonths sharpe_months_on_tf; sharpe_months_on_tf.SetTimeFrame(tf_str); //--- selecionamos os rendimentos para o mês i for(int m = 1; m <= 12; m++) { Return month_returns[]; GetReturnsByMonth(returns,m,month_returns); //--- calculamos as estatísticas anuais double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns); sharpe_months_on_tf.Sharpe(m,sharpe_annual); } //--- adicionamos os valores do índice de Sharpe por 12 meses no timeframe i sharpe_by_months[i] = sharpe_months_on_tf; } //--- exibimos uma tabela de valores de Sharpe anuais mês a mês em todos os timeframes ArrayPrint(sharpe_by_months,3); } /* Resultado Calculate Sharpe Annual on EURUSD for 2020 year [TF] [Jan] [Feb] [Marc] [Apr] [May] [June] [July] [Aug] [Sept] [Oct] [Nov] [Dec] [ 0] "PERIOD_M1" -2.856 -1.340 0.120 -0.929 2.276 1.534 6.836 2.154 -2.697 -1.194 3.891 4.140 [ 1] "PERIOD_M2" -2.919 -1.348 0.119 -0.931 2.265 1.528 6.854 2.136 -2.717 -1.213 3.845 4.125 [ 2] "PERIOD_M3" -2.965 -1.340 0.118 -0.937 2.276 1.543 6.920 2.159 -2.745 -1.212 3.912 4.121 [ 3] "PERIOD_M4" -2.980 -1.341 0.119 -0.937 2.330 1.548 6.830 2.103 -2.765 -1.219 3.937 4.110 [ 4] "PERIOD_M5" -2.929 -1.312 0.120 -0.935 2.322 1.550 6.860 2.123 -2.729 -1.239 3.971 4.076 [ 5] "PERIOD_M6" -2.945 -1.364 0.119 -0.945 2.273 1.573 6.953 2.144 -2.768 -1.239 3.979 4.082 [ 6] "PERIOD_M10" -3.033 -1.364 0.119 -0.934 2.361 1.584 6.789 2.063 -2.817 -1.249 4.087 4.065 [ 7] "PERIOD_M12" -2.952 -1.358 0.118 -0.956 2.317 1.609 6.996 2.070 -2.933 -1.271 4.115 4.014 [ 8] "PERIOD_M15" -3.053 -1.367 0.118 -0.945 2.377 1.581 7.132 2.078 -2.992 -1.274 4.029 4.047 [ 9] "PERIOD_M20" -2.998 -1.394 0.117 -0.920 2.394 1.532 6.884 2.065 -3.010 -1.326 4.074 4.040 [10] "PERIOD_M30" -3.008 -1.359 0.116 -0.957 2.379 1.585 7.346 2.084 -2.934 -1.323 4.139 4.034 [11] "PERIOD_H1" -2.815 -1.373 0.116 -0.966 2.398 1.601 7.311 2.221 -3.136 -1.374 4.309 4.284 */
Pode-se observar que os valores do índice anual para cada mês são muito próximos em todos os timeframes em que os cálculos foram realizados. Para uma melhor apresentação, vamos mostrar os resultados como uma superfície 3D usando um diagrama do Excel.
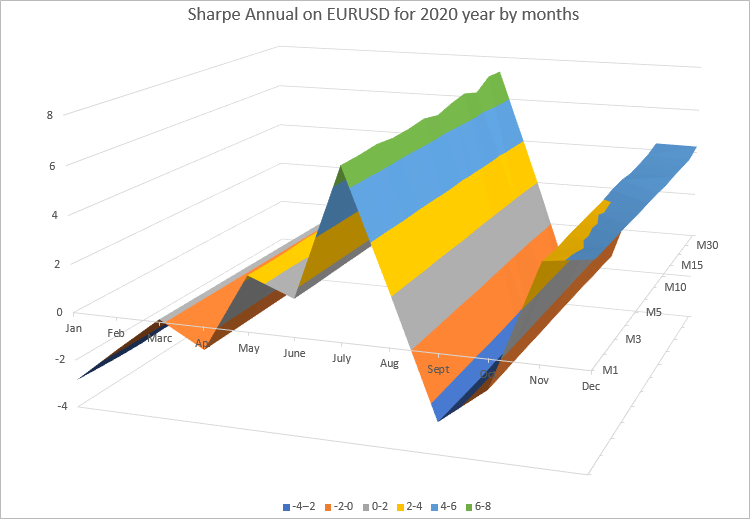
O gráfico mostra claramente que os valores do índice de Sharpe anual mudam a cada mês. O que depende de como o gráfico EURUSD mudou no mês em questão. Mas, além disso, o valor do índice de Sharpe anual para cada mês em todos os timeframes quase não muda.
Assim, podemos calculá-lo em qualquer timeframe, sendo que o valor resultante também não depende do número de barras em que os rendimentos foram obtidos. Isso significa que o algoritmo de cálculo acima pode ser usado em testes, otimização e durante o monitoramento em tempo real. O principal é que a matriz de rendimentos não deve ser muito pequena.
Índice de Sortino
Ao calcular o índice de Sharpe, a volatilidade total das cotações, tanto para cima quanto para baixo, é considerada como risco. No entanto, um aumento no valor de uma carteira é benéfico para o investidor, enquanto uma diminuição em seu valor pode acarretar prejuízos. Por isso, o risco real no índice é superestimado. O índice de Sortino, desenvolvido no início da década de 1990 por Frank Sortino, resolve esse problema.
Como seus antecessores, Sortino considera o rendimento futuro como uma variável aleatória igual ao seu valor esperado e o risco como uma dispersão. A rentabilidade e o risco são determinados com base nos valores históricos das cotações para um determinado período. Assim como no cálculo do índice de Sharpe, a rentabilidade é dividida pelo risco.
Sortino notou que o risco, definido como a dispersão total dos rendimentos (ou seja, a volatilidade total), depende tanto de variações positivas quanto negativas. Sortino substituiu a dispersão total por uma semidispersão que leva em conta apenas as quedas nos ativos. A semidispersão é referida em várias publicações como volatilidade para baixo, dispersão negativa, menor dispersão ou desvio padrão de perdas.
O índice de Sortino é calculado da mesma forma que o de Sharpe, só que os rendimentos positivos são excluídos do cálculo da volatilidade. Isso permite reduzir a medida de risco e aumentar o valor do índice.
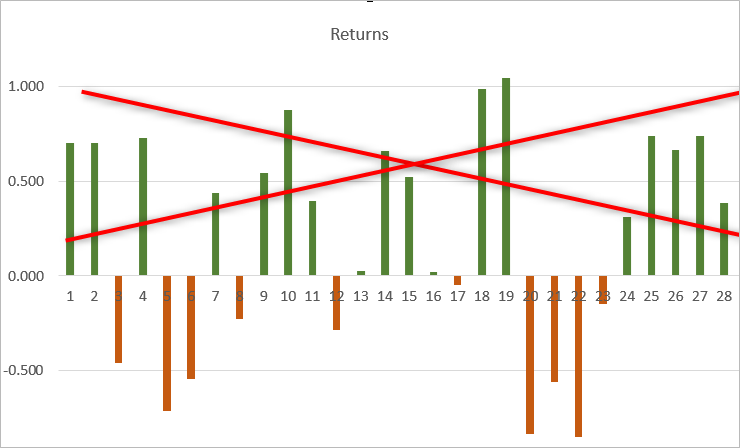
Código de exemplo para calcular o índice de Sortino com base no cálculo do índice de Sharpe. São pegados apenas rendimentos negativos para calcular a "semidispersão".
//+------------------------------------------------------------------+ //| Calculamos os índices de Sharpe e de Sortino | //+------------------------------------------------------------------+ void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino) { avr = ArrayMean(returns); std = ArrayStd(returns); sharpe = (std == 0) ? 0 : avr / std; //--- agora removemos os retornos positivos e calculamos o índice de Sortino double negative_only[]; int size = ArraySize(returns); ArrayResize(negative_only,size); ZeroMemory(negative_only); //--- copiamos apenas os rendimentos negativos for(int i = 0; i < size; i++) negative_only[i] = (returns[i] > 0) ? 0 : returns[i]; double semistd = ArrayStd(negative_only); sortino = avr / semistd; return; }
O script CalculateSortino_All_TF.mq5 anexado ao artigo fornece os seguintes resultados de EURUSD para 2020:
[TF] [Minutes] [Rates] [Avg] [Std] [SharpeAnnual] [SortinoAnnual] [Ratio] [ 0] "M1" 1 373023 0.00000024 0.00014182 1.01769617 1.61605380 1.58795310 [ 1] "M2" 2 186573 0.00000048 0.00019956 1.02194170 1.62401856 1.58914991 [ 2] "M3" 3 124419 0.00000072 0.00024193 1.03126142 1.64332243 1.59350714 [ 3] "M4" 4 93302 0.00000096 0.00028000 1.02924195 1.62618200 1.57998030 [ 4] "M5" 5 74637 0.00000120 0.00031514 1.02303684 1.62286584 1.58632199 [ 5] "M6" 6 62248 0.00000143 0.00034122 1.03354379 1.63789024 1.58473231 [ 6] "M10" 10 37349 0.00000239 0.00044072 1.03266766 1.63461839 1.58290848 [ 7] "M12" 12 31124 0.00000286 0.00047632 1.04525580 1.65215986 1.58062730 [ 8] "M15" 15 24900 0.00000358 0.00053223 1.04515816 1.65256608 1.58116364 [ 9] "M20" 20 18675 0.00000477 0.00061229 1.04873529 1.66191269 1.58468272 [10] "M30" 30 12450 0.00000716 0.00074023 1.06348332 1.68543441 1.58482449 [11] "H1" 60 6225 0.00001445 0.00101979 1.10170316 1.75890688 1.59653431 [12] "H2" 120 3115 0.00002880 0.00145565 1.08797046 1.73062372 1.59068999 [13] "H3" 180 2076 0.00004305 0.00174762 1.10608991 1.77619289 1.60583048 [14] "H4" 240 1558 0.00005746 0.00200116 1.11659184 1.83085734 1.63968362 [15] "H6" 360 1038 0.00008643 0.00247188 1.11005321 1.79507001 1.61710267 [16] "H8" 480 779 0.00011508 0.00288226 1.09784908 1.74255746 1.58724682 [17] "H12" 720 519 0.00017188 0.00320405 1.20428761 2.11045830 1.75245371 [18] "D1" 1440 259 0.00035582 0.00470188 1.20132966 2.04624198 1.70331429 [19] "W1" 10080 51 0.00193306 0.01350157 1.03243721 1.80369984 1.74703102 [20] "MN1" 43200 12 0.00765726 0.01776075 1.49349076 5.00964481 3.35431926
Observa-se que praticamente em todos os timeframes, o valor anual do Sortino é 1,60 vezes maior que o índice de Sharpe. Mas, ao calcular os resultados da negociação, fica claro que não haverá um padrão tão claro. Por isso, faz sentido comparar estratégias/carteiras usando ambos os indicadores.
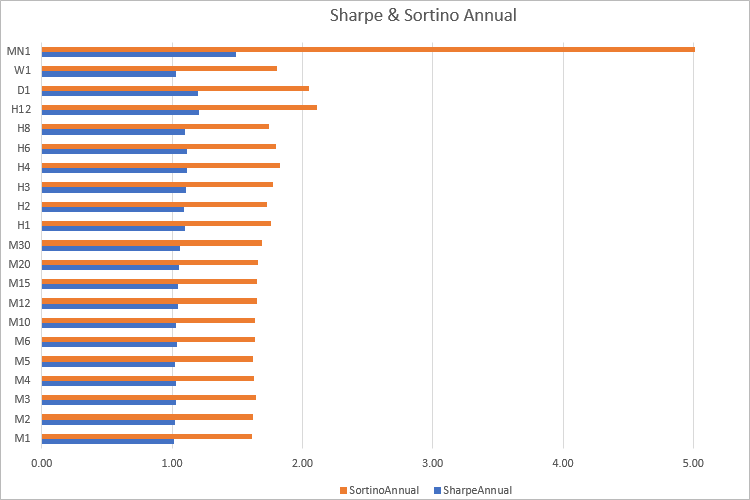
A diferença entre os dois é que o Índice de Sharpe mostra principalmente a volatilidade, enquanto o Índice de Sortino realmente mostra o nível de rendimento por unidade de risco. Mas não se esqueça de que todos esses cálculos são feitos sobre o histórico, e os bons valores apresentados pelos indicadores não garantem lucros no futuro.
Exemplo de cálculo do índice Sharpe no testador de estratégia MetaTrader 5
O Índice de Sharpe foi desenvolvido para avaliar carteiras com ações. O preço das ações muda todos os dias, portanto, o tamanho dos ativos também muda todos os dias. As estratégias de negociação por padrão não implicam a presença de posições abertas, logo, parte do tempo o estado da conta de negociação permanecerá inalterado. Isso significa que, na ausência de posições abertas, receberemos rendimentos nulos e o cálculo do índice Sharpe com esses dados não será confiável. Por isso, apenas as barras onde o status da conta muda devem ser levadas em consideração. A alternativa mais adequada seria remover os valores de capital líquido em cada último tick da barra. Isso permitirá calcular o índice de Sharpe para qualquer modo de geração de ticks no testador de estratégia MetaTrader 5.
O segundo ponto a considerar é que o incremento percentual dos preços, que normalmente é considerado como Return[i]=(CloseCurrent-ClosePrevious)/ClosePrevious, tem uma certa desvantagem nos cálculos. Nomeadamente, se o preço diminuir em 5% e depois aumentar em 5%, não obteremos o valor inicial. Por isso, em vez do usual incremento de preço relativo, os estudos estatísticos costumam utilizar o logaritmo do incremento de preço. A rentabilidade logarítmica não têm essa desvantagem própria da rentabilidade linear. É calculada pela fórmula:
Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)
A rentabilidade logarítmica é conveniente porque pode ser somada, pois a soma dos logaritmos é equivalente ao produto dos rendimentos relativos.
Assim, o algoritmo para calcular o índice de Sharpe muda minimamente.
//--- calculamos os logaritmos dos incrementos a partir da matriz de capital líquido for(int i = 1; i < m_bars_counter; i++) { //--- somente adicionamos se o capital líquido tiver mudado if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // logaritmo do incremento aver += log_return; // logaritmo médio dos incrementos AddReturn(log_return); // preenchemos a matriz de logaritmos a partir dos incrementos counter++; // contador de rendimentos } prev_equity = m_equities[i]; } //--- se não houver valores suficientes para calcular o índice de Sharpe, retornamos 0 if(counter <= 1) return(0); //--- valor médio do logaritmo do incremento aver /= counter; //--- calculamos o desvio padrão for(int i = 0; i < counter; i++) std += (m_returns[i] - aver) * (m_returns[i] - aver); std /= counter; std = MathSqrt(std); //--- índice de Sharpe no timeframe atual double sharpe = aver / std;
O código de cálculo completo é implementado como um arquivo de inclusão Sharpe.mqh anexado ao artigo. Para calcular o índice de Sharpe como um critério de otimização personalizado, anexamos este arquivo ao Expert Advisor e adicionamos algumas linhas de código. Vamos mostrar como fazer isso usando o EA "MACD Sample.mq5" da distribuição padrão do MetaTrader 5 como exemplo.
#define MACD_MAGIC 1234502 //--- #include <Trade\Trade.mqh> #include <Trade\SymbolInfo.mqh> #include <Trade\PositionInfo.mqh> #include <Trade\AccountInfo.mqh> #include "Sharpe.mqh" //--- input double InpLots = 0.1;// Lots input int InpTakeProfit = 50; // Take Profit (in pips) input int InpTrailingStop = 30; // Trailing Stop Level (in pips) input int InpMACDOpenLevel = 3; // MACD open level (in pips) input int InpMACDCloseLevel = 2; // MACD close level (in pips) input int InpMATrendPeriod = 26; // MA trend period //--- int ExtTimeOut = 10; // time out in seconds between trade operations CReturns returns; .... //+------------------------------------------------------------------+ //| Expert new tick handling function | //+------------------------------------------------------------------+ void OnTick(void) { static datetime limit_time = 0; // last trade processing time + timeout //--- adicionamos o capital líquido atual atual à matriz para calcular o índice de Sharpe MqlTick tick; SymbolInfoTick(_Symbol, tick); returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY)); //--- don't process if timeout if(TimeCurrent() >= limit_time) { //--- check for data if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod) { //--- change limit time by timeout in seconds if processed if(ExtExpert.Processing()) limit_time = TimeCurrent() + ExtTimeOut; } } } //+------------------------------------------------------------------+ //| Tester function | //+------------------------------------------------------------------+ double OnTester(void) { //--- calculamos o índice de Sharpe double sharpe = returns.OnTester(); return(sharpe); } //+------------------------------------------------------------------+
O código resultante será salvo com o nome "MACD Sample Sharpe.mq5", também anexado ao artigo.
Vamos executar a otimização genética do EURUSD M10 para 2020 selecionando um critério de otimização personalizado.
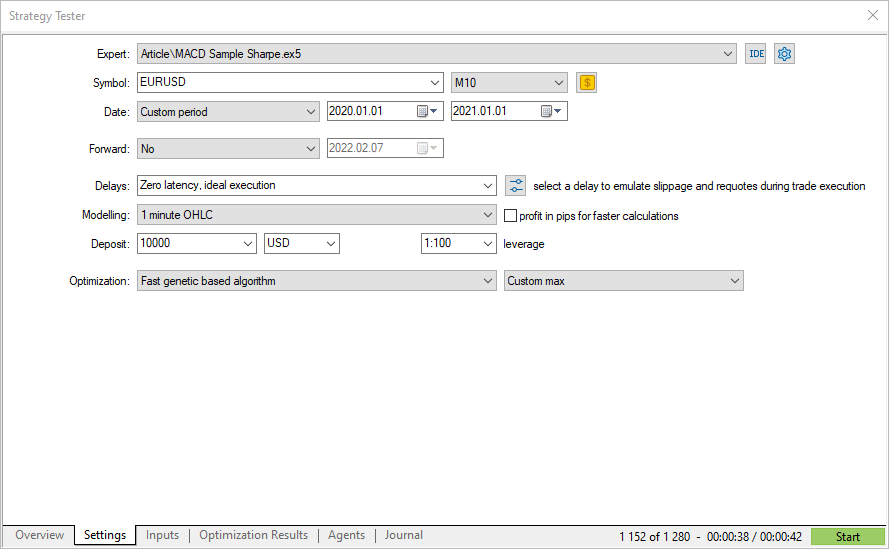
Os valores obtidos do critério personalizado coincidem com o índice de Sharpe calculado pelo testador de estratégia. Agora você conhece o mecanismo de cálculo e como interpretar os resultados.
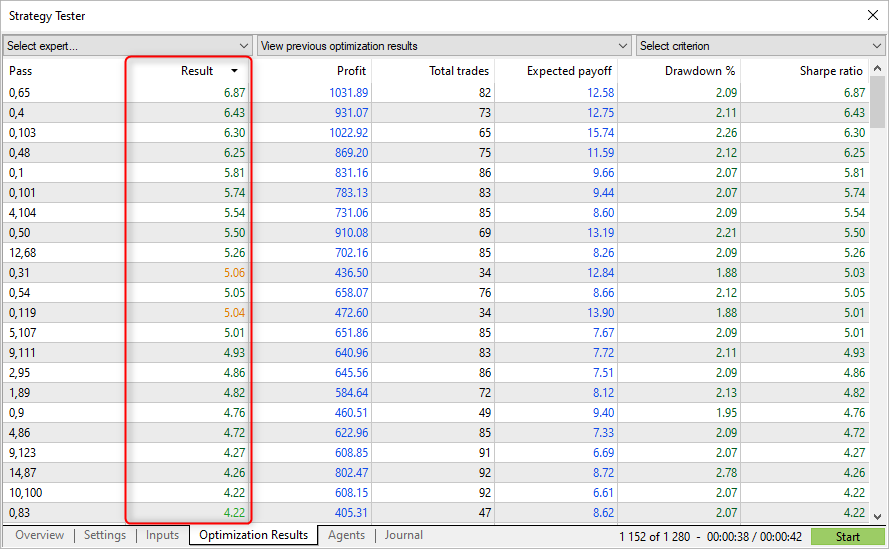
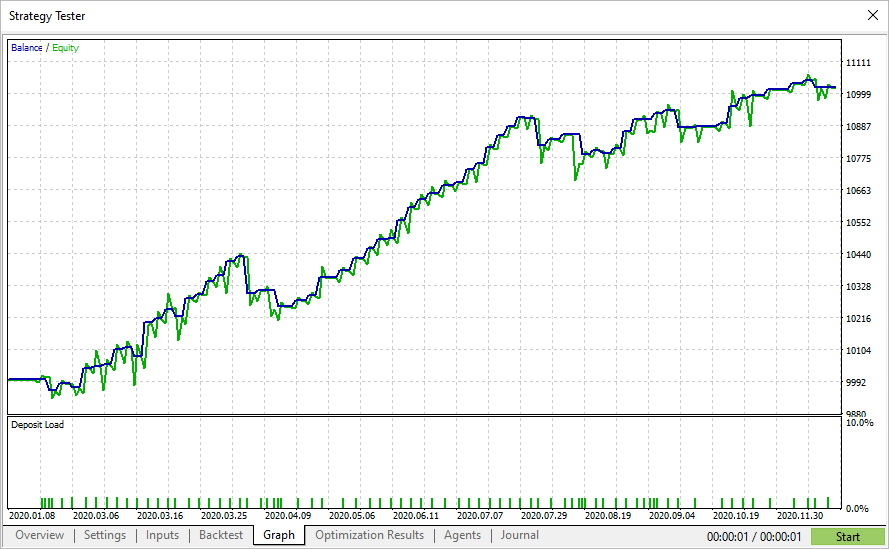
As rodadas com o índice de Sharpe máximo nem sempre mostram o maior lucro no testador, mas permitem encontrar parâmetros com um gráfico de capital líquido suave. Em tais gráficos, como regra, não há crescimento acentuado, mas também não há grandes quedas e rebaixamentos no capital líquido.
Assim, a otimização do índice de Sharpe de fato permite buscar parâmetros mais estáveis em comparação com outros critérios de otimização.
Vantagens e desvantagens
Os índices de Sharpe e de Sortino permitem determinar se o lucro recebido compensa ou não o risco associado. Outra vantagem comparada às medições de risco alternativas é que podem ser aplicados a todos os tipos de ativos. Por exemplo, é possível comparar o ouro com a prata usando o índice de Sharpe porque não requer uma referência externa específica a fim de avaliar. Assim, podem ser aplicados a estratégias individuais ou a títulos, bem como a carteiras em fundos comuns.
A desvantagem dessas ferramentas é que o cálculo pressupõe uma distribuição normal dos rendimentos. Na realidade, esse requisito geralmente não é atendido, no entanto, os índices de Sharpe e de Sortino são os mais simples e compreensíveis na hora de comparar diferentes estratégias e carteiras.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/9171
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
 Desenvolvendo um EA de negociação do zero (Parte 08): Um salto conceitual (I)
Desenvolvendo um EA de negociação do zero (Parte 08): Um salto conceitual (I)
 Desenvolvendo um EA de negociação do zero (Parte 07): Adicionando o Volume At Price (I)
Desenvolvendo um EA de negociação do zero (Parte 07): Adicionando o Volume At Price (I)
 Desenvolvendo um EA de negociação do zero (Parte 09): Um salto conceitual (II)
Desenvolvendo um EA de negociação do zero (Parte 09): Um salto conceitual (II)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
O Sharpe em logaritmos não depende do tamanho do depósito somente no caso de negociação com reinvestimento.
Mas, nesse caso, o Sharpe em incrementos simples não depende do tamanho do depósito.
Portanto, não entendo por que devo usar o Sharpe em logaritmos.
Ler o logaritmo do preço
Você mesmo encontrará outras referências
Leia o logaritmo do preço
Você mesmo encontrará outras referências
Outra nuance extremamente importante é que, nesse script, somente as barras em que houve uma mudança no patrimônio líquido são levadas em consideração no cálculo do Sharpe:
//--- add only if equity has changed if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // incrementar o logaritmo aver += log_return; // logaritmo médio dos incrementos AddReturn(log_return); // preencher a matriz de logaritmos incrementais counter++; // contador de retornos } prev_equity = m_equities[i];A alteração média é então encontrada dividindo-se pelo número de tais barras:
No entanto, a transição para os sharps anuais baseia-se na proporção do período de tempo, como se todas as barras do tf atual fossem contadas no cálculo:
Ou seja, mais uma vez: o script encontra a média de sharps por 1 barra com mudança de patrimônio e, em seguida, para encontrar a anual, multiplica-a não pelo número dessas barras em um ano, mas pelo número total de barras desse tf em um ano (sua raiz, é claro). Isso é errôneo e superestima o valor final.
Aparentemente, o Sharpe é calculado da mesma forma no testador?
o script encontra o Sharpe médio por 1 barra com mudança de patrimônio e, em seguida, para encontrar o anual, multiplica-o não pelo número dessas barras em um ano, mas pelo número total de barras desse tf em um ano (sua raiz, é claro). O que é errôneo e superestima o valor final
Eu também notei isso. Por isso, em minha versão, adicionei uma opção para levar em conta as barras zero.