取引における数学：シャープレシオとソルティノレシオ

MetaTrader 5 — トレーディング | 13 4月 2022, 10:39

1 808

投資収益率は、投資家や初心者のトレーダーが取引効率の分析に使用する最も明白な指標です。プロのトレーダーは、シャープレシオやソルティノレシオなどのより信頼性の高いツールを使用して、ストラテジーを分析します。この記事では、これらの比率がどのように計算されるかを理解するための簡単な例を検討します。取引ストラテジーの評価の詳細は、「トレーディングにおける数学:トレード結果の推定方法」稿で考察されました。この記事を読んで知識を更新したり、新しいことを学んだりすることをお勧めします。

シャープレシオ

経験豊富な投資家やトレーダーは、一貫した結果を得るために、しばしば複数のストラテジーで取引してさまざまな資産に投資します。これは、投資ポートフォリオの作成を意味するスマートな投資の概念の1つです。証券/ストラテジーの各ポートフォリオには、独自のリスクと利益率のパラメータがあり、何らかの方法で比較する必要があります。

このような比較で最も参照されるツールの1つは、1966年にノーベル賞受賞者のウィリアム・F・シャープによって開発されたシャープレシオです。比率の計算では、平均収益率、収益の標準偏差、リスクのない利益率などの基本的なパフォーマンス指標が使用されます。

シャープレシオの欠点は、分析に使用されるソースデータが正規分布している必要があることです。つまり、利益率分布グラフは対称である必要があり、鋭いピークや下降があってはなりません。

シャープレシオは、次の式を使用して計算されます。

シャープレシオ = (Return - RiskFree)/Std

ここで

Return — 特定の期間の平均収益率(例: 月、四半期、年)
RiskFree — 同じ期間のリスクフリーの収益率。従来、これらには、銀行預金、債券、および100％の信頼性を備えたその他の最小リスク資産が含まれます。
Std — 同じ期間のポートフォリオ利益率の標準偏差。利益率が期待値から大きく外れるほど、トレーダーの口座またはポートフォリオ資産が経験するリスクとボラティリティが高くなります。

リターン

利益率は、特定の期間における資産の価値の変化として計算されます。利益率の値は、シャープレシオが計算されるのと同じ期間に使用されます。通常考慮されるのは年ごとのシャープレシオですが、四半期、月次、日次の値を計算することもできます。利益率は次の式で計算されます。

Return[i] = (Close[i]-Close[i-1])/Close[i-1]

ここで

Return[i] — 期間の利益率
Close[i] — i番目の間隔の終了時の資産の価値
Close[i-1] — 前の間隔の終了時の資産の価値

つまり、利益率は、選択した期間の資産価値の相対的な変化として記述できます。

Return[i] = Delta[i]/Previous

ここで

Delta[i] = (Close[i]-Close[i-1]) — 選択した期間の資産価値の絶対的な変化
Previous = Close[i-1] — 前の間隔の終了時の資産の価値

日次値を使用して1年間のシャープレシオを計算するには、その年の各日の利益率の値を使用し、利益率の合計を計算の日数で割ったものとして平均日次利益率を計算する必要があります。

Return = Sum(Return[i])/N

ここで、Nは日数です。

リスクのない利益率

常にリスクがあるため、リスクのない利益率の概念には条件が付きます。シャープレシオは、同じ期間での異なるストラテジー/ポートフォリオの比較に使用されるため、ゼロのリスクのない利益率を数式で使用できます。つまり

RiskFree = 0

標準偏差または利益率

標準偏差は、確率変数が平均値からどのように逸脱しているかを示します。最初に利益率の平均値が計算され、次に平均値からの利益率の二乗偏差が合計されます。結果の合計を利益率の数で割って分散を求めます。分散の平方根は標準偏差です。

D = Sum((Return - Return[i])^2 )/N

STD = SQRT(D)

標準偏差の計算例は、前述の記事に記載されています。

任意の時間枠でのシャープレシオの計算と年間値への変換

シャープレシオの計算方法は1966年から変わっていません。この計算方法が広く認識された後、変数はその現代的な名前を受け取りました。当時、ファンドとポートフォリオのパフォーマンス評価は、数年間受け取った利益率に基づいていました。その後、月次データで計算が行われ、結果のシャープレシオは年次値にマッピングされました。この方法では、2つのファンド、ポートフォリオ、またはストラテジーを比較できます。

シャープレシオは、さまざまな期間や時間枠から年間値に簡単にスケーリングできます。これは、結果値に現在の間隔に対する年間間隔の比率の平方根を乗算することによって行われます。次の例を考えてみましょう。

日次利益率の値(SharpeDaily)を使用してシャープレシオを計算したとします。結果を年次値(SharpeAnnual)に変換する必要があります。年率は、期間の比率の平方根に比例します。つまり、1年に1日あたりの間隔がいくつ収まるかです。1年間に252営業日があるため、1日の収益ベースのシャープレシオに252の平方根を掛ける必要があります。これは、年間のシャープレシオになります。

SharpeAnnual = SQRT(252)*SharpeDaily // 252 working days in a year

値がH1の時間枠に基づいて計算される場合、同じ原則を使用します。まずSharpeHourlyをSharpeDailyに変換してから、年間のSharpe比率を計算します。1つのD1バーには24個のH1バーが含まれているため、式は次のようになります。

SharpeDaily = SQRT(24)*SharpeHourly   // 24 hours fit into D1

すべての金融商品が24時間取引されているわけではありません。ただし、同じ金融商品のテスターで取引ストラテジーを評価する場合、比較は同じテスト間隔と同じ時間枠で実行されるため、これは重要ではありません。

シャープレシオを使用したストラテジーの評価

ストラテジー/ポートフォリオのパフォーマンスに応じて、シャープレシオは異なる値(負を含む)を持つ可能性があります。シャープレシオを年間値に変換すると、古典的な方法での解釈が可能になります。

値	意味	説明
シャープレシオ < 0	悪い	このストラテジーは不採算です。
0 < シャープレシオ < 1.0	未定義	リスクには利益がありません。このようなストラテジーは、代替手段がない場合に検討できます。
シャープレシオ ≥ 1.0	良好	シャープレシオが1より大きい場合、リスクが報われ、ポートフォリオ/ストラテジーが正の結果を示す可能性があることを意味する可能性があります
シャープレシオ ≥ 3.0	非常に良好	高い値は、特定の各取引で損失が発生する可能性が非常に低いことを示します。

シャープ係数は通常の統計変数であることを忘れないでください。これは、利益率とリスクの比率を反映しています。したがって、さまざまなポートフォリオやストラテジーを分析する場合は、シャープレシオを推奨値と相関させるか、関連する値と比較することが重要です。

2020年EURUSDのシャープレシオ計算

シャープレシオはもともと、通常多くの株式で構成されるポートフォリオを評価するために開発されました。株式の価値は日々変化し、それに応じてポートフォリオの価値も変化します。値と利益率の変化は、任意の時間枠で測定できます。EURUSDの計算を見てみましょう。

計算は、H1とD1の2つの時間枠で実行されます。次に、結果を年次値に変換して比較し、違いがあるかどうかを確認します。計算には2020年のバー終値を使用します。

MQL5のコード

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   double H1_close[],D1_close[];
   double h1_returns[],d1_returns[];
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nCalculate the mean and standard deviation of returns on H1 bars");
      Print("H1 bars=",ArraySize(H1_close));
      GetReturns(H1_close,h1_returns);
      double average = ArrayMean(h1_returns);
      PrintFormat("H1 average=%G",average);
      double std = ArrayStd(h1_returns);
      PrintFormat("H1 std=%G",std);
      double sharpe_H1 = average / std;
      PrintFormat("H1 Sharpe=%G",sharpe_H1);
      double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_H1);
     }

   bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close);
   if(bars == -1)
      Print("CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021 failed. Error ",GetLastError());
   else
     {
      Print("\nCalculate the mean and standard deviation of returns on D1 bars");     
      Print("D1 bars=",ArraySize(D1_close));
      GetReturns(D1_close,d1_returns);
      double average = ArrayMean(d1_returns);
      PrintFormat("D1 average=%G",average);
      double std = ArrayStd(d1_returns);
      PrintFormat("D1 std=%G",std);
      double sharpe_D1 = average / std;
      double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns));
      Print("Sharpe_annual(H1)=", sharpe_annual_D1);
     }
  }

//+------------------------------------------------------------------+
//|  Fills the returns[] array of returns                            |
//+------------------------------------------------------------------+
void GetReturns(const double & values[], double & returns[])
  {
   int size = ArraySize(values);
//--- if less than 2 values, return an empty array of returns
   if(size < 2)
     {
      ArrayResize(returns,0);
      PrintFormat("%s: Error. ArraySize(values)=%d",size);
      return;
     }
   else
     {
      //--- fill returns in a loop
      ArrayResize(returns, size - 1);
      double delta;
      for(int i = 1; i < size; i++)
        {
         returns[i - 1] = 0;
         if(values[i - 1] != 0)
           {
            delta = values[i] - values[i - 1];
            returns[i - 1] = delta / values[i - 1];
           }
        }
     }
//---
  }
//+------------------------------------------------------------------+
//|  Calculates the average number of array elements                 |
//+------------------------------------------------------------------+
double ArrayMean(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = 0;
   for(int i = 0; i < size; i++)
      mean += array[i];
   mean /= size;
   return(mean);
  }
//+------------------------------------------------------------------+
//|  Calculates the standard deviation of array elements             |
//+------------------------------------------------------------------+
double ArrayStd(const double & array[])
  {
   int size = ArraySize(array);
   if(size < 1)
     {
      PrintFormat("%s: Error, array is empty",__FUNCTION__);
      return(0);
     }
   double mean = ArrayMean(array);
   double std = 0;
   for(int i = 0; i < size; i++)
      std += (array[i] - mean) * (array[i] - mean);
   std /= size;
   std = MathSqrt(std);
   return(std);
  }  
//+------------------------------------------------------------------+

/*
Result

Calculate the mean and standard deviation of returns on H1 bars
H1 bars:6226
H1 average=1.44468E-05
H1 std=0.00101979
H1 Sharpe=0.0141664
Sharpe_annual(H1)=1.117708053392263

Calculate the mean and standard deviation of returns on D1 bars
D1 bars:260
D1 average=0.000355823
D1 std=0.00470188
Sharpe_annual(H1)=1.2179005039019222

*/

MetaTrader5ライブラリを使用して計算するPythonコード

import math
from datetime import datetime
import MetaTrader5 as mt5

# display data on the MetaTrader 5 package
print("MetaTrader5 package author: ", mt5.__author__)
print("MetaTrader5 package version: ", mt5.__version__)

# import the 'pandas' module for displaying data obtained in the tabular form
import pandas as pd

pd.set_option('display.max_columns', 50)  # how many columns to show
pd.set_option('display.width', 1500)  # max width of the table to show
# import pytz module for working with the time zone
import pytz

# establish connection to the MetaTrader 5 terminal
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# set time zone to UTC
timezone = pytz.timezone("Etc/UTC")
# create datetime objects in the UTC timezone to avoid the local time zone offset
utc_from = datetime(2020, 1, 1, tzinfo=timezone)
utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone)
# get EURUSD H1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone
rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to)
# also get D1 bars in the interval 2020.01.01 00:00 - 2020.31.12 13:00 in the UTC timezone
rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to)
# shut down connection to the MetaTrader 5 terminal and continue processing obtained bars
mt5.shutdown()

# create DataFrame out of the obtained data
rates_frame = pd.DataFrame(rates_H1)

# add the "Return" column
rates_frame['return'] = 0.0
# now calculate the returns as return[i] = (close[i] - close[i-1])/close[i-1]
prev_close = 0.0
for i, row in rates_frame.iterrows():
    close = row['close']
    rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0
    prev_close = close

print("\nCalculate the mean and standard deviation of returns on H1 bars")
print('H1 rates:', rates_frame.shape[0])
ret_average = rates_frame[1:]['return'].mean()  # skip the first row with zero return
print('H1 return average=', ret_average)
ret_std = rates_frame[1:]['return'].std(ddof=0) # skip the first row with zero return
print('H1 return std =', ret_std)
sharpe_H1 = ret_average / ret_std
print('H1 Sharpe = Average/STD = ', sharpe_H1)

sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1)
print('Sharpe_annual(H1) =', sharpe_annual_H1)

# now calculate the Sharpe ratio on the D1 timeframe
rates_daily = pd.DataFrame(rates_D1)

# add the "Return" column
rates_daily['return'] = 0.0
# calculate returns
prev_return = 0.0
for i, row in rates_daily.iterrows():
    close = row['close']
    rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0
    prev_return = close

print("\nCalculate the mean and standard deviation of returns on D1 bars")
print('D1 rates:', rates_daily.shape[0])
daily_average = rates_daily[1:]['return'].mean()
print('D1 return average=', daily_average)
daily_std = rates_daily[1:]['return'].std(ddof=0)
print('D1 return std =', daily_std)
sharpe_daily = daily_average / daily_std
print('D1 Sharpe =', sharpe_daily)

sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1)
print('Sharpe_annual(D1) =', sharpe_annual_D1)

Result
Calculate the mean and standard deviation of returns on H1 bars

H1 rates: 6226
H1 return average= 1.4446773215242986e-05
H1 return std = 0.0010197932969323495
H1 Sharpe = Average/STD = 0.014166373968823358
Sharpe_annual(H1) = 1.117708053392236

Calculate the mean and standard deviation of returns on D1 bars
D1 rates: 260
D1 return average= 0.0003558228355051694
D1 return std = 0.004701883757646081
D1 Sharpe = 0.07567665511222807
Sharpe_annual(D1) = 1.2179005039019217

ご覧のとおり、MQL5とPythonの計算結果は同じです。ソースコードは以下に添付されています(CalculateSharpe_2TF)

H1バーとD1バーから計算された年次シャープレシオが異なる(それぞれ1.117708と1.217900)ため、その理由を調べてみましょう。

すべての時間枠での2020年EURUSDの年次シャープレシオの計算

それでは、すべての時間枠での年次シャープレシオを計算してみましょう。これを行うために、取得したデータを表に収集します。

TF - 時間枠
Minutes - 時間枠内の分数
Rates - この期間の年間バー数
Avg - 時間枠でのバーあたりの平均収益率(パーセント)(バーあたりの平均価格変動パーセント)
Std - 時間枠でのバーあたりの標準偏差(パーセント)(この時間枠での価格変動率)
SharpeTF - 指定された時間枠で計算されたシャープレシオ
SharpeAnnual - この時間枠に基づいて計算された年間シャープレシオシャープレシオ

以下は計算コードブロックです。完全なコードは、記事に添付されているCalculateSharpe_All_TF.mq5ファイルにあります。

//--- structure to print statistics to log
struct Stats
  {
   string            TF;
   int               Minutes;
   int               Rates;
   double            Avg;
   double            Std;
   double            SharpeTF;
   double            SharpeAnnual;
  };
//--- array of statistics by timeframes
Stats stats[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- arrays for close prices
   double H1_close[],D1_close[];
//--- arrays of returns
   double h1_returns[],d1_returns[];
//--- arrays of timeframes on which the Sharpe coefficient will be calculated
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,
                                   PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1
                                  };

   ArrayResize(stats,ArraySize(timeframes));
//--- timeseries request parameters
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print(symbol);
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- get the array of returns on the specified timeframe
      double returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      //--- calculate statistics
      GetStats(returns,avr,std,sharpe);
      double sharpe_annual = sharpe * MathSqrt(ArraySize(returns));
      PrintFormat("%s  aver=%G%%   std=%G%%  sharpe=%G  sharpe_annual=%G",
                  EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual);
      //--- fill the statistics structure
      Stats row;
      string tf_str = EnumToString(timeframes[i]);
      StringReplace(tf_str,"PERIOD_","");
      row.TF = tf_str;
      row.Minutes = PeriodSeconds(timeframes[i]) / 60;
      row.Rates = ArraySize(returns);
      row.Avg = avr;
      row.Std = std;
      row.SharpeTF = sharpe;
      row.SharpeAnnual = sharpe_annual;
      //--- add a row for the timeframe statistics
      stats[i] = row;
     }
//--- print statistics on all timeframes to log
   ArrayPrint(stats,8);
  }

/*
Result

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeTF] [SharpeAnnual]
[ 0] "M1"          1  373023 0.00000024 0.00168942 0.00168942     1.03182116
[ 1] "M2"          2  186573 0.00000048 0.00239916 0.00239916     1.03629642
[ 2] "M3"          3  124419 0.00000072 0.00296516 0.00296516     1.04590258
[ 3] "M4"          4   93302 0.00000096 0.00341717 0.00341717     1.04378592
[ 4] "M5"          5   74637 0.00000120 0.00379747 0.00379747     1.03746116
[ 5] "M6"          6   62248 0.00000143 0.00420265 0.00420265     1.04854166
[ 6] "M10"        10   37349 0.00000239 0.00542100 0.00542100     1.04765562
[ 7] "M12"        12   31124 0.00000286 0.00601079 0.00601079     1.06042363
[ 8] "M15"        15   24900 0.00000358 0.00671964 0.00671964     1.06034161
[ 9] "M20"        20   18675 0.00000477 0.00778573 0.00778573     1.06397070
[10] "M30"        30   12450 0.00000716 0.00966963 0.00966963     1.07893298
[11] "H1"         60    6225 0.00001445 0.01416637 0.01416637     1.11770805
[12] "H2"        120    3115 0.00002880 0.01978455 0.01978455     1.10421905
[13] "H3"        180    2076 0.00004305 0.02463458 0.02463458     1.12242890
[14] "H4"        240    1558 0.00005746 0.02871564 0.02871564     1.13344977
[15] "H6"        360    1038 0.00008643 0.03496339 0.03496339     1.12645075
[16] "H8"        480     779 0.00011508 0.03992838 0.03992838     1.11442404
[17] "H12"       720     519 0.00017188 0.05364323 0.05364323     1.22207717
[18] "D1"       1440     259 0.00035582 0.07567666 0.07567666     1.21790050
[19] "W1"      10080      51 0.00193306 0.14317328 0.14317328     1.02246174
[20] "MN1"     43200      12 0.00765726 0.43113365 0.43113365     1.49349076

*/

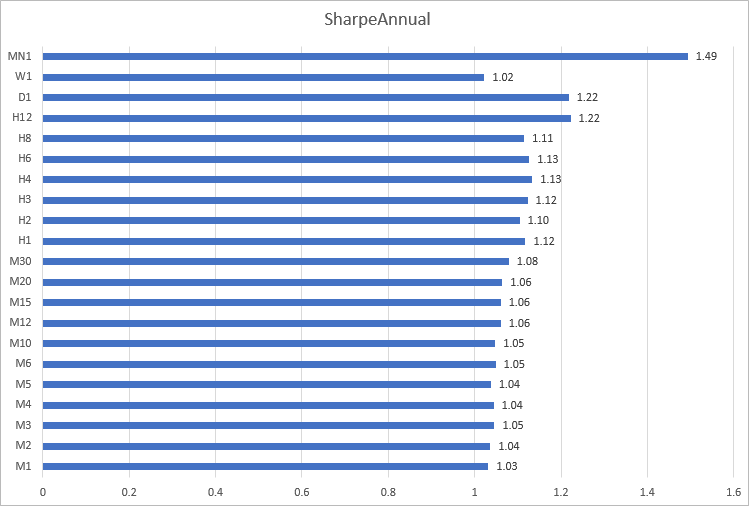
さまざまな時間枠での2020年のEURUSDのシャープレシオのヒストグラムを作成しましょう。ここで、M1からM30までの微細な時間枠での計算では、1.03から1.08までの近い結果が得られることがわかります。最も一貫性のない結果は、H12からMN1までの時間枠で得られました。

さまざまな時間枠での2020年EURUSD年次シャープレシオの計算

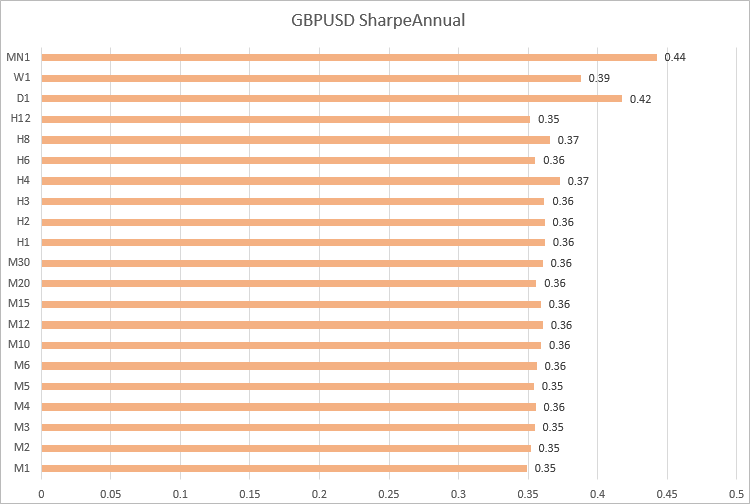
2020年のGBPUSD、USDJPY、USDCHFのシャープレシオの計算

さらに3つの通貨ペアについて同様の計算を実行してみましょう。

GBPUSDのシャープレシオの値はM1からH12までの時間枠で類似しています。

さまざまな時間枠での2020年GBPUSDの年次シャープレシオの計算

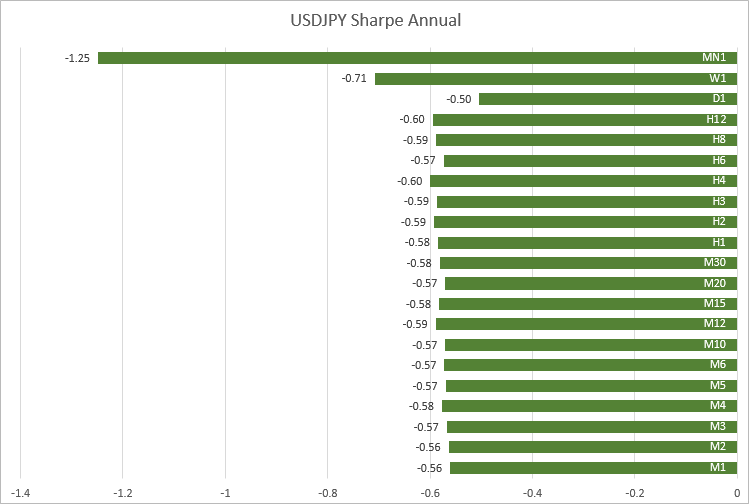
USDJPYの値はM1からH12までの時間枠でも近い(-0.56から-0.60)です。

さまざまな時間枠での2020年USDJPYの年次シャープレシオの計算

USDCHFではM1からM30までの時間枠で同様の値が取得されました。時間枠が長くなると、シャープレシオは変動します。

さまざまな時間枠での2020年USDCHFの年次シャープレシオの計算

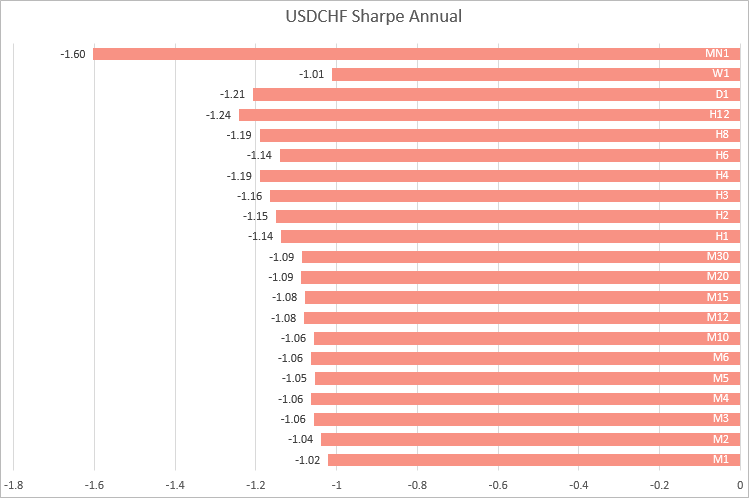
したがって、4つの主要な通貨ペアの例に基づいて、シャープレシオの最も安定した計算はM1からM30までの時間枠で得られると結論付けることができます。これは、異なる銘柄で機能するストラテジーを比較する場合、より短い時間枠の利益率を使用して比率を計算する方がよいことを意味します。

2020年EURUSDの年次シャープレシオの月次の計算

2020年の各月の月次利益率を使用して、M1からH1までの時間枠での年次シャープレシオを計算してみましょう。CalculateSharpe_Months.mq5スクリプトの完全なコードが記事に添付されています。

//--- structure to store returns
struct Return
  {
   double            ret;   // return
   datetime          time;  // date
   int               month; // month
  };
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   SharpeMonths sharpe_by_months[];
//--- arrays of timeframes on which the Sharpe coefficient will be calculated
   ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5,
                                   PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20,
                                   PERIOD_M30,PERIOD_H1
                                  };
   ArrayResize(sharpe_by_months,ArraySize(timeframes));
//--- timeseries request parameters
   string symbol = Symbol();
   datetime from = D'01.01.2020';
   datetime to = D'01.01.2021';
   Print("Calculate Sharpe Annual on ",symbol, " for 2020 year");
   for(int i = 0; i < ArraySize(timeframes); i++)
     {
      //--- get the array of returns on the specified timeframe
      Return returns[];
      GetReturns(symbol,timeframes[i],from,to,returns);
      double avr,std,sharpe;
      //--- Calculate statistics for the year
      GetStats(returns,avr,std,sharpe);
      string tf_str = EnumToString(timeframes[i]);
      //--- calculate the annual Sharpe ratio for each month
      SharpeMonths sharpe_months_on_tf;
      sharpe_months_on_tf.SetTimeFrame(tf_str);
      //--- select returns for i-th month
      for(int m = 1; m <= 12; m++)
        {
         Return month_returns[];
         GetReturnsByMonth(returns,m,month_returns);
         //--- Calculate statistics for the year
         double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns);
         sharpe_months_on_tf.Sharpe(m,sharpe_annual);
        }
      //--- add Sharpe ratio for 12 months on timeframe i
      sharpe_by_months[i] = sharpe_months_on_tf;
     }
//--- display the table of annual Sharpe values by months on all timeframes
   ArrayPrint(sharpe_by_months,3);
  }

/*
Result

Calculate Sharpe Annual on EURUSD for 2020 year
             [TF]  [Jan]  [Feb] [Marc]  [Apr] [May] [June] [July] [Aug] [Sept]  [Oct] [Nov] [Dec]
[ 0] "PERIOD_M1"  -2.856 -1.340  0.120 -0.929 2.276  1.534  6.836 2.154 -2.697 -1.194 3.891 4.140
[ 1] "PERIOD_M2"  -2.919 -1.348  0.119 -0.931 2.265  1.528  6.854 2.136 -2.717 -1.213 3.845 4.125
[ 2] "PERIOD_M3"  -2.965 -1.340  0.118 -0.937 2.276  1.543  6.920 2.159 -2.745 -1.212 3.912 4.121
[ 3] "PERIOD_M4"  -2.980 -1.341  0.119 -0.937 2.330  1.548  6.830 2.103 -2.765 -1.219 3.937 4.110
[ 4] "PERIOD_M5"  -2.929 -1.312  0.120 -0.935 2.322  1.550  6.860 2.123 -2.729 -1.239 3.971 4.076
[ 5] "PERIOD_M6"  -2.945 -1.364  0.119 -0.945 2.273  1.573  6.953 2.144 -2.768 -1.239 3.979 4.082
[ 6] "PERIOD_M10" -3.033 -1.364  0.119 -0.934 2.361  1.584  6.789 2.063 -2.817 -1.249 4.087 4.065
[ 7] "PERIOD_M12" -2.952 -1.358  0.118 -0.956 2.317  1.609  6.996 2.070 -2.933 -1.271 4.115 4.014
[ 8] "PERIOD_M15" -3.053 -1.367  0.118 -0.945 2.377  1.581  7.132 2.078 -2.992 -1.274 4.029 4.047
[ 9] "PERIOD_M20" -2.998 -1.394  0.117 -0.920 2.394  1.532  6.884 2.065 -3.010 -1.326 4.074 4.040
[10] "PERIOD_M30" -3.008 -1.359  0.116 -0.957 2.379  1.585  7.346 2.084 -2.934 -1.323 4.139 4.034
[11] "PERIOD_H1"  -2.815 -1.373  0.116 -0.966 2.398  1.601  7.311 2.221 -3.136 -1.374 4.309 4.284

*/

月ごとの年比率の値は、計算を実行したすべての時間枠で非常に近いことがわかります。より良いプレゼンテーションのために、Excelダイアグラムを使用して結果を3Dサーフェスとしてレンダリングしましょう。

月および時間枠ごとの2020年EURUSD年次シャープレシオの3Dチャート

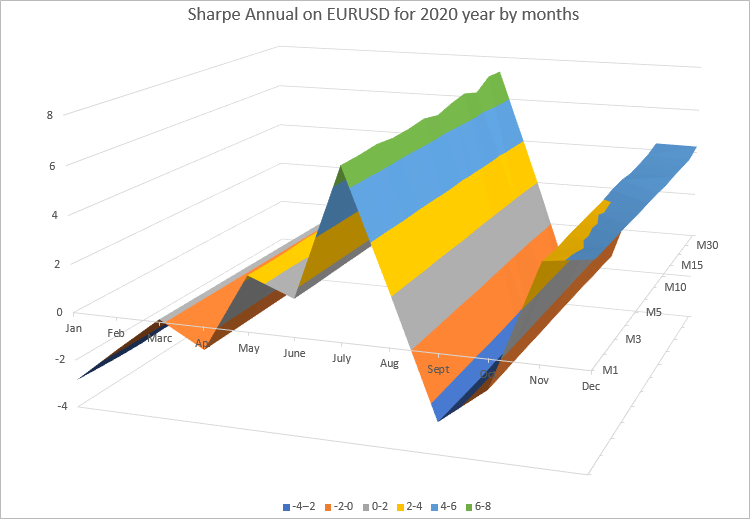
このダイアグラムは、年次シャープレシオの値が毎月変化することを明確に示しています。これは、EURUSDが今月どのように変化したかによって異なります。一方、すべての時間枠での月ごとの年次シャープレシオはほとんど変化しません。

したがって、年次シャープレシオは任意の時間枠で計算できますが、結果値は、利益率が得られたバーの数にも依存します。これは、この計算アルゴリズムをリアルタイムでのテスト、最適化、および監視に使用できることを意味します。唯一の前提条件は、十分な数の利益率の配列を持つことです。

ソルティノレシオ

シャープレシオの計算では、リスクは、資産の増減の両方で、相場の完全なボラティリティです。ただし、ポートフォリオの価値の増加は投資家にとっては良いことである一方、損失はその減少にのみ関連しています。したがって、比率の実際のリスクは誇張されています。 1990年代初頭にフランクソルティノによって開発されたソルティノレシオは、この問題に対処しています。

前任者と同様に、F。ソルティノは、将来の利益率を数学的な期待値に等しい確率変数と見なし、リスクは分散と見なします。利益率とリスクは、一定期間の過去の相場に基づいて決定されます。シャープレシオの計算と同様に、利益率はリスクで除算されます。

ソルティノは、利益率の全分散(または完全なボラティリティ)として定義されるリスクは、正と負の両方の変化に依存すると述べました。ソルティノは、全体的なボラティリティを、資産の減少のみを考慮したセミボラティリティに置き換えました。半ボラティリティは、有害なボラティリティ、下振れリスク、下向きの偏差、負のボラティリティ、または下向きの標準偏差とも呼ばれます。

ソルティノレシオの計算はシャープの計算と似ていますが、唯一の違いは、正の利益率がボラティリティの計算から除外されていることです。これにより、リスク尺度が減少し、比率の重みが増加します。

正と負の利益率

シャープレシオに基づいてソルティノレシオを計算するコード例。半分散は、負の利益率を使用してのみ計算されます。

//+------------------------------------------------------------------+
//|  Calculates Sharpe and Sortino ratios                            |
//+------------------------------------------------------------------+
void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino)
  {
   avr = ArrayMean(returns);
   std = ArrayStd(returns);
   sharpe = (std == 0) ? 0 : avr / std;
//--- now, remove negative returns and calculate the Sortino ratio
   double negative_only[];
   int size = ArraySize(returns);
   ArrayResize(negative_only,size);
   ZeroMemory(negative_only);
//--- copy only negative returns
   for(int i = 0; i < size; i++)
      negative_only[i] = (returns[i] > 0) ? 0 : returns[i];
   double semistd = ArrayStd(negative_only);
   sortino = avr / semistd;   
   return;
  }

この記事に添付されているスクリプトCalculateSortino_All_TF.mq5は、2020年のEURUSDで次の結果を生成します。

      [TF] [Minutes] [Rates]      [Avg]      [Std] [SharpeAnnual] [SortinoAnnual]    [Ratio]
[ 0] "M1"          1  373023 0.00000024 0.00014182     1.01769617      1.61605380 1.58795310
[ 1] "M2"          2  186573 0.00000048 0.00019956     1.02194170      1.62401856 1.58914991
[ 2] "M3"          3  124419 0.00000072 0.00024193     1.03126142      1.64332243 1.59350714
[ 3] "M4"          4   93302 0.00000096 0.00028000     1.02924195      1.62618200 1.57998030
[ 4] "M5"          5   74637 0.00000120 0.00031514     1.02303684      1.62286584 1.58632199
[ 5] "M6"          6   62248 0.00000143 0.00034122     1.03354379      1.63789024 1.58473231
[ 6] "M10"        10   37349 0.00000239 0.00044072     1.03266766      1.63461839 1.58290848
[ 7] "M12"        12   31124 0.00000286 0.00047632     1.04525580      1.65215986 1.58062730
[ 8] "M15"        15   24900 0.00000358 0.00053223     1.04515816      1.65256608 1.58116364
[ 9] "M20"        20   18675 0.00000477 0.00061229     1.04873529      1.66191269 1.58468272
[10] "M30"        30   12450 0.00000716 0.00074023     1.06348332      1.68543441 1.58482449
[11] "H1"         60    6225 0.00001445 0.00101979     1.10170316      1.75890688 1.59653431
[12] "H2"        120    3115 0.00002880 0.00145565     1.08797046      1.73062372 1.59068999
[13] "H3"        180    2076 0.00004305 0.00174762     1.10608991      1.77619289 1.60583048
[14] "H4"        240    1558 0.00005746 0.00200116     1.11659184      1.83085734 1.63968362
[15] "H6"        360    1038 0.00008643 0.00247188     1.11005321      1.79507001 1.61710267
[16] "H8"        480     779 0.00011508 0.00288226     1.09784908      1.74255746 1.58724682
[17] "H12"       720     519 0.00017188 0.00320405     1.20428761      2.11045830 1.75245371
[18] "D1"       1440     259 0.00035582 0.00470188     1.20132966      2.04624198 1.70331429
[19] "W1"      10080      51 0.00193306 0.01350157     1.03243721      1.80369984 1.74703102
[20] "MN1"     43200      12 0.00765726 0.01776075     1.49349076      5.00964481 3.35431926

ほとんどすべての時間枠で、ソルティノレシオはシャープレシオの1.60倍であることがわかります。もちろん、取引結果に基づいて比率を計算する場合、そのような明確な依存関係はありません。したがって、両方の比率を使用してストラテジー/ポートフォリオを比較することは理にかなっています。

2020年のEURUSDのシャープレシオとソルティノレシオ

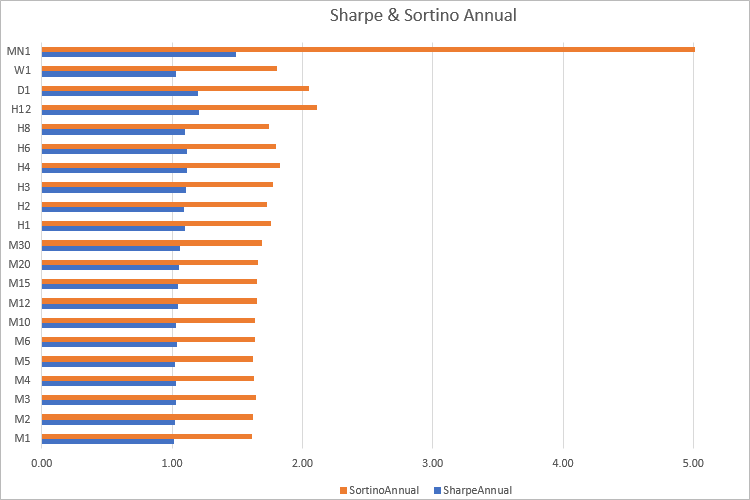
これら2つの指標の違いは、シャープレシオは主にボラティリティを反映しているのに対し、ソルティノレシオは実際にはリスクの単位あたりの比率または利益率を示していることです。ただし、計算は履歴に基づいて行われるため、良い結果が将来の利益を保証することはできません。

MetaTrader5ストラテジーテスターでのシャープレシオ計算の例

シャープレシオは、もともと株式を含むポートフォリオを評価するために開発されました。株価は日々変化するため、資産の価値も日々変化します。デフォルトでは、取引ストラテジーはポジションの存在を意味しないため、一部の時間、取引口座の状態は変更されません。これは、ポジションがない場合、ゼロの利益率値を受け取るため、シャープの計算が間違っていることを意味します。したがって、計算では、取引口座の状態が変更されたバーのみが使用されます。最も適切なオプションは、各バーの最後のティックの株式価値を分析することです。これにより、MetaTrader5ストラテジーテスターの任意のティック生成モードでシャープレシオを計算できるようになります。

考慮すべきもう1つのポイントは、通常はReturn [i] =(CloseCurrent-ClosePrevious)/ ClosePreviousとして計算されるパーセンテージの価格増分には、計算に一定の欠点があることです。価格が5％下がってから5％上がると、初期値は得られません。そのため、通常の相対価格増分の代わりに、統計調査では通常、価格増分の対数が使用されます。対数利益率(対数利益率)には、線形利益率のこの欠点はありません。値は次のように計算されます。

Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)

対数の合計は相対的な利益率の積に等しいため、対数の利益率は合計できるので便利です。

したがって、シャープレシオの計算アルゴリズムには最小限の調整が必要です。

//--- calculate the logarithms of increments using the equity array
   for(int i = 1; i < m_bars_counter; i++)
     {
      //--- only add if equity has changed
      if(m_equities[i] != prev_equity)
        {
         log_return = MathLog(m_equities[i] / prev_equity); // increment logarithm
         aver += log_return;            // average logarithm of increments
         AddReturn(log_return);         // fill the array of increment logarithms
         counter++;                     // counter of returns
        }
      prev_equity = m_equities[i];
     }
//--- if values are not enough for Sharpe calculation, return 0
   if(counter <= 1)
      return(0);
//--- average value of the increment logarithm
   aver /= counter;
//--- calculate standard deviation
   for(int i = 0; i < counter; i++)
      std += (m_returns[i] - aver) * (m_returns[i] - aver);
   std /= counter;
   std = MathSqrt(std);
//--- Sharpe ratio on the current timeframe
   double sharpe = aver / std;

完全な計算コードは、記事に添付されているインクルードファイルSharpe.mqhとして実装されています。カスタム最適化基準としてシャープレシオを計算するには、このファイルをエキスパートアドバイザーに接続し、数行のコード行を追加します。例として、標準のMetaTrader5パックのMACDSample.mq5EAを使用してそれを行う方法を見てみましょう。

#define MACD_MAGIC 1234502
//---
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\PositionInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include "Sharpe.mqh"
//---
input double InpLots          = 0.1;// Lots
input int    InpTakeProfit    = 50; // Take Profit (in pips)
input int    InpTrailingStop  = 30; // Trailing Stop Level (in pips)
input int    InpMACDOpenLevel = 3;  // MACD open level (in pips)
input int    InpMACDCloseLevel = 2; // MACD close level (in pips)
input int    InpMATrendPeriod = 26; // MA trend period
//---
int ExtTimeOut = 10; // time out in seconds between trade operations
CReturns   returns;
....
//+------------------------------------------------------------------+
//| Expert new tick handling function                                |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   static datetime limit_time = 0; // last trade processing time + timeout
//--- add current equity to the array to calculate the Sharpe ratio
   MqlTick tick;
   SymbolInfoTick(_Symbol, tick);
   returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY));
//--- don't process if timeout
   if(TimeCurrent() >= limit_time)
     {
      //--- check for data
      if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod)
        {
         //--- change limit time by timeout in seconds if processed
         if(ExtExpert.Processing())
            limit_time = TimeCurrent() + ExtTimeOut;
        }
     }
  }
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester(void)
  {
//--- calculate Sharpe ratio
   double sharpe = returns.OnTester();
   return(sharpe);
  }
//+------------------------------------------------------------------+

結果のコードを「MACDSampleSharpe.mq5」として保存します。関連するファイルも以下に添付されています。

カスタム最適化基準を選択して、EURUSDM102020の遺伝的最適化を実行してみましょう。

カスタム基準を使用したエキスパートアドバイザーの遺伝的最適化のためのテスター設定

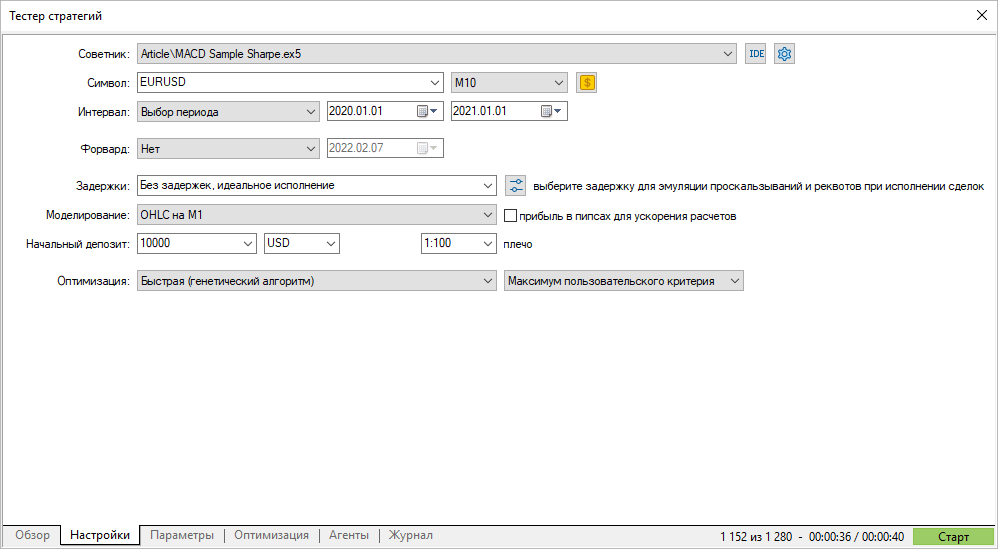
得られたカスタム基準値は、ストラテジーテスターによって計算されたシャープレシオと一致します。これで、計算メカニズムと、得られた結果の解釈方法がわかりました。

カスタム基準を使用したエキスパートアドバイザーの遺伝的最適化の結果

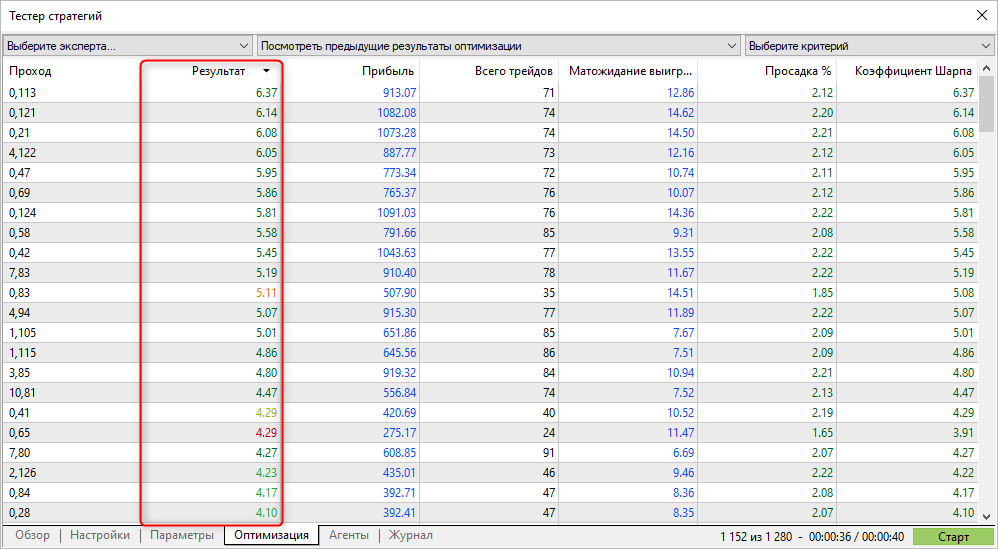
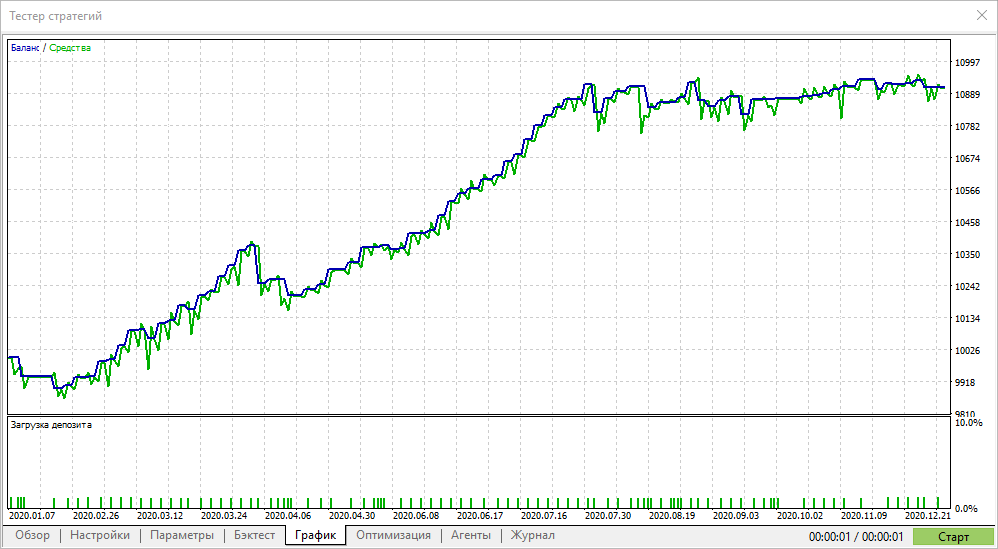
シャープレシオが最も高いパスは、テスターで常に最高の利益を示すとは限りませんが、スムーズなエクイティグラフでパラメーターを見つけることができます。このようなグラフは通常、急激な成長を示していませんが、大きな落ち込みや株式のドローダウンもありません。

これは、シャープレシオによる最適化を使用すると、他の最適化基準と比較して、より安定したパラメーターを見つけることができることを意味します。

シャープレシオ6.14のエキスパートアドバイザーのテストを示すグラフ >

長所と短所

シャープレシオとソルティノレシオにより、受け取った利益が関連するリスクをカバーしているかどうかを判断できます。代替のリスク尺度に対するもう1つの利点は、計算をすべてのタイプの資産に適用できることです。たとえば、評価に特定の外部ベンチマークを必要としないため、シャープレシオを使用して金と銀を比較できます。したがって、比率は、資産またはストラテジーポートフォリオだけでなく、個々のストラテジーまたは証券にも適用できます。

これらのツールの欠点は、計算が正規分布の利益率を想定していることです。実際には、この要件が満たされることはめったにありません。それでも、シャープレシオとソルティノレシオは、さまざまなストラテジーやポートフォリオの比較を可能にする最もシンプルで理解しやすいツールです。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/9171

添付されたファイル |

ZIPをダウンロード

CalculateSharpe_2TF.mq5 (9.48 KB)

CalculateSharpe_2TF.py (6.44 KB)

CalculateSharpe_Months.mq5 (21.8 KB)

CalculateSharpe_All_TF.mq5 (14.87 KB)

CalculateSortino_All_TF.mq5 (21.49 KB)

Sharpe.mqh (10.15 KB)

MACD_Sample_Sharpe.mq5 (37.11 KB)

MQL5.zip (19.95 KB)