Mathématiques en trading : ratios de Sharpe et de Sortino
Le retour sur investissement est l'indicateur le plus évident que les investisseurs et les traders débutants utilisent pour l'analyse de l'efficacité du trading. Les traders professionnels utilisent des outils plus fiables pour analyser les stratégies, tels que les ratios de Sharpe et de Sortino, entre autres. Dans cet article, nous allons considérer des exemples simples pour comprendre comment ces ratios sont calculés. Les spécificités de l'évaluation des stratégies de trading ont déjà été examinées dans l'article "Mathématiques dans le trading. Comment estimer les résultats de trading". Il est recommandé de lire l'article pour rafraîchir vos connaissances ou pour apprendre quelque chose de nouveau.
Ratio de Sharpe
Les investisseurs et traders expérimentés tradent souvent plusieurs stratégies et investissent dans différents actifs dans le but d'obtenir des résultats cohérents. C'est l'un des concepts d'investissement intelligent qui implique la constitution d'un portefeuille d'investissement. Chaque portefeuille de titres/stratégies a ses propres paramètres de risque et de rendement, qui devraient en quelque sorte être comparés.
L'un des outils les plus référencés pour une telle comparaison est le ratio de Sharpe, qui a été développé en 1966 par le lauréat du prix Nobel William F. Sharpe. Le calcul du ratio utilise des mesures de performance de base, notamment le taux de rendement moyen, l'écart type de rendement et le rendement sans risque.
L'inconvénient du ratio de Sharpe est que les données sources utilisées pour l'analyse doivent être normalement distribuées. En d'autres termes, le graphique de distribution des rendements doit être symétrique et ne doit pas présenter de pics ou de chutes brusques.
Le ratio de Sharpe est calculé selon la formule suivante :
Ratio de Sharpe = (Rendement - SansRisque)/Std
Avec :
- Rendement — le taux de rendement moyen pour une certaine période. Par exemple, pour un mois, un trimestre, une année, etc.
- SansRisque — taux de rendement sans risque pour la même période. Traditionnellement, il s'agit de dépôts bancaires, d'obligations et d'autres actifs à risque minimum avec une fiabilité à 100 %.
- Std — écart type des rendements du portefeuille pour la même période. Plus les rendements s'écartent de la valeur attendue, plus le risque et la volatilité subis par le compte ou les actifs du portefeuille du trader sont élevés.
Rendement
Le rendement est calculé comme une variation de la valeur des actifs pendant un certain intervalle. Les valeurs de retour sont utilisées pour la même période pour laquelle le ratio de Sharpe est calculé. Habituellement, le ratio de Sharpe annuel est pris en compte, mais il est également possible de calculer des valeurs trimestrielles, mensuelles ou même quotidiennes. Le rendement est calculé par la formule suivante :
Rendement[i] = (Close[i]-Close[i-1])/Close[i-1]
Avec :
- Rendement[i] — retour pour l'intervalle i ;
- Close[i] — la valeur des actifs à la fin du i-ième intervalle ;
- Close[i-1] — la valeur des actifs à la fin de l'intervalle précédent.
En d'autres termes, le rendement peut être écrit comme une variation relative de la valeur de l'actif pour la période sélectionnée :
Rendement[i] = Delta[i]/Précédent
Avec :
- Delta[i] = (Close[i]-Close[i-1]) — variation absolue de la valeur de l'actif pour la période sélectionnée ;
- Précédent = Close[i-1] — la valeur des actifs à la fin de l'intervalle précédent.
Pour calculer le ratio de Sharpe pour une période d'un an en utilisant des valeurs quotidiennes, nous devons utiliser les valeurs de rendement pour chaque jour de l'année et calculer le rendement quotidien moyen comme une somme des rendements divisée par le nombre de jours dans le calcul.
Rendement = Somme(Rendement[i])/N
où N est le nombre de jours.
Rendement sans risque
La notion de rendement sans risque est conditionnelle, puisqu'il y a toujours un risque. Étant donné que le ratio de Sharpe est utilisé pour comparer différentes stratégies/portefeuilles dans les mêmes intervalles de temps, le rendement sans risque zéro peut être utilisé dans la formule. C'est-à-dire,
SansRisque = 0
Écart-type ou rendement
L'écart type montre comment les variables aléatoires s'écartent d'une valeur moyenne. Tout d'abord, la valeur de rendement moyenne est calculée, puis les écarts au carré des rendements par rapport à la valeur moyenne sont additionnés. La somme résultante est divisée par le nombre de retours pour obtenir la dispersion. La racine carrée de la dispersion est l'écart type.
D = Sum((Rendement - Rendement[i])^2 )/N
STD = SQRT(D)
Un exemple de calcul de l'écart type est fourni dans l'article mentionné précédemment.
Calculer le ratio de Sharpe sur n'importe quelle période et le convertir en une valeur annuelle
La méthode de calcul du ratio de Sharpe n'a pas changé depuis 1966. La variable a reçu son nom moderne après que cette méthodologie de calcul ait été largement reconnue. À cette époque, les évaluations de la performance des fonds et des portefeuilles étaient basées sur les rendements reçus pendant plusieurs années. Plus tard, des calculs ont été effectués sur des données mensuelles, tandis que le ratio de Sharpe résultant a été cartographié en une valeur annuelle. Cette méthode permet de comparer deux fonds, portefeuilles ou stratégies.
Le ratio de Sharpe peut être facilement mis à l'échelle à partir de différentes périodes et délais en une valeur annuelle. Cela se fait en multipliant la valeur résultante par la racine carrée du rapport de l'intervalle annuel à l'intervalle actuel. Considérons l'exemple suivant.
Supposons que nous ayons calculé le ratio de Sharpe à l'aide des valeurs de rendement quotidiennes — SharpeDaily. Le résultat doit être converti en valeur annuelle SharpeAnnual. Le rapport annuel est proportionnel à la racine carrée du rapport des périodes, c'est-à-dire combien d'intervalles quotidiens correspondent à une année. Puisqu'il y a 252 jours ouvrables dans une année, le ratio de Sharpe basé sur le rendement quotidien doit être multiplié par la racine carrée de 252. Ce sera le ratio de Sharpe annuel :
SharpeAnnual = SQRT(252)*SharpeDaily // 252 jours ouvrés par an
Si la valeur est calculée sur la base de la période H1, nous utilisons le même principe - convertissez d'abord SharpeHourly en SharpeDaily, puis calculez le ratio annuel de Sharpe. Une barre D1 comprend 24 barres H1, c'est pourquoi la formule sera la suivante :
SharpeDaily = SQRT(24)*SharpeHourly // 24 heures correspondent à D1
Tous les instruments financiers ne sont pas négociés 24 heures sur 24. Mais ce n'est pas important lors de l'évaluation des stratégies de trading dans le testeur pour le même instrument financier, puisque la comparaison est effectuée pour le même intervalle de test et la même période.
Évaluer les stratégies à l'aide du ratio de Sharpe
Selon la performance de la stratégie/du portefeuille, le ratio de Sharpe peut avoir des valeurs différentes, voire négatives. La conversion du ratio de Sharpe en une valeur annuelle permet son interprétation de manière classique : | Valeur | Signification | Description |
|---|---|---|
| Sharpe Ratio < 0 | Mauvais | La stratégie n'est pas rentable |
| 0 < Sharpe Ratio < 1.0 | Indéfini | Le risque ne paie pas. De telles stratégies peuvent être envisagées lorsqu'il n'y a pas d'alternatives |
| Sharpe Ratio ≥ 1.0 | Bon | Si le ratio de Sharpe est supérieur à un, cela peut signifier que le risque est payant et que le portefeuille/stratégie peut afficher des résultats positifs |
| Sharpe Ratio ≥ 3.0 | Très bon | Une valeur élevée indique que la probabilité d'obtenir une perte dans chaque transaction particulière est très faible |
N'oubliez pas que le coefficient de Sharpe est une variable statistique régulière. Il reflète le rapport entre les rendements et le risque. Par conséquent, lors de l'analyse de différents portefeuilles et stratégies, il est important de corréler le ratio de Sharpe avec les valeurs recommandées ou de comparer avec les valeurs pertinentes.
Calcul du ratio de Sharpe pour l'EURUSD, 2020
Le ratio de Sharpe a été développé à l'origine pour évaluer des portefeuilles qui se composent généralement de nombreuses actions. La valeur des actions change tous les jours et la valeur du portefeuille change en conséquence. Une variation de la valeur et des rendements peut être mesurée à tout moment. Voyons les calculs pour EURUSD.
Les calculs seront effectués sur deux horizons de temps, H1 et D1. Ensuite, nous convertirons les résultats en valeurs annuelles et les comparerons pour voir s'il y a une différence. Nous utiliserons les prix de clôture de la barre pour 2020 pour les calculs.
Coder en MQL5
//+------------------------------------------------------------------+ //| Fonction de démarrage du script | //+------------------------------------------------------------------+ void OnStart() { //--- double H1_close[],D1_close[]; double h1_returns[],d1_returns[]; datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; int bars = CopyClose("EURUSD",PERIOD_H1,from,to,H1_close); if(bars == -1) Print("Echec de CopyClose(\"EURUSD\",PERIOD_H1,01.01.2020,01.01.2021. Erreur ",GetLastError()); else { Print("\nCalcule la moyenne et l'écart-type des rendements des barres H1"); Print("H1 bars=",ArraySize(H1_close)); GetReturns(H1_close,h1_returns); double average = ArrayMean(h1_returns); PrintFormat("Moyenne H1 = %G",average); double std = ArrayStd(h1_returns); PrintFormat("Ecart-type H1 = %G",std); double sharpe_H1 = average / std; PrintFormat("Sharpe H1 = %G",sharpe_H1); double sharpe_annual_H1 = sharpe_H1 * MathSqrt(ArraySize(h1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_H1); } bars = CopyClose("EURUSD",PERIOD_D1,from,to,D1_close); if(bars == -1) Print("Echec de CopyClose(\"EURUSD\",PERIOD_D1,01.01.2020,01.01.2021. Erreur ",GetLastError()); else { Print("\nCalcule la moyenne et l'écart-type des rendements des barres D1 "); Print("Barres D1 = ",ArraySize(D1_close)); GetReturns(D1_close,d1_returns); double average = ArrayMean(d1_returns); PrintFormat("Moyenne D1 = %G",average); double std = ArrayStd(d1_returns); PrintFormat("Ecart-type D1 = %G",std); double sharpe_D1 = average / std; double sharpe_annual_D1 = sharpe_D1 * MathSqrt(ArraySize(d1_returns)); Print("Sharpe_annual(H1)=", sharpe_annual_D1); } } //+------------------------------------------------------------------+ //| Remplit le tableau returns[] des rendements | //+------------------------------------------------------------------+ void GetReturns(const double & values[], double & returns[]) { int size = ArraySize(values); //--- si moins de 2 valeurs, retourne un tableau vide if(size < 2) { ArrayResize(returns,0); PrintFormat("%s: Erreur. ArraySize(values)=%d",size); return; } else { //--- remplit les rendements dans une boucle ArrayResize(returns, size - 1); double delta; for(int i = 1; i < size; i++) { returns[i - 1] = 0; if(values[i - 1] != 0) { delta = values[i] - values[i - 1]; returns[i - 1] = delta / values[i - 1]; } } } //--- } //+------------------------------------------------------------------+ //| Calcule le nombre moyen d'éléments du tableau //|+------------------------------------------------------------------+ double ArrayMean(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Erreur, tableau est vide",__FUNCTION__); return(0); } double mean = 0; for(int i = 0; i < size; i++) mean += array[i]; mean /= size; return(mean); } //+------------------------------------------------------------------+ //| Calcule l'écart type des éléments du tableau | //+------------------------------------------------------------------+ double ArrayStd(const double & array[]) { int size = ArraySize(array); if(size < 1) { PrintFormat("%s: Erreur, le tableau est vide",__FUNCTION__); return(0); } double mean = ArrayMean(array); double std = 0; for(int i = 0; i < size; i++) std += (array[i] - mean) * (array[i] - mean); std /= size; std = MathSqrt(std); return(std); } //+------------------------------------------------------------------+ /* Résultat Calcule la moyenne et l'écart-type des rendements des barres H1 Barres H1 : 6226 Moyenne H1 = 1.44468E-05 Ecart-type H1 = 0.00101979 Sharpe H1 = 0.0141664 Sharpe_annual(H1)=1.117708053392263 Calcule la moyenne et l'écart-type des rendements des barres D1 Barres D1 : 260 Moyenne D1 =0.000355823 Ecart-type D1 = 0.00470188 Sharpe_annual(H1)=1.2179005039019222 */
Code Python pour calculer à l'aide de la bibliothèque MetaTrader 5
import math from datetime import datetime import MetaTrader5 as mt5 # affiche les informations du package MetaTrader 5 print("Auteur du package MetaTrader5 : ", mt5.__author__) print("Version du package MetaTrader5 : ", mt5.__version__) # importe le module 'pandas' pour afficher les données obtenues sous forme tabulaire import pandas as pd pd.set_option('display.max_columns', 50) # nombre de colonnes à afficher pd.set_option('display.width', 1500) # largeur max du tableau à afficher # importe le module pytz pour utiliser le fuseau horaire import pytz # établit la connexion avec le terminal MetaTrader 5 if not mt5.initialize(): print("Echec de initialize()") mt5.shutdown() # définit le fuseau horaire en GMT timezone = pytz.timezone("Etc/UTC") # crée les objets datetime dans le fuseau horaire GMT pour éviter le décalage du fuseau horaire local utc_from = datetime(2020, 1, 1, tzinfo=timezone) utc_to = datetime(2020, 12, 31, hour=23, minute=59, second=59, tzinfo=timezone) # récupère les barres EURUSD H1 dans l'intervalle 2020.01.01 00:00 - 2020.31.12 13:00 dans le fuseau horaire GMT rates_H1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_H1, utc_from, utc_to) # récupère également les barres D1 dans l'intervalle 2020.01.01 00:00 - 2020.31.12 13:00 dans le fuseau horaire GMT rates_D1 = mt5.copy_rates_range("EURUSD", mt5.TIMEFRAME_D1, utc_from, utc_to) # stoppe la connexion au terminal MetaTrader 5 et continue de traiter les barres obtenues mt5.shutdown() # crée le DataFrame à partir des données obtenues rates_frame = pd.DataFrame(rates_H1) # ajoute la colonne "Return" (Rendement) rates_frame['return'] = 0.0 # calcule maintenant le rendement comme étant return[i] = (close[i] - close[i-1])/close[i-1] prev_close = 0.0 for i, row in rates_frame.iterrows(): close = row['close'] rates_frame.at[i, 'return'] = close / prev_close - 1 if prev_close != 0.0 else 0.0 prev_close = close print("\nCalcule la moyenne et l'écart-type des barres H1") print('H1 rates:', rates_frame.shape[0]) ret_average = rates_frame[1:]['return'].mean() # saute la 1ère ligne avec un rendement 0 print('Rendement moyen H1 = ', ret_average) ret_std = rates_frame[1:]['return'].std(ddof=0) # saute la 1ère ligne avec un rendement 0 print('Ecart-type du rendement H1 = ', ret_std) sharpe_H1 = ret_average / ret_std print('Sharpe H1 = Moyenne/EcartType = ', sharpe_H1) sharpe_annual_H1 = sharpe_H1 * math.sqrt(rates_H1.shape[0]-1) print('Sharpe_annual(H1) =', sharpe_annual_H1) # calcule maintenant le ratio de Sharpe sur la période D1 rates_daily = pd.DataFrame(rates_D1) # ajoute la colonne "Return" (Rendement) rates_daily['return'] = 0.0 # calcule les rendements prev_return = 0.0 for i, row in rates_daily.iterrows(): close = row['close'] rates_daily.at[i, 'return'] = close / prev_return - 1 if prev_return != 0.0 else 0.0 prev_return = close print("\nCalcule la moyenne et l'écart-type des barres D1") print('Taux D1 :', rates_daily.shape[0]) daily_average = rates_daily[1:]['return'].mean() print('Rendement moyen D1 = ', daily_average) daily_std = rates_daily[1:]['return'].std(ddof=0) print('Ecart-type du rendement D1 = ', daily_std) sharpe_daily = daily_average / daily_std print('Sharpe D1 =', sharpe_daily) sharpe_annual_D1 = sharpe_daily * math.sqrt(rates_daily.shape[0]-1) print('Sharpe_annual(D1) =', sharpe_annual_D1) Résultat Calcule la moyenne et l'écart-type des barres H1 Taux H1 : 6226 Rendement moyen H1 = 1.4446773215242986e-05 Ecart-type du rendement H1 = 0.0010197932969323495 Sharpe H1 = Moyenne/EcartType = 0.014166373968823358 Sharpe_annual(H1) = 1.117708053392236 Calcule la moyenne et l'écart-type des barres D1 Taux D1 : 260 Rendement moyen D1 = 0.0003558228355051694 Ecart-type du rendement D1 = 0.004701883757646081 Sharpe D1 = 0.07567665511222807 Sharpe_annual(D1) = 1.2179005039019217
Comme vous pouvez le voir, les résultats des calculs MQL5 et Python sont les mêmes. Les codes sources sont joints ci-dessous (CalculateSharpe_2TF).
Les ratios de Sharpe annuels calculés à partir des barres H1 et D1 diffèrent : 1,117708 et 1,217900. Essayons d'en découvrir la raison.
Calcul du ratio annuel de Sharpe sur l'EURUSD pour 2020 sur toutes les périodes
Maintenant, calculons le ratio de Sharpe annuel sur toutes les échéances. Pour ce faire, nous collectons les données obtenues dans un tableau :
- TF — période
- Minutes — nombre de minutes dans une période
- Rates - nombre de barres par an sur cette période
- Avg — rendement moyen par barre sur la période en pourcentage (pourcentage de variation de prix moyen par barre)
- Std — écart type par barre sur la période en pourcentage (pourcentage de volatilité des prix sur cette période)
- SharpeTF — Ratio de Sharpe calculé sur la période donnée
- SharpeAnnuel — ratio de Sharpe annuel calculé sur la base de cette période Ratio de Sharpe
Vous trouverez ci-dessous le bloc de code de calcul. Le code complet est disponible dans le fichier CalculateSharpe_All_TF.mq5 joint à l'article.
//--- structure pour afficher les statistiques à journaliser struct Stats { string TF; int Minutes; int Rates; double Avg; double Std; double SharpeTF; double SharpeAnnual; }; //--- tableau des statistiques par périodes Stats stats[]; //+------------------------------------------------------------------+ //| Fonction de démarrage du script | //+------------------------------------------------------------------+ void OnStart() { //--- tableaux des prix de clôture double H1_close[],D1_close[]; //--- tableaux des rendements double h1_returns[],d1_returns[]; //--- tableaux des périodes sur lesquelles les coefficients de Sharpe seront calculés ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4, PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1 }; ArrayResize(stats,ArraySize(timeframes)); //--- paramètres de la requête timeseries string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print(symbol); for(int i = 0; i < ArraySize(timeframes); i++) { //--- récupère le tableau des rendements sur la période spécifiée double returns[]; GetReturns(symbol,timeframes[i],from,to,returns); //--- calcule les statistiques GetStats(returns,avr,std,sharpe); double sharpe_annual = sharpe * MathSqrt(ArraySize(returns)); PrintFormat("%s aver=%G%% std=%G%% sharpe=%G sharpe_annual=%G", EnumToString(timeframes[i]), avr * 100,std * 100,sharpe,sharpe_annual); //--- remplit la structure des statistiques Stats row; string tf_str = EnumToString(timeframes[i]); StringReplace(tf_str,"PERIOD_",""); row.TF = tf_str; row.Minutes = PeriodSeconds(timeframes[i]) / 60; row.Rates = ArraySize(returns); row.Avg = avr; row.Std = std; row.SharpeTF = sharpe; row.SharpeAnnual = sharpe_annual; //--- ajoute une ligne pour les statisqtiques de la période stats[i] = row; } //--- affiche les statistiques de toutes les périodes à journaliser ArrayPrint(stats,8); } /* Résultat [TF] [Minutes] [Taux] [Moyenne] [Ecart Type] [SharpeTF] [SharpeAnnual] [ 0] "M1" 1 373023 0.00000024 0.00168942 0.00168942 1.03182116 [ 1] "M2" 2 186573 0.00000048 0.00239916 0.00239916 1.03629642 [ 2] "M3" 3 124419 0.00000072 0.00296516 0.00296516 1.04590258 [ 3] "M4" 4 93302 0.00000096 0.00341717 0.00341717 1.04378592 [ 4] "M5" 5 74637 0.00000120 0.00379747 0.00379747 1.03746116 [ 5] "M6" 6 62248 0.00000143 0.00420265 0.00420265 1.04854166 [ 6] "M10" 10 37349 0.00000239 0.00542100 0.00542100 1.04765562 [ 7] "M12" 12 31124 0.00000286 0.00601079 0.00601079 1.06042363 [ 8] "M15" 15 24900 0.00000358 0.00671964 0.00671964 1.06034161 [ 9] "M20" 20 18675 0.00000477 0.00778573 0.00778573 1.06397070 [10] "M30" 30 12450 0.00000716 0.00966963 0.00966963 1.07893298 [11] "H1" 60 6225 0.00001445 0.01416637 0.01416637 1.11770805 [12] "H2" 120 3115 0.00002880 0.01978455 0.01978455 1.10421905 [13] "H3" 180 2076 0.00004305 0.02463458 0.02463458 1.12242890 [14] "H4" 240 1558 0.00005746 0.02871564 0.02871564 1.13344977 [15] "H6" 360 1038 0.00008643 0.03496339 0.03496339 1.12645075 [16] "H8" 480 779 0.00011508 0.03992838 0.03992838 1.11442404 [17] "H12" 720 519 0.00017188 0.05364323 0.05364323 1.22207717 [18] "D1" 1440 259 0.00035582 0.07567666 0.07567666 1.21790050 [19] "W1" 10080 51 0.00193306 0.14317328 0.14317328 1.02246174 [20] "MN1" 43200 12 0.00765726 0.43113365 0.43113365 1.49349076 */
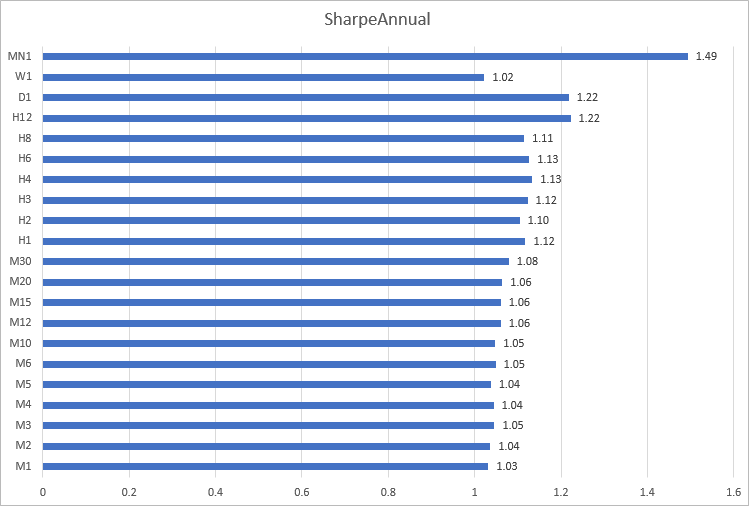
Construisons un histogramme du ratio de Sharpe sur l'EURUSD pour 2020 sur les différentes échéances. On voit ici que les calculs sur des plages de temps minute, de M1 à M30, donnent des résultats proches : de 1,03 à 1,08. Les résultats les plus incohérents ont été obtenus sur des échéances allant de H12 à MN1.
Calcul du ratio de Sharpe pour GBPUSD, USDJPY et USDCHF pour 2020
Effectuons des calculs similaires pour trois autres paires de devises.
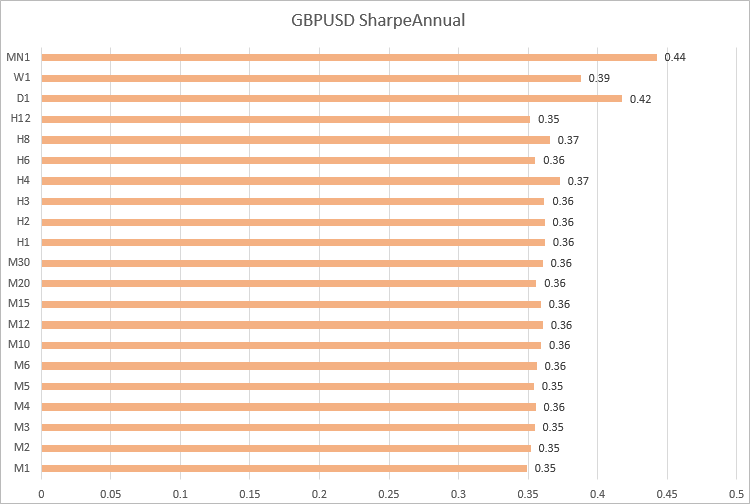
GBPUSD, les valeurs du ratio de Sharpe sont similaires sur les échéances de M1 à S12.
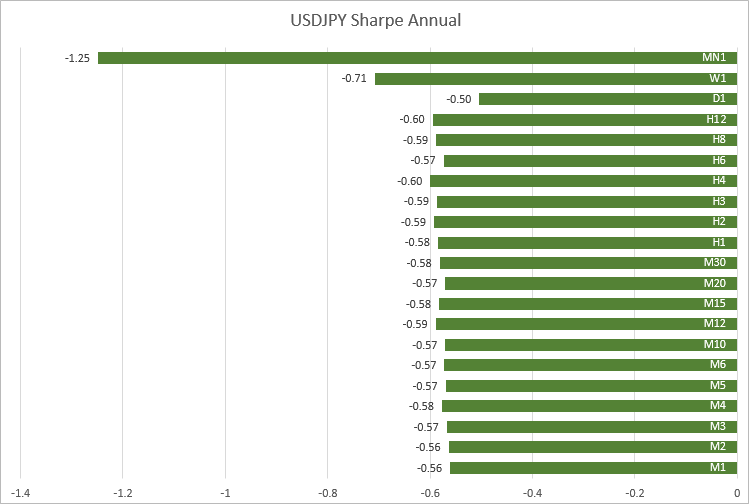
USDJPY, les valeurs sont également proches sur les échéances de M1 à H12 : -0,56 à -0,60.
USDCHF, des valeurs similaires ont été obtenues sur des échéances allant de M1 à M30. À mesure que la période augmente, le ratio de Sharpe fluctue.
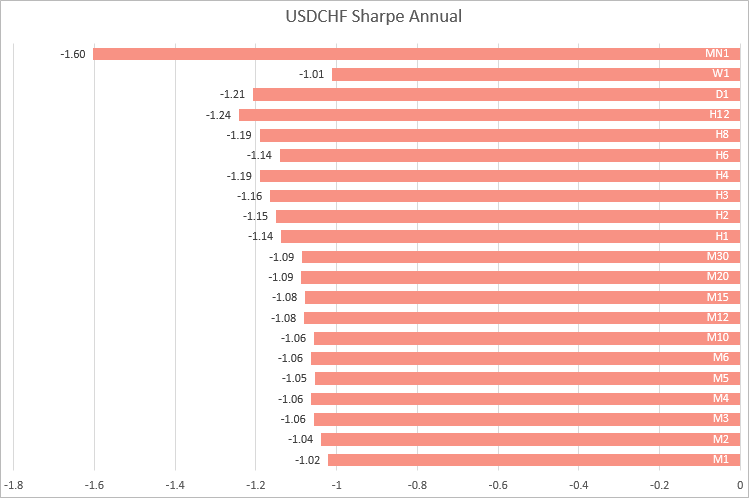
Ainsi, sur la base des exemples de quatre paires de devises majeures, nous pouvons conclure que les calculs les plus stables du ratio de Sharpe sont obtenus sur des échéances allant de M1 à M30. Cela signifie qu'il est préférable de calculer le ratio en utilisant des rendements à plus court terme, lorsque vous souhaitez comparer des stratégies fonctionnant sur différents symboles.
Calcul du ratio annuel de Sharpe sur l'EURUSD pour 2020 par mois
Utilisons les rendements mensuels de chaque mois de 2020 et calculons le ratio de Sharpe annuel sur des périodes allant de M1 à H1. Le code complet du script CalculateSharpe_Months.mq5 est joint à l'article.
//--- structure pour stocker les rendements struct Return { double ret; // return datetime time; // date int month; // month }; //+------------------------------------------------------------------+ //| Fonction de démarrage du script | //+------------------------------------------------------------------+ void OnStart() { SharpeMonths sharpe_by_months[]; //--- tableaux des périodes sur lesquelles le ratio de Sharpe sera calculé ENUM_TIMEFRAMES timeframes[] = {PERIOD_M1,PERIOD_M2,PERIOD_M3,PERIOD_M4,PERIOD_M5, PERIOD_M6,PERIOD_M10,PERIOD_M12,PERIOD_M15,PERIOD_M20, PERIOD_M30,PERIOD_H1 }; ArrayResize(sharpe_by_months,ArraySize(timeframes)); //--- Paramètres de la requpete timeseries string symbol = Symbol(); datetime from = D'01.01.2020'; datetime to = D'01.01.2021'; Print("Calcule Sharpe Annual sur ",symbol, " pour l'année 2020"); for(int i = 0; i < ArraySize(timeframes); i++) { //--- récupère le tableau des rendements sur la période spécifiée Return returns[]; GetReturns(symbol,timeframes[i],from,to,returns); double avr,std,sharpe; //--- Calcule les statistiques de l'année GetStats(returns,avr,std,sharpe); string tf_str = EnumToString(timeframes[i]); //--- calcule le ratio de Sharpe annuel pour chaque mois SharpeMonths sharpe_months_on_tf; sharpe_months_on_tf.SetTimeFrame(tf_str); //--- sélectionne les rendements du i-ème mois for(int m = 1; m <= 12; m++) { Return month_returns[]; GetReturnsByMonth(returns,m,month_returns); //--- Calcule les statistiques de l'année double sharpe_annual = CalculateSharpeAnnual(timeframes[i],month_returns); sharpe_months_on_tf.Sharpe(m,sharpe_annual); } //--- ajoute le ratio de Sharpe pour les 12 mois sur la période i sharpe_by_months[i] = sharpe_months_on_tf; } //--- affiche le tableau des valeurs annuelles de Sharpe par mois sur toutes les périodes ArrayPrint(sharpe_by_months,3); } /* Résultat Calcule Sharpe Annual sur EURUSD pour l'année 2020 [TF] [Jan] [Feb] [Marc] [Apr] [May] [June] [July] [Aug] [Sept] [Oct] [Nov] [Dec] [ 0] "PERIOD_M1" -2.856 -1.340 0.120 -0.929 2.276 1.534 6.836 2.154 -2.697 -1.194 3.891 4.140 [ 1] "PERIOD_M2" -2.919 -1.348 0.119 -0.931 2.265 1.528 6.854 2.136 -2.717 -1.213 3.845 4.125 [ 2] "PERIOD_M3" -2.965 -1.340 0.118 -0.937 2.276 1.543 6.920 2.159 -2.745 -1.212 3.912 4.121 [ 3] "PERIOD_M4" -2.980 -1.341 0.119 -0.937 2.330 1.548 6.830 2.103 -2.765 -1.219 3.937 4.110 [ 4] "PERIOD_M5" -2.929 -1.312 0.120 -0.935 2.322 1.550 6.860 2.123 -2.729 -1.239 3.971 4.076 [ 5] "PERIOD_M6" -2.945 -1.364 0.119 -0.945 2.273 1.573 6.953 2.144 -2.768 -1.239 3.979 4.082 [ 6] "PERIOD_M10" -3.033 -1.364 0.119 -0.934 2.361 1.584 6.789 2.063 -2.817 -1.249 4.087 4.065 [ 7] "PERIOD_M12" -2.952 -1.358 0.118 -0.956 2.317 1.609 6.996 2.070 -2.933 -1.271 4.115 4.014 [ 8] "PERIOD_M15" -3.053 -1.367 0.118 -0.945 2.377 1.581 7.132 2.078 -2.992 -1.274 4.029 4.047 [ 9] "PERIOD_M20" -2.998 -1.394 0.117 -0.920 2.394 1.532 6.884 2.065 -3.010 -1.326 4.074 4.040 [10] "PERIOD_M30" -3.008 -1.359 0.116 -0.957 2.379 1.585 7.346 2.084 -2.934 -1.323 4.139 4.034 [11] "PERIOD_H1" -2.815 -1.373 0.116 -0.966 2.398 1.601 7.311 2.221 -3.136 -1.374 4.309 4.284 */
On constate que les valeurs des ratios annuels pour chaque mois sont très proches sur toutes les échelles de temps sur lesquelles nous avons effectué les calculs. Pour une meilleure présentation, rendons les résultats sous forme de surface 3D à l'aide d'un diagramme Excel.
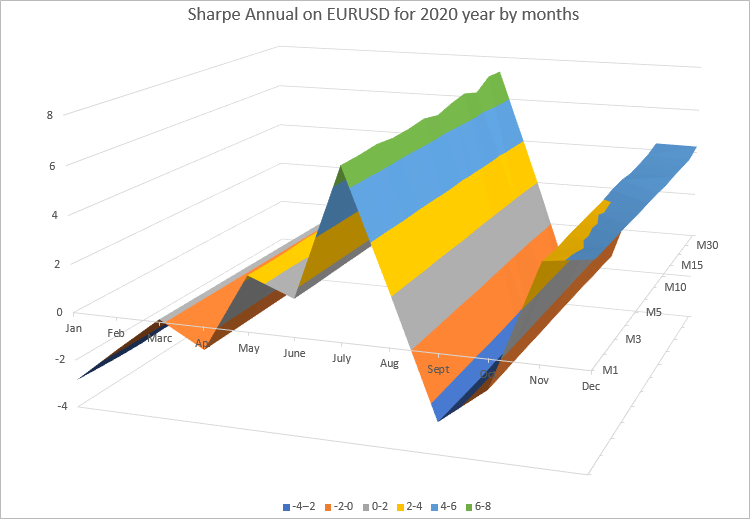
Le diagramme montre clairement que les valeurs du ratio de Sharpe annuel changent tous les mois. Cela dépend de l'évolution de l'EURUSD ce mois-ci. En revanche, le ratio annuel de Sharpe pour chaque mois sur toutes les échéances ne change presque pas.
Ainsi, le ratio de Sharpe annuel peut être calculé sur n'importe quelle période, tandis que la valeur résultante dépend également du nombre de barres sur lesquelles des rendements ont été obtenus. Cela signifie que cet algorithme de calcul peut être utilisé dans les tests, l'optimisation et la surveillance en temps réel. La seule condition préalable est d'avoir un éventail de retours suffisamment large.
Ratio de Sortino
Dans le calcul du ratio de Sharpe, le risque est la pleine volatilité des cotations, à la fois à la hausse et à la baisse des actifs. Mais l'augmentation de la valeur du portefeuille est bonne pour l'investisseur, tandis que la perte n'est liée qu'à sa diminution. Par conséquent, le risque réel dans le ratio est surestimé. Le ratio de Sortino développé au début des années 1990 par Frank Sortino répond à ce problème.
Comme ses prédécesseurs, F. Sortino considère le rendement futur comme une variable aléatoire égale à son espérance mathématique, tandis que le risque est considéré comme une variance. Le rendement et le risque sont déterminés sur la base des cotations historiques pour une certaine période. Comme dans le calcul du ratio de Sharpe, le rendement est divisé par le risque.
Sortino a noté que le risque défini comme la variance totale des rendements (ou la volatilité totale) dépend à la fois des changements positifs et négatifs. Sortino a remplacé la volatilité globale totale par une semi-volatilité qui ne considère qu'une diminution des actifs. La semi-volatilité est également appelée volatilité nuisible, risque de baisse, déviation à la baisse, volatilité négative ou écart type à la baisse.
Le calcul du ratio de Sortino est similaire à celui de Sharpe, à la seule différence que les rendements positifs sont exclus du calcul de la volatilité. Cela réduit la mesure du risque et augmente le poids du ratio.
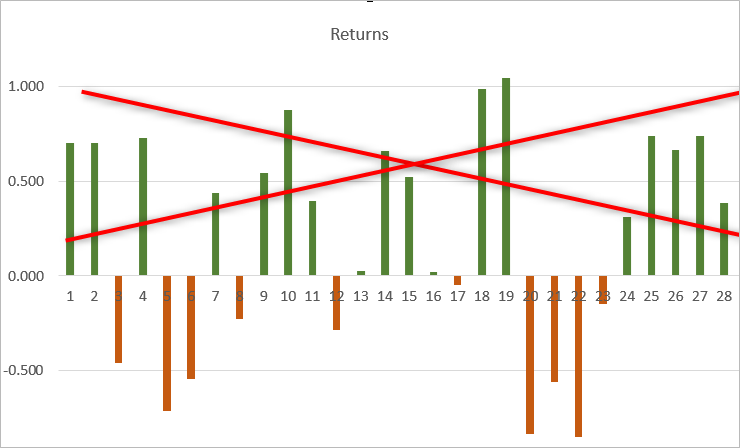
Exemple de code calculant le ratio de Sortino basé sur le ratio de Sharpe. La semi-dispersion est calculée uniquement en utilisant des rendements négatifs.
//+------------------------------------------------------------------+ //| Calculae les ratios de Sharpe et de Sortino | //+------------------------------------------------------------------+ void GetStats(ENUM_TIMEFRAMES timeframe, const double & returns[], double & avr, double & std, double & sharpe, double & sortino) { avr = ArrayMean(returns); std = ArrayStd(returns); sharpe = (std == 0) ? 0 : avr / std; //--- supprime les rendements négatifs et calcule le ratio de Sortino double negative_only[]; int size = ArraySize(returns); ArrayResize(negative_only,size); ZeroMemory(negative_only); //--- ne copie que les rendements négatifs for(int i = 0; i < size; i++) negative_only[i] = (returns[i] > 0) ? 0 : returns[i]; double semistd = ArrayStd(negative_only); sortino = avr / semistd; return; }
Le script CalculateSortino_All_TF.mq5 joint à cet article génère les résultats suivants sur l'EURUSD, pour 2020 :
[TF] [Minutes] [Periodes] [Avg] [Std] [SharpeAnnual] [SortinoAnnual] [Ratio] [ 0] "M1" 1 373023 0.00000024 0.00014182 1.01769617 1.61605380 1.58795310 [ 1] "M2" 2 186573 0.00000048 0.00019956 1.02194170 1.62401856 1.58914991 [ 2] "M3" 3 124419 0.00000072 0.00024193 1.03126142 1.64332243 1.59350714 [ 3] "M4" 4 93302 0.00000096 0.00028000 1.02924195 1.62618200 1.57998030 [ 4] "M5" 5 74637 0.00000120 0.00031514 1.02303684 1.62286584 1.58632199 [ 5] "M6" 6 62248 0.00000143 0.00034122 1.03354379 1.63789024 1.58473231 [ 6] "M10" 10 37349 0.00000239 0.00044072 1.03266766 1.63461839 1.58290848 [ 7] "M12" 12 31124 0.00000286 0.00047632 1.04525580 1.65215986 1.58062730 [ 8] "M15" 15 24900 0.00000358 0.00053223 1.04515816 1.65256608 1.58116364 [ 9] "M20" 20 18675 0.00000477 0.00061229 1.04873529 1.66191269 1.58468272 [10] "M30" 30 12450 0.00000716 0.00074023 1.06348332 1.68543441 1.58482449 [11] "H1" 60 6225 0.00001445 0.00101979 1.10170316 1.75890688 1.59653431 [12] "H2" 120 3115 0.00002880 0.00145565 1.08797046 1.73062372 1.59068999 [13] "H3" 180 2076 0.00004305 0.00174762 1.10608991 1.77619289 1.60583048 [14] "H4" 240 1558 0.00005746 0.00200116 1.11659184 1.83085734 1.63968362 [15] "H6" 360 1038 0.00008643 0.00247188 1.11005321 1.79507001 1.61710267 [16] "H8" 480 779 0.00011508 0.00288226 1.09784908 1.74255746 1.58724682 [17] "H12" 720 519 0.00017188 0.00320405 1.20428761 2.11045830 1.75245371 [18] "D1" 1440 259 0.00035582 0.00470188 1.20132966 2.04624198 1.70331429 [19] "W1" 10080 51 0.00193306 0.01350157 1.03243721 1.80369984 1.74703102 [20] "MN1" 43200 12 0.00765726 0.01776075 1.49349076 5.00964481 3.35431926
On peut voir que dans presque toutes les périodes, la valeur de Sortino est de 1,60 fois le ratio de Sharpe. Bien sûr, il n'y aura pas une telle dépendance claire lors du calcul des ratios basés sur les résultats de trading. Par conséquent, il est logique de comparer les stratégies/portefeuilles en utilisant les deux ratios.
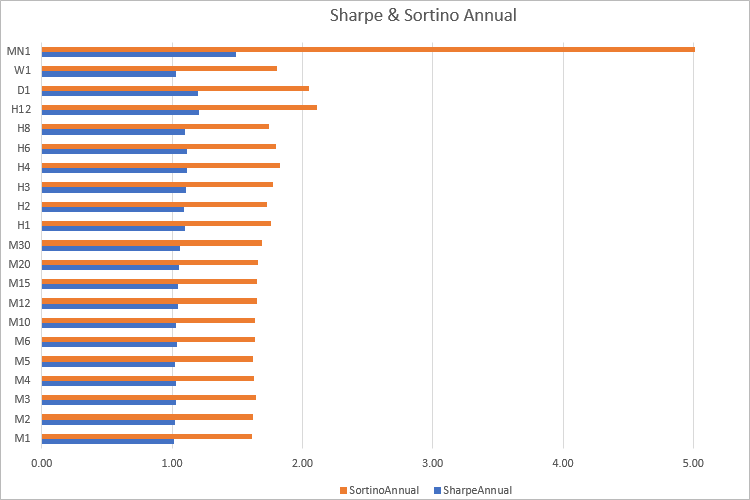
La différence entre ces deux mesures est que le ratio de Sharpe reflète principalement la volatilité, tandis que le ratio de Sortino montre vraiment le ratio ou le rendement par unité de risque. Mais n'oubliez pas que les calculs sont effectués sur la base de l'historique, donc de bons résultats ne peuvent garantir des bénéfices futurs.
Exemple de calcul du ratio de Sharpe dans le testeur de stratégie MetaTrader 5
Le ratio de Sharpe a été développé à l'origine pour évaluer les portefeuilles contenant des actions. Les prix des actions changent tous les jours et, par conséquent, la valeur des actifs change également tous les jours. Par défaut, les stratégies de trading n'impliquent pas l'existence de positions ouvertes, donc une partie du temps, l'état d'un compte de trading restera inchangé. Cela signifie que lorsqu'il n'y a pas de positions ouvertes, nous recevrons des valeurs de retour nulles, et donc les calculs de Sharpe seront erronés pour eux. Par conséquent, les calculs n'utiliseront que les barres sur lesquelles l'état du compte de trading a changé. L'option la plus appropriée consiste à analyser les valeurs des actions sur le dernier tick de chaque barre. Cela permettra le calcul du ratio de Sharpe avec n'importe quel mode de génération de ticks dans le testeur de stratégie MetaTrader 5.
Un autre point à prendre en compte est que l'incrément de prix en pourcentage, qui est généralement calculé comme Return[i]=(CloseCurrent-ClosePrevious)/ClosePrevious, présente un certain inconvénient dans les calculs. C'est comme suit : si le prix baisse de 5 % puis augmente de 5 %, nous n'obtiendrons pas la valeur initiale. C'est pourquoi, au lieu de l'augmentation de prix relative habituelle, les études statistiques utilisent généralement le logarithme de l'augmentation de prix. Les retours logarithmiques (rendements logarithmiques) n'ont pas cet inconvénient des retours linéaires. La valeur est calculée comme suit :
Log_Return =ln(Current/Previous) = ln(Current) — ln(Previous)
Les retours logarithmiques sont pratiques car ils peuvent être additionnés car la somme des logarithmes est équivalente au produit des retours relatifs.
Ainsi, l'algorithme de calcul du ratio de Sharpe nécessite des ajustements minimaux.
//--- calcule les logarithmes des incréments en utilisant le tableau des equities for(int i = 1; i < m_bars_counter; i++) { //--- ne l'ajoute que si l'equity a changé if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // logarithme de l'incrément aver += log_return; // logarithme moyen des incréments AddReturn(log_return); // remplit le tableau des logarithmes d'incréments counter++; // compteur des rendements } prev_equity = m_equities[i]; } //--- si les valeurs ne sont pas suffisantes pour le calcul de Sharpe, retourne 0 if(counter <= 1) return(0); //--- valeur moyenne du logarithme d'incrément aver /= counter; //--- calcule l'écart-type for(int i = 0; i < counter; i++) std += (m_returns[i] - aver) * (m_returns[i] - aver); std /= counter; std = MathSqrt(std); //--- ratio de Sharpe sur la période actuelle double sharpe = aver / std;
Le code de calcul complet est implémenté sous la forme d'un fichier inclus Sharpe.mqh qui est joint à l'article. Pour calculer le ratio de Sharpe comme critère d'optimisation personnalisé, connectez ce fichier à votre Expert Advisor et ajoutez quelques lignes de code. Voyons comment le faire en utilisant le MACD Sample.mq5 EA du pack standard MetaTrader 5 à titre d'exemple.
#define MACD_MAGIC 1234502 //--- #include <Trade\Trade.mqh> #include <Trade\SymbolInfo.mqh> #include <Trade\PositionInfo.mqh> #include <Trade\AccountInfo.mqh> #include "Sharpe.mqh" //--- input double InpLots = 0.1;// Lots input int InpTakeProfit = 50; // Take Profit (en pips) input int InpTrailingStop = 30; // Niveau du Trailing Stop (en pips) input int InpMACDOpenLevel = 3; // Niveau d'ouverture du MACD (en pips) input int InpMACDCloseLevel = 2; // Niveau de clôture du MACD (en pips) input int InpMATrendPeriod = 26; // Période de la tendance //--- int ExtTimeOut = 10; // time out en secondes entre les opérations de trading CReturns returns; .... //+------------------------------------------------------------------+ //| Fonction de gestion d'un nouveau tick | //+------------------------------------------------------------------+ void OnTick(void) { static datetime limit_time = 0; // heure du dernière trade traité + timeout //--- ajoute le symbole actuel au tableau pour calculer le ratio de Sharpe MqlTick tick; SymbolInfoTick(_Symbol, tick); returns.OnTick(tick.time, AccountInfoDouble(ACCOUNT_EQUITY)); //--- aucun traitement en cas de timeout if(TimeCurrent() >= limit_time) { //--- vérifie les données if(Bars(Symbol(), Period()) > 2 * InpMATrendPeriod) { //--- change l'heure de limite avec le timeout en secondes si traité if(ExtExpert.Processing()) limit_time = TimeCurrent() + ExtTimeOut; } } } //+------------------------------------------------------------------+ //| Tester function | //+------------------------------------------------------------------+ double OnTester(void) { //--- calcule le ratio de Sharpe double sharpe = returns.OnTester(); return(sharpe); } //+------------------------------------------------------------------+
Enregistrez le code résultant sous "MACD Sample Sharpe.mq5" - le fichier correspondant est également joint ci-dessous.
Exécutons une optimisation génétique pour EURUSD M10 2020, en sélectionnant un critère d'optimisation personnalisé.
Les valeurs des critères personnalisés obtenues coïncident avec le ratio de Sharpe calculé par le testeur de stratégie. Vous connaissez maintenant les mécanismes de calcul ainsi que la manière d'interpréter les résultats obtenus.
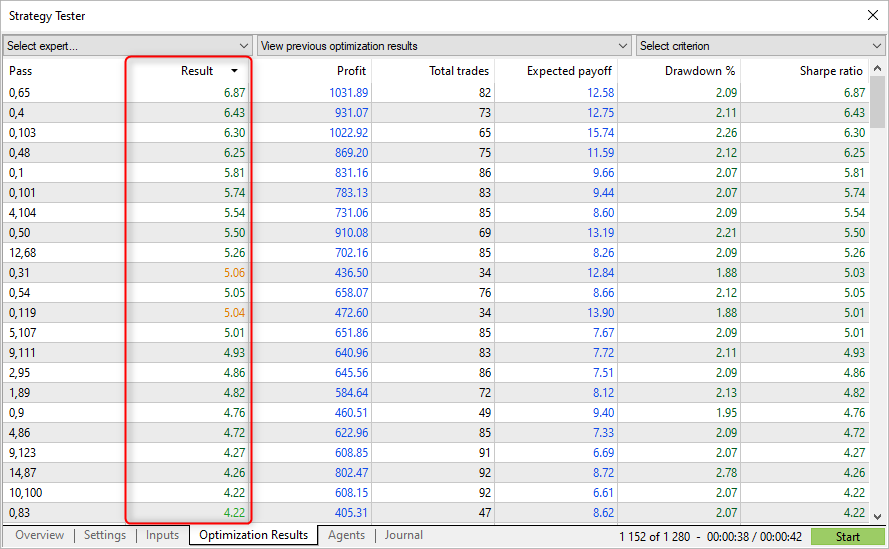
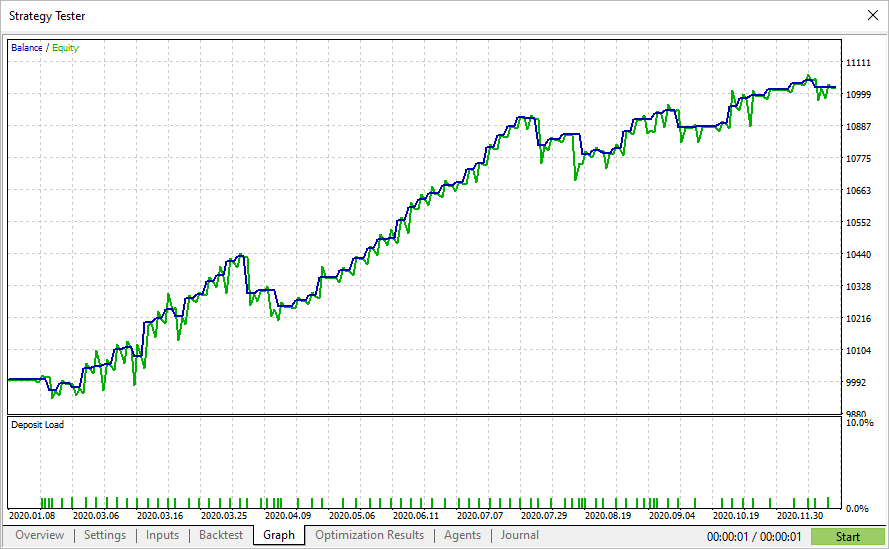
Les passes avec le ratio de Sharpe le plus élevé ne montrent pas toujours le profit le plus élevé dans le testeur, mais elles permettent de trouver des paramètres avec un graphique d'équité lisse. De tels graphiques ne montrent généralement pas de forte croissance, mais il n'y a pas non plus de grosses chutes ni de baisses de capital.
Cela signifie qu'en utilisant l'optimisation par le ratio de Sharpe, il est possible de trouver des paramètres plus stables, par rapport aux autres critères d'optimisation.
Avantages et inconvénients
Les ratios de Sharpe et de Sortino permettent de déterminer si le bénéfice reçu couvre ou non le risque associé. Un autre avantage par rapport aux autres mesures de risque est que les calculs peuvent être appliqués à tous les types d'actifs. Par exemple, vous pouvez comparer l'or à l'argent en utilisant le ratio de Sharpe car il ne nécessite pas d'évaluation externe spécifique. Ainsi, les ratios peuvent être appliqués à des stratégies ou des titres individuels, ainsi qu'à des portefeuilles d'actifs ou de stratégie.
L'inconvénient de ces outils est que le calcul suppose une distribution normale des rendements. En réalité, cette exigence est rarement remplie. Néanmoins, les ratios de Sharpe et de Sortino sont les outils les plus simples et les plus compréhensibles permettant de comparer différentes stratégies et portefeuilles.
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/9171
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.
 Better programmer (Partie 05) : Comment devenir un développeur plus rapide
Better programmer (Partie 05) : Comment devenir un développeur plus rapide
 Better Programmer (Partie 04): Comment devenir un développeur plus rapide
Better Programmer (Partie 04): Comment devenir un développeur plus rapide
 Better Programmer (Part 06) : 9 habitudes qui mènent à un codage efficace
Better Programmer (Part 06) : 9 habitudes qui mènent à un codage efficace
 Better Programmer (Partie 03): Abandonnez ces 5 choses pour devenir un programmeur MQL5 performant
Better Programmer (Partie 03): Abandonnez ces 5 choses pour devenir un programmeur MQL5 performant
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Le Sharpe sur les logarithmes ne dépend pas de la taille du dépôt uniquement dans le cas de transactions avec réinvestissement.
Mais dans ce cas, le Sharpe sur les incréments simples ne dépend pas de la taille du dépôt.
Par conséquent, je ne comprends pas pourquoi je devrais utiliser le Sharpe sur les logarithmes.
Lire le logarithme du prix
Vous trouverez vous-même d'autres références
Lire le logarithme du prix
Vous trouverez vous-même d'autres références
Une autre nuance très importante est que dans ce script, seules les barres où il y a eu un changement d'équité sont prises en compte dans le calcul du Sharpe :
//--- add only if equity has changed if(m_equities[i] != prev_equity) { log_return = MathLog(m_equities[i] / prev_equity); // incrémente le logarithme aver += log_return; // logarithme moyen des incréments AddReturn(log_return); // remplir le tableau des logarithmes incrémentaux counter++; // compteur de retours } prev_equity = m_equities[i];La variation moyenne est alors trouvée en divisant par le nombre de ces barres :
Cependant, la transition vers le sharpe annuel est basée sur le ratio de la période de temps, comme si toutes les barres de la période de temps actuelle étaient prises en compte dans le calcul :
C'est-à-dire, une fois de plus : le script trouve la moyenne des sharps pour 1 barre avec changement d'équité, et ensuite, pour trouver le sharps annuel, le multiplie non pas par le nombre de telles barres dans une année, mais par le nombre total de barres de cette période de temps dans une année (sa racine, bien sûr). Ce qui est erroné et surestime le chiffre final.
Apparemment, le Sharpe est calculé de la même manière dans le testeur ?
le script trouve le Sharpe moyen pour 1 barre avec changement d'équité, et ensuite, pour trouver le Sharpe annuel, le multiplie non pas par le nombre de telles barres dans une année, mais par le nombre total de barres de ce tf dans une année (sa racine, bien sûr). Ce qui est erroné et surestime le chiffre final
J'ai également remarqué cela. C'est pourquoi, dans ma version, j'ai ajouté une option permettant de prendre en compte les barres nulles.