Tiefe Neuronale Netzwerke (Teil VIII). Erhöhung der Klassifizierungsqualität von Ensembles mit Bagging
727
1
Inhalt
- Einführung
- Vorbereitung der Anfangsdaten
- Verarbeiten des Rauschens in der Untermenge pretrain
- Trainieren von Ensembles der Klassifikatoren von Neuronalen Netzen Training mit rauschgeminderten Anfangsdaten und berechnen kontinuierlicher Prognosen der Neuronalen Netze mit der Untermenge test
- Bestimmen der Schwellenwerte der erhaltenen kontinuierlichen Prognosen, ihr konvertieren Klassenlables und berechnen der Metriken der Neuronalen Netze
- Testen der Ensembles
- Optimieren der Hyperparameter von Ensembles von Klassifikatoren von Neuronalen Netzen
- Optimieren der Hyperparameter in der Nachbearbeitung
- Kombinieren der besten Ensembles zum Superensemble inklusive deren Ausgaben
- Analyse der Versuchsergebnisse
- Schlussfolgerung
- Anlagen
Einführung
In den beiden vorhergehenden Artikeln (1, 2) haben wir ein Ensemble von ELM-Klassifikatoren für neuronale Netze erstellt. Damals diskutierten wir, wie die Klassifizierungsqualität verbessert werden kann. Unter den vielen möglichen Lösungen wurden zwei gewählt: Reduzierung der Auswirkungen von Rauschproben und Auswahl des optimalen Schwellenwerts, durch den die kontinuierlichen Vorhersagen der neuronalen Netzwerke des Ensembles in Klassenlabels umgewandelt werden. In diesem Artikel schlage ich vor, experimentell zu testen, wie sich das auf die Klassifizierungsqualität auswirkt:
- Methoden zur Rauschminderung,
- Schwellenwerttypen,
- Optimierung der Hyperparameter der neuronalen Netze des Ensembles und der Nachbearbeitung.
Dann vergleichen wir die Qualität der Klassifizierung, die durch Mittelwertbildung und einfache Mehrheitsabstimmung des Superensembles, das sich aus den besten Ensembles zusammensetzt, nach den Optimierungsergebnissen. Alle Berechnungen werden in der Umgebung von R 3.4.4.4 durchgeführt.
1. Vorbereitung der Anfangsdaten
Zur Vorbereitung der ersten Daten verwenden wir die zuvor beschriebenen Skripte.
Wir laden im ersten Block (Library) die notwendigen Funktionen und Bibliotheken.
Im zweiten Block (prepare) werden unter Verwendung der Anführungszeichen mit vom Terminal übergebenen Zeitstempeln die Indikatorwerte (in diesem Fall sind dies digitale Filter) und zusätzliche Variablen auf OHLC-Basis berechnet. Wir kombinieren diesen Datensatz in den Datenrahmen dt. Dann definieren wir die Parameter von Ausreißern in diesen Daten und berechnen sie. Wir definieren dann die Normierungsparameter und normieren die Daten. Wir erhalten den resultierenden Satz von Eingangsdaten DTcap.n.
Wir erzeugen im dritten Block (Daten X1) zwei Gruppen:
- data1 - enthält alle 13 Indikatoren mit den Zeitstempeln Data und dem Ziel Class;
- X1 - der gleiche Satz von Prädiktoren, aber ohne Zeitstempel. Das Ziel wird in einen Zahlenwert (0, 1) umgewandelt.
Wir erzeugen im vierten Block (Daten X2) auch zwei Sätze:
- data2 - enthält 7 Prädiktoren und einen Zeitstempel (Daten, CO, HO, LO, HL, dC, dH, dL);
- Х - die gleichen Prädiktoren, aber ohne Zeitstempel.
#--1--Library------------- patch <- "C:/Users/Vladimir/Documents/Market/Statya_DARCH2/PartVIII/PartVIII/" source(file = paste0(patch,"importar.R")) source(file = paste0(patch,"Library.R")) source(file = paste0(patch,"FunPrepareData_VII.R")) source(file = paste0(patch,"FUN_Stacking_VIII.R")) import_fun(NoiseFiltersR, GE, noise) #--2-prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt$features, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) meth <- qc(expoTrans, range)# "spatialSign" "expoTrans" "range" "spatialSign", preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) DTcap.n <- NormData(DTcap, preproc = preproc) }, env) #--3-Data X1------------- evalq({ subset <- qc(pretrain, train, test, test1) foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 names(data1) <- subset X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 names(X1) <- subset }, env) #--4-Data-X2------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 names(data2) <- subset X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 names(X2) <- subset rm(dt, DT, pre.outl, DTcap, meth, preproc) }, env)
Im fünften Block (bestF) sortieren wir die Prädiktoren der Menge Х in aufsteigender Reihenfolge ihrer Bedeutung (orderX1). Wir wählen diejenigen von ihnen mit einem Koeffizienten über 0,5 (featureX1). Wir drucken die Koeffizienten und Namen der ausgewählten Prädiktoren.
#--5--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") -> rx1 rx1$stopri[ ,1] -> orderX1 featureX1 <- dp$filter(rx1$stopri %>% as.data.frame(), rx1$stopri[ ,2] > 0.5) %>% dp$select(V1) %>% unlist() %>% unname() }, env) print(env$rx1$stopri) [,1] [,2] [1,] 6 1.0423206 [2,] 12 1.0229287 [3,] 7 0.9614459 [4,] 10 0.9526798 [5,] 5 0.8884596 [6,] 1 0.8055126 [7,] 3 0.7959655 [8,] 11 0.7594309 [9,] 8 0.6960105 [10,] 2 0.6626440 [11,] 4 0.4905196 [12,] 9 0.3554887 [13,] 13 0.2269289 colnames(env$X1$pretrain$x)[env$featureX1] [1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl" [10] "stlm"
Die gleiche Berechnung wird mit dem zweiten Datensatz Х2 durchgeführt. Wir erhalten orderX2 und featureX2.
evalq({
orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx2
rx2$stopri[ ,1] -> orderX2
featureX2 <- dp$filter(rx2$stopri %>% as.data.frame(), rx2$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx2$stopri)
[,1] [,2]
[1,] 1 1.6650259
[2,] 5 1.6636689
[3,] 3 0.7751799
[4,] 2 0.7751351
[5,] 6 0.5692846
[6,] 7 0.5496889
[7,] 4 0.4970882
colnames(env$X2$pretrain$x)[env$featureX2]
[1] "CO" "dC" "LO" "HO" "dH" "dL"
Damit ist die Vorbereitung der ersten Daten für die Experimente abgeschlossen. Wir haben zwei Datensätze X1/data1, X2/data2 und Prädiktoren orderX1, orderX2 nach Bedeutung geordnet vorbereitet. Alle oben genannten Skripte befinden sich in der Datei Prepare_VIII.R.
2. Verarbeiten des Rauschens in der Untermenge pretrain
Viele Autoren von Artikeln, darunter auch ich, widmeten ihre Publikationen der Filterung von verrauschten Vorhersagen. Hier schlage ich vor, ein weiteres, ebenso wichtiges, aber weniger genutztes Merkmal zu untersuchen - die Identifizierung und Verarbeitung von verrauschten Stichproben in Datensätzen. Warum werden also einige Beispiele in Datensätzen als Rauschen betrachtet und mit welchen Methoden können sie verarbeitet werden? Ich werde versuchen, es zu erklären.
So stehen wir vor der Aufgabe der Klassifizierung, während wir über einen Trainingssatz von Prädiktoren und ein Ziel verfügen. Das Ziel wird als gut auf die interne Struktur des Trainingssets abgestimmt angesehen. Aber in Wirklichkeit ist die Datenstruktur der Prädiktoren viel komplizierter als die vorgeschlagene Struktur des Ziels. Es stellt sich heraus, dass das Set Beispiele enthält, die dem Ziel gut entsprechen, während es einige gibt, die ihm überhaupt nicht entsprechen und das Modell beim Lernen stark verzerren. Dies führt zu einer Qualitätsminderung der Modellklassifizierung. Die Ansätze zur Identifizierung und Verarbeitung der Rauschproben wurden bereits detailliert betrachtet. Hier wird überprüft, wie sich drei Verarbeitungsmethoden auf die Klassifizierungsqualität auswirken:
- Korrektur der fälschlicherweise beschrifteten Beispiele;
- Entfernen dieser aus dem Datensatz;
- Zuordnen zu einer eigenen Klasse.
Die Rauschproben werden mit der Funktion NoiseFiltersR::GE() identifiziert und verarbeitet. Sie sucht nach den Rauschproben und modifiziert deren Kennzeichnung (korrigiert fehlerhafte Kennzeichnungen). Beispiele, die nicht mit neuer Kennzeichnung versehen werden können, werden entfernt. Die identifizierten Rauschproben können auch manuell aus dem Set entfernt oder in eine separate Klasse verschoben werden, indem ihnen ein neues Kennzeichnung zugewiesen wird. Alle oben genannten Berechnungen werden auf der Teilmenge "pretrain" durchgeführt, da sie für das Training des Ensembles verwendet werden. Das ist dann das Ergebnis der Funktion:
#---------------------------
import_fun(NoiseFiltersR, GE, noise)
#-----------------------
evalq({
out <- noise(x = data1[[1]] %>% dp$select(-Data))
summary(out, explicit = TRUE)
}, env)
Filter GE applied to dataset
Call:
GE(x = data1[[1]] %>% dp$select(-Data))
Parameter:
k: 5
kk: 3
Results:
Number of removed instances: 0 (0 %)
Number of repaired instances: 819 (20.46988 %)
Explicit indexes for removed instances:
.......
Ausgegebene Struktur der Funktion out:
> str(env$out) List of 7 $ cleanData :'data.frame': 4001 obs. of 14 variables: ..$ ftlm : num [1:4001] 0.293 0.492 0.47 0.518 0.395 ... ..$ stlm : num [1:4001] 0.204 0.185 0.161 0.153 0.142 ... ..$ rbci : num [1:4001] -0.0434 0.1156 0.1501 0.25 0.248 ... ..$ pcci : num [1:4001] -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... ..$ fars : num [1:4001] 0.208 0.255 0.246 0.279 0.267 ... ..$ v.fatl: num [1:4001] 0.4963 0.4635 0.0842 0.3707 0.0542 ... ..$ v.satl: num [1:4001] -0.0146 0.0248 -0.0353 0.1797 0.1205 ... ..$ v.rftl: num [1:4001] -0.2695 -0.0809 0.1752 0.3637 0.5305 ... ..$ v.rstl: num [1:4001] 0.398 0.362 0.386 0.374 0.357 ... ..$ v.ftlm: num [1:4001] 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... ..$ v.stlm: num [1:4001] -0.275 -0.226 -0.285 -0.11 -0.148 ... ..$ v.rbci: num [1:4001] 0.5374 0.4811 0.0978 0.2992 -0.0141 ... ..$ v.pcci: num [1:4001] -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ... $ remIdx : int(0) $ repIdx : int [1:819] 16 27 30 31 32 34 36 38 46 58 ... $ repLab : Factor w/ 2 levels "-1","1": 2 2 2 1 1 2 2 2 1 1 ... $ parameters:List of 2 ..$ k : num 5 ..$ kk: num 3 $ call : language GE(x = data1[[1]] %>% dp$select(-Data)) $ extraInf : NULL - attr(*, "class")= chr "filter"
Wobei:
- out$cleanData - der Datensatz nach Korrektur der Kennzeichnung der Rauschproben,
- out$remIdx - - Indexe der entfernten Samples (keine im Out-Beispiel),
- out$repIdx - Indexe der Teilmengen mit umbenannten Zielen,
- out$repLab - neue Kennzeichnungen dieser Rauschproben. So können wir sie aus dem Datensatz entfernen oder ihnen mit out$repIdx eine neue Kennzeichnung zuweisen.
Sobald die Indizes der Rauschproben bestimmt sind, bereiten wir vier Datensätze für das Training der Ensembles vor, die in der Struktur denoiseX1pretrain kombiniert sind.
- denoiseX1pretrain$origin - das ursprüngliche Vorübungs-Set;
- denoiseX1pretrain$reparated - Datensatz mit der Kennzeichnung der korrigierten Rauschproben;
- denoiseX1pretrain$removed - Datensatz mit den entfernten Rauschproben;
- denoiseX1pretrain$relabe - Datensatz mit den Rauschproben, den eine neuee Kennzeichnung zugewiesen wurde (d.h. das Ziel hat nun drei Klassen).
#--2-Data Xrepair-------------
#library(NoiseFiltersR)
evalq({
out <- noise(x = data1$pretrain %>% dp$select(-Data))
Yrelab <- X1$pretrain$y
Yrelab[out$repIdx] <- 2L
X1rem <- data1$pretrain[-out$repIdx, ] %>% dp$select(-Data)
denoiseX1pretrain <- list(origin = list(x = X1$pretrain$x, y = X1$pretrain$y),
repaired = list(x = X1$pretrain$x, y = out$cleanData$Class %>%
as.numeric() %>% subtract(1)),
removed = list(x = X1rem %>% dp$select(-Class),
y = X1rem$Class %>% as.numeric() %>% subtract(1)),
relabeled = list(x = X1$pretrain$x, y = Yrelab))
rm(out, Yrelab, X1rem)
}, env)
Die Teilmengen denoiseX1pretrain$origin|repaired|relabeled haben die gleichen Prädiktoren х, aber das Ziel у ist in jedem Satz unterschiedlich. Werfen wir einen Blick auf ihre Struktur:
#------------------------- env$denoiseX1pretrain$repaired$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$relabeled$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$repaired$y %>% table() . 0 1 1888 2113 env$denoiseX1pretrain$removed$y %>% table() . 0 1 1509 1673 env$denoiseX1pretrain$relabeled$y %>% table() . 0 1 2 1509 1673 819
Da die Anzahl der Proben im Datensatz denoiseX1pretrain$removed sich änderte, prüfen wir, wie sich die Signifikanz der Prädiktoren verändert hat:
evalq({
orderF(x = denoiseX1pretrain$removed$x %>% as.matrix(),
type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx1rem
rx1rem$stopri[ ,1] -> orderX1rem
featureX1rem <- dp$filter(rx1rem$stopri %>% as.data.frame(),
rx1rem$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx1rem$stopri)
[,1] [,2]
[1,] 6 1.0790642
[2,] 12 1.0320772
[3,] 7 0.9629750
[4,] 10 0.9515987
[5,] 5 0.8426669
[6,] 1 0.8138830
[7,] 3 0.7934568
[8,] 11 0.7682185
[9,] 8 0.6720211
[10,] 2 0.6355753
[11,] 4 0.5159589
[12,] 9 0.3670544
[13,] 13 0.2170575
colnames(env$X1$pretrain$x)[env$featureX1rem]
[1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl"
[10] "stlm" "pcci"
Die Reihenfolge und Zusammensetzung der besten Prädiktoren hat sich geändert. Dies muss beim Training von Ensembles berücksichtigt werden.
Also, wir haben 4 Teilmengen bereit: denoiseX1pretrain$origin, repaired, removed, relabeled. Sie werden für die Ausbildung der ELM-Ensembles verwendet. Skripte zur Rauschminderung der Daten befinden sich in der Datei Denoise.R. Die Struktur der Ausgangsdaten Х und denoiseX1pretrain sieht wie folgt aus:
Abb. 1. Die Struktur der Anfangsdaten.
3. Trainieren von Ensembles der Klassifikatoren von Neuronalen Netzen Training mit rauschgeminderten Anfangsdaten und berechnen kontinuierlicher Prognosen der Neuronalen Netze mit der Untermenge test
Schreiben wir eine Funktion zum Trainieren des Ensembles und zum Empfangen von Vorhersagen, die später als Eingabedaten für den trainierbaren Kombinierer im Stapel-Ensemble dienen.
Solche Berechnungen wurden bereits im vorherigen Artikel durchgeführt, daher werden deren Details nicht diskutiert. Kurz gesagt:
- In Block 1 (Eingang) die Konstanten definieren;
- In Block 2 (createEns) die Funktion CreateEns() definieren, die ein Ensemble von einzelnen neuronalen Netzwerk-Klassifikatoren mit konstanten Parametern und reproduzierbarer Initialisierung erzeugen würde;
- In Block 3 (GetInputData) berechnet die Funktion GetInputData() die Vorhersagen von drei Teilmengen Х$ train/test/test1 mit dem Ensemble Ens.
#--1--Input------------- evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear n <- 500 r = 7L SEED <- 12345 #--2-createENS---------------------- createEns <- function(r = 7L, nh = 5L, fact = 7L, X, Y){ Xtrain <- X[ , featureX1] k <- 1 rng <- RNGseq(n, SEED) #---creste Ensemble--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Y[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #--3-GetInputData -FUN----------- GetInputData <- function(Ens, X, Y){ #---predict-InputPretrain-------------- Xtrain <- X[ ,featureX1] k <- 1 rng <- RNGseq(n, SEED) #---create Ensemble--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 predict(Ens[[i]], newdata = Xtrain[-idx, ]) } %>% unname() -> InputPretrain #---predict-InputTrain-- Xtest <- X1$train$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> InputTrain #[ ,n] #---predict--InputTest---- Xtest1 <- X1$test$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---predict--InputTest1---- Xtest2 <- X1$test1$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---res------------------------- return(list(InputPretrain = InputPretrain, InputTrain = InputTrain, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
Wir haben bereits den Satz denoiseX1pretrain mit vier Datengruppen für Trainingsensembles: Originale (origin), korrigierte (repaired), entfernte (removed) und neu gekennzeichnete (relabeled) Rauschproben. Nach dem Training des Ensembles auf jeder dieser Datengruppen erhalten wir vier Ensembles. Unter Verwendung dieser Ensembles mit der Funktion GetInputData() erhalten wir vier Gruppen von Vorhersagen in drei Teilmengen: train, test und test1. Nachfolgend sind die Skripte für jedes Ensemble in der erweiterten Form separat aufgeführt (nur zum Debuggen und besseren Verständnis).
#---4--createEns--origin-------------- evalq({ Ens.origin <- vector(mode = "list", n) res.origin <- vector("list", 4) x <- denoiseX1pretrain$origin$x %>% as.matrix() y <- denoiseX1pretrain$origin$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.origin GetInputData(Ens = Ens.origin, X = x, Y = y) -> res.origin }, env) #---4--createEns--repaired-------------- evalq({ Ens.repaired <- vector(mode = "list", n) res.repaired <- vector("list", 4) x <- denoiseX1pretrain$repaired$x %>% as.matrix() y <- denoiseX1pretrain$repaired$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.repaired GetInputData(Ens = Ens.repaired, X = x, Y = y) -> res.repaired }, env) #---4--createEns--removed-------------- evalq({ Ens.removed <- vector(mode = "list", n) res.removed <- vector("list", 4) x <- denoiseX1pretrain$removed$x %>% as.matrix() y <- denoiseX1pretrain$removed$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.removed GetInputData(Ens = Ens.removed, X = x, Y = y) -> res.removed }, env) #---4--createEns--relabeled-------------- evalq({ Ens.relab <- vector(mode = "list", n) res.relab <- vector("list", 4) x <- denoiseX1pretrain$relabeled$x %>% as.matrix() y <- denoiseX1pretrain$relabeled$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.relab GetInputData(Ens = Ens.relab, X = x, Y = y) -> res.relab }, env)
Die Struktur der Vorhersageergebnisse der Ensembles ist nachfolgend gezeigt:
> env$res.origin %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.747 0.774 0.733 0.642 0.28 ... $ InputTrain : num [1:1001, 1:500] 0.742 0.727 0.731 0.66 0.642 ... $ InputTest : num [1:501, 1:500] 0.466 0.446 0.493 0.594 0.501 ... $ InputTest1 : num [1:251, 1:500] 0.093 0.101 0.391 0.547 0.416 ... > env$res.repaired %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.815 0.869 0.856 0.719 0.296 ... $ InputTrain : num [1:1001, 1:500] 0.871 0.932 0.889 0.75 0.737 ... $ InputTest : num [1:501, 1:500] 0.551 0.488 0.516 0.629 0.455 ... $ InputTest1 : num [1:251, 1:500] -0.00444 0.00877 0.35583 0.54344 0.40121 ... > env$res.removed %>% str() List of 4 $ InputPretrain: num [1:955, 1:500] 0.68 0.424 0.846 0.153 0.242 ... $ InputTrain : num [1:1001, 1:500] 0.864 0.981 0.784 0.624 0.713 ... $ InputTest : num [1:501, 1:500] 0.755 0.514 0.439 0.515 0.156 ... $ InputTest1 : num [1:251, 1:500] 0.105 0.108 0.511 0.622 0.339 ... > env$res.relab %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 1.11 1.148 1.12 1.07 0.551 ... $ InputTrain : num [1:1001, 1:500] 1.043 0.954 1.088 1.117 1.094 ... $ InputTest : num [1:501, 1:500] 0.76 0.744 0.809 0.933 0.891 ... $ InputTest1 : num [1:251, 1:500] 0.176 0.19 0.615 0.851 0.66 ...
Schauen wir, wie die Verteilung dieser Ausgaben/Eingaben aussehen. Hier die ersten 10 Ausgaben des Satzes InputTrain[ ,1:10]:
#------Ris InputTrain------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTrain[ ,1:10], horizontal = T, main = "res.origin$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTrain[ ,1:10], horizontal = T, main = "res.repaired$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTrain[ ,1:10], horizontal = T, main = "res.removed$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTrain[ ,1:10], horizontal = T, main = "res.relab$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
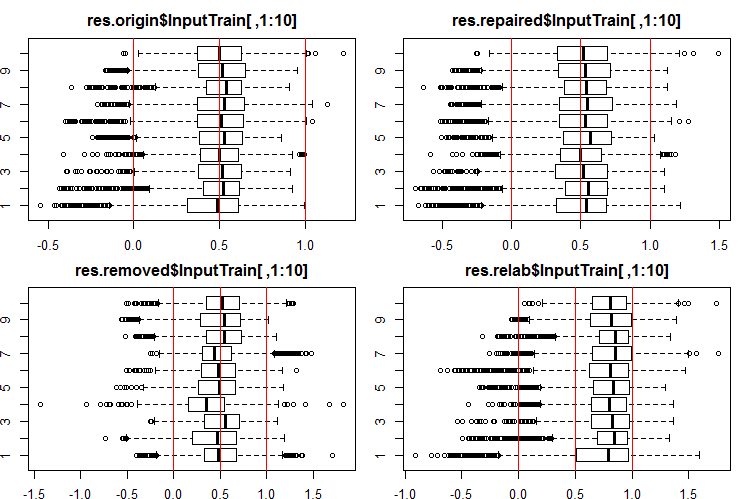
Abb. 2. Verteilung der Vorhersagen der Ausgabe von InputTrain unter Verwendung verschiedener Ensembles.
Sehen wir hier die 10 ersten Ausgaben des Satzes InputTest[ ,1:10]:
#------Ris InputTest------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2), las = 1) boxplot(env$res.origin$InputTest[ ,1:10], horizontal = T, main = "res.origin$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest[ ,1:10], horizontal = T, main = "res.repaired$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest[ ,1:10], horizontal = T, main = "res.removed$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest[ ,1:10], horizontal = T, main = "res.relab$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
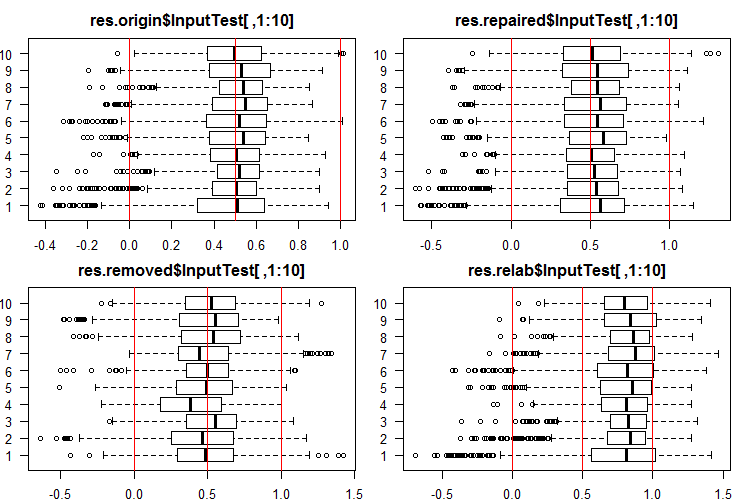
Abb. 3. Verteilung der Vorhersagen der Ausgabe von InputTest unter Verwendung verschiedener Ensembles.
Sehen wir hier die 10 ersten Ausgaben des Satzes InputTest1[ ,1:10]:
#------Ris InputTest1------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTest1[ ,1:10], horizontal = T, main = "res.origin$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest1[ ,1:10], horizontal = T, main = "res.repaired$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest1[ ,1:10], horizontal = T, main = "res.removed$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest1[ ,1:10], horizontal = T, main = "res.relab$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
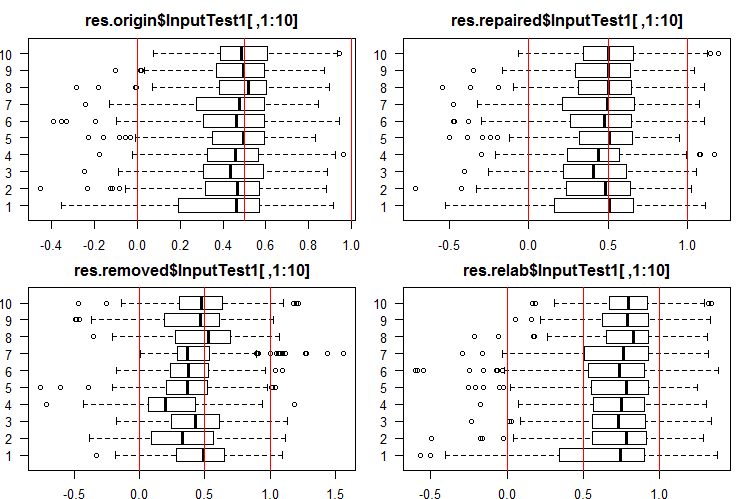
Abb. 4. Verteilung der Vorhersagen der Ausgabe von InputTest1 unter Verwendung verschiedener Ensembles.
Die Verteilung aller Vorhersagen unterscheidet sich stark von den Vorhersagen, die aus den Daten gewonnen wurden, die durch die Methode SpatialSign in den vorangegangenen Experimenten normiert wurden. Sie können mit verschiedenen Normalisierungsmethoden selbst experimentieren.
Nach der Berechnung der Vorhersage von Teilmengen X1$train/test/test1 mit jedem Ensemble erhalten wir vier Datengruppen - res.origin, res.repaired, res.removed und res.relab, mit Verteilungen in den Abbildungen 2 - 4.
Bestimmen wir die Klassifizierungsqualität jedes Ensembles und wandeln die kontinuierlichen Vorhersagen in Klassenlabel.
4. Bestimmen der Schwellenwerte der erhaltenen kontinuierlichen Prognosen, ihr konvertieren Klassenlables und berechnen der Metriken der Neuronalen Netze
Um die fortlaufenden Daten in Klassenlables umzuwandeln, werden eine oder mehrere Schwellenwerte für die Aufteilung in diese Klassen verwendet. Die kontinuierlichen Vorhersagen der Satzes InputTrain, die aus dem fünften neuronalen Netz aller Ensembles stammen, sehen wie folgt aus:
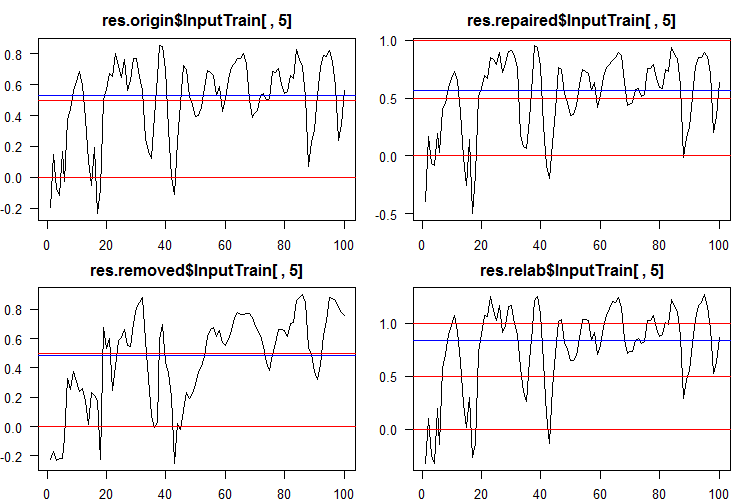
Abb. 5. Kontinuierliche Vorhersagen des fünften neuronalen Netzes verschiedener Ensembles.
Wie wir sehen können, sind die Diagramme der kontinuierlichen Vorhersage der origin, repaired, relabeled Modelle ähnlich in der Form, haben aber einen anderen Bereich. Die Linie der Vorhersage des removed Modells ist in ihrer Form erheblich unterschiedlich.
Um die nachfolgenden Berechnungen zu vereinfachen, sammeln wir alle Modelle und deren Vorhersagen in einer Struktur predX1. Schreiben wir dazu eine kompakte Funktion, die alle Berechnungen in einem Zyklus wiederholt. Es gibt das Skript und ein Bild der predX1 Struktur:
library("doFuture")
#---predX1------------------
evalq({
group <- qc(origin, repaired, removed, relabeled)
predX1 <- vector("list", 4)
foreach(i = 1:4, .packages = "elmNN") %do% {
x <- denoiseX1pretrain[[i]]$x %>% as.matrix()
y <- denoiseX1pretrain[[i]]$y
SEED = 12345
createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> ens
GetInputData(Ens = ens, X = x, Y = y) -> pred
return(list(ensemble = ens, pred = pred))
} -> predX1
names(predX1) <- group
}, env)
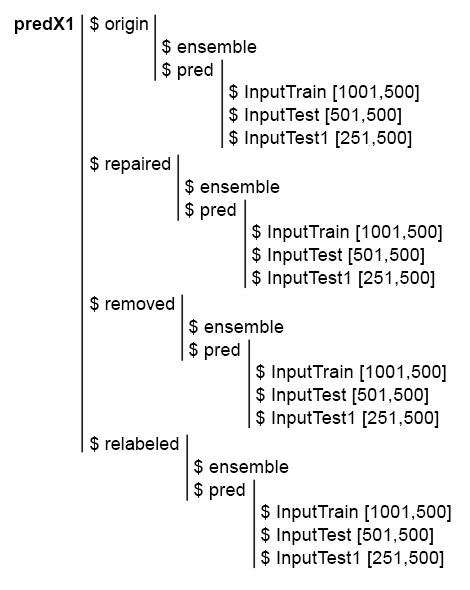
Abb. 6. Struktur des Satzes predX1
Vergessen wir nicht dass, um die Metriken der Vorhersagequalität des Ensembles zu erhalten, zwei Operationen durchgeführt werden müssen: Bereinigung (pruning) und Mittelung (oder einfache Mehrheitsentscheidung). Für die Bereinigung ist es notwendig, alle Ausgaben der einzelnen neuronalen Netze des Ensembles von der Endlosform in Klassenlabels zu konvertieren. Definiere dann die Metriken der einzelnen neuronalen Netze und wähle eine bestimmte Anzahl von ihnen mit den besten Ergebnissen. Dann mitteln wir die kontinuierlichen Vorhersagen dieser besten neuronalen Netze und erhalten eine kontinuierliche durchschnittliche Vorhersage des Ensembles. Definieren wir noch einmal den Schwellenwert, wandeln ihn die gemittelte Vorhersage in Klassenlabel um und berechnen die Endwerte der Klassifizierungsqualität des Ensembles.
Daher ist es notwendig, die kontinuierliche Vorhersage zweimal in Klassenlabels umzuwandeln. Die Umwandlungsschwellenwerte in diesen beiden Phasen können entweder gleich oder unterschiedlich sein. Welche Varianten von Schwellenwerten können verwendet werden?
- Der voreingestellte Schwellenwert. In diesem Fall ist er gleich 0,5.
- Schwellenwert gleich dem Median. Ich denke, er ist zuverlässiger. Der Median kann jedoch nur auf dem Validierungssatz bestimmt werden, während er nur beim Testen der nachfolgenden Teilmengen angewendet werden kann. Zum Beispiel definieren wir die Schwellenwerte für die Teilmenge InputTrain, die später für die Teilmengen InputTest und InputTest1 verwendet werden.
- Schwellenwert optimiert für verschiedene Kriterien. Dies kann beispielsweise der minimale Klassifizierungsfehler, die maximale Genauigkeit "1" oder "0" usw. sein. Die optimalen Schwellenwerte werden immer auf der Teilmenge InputTrain bestimmt und auf der Teilmenge InputTest und InputTest1 verwendet.
- Bei der Mittelung der Ergebnisse der besten neuronalen Netze kann die Kalibrierung verwendet werden. Einige Autoren schreiben, dass nur gut kalibrierte Ergebnisse gemittelt werden können. Die Bestätigung dieser Aussage ist außerhalb des Anwendungsbereichs dieses Artikels.
Der optimale Schwellenwert wird mit der Funktion InformationValue::optimalCutoff() bestimmt. Sie ist im Paket ausführlich beschrieben.
Um die Schwellenwerte für die Punkte 1 und 2 festzulegen, sind keine zusätzlichen Berechnungen erforderlich. Um die optimalen Schwellenwerte für Punkt 3 zu berechnen, schreiben wir die Funktion GetThreshold().
#--function------------------------- evalq({ import_fun("InformationValue", optimalCutoff, CutOff) import_fun("InformationValue", youdensIndex, th_youdens) GetThreshold <- function(X, Y, type){ switch(type, half = 0.5, med = median(X), mce = CutOff(Y, X, "misclasserror"), both = CutOff(Y, X,"Both"), ones = CutOff(Y, X, "Ones"), zeros = CutOff(Y, X, "Zeros") ) } }, env)
Es werden nur die ersten vier in dieser Funktion beschriebenen Arten von Schwellenwerten (half, med, mce, mce, both) berechnet. Die ersten beiden sind die Schwellenwerte von half und median. Der Schwellenwert mce liefert den minimalen Klassifizierungsfehler, der Schwellenwert both - den maximalen Wert des Koeffizienten youdensIndex = (sensitivity + specificity —1). Die Berechnungsreihenfolge sieht wie folgt aus:
1. Wir berechnen im Satz predX1 die vier Arten von Schwellenwerten für jedes der 500 neuronalen Netze des Ensembles auf der Untermenge InputTrain, getrennt in jeder Datengruppe (origin, repaired, removed und relabeled).
2. Anschließend werden unter Verwendung dieser Schwellenwerte die kontinuierlichen Vorhersagen aller neuronalen Netzwerke in allen Teilmengen (train|test|test1) in Klassen umgewandelt und die Durchschnittswerte F1 bestimmt. Wir erhalten vier Gruppen von Metriken, die jeweils drei Teilmengen enthalten. Nachfolgend ein Schritt-für-Schritt-Skript für die Gruppe origin.
Wir definiere 4 Arten von Schwellenwerten für die Teilmenge predX1$origin$pred$InputTrain:
#--threshold--train--origin--------
evalq({
Ytest = X1$train$y
Ytest1 = X1$test$y
Ytest2 = X1$test1$y
testX1 <- vector("list", 4)
names(testX1) <- group
type <- qc(half, med, mce, both)
registerDoFuture()
cl <- makeCluster(4)
plan(cluster, workers = cl)
foreach(i = 1:4, .combine = "cbind") %dopar% {# type
foreach(j = 1:500, .combine = "c") %do% {
GetThreshold(predX1$origin$pred$InputTrain[ ,j], Ytest, type[i])
}
} -> testX1$origin$Threshold
stopCluster(cl)
dimnames(testX1$origin$Threshold) <- list(NULL,type)
}, env)
Wir verwenden zwei verschachtelte Schleifen in jeder Berechnung. Wir wählen in der äußeren Schleife den Schwellentyp aus, erstellen einen Cluster und parallelisieren die Berechnung auf 4 Kerne. In der inneren Schleife iterieren wir über die Vorhersagen InputTrain von jedem der 500 neuronalen Netze, die das Ensemble umfassen. Es werden 4 Arten von Schwellenwerten definiert. Die Struktur der erhaltenen Daten schaut so aus:
> env$testX1$origin$Threshold %>% str() num [1:500, 1:4] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "half" "med" "mce" "both" > env$testX1$origin$Threshold %>% head() half med mce both [1,] 0.5 0.5033552 0.3725180 0.5125180 [2,] 0.5 0.4918041 0.5118821 0.5118821 [3,] 0.5 0.5005034 0.5394191 0.5394191 [4,] 0.5 0.5138439 0.4764055 0.5164055 [5,] 0.5 0.5241393 0.5165478 0.5165478 [6,] 0.5 0.4673319 0.4508287 0.4608287
Unter Verwendung der erhaltenen Schwellenwerte konvertieren wir die kontinuierlichen Vorhersagen der Gruppe origin der Untermenge train, test und test1 in Klassenlables und berechnen die Metriken (mean(F1)).
#--train--------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTrain[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTrainScore
dimnames(testX1$origin$InputTrainScore)[[2]] <- type
}, env)
#--test-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTestScore
dimnames(testX1$origin$InputTestScore)[[2]] <- type
}, env)
#--test1-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest1[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTest1Score
dimnames(testX1$origin$InputTest1Score)[[2]] <- type
}, env)
Hier ist die Verteilung der Metriken in der Gruppe origin und drei ihrer Teilmengen. Das folgende Skript für die Gruppe origin:
k <- 1L #origin # k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
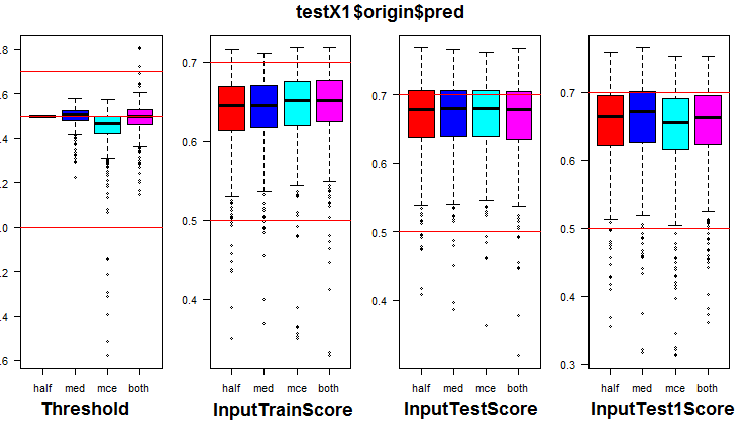
Abb. 7. Verteilung der Schwellenwerte und Metriken der Gruppe origin
Die Visualisierung zeigte, dass die Verwendung von "med" als Schwellenwert für die Datengruppe origin keine sichtbare Verbesserung der Qualität gegenüber dem Schwellenwert "half" bewirkt.
Wir berechnen alle 4 Arten von Schwellenwerten in allen Gruppen (man sollte darauf vorbereitet sein, dass es ziemlich viel Zeit und Speicher in Anspruch nimmt).
library("doFuture") #--threshold--train--------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y registerDoFuture() cl <- makeCluster(4) plan(cluster, workers = cl) while (k <= 4) { # group foreach(i = 1:4, .combine = "cbind") %dopar% {# type foreach(j = 1:500, .combine = "c") %do% { GetThreshold(predX1[[k]]$pred$InputTrain[ ,j], Ytest, type[i]) } } -> testX1[[k]]$Threshold dimnames(testX1[[k]]$Threshold) <- list(NULL,type) k <- k + 1 } stopCluster(cl) }, env)
Unter Verwendung der erhaltenen Schwellenwerte berechnen wir in allen Gruppen und Untermengen:
#--train-------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTrain[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTrainScore dimnames(testX1[[k]]$InputTrainScore)[[2]] <- type k <- k + 1 } }, env) #--test----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTestScore dimnames(testX1[[k]]$InputTestScore)[[2]] <- type k <- k + 1 } }, env) #--test1----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest1[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTest1Score dimnames(testX1[[k]]$InputTest1Score)[[2]] <- type k <- k + 1 } }, env)
Zu jeder Datengruppe haben wir Metriken von jedem der 500 neuronalen Netze des Ensembles mit vier verschiedenen Schwellenwerten in drei Teilmengen hinzugefügt.
Sehen wir, wie die Metriken in jeder Gruppe und Teilmenge verteilt sind. Das Skript wird für die Teilmenge repaired bereitgestellt. Es ist ähnlich für andere Gruppen, nur die Gruppennummer ändert sich. Aus Gründen der Übersichtlichkeit werden die Diagramme aller Gruppen in einem dargestellt.
# k <- 1L #origin k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
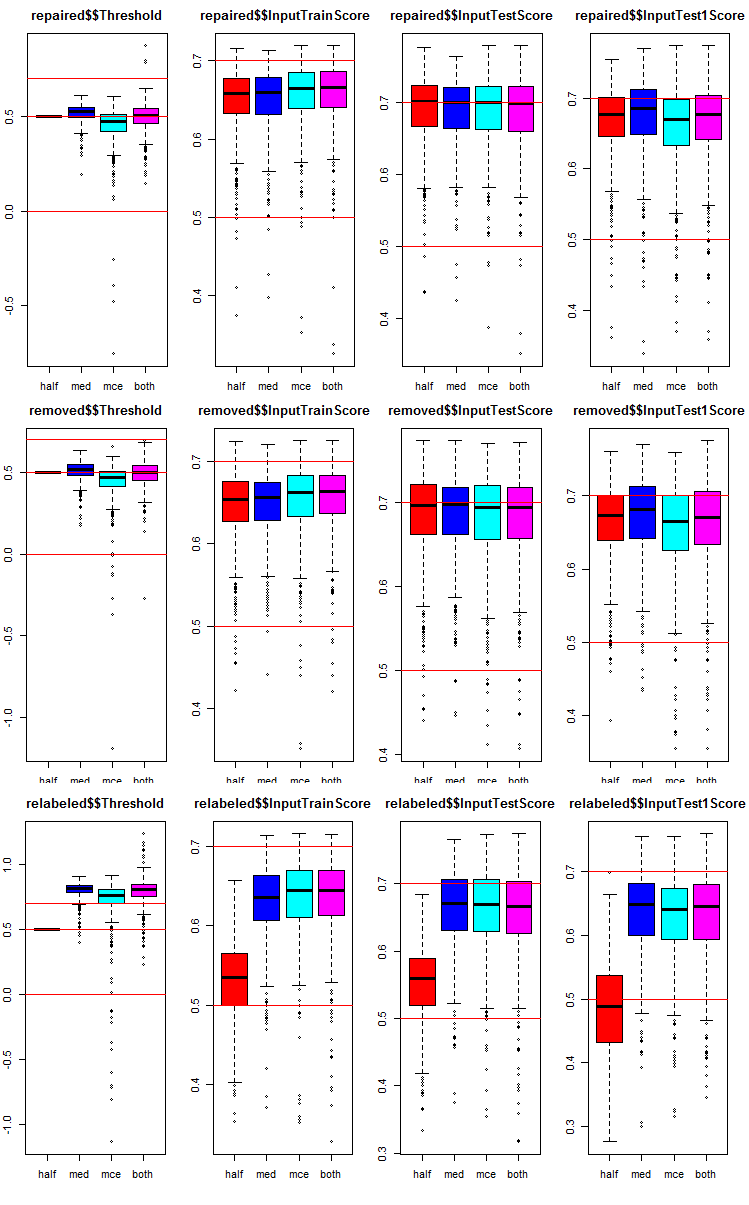
Abb. 8. Verteilungsgrafiken der Vorhersagemetriken der einzelnen neuronalen Netze des Ensembles in drei Datengruppen mit drei Teilmengen und vier verschiedenen Schwellenwerten.
Gemeinsam in allen Gruppen:
- Metriken der Untergruppe test (InputTestScore) sind viel besser als Metriken der Validierungsgruppe (InputTrainScore);
- Metriken der zweiten Untergruppe test (InputTest1Score) sind deutlich schlechter als Metriken der ersten Testsubgruppe;
- Schwellenwert vom Typ "half" zeigt in allen Teilmengen nicht schlechtere Ergebnisse als andere, mit Ausnahme von relabeled.
5. Testen der Ensembles
5.1. Bestimmung von 7 neuronalen Netzwerken mit den besten Metriken in jedem Ensemble und in jeder Datengruppe im InputTrain Teilmenge
Durchführung der Bereinigung (pruning). In jeder Datengruppe des testX1-Subsets ist es notwendig, 7 Werte von InputTrainScoremit den größten Werten des Mittelwerts F1 auszuwählen. Ihre Indizes werden die Indizes der besten neuronalen Netze im Ensemble sein. Das Skript ist unten angegeben und befindet sich auch in der Datei Test.R.
#--bestNN---------------------------------------- evalq({ nb <- 3L k <- 1L while (k <= 4) { foreach(j = 1:4, .combine = "cbind") %do% { testX1[[k]]$InputTrainScore[ ,j] %>% order(decreasing = TRUE) %>% head(2*nb + 1) } -> testX1[[k]]$bestNN dimnames(testX1[[k]]$bestNN) <- list(NULL, type) k <- k + 1 } }, env)
Wir erhielten Indizes der neuronalen Netze mit den besten Ergebnissen in vier Datengruppen (origin, repaired, removed, relabeled). Betrachten wir sie genauer und vergleichen wir, wie sehr sich diese besten neuronalen Netze je nach Datengruppe und Schwellentyp unterscheiden.
> env$testX1$origin$bestNN half med mce both [1,] 415 75 415 415 [2,] 191 190 220 220 [3,] 469 220 191 191 [4,] 220 469 469 469 [5,] 265 287 57 444 [6,] 393 227 393 57 [7,] 75 322 444 393 > env$testX1$repaired$bestNN half med mce both [1,] 393 393 154 154 [2,] 415 92 205 205 [3,] 205 154 220 220 [4,] 462 190 393 393 [5,] 435 392 287 287 [6,] 392 220 90 90 [7,] 265 287 415 415 > env$testX1$removed$bestNN half med mce both [1,] 283 130 283 283 [2,] 207 110 300 300 [3,] 308 308 110 110 [4,] 159 134 192 130 [5,] 382 207 207 192 [6,] 192 283 130 308 [7,] 130 114 134 207 env$testX1$relabeled$bestNN half med mce both [1,] 234 205 205 205 [2,] 69 287 469 469 [3,] 137 191 287 287 [4,] 269 57 191 191 [5,] 344 469 415 415 [6,] 164 75 444 444 [7,] 184 220 57 57
Man sieht, dass die Indizes neuronaler Netze mit den Schwellentypen "mce" und "both" sehr oft übereinstimmen.
5.2. Mittelung kontinuierlicher Vorhersagen dieser 7 besten neuronalen Netze.
Nach der Auswahl der 7 besten neuronalen Netze, berechnen wir diese in jeder Datengruppe, in Teilmengen InputTrain, InputTest, InputTest1 und nach jedem Schwellentyp. Skript zur Verarbeitung der InputTrain Teilmenge in 4 Gruppen:
#--Averaging--train------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTrain[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TrainYpred dimnames(testX1[[k]]$TrainYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Schauen wir uns die Struktur und die statistischen Zahlen der erhaltenen, gemittelten, kontinuierlichen Vorhersagen ind dr Datengruppe repaired:
> env$testX1$repaired$TrainYpred %>% str() num [1:1001, 1:4] 0.849 0.978 0.918 0.785 0.814 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "Y.aver_half" "Y.aver_med" "Y.aver_mce" "Y.aver_both" > env$testX1$repaired$TrainYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.2202 Min. :-0.4021 Min. :-0.4106 Min. :-0.4106 1st Qu.: 0.3348 1st Qu.: 0.3530 1st Qu.: 0.3512 1st Qu.: 0.3512 Median : 0.5323 Median : 0.5462 Median : 0.5462 Median : 0.5462 Mean : 0.5172 Mean : 0.5010 Mean : 0.5012 Mean : 0.5012 3rd Qu.: 0.7227 3rd Qu.: 0.7153 3rd Qu.: 0.7111 3rd Qu.: 0.7111 Max. : 1.1874 Max. : 1.0813 Max. : 1.1039 Max. : 1.1039
Die Statistik der letzten beiden Schwellenwerte ist auch hier identisch. HIer sind die Skripte für die beiden verbleibenden Untermengen InputTest, InputTest1:
#--Averaging--test------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TestYpred dimnames(testX1[[k]]$TestYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env) #--Averaging--test1------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest1[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$Test1Ypred dimnames(testX1[[k]]$Test1Ypred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Schauen wir uns die Statistik der Untermenge InputTest der Datengruppe repaired:
> env$testX1$repaired$TestYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.1524 Min. :-0.5055 Min. :-0.5044 Min. :-0.5044 1st Qu.: 0.2888 1st Qu.: 0.3276 1st Qu.: 0.3122 1st Qu.: 0.3122 Median : 0.5177 Median : 0.5231 Median : 0.5134 Median : 0.5134 Mean : 0.5114 Mean : 0.4976 Mean : 0.4946 Mean : 0.4946 3rd Qu.: 0.7466 3rd Qu.: 0.7116 3rd Qu.: 0.7149 3rd Qu.: 0.7149 Max. : 1.1978 Max. : 1.0428 Max. : 1.0722 Max. : 1.0722
Die Statistik der letzten beiden Schwellenwerttypen ist auch hier identisch.
5.3. Definition der Schwellenwerte für die gemittelten kontinuierlichen Vorhersagen
Jetzt haben wir die Vorhersagen für jedes Ensemble gemittelt. Sie müssen in Klassenlabels und die endgültigen Qualitätskennzahlen für alle Datengruppen und Schwellentypen umgewandelt werden. Um dies zu erreichen, bestimmen wir, ähnlich wie bei den vorherigen Berechnungen, die besten Schwellenwerte, indem wir nur die InputTrain-Subsets verwenden. Das untenstehende Skript berechnet die Schwellenwerte in jeder Gruppe und in jeder Teilmenge:
#-th_aver------------------------------ evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold GetThreshold(testX1[[k]]$TrainYpred[ ,j], Ytest, type[i]) } } -> testX1[[k]]$th_aver dimnames(testX1[[k]]$th_aver) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env)
5.4. Umwandlung der gemittelten kontinuierlichen Vorhersagen der Ensembles in Klassenbezeichnungen und Berechnung der Metriken der Ensembles auf den Teilmengen InputTrain, InputTest und InputTest1 aller Datengruppen.
Mit den oben berechneten th_aver Schwellenwerten bestimmen wir die Kennzahlen:
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TrainScore dimnames(testX1[[k]]$TrainScore) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest1, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TestScore dimnames(testX1[[k]]$TestScore) <- list(type, colnames(testX1[[k]]$TestYpred)) k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest2, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$Test1Score dimnames(testX1[[k]]$Test1Score) <- list(type, colnames(testX1[[k]]$Test1Ypred)) k <- k + 1 } }, env)
Erstellen wir eine Übersichtstabelle und analysieren die erhaltenen Kennzahlen. Beginnen wir mit der Gruppe origin (ihre Rauschproben wurden in keiner Weise verarbeitet). Wir suchen die Ergebnisse TestScore und Test1Score. Die Ergebnisse der Untermengen TestTrain sind indikativ, sie werden zum Vergleich mit den Testergebnissen benötigt:
> env$testX1$origin$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.711 0.708 0.712 0.712 med 0.711 0.713 0.707 0.707 mce 0.712 0.704 0.717 0.717 both 0.711 0.706 0.717 0.717 > env$testX1$origin$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.750 0.738 0.745 0.745 med 0.748 0.742 0.746 0.746 mce 0.742 0.720 0.747 0.747 both 0.748 0.730 0.747 0.747 > env$testX1$origin$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.735 0.732 0.716 0.716 med 0.733 0.753 0.745 0.745 mce 0.735 0.717 0.716 0.716 both 0.733 0.750 0.716 0.716
Was zeigt die vorgeschlagene Tabelle?
Das beste Ergebnis von 0,750 in TestScore zeigte die Variante mit dem Schwellenwert "half" in beiden Transformationen (sowohl beim Beschneiden als auch bei der Mittelung). Die Qualität sinkt jedoch auf 0,735 in der Untermenge Test1Score.
Ein stabileres Ergebnis von ~0,745 in beiden Teilmengen zeigen die Schwellenvarianten (med, mce, both) beim Bereinigen und med bei der Mittelwertbildung.
Siehe nächste Datengruppe - repaired (mit der korrigierten Kennzeichnung der Rauschproben):
> env$testX1$repaired$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.711 0.717 0.717 med 0.709 0.709 0.713 0.713 mce 0.728 0.714 0.709 0.709 both 0.728 0.711 0.717 0.717 > env$testX1$repaired$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.759 0.761 0.756 0.756 med 0.754 0.748 0.747 0.747 mce 0.758 0.755 0.743 0.743 both 0.758 0.732 0.754 0.754 > env$testX1$repaired$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.744 0.724 0.724 med 0.738 0.748 0.744 0.744 mce 0.697 0.720 0.677 0.677 both 0.697 0.743 0.731 0.731
Das beste in der Tabelle angezeigte Ergebnis ist 0,759 in der Kombination half/half. Ein stabileres Ergebnis von ~0,750 in beiden Untermengen zeigen die Schwellenvarianten (halb, med, mce, both) beim Bereinigen und med bei der Mittelwertbildung.
Siehe nächste Datengruppe - removed (wobei die Rauschproben aus dem Set entfernt wurden):
> env$testX1$removed$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.720 0.724 0.718 med 0.715 0.717 0.715 0.717 mce 0.721 0.722 0.725 0.723 both 0.721 0.720 0.725 0.723 > env$testX1$removed$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.761 0.769 0.761 0.751 med 0.752 0.749 0.760 0.752 mce 0.749 0.755 0.753 0.737 both 0.749 0.736 0.753 0.760 > env$testX1$removed$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.712 0.732 0.716 0.720 med 0.729 0.748 0.740 0.736 mce 0.685 0.724 0.721 0.685 both 0.685 0.755 0.721 0.733
Analysieren wir die Tabelle. Das beste Ergebnis von 0,769 in TestScore zeigte die Variante mit den Schwellenwerten med/half. Die Qualität sinkt jedoch auf 0,732 in der Teilmenge Test1Score. Für die Teilmenge TestScore ergibt die beste Kombination von Schwellenwerten beim Bereinigen (halb, med, mce, both) und half, wenn die Mittelung die besten Werte aller Gruppen ergibt.
Siehe die letzte Datengruppe - relabeled (mit den Rauschproben isoliert zu einer separaten Klasse):
> env$testX1$relabeled$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.672 0.559 0.529 0.529 med 0.715 0.715 0.711 0.711 mce 0.712 0.715 0.717 0.717 both 0.710 0.718 0.720 0.720 > env$testX1$relabeled$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.572 0.555 0.555 med 0.736 0.748 0.746 0.746 mce 0.739 0.747 0.745 0.745 both 0.710 0.756 0.754 0.754 > env$testX1$relabeled$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.664 0.498 0.466 0.466 med 0.721 0.748 0.740 0.740 mce 0.739 0.732 0.716 0.716 both 0.734 0.737 0.735 0.735
Die besten Ergebnisse für diese Gruppe werden durch die folgende Kombination von Schwellenwerten erzielt: (med, mce, both) beim Bereinigen und beides oder med bei der Mittelung.
Denken wir daran, dass man andere Werte als meine bekommen kann.
Die folgende Abbildung zeigt die Datenstruktur von testX1 nach allen oben genannten Berechnungen:
Abb. 9. Die Datenstruktur von testX1.
6. Optimieren der Hyperparameter von Ensembles von Klassifikatoren von Neuronalen Netzen
Alle bisherigen Berechnungen wurden an Ensembles mit den gleichen Hyperparametern neuronaler Netze durchgeführt, die auf persönlichen Erfahrungen basieren. Wie man weiß, müssen die Hyperparameter neuronaler Netze, wie auch andere Modelle, für einen bestimmten Datensatz optimiert werden, um bessere Ergebnisse zu erzielen. Für das Training verwenden wir die Daten nach der Rauschminderung, die in 4 Gruppen unterteilt sind (origin, repaired, removed und relabeled). Daher ist es notwendig, optimale Hyperparameter der neuronalen Netze des Ensembles genau für diese Mengen zu erhalten. Alle Fragen zur Bayes'schen Optimierung wurden im vorherigen Artikel ausführlich diskutiert, so dass ihre Details hier nicht weiter besprochen werden.
4 Hyperparameter neuronaler Netze werden optimiert:
- Die Anzahl der Prädiktoren - numFeature = c(3L, 13L) im Bereich von 3 bis 13;
- Der Prozentsatz der in der Ausbildung verwendeten Proben - r = c(1L, 10L) im Bereich von 10 % bis 100 %;
- Die Anzahl der Neuronen in der verborgenen Schicht - nh = c(1L, 51L) im Bereich von 1 bis 51;
- Typ der Aktivierungsfunktion - fact = c(1L, 10L) Index in der Liste der Aktivierungsfunktionen Fact.
Setzten der Konstanten:
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L) ) }, env)
Wir schreiben eine Fitnessfunktion, die den Qualitätsindikator Score = meаn(F1) und die Vorhersage des Ensembles in Klassenlabels zurückgibt. Die Bereinigung (Auswahl der besten neuronalen Netze im Ensemble) und die Mittelung der kontinuierlichen Vorhersage erfolgt mit dem gleichen Schwellenwert = 0,5. Es erwies sich früher als eine sehr gute Option - zumindest für die erste Annäherung. Hier ist das Skript:
#---Fitnes -FUN----------- evalq({ n <- 500 numEns <- 3 # SEED <- c(12345, 1235809) fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) k <- 1 rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Die auskommentierte SEED-Variable hat zwei Werte. Dies ist notwendig, um die Auswirkungen dieses Parameters auf das Ergebnis experimentell zu überprüfen. Ich habe die Optimierung mit den gleichen Anfangsdaten und Parametern durchgeführt, aber mit zwei verschiedenen Werten von SEED. Das beste Ergebnis wurde mit SEED = 1235809 erzielt. Dieser Wert wird in den folgenden Skripten verwendet. Aber die erhaltenen Hyperparameter und Klassifizierungsqualitätswerte werden für beide Werte von SEED bereitgestellt. Jeder kann mit anderen Werten experimentieren.
Überprüfen wir, ob die Fitnessfunktion funktioniert, wie lange ein Durchlauf ihrer Berechnungen dauert und das Ergebnis sehen:
evalq({
Ytrain <- X1$pretrain$y
Ytest <- X1$train$y
Ytest1 <- X1$test$y
Xtrain <- X1$pretrain$x
Xtest <- X1$train$x
Xtest1 <- X1$test$x
orderX <- orderX1
SEED <- 1235809
system.time(
res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
)
}, env)
user system elapsed
5.89 0.00 5.99
env$res$Score
[1] 0.741
Nachfolgend ist das Skript zur Optimierung der Hyperparameter neuronaler Netze nacheinander für jede Gruppe von Rauschunterdrückungen. Wir verwenden 20 Punkte der anfänglichen zufälligen Initialisierung und 20 nachfolgende Iterationen.
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100, control = c(100, 50, 8)) } -> OPT_Res1 group <- qc(origin, repaired, removed, relabeled) names(OPT_Res1) <- group }, env)
Sobald man mit der Ausführung des Skripts beginnt, muss man sich etwa eine halbe Stunde gedulden (je nach Hardware). Wir sortieren die erhaltenen Werte in absteigender Reihenfolge und wählen die drei besten aus. Diese Werte werden den Variablen best.res (für SEED = 12345) und best.res1 (für SEED = 1235809) zugeordnet.
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res
names(best.res) <- group
}, env)
evalq({
foreach(i = 1:4) %do% {
OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res1
names(best.res1) <- group
}, env)
Hier die Werte von best.res
env$best.res # $origin # Round numFeature r nh fact Value # 1 39 10 7 20 2 0.769 # 2 12 6 4 38 2 0.766 # 3 38 4 3 15 2 0.766 # # $repaired # Round numFeature r nh fact Value # 1 5 10 5 20 7 0.767 # 2 7 5 2 36 9 0.766 # 3 28 5 10 6 8 0.766 # # $removed # Round numFeature r nh fact Value # 1 1 11 6 44 9 0.764 # 2 8 8 6 26 7 0.764 # 3 19 12 1 40 5 0.763 # # $relabeled # Round numFeature r nh fact Value # 1 24 9 10 1 10 0.746 # 2 7 9 9 2 8 0.745 # 3 32 4 1 1 10 0.738
Das Gleiche für die Werte von best.res1:
> env$best.res1 $origin Round numFeature r nh fact Value 1 19 8 3 41 2 0.777 2 32 8 1 33 2 0.777 3 23 6 1 35 1 0.770 $repaired Round numFeature r nh fact Value 1 26 9 4 17 3 0.772 2 33 11 9 30 9 0.771 3 38 5 4 17 2 0.770 $removed Round numFeature r nh fact Value 1 30 5 4 17 2 0.770 2 8 8 2 13 6 0.769 3 32 5 3 22 7 0.766 $relabeled Round numFeature r nh fact Value 1 34 12 5 8 9 0.777 2 33 9 5 4 9 0.763 3 36 12 7 4 9 0.760
Wie man erkennen kann, sehen diese Ergebnisse besser aus. Zum Vergleich: Wir können nicht die ersten drei Ergebnisse drucken, sondern zehn: Die Unterschiede werden noch deutlicher sichtbar.
Jeder Optimierungslauf erzeugt unterschiedliche Hyperparameterwerte und Ergebnisse. Die Hyperparameter können durch verschiedene RNG-Einstellungen sowie durch eine spezifische Start-Initialisierung optimiert werden.
Sammeln wir die besten Hyperparameter der neuronalen Netze der Ensembles für 4 Datengruppen. Sie werden später benötigt, um Ensembles mit optimalen Hyperparametern zu bilden.
#---best.param-------------------
evalq({
foreach(i = 1:4, .combine = "rbind") %do% {
OPT_Res1[[i]]$Best_Par %>% unname()
} -> best.par1
dimnames(best.par1) <- list(group, qc(numFeature, r, nh, fact))
}, env)
The hyperparameters:
> env$best.par1 numFeature r nh fact origin 8 3 41 2 repaired 9 4 17 3 removed 5 4 17 2 relabeled 12 5 8 9
Alle Skripte dieses Skripte befinden sich in der Datei Optim_VIII.R.
7. Optimierung der Hyperparameter der Nachbearbeitung (Schwellenwerte für die Bereinigung und Mittelung)
Die Optimierung der Hyperparameter der neuronalen Netze führt zu einer leichten Erhöhung der Klassifizierungsqualität. Wie bereits erwähnt, hat die Kombination von Schwellentypen beim Bereinigen und Mitteln einen stärkeren Einfluss auf die Klassifizierungsqualität.
Wir haben die Hyperparameter bereits mit einer konstanten Kombination von Schwellenwerten half/half optimiert. Vielleicht ist diese Kombination nicht optimal. Wiederholen wir die Optimierung mit zwei zusätzlichen optimierten Parametern th1 = c(1L, 2L)) - Schwellentyp beim Beschneiden des Ensembles (Auswahl der besten neuronalen Netze) - und th2 = c(1L, 4L) - Schwellentyp beim Umwandeln der gemittelten Vorhersage des Ensembles in Klassenbezeichnungen. Definieren wir die Konstanten und die Wertebereiche der zu optimierenden Hyperparameter.
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds_m <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L), th1 = c(1L, 2L), th2 = c(1L, 4L) ) }, env)
Nun zur Fitnessfunktion. Es wurde leicht modifiziert: zwei Parameter, th1, th2 wurden hinzugefügt. Wir berechnen im Funktionskörper und im 'best' Block den Schwellenwert in Abhängigkeit von th1. Im Block "Testdurchschnitt" bestimmen wir den Schwellenwert mit der Funktion GetThreshold() in Abhängigkeit vom Schwellentyp th2.
#---Fitnes -FUN----------- evalq({ n <- 500L numEns <- 3L # SEED <- c(12345, 1235809) fitnes_m <- function(numFeature, r, nh, fact, th1, th2){ bestF <- orderX %>% head(numFeature) k <- 1L rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- ifelse(th1 == 1L, 0.5, median(y.pr)) -> th foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > th, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred th <- GetThreshold(ensPred, Yts$Ytest1, type[th2]) ifelse(ensPred > th, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Prüfen wir wie viel Zeit ein Iteration dieser Funktion benötigt und ob sie arbeitet:
#---res fitnes------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Xtrain <- X1$pretrain$x Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 th1 <- 1 th2 <- 4 system.time( res_m <- fitnes_m(numFeature = 10, r = 7, nh = 5, fact = 2, th1, th2) ) }, env) user system elapsed 6.13 0.04 6.32 > env$res_m$Score [1] 0.748
Die Ausführungszeit der Funktion hat sich deutlich geändert. Danach starten wit die Optimierung und warten auf das Ergebnis:
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res1 <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes_m, bounds = bonds_m, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100) #, control = c(100, 50, 8)) } -> OPT_Res_m group <- qc(origin, repaired, removed, relabeled) names(OPT_Res_m) <- group }, env)
Die Auswahl der besten 10 erhaltenen Hyperparameter für jede Datengruppe:
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res_m[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(10)
} -> best.res_m
names(best.res_m) <- group
}, env)
$origin
Round numFeature r nh fact th1 th2 Value
1 19 8 3 41 2 2 4 0.778
2 25 6 8 51 8 2 4 0.778
3 39 9 1 22 1 2 4 0.777
4 32 8 1 21 2 2 4 0.772
5 10 6 5 32 3 1 3 0.769
6 22 7 2 30 9 1 4 0.769
7 28 6 10 25 5 1 4 0.769
8 30 7 9 33 2 2 4 0.768
9 40 9 2 48 10 2 4 0.768
10 23 9 1 2 10 2 4 0.767
$repaired
Round numFeature r nh fact th1 th2 Value
1 39 7 8 39 8 1 4 0.782
2 2 5 8 50 3 2 3 0.775
3 3 12 6 7 8 1 1 0.769
4 24 5 10 45 5 2 3 0.769
5 10 7 8 40 2 1 4 0.768
6 13 5 8 40 2 2 4 0.768
7 9 6 9 13 2 2 3 0.766
8 19 5 7 46 6 2 1 0.765
9 40 9 8 50 6 1 4 0.764
10 20 9 3 28 9 1 3 0.763
$removed
Round numFeature r nh fact th1 th2 Value
1 40 7 2 39 8 1 3 0.786
2 13 5 3 48 3 2 3 0.776
3 8 5 6 18 1 1 1 0.772
4 5 5 10 24 3 1 3 0.771
5 29 13 7 1 1 1 4 0.771
6 9 7 3 25 7 1 4 0.770
7 17 9 2 17 1 1 4 0.770
8 19 7 7 25 2 1 3 0.768
9 4 10 6 19 7 1 3 0.765
10 2 4 4 47 7 2 3 0.764
$relabeled
Round numFeature r nh fact th1 th2 Value
1 7 8 1 13 1 2 4 0.778
2 26 8 1 19 6 2 4 0.768
3 3 6 3 45 4 2 2 0.766
4 20 6 2 40 10 2 2 0.766
5 13 4 3 18 2 2 3 0.762
6 10 10 6 4 8 1 3 0.761
7 31 11 10 16 1 2 4 0.760
8 15 13 7 7 1 2 3 0.759
9 5 7 3 20 2 1 4 0.758
10 9 9 3 22 8 2 3 0.758
Es gibt eine kleine Verbesserung der Qualität. Die besten Hyperparameter für jede Datengruppe unterscheiden sich stark von den Hyperparametern, die bei der vorherigen Optimierung erhalten wurden, ohne Berücksichtigung der unterschiedlichen Kombination von Schwellenwerten. Die beste Qualität der Ergebnisse wird durch Datengruppen von Rauschproben mit neuer Kennzeichnung (repaired) und den entfernten ( removed) erreicht.
#---best.param------------------- evalq({ foreach(i = 1:4, .combine = "rbind") %do% { OPT_Res_m[[i]]$Best_Par %>% unname() } -> best.par_m dimnames(best.par_m) <- list(group, qc(numFeature, r, nh, fact, th1, th2)) }, env) # > env$best.par_m------------------------ # numFeature r nh fact th1 th2 # origin 8 3 41 2 2 4 # repaired 7 8 39 8 1 4 # removed 7 2 39 8 1 3 # relabeled 8 1 13 1 2 4
Die verwendeten Skripte dieses Teils befinden sich in der Datei Optim_mVIII.R.
8. Kombinieren der besten Ensembles zum Superensemble inklusive deren Ausgaben
Wir kombinieren mehrere beste Ensembles zu einem Superensemble, und deren Ergebnisse werden mit einfacher Mehrheit kaskadiert.
Zuerst kombinieren wir die Ergebnisse mehrerer bester Ensembles, die während der Optimierung erhalten wurden. Nach der Optimierung gibt die Funktion nicht nur die besten Hyperparameter zurück, sondern auch die Historie der Vorhersagen in Klassenlabels bei allen Iterationen. Wir erzeugen ein Superensemble aus den 5 besten Ensembles jeder Datengruppe und überprüfen mit einfacher Mehrheit, ob sich die Klassifizierungsqualität in dieser Variante verbessert.
Die Berechnungen werden in der folgenden Reihenfolge durchgeführt:
- Sequentiell über 4 Datengruppen in einer Schleife iterieren;
- Bestimmen der Indizes der 5 besten Vorhersagen in jeder Datengruppe;
- Die Vorhersagen mit diesen Indizes zu einem Datenrahmen zusammenfassen;
- Die Klassenbezeichnung in allen Vorhersagen von "0" auf "-1" ändern;
- Summe dieser Vorhersagen Zeile für Zeile;
- Umwandeln dieser summierten Werte gemäß der Bedingung in Klassenbeschriftungen (-1, 0, 1): wenn der Wert größer als 3 ist, dann Klasse = 1; wenn kleiner als -3, dann Klasse = -1; ansonsten Klasse = 0
Hier ist das Skript, das diese Berechnungen durchführt:
#--Index-best-------------------
evalq({
prVot <- vector("list", 4)
foreach(i = 1:4) %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(.) ifelse(. == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x)) ->.;
ifelse(. > 3, 1, ifelse(. < -3, -1, 0))
} -> prVot
names(prVot) <- group
}, env)
Wir haben eine zusätzliche dritte Klasse "0". Wenn "-1", ist es "Verkaufen", "1" ist "Kaufen" und "0" ist "nicht sicher". Wie der Expert Advisor auf dieses Signal reagiert, liegt in der Verantwortung des Benutzers. Er kann sich vom Markt fernhalten, oder er kann auf dem Markt sein und nichts tun und auf ein neues Signal zum Handeln warten. Die Verhaltensmodelle sollten beim Testen des Experten erstellt und überprüft werden.
Um die Metriken zu erhalten, ist es notwendig:
- Sequentiell über jede Datengruppe in einer Schleife iterieren;
- Im Istwert des Ziels Ytest1, das Klassenlabel "0" durch das Label "-1" ersetzen;
- Das oben erhaltene tatsächliche und vorhergesagte Ziel PRVot in einem Datenrahmen kombinieren;
- Entfernen der Zeilen mit dem Wert von prVot = 0 aus dem Datenrahmen;
- Berechnen der Metrik.
Berechnen wir das Ergebnis und sehen es uns an.
evalq({
foreach(i = 1:4) %do% { #group
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = prVot[[i]]) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred)
} -> Score
names(Score) <- group
}, env)
env$Score
$origin
$origin$metrics
Accuracy Precision Recall F1
-1 0.806 0.809 0.762 0.785
1 0.806 0.804 0.845 0.824
$origin$confMatr
Confusion Matrix und Statistik
predicted
actual -1 1
-1 157 49
1 37 201
Accuracy : 0.8063
95% CI : (0.7664, 0.842)
No Information Rate : 0.5631
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6091
Mcnemar's Test P-Value : 0.2356
Sensitivity : 0.8093
Specificity : 0.8040
Pos Pred Value : 0.7621
Neg Pred Value : 0.8445
Prevalence : 0.4369
Detection Rate : 0.3536
Detection Prevalence : 0.4640
Balanced Accuracy : 0.8066
'Positive' Class : -1
$repaired
$repaired$metrics
Accuracy Precision Recall F1
-1 0.82 0.826 0.770 0.797
1 0.82 0.816 0.863 0.839
$repaired$confMatr
Confusion Matrix und Statistik
predicted
actual -1 1
-1 147 44
1 31 195
Accuracy : 0.8201
95% CI : (0.7798, 0.8558)
No Information Rate : 0.5731
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6358
Mcnemar's Test P-Value : 0.1659
Sensitivity : 0.8258
Specificity : 0.8159
Pos Pred Value : 0.7696
Neg Pred Value : 0.8628
Prevalence : 0.4269
Detection Rate : 0.3525
Detection Prevalence : 0.4580
Balanced Accuracy : 0.8209
'Positive' Class : -1
$removed
$removed$metrics
Accuracy Precision Recall F1
-1 0.819 0.843 0.740 0.788
1 0.819 0.802 0.885 0.841
$removed$confMatr
Confusion Matrix und Statistik
predicted
actual -1 1
-1 145 51
1 27 207
Accuracy : 0.8186
95% CI : (0.7789, 0.8539)
No Information Rate : 0.6
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.6307
Mcnemar's Test P-Value : 0.009208
Sensitivity : 0.8430
Specificity : 0.8023
Pos Pred Value : 0.7398
Neg Pred Value : 0.8846
Prevalence : 0.4000
Detection Rate : 0.3372
Detection Prevalence : 0.4558
Balanced Accuracy : 0.8227
'Positive' Class : -1
$relabeled
$relabeled$metrics
Accuracy Precision Recall F1
-1 0.815 0.809 0.801 0.805
1 0.815 0.820 0.828 0.824
$relabeled$confMatr
Confusion Matrix und Statistik
predicted
actual -1 1
-1 157 39
1 37 178
Accuracy : 0.8151
95% CI : (0.7741, 0.8515)
No Information Rate : 0.528
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6292
Mcnemar's Test P-Value : 0.9087
Sensitivity : 0.8093
Specificity : 0.8203
Pos Pred Value : 0.8010
Neg Pred Value : 0.8279
Prevalence : 0.4720
Detection Rate : 0.3820
Detection Prevalence : 0.4769
Balanced Accuracy : 0.8148
'Positive' Class : -1
#---------------------------------------
Die Qualität hat sich in allen Gruppen deutlich verbessert. Die besten Ergebnisse von "Balanced Accuracy" wurden in den Gruppen removed (0.8227) und repaired (0.8209) erzielt.
Kombinieren wir die Prognosen der Gruppe auch mit einfacher Mehrheit. Führen wir die Kombination in Kaskade durch:
- Über alle Datengruppen in einer Schleife iterieren;
- Bestimmen der Indizes der Durchläufe mit den besten Ergebnissen;
- Auswählen der Vorhersagen für diese besten Durchläufe;
- Ersetzen in jeder Spalte das Klassenlabel "0" durch das Label "-1";
- Zeilenweise summieren der Vorhersagen in der Gruppe.
Sehen wir uns das erzielte Ergebnis an:
#--Index-best-------------------
evalq({
foreach(i = 1:4, .combine = "+") %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(x) ifelse(x == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x))
} -> prVotSum
}, env)
> env$prVotSum %>% table()
.
-20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 14 16 18 20
166 12 4 6 7 6 5 3 6 1 4 4 5 6 5 10 7 3 8 24 209
Belassen wir nur den größten Wert für die Abstimmung und Berechnung der Metrik:
evalq({
pred <- {prVotSum ->.;
ifelse(. > 18, 1, ifelse(. < -18, -1, 0))}
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = pred) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred) -> ScoreSum
}, env)
env$ScoreSum
> env$ScoreSum
$metrics
Accuracy Precision Recall F1
-1 0.835 0.849 0.792 0.820
1 0.835 0.823 0.873 0.847
$confMatr
Confusion Matrix und Statistik
predicted
actual -1 1
-1 141 37
1 25 172
Accuracy : 0.8347
95% CI : (0.7931, 0.8708)
No Information Rate : 0.5573
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6674
Mcnemar's Test P-Value : 0.1624
Sensitivity : 0.8494
Specificity : 0.8230
Pos Pred Value : 0.7921
Neg Pred Value : 0.8731
Prevalence : 0.4427
Detection Rate : 0.3760
Detection Prevalence : 0.4747
Balanced Accuracy : 0.8362
'Positive' Class : -1
Dies ergab eine sehr gute Bewertung der Balanced Accuracy = 0,8362.
Die in diesem Abschnitt beschriebenen Skripte befinden sich in der Datei Voting.R.
Aber wir dürfen eine Kleinigkeit nicht vergessen. Bei der Optimierung der Hyperparameter haben wir das Testset InputTest verwendet. Das bedeutet, dass wir mit dem nächsten Testset InputTest1 arbeiten können. Die Kombination der Ensembles beim Kaskadieren führt höchstwahrscheinlich zu dem gleichen positiven Effekt ohne Optimierung der Hyperparameter. Überprüfen wir die zuvor erhaltenen Durchschnittswerte.
Wir kombinieren die gemittelten Ergebnisse der in Abschnitt 5.2 erhaltenen Ensembles.
Wir wiederholen die in Abschnitt 5.4 beschriebenen Berechnungen mit einer Änderung. Bei der Konvertierung der kontinuierlichen gemittelten Vorhersage in Klassenbezeichnungen sind diese Bezeichnungen[-1, 0, 1]. Die Reihenfolge der Berechnung in jeder Teilmenge Train/Test/Test1:
- Sequentiell über 4 Datengruppen in einer Schleife iterieren;
- Durch 4 Arten der bereinigten Schwellenwerte;
- Durch 4 Arten der gemittelten Schwellenwerte;
- Umwandeln der kontinuierlich gemittelten Vorhersage des Ensembles in Klassenlabels[-1, 1];
- Diese summieren durch 4 Arten von gemittelten Schwellenwerte;
- Umbenennen der Summe mit neuen Kennzeichnungen[-1, 0, 1];
- Hinzufügen des erhaltenen Ergebnisses zur Struktur VotAver.
#---train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) VotAver <- vector("list", 4) names(VotAver) <- group while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Train.clVoting dimnames(VotAver[[k]]$Train.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test------------------------------ evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test.clVoting dimnames(VotAver[[k]]$Test.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test1------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test1.clVoting dimnames(VotAver[[k]]$Test1.clVoting) <- list(NULL, type) k <- k + 1 } }, env)
Sobald die neu benannten gemittelten Vorhersagen in Teilmengen und Gruppen bestimmt sind, berechnen wir deren Metriken. Reihenfolge der Berechnungen:
- Iterieren über die Gruppen in einer Schleife;
- Iterieren über 4 Arten der gemittelten Schwellenwerte;
- Umbenennen der die Klassenlables in der aktuellen Vorhersage von "0" auf "-1" ändern;
- Kombinieren der aktuellen und der umbenannten Vorhersage im Datenrahmen;
- Entfernen der Zeilen mit der Vorhersage gleich 0 aus dem Datenrahmen;
- Berechnen der Kennzahlen und hinzufügen zur Struktur VotAver.
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TrainScoreVot names(VotAver[[k]]$TrainScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest1 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TestScoreVot names(VotAver[[k]]$TestScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest2 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$Test1ScoreVot names(VotAver[[k]]$Test1ScoreVot) <- type k <- k + 1 } }, env)
Sammeln wir die Daten in lesbarer Form und schauen wir sie uns an:
#----TrainScoreVot-------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TrainScoreVot %>% unlist() %>% unname()
} -> TrainScoreVot
dimnames(TrainScoreVot) <- list(group, type)
}, env)
> env$TrainScoreVot
half med mce both
origin 0.738 0.750 0.742 0.752
repaired 0.741 0.743 0.741 0.741
removed 0.748 0.755 0.755 0.755
relabeled 0.717 0.741 0.740 0.758
#-----TestScoreVot----------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TestScoreVot %>% unlist() %>% unname()
} -> TestScoreVot
dimnames(TestScoreVot) <- list(group, type)
}, env)
> env$TestScoreVot
half med mce both
origin 0.774 0.789 0.797 0.804
repaired 0.777 0.788 0.778 0.778
removed 0.801 0.808 0.809 0.809
relabeled 0.773 0.789 0.802 0.816
#----Test1ScoreVot--------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$Test1ScoreVot %>% unlist() %>% unname()
} -> Test1ScoreVot
dimnames(Test1ScoreVot) <- list(group, type)
}, env)
> env$Test1ScoreVot
half med mce both
origin 0.737 0.757 0.757 0.755
repaired 0.756 0.743 0.754 0.754
removed 0.759 0.757 0.745 0.745
relabeled 0.734 0.705 0.697 0.713
Die besten Ergebnisse wurden mit der getesteten Untergruppe in der Datengruppe "removed" mit der Verarbeitung von Rauschproben erzielt.
Kombinieren wir die Ergebnisse in jeder Teilmenge jeder Datengruppe durch Typen der Mittelung.
#==Variant-2========================================== #--TrainScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Train.clVoting ->.; apply(., 1, function(x) sum(x)) ->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Train.clVotingSum ifelse(Ytest == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TrainScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--TestScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test.clVotingSum ifelse(Ytest1 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TestScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--Test1ScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test1.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test1.clVotingSum ifelse(Ytest2 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$Test1ScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env)
Sammeln wir die Ergebnisse in lesbarer Form.
evalq({
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TrainScoreVotSum %>% unlist() %>% unname()
} -> TrainScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TestScoreVotSum %>% unlist() %>% unname()
} -> TestScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$Test1ScoreVotSum %>% unlist() %>% unname()
} -> Test1ScoreVotSum
ScoreVotSum <- cbind(TrainScoreVotSum, TestScoreVotSum, Test1ScoreVotSum)
dimnames(ScoreVotSum ) <- list(group, qc(TrainScoreVotSum, TestScoreVotSum,
Test1ScoreVotSum))
}, env)
> env$ScoreVotSum
TrainScoreVotSum TestScoreVotSum Test1ScoreVotSum
origin 0.763 0.807 0.762
repaired 0.752 0.802 0.748
removed 0.761 0.810 0.765
relabeled 0.766 0.825 (!!) 0.711
Berücksichtigen wir die Ergebnisse des Testsets. Überraschenderweise hatte die Methode relabeled das beste Ergebnis. Die Ergebnisse in allen Gruppen sind viel besser als die in Abschnitt 5.4 erzielten. Das Verfahren zur Kombination der Ensemble-Ausgaben in Kaskade durch einfache Mehrheitsabstimmung führt zu einer Verbesserung der Klassifizierungsqualität (Genauigkeit) von 5% auf 7%.
Die Skripte aus diesem Abschnitt befinden sich in der Datei Voting_aver.R. Die Struktur der erhaltenen Daten ist in der folgenden Abbildung dargestellt:
Abb. 10. Die Datenstruktur von VotAver.
Das Bild unten bietet ein vereinfachtest Schema aller Berechnungen: Es zeigt die Entwicklungsschritte, die verwendeten Skripte und Datenstrukturen.
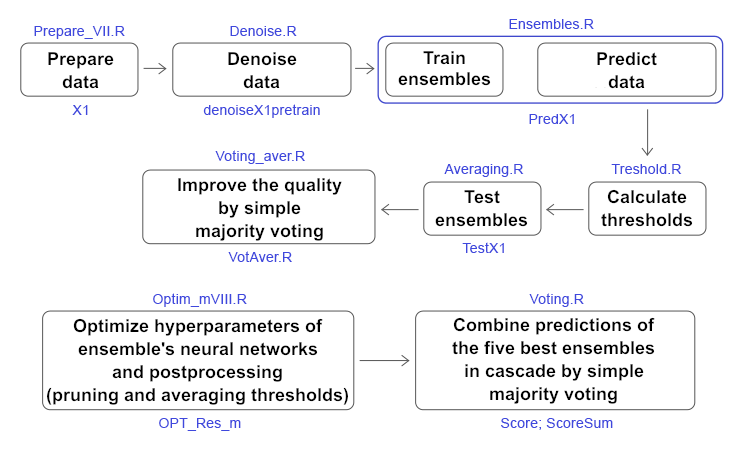
Abb. 11. Struktur und die Abfolge der wichtigsten Berechnungen in diesem Artikel.
8. Analyse der Versuchsergebnisse
Wir haben die Rauschproben aus den Anfangsdatensätzen in den Untermengen Pretrain (!) auf drei Arten verarbeitet:
- Die mit "erroneously" gekennzeichneten Daten neu zugeordnet, ohne die Anzahl der Klassen zu ändern (repaired);
- Die "Rauschproben" aus der Teilmenge entfernt (removed);
- Die "Rauschproben" in einer separaten Klasse isoliert (relabeled).
Vier Gruppen von Daten (origin, repaired, removed, relabeled) wurden in der Struktur denoiseX1pretrain erhalten. Verwenden wir sie, um das aus 500 neuronalen ELM-Netzwerkklassifikatoren bestehende Ensemble zu trainieren. Wir erhalten vier Ensembles. Wir berechnen die kontinuierlichen Vorhersagen von drei Teilmengen Х$train/test/test1 mit diesen 4 Ensembles und sammeln sie in der Struktur predX1.
Dann berechnen wir 4 Arten von Schwellenwerten für kontinuierliche Vorhersagen von jedem der 500 neuronalen Netze jedes Ensembles auf der Untergruppe InputTrain (!). Wir konvertieren anhand dieser Schwellenwerte die kontinuierlichen Vorhersagen in die Klassenlables (0, 1). Wir berechnen die Metriken (mean(F1)) für jedes neuronale Netzwerk der Ensembles und sammeln sie in der Struktur testX1$$$(InputTrainScore|InputTestScore|InputTestScore|InputTest1Score). Visualisierung der Verteilung der Metriken in 4 Datengruppen und 3 Teilmengen zeigt:
- Erstens sind die Metriken auf der ersten Testuntermenge in allen Gruppen höher als auf InputTrainS;
- Zweitens sind die Metriken in den Gruppen repaired und removed optisch höher als in zwei anderen.
Wählen wir nun die 7 besten neuronalen Netze mit den größten Werten von mean(F1) in jedem Ensemble aus und berechnen deren kontinuierliche Vorhersagen. Wir fügen deren Werte zur Struktur testX1$$$(TrainYpred|TestYpred|TestYpred|Test1Ypred) hinzu. Wir berechnen die Schwellenwerte th_aver auf der Teilmenge TrainYpred, bestimmen die Metriken aller gemittelten kontinuierlichen Vorhersagen und fügen sie der Struktur testX1$$$(TrainScore|TestScore|TestScore|Test1Score) hinzu. Jetzt können sie analysiert werden.
Mit einer unterschiedlichen Kombination der Bereinigungs- und Mittelwertschwellen in verschiedenen Datengruppen erhalten wir Kennzahlen im Bereich von 0,75 - 0,77. Das beste Ergebnis wurde in der Gruppe removed erzielt, wobei die "Rauschproben" entfernt wurden.
Die Optimierung der Hyperparameter der neuronalen Netze ermöglicht einen stabilen Anstieg der Kennzahlen um 0,77+ in allen Gruppen.
Die Optimierung der Hyperparameter der neuronalen Netze und die Schwellenwerte für die Nachbearbeitung (Beschneiden und Mitteln) liefern ein stabil hohes Ergebnis von etwa 0,78+ in allen Gruppen mit den verarbeiteten "Rausch"-Samples.
Wir erstellen ein Superensemble aus mehreren Ensembles mit den optimalen Hyperparametern, nehmen die Vorhersagen dieser Ensembles und kombinieren sie mit einfacher Mehrheit in jeder Datengruppe. Als Ergebnis erhalten wir die Metriken in den Gruppen repaired und removed im Bereich von 0,82+. Kombiniert man diese Vorhersagen der Superensembles auch mit einfacher Mehrheit, erhält man den Endwert von 0,836. So führt die Kombination der Vorhersagen in einer Kaskade mit einfacher Mehrheit zu einer Qualitätsverbesserung von 6-7%.
Überprüfen wir diese Aussage auf die gemittelten Vorhersagen des frühher erhaltenen Ensembles. Nachdem wir die Berechnungen und Konvertierungen in den Gruppen wiederholt haben, erhalten wir Metriken von 0,8+ in der Gruppe entfernt der Teilmenge Test. Wenn wir die Kombination in einer Kaskade fortsetzen, erhalten wir in der Untermenge Test in allen Datengruppen Kennzahlen mit Werten von 0,8+.
Es kann der Schluss gezogen werden, dass die Kombination der Ensemble-Vorhersagen in einer Kaskade durch einfache Abstimmung die Klassifizierungsqualität tatsächlich verbessert.
Schlussfolgerung
In diesem Artikel wurden drei Methoden zur Verbesserung der Qualität von Bagging-Ensembles betrachtet, sowie die Optimierung von Hyperparametern der neuronalen Netzwerke und der Nachbearbeitung des Ensembles. Basierend auf den Ergebnissen der Experimente können die folgenden Schlussfolgerungen gezogen werden:
- Die Verarbeitung der Rauschproben mit den Methoden repaired und removed verbessert die Klassifizierungsqualität von Ensembles erheblich;
- Die Wahl der Schwellenwertart für die Bereinigung und Mittelwertbildung sowie deren Kombination hat einen wesentlichen Einfluss auf die Klassifizierungsqualität;
- Die Kombination mehrerer Ensembles zu einem Superensemble mit ihren Vorhersagen, die in einer Kaskade mit einfacher Mehrheitsentscheidung kombiniert werden, ergibt die größte Steigerung der Klassifizierungsqualität;
- Die Optimierung der Hyperparameter der neuronalen Netze des Ensembles und der Nachbearbeitung verbessert leicht die Klassifizierungsqualität. Es ist ratsam, die erste Optimierung an neuen Daten durchzuführen und sie regelmäßig zu wiederholen, wenn die Qualität nachlässt. Die Periodizität wird experimentell bestimmt.
Anlagen
GitHub/PartVIII hält folgende Dateien bereit:
- Importar.R — Paket-Import Funktionen.
- Library.R — benötigte Bibliotheken.
- FunPrepareData_VII.R — Funktionen zur Vorbereitung der Anfangsdaten.
- FunStacking_VIII.R — Funktion für das Erstellen und Testen von Ensembles.
- Prepare_VIII.R — Funktionen und Skripte zur Vorbereitung der Anfangsdaten für trainierbare Kombinierer.
- Denoise.R — Skripte zur Verarbeitung von Rauschproben.
- Ensemles.R — Skripte zum Erstellen von Ensembles.
- Threshold.R — Skript zur Bestimmung von Schwellenwerte.
- Test.R — Skripte zum Testen von Ensembles.
- Averaging.R — Skripte zum Mitteln von kontinuierlichen Ausgaben von Ensembles.
- Voting_aver.R — Kombinieren gemittelter Ausgaben in einer Kaskade durch einfach Mehrheitsabstimmung.
- Optim_VIII.R — Skripte zum Optimieren der Hyperparameter von Neuronalen Netzen.
- Optim_mVIII.R — Skripte zum Optimieren der Hyperparameter von Neuronalen Netzen und der Nachbearbeitung.
- Voting.R — kombinieren der Ausgaben von Superensembles in einer Kaskade durch einfache Mehrheitsabstimmung.
- SessionInfo_VII.txt — Liste der in diesem Artikel verwendeten Pakete.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/4722
PairPlot basiert auf CGraphic dient der Analyse von Korrelationen zwischen Datenarrays (Zeitreihen)
50.000 ausgeführte Aufträge im Rahmen des Freelance-Service bei MQL5.com
Kombinieren der Strategien von Trend- und Seitwärtsbewegung
Entwicklung von Bestandsindikatoren mit Volumensteuerung am Beispiel des Delta-Indikators
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Обсуждение и вопросы по коду можно сделать в ветке
Удачи