
深度神经网络 (第 IV 部)。创建, 训练和测试神经网络模型
内容
概述
主要研究方向和应用
目前, 深度神经网络的研究与应用主要有两条。它们在隐藏层中初始化神经元权重的方法不同。
方法 1: 神经网络对于隐藏层中的神经元初始化方法非常敏感, 尤其是如果隐藏层的数量增加 (大于3)。G.Hynton 教授率先尝试解决这个问题。他的方法背后蕴含的思路是在隐藏层中始创神经元的权重, 而权重是在无监督训练由 RBM (受限玻耳兹曼机器) 或 AE (autoencoder) 构成的自动关联神经网络期间获得。这些堆叠的 RBM (SRBM) 和堆叠的 AE (SAE) 用大量未标记的数据进行训练。这种训练旨在突显数据中的隐藏结构 (表示, 图像) 和关系。在预训练中将 MLP 置于非常接近最优解的空间, 并用由此获得的 MLP 权重值初始化神经元。这能够减少标记数据的数量, 以及随后的 MLP 微调 (训练) 期间的世代数。在实际应用的许多领域这些都是极端重要的优势, 尤其是在处理大量数据时。
方法 2: 由 Yoshua Bengio 率领的另一批科学家创建了隐藏神经元初始化的具体方法, 具体的激活函数, 稳定和训练方法。这个方向的成功与深层卷积神经网络和复发神经网络 (DCNN, RNN) 的广泛发展有关。这种神经网络在图像识别, 从一种语言到另一种语言的口语翻译, 文字分析和分类方面表现出极高效率。开发这些神经网络的思路和方法也开始用于 MLP。
目前, 这两种方法的运用都很活跃。应该注意的是, 利用近乎相同的结果, 预训练神经网络需要较少的计算资源和少量的训练样本。这是一个重要的优点。我个人喜欢预训练深度神经网络。我相信未来属于无监督学习。
软件包 R 能够用来开发和使用 DNN
R 拥有众多的软件包, 可用于创建和使用具有不同复杂度和能力集合的 DNN。
软件包能够创建, 训练并测试预训练 DNN:
- deepnet 是一个简单的软件包, 没有很多设置和参数。可以创建预训练 SAE 神经网络和 SRBM 。 在之前的文章中, 我们研过使用此软件包实际实现智能系统。使用 RBM 进行预训练会产生较不稳定的结果。这个软件包适合首次遇到这一题材, 并学习这种网络的特性。使用正确的方法, 可以在智能系统中使用。RcppDL 是这个软件包的一个版本, 以 С++ 编写, 稍微短小。
- darch v.0.12 是一个复杂, 灵活的软件包, 拥有很多参数和设置。推荐设置为省缺设置。该软件包允许创建和设置任意复杂度和配置的神经网络。使用 SRBM 进行预训练。此软件包适合于高级用户。我们将稍后详细讨论其能力。
软件包在以下情况下无需预训练即可创建, 训练和测试 DNN:
- H2O 是 一个用于处理大型数据 (>1M 行和 >1K 列) 的软件包。其内使用的深度神经网络具有已开发的正则化系统。它的能力已超越我们的领域, 但这不应该阻止我们使用它。
- mxnet 不仅能够创建 MLP, 而且可以创建复杂的复发网络, 卷积和 LSTM 神经网络。该软件包具有多种语言的 API, 包括 R 和 Python。该软件包的理念与上面列出的那些不同。这是因为开发者主要为 Python 编写软件包。用于 R 的 mxnet 软件包比 Python 的软件包更轻量, 功能更少。但这不会令该软件包更糟。
深度和复发网络的题材在 Python 环境中得到了很好的开发。有许多有趣的软件包用于构建 R 中所没有的这种类型的神经网络。有些 R 软件包允许运行以 Python 编写的程序/模块:
- PythonInR 和 reticulate 是两个可以在 R 中运行任何 Python 代码的软件包。为此, 您需要在计算机上安装 Python 2/3。
- kerasr 是一个深度学习十分流行的 keras 函数库的 R 接口。
- tensorflow 是一个在 R 环境中提供访问完整 TensorFow API 的软件包。
最近, 微软发布了一个 cntk v.2.1 (计算网络工具包) GitHub 函数库。它可用作可比 Keras 的后端。建议针对我们的问题进行测试。
Yandex 正在保持前进 - 其内函数库 CatBoost 是以开源提供。该函数库可用于利用不同类型的数据训练模型。这包括难以表述的数据, 举例来说, 云类型和商品类型。源代码, 文档, 基准和必要的工具已经遵照 Apache 2.0 许可协议在 GitHub 上发布 。尽管事实上这些不是神经网络, 而只是提升了树林, 但建议测试其算法, 特别是那些包含来自 R 的 API。</ s3>
1. 软件包能力的简要说明
darch 版本的软件包。0.12.0 提供了广泛的功能, 不仅可以创建和训练模型, 还可以根据您的需求和喜好量身定做。在 以前的文章 中研究过的软件包版本 (0.10.0) 中已引入了重大变更。添加了新的激活, 初始化和稳定函数。最引人注目的新奇之处在于, 所有内容都被带入一个函数 darch(), 这是一个构造函数。支持图形卡。在训练之后, 该函数返回一个 DArch 类的对象。对象的结构如图例.1 所示。predict() 和 darchTest() 函数返回有关新数据或分类度量的预测。

图例.1. DArch 对象的结构
所有参数都有省缺值。这些值通常未经优化。所有这些参数可以分为三组 - 一般, 针对 RBM 以及针对 NN。我们稍后会详细研究一些细节。
| 函数 | 类型 |
|---|---|
| 初始化函数 |
|
| 激活函数 |
|
| 训练函数 |
|
| 训练等级 |
|
| 稳定函数 |
|
| 动量 |
|
| 停止条件 |
|
深度神经网络由连接到自动相关网络 (SRBM) 中的 n 个 RBM (n = 层-1), 且有多层的实际神经网络 MLP 组成。RBM 的逐层训练是对无标记数据的无监督训练。神经网络的微调需要监督, 并在标记数据上进行。
利用参数将这些训练阶段切分, 令我们有机会使用不同体量的数据 (不同的结构!!), 并基于一个预训练获得几个精细调整的模型。如果预训练和微调的数据相同, 则训练可以一次性进行, 而无需将其分为两个阶段。预训练可以跳过 (rbm.numEpochs = 0; darch.numEpochs = 10))。在这种情况下, 您只能使用多层神经网络或只训练 RBM ( rbm.numEpochs = 10; darch.numEpochs = 0)。您仍然可以访问所有内部参数。
经过训练的神经网络可以根据需要进一步在新数据基础上进行训练。只有有限数量的模型才有可能。由复杂受限 Boltzmann 机 (DNRBM) 初始化的深度神经网络的结构图显示在图例.2 中
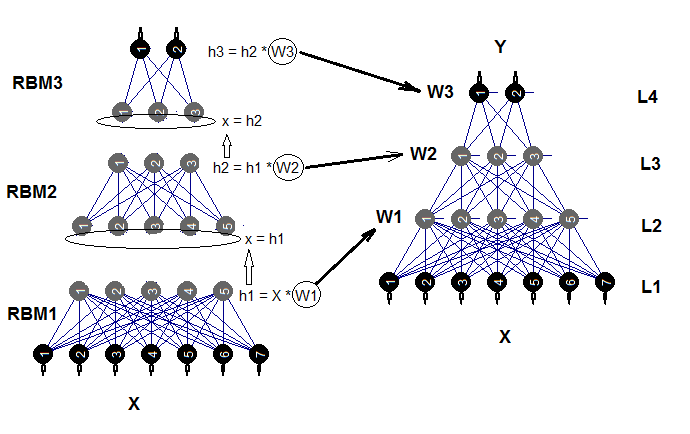
图例.2. DNSRBM 的结构图
1.1. 神经元的初始化函数
软件包中有两个主要的神经元初始化函数。
- generateWeightsUniform() 使用 runif(n, min, max) 函数, 且实现如下:
> generateWeightsUniform function (numUnits1, numUnits2, weights.min = getParameter(".weights.min", -0.1, ...), weights.max = getParameter(".weights.max", 0.1, ...), ...) { matrix(runif(numUnits1 * numUnits2, weights.min, weights.max), nrow = numUnits1, ncol = numUnits2) } <environment: namespace:darch>
numUnits1 是上一层神经元的数量, 而 numUnits2 是当前图层上的神经元数目。
- generateWeightsNormal() 使用 rnorm(n, mean, sd) 函数, 且在软件包中实现如下:
> generateWeightsNormal function (numUnits1, numUnits2, weights.mean = getParameter(".weights.mean", 0, ...), weights.sd = getParameter(".weights.sd", 0.01, ...), ...) { matrix(rnorm(numUnits1 * numUnits2, weights.mean, weights.sd), nrow = numUnits1, ncol = numUnits2) } <environment: namespace:darch>
其它四个函数正在使用这两个函数, 但使用特定函数定义 min, max, mean 和 sd。您在终端中输入无括号的函数名称, 即可学习它们。
1.2. 神经元的激活函数
除了标准的激活功能, 该软件包还推荐了广泛的新函数。这是它们当中的一些:
x <- seq(-5, 5, 0.1) par(mfrow = c(2,3)) plot(x, y = 1/(1 + exp(-x)), t = "l", main = "sigmoid") abline(v = 0, col = 2) plot(x, y = tanh(x), t = "l", main = "tanh") abline(v = 0, h = 0, col = 2) plot(x, y = log(1 + exp(x)), t = "l", main = "softplus"); abline(v = 0, col = 2) plot(x, y = ifelse(x > 0, x ,exp(x) - 1), t = "l", main = "ELU") abline(h = 0, v = 0, col = 2) plot(x, y = ifelse(x > 0, x , 0), t = "l", main = "ReLU") abline(h = 0, v = 0, col = 2) par(mfrow = c(1,1))
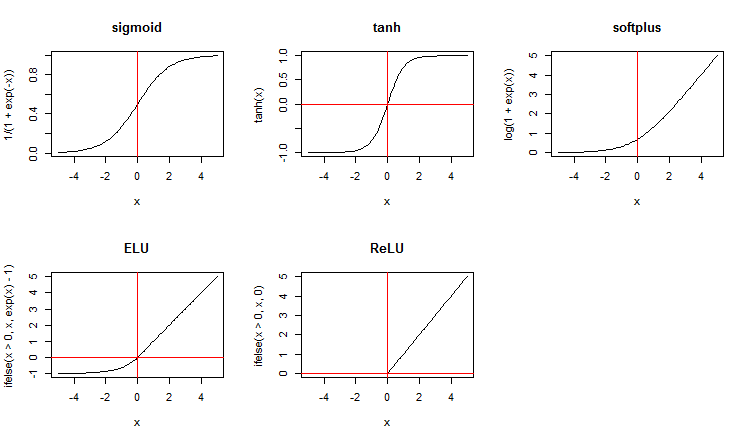
图例.3. 神经元的激活函数
我们来分别研究 maxout 激活函数。此函数来自于卷积网络。神经网络的隐藏层由 poolSize 的大小划分。隐藏层中的神经元数量必须由池的大小整除。对于训练, 从池中选择最大激活的神经元并将其发送到输入。池中神经元的激活函数分别设置。简单来说, 这是一个在过滤步骤中的能力受限的双层 (卷积 + 最大池化)。根据各种发表的言论, 它与 dropout 配合会产生优良结果。图例. 4. 示意性地展示拥有 8 个神经元和两个不同池大小的隐藏层
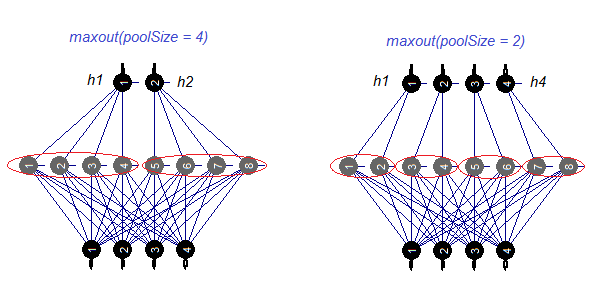
图例.4. maxout 激活函数
1.3. 训练方法
不幸地是, 在软件包里只有两个训练方法 - 基本版和改进版的 backpropagation 和 rprop , 在后向传播是带有/不带有权重更新。还有一种可能是借助 bp.learnRateScale. 乘数改变训练等级。
1.4. 调节和稳定方法
- dropout 是在训练期间隐藏层一部分神经元的退脱 (权重归零)。神经元按照随机顺序归零。要退脱的神经元相对数量由 darch.dropout 参数定义。每个隐藏层中的退脱级别可能不同。可以为每个批次或每个世代生成退脱掩码。
- dropconnect 正在关闭当前层一部分神经元与上一层神经元之间的连接。连接按照随机顺序切断。要切割的相对连接数量由相同的参数 darch.dropout 定义 (通常不大于 0.5)。根据一些发表言论, dropconnect 展示出比退脱更好的结果。
- dither 是防止输入数据抖动从而导致重复训练的一种方式。
- weightDecay 在更新之前, 每个神经元的权重将乘以 (1 — weightDecay) 。
- normalizeWeights 是将来自上述 (L2 范数) 的可能限制的神经元权重的输入向量常规化的一种方法
前三种方法只能单独使用。
1.5. 培训 RBM 的方法和参数
有两种训练 SRBM 的方式。在 rbm.numEpochs 期间, RBM 每次训练一遍, 或者每个 RBM 每次训练一个世代。由 rbm.consecutive: 参数选择这些方法之一。TRUE 或省缺值是第一种方法, FALSE 是第二种方法。图例.5 展示两种训练计划的变种。rbm.lastLayer 可以用来指定哪个层次的 SRBM 应该停止预训练。若为 0, 则要对所有层进行训练, 若为 (-1) 则上层保留不训练。这是有道理的, 因为上层必须分开训练, 且需要更长时间。其它参数不需要额外的解释。
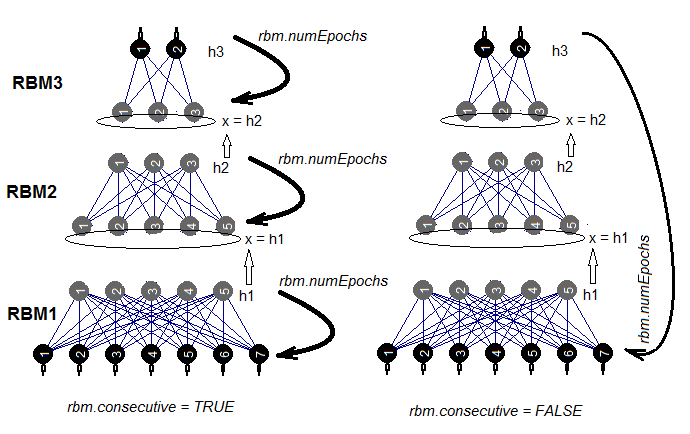
图例.5. 两种训练 SRBM 的方法
1.6. 训练 DNN 的方法和参数
DNN 可以通过两种方式进行训练 - 预训练和没有预训练。这些方法中使用的参数是完全不同的。例如, 在有 预训练 的训练中使用具体的初始化和正则化方法没有任何意义。事实上, 使用这些方法可能会使结果更糟。背后的原因是, 在预训练之后, 隐藏层中的神经元权重将被放置在接近最优值的区域, 且它们仅需微调。为了在没有预训练的训练中实现相同的结果, 将使用所有可用的初始化和正则化方法。通常, 这种训练神经网络方式需要更长的时间。
所以, 我们将重点关注带预训练的训练。通常, 它分两个阶段进行。
- 在一大批未标记的数据上训练 SRBM。预训练参数分别设置。因此, 我们有一个由 SRBM 权重始创的神经网络。 然后用自己的训练参数对具有标记数据的神经网络的上层进行训练。这样, 我们有一个已训练上层, 且低层已始创权重的神经网络。将其另存为独立对象供进一步使用。
- 在第二阶段, 我们将使用少量标记样本, 针对神经网络的所有层进行低等级和较少世代数量的训练。这是网络的微调。神经网络已得到训练。
分阶段预培训, 微调和进一步培训的可能性, 不仅为 DNN, 也为 DNN 委员会的训练创建算法提供了不可思议的灵活性。图例.6. 体现 DNN 和 DNN 委员会训练的几个变体。
- 变体 а: 在微调期间, 在每个 n 世代保存 DNN。这样我们将得到经不同程度训练的一些 DNN。后来, 这些神经网络中的每一个可以单独使用, 或作为委员会的一部分使用。这种情况的缺点是所有 DNN 都在相同的数据上训练, 因为它们都具有相同的训练参数。
- 变体 b: 使用不同数据集合 (滑动窗口, 成长窗口等) 和不同参数来并行微调已始创 DNN。结果就是, 我们将有一个 DNN, 其产生的相关预测比变体 a 的更少。
- 变体 c: 利用不同数据集合和参数 顺序 微调已始创 DNN。保存中间模型。这就是我们以前所说的进一步训练。每当有足够的新数据时, 可以执行此操作。
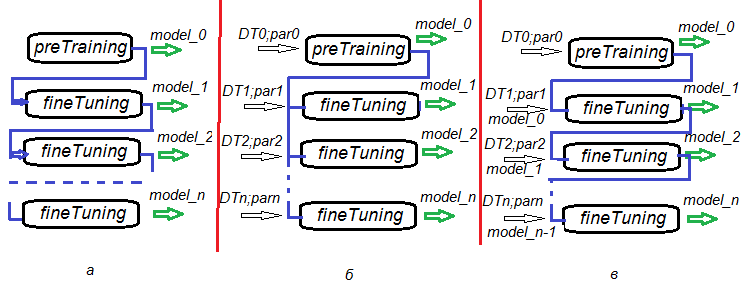
图例.6. 训练 DNN 的变体
2. 依据所使用的参数测试 DNN 的工作品质。
2.1. 实验
2.1.1. 输入数据 (准备)
我们将使用文章前一部分的数据和函数 (1, 2, 3)。在那里我们详细讨论了初步数据准备的各种变体。我将简要复述我们即将进行的初步准备阶段。OHLCV 是初始数据, 与以前一样。输入数据为数字滤波器, 输出数据为之字折线。可以使用函数和工作空间 Cotir.RData 的图像。
为执行而进行的准备数据阶段将在单独的函数中收集:
- PrepareData() — 创建初始数据集合并清理 NA;
- SplitData() — 将初始数据集合化分为预训练, 训练, 验证, 测试子集;
- CappingData() — 在所有子集中识别并插补异常值。
为了节省文章的篇幅, 我不会在此给出这些函数的列表。它们可以从 GitHub 下载, 因为在以前的文章中已经详细地研究过了。我们稍后会查看结果。我们不会在初步处理过程中讨论数据变换的所有方法。其中许多是众所周知的并被广泛使用。我们将使用一种较为不知名的方法, 即 离散化 (有监督和无监督)。在第二篇文章中, 我们研究了 两个有监督离散化软件包 (discretization 和 smbinning)。它们包含不同的离散算法。
我们将研究把连续变量分割为箱体的不同方法, 以及在模型中使用这些离散变量的方法。
什么是分箱?
分箱是用于建模评分的术语。它被称为机器学习中的离散化。这是将连续变量变换为有限数量的间隔 (箱体) 的过程。这有助于理解其分布以及与二进制目标变量的关系。在此过程中创建的箱体可成为模型中使用的预测特性的特征。
为什么要分箱?
尽管对分箱有一些保留, 但它具有显著的优势。
- 它允许将缺失数据 (NA) 和其它特殊计算 (举例如, 除以零) 包括在模型中。
- 它控制或减轻异常值对模型的影响。
- 它解决了预测因子中不同尺度的问题, 使最终模型中的权重系数相当。
无监督离散化
无监督离散化将连续函数分割为箱体, 而不考虑任何其它信息。分割有两种选择。它们是等长箱体和等频箱体。
| 选项 |
目标 |
示例 |
缺点 |
|---|---|---|---|
| 等长箱体 |
理解变量的分布 |
相同长度沙堡的经典直方图, 可以使用不同的规则 (sturges, rice ets) 计算 |
沙堡中的记录数量可能太小, 无法正确计算 |
| 等频箱体 |
使用诸如不良率指标来分析与二进制目标变量的关系 |
四分位数和百分位数 | 选定的截止点不能将依靠目标变量查证的箱体之间的差异最大化。 |
有监督离散化
有监督离散化将连续变量分割为投影到目标变量中的箱体。这里的关键在于找到能够最大限度地提高组间差异的截止点。
使用诸如 ChiMerge 或递归分区之类的算法, 分析人员可以在几秒内快速找到最优点, 并使用诸如证据权重 (WoE) 和信息值 (IV) 等指数来评估其与目标变量的关系。
WoE 可用作在有监督学习算法的预处理阶段变换预测变量的工具。在预测因子的离散化过程中, 我们可以用它们的新名义变量或者它们的 WoE 值代替它们。第二个变体很有趣, 因为它允许将名义变量 (factor) 变换成伪变量。这样可以显著提高分类质量。
WOE 和 IV 在数据分析中扮演了两个不同的角色:
- WOE 描述了预测因子与二进制目标变量的关系。
- IV 衡量这些关系的强度。
我们来厘清 WOE 和 IV 正在使用何种图表和公式。我们回想在 文章的第二部分 将 v.fatl 变量分成 10 等份的图表。
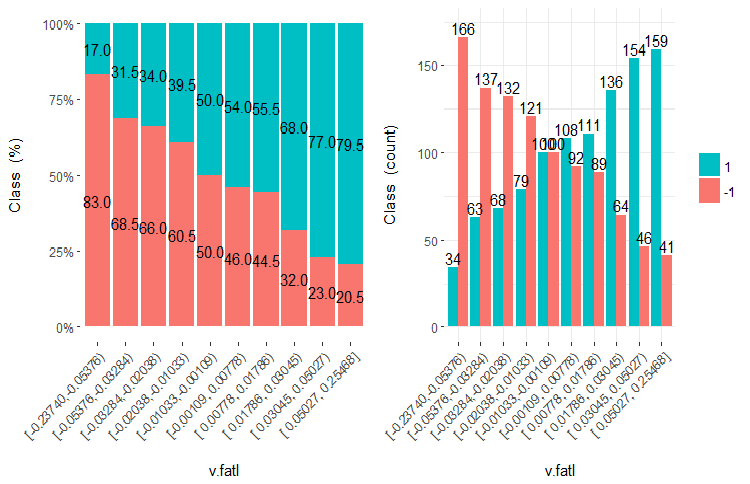
图例.7. v.fatal 变量分为 10 个相同频率的区域
数据预测能力 (WOE)
如您所见, 每个箱体都有进入类 "1" 和类 "-1" 的样本。WoEi 箱体的预测能力用公式计算
WoEi = ln(Gi/Bi)*100
其中:
Gi — 在变量的每个箱体中 "优良" 样本的相对频率 (在我们的例子中 "优良" = "1");
Bi — 在变量的每个箱体中 "不良" 样本的相对频率 (在我们的例子中 "不良" = "-1")。
如果 WoEi = 1, 这意味着该箱体中的 "优良" 和 "不良" 样本的数量大致相同, 那么该箱体的预测能力是 0。如果 "优良" 样本数量上超过 "不良", WOE >0, 反之亦然。
信息值 (IV)
这是识别变量意义和衡量 "优良" 和 "不良" 样本分布差异的最常用措施。信息值可以用公式计算:
IV = ∑ (Gi – Bi) ln (Gi/Bi)
变量的信息值等于变量所有箱体的总和。该系数的值可以解释如下:
- 低于 0,02 — 统计不显著的变量;
- 0,02 – 0,1 — 统计微弱的变量;
- 0,1 – 0,3 — 统计显著的变量;
- 0,3 及以上 — 统计强壮的变量。
然后, 使用各种算法和优化准则合并/划分箱体, 令这些箱体之间的差异尽可能大。例如, smbinning 软件包使用递归分区进行数值分类 并用信息值来制定最佳截止点。discretization 软件包利用 ChiMerge 和 MDL 解决了这个问题。应当记住, 截止点是在训练集合上获得, 并用于划分验证和测试集合。
有若干软件包允许以一种或其它方式将数字变量离散化。它们是 discretization, smbinning, Information, InformationValue 和 woebinning。我们需要将测试数据设置为离散的, 然后使用该信息划分验证和测试集合。我们也希望对结果进行直观控制。出于这些需求, 我选择了 woebinning 软件包。
该软件包自动分割 数值和因子, 并将其绑定到二进制目标变量。这里提供两种方法:
- 精细和粗略分类的实现逐次理顺粒度的类别和等级;
- 通过迭代经二进制切分得到的初始箱体按照树状方法分段。
两个进程依据 WOE 的相似值合并已分割箱体, 且基于 IV 准则停止。软件包可与独立变量或整体数据帧一起使用。这样就提供了灵活的工具, 用于研究进行分箱的各种解决方案以及在新数据上的扩展。
我们来进行计算。我们已从终端加载了报价到我们的工作环境 (或来自 GitHub 的工作环境 Cotir.RData 的图像)。计算顺序和结果:
- PrepareData() — 创建初始数据集合 dt[7906, 14], 将 NA 清除。该集合包括临时标签 Data, 输入变量 (12) 和目标变量 Class (两等级 "-1" 和 "+1" 的因子)。
- SplitData() — 将初始数据集合 dt[] 按照 2000/1000/500/500 的比率化为子集 pretrain, train, val, test, 将它们联组成数据帧 DT[4, 4000, 14]。
- CappingData() — 识别并插补所有子集中的异常值, 得到 DTcap[4, 4000, 14] 集合。尽管事实上离散化对于异常值是宽容的, 但我们将会插补它们。您可以无需这个阶段进行实验。正如您记忆的那样, 异常值 (pre.out) 的参数在预训练的子集中定义。使用这些参数处理训练/验证/测试集合。
- NormData() — 使用来自 caret 软件包的 spatialSing 方法常规化集合。类似于插补异常值, 常规化的参数 (preproc) 在预训练子集上定义。使用这些参数处理训练/验证/测试样品。我们已有了 DTcap.n[4, 4000, 14] 作为结果。
- DiscretizeData() — 定义离散化参数 (preCut), 变量品质和它们的箱体处于 WOE 和 IV 的辐射下。
evalq({
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DT <- SplitData(dt, 2000, 1000, 500,500)
pre.outl <- PreOutlier(DT$pretrain)
DTcap <- CappingData(DT, impute = T, fill = T, dither = F,
pre.outl = pre.outl)
preproc <- PreNorm(DTcap, meth = meth)
DTcap.n <- NormData(DTcap, preproc = preproc)
preCut <- PreDiscret(DTcap.n)
}, env)
我们将所有变量的离散化数据放入表格中, 并查看它们:
evalq(tabulate.binning <- woe.binning.table(preCut), env) > env$tabulate.binning $`WOE Table for v.fatl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.3904381926 154 7.7% 130 24 13.2% 2.4% 15.6% 171.3 0.185 2 <= -0.03713814085 769 38.5% 498 271 50.4% 26.8% 35.2% 63.2 0.149 3 <= 0.1130198981 308 15.4% 141 167 14.3% 16.5% 54.2% -14.5 0.003 4 <= Inf 769 38.5% 219 550 22.2% 54.3% 71.5% -89.7 0.289 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.626 $`WOE Table for ftlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.2344708291 462 23.1% 333 129 33.7% 12.7% 27.9% 97.2 0.204 2 <= -0.01368798447 461 23.1% 268 193 27.1% 19.1% 41.9% 35.2 0.028 3 <= 0.1789073635 461 23.1% 210 251 21.3% 24.8% 54.4% -15.4 0.005 4 <= Inf 616 30.8% 177 439 17.9% 43.4% 71.3% -88.4 0.225 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.463 $`WOE Table for rbci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1718377948 616 30.8% 421 195 42.6% 19.3% 31.7% 79.4 0.185 2 <= -0.09060410462 153 7.6% 86 67 8.7% 6.6% 43.8% 27.4 0.006 3 <= 0.3208178176 923 46.2% 391 532 39.6% 52.6% 57.6% -28.4 0.037 4 <= Inf 308 15.4% 90 218 9.1% 21.5% 70.8% -86.1 0.107 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.335 $`WOE Table for v.rbci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1837437563 616 30.8% 406 210 41.1% 20.8% 34.1% 68.3 0.139 2 <= 0.03581374495 461 23.1% 253 208 25.6% 20.6% 45.1% 22.0 0.011 3 <= 0.2503922644 461 23.1% 194 267 19.6% 26.4% 57.9% -29.5 0.020 4 <= Inf 462 23.1% 135 327 13.7% 32.3% 70.8% -86.1 0.161 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.331 $`WOE Table for v.satl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.01840058612 923 46.2% 585 338 59.2% 33.4% 36.6% 57.3 0.148 2 <= 0.3247097195 769 38.5% 316 453 32.0% 44.8% 58.9% -33.6 0.043 3 <= 0.4003869443 154 7.7% 32 122 3.2% 12.1% 79.2% -131.4 0.116 4 <= Inf 154 7.7% 55 99 5.6% 9.8% 64.3% -56.4 0.024 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.330 $`WOE Table for v.stlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4030051922 154 7.7% 118 36 11.9% 3.6% 23.4% 121.1 0.102 2 <= -0.1867821117 462 23.1% 282 180 28.5% 17.8% 39.0% 47.3 0.051 3 <= 0.1141896118 615 30.8% 301 314 30.5% 31.0% 51.1% -1.8 0.000 4 <= Inf 769 38.5% 287 482 29.0% 47.6% 62.7% -49.4 0.092 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.244 $`WOE Table for pcci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1738420887 616 30.8% 397 219 40.2% 21.6% 35.6% 61.9 0.115 2 <= -0.03163945242 307 15.3% 165 142 16.7% 14.0% 46.3% 17.4 0.005 3 <= 0.2553612644 615 30.8% 270 345 27.3% 34.1% 56.1% -22.1 0.015 4 <= Inf 462 23.1% 156 306 15.8% 30.2% 66.2% -65.0 0.094 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.228 $`WOE Table for v.ftlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.03697698898 923 46.2% 555 368 56.2% 36.4% 39.9% 43.5 0.086 2 <= 0.2437475615 615 30.8% 279 336 28.2% 33.2% 54.6% -16.2 0.008 3 <= Inf 462 23.1% 154 308 15.6% 30.4% 66.7% -66.9 0.099 5 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.194 $`WOE Table for v.rftl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1578370554 616 30.8% 372 244 37.7% 24.1% 39.6% 44.6 0.060 2 <= 0.1880959621 768 38.4% 384 384 38.9% 37.9% 50.0% 2.4 0.000 3 <= 0.3289762494 308 15.4% 129 179 13.1% 17.7% 58.1% -30.4 0.014 4 <= Inf 308 15.4% 103 205 10.4% 20.3% 66.6% -66.4 0.065 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.140 $`WOE Table for stlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4586732186 154 7.7% 60 94 6.1% 9.3% 61.0% -42.5 0.014 2 <= -0.1688696056 462 23.1% 266 196 26.9% 19.4% 42.4% 32.9 0.025 3 <= 0.2631157075 922 46.1% 440 482 44.5% 47.6% 52.3% -6.7 0.002 4 <= 0.3592235072 154 7.7% 97 57 9.8% 5.6% 37.0% 55.6 0.023 5 <= 0.4846279843 154 7.7% 81 73 8.2% 7.2% 47.4% 12.8 0.001 6 <= Inf 154 7.7% 44 110 4.5% 10.9% 71.4% -89.2 0.057 8 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.122 $`WOE Table for v.rstl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4541701981 154 7.7% 94 60 9.5% 5.9% 39.0% 47.3 0.017 2 <= -0.3526306487 154 7.7% 62 92 6.3% 9.1% 59.7% -37.1 0.010 3 <= -0.2496412214 154 7.7% 53 101 5.4% 10.0% 65.6% -62.1 0.029 4 <= -0.08554320418 307 15.3% 142 165 14.4% 16.3% 53.7% -12.6 0.002 5 <= 0.360854678 923 46.2% 491 432 49.7% 42.7% 46.8% 15.2 0.011 6 <= Inf 308 15.4% 146 162 14.8% 16.0% 52.6% -8.0 0.001 8 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.070 $`WOE Table for v.pcci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4410911486 154 7.7% 92 62 9.3% 6.1% 40.3% 41.9 0.013 2 <= -0.03637567714 769 38.5% 400 369 40.5% 36.5% 48.0% 10.5 0.004 3 <= 0.1801156117 461 23.1% 206 255 20.9% 25.2% 55.3% -18.9 0.008 4 <= 0.2480148615 154 7.7% 84 70 8.5% 6.9% 45.5% 20.6 0.003 5 <= 0.3348752487 154 7.7% 67 87 6.8% 8.6% 56.5% -23.7 0.004 6 <= 0.4397404288 154 7.7% 76 78 7.7% 7.7% 50.6% -0.2 0.000 7 <= Inf 154 7.7% 63 91 6.4% 9.0% 59.1% -34.4 0.009 9 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.042
该表格的每个变量具有以下值:
- Final.Bin — 箱体边界;
- Total.Count — 箱体中的样品总数;
- Total.Distr — 箱体中样品的相对数量;
- 0.Count — 属于 "0" 类别的样本数量;
- 1.Count — 属于 "1" 类别的样本数量;
- 0.Distr — — 属于 "0" 类别的样本相对数量;
- 1.Distr — 属于 "1" 类别的样本相对数量;
- 1.Rate — 类别 "1" 的样本数量与类别 "0" 的样本数量的百分比
- WOE — 箱体的预测能力;
- IV — 箱体的统计重要性。
图形表述将更具说明性。根据这个表格, 按照 IV 的增加顺序绘制所有变量的 WOE 图表:
> evalq(woe.binning.plot(preCut), env)
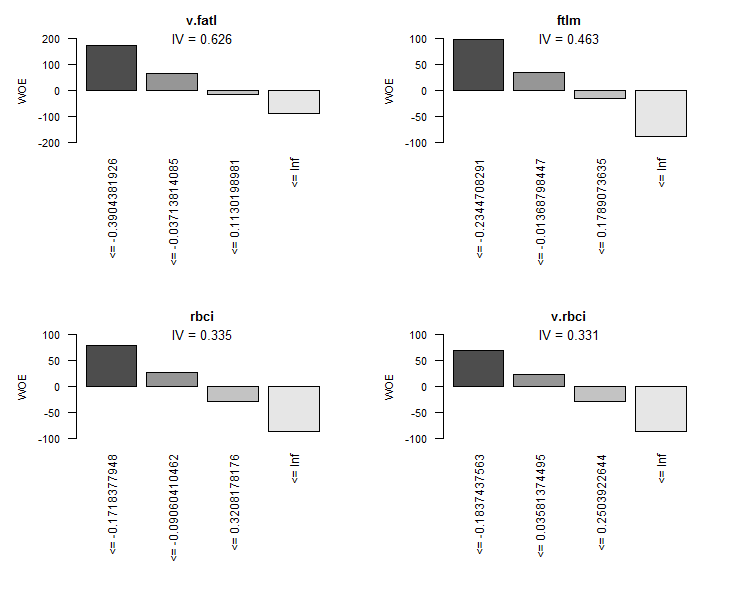
图例.8. WOE 的 4 个最佳变量
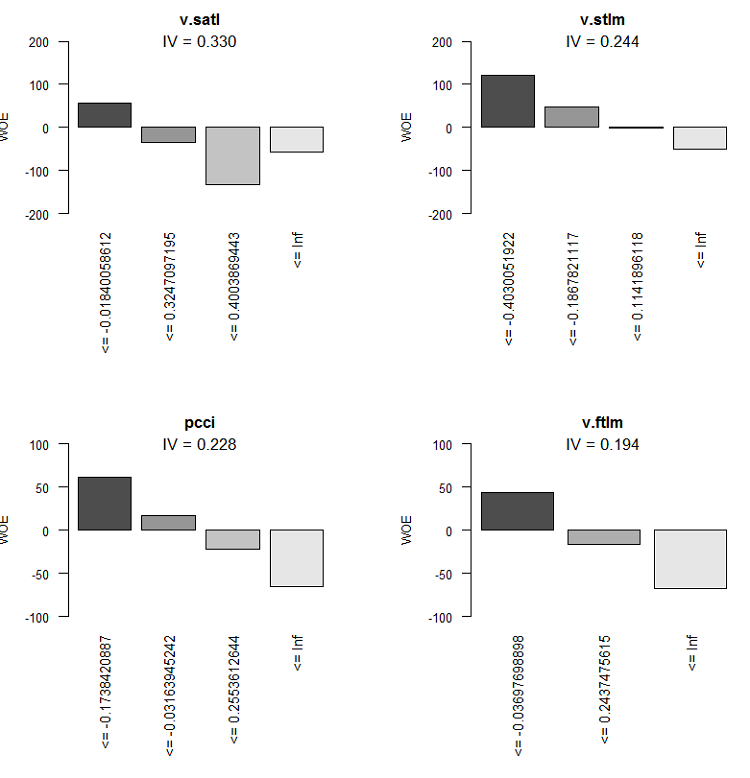
图例.9. WOE 变量 5-8
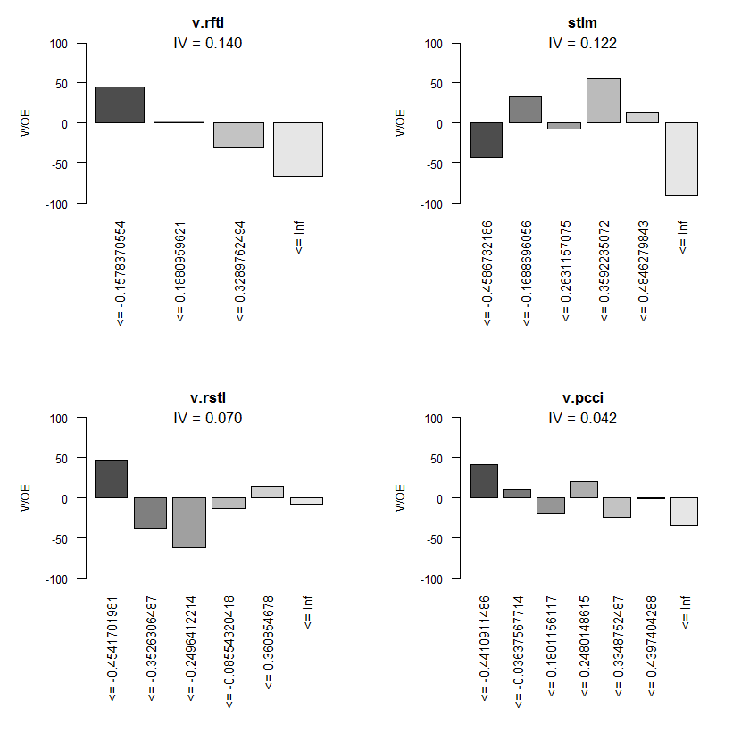
图例.10. WOE 输入变量 9-12
按照其 IV 的变量总范围图表。
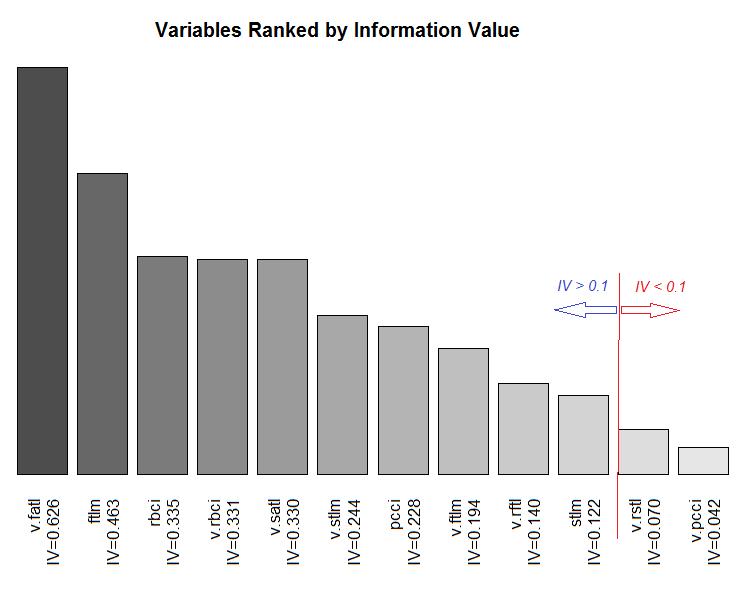
图例.11. 按照其 IV 的变量总范围。
我们不会使用两个不重要的变量 v.rstl 和 v.pcci, 其中 IV < 0.1。我们从图表中可以看出, 在 10 个重要变量中, 只有 v.satl 和 stlm 与目标变量具有非线性关系。其它变量具有线性关系。
对于进一步的实验, 我们需要创建三个集合。它们是:
- DTbin 是一个数据集合, 其中连续的数字预测因子被变换为等级数等于它们被分割成的箱体数量的因子;
- DTdum 是一个数据集合, 其中 DTbin 数据集合的预测因子被变换为伪二进制变量;
- DTwoe 是一个数据集合, 其中预测因子通过用这些等级的 WOE 值替换等级自身被变换为数字变量。
第一个集合 DTbin 需要进行训练, 并获取基本模型的度量。第二个和第三个集合将用于训练 DNN, 并比较两种转化方法的效率。
woebinning 软件包的 woe.binning.deploy() 函数可令我们相对简单地解决这一问题。以下数据必须传递给函数:
- 含有预测因子的数据帧和目标变量, 其中目标变量的值必须为 0 或 1;
- 前一阶段获得的离散参数 (preCut);
- 必须分类的变量名称。如果所有变量都必须分类, 那么只需指定数据帧的名称;
- 指定无需分类变量的最小 IV;
- 指定我们想要获得哪些附加变量 (除了分类的变量)。有两个变体 - "woe" 和 "dum"。
该函数返回一个包含初始变量, 分类变量和其它变量 (如果已指定) 的数据帧。新创建变量的名称是通过将相应的前缀或后缀添加到初始变量名称来创建的。以这种方式, 所有其它变量的前缀都是 "dum" 或 "woe", 分类变量具有后缀 "binned"。我们编写函数 DiscretizeData(), 其中使用 woe.binning.deploy() 变换初始数据集合。
DiscretizeData <- function(X, preCut, var){ require(foreach) require(woeBinning) DTd <- list() foreach(i = 1:length(X)) %do% { X[[i]] %>% select(-Data) %>% targ.int() %>% woe.binning.deploy(preCut, min.iv.total = 0.1, add.woe.or.dum.var = var) -> res return(res) } -> DTd list(pretrain = DTd[[1]] , train = DTd[[2]] , val = DTd[[3]] , test = DTd[[4]] ) -> DTd return(DTd) }
函数的输入参数是含有 pretrain/train/val/test 插槽的初始数据 (list X), 离散参数 preCut 和附加变量类型 (string var)。
函数会从每个插槽里移除 "Data" 变量, 并修改目标变量 - 因子 "Class" 改为数字目标变量 "Cl"。有基于此, 它将发送 woe.binning.deploy() 到函数输入。我们在函数的入口参数里附带指定最小 IV = 0.1 以便将变量包含到输出集合。在输出端, 我们将收到一个包含相同插槽 预训练/训练/验证/测试 的列表。在每个插槽中, 已分类变量, 若有请求, 额外的变量将被添加到初始变量中。我们来计算所有需要的集合, 并从 DTcap.n 中添加原始数据。
evalq({
require(dplyr)
require(foreach)
DTbin = DiscretizeData(DTcap.n, preCut = preCut, var = "")
DTwoe = DiscretizeData(DTcap.n, preCut = preCut, var = "woe")
DTdum = DiscretizeData(DTcap.n, preCut = preCut, var = "dum")
X.woe <- list()
X.bin <- list()
X.dum <- list()
foreach(i = 1:length(DTcap.n)) %do% {
DTbin[[i]] %>% select(contains("binned")) -> X.bin[[i]]
DTdum[[i]] %>% select(starts_with("dum")) -> X.dum[[i]]
DTwoe[[i]] %>% select(starts_with("woe")) %>%
divide_by(100) -> X.woe[[i]]
return(list(bin = X.bin[[i]], woe = X.woe[[i]],
dum = X.dum[[i]], raw = DTcap.n[[i]]))
} -> DTcut
list(pretrain = DTcut[[1]],
train = DTcut[[2]],
val = DTcut[[3]],
test = DTcut[[4]] ) -> DTcut
rm(DTwoe, DTdum, X.woe, X.bin, X.dum)
},
env)
由于 WOE 是一个百分比值, 我们可以将 WOE 除以 100, 并获得可以发送到神经网络的输入变量值, 而无需额外的常规化。我们来看看获得的插槽结构, 譬如 DTcut$val。
> env$DTcut$val %>% str() List of 4 $ bin:'data.frame': 501 obs. of 10 variables: ..$ v.fatl.binned: Factor w/ 5 levels "(-Inf,-0.3904381926]",..: 1 1 3 2 4 3 4 4 4 4 ... ..$ ftlm.binned : Factor w/ 5 levels "(-Inf,-0.2344708291]",..: 2 1 1 1 2 2 3 4 4 4 ... ..$ rbci.binned : Factor w/ 5 levels "(-Inf,-0.1718377948]",..: 2 1 2 1 2 3 3 3 4 4 ... ..$ v.rbci.binned: Factor w/ 5 levels "(-Inf,-0.1837437563]",..: 1 1 3 2 4 3 4 4 4 4 ... ..$ v.satl.binned: Factor w/ 5 levels "(-Inf,-0.01840058612]",..: 1 1 1 1 1 1 1 1 1 2 ... ..$ v.stlm.binned: Factor w/ 5 levels "(-Inf,-0.4030051922]",..: 2 2 3 2 3 2 3 3 4 4 ... ..$ pcci.binned : Factor w/ 5 levels "(-Inf,-0.1738420887]",..: 1 1 4 2 4 2 4 2 2 3 ... ..$ v.ftlm.binned: Factor w/ 4 levels "(-Inf,-0.03697698898]",..: 1 1 3 2 3 2 3 3 2 2 ... ..$ v.rftl.binned: Factor w/ 5 levels "(-Inf,-0.1578370554]",..: 2 1 1 1 1 1 1 2 2 2 ... ..$ stlm.binned : Factor w/ 7 levels "(-Inf,-0.4586732186]",..: 2 2 2 2 1 1 1 1 1 2 ... $ woe:'data.frame': 501 obs. of 10 variables: ..$ woe.v.fatl.binned: num [1:501] 1.713 1.713 -0.145 0.632 -0.897 ... ..$ woe.ftlm.binned : num [1:501] 0.352 0.972 0.972 0.972 0.352 ... ..$ woe.rbci.binned : num [1:501] 0.274 0.794 0.274 0.794 0.274 ... ..$ woe.v.rbci.binned: num [1:501] 0.683 0.683 -0.295 0.22 -0.861 ... ..$ woe.v.satl.binned: num [1:501] 0.573 0.573 0.573 0.573 0.573 ... ..$ woe.v.stlm.binned: num [1:501] 0.473 0.473 -0.0183 0.473 -0.0183 ... ..$ woe.pcci.binned : num [1:501] 0.619 0.619 -0.65 0.174 -0.65 ... ..$ woe.v.ftlm.binned: num [1:501] 0.435 0.435 -0.669 -0.162 -0.669 ... ..$ woe.v.rftl.binned: num [1:501] 0.024 0.446 0.446 0.446 0.446 ... ..$ woe.stlm.binned : num [1:501] 0.329 0.329 0.329 0.329 -0.425 ... $ dum:'data.frame': 501 obs. of 41 variables: ..$ dum.v.fatl.-Inf.-0.3904381926.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.-0.03713814085.0.1130198981.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.-0.3904381926.-0.03713814085.binned: num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.0.1130198981.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-0.2344708291.-0.01368798447.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-Inf.-0.2344708291.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-0.01368798447.0.1789073635.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.0.1789073635.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ....................................................................................... ..$ dum.stlm.-Inf.-0.4586732186.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.-0.1688696056.0.2631157075.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.2631157075.0.3592235072.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.3592235072.0.4846279843.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.4846279843.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... $ raw:'data.frame': 501 obs. of 14 variables: ..$ Data : POSIXct[1:501], format: "2017-02-23 15:30:00" "2017-02-23 15:45:00" ... ..$ ftlm : num [1:501] -0.223 -0.374 -0.262 -0.31 -0.201 ... ..$ stlm : num [1:501] -0.189 -0.257 -0.271 -0.389 -0.473 ... ..$ rbci : num [1:501] -0.0945 -0.1925 -0.1348 -0.1801 -0.1192 ... ..$ pcci : num [1:501] -0.5714 -0.2602 0.4459 -0.0478 0.2596 ... ..$ v.fatl: num [1:501] -0.426 -0.3977 0.0936 -0.1512 0.1178 ... ..$ v.satl: num [1:501] -0.35 -0.392 -0.177 -0.356 -0.316 ... ..$ v.rftl: num [1:501] -0.0547 -0.2065 -0.3253 -0.4185 -0.4589 ... ..$ v.rstl: num [1:501] 0.0153 -0.0273 -0.0636 -0.1281 -0.15 ... ..$ v.ftlm: num [1:501] -0.321 -0.217 0.253 0.101 0.345 ... ..$ v.stlm: num [1:501] -0.288 -0.3 -0.109 -0.219 -0.176 ... ..$ v.rbci: num [1:501] -0.2923 -0.2403 0.1909 0.0116 0.2868 ... ..$ v.pcci: num [1:501] -0.0298 0.3738 0.6153 -0.5643 0.2742 ... ..$ Class : Factor w/ 2 levels "-1","1": 1 1 1 1 2 2 2 2 2 1 ...
如您所见, bin 插槽包含 10 个不同等级数量的因子变量。它们带有后缀 "binned"。woe 插槽包含 10 个变量, 其因子等级因其 WOE 而改变 (它们具有 "woe" 前缀)。dum 插槽有 41 个数字变量 dummy, 含有得自经逐一编码的因子变量 (带前缀 "dum") 的数值 (0, 1)。原始 插槽中有 14 个变量。它们是 Data — 时间戳, Class — 目标因子变量和 12 个数字预测因子。
我们已有进一步实验所需的所有数据。下面列出的对象如今应该在环境 env 中。我们将含有这些对象的工作区域保存到 PartIV.RData 文件中。
> ls(env) [1] "Close" "Data" "dt" "DT" "DTbin" "DTcap" "DTcap.n" "DTcut" "High" [10] "i" "Low" "Open" "pre.outl" "preCut" "preproc" "Volume"
2.1.2. 基本比较模型
我们将使用已在 OneR 软件包里实现的 OneR 模型作为基准模型。该模型简单, 可靠, 易于解释。关于算法的信息可以在软件包描述中找到。该模型仅配合箱体数据运作。该软件包包含辅助函数, 可将数字变量以不同的方式离散化。由于我们已经将预测因子变换成了因子, 所以我们不需要它们。
现在, 我会详细说明示意下面的计算。通过从 DTcut 中提取相应的插槽并在其中添加目标变量 Class 来创建训练/验证/测试集合。我们将利用训练集合训练模型。
> evalq({
+ require(OneR)
+ require(dplyr)
+ require(magrittr)
+ train <- cbind(DTcut$train$bin, Class = DTcut$train$raw$Class) %>% as.data.frame()
+ val <- cbind(DTcut$val$bin, Class = DTcut$val$raw$Class) %>% as.data.frame()
+ test <- cbind(DTcut$test$bin, Class = DTcut$test$raw$Class) %>% as.data.frame()
+ model <- OneR(data = train, formula = NULL, ties.method = "chisq", #c("first","chisq"
+ verbose = TRUE) #FALSE, TRUE
+ }, env)
加载所需软件包: OneR
Attribute Accuracy
1 * v.satl.binned 63.14%
2 v.fatl.binned 62.64%
3 ftlm.binned 62.54%
4 pcci.binned 61.44%
5 v.rftl.binned 59.74%
6 v.rbci.binned 58.94%
7 rbci.binned 58.64%
8 stlm.binned 58.04%
9 v.stlm.binned 57.54%
10 v.ftlm.binned 56.14%
---
Chosen attribute due to accuracy
and ties method (if applicable): '*'
Warning message:
In OneR(data = train, formula = NULL, ties.method = "chisq", verbose = TRUE) :
data contains unused factor levels
模型所选 v.satl.binned 变量基准精度 63.14%, 作为创建规则的基准。我们来看看这个模型的一般信息:
> summary(env$model) Call: OneR(data = train, formula = NULL, ties.method = "chisq", verbose = FALSE) Rules: If v.satl.binned = (-Inf,-0.01840058612] then Class = -1 If v.satl.binned = (-0.01840058612,0.3247097195] then Class = 1 If v.satl.binned = (0.3247097195,0.4003869443] then Class = 1 If v.satl.binned = (0.4003869443, Inf] then Class = 1 Accuracy: 632 of 1001 instances classified correctly (63.14%) Contingency table: v.satl.binned Class (-Inf,-0.01840058612] (-0.01840058612,0.3247097195] (0.3247097195,0.4003869443] (0.4003869443, Inf] Sum -1 * 325 161 28 37 551 1 143 * 229 * 35 * 43 450 Sum 468 390 63 80 1001 --- Maximum in each column: '*' Pearson's Chi-squared test: X-squared = 74.429, df = 3, p-value = 4.803e-16
图形表示的训练结果:
plot(env$model)

图例.12. 模型中按类别 v.satl.binned 变量分类分布
训练期间预测的准确性不是很高。我们将看到这个模型在验证集合上展示出什么样的准确度:
> evalq(res.val <- eval_model(predict(model, val %>% as.data.frame()), val$Class), + env) Confusion matrix (absolute): Actual Prediction -1 1 Sum -1 106 87 193 1 100 208 308 Sum 206 295 501 Confusion matrix (relative): Actual Prediction -1 1 Sum -1 0.21 0.17 0.39 1 0.20 0.42 0.61 Sum 0.41 0.59 1.00 Accuracy: 0.6267 (314/501) Error rate: 0.3733 (187/501) Error rate reduction (vs. base rate): 0.0922 (p-value = 0.04597)
以及在测试集合上:
> evalq(res.test <- eval_model(predict(model, test %>% as.data.frame()), test$Class), + env) Confusion matrix (absolute): Actual Prediction -1 1 Sum -1 130 102 232 1 76 193 269 Sum 206 295 501 Confusion matrix (relative): Actual Prediction -1 1 Sum -1 0.26 0.20 0.46 1 0.15 0.39 0.54 Sum 0.41 0.59 1.00 Accuracy: 0.6447 (323/501) Error rate: 0.3553 (178/501) Error rate reduction (vs. base rate): 0.1359 (p-value = 0.005976)
结果并不令人鼓舞。错误率降低 展示出准确性相对于基准 (0.5) 等级是如何增加的。p (<0.05) 的低值表示该模型能够比基本水平更好地产生预测。测试集合的精度为 0.6447 (323/501), 高于验证集合的准确性。测试集合相比验证集合更远离训练集。这一结果将作为比较我们未来模型的预测结果的参考点。
2.1.3. DNN 的结构
我们将使用三个数据集合进行训练和测试:
- DTcut$$raw — 12 个输入变量 (异常值插补和常规化)。
- DTcut$$dum — 41 个二进制变量。
- DTcut$$woe — 10 个数值变量。
我们将使用所有数据集合的 Class 变量 = 含两个等级的因子。神经网络的结构:
- DNNraw - layers = c(12, 16, 8(2), 2), 激活函数 c(tanh, maxout(lin), softmax)
- DNNwoe - layers = c(10, 16, 8(2), 2), 激活函数 c(tanh, maxout(lin), softmax)
- DNNdum - layers = c(41, 50, 8(2), 2), 激活函数 c(ReLU, maxout(ReLU), softmax)
以下示意图显示了 DNNwoe 神经网络的结构。神经网络有一个输入层, 两个隐藏层和一个输出层。另两个神经网络 (DNNdum, DNNraw) 具有相似的结构。它们仅有的不同之处在于层中的神经元数量和激活函数。
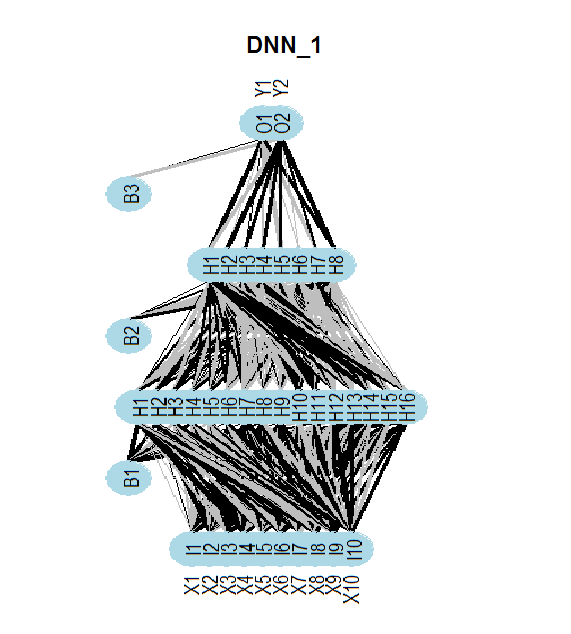
图例.13. 神经网络 DNNwoe 结构
2.1.4. 培训变数
带预训练
训练有两个阶段
- 在预训练集合之上的 SRBM 预训练, 随后仅训练神经网络的上层, 在训练集合和参数之上进行验证 — par_0;
- 使用训练/验证集合和参数 par_1 对整个网络进行微调。
我们可以保存微调的中间模型, 但不是强制性的。展现最佳训练结果的模型将被保存。这两个阶段的参数应该包含:
- par_0 — 神经网络的一般参数, RBM 训练参数和 DNN 上层训练参数;
- par_1 — DNN 所有层的训练参数。
所有 DArch 的参数都有省缺值。如果我们在训练的某个阶段需要不同的参数, 我们可以通过列表设置它们, 并且它们将覆盖省缺参数。在训练的第一阶段之后, 我们将获得具有参数和训练结果 (训练误差, 测试误差等) 的 DArch 结构, 以及含有已训练 SRBM 的权重始创的神经网络。若要完成第二阶段的训练, 您需要将第一阶段获得的 DArch 结构纳入训练阶段的参数清单。自认而然地, 我们需要一个训练和验证集合。
我们来研究第一阶段训练所需的参数 (SRBM 的预训练和神经网络上层的训练) 并运行它:
##=====CODE I etap=========================== evalq({ require(darch) require(dplyr) require(magrittr) Ln <- c(0, 16, 8, 0)# // 输入和输出神经元的数量将从数据集合中自动识别 nEp_0 <- 25 #------------------ par_0 <- list( layers = Ln, # // 我们把这个参数放在列表中 (为简单起见) seed = 54321,# // 如果我们想在初始化期间获得相同的数据 logLevel = 5, # // 我们需要什么等级的信息输出 # params RBM======================== rbm.consecutive = F, # 每个 RBM 一次训练一个世代 rbm.numEpochs = nEp_0, rbm.batchSize = 50, rbm.allData = TRUE, rbm.lastLayer = -1, # // 不要训练 SRBM 的上层 rbm.learnRate = 0.3, rbm.unitFunction = "tanhUnitRbm", # params NN ======================== darch.batchSize = 50, darch.numEpochs = nEp_0,# // 为了简单起见, 将此参数从列表中删除 darch.trainLayers = c(F,F,T), #обучать //仅上层 darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = 0.5, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.1,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = "linearUnit") #--------------------------- DNN_default <- darch(darch = NULL, paramsList = par_0, x = DTcut$pretrain$woe %>% as.data.frame(), y = DTcut$pretrain$raw$Class %>% as.data.frame(), xValid = DTcut$train$woe %>% as.data.frame(), yValid = DTcut$train$raw$Class %>% as.data.frame() ) }, env)训练第一阶段彻底完成的结果:
........................... INFO [2017-09-11 14:12:19] Classification error on Train set (best model): 31.95% (639/2000) INFO [2017-09-11 14:12:19] Train set (best model) Cross Entropy error: 1.233 INFO [2017-09-11 14:12:19] Classification error on Validation set (best model): 35.86% (359/1001) INFO [2017-09-11 14:12:19] Validation set (best model) Cross Entropy error: 1.306 INFO [2017-09-11 14:12:19] Best model was found after epoch 3 INFO [2017-09-11 14:12:19] Final 0.632 validation Cross Entropy error: 1.279 INFO [2017-09-11 14:12:19] Final 0.632 validation classification error: 34.42% INFO [2017-09-11 14:12:19] Fine-tuning finished after 5.975 secs
神经网络训练的第二阶段:
##=====CODE II etap=========================== evalq({ require(darch) require(dplyr) require(magrittr) nEp_1 <- 100 bp.learnRate <- 1 par_1 <- list( layers = Ln, seed = 54321, logLevel = 5, rbm.numEpochs = 0,# SRBM is not to be trained! darch.batchSize = 50, darch.numEpochs = nEp_1, darch.trainLayers = c(T,T,T), #TRUE, darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = bp.learnRate, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.1,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation backpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = exponentialLinearUnit, darch.elu.alpha = 2) #------------------------------ DNN_1 <- darch( darch = DNN_default, paramsList = par_1, x = DTcut$train$woe %>% as.data.frame(), y = DTcut$train$raw$Class %>% as.data.frame(), xValid = DTcut$val$woe %>% as.data.frame(), yValid = DTcut$val$raw$Class %>% as.data.frame() ) }, env)
训练第二阶段的结果:
........................... INFO [2017-09-11 15:48:37] Finished epoch 100 of 100 after 0.279 secs (3666 patterns/sec) INFO [2017-09-11 15:48:37] Classification error on Train set (best model): 31.97% (320/1001) INFO [2017-09-11 15:48:37] Train set (best model) Cross Entropy error: 1.225 INFO [2017-09-11 15:48:37] Classification error on Validation set (best model): 31.14% (156/501) INFO [2017-09-11 15:48:37] Validation set (best model) Cross Entropy error: 1.190 INFO [2017-09-11 15:48:37] Best model was found after epoch 96 INFO [2017-09-11 15:48:37] Final 0.632 validation Cross Entropy error: 1.203 INFO [2017-09-11 15:48:37] Final 0.632 validation classification error: 31.44% INFO [2017-09-11 15:48:37] Fine-tuning finished after 37.22 secs
训练第二阶段预测误差变化图:
plot(env$DNN_1, y = "raw")
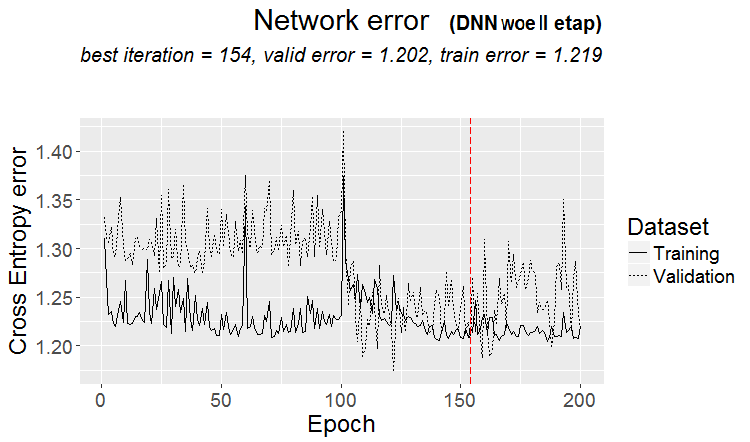
图例.14. 训练第二阶段期间分类错误的变化
我们来看一下测试集合上最终模型的分类错误:
#-----------
evalq({
xValid = DTcut$test$woe %>% as.data.frame()
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(DNN_1, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict)
}, env)
Incorrect classifications on all examples: 166 (33.13%)
Confusion Matrix and Statistics
Reference
Prediction -1 1
-1 129 77
1 89 206
Accuracy : 0.6687
95% CI : (0.6255, 0.7098)
No Information Rate : 0.5649
P-Value [Acc > NIR] : 1.307e-06
Kappa : 0.3217
Mcnemar's Test P-Value : 0.3932
Sensitivity : 0.5917
Specificity : 0.7279
Pos Pred Value : 0.6262
Neg Pred Value : 0.6983
Prevalence : 0.4351
Detection Rate : 0.2575
Detection Prevalence : 0.4112
Balanced Accuracy : 0.6598
'Positive' Class : -1
#----------------------------------------
这些数据集合 (woe) 与这些参数的精度远离最优值, 远高于基本模型的准确性。通过优化 DNN 的超参数具有提高精度的重大潜力。如果重复计算, 则数据可能与文章中的并不完全一致。
我们把脚本带进一个更加紧凑的形式, 以便与其它数据集合进一步的计算。我们 woe 集合编写一个函数:
#------------------- DNN.train.woe <- function(param, X){ require(darch) require(magrittr) darch( darch = NULL, paramsList = param[[1]], x = X[[1]]$woe %>% as.data.frame(), y = X[[1]]$raw$Class %>% as.data.frame(), xValid = X[[2]]$woe %>% as.data.frame(), yValid = X[[2]]$raw$Class %>% as.data.frame() ) %>% darch( ., paramsList = param[[2]], x = X[[2]]$woe %>% as.data.frame(), y = X[[2]]$raw$Class %>% as.data.frame(), xValid = X[[3]]$woe %>% as.data.frame(), yValid = X[[3]]$raw$Class %>% as.data.frame() ) -> Darch return(Darch) }
以紧凑的形式重复计算 DTcut$$woe 数据集合:
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_0 <- 25
nEp_1 <- 25
rbm.learnRate = c(0.5,0.3,0.1)
bp.learnRate <- c(0.5,0.3,0.1)
list(par_0, par_1) %>% DNN.train.woe(DTcut) -> Dnn.woe
xValid = DTcut$test$woe %>% as.data.frame()
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.woe, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.woe
}, env)
针对 DTcut$$ 原始数据集合进行计算:
#-------------------------
DNN.train.raw <- function(param, X){
require(darch)
require(magrittr)
darch( darch = NULL, paramsList = param[[1]],
x = X[[1]]$raw %>% tbl_df %>% select(-c(Data, Class)),
y = X[[1]]$raw$Class %>% as.data.frame(),
xValid = X[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)),
yValid = X[[2]]$raw$Class %>% as.data.frame()
) %>%
darch( ., paramsList = param[[2]],
x = X[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)),
y = X[[2]]$raw$Class %>% as.data.frame(),
xValid = X[[3]]$raw %>% tbl_df %>% select(-c(Data, Class)),
yValid = X[[3]]$raw$Class %>% as.data.frame()
) -> Darch
return(Darch)
}
#-------------------------------
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_0 <- 25
nEp_1 <- 25
rbm.learnRate = c(0.5,0.3,0.1)
bp.learnRate <- c(0.5,0.3,0.1)
list(par_0, par_1) %>% DNN.train.raw(DTcut) -> Dnn.raw
xValid = DTcut$test$raw %>% tbl_df %>% select(-c(Data, Class))
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.raw, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.raw
}, env)
#----------------------------
以下是该集合的分类错误变化的结果和图表:
> env$cM.raw
Confusion Matrix and Statistics
Reference
Prediction -1 1
-1 133 73
1 86 209
Accuracy : 0.6826
95% CI : (0.6399, 0.7232)
No Information Rate : 0.5629
P-Value [Acc > NIR] : 2.667e-08
Kappa : 0.3508
Mcnemar's Test P-Value : 0.3413
Sensitivity : 0.6073
Specificity : 0.7411
Pos Pred Value : 0.6456
Neg Pred Value : 0.7085
Prevalence : 0.4371
Detection Rate : 0.2655
Detection Prevalence : 0.4112
Balanced Accuracy : 0.6742
'Positive' Class : -1
#--------------------------------------
plot(env$Dnn.raw, y = "raw")
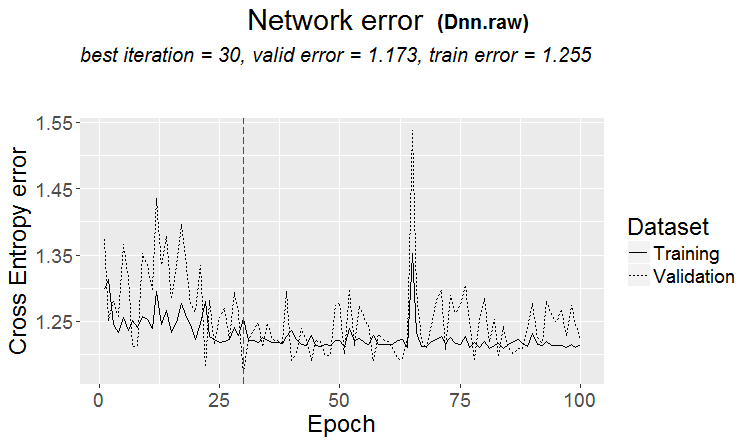
图例.15. 第二阶段分类误差变化
我无法用 DTcut$$dum 数据训练神经网络。您可自行尝试这样做。例如, 输入 DTcut$$bin 数据, 并将训练参数排列成要转换为伪变量的预测因子。
不带预训练的训练
我们来训练神经网络, 无需在预训练/训练/验证集合上使用相同的数据 (woe, raw) 进行预训练。我们来看看结果.
#-------WOE---------------- evalq({ require(darch) require(magrittr) Ln <- c(0, 16, 8, 0) nEp_1 <- 100 bp.learnRate <- c(0.5,0.7,0.1) #--param---------------- par_1 <- list( layers = Ln, seed = 54321, logLevel = 5, rbm.numEpochs = 0,# SRBM is not to be trained! darch.batchSize = 50, darch.numEpochs = nEp_1, darch.trainLayers = c(T,T,T), #TRUE, darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = bp.learnRate, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.0,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation backpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = exponentialLinearUnit, darch.elu.alpha = 2) #--train--------------------------- darch( darch = NULL, paramsList = par_1, x = DTcut[[1]]$woe %>% as.data.frame(), y = DTcut[[1]]$raw$Class %>% as.data.frame(), xValid = DTcut[[2]]$woe %>% as.data.frame(), yValid = DTcut[[2]]$raw$Class %>% as.data.frame() ) -> Dnn.woe.I #---test-------------------------- xValid = DTcut$val$woe %>% as.data.frame() yValid = DTcut$val$raw$Class %>% as.vector() Ypredict <- predict(Dnn.woe.I, newdata = xValid, type = "class") numIncorrect <- sum(Ypredict != yValid) cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (", round(numIncorrect/nrow(xValid)*100, 2), "%)\n")) caret::confusionMatrix(yValid, Ypredict) -> cM.woe.I }, env) #---------Ris16------------------------------------ plot(env$Dnn.woe.I, type = "class") env$cM.woe.I
度量:
....................................................... INFO [2017-09-14 10:38:01] Classification error on Train set (best model): 28.7% (574/2000) INFO [2017-09-14 10:38:01] Train set (best model) Cross Entropy error: 1.140 INFO [2017-09-14 10:38:02] Classification error on Validation set (best model): 35.86% (359/1001) INFO [2017-09-14 10:38:02] Validation set (best model) Cross Entropy error: 1.299 INFO [2017-09-14 10:38:02] Best model was found after epoch 67 INFO [2017-09-14 10:38:02] Final 0.632 validation Cross Entropy error: 1.241 INFO [2017-09-14 10:38:02] Final 0.632 validation classification error: 33.23% INFO [2017-09-14 10:38:02] Fine-tuning finished after 37.13 secs Incorrect classifications on all examples: 150 (29.94%) > env$cM.woe.I Confusion Matrix and Statistics Reference Prediction -1 1 -1 144 62 1 88 207 Accuracy : 0.7006 95% CI : (0.6584, 0.7404) No Information Rate : 0.5369 P-Value [Acc > NIR] : 5.393e-14 Kappa : 0.3932 Mcnemar's Test P-Value : 0.04123 Sensitivity : 0.6207 Specificity : 0.7695 Pos Pred Value : 0.6990 Neg Pred Value : 0.7017 Prevalence : 0.4631 Detection Rate : 0.2874 Detection Prevalence : 0.4112 Balanced Accuracy : 0.6951 'Positive' Class : -1
训练期间分类误差变化图表:
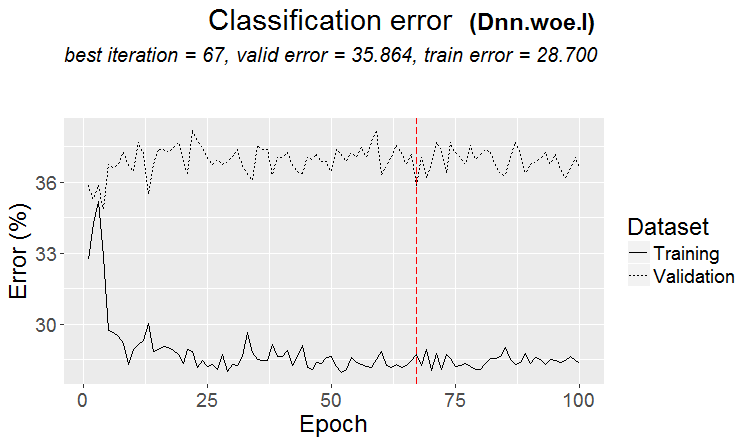
图例.16. $woe 集合上的无预训练分类误差变化
针对相同的集合 $raw:
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_1 <- 100
bp.learnRate <- c(0.5,0.7,0.1)
#--param-----------------------------
par_1 <- list(
layers = Ln,
seed = 54321,
logLevel = 5,
rbm.numEpochs = 0,# SRBM is not to be trained!
darch.batchSize = 50,
darch.numEpochs = nEp_1,
darch.trainLayers = c(T,T,T), #TRUE,
darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"),
bp.learnRate = bp.learnRate,
bp.learnRateScale = 1,
darch.weightDecay = 0.0002,
darch.dither = F,
darch.dropout = c(0.1,0.2,0.1),
darch.fineTuneFunction = backpropagation, #rpropagation backpropagation
normalizeWeights = T,
normalizeWeightsBound = 1,
darch.weightUpdateFunction = c("weightDecayWeightUpdate",
"maxoutWeightUpdate",
"weightDecayWeightUpdate"),
darch.dropout.oneMaskPerEpoch = T,
darch.maxout.poolSize = 2,
darch.maxout.unitFunction = exponentialLinearUnit,
darch.elu.alpha = 2)
#---train------------------------------
darch( darch = NULL, paramsList = par_1,
x = DTcut[[1]]$raw %>% tbl_df %>% select(-c(Data, Class)) ,
y = DTcut[[1]]$raw$Class %>% as.vector(),
xValid = DTcut[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)) ,
yValid = DTcut[[2]]$raw$Class %>% as.vector()
) -> Dnn.raw.I
#---test--------------------------------
xValid = DTcut[[3]]$raw %>% tbl_df %>% select(-c(Data, Class))
yValid = DTcut[[3]]$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.raw.I, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.raw.I
}, env)
#---------Ris17----------------------------------
env$cM.raw.I
plot(env$Dnn.raw.I, type = "class")
度量:
INFO [2017-09-14 11:06:13] Classification error on Train set (best model): 30.75% (615/2000) INFO [2017-09-14 11:06:13] Train set (best model) Cross Entropy error: 1.189 INFO [2017-09-14 11:06:13] Classification error on Validation set (best model): 33.67% (337/1001) INFO [2017-09-14 11:06:13] Validation set (best model) Cross Entropy error: 1.236 INFO [2017-09-14 11:06:13] Best model was found after epoch 45 INFO [2017-09-14 11:06:13] Final 0.632 validation Cross Entropy error: 1.219 INFO [2017-09-14 11:06:13] Final 0.632 validation classification error: 32.59% INFO [2017-09-14 11:06:13] Fine-tuning finished after 35.47 secs Incorrect classifications on all examples: 161 (32.14%) > #---------Ris17---------------------------------- > env$cM.raw.I Confusion Matrix and Statistics Reference Prediction -1 1 -1 140 66 1 95 200 Accuracy : 0.6786 95% CI : (0.6358, 0.7194) No Information Rate : 0.5309 P-Value [Acc > NIR] : 1.283e-11 Kappa : 0.3501 Mcnemar's Test P-Value : 0.02733 Sensitivity : 0.5957 Specificity : 0.7519 Pos Pred Value : 0.6796 Neg Pred Value : 0.6780 Prevalence : 0.4691 Detection Rate : 0.2794 Detection Prevalence : 0.4112 Balanced Accuracy : 0.6738 'Positive' Class : -1
分类误差变化图表:
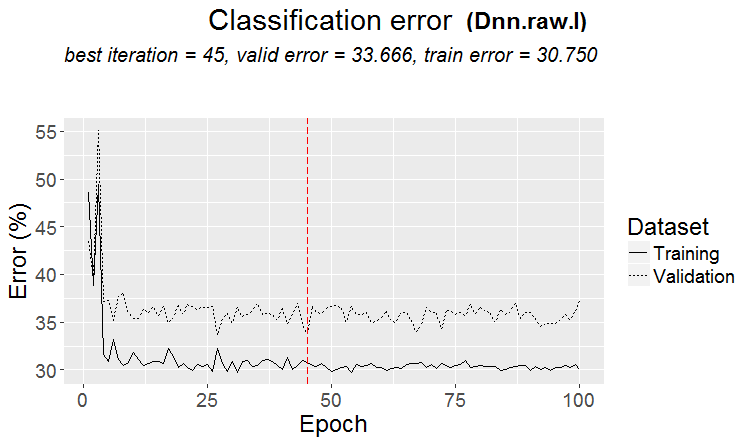
图例.17. $raw 集合上的无预训练分类误差变化
2.2. 结果分析
让我们将实验结果放在一张表格中:
| 训练类型 | 集合 $woe | 集合 $raw |
|---|---|---|
| 带预训练 | 0.6687 (0.6255 - 0.7098) | 0.6826(0.6399 - 0.7232) |
| 不带预训练 | 0.7006(0.6589 - 0.7404) | 0.6786(0.6359 - 0.7194) |
带预训练的分类误差在两集合中几乎相同。它在 30+/-4% 的范围内。尽管误差较小, 但是从分类误差变化的图表可以看出, 在没有预训练的情况下训练中出现了重复训练 (验证和测试集合中的误差明显大于训练误差)。因此, 我们将在进一步的实验中使用带预训练的训练。
结果并不比基本模型的结果大很多。我们有可能通过优化一些超参数来改善特性。我们将在下一篇文章中做到这一点。
结束语
尽管有限制 (例如, 只有两种基本的训练方法), darch 软件包允许创建不同结构和参数的神经网络。这个软件包是深入研究神经网络的优秀工具。
DNN 的弱特性, 主要通过使用省缺参数或接近它们的参数来解释。在 $raw 集合之前, $woe 没有展现出任何优势。因此, 在下一篇文章中, 我们将:
- 优化早前创建的 DNN.woe 中的一部分超参数;
- 将使用 TensorFlow 函数库创建一个 DNN, 对其进行测试, 并与 DNN (darch) 进行比较;
- 将创建一个不同类型 (袋式, 堆叠式) 神经网络的集合, 并看看它如何提高预测的质量。
应用
GitHub/PartIV 包括:
- FunPrepareData.R — 用于准备数据的函数
- RunPrepareData.R — 用于准备数据的脚本
- Experiment.R — 用于运行实验的脚本
- Part_IV.RData — 含有准备数据阶段之后获得的所有对象的工作区域图像
- SessionInfo.txt — 关于使用软件的信息
- Darch_default.txt — 具有省缺值的 DArch 结构的参数列表
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/3473
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 深度神经网络 (第 III 部)。样品选择和降维
深度神经网络 (第 III 部)。样品选择和降维
 TradeObjects: 基于 MetaTrader 图形对象的自动化交易
TradeObjects: 基于 MetaTrader 图形对象的自动化交易
 使用云存储服务来进行终端之间的数据交换
使用云存储服务来进行终端之间的数据交换

Благодарим вас за использование моего пакета OneR.DNN не намного лучше, чем модель OneR!
这只适用于使用默认参数 的 DNN。在优化超参数的情况下,DNN 的结果要好得多。请参见第五部分。
祝您好运
这只适用于使用默认参数的 DNN。使用优化的超参数,DNN 会显示出更好的结果。请参见第五部分。
祝好运
交易结果出来了吗?
大家都回到醪糟 中去了。这是另一个话题。