
Прогнозирование временных рядов при помощи экспоненциального сглаживания (окончание)
Введение
В статье "Прогнозирование временных рядов при помощи экспоненциального сглаживания" [1] были кратко представлены модели экспоненциального сглаживания, продемонстрирован один из возможных подходов к оптимизации параметров моделей и в конечном итоге создан индикатор, производящий прогнозирование на основе модели линейного тренда с демпфированием. В данной статье будет предпринята попытка в некоторой степени увеличить точность прогноза этого индикатора.
Прогнозирование котировок валют является сложной задачей, и получить достаточно достоверный прогноз даже на три-четыре шага вперед достаточно трудно. Тем не менее, как и в опубликованной ранее статье, в дальнейшем будем строить прогнозы на 12 шагов вперед, понимая, что на таком большом горизонте получить удовлетворительных результатов не удастся. Поэтому в первую очередь следует обращать внимание на несколько первых шагов прогноза, для которых доверительный интервал оказывается наименьшим.
Прогноз на 10-12 шагов вперед в основном предназначен для демонстрации особенностей поведения различных моделей и методов прогноза. В любом случае, границы доверительного интервала помогут оценить достоверность полученного прогноза для каждого горизонта. Основной целью данной статьи является демонстрация некоторых методов, с помощью которых можно попробовать модернизировать индикатор, опубликованный в статье [1].
Используемый для построения индикаторов алгоритм поиска минимума функции многих переменных был рассмотрен в прошлой статье, поэтому повторного его описания приводить не будем. Для того чтобы не перегружать статью, теоретические выкладки будут представлены в минимальном объеме.
1. Исходный индикатор
В качестве отправной точки будем использовать индикатор IndicatorES.mq5 (см. статью [1]).
Для компиляции индикатора необходимы расположенные в одном каталоге файлы IndicatorES.mq5, CIndicatorES.mqh и PowellsMethod.mqh. Файлы размещены в конце статьи в архиве files2.zip.
Напомним выражения, определяющие используемую для построения этого индикатора модель экспоненциального сглаживания линейного роста с демпфированием.
![]()
![]()
![]()
Где:
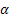 - параметр сглаживания уровня последовательности [0,1];
- параметр сглаживания уровня последовательности [0,1];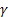 - параметр сглаживания тренда [0,1];
- параметр сглаживания тренда [0,1];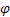 - параметр демпфирования [0,1];
- параметр демпфирования [0,1];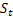 - сглаженный уровень последовательности, вычисленный в момент времени t после поступления значения
- сглаженный уровень последовательности, вычисленный в момент времени t после поступления значения 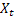 ;
;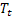 - сглаженный аддитивный тренд, вычисленный в момент времени t;
- сглаженный аддитивный тренд, вычисленный в момент времени t;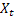 - значение последовательности в момент времени t;
- значение последовательности в момент времени t;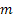 - количество шагов вперед, на которое делается прогноз;
- количество шагов вперед, на которое делается прогноз;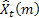 - прогноз на m шагов вперед сделанный в момент времени t;
- прогноз на m шагов вперед сделанный в момент времени t;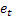 - ошибка прогнозирования на один шаг вперед на момент времени t,
- ошибка прогнозирования на один шаг вперед на момент времени t, 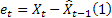 .
.
Единственным входным параметром индикатора является значение, определяющее длину интервала, по которому будет производиться оптимизация параметров модели и выбор начальных значений (интервал обучения). После определения оптимальных величин параметров модели по заданному интервалу производится расчет и построение непосредственно прогноза, доверительного интервала и линии, соответствующей прогнозу модели на один шаг вперед. Оптимизация параметров и построение прогноза происходит при каждом формировании нового бара.
Так как данный индикатор предполагается модернизировать, то для оценки влияния вносимых нами изменений будем использовать тестовые последовательности, размещенные в конце статьи в архиве Files2.zip. Внутри архива в каталоге \Dataset2 находятся файлы с сохраненными котировками EURUSD, USDCHF, USDJPY и индексом доллара DXY. Каждый из них сохранен для трех таймфреймов M1, H1, D1. В файлах сохранены значения "open", причем самое позднее по времени значение расположено в конце файла. Файлы содержат по 1200 элементов.
Ошибки прогнозирования будем оценивать, производя вычисление коэффициента "Mean Absolute Percentage Error" (MAPE)
![]()
Разделим каждую из двенадцати тестовых последовательностей на пятьдесят перекрывающихся отрезков по 80 элементов в каждом и далее для каждого из них произведем вычисление значения MAPE. Среднюю величину полученных таким образом оценок будем использовать в качестве показателя ошибки прогноза для сравниваемых индикаторов. Таким же образом будем вычислять значения MAPE для ошибок прогноза на два и три шага вперед. В дальнейшем такие усредненные оценки будем обозначать:
- MAPE1 – усредненная оценка ошибки прогноза на один шаг вперед;
- MAPE2 – усредненная оценка ошибки прогноза на два шага вперед;
- MAPE3 – усредненная оценка ошибки прогноза на три шага вперед;
- MAPE1-3 – среднее значение (MAPE1+MAPE2+MAPE3)/3.
При вычислении значения MAPE на каждом шаге происходит деление абсолютного значения величины ошибки прогноза на текущее значение последовательности. Чтобы при этом избежать деления на ноль или получения отрицательных значений, необходимо чтобы входные последовательности, как в нашем случае, принимали только отличные от нуля положительные значения.
Для нашего исходного индикатора значения этих оценок приведены в таблице 1.
| MAPE1 | MAPE2 | MAPE3 | MAPE1-3 | |
|---|---|---|---|---|
| IndicatorES | 0.2099 | 0.2925 |
0.3564 | 0.2863 |
Таблица 1. Оценка ошибок прогнозирования исходного индикатора
Данные приведенные в таблице 1 получены при помощи скрипта Errors_IndicatorES.mq5 (в конце статьи в архиве files2.zip). Для компиляции и запуска скрипта необходимо, чтобы файлы CIndicatorES.mqh и PowellsMethod.mqh были расположены в том же каталоге что и Errors_IndicatorES.mq5, а входные последовательности были размещены в каталоге Files\Dataset2\.
Получив исходные оценки ошибок прогнозирования, можно перейти к модернизации данного индикатора.
2. Критерий оптимизации
В исходном индикаторе из статьи "Прогнозирование временных рядов при помощи экспоненциального сглаживания" параметры модели определялись путем минимизации суммы квадратов ошибки прогнозирования на один шаг вперед. Логично предположить, что оптимальные для прогноза на один шаг параметры модели могут не обеспечить минимум ошибок при прогнозе на большее количество шагов вперед. Конечно, хотелось бы минимизировать ошибки прогнозирования на 10-12 шагов вперед, но для рассматриваемых нами последовательностей получить удовлетворительный результат прогноза на таком интервале не представляется возможным.
Поэтому будем реалистами и в качестве первой модернизации нашего индикатора при оптимизации параметров модели будем использовать сумму квадратов ошибки предсказания на один, два и три шага вперед. При этом можно ожидать, что в среднем на интервале первых трех шагов прогноза удастся несколько снизить среднее количество ошибок.
Конечно, такая модернизация исходного индикатора не затрагивает основных принципов его построения, а только изменяет критерий оптимизации параметров, поэтому нельзя ожидать увеличения точности прогноза в разы, но, тем не менее, количество ошибок прогнозирования на два и три шага вперед должно несколько снизиться.
Для сравнения результатов прогнозирования был создан класс CMod1, аналогичный классу CIndicatorES из предыдущей статьи, в котором была изменена целевая функция func.
Функция func исходного класса CIndicatorES:
double CIndicatorES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=0;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(Dlen*MathLog(k1*k2*k3*sse)); }
После внесения изменений функция func приняла вид
double CMod1::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,err,ae,pt,phi2,phi3,a; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95; // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 phi2=phi+phi*phi; phi3=phi2+phi*phi*phi; err=0; for(i=0;i<Dlen-2;i++) { e=Dat[i]-(s+phi*t); err+=e*e; a=Dat[i+1]-(s+phi2*t); err+=a*a; a=Dat[i+2]-(s+phi3*t); err+=a*a; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } e=Dat[Dlen-2]-(s+phi*t); err+=e*e; a=Dat[Dlen-1]-(s+phi2*t); err+=a*a; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; a=Dat[Dlen-1]-(s+phi*t); err+=a*a; return(k1*k2*k3*err); }
Теперь при вычислении целевой функции используется сумма квадратов ошибок прогнозирования на один, два и три шага вперед.
Далее на базе этого класса был создан скрипт Errors_Mod1.mq5, позволяющий, как и уже упомянутый скрипт Errors_IndicatorES.mq5, произвести оценку ошибок прогнозирования. Файлы CMod1.mqh и Errors_Mod1.mq5 размещены в конце статьи в архиве files2.zip.
В таблице 2 приведены оценки ошибок прогноза для исходного и модернизированного варианта.
| MAPE1 | MAPE2 | MAPE3 | MAPE1-3 | |
|---|---|---|---|---|
| IndicatorES | 0.2099 | 0.2925 | 0.3564 | 0.2863 |
| Mod1 | 0.2144 | 0.2898 | 0.3486 | 0.2842 |
Таблица 2. Сравнение оценок ошибок прогнозирования
Как видим, для рассматриваемых последовательностей коэффициенты ошибок MAPE2, MAPE3 и среднее значение MAPE1-3 действительно удалось несколько снизить. Поэтому сохраним этот вариант и приступим к дальнейшей модификации нашего индикатора.
3. Адаптация параметров в процессе сглаживания
Идея изменения параметров сглаживания в зависимости от текущих значений входной последовательности не нова и продиктована желанием корректировать коэффициенты сглаживания таким образом, чтобы при любом изменении характера входной последовательности они оставались оптимальными. Описание некоторых способов адаптации коэффициентов сглаживания можно найти в литературе [2], [3].
Рассчитывая на то, что использование адаптивной модели экспоненциального сглаживания позволит нам дополнительно увеличить точность прогнозирования нашего индикатора, попробуем в качестве следующей модернизации использовать модель с динамически изменяющимся коэффициентом сглаживания.
К сожалению, большинство известных методов адаптации при использовании их в алгоритмах прогнозирования далеко не всегда приводят к желаемому результату. Выбор подходящего способа адаптации может оказаться слишком громоздкой и трудоемкой задачей, поэтому в данном случае воспользуемся выводами, приведенными в литературе [4] и попытаемся реализовать метод "Smooth Transition Exponential Smoothing" (STES) представленный в статье [5].
В указанной статье суть метода представлена в краткой и ясной форме, поэтому не будем пересказывать ее, а сразу представим выражения для нашей модели (см. начало данной статьи) с учетом использования адаптивного коэффициента сглаживания.
![]()
![]()
![]()
![]()
Как видим, теперь значение коэффициента сглаживания альфа вычисляется на каждом шаге алгоритма и зависит от квадрата ошибки предсказания. Влияние ошибки предсказания на величину альфа определяется значениями коэффициентов b и g. В остальном выражения для используемой модели не изменились. Дополнительную информацию по использованию метода STES можно найти в статье [6].
Если в предыдущих вариантах по заданной входной последовательности производился поиск оптимального значения коэффициента альфа, то теперь оптимизации подлежат два коэффициента адаптации b и g, а величина альфа будет динамически определяться в процессе сглаживания входной последовательности.
Данная модернизация реализована в виде класса CMod2. Основные изменения (как и в прошлый раз) затронули в основном функцию func, которая теперь будет выглядеть следующим образом.
double CMod2::func(const double &p[]) { int i; double s,t,alp,gam,phi,sb,sg,k1,k2,e,err,ae,pt,phi2,phi3,a; s=p[0]; t=p[1]; gam=p[2]; phi=p[3]; sb=p[4]; sg=p[5]; k1=1; k2=1; if (gam>0.95){k1+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k1+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k2+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k2+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 phi2=phi+phi*phi; phi3=phi2+phi*phi*phi; err=0; for(i=0;i<Dlen-2;i++) { e=Dat[i]-(s+phi*t); err+=e*e; a=Dat[i+1]-(s+phi2*t); err+=a*a; a=Dat[i+2]-(s+phi3*t); err+=a*a; alp=0.05+0.9/(1+MathExp(sb+sg*e*e)); // 0.05 < Alpha < 0.95 ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } e=Dat[Dlen-2]-(s+phi*t); err+=e*e; a=Dat[Dlen-1]-(s+phi2*t); err+=a*a; alp=0.05+0.9/(1+MathExp(sb+sg*e*e)); // 0.05 < Alpha < 0.95 ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; a=Dat[Dlen-1]-(s+phi*t); err+=a*a; return(k1*k2*err); }
При создании данной функции в выражение, определяющее величину коэффициента альфа, внесены некоторые изменения. Это сделано для того, чтобы ограничить максимально и минимально возможную величину этого коэффициента значениями 0.05 и 0.95 соответственно.
На базе класса CMod2 был написан скрипт Errors_Mod2.mq5, позволяющий, как и в прошлый раз, произвести оценку ошибок прогнозирования. Файлы CMod2.mqh и Errors_Mod2.mq5 размещены в конце статьи в архиве files2.zip.
В таблице 3 приведены результаты работы этого скрипта.
| MAPE1 | MAPE2 | MAPE3 | MAPE1-3 | |
|---|---|---|---|---|
| IndicatorES | 0.2099 | 0.2925 | 0.3564 | 0.2863 |
| Mod1 | 0.2144 | 0.2898 | 0.3486 | 0.2842 |
| Mod2 | 0.2145 | 0.2832 | 0.3413 | 0.2797 |
Таблица 3. Сравнение оценок ошибок прогнозирования
Как следует из таблицы 3, использование адаптивного коэффициента сглаживания в среднем для наших тестовых последовательностей позволило дополнительно немного снизить ошибки прогнозирования. Таким образом, после двух произведенных модернизаций коэффициент ошибок MAPE1-3 удалось снизить примерно на два процента.
Несмотря на то, что результат наших модернизаций оказался весьма скромным, все же остановимся на полученном варианте и оставим дальнейшие модернизации за рамками данной статьи. В качестве следующего шага интересно было бы использовать преобразование Бокса-Кокса (Box-Cox transformation). Это преобразование чаще всего используют для того чтобы приблизить закон распределения исходной последовательности к нормальному.
В нашем случае его можно было бы применить для преобразования исходной последовательности, осуществления прогноза и затем обратного преобразования прогноза. При этом используемый коэффициент преобразования должен быть выбран таким образом, чтобы минимизировать результирующую ошибку прогнозирования. Пример использования преобразования Бокса-Кокса при прогнозировании последовательностей можно найти в статье [7].
4. Доверительный интервал прогноза (Prediction Intervals)
В исходном индикаторе IndicatorES.mq5 (из прошлой статьи) доверительный интервал прогноза вычислялся в соответствии с аналитическими выражениями, выведенными для выбранной модели экспоненциального сглаживания [8]. В нашем случае после внесения изменений изменилась и используемая нами модель. Так как теперь коэффициент сглаживания стал переменным, использовать для определения доверительного интервала указанные аналитические выражения будет уже некорректно.
Дополнительным аргументом в пользу изменения способа определения доверительного интервала может служить тот факт, что используемые ранее аналитические выражения были выведены исходя из предположения симметричности и нормальности закона распределения ошибок прогнозирования. Для нашего класса последовательностей эти условия не выполняются, и распределение ошибок прогнозирования может не быть нормальным и симметричным.
В исходном индикаторе при определении доверительного интервала сначала по входной последовательности вычислялась дисперсия ошибки прогнозирования на один шаг вперед, а затем уже на основании ее величины при помощи аналитических выражений определялась дисперсия для прогноза на два, три и так далее шагов.
Для того чтобы избежать использования аналитических выражений можно воспользоваться простейшим вариантом, когда дисперсия прогноза на два, три и так далее шагов вперед оценивается непосредственно по входной последовательности, так же как и дисперсия прогноза на один шаг вперед. Но такой подход имеет существенный недостаток - при коротких входных последовательностях оценка доверительного интервала будет иметь огромный разброс, а вычисление дисперсии и среднеквадратичной ошибки не позволит снять ограничения на предполагаемую нормальность ошибок.
Выходом из положения в данном случае может служить использование непараметрического бутстрапа (ресамплинг) [9]. Суть идеи можно выразить простыми словами - если случайным образом (равномерный закон распределения) производить выборку с возвратом из исходной последовательности, то созданная таким образом искусственная последовательность будет иметь такой же закон распределения, что и исходная.
Предположим, что у нас имеется входная последовательность размером N элементов, тогда, генерируя псевдослучайную последовательность с равномерным законом распределения в диапазоне [0,N-1] и используя эти значения в качестве индексов при выборке из входного массива, можно сформировать искусственную последовательность значительно большей длины, чем исходная. При этом закон распределения у сгенерированной последовательности будет такой же (почти такой же), как и у исходной.
Порядок использования бутстрапа при оценке доверительных интервалов может быть следующим:
- Для полученной нами в процессе модификации модели экспоненциального сглаживания по входной последовательности определим оптимальные величины исходных значений модели, ее коэффициентов и коэффициентов адаптации. Поиск оптимальных параметров производится, как и раньше, при помощи алгоритма, реализующего метод поиска Пауэлла;
- Используя найденные оптимальные параметры модели, "пройдем" по исходной последовательности и сформируем массив ошибок прогноза на один шаг вперед. Массив будет содержать количество элементов, равное длине входной последовательности N;
- Отцентрируем ошибки, вычитая из каждого элемента массива ошибок их среднее значение;
- Используя генератор псевдослучайной последовательности, будем генерировать индексы в диапазоне [0,N-1] и использовать их для формирования искусственной последовательности ошибок длинной 9999 элементов (ресамплинг);
- Подставляя в выражения, описывающие используемую нами модель, значения из искусственно созданного массива ошибок, сформируем массив, содержащий 9999 значений псевдо-входной последовательности. Другими словами – если раньше в выражения модели подставлялись значения входной последовательности, и при этом вычислялась ошибка прогнозирования, то в данном случае производим обратные вычисления. Для каждого элемента массива подставляем значение ошибки и вычисляем при этом входное значение. В результате получим массив из 9999 элементов содержащий последовательность с таким же законом распределения, как и входная последовательность, но при этом имеющую достаточную длину для непосредственной оценки доверительных интервалов прогноза.
Далее, используя сформированную нами достаточно длинную последовательность, произведем оценку доверительных интервалов. Для этого используем тот факт, что если сформировать массив ошибок прогнозирования и отсортировать его по возрастанию, то для массива содержащего 9999 величин, ячейки массива с индексами 249 и 9749 будут содержать значения соответствующие границам 95% доверительного интервала [10].
Для более точного определения вероятностных границ длина массива выбирается нечетной. В нашем случае для определения границ доверительных интервалов прогноза необходимо проделать следующие шаги:
- Используя найденные ранее оптимальные значения параметров модели, "проходим" по сгенерированной последовательности и формируем массив, содержащий 9999 ошибок прогноза на один шаг вперед;
- Сортируем полученный массив;
- Выбираем из сортированного массива ошибок значения с индексами 249 и 9749, которые и будут являться границами 95% доверительного интервала;
- Повторяем шаги 1, 2 и 3 для ошибок прогнозирования на два, три и так далее шагов вперед.
Такой способ определения доверительных интервалов имеет и преимущества и недостатки.
К преимуществам можно отнести отсутствие предположений о характере закона распределения ошибок прогноза. Совсем не обязательно чтобы они имели нормальный или симметричный закон распределения. Кроме того, такой метод может быть использован тогда, когда невозможно вывести аналитические выражения для используемой модели.
К недостаткам следует отнести резкое увеличение требуемого объема вычислений и чувствительность разброса оценок от качества используемого генератора псевдослучайной последовательности.
Представленный метод определения доверительных интервалов при помощи ресамплинга и квантилей является достаточно примитивным, и наверняка имеются способы его улучшения. Но так как в нашем случае доверительные интервалы предназначены только для визуальной оценки, точности такого метода может оказаться вполне достаточно.
5. Вариант модифицированного индикатора
С учетом представленных в статье модернизаций был создан индикатор ForecastES.mq5. При этом для ресамплинга был использован генератор псевдослучайной последовательности, представленный ранее в статье [11]. Со штатным генератором MathRand() были получены несколько худшие результаты. Возможно, из-за недостаточно широкого диапазона генерируемых им значений [0,32767].
При компиляции индикатора ForecastES.mq5 в том же каталоге должны быть размещены файлы PowellsMethod.mqh, CForeES.mqh и RNDXor128.mqh. Все эти файлы находятся в архиве fore.zip.
Ниже приведен исходный код индикатора ForecastES.mq5.
//----------------------------------------------------------------------------------- // ForecastES.mq5 // 2012, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2012, victorg." #property link "https://www.mql5.com" #property version "1.02" #property description "Forecasting based on the exponential smoothing." #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "ConfUp" // Confidence interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCrimson #property indicator_style3 STYLE_DOT #property indicator_width3 1 #property indicator_label4 "ConfDn" // Confidence interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCrimson #property indicator_style4 STYLE_DOT #property indicator_width4 1 input int nHist=80; // History bars, nHist>=24 #include "CForeES.mqh" #include "RNDXor128.mqh" #define NFORE 12 #define NBOOT 9999 double Hist[],Fore[],Conf1[],Conf2[]; double Data[],Err[],BSDat[],Damp[NFORE],BSErr[NBOOT]; int NDat; CForeES Es; RNDXor128 Rnd; //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NDat=nHist; if(NDat<24)NDat=24; MqlRates rates[]; CopyRates(NULL,0,0,NDat,rates); // Load missing data ArrayResize(Data,NDat); ArrayResize(Err,NDat); ArrayResize(BSDat,NBOOT+NFORE); SetIndexBuffer(0,Hist,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,Fore,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFORE); SetIndexBuffer(2,Conf1,INDICATOR_DATA); // Confidence interval PlotIndexSetString(2,PLOT_LABEL,"ConfUp"); PlotIndexSetInteger(2,PLOT_SHIFT,NFORE); SetIndexBuffer(3,Conf2,INDICATOR_DATA); // Confidence interval PlotIndexSetString(3,PLOT_LABEL,"ConfDN"); PlotIndexSetInteger(3,PLOT_SHIFT,NFORE); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,j,k,start; double s,t,alp,gam,phi,sb,sg,e,f,a,a1,a2; if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar start=rates_total-NDat; //----------------------- PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE); for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data Es.CalcPar(Data); // Optimization of parameters s=Es.GetPar(0); t=Es.GetPar(1); gam=Es.GetPar(2); phi=Es.GetPar(3); sb=Es.GetPar(4); sg=Es.GetPar(5); //---- a=phi; Damp[0]=phi; for(j=1;j<NFORE;j++){a=a*phi; Damp[j]=Damp[j-1]+a;} // Phi table //---- f=s+phi*t; for(i=0;i<NDat;i++) // History { e=Data[i]-f; Err[i]=e; alp=0.05+0.9/(1+MathExp(sb+sg*e*e)); // 0.05 < Alpha < 0.95 a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); Hist[start+i]=f; // History } for(j=0;j<NFORE;j++)Fore[rates_total-NFORE+j]=s+Damp[j]*t; // Forecast //---- a=0; for(i=0;i<NDat;i++)a+=Err[i]; a/=NDat; for(i=0;i<NDat;i++)Err[i]-=a; // alignment of the array of errors //---- f=Es.GetPar(0)+phi*Es.GetPar(1); for(i=0;i<NBOOT+NFORE;i++) // Resampling { j=(int)(NDat*Rnd.Rand_01()); if(j>NDat-1)j=NDat-1; e=Err[j]; BSDat[i]=f+e; alp=0.05+0.9/(1+MathExp(sb+sg*e*e)); // 0.05 < Alpha < 0.95 a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=s+phi*t; } //---- for(j=0;j<NFORE;j++) // Prediction intervals { s=Es.GetPar(0); t=Es.GetPar(1); f=s+phi*t; for(i=0,k=0;i<NBOOT;i++,k++) { BSErr[i]=BSDat[i+j]-(s+Damp[j]*t); e=BSDat[i]-f; a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); } ArraySort(BSErr); Conf1[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[249]; Conf2[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[9749]; } return(rates_total); } //-----------------------------------------------------------------------------------Для большей наглядности программный код индикатора по возможности был написан "линейно". Никакой оптимизации при его написании производить не предполагалось.
На рисунках 1 и 2 приведены результаты работы индикатора для двух различных ситуаций.
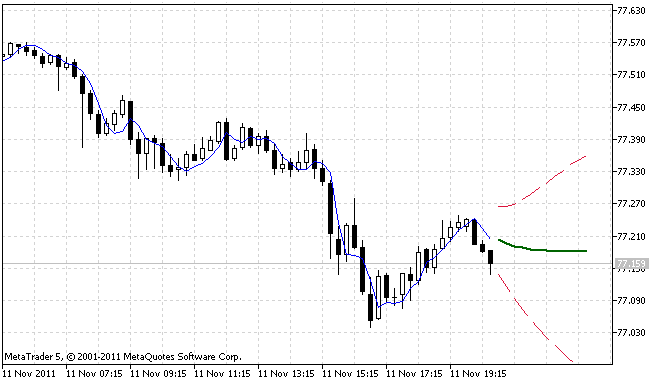
Рисунок 1. Первый пример работы индикатора ForecastES.mq5
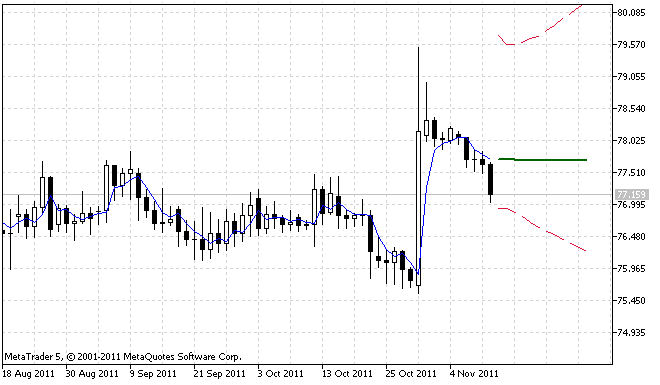
Рисунок 2. Второй пример работы индикатора ForecastES.mq5
На рисунке 2 хорошо видно, что 95% доверительный интервал прогноза несимметричен. Это следствие того, что входная последовательность имеет большой выброс, который привел к несимметричному распределению ошибок прогноза.
Ранее на сайтах www.mql4.com и www.mql5.com публиковались индикаторы-экстраполяторы. Возьмем один из них - ar_extrapolator_of_price.mq5 и, установив значения его параметров, как показано на рисунке 3, сравним его результаты с результатами созданного нами индикатора.
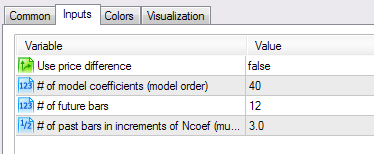
Рисунок 3. Установки индикатора ar_extrapolator_of_price.mq5
Сравнение работы этих двух индикаторов производилось визуально на разных таймфреймах котировок EURUSD и USDCHF. На первый взгляд общее направление прогноза у индикаторов в большинстве случаев совпадает. Хотя, при длительном наблюдении могут встретиться и серьезные расхождения. При этом, конечно, ar_extrapolator_of_price.mq5 всегда будет давать более ломанную прогнозную линию.
На рисунке 4 показан пример одновременной работы индикаторов ForecastES.mq5 и ar_extrapolator_of_price.mq5.
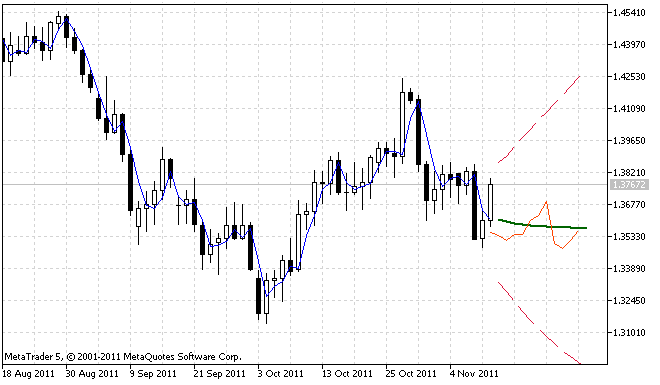
Рисунок 4. Сравнение результатов прогнозирования
Прогнозная линия индикатора ar_extrapolator_of_price.mq5 показана на рисунке 4 сплошной оранжево-красной линией.
Заключение
В результате публикации данной и предыдущей статьи:
- Были представлены модели экспоненциального сглаживания, используемые при прогнозировании временных последовательностей;
- Предложена их программная реализация;
- Кратко рассмотрены вопросы выбора оптимальных начальных значений и параметров моделей;
- Приведена программная реализация алгоритма поиска минимума функции многих переменных методом Пауэлла;
- Приведены программные примеры оптимизации параметров модели прогнозирования по входной последовательности;
- Продемонстрированы некоторые простейшие примеры модернизации алгоритма прогнозирования;
- Кратко рассмотрен способ оценки доверительных интервалов прогноза с использованием бутстрапа и квантилей;
- Создан индикатор ForecastES.mq5 осуществляющий прогнозирование котировок и включающий в себя рассмотренные в статьях приемы и алгоритмы;
- Приведены некоторые ссылки на статьи и журналы и книги, имеющие отношение к данной теме.
В отношении созданного в конечном итоге индикатора ForecastES.mq5 необходимо заметить, что используемый для оптимизации алгоритм, реализующий метод Пауэлла, в определенных случаях может не определить с заданной точностью минимум целевой функции. При этом будет достигнуто максимально разрешенное количество итераций и в журнал будет выведено соответствующее сообщение. Но в коде индикатора эта ситуация никак не обрабатывается. Для демонстрации алгоритмов, представленных в статье, это вполне допустимо, но для серьезных приложений такую ситуацию необходимо отслеживать и как-то обрабатывать.
В качестве дальнейшего направления развития прогнозирующего индикатора можно предложить использовать на каждом шаге одновременно несколько различных моделей прогнозирования с дальнейшим выбором одного из них, например, по информационному критерию Акаике. Или в случае использования нескольких близких по характеру моделей вычислять средневзвешенное значение их результатов прогноза. При этом коэффициенты взвешивания могут выбираться в зависимости от коэффициента ошибок прогноза каждой модели.
Тематика, связанная с прогнозированием временных рядов настолько широка что, к сожалению, в данных статьях не удалось затронуть и малой доли связанных с ней вопросов. Но хочется надеяться, что эти публикации помогут привлечь интерес читателя к вопросам прогнозирования и к дальнейшим работам в этой области.
Ссылки
- "Прогнозирование временных рядов при помощи экспоненциального сглаживания".
- Лукашин Ю.П., Адаптивные методы краткосрочного прогнозирования временных рядов: Учебное пособие. - М.: Финансы и статистика, 2003.-416 с.
- Булашев С.В. Статистика для трейдеров. - М.: Компания Спутник +, 2003. - 245 с.
- Everette S. Gardner Jr., Exponential smoothing: The state of the art – Part II. June 3, 2005.
- James W. Taylor, Smooth Transition Exponential Smoothing. Journal of Forecasting, 2004, Vol. 23, pp. 385-394.
- James W. Taylor, Volatility Forecasting with Smooth Transition Exponential Smoothing. International Journal of Forecasting, 2004, Vol. 20, pp. 273-286.
- Alysha M De Livera. Automatic forecasting with a modified exponential smoothing state space framework. 28 April 2010, Department of Econometrics and Business Statistics, Monash University, VIC 3800 Australia.
- Rob J Hyndman et al. Prediction intervals for exponential smoothing using two new classes of state space models. 30 January 2003.
- Журнал "Квантиль". №3, сентябрь 2007 г.
- http://ru.wikipedia.org/wiki/Квантиль
- "Анализ основных характеристик временных рядов".
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Интервью с Александром Элдером: "Я хочу быть психиатром на рынке"
Интервью с Александром Элдером: "Я хочу быть психиатром на рынке"
 Лига Чемпионов ATC: Интервью с Борисом Одинцовым (ATC 2011)
Лига Чемпионов ATC: Интервью с Борисом Одинцовым (ATC 2011)
 Интервью с Виталием Антоновым (ATC 2011)
Интервью с Виталием Антоновым (ATC 2011)
 Разработка эксперта средствами UML
Разработка эксперта средствами UML
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Виктор, у Вас нет модификации индикаторов со сдвигом по истории? Не только для последнего бара. Хотелось бы приблизительно оценить эффективность реализованных Вами методов.
Нет, сдвинутых индикаторов я не делал.
В файле ForecastES.mq5 исправлены обнаруженные ошибки. Обновленный файл ForecastES.mq5 как и прежде находится в архиве Fore.zip.
Опубликована новая статья Прогнозирование временных рядов с помощью экспоненциального сглаживания (продолжение):
Автор: Виктор
Я много раз пытался найти этот модифицированный новый индикатор в разделе Code Base MT5, но так и не нашел.
Не могли бы вы добавить его в кодовую базу МТ5, чтобы я мог легко скачать его и протестировать? Или, пожалуйста, предоставьте мне модифицированный индикатор и как загрузить его в мой MT5?
Есть ли у вас то же самое для MT4?
Любой, кто может помочь, пожалуйста.
Спасибо
Форум о трейдинге, автоматизированных торговых системах и тестировании торговых стратегий
Обсуждение статьи "Прогнозирование временных рядов с помощью экспоненциального сглаживания"
newdigital, 2014.06.06 21:48
Как стать бесстрашным трейдером на Форекс
- Должны ли вы знать, что произойдет дальше?
- Есть ли лучший способ?
- Стратегии, когда вы знаете, что не знаете
"Хорошее инвестирование - это своеобразный баланс между убежденностью в необходимости следовать своим идеям и гибкостью, чтобы понять, когда вы совершили ошибку".-Майкл Стейнхардт
"95 % торговых ошибок, которые вы, скорее всего, совершите, будут обусловлены вашим отношением к тому, что вы можете ошибиться, потерять деньги, упустить и оставить деньги на столе - четыре торговых страха"
-Марк Дуглас, Trading In the Zone
Многие трейдеры очаровываются идеей прогнозирования. Кажется, что необходимость прогнозирования является неотъемлемой частью успешной торговли. В конце концов, рассуждаете вы, я должен знать, что произойдет дальше, чтобы заработать деньги, верно? К счастью, это не так, и в этой статье мы расскажем о том, как можно хорошо торговать, не зная, что произойдет дальше.
Обязательно ли знать, что произойдет дальше?
Хотя знать, что произойдет дальше, было бы полезно, никто не может знать наверняка. Причина, по которой инсайдерская торговля является преступлением, которое часто проверяется на фондовых рынках, может помочь вам увидеть, что некоторые трейдеры настолько отчаянно хотят знать будущее, что готовы обманывать и платить жесткий штраф, когда их поймают. Короче говоря, опасно думать об определенном будущем, когда на кону стоят ваши деньги, и лучше всего при заключении сделки думать о гранях, а не об определенности.
Проблема с мыслью о том, что вы должны знать, какое будущее ждет вашу сделку, заключается в том, что, когда с вашей сделкой случается что-то неблагоприятное по сравнению с вашими ожиданиями, возникает страх. Сам по себе страх - это не плохо. Однако большинство трейдеров, поставив на кон свои деньги, часто замирают и не могут завершить сделку.
Если вам не нужно знать, что произойдет дальше, то что же вам нужно? Список на удивление короткий и простой, но важнее всего, чтобы вы не думали, что знаете, что произойдет, потому что в этом случае вы, скорее всего, переборщите с кредитным плечом и преуменьшите риски, которые постоянно присутствуют в мире трейдинга.
- Чистый край, по которому вам удобно входить в сделку
- Хорошо определенная точка аннулирования, в которой ваша торговая установка больше не является
- Потенциальная точка входа на развороте
- Соответствующий размер сделки / управление капиталом
Есть ли лучший способ?Вчера Европейский центральный банк принял решение о снижении ставки рефинансирования и депозитной ставки. Многие трейдеры шли на это заседание с короткими позициями, однако пара EURUSD преодолела ~250% дневного диапазона ATR и закрылась вблизи максимумов, что свидетельствует о силе EURUSD. Проще говоря, результат оказался за пределами возможного для большинства трейдеров, и если вы вошли в короткую позицию и были охвачены страхом, то, скорее всего, не закрыли ее и стали очередной "жертвой рынка", что по-другому можно назвать жертвой собственного страха проиграть.
Так как же лучше поступить? Хотите верьте, хотите нет, но нужно подходить к рынку, понимая, насколько эмоциональными могут быть рынки и что лучше не привязываться к тому, куда рынок "должен пойти". Многие трейдеры держатся за убыточную сделку не для того, чтобы улучшить состояние своего счета, а скорее для того, чтобы защитить свое эго. Конечно, лучший путь в трейдинге - это сосредоточиться на защите собственного капитала и оставить свое эго за дверью торгового зала, чтобы оно не влияло на вашу торговлю негативно.
Стратегии, когда вы знаете, что не знаете
.
Есть одна общая черта у трейдеров, которые могут торговать без страха. Они закладывают убыточные сделки в свой подход. Это похоже на гамбит в шахматах, и он лишает многих трейдеров преимущества и силы, которую дает страх. Для тех, кто не играет в шахматы, гамбит - это игра, в которой вы жертвуете малозначимой фигурой, например пешкой, ради получения преимущества. В трейдинге гамбит может стать вашей первой сделкой, которая позволит вам лучше почувствовать преимущество, которое вы ощущаете в момент заключения сделки.
USD Hedge Джеймса Стэнли - отличный пример стратегии, которая работает в предположении, что одна сделка окажется проигрышной. В чем ее смысл? Она заранее предполагает убытки и позволяет вам торговать без страха, который мучает многих трейдеров. Еще один инструмент, который вы можете использовать, чтобы определить, идет ли тренд в вашу пользу или против вас, - это фрактал.
Если посмотреть за пределы мира трейдинга и шахмат, то есть и другие виды бизнеса, которые предполагают убытки и поэтому способны действовать с ясной головой, когда убытки наступают. Это казино и страховые компании. Оба этих бизнеса предполагают убытки и работают только в соответствии с просчитанным риском, они действуют без страха, и вы тоже сможете, если будете предполагать небольшие потери как часть своей стратегии.
Еще одна замечательная цитата Марка Дугласа:
"Чем меньше меня волновало, ошибаюсь я или нет, тем яснее становились вещи, что значительно облегчало вхождение и выход из позиций, сокращение потерь, чтобы мысленно быть готовым воспользоваться следующей возможностью". -Марк Дуглас
Счастливого трейдинга!
Источник