
Ядерная оценка неизвестной плотности вероятности
Введение
Совершенствование языка MQL5 в плане его быстродействия и постоянный рост производительности персональных компьютеров привели к тому, что пользователи платформы MetaTrader 5 все чаще для анализа рынка стали использовать достаточно сложные, развитые математические методы. Эти методы могут принадлежать различным областям экономики, эконометрики, статистики, но в любом случае при их использовании приходится сталкиваться с таким понятием как функция плотности вероятности.
Многие распространенные методы анализа разрабатывались исходя из предположения о нормальности распределения самих данных или о нормальности ошибок в используемой модели. Кроме того, часто для оценки результатов анализа важно знать распределение различных компонент используемой модели. И в том, и в другом случае возникает задача создания, по возможности универсального "инструмента", позволяющего производить оценку неизвестной плотности вероятности.
В данной статье предпринимается попытка создания класса, реализующего более или менее универсальный алгоритм оценки неизвестной функции плотности вероятности. Первоначальная идея заключалась в том, чтобы при этом не использовать никаких внешних средств, то есть предполагалось, что все должно быть реализовано только средствами MQL5. Но в результате от этой первоначальной идеи пришлось несколько отклониться. Понятно, что задача визуальной оценки плотности вероятности включает в себя две самостоятельные части.
Непосредственно вычисление самой оценки и ее визуализация, то есть отображение в виде графика или диаграммы. Вычисления, конечно, реализованы средствами MQL5, а визуализацию пришлось реализовать путем создания HTML-странички и отображением ее в WEB-браузере. Такое решение было выбрано в связи с желанием получить в конечном итоге графический результат в векторной форме.
Но, так как расчетная часть и отображение результатов расчета реализованы отдельно друг от друга, то читатель, конечно, может осуществить визуализацию любым другим доступным ему способом. Тем более что в недалеком будущем можно ожидать появления в составе MetaTrader 5 различного рода библиотек, наверное, в том числе и графических (насколько известно, работа в этом направлении сейчас ведется). В случае появления в составе MetaTrader 5 развитых средств, предназначенных для построения графиков и диаграмм, переделать в предлагаемом решении отображающую часть, при желании будет несложно.
Следует сразу оговориться, что создать действительно универсальный алгоритм для оценки плотности вероятности последовательностей на поверку оказалось недостижимой задачей. Хотя предложенное в статье решение и не является узкоспециализированным, но и назвать его действительно полностью универсальным нельзя. Проблема заключается в том, что, например, для колоколообразных распределений, подобных нормальному и экспоненциальному, критерии оптимальности при оценке плотности оказываются совершенно различными.
Поэтому, если имеется предварительная информация о характере оцениваемого распределения, то всегда можно выбрать решение, которое будет наиболее подходящим для данного конкретного случая. Но, тем не менее, в дальнейшем будем считать, что о характере оцениваемой плотности нам ничего не известно. Наверняка такой подход в какой-то степени повлияет на качество оценок, но будем надеяться, что это окупится за счет возможности производить оценки совершенно различных по характеру плотностей.
В связи с тем, что при анализе рыночной информации чаще всего приходится иметь дело с нестационарными последовательностями, наибольший интерес может представлять оценка плотности последовательностей малой и средней длины. Это принципиальный момент, который во многом определяет выбор используемого метода оценки.
Для действительно длинных последовательностей, которые содержат больше миллиона значений, с большим успехом могут использоваться гистограммы и P-spline. Но для последовательности, содержащей 10-20 значений, с эффективным построением гистограмм возникают некоторые проблемы. Поэтому далее в статье будем ориентироваться в первую очередь на последовательности имеющие длину от 10 до примерно 10000 значений.
1. Методы оценки плотности вероятности
В настоящее время известно большое количество более или менее популярных методов оценки плотности вероятности. Упоминание о них можно легко найти в сети, воспользовавшись поиском, например, по ключевым словам "оценка плотности вероятности", "плотность вероятности"," density estimation" и так далее. Но, к сожалению, выбрать из них самый лучший метод не удалось. Все они в равной степени обладают как определенными преимуществами, так и недостатками.
Традиционно, для оценки плотности используются гистограммы [1]. Использование гистограмм или сглаженных гистограмм способно обеспечить высокое качество оценок плотности вероятности, но лишь в случае последовательностей большой длины. Как уже упоминалось ранее, разделить короткую последовательность на большое количество групп не представляется возможным, а гистограмма, состоящая из 2-3 столбцов, не может составить представления о законе распределения плотности вероятности такой последовательности. Поэтому от использования гистограмм пришлось отказаться.
Другим достаточно известным методом оценки является ядерная оценка плотности (kernel density estimation) [2]. Хорошие иллюстрации, поясняющие суть использования ядерного сглаживания можно найти по ссылке [3]. В конечном итоге, несмотря на все недостатки присущие этому методу, выбор пал именно на него. Некоторые моменты, связанные с реализацией этого метода, будут кратко рассмотрены далее.
Среди прочих методов оценки плотности хотелось бы упомянуть о весьма интересном методе, в котором используется алгоритм "Expectation–maximization" [4]. Этот алгоритм позволяет разделить последовательность на отдельные компоненты имеющие, например, нормальное распределение. После определения параметров отдельных компонент можно просуммировав полученные кривые распределения получить оценку плотности. Упоминание о данном методе можно найти в публикации, размещенной по ссылке [5]. Этот метод, как впрочем, и масса других, при подготовке статьи не был реализован и не тестировался. Большое количество предлагаемых в различных источниках методов оценки плотности не позволяет практически исследовать каждый из них.
Перейдем к рассмотрению выбранного для реализации метода – метода ядерной оценки плотности.
2. Ядерная оценка плотности вероятности
Ядерная оценка плотности вероятности основывается на методе ядерного сглаживания. Познакомиться с принципами этого метода можно, например, в литературе [6], [7].
Основная идея ядерного сглаживания достаточно проста. Пользователи MetaTrader 5 хорошо знакомы с индикатором Moving Average (MA). Работу этого индикатора легко представить себе в виде скользящего по последовательности окна, внутри которого происходит усреднение взвешенных значений последовательности. При этом форма окна может быть прямоугольной, экспоненциальной или какой-либо другой. Легко заметить, что такое же скользящее окно мы видим и при ядерном сглаживании (например, [3]) только, в этом случае окно симметричное.
Примеры наиболее часто используемых при ядерном сглаживании окон можно найти по ссылке [8]. В случае если при ядерном сглаживании используется регрессия нулевого порядка, то взвешенные значения последовательности, которые попали в окно (ядро), так же как и в случае с MA, просто усредняются. Такое же применение оконной функции мы можем видеть и в случае, когда сталкиваемся с вопросами связанными с фильтрацией. Только теперь та же самая процедура будет представлена несколько иначе - при помощи амплитудно-частотной и фазо-частотной характеристики, а ядро (окно) будет называться импульсной характеристикой фильтра.
Приведенные примеры демонстрируют тот факт, что одно и то же явление зачастую может быть представлено различными способами. Что, несомненно, обогащает математический аппарат, но иногда при обсуждении вопросов связанных с данной тематикой может вносить и некоторую путаницу.
Хотя ядерная оценка плотности использует те же самые принципы, что и ядерное сглаживание, о котором уже упоминалось, ее алгоритм имеет некоторые особенности.
Обратимся к выражению, определяющему процедуру оценки плотности в одной точке.
![]()
где
- x - последовательность длиной n;
- K - симметричное ядро;
- h - диапазон, параметр сглаживания.
В дальнейшем для оценок плотности будем использовать только Гауссово ядро:
![]()
Как следует из приведенного ранее выражения, плотность в точке X вычисляется как сумма значений ядра для величин, определяемых разностями между значением X и значениями последовательности. При этом точки X, в которых вычисляется плотность, могут и не совпадать со значениями самой последовательности.
Перечислим основные шаги практической реализации алгоритма ядерной оценки плотности.
- Производим оценку среднего значения и стандартного отклонения входной последовательности.
- Производим нормализацию входной последовательности. Из каждого ее значения вычитаем ранее найденное среднее и делим на величину стандартного отклонения. После такой нормализации исходная последовательность будет иметь нулевое среднее и стандартное отклонение, равное единице. Непосредственно для вычисления плотности такая нормализация не обязательна, но она позволит унифицировать результирующие графики, так как для любой последовательности на шкале X будут располагаться значения, выраженные в единицах стандартного отклонения.
- Находим максимальное и минимальное значение в нормализованной последовательности.
- Создаем два массива, размер которых должен соответствовать желаемому количеству отображаемых на результирующем графике точек. Например, если график предполагается строить по 200 точкам, то размер массивов должен составлять соответственно по 200 значений.
- Оставляем один из созданных массивов для хранения результата, а в другом сформируем значения точек, для которых будет производиться оценка плотности. Для этого в диапазоне между найденными ранее максимальным и минимальным значениями сформируем 200 (для данного примера) равноотстоящих величин и сохраним их в подготовленном массиве.
- Используя приведенное ранее выражение, произведем оценку плотности в 200 (для нашего примера) тестовых точках, сохраняя результат в подготовленном на шаге 4 массиве.
Ниже приведена программная реализация этого алгоритма.
//+------------------------------------------------------------------+ //| CDens.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CDens:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth public: void CDens(void); int Density(double &x[],double hh); void NTpoints(int n); private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CDens::CDens(void) { NTpoints(200); // Default number of test points } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CDens::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Density | //+------------------------------------------------------------------+ int CDens::Density(double &x[],double hh) { int i; double a,b,min,max,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) min=X[ArrayMinimum(X)]; max=X[ArrayMaximum(X)]; b=(max-min)/(Np-1.0); for(i=0;i<Np;i++)T[i]=min+b*(double)i; // Create test points //-------------------------------- Bandwidth selection h=hh; if(h<0.001)h=0.001; H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Gaussian kernel density estimation | //+------------------------------------------------------------------+ void CDens::kdens(double h) { int i,j; double a,b,c; c=MathSqrt(M_PI+M_PI)*N*h; for(i=0;i<Np;i++) { a=0; for(j=0;j<N;j++) { b=(T[i]-X[j])/h; a+=MathExp(-b*b*0.5); } Y[i]=a/c; // pdf } } //--------------------------------------------------------------------
Метод NTpoints() позволяет установить необходимое количество тестовых равноотстоящих точек, для которых будет производиться оценка плотности. Обращение к этому методу должно производиться до обращения к методу Density(). При обращении к методу Density() ему в качестве параметров передается ссылка на массив, содержащий входные данные и значение диапазона (параметра сглаживания).
В случае удачного завершения метод Density() возвращает ноль, а в массивах T[] и Y[] данного класса будут размещены значения тестовых точек и результаты оценок соответственно.
Размеры этих массивов задаются при обращении к NTpoints(), а по умолчанию их размер составляет 200 значений.
Следующий пример скрипта демонстрирует порядок использования представленного класса CDens.
#include "CDens.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i; int ndata=1000; // Input data length int npoint=300; // Number of test points double X[]; // Array for data double T[]; // Test points for pdf estimating double Y[]; // Array for result ArrayResize(X,ndata); ArrayResize(T,npoint); ArrayResize(Y,npoint); for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data CDens *kd=new CDens; kd.NTpoints(npoint); // Setting number of test points kd.Density(X,0.22); // Density estimation with h=0.22 ArrayCopy(T,kd.T); // Copy test points ArrayCopy(Y,kd.Y); // Copy result (pdf) delete(kd); // Result: T[]-test points, Y[]-density estimation } //--------------------------------------------------------------------
В этом примере подготавливаются массивы для хранения входной последовательности тестовых точек и результатов оценки. Затем, для примера, массив X[] заполняется случайными значениями. После того как данные подготовлены, создается экземпляр класса CDens.
Далее обращением к методу NTpoints() задается необходимое количество тестовых точек, в данном примере npoint=300. Если нет необходимости изменять заданное по умолчанию количество точек, то обращение к методу NTpoints() можно исключить.
После обращения к методу Density() вычисленные значения копируются в заранее подготовленные массивы, и затем удаляется созданный ранее экземпляр класса CDens. Приведенный пример демонстрирует только взаимодействие с классом CDens и никаких дальнейших действий с полученными результатами (массивы T[] и Y[]) не производится.
Если эти результаты предполагается использовать для построения графика, то это несложно сделать, отложив по шкале X графика значения из массива T[], а по шкале Y - соответствующие значения из массива Y[].
3. Выбор оптимального диапазона
На рисунке 1 показаны графики оценки плотности для последовательности с нормальным законом распределения и различными значениями диапазона h.
Оценки произведены при помощи приведенного выше класса CDens. Графики были построены в виде HTML-страницы. В конце статьи будет представлен используемый в статье способ построения таких графиков. О построении графиков и диаграмм в формате HTML можно посмотреть в публикации [9].
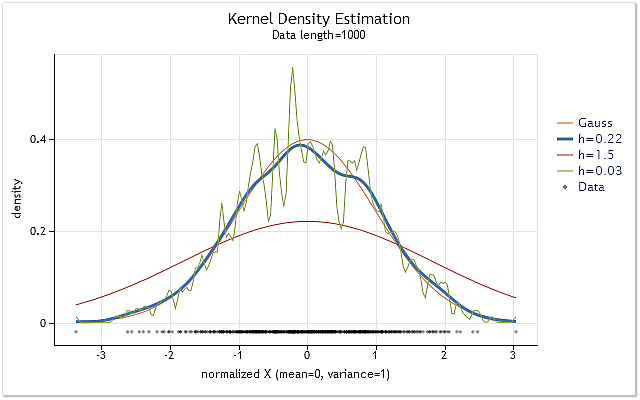
Рис. 1. Оценка плотности для различных значений диапазона h
На рисунке 1 кроме трех оценок плотности показана и истинная кривая плотности нормального распределения (Гауссово распределение). Нетрудно заметить, что в данном случае наиболее приемлемый результат оценки был получен при h=0.22. В двух других случаях наблюдается явное "пересглаживание" и "недосглаживание".
Рисунок 1 хорошо иллюстрирует насколько важным, при использовании ядерной оценки плотности, является правильный выбор диапазона h. При неудачном выборе значения h оценка будет иметь большое смещение по отношению к истинной плотности или слишком большую дисперсию.
Оптимальному выбору диапазона h посвящено много различных работ. Часто при выборе h используется предложенная Сильверманом (Silverman's rule of thumb) достаточно простая и хорошо себя зарекомендовавшая оценка (cм. [10]).
![]()
Здесь A – наименьшее из значений стандартного отклонения последовательности и интерквартильного диапазона последовательности, деленого на 1.34.
Учитывая, что в приведенном ранее классе CDens входная последовательность после нормализации имеет стандартное отклонение равное единице, нетрудно реализовать данное правило, используя следующий фрагмент кода:
ArraySort(X); i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb
Данная оценка хорошо подходит для последовательностей с плотностью вероятности, по форме близкой к нормальной.
Во многих случаях, при отклонении формы оцениваемой плотности от нормальной, учет интерквартильного диапазона позволяет скорректировать в меньшую сторону значение величины h, что делает предложенную оценку достаточно универсальной. Поэтому данное эмпирическое правило имеет смысл использовать в качестве начальной базовой оценки значения h, тем более что при этом не приходится производить громоздких вычислений.
Кроме асимптотических и эмпирических оценок значения диапазона h существуют также различные методы, построенные на предварительном анализе непосредственно самой входной последовательности. В этом случае оптимальная величина h определяется с учетом предварительной оценки характера неизвестной плотности. Сравнение эффективности некоторых из этих методов можно найти в публикациях [11],[12].
Судя по результатам тестов, опубликованным в различных источниках, одним из наиболее эффективных методов оценки диапазона является "Sheather-Jones plug-in method", далее SJPI. Остановим свой выбор именно на этом методе. Для того чтобы не перегружать статью громоздкими математическими выражениями, обсудим далее лишь некоторые особенности данного метода. При необходимости, с математикой этого метода можно познакомиться в публикации [13].
Используемое нами Гауссово ядро является ядром с неограниченным носителем (т.е. оно определено при изменении его параметра от минус до плюс бесконечности). Как следует из приведенного ранее выражения, при прямом способе вычисления и ядре с неограниченным носителем, для оценки плотности в M точках последовательности длиной N, нам понадобится O(M*N) операций. Для случая, когда необходимо произвести оценку в каждой из точек последовательности, эта величина возрастает до O(N*N) операций и время, затрачиваемое на вычисление, будет возрастать пропорционально квадрату длины последовательности.
Такая высокая потребность в вычислительных ресурсах является одним из основных недостатков метода ядерного сглаживания. С реализацией SJPI-метода, в плане требуемого объема вычислений, дело обстоит не лучше. Не вдаваясь в подробности, отметим, что при реализации SJPI-метода нам необходимо сначала дважды вычислить сумму производных от плотности по всей длине входной последовательности.
Затем, используя полученные результаты, следует многократно вычислять оценку, значение которой должно быть равным нулю. Для поиска аргумента, при котором эта функция равна нулю, может использоваться Newton-Raphson метод [14]. При прямом методе вычисления расчет оптимального значения диапазона SJPI-методом может потребовать примерно до десяти раз больше времени, чем непосредственно само вычисление оценок плотности.
Известны различные методы ускорения расчетов при ядерном сглаживании и ядерной оценке плотности. В нашем случае используется Гауссово ядро, значения которого мы можем считать пренебрежительно малыми для величин аргумента превышающих 4. Поэтому если значение аргумента больше 4, то вычисление значения ядра можно не производить, тем самым частично сократив требуемое количество вычислений. При построении графика такой оценки, по сравнению с полным вариантом расчета, какую-либо разницу вряд ли удастся заметить.
Другим простым способом ускорения расчетов может служить сокращение количества точек, для которых производится оценка. Как уже упоминалось, если M меньше N, то количество требуемых операций сократится с O(N*N) до O(M*N). Если мы имеем длинную последовательность, например, N=100000, то производя оценки только в M=200 точках, мы получим весьма существенный выигрыш по времени вычислений.
Для сокращения требуемого количества вычислений используются и более сложные методы, например, оценки с использованием алгоритма быстрого преобразования Фурье или вейвлет-преобразования. Для действительно длинных последовательностей могут с успехом использоваться и методы, основанные на сокращении размерности входной последовательности, например, "Data binning" [15].
Кроме перечисленных способов ускорения расчетов, в случае, если используется Гауссово ядро, может быть применено и быстрое Гауссово преобразование [16]. Для реализации SJPI-метода оценки значения диапазона воспользуемся основанном на Гауссовом преобразовании алгоритме, опубликованном по ссылке [17]. По этой ссылке можно найти и публикации с описанием метода, и программные коды, реализующие предложенный алгоритм.
4. Sheather-Jones plug-in (SJPI)
Опять же, как и в случае с математическими выражениями, определяющими суть метода SJPI, не будем копировать в данную статью и математические выкладки, связанные с реализацией, представленного по ссылке [17] алгоритма. Заинтересованный читатель может в случае необходимости самостоятельно познакомится с публикациями, размещенными по ссылке [17].
На базе материалов, размещенных по ссылке [17], был создан класс CSJPlugin, который предназначен для вычисления оптимального значения диапазона h и включает в себя только один доступный (public) метод – double CSJPlugin::SelectH(double &px[],double h,double stdev=1).
При обращении к этому методу в качестве параметров ему передаются следующие аргументы:
- double &px[] – ссылка на массив, содержащий исходную последовательность;
- double h – начальное значение диапазона h, относительно которого будет производится поиск при решении уравнений алгоритмом Ньютона-Рапсона. Желательно чтобы это значение было как можно ближе к искомому, это может существенно сократить время, затраченное на решение уравнений, и поможет снизить вероятность возникновения ситуаций, при которых метод Newton-Raphson может потерять устойчивость. В качестве начального значения h можно использовать величину, найденную по эмпирическому правилу Сильвермана;
- double stdev=1 – значение стандартного отклонения исходной последовательности. По умолчанию равно единице. В нашем случае изменять принятую по умолчанию величину не понадобится, так как данный метод предполагается использовать совместно с приведенным ранее классом CDens, в котором исходная последовательность уже нормирована и всегда имеет равное единице стандартное отклонение.
В случае успешного завершения метод SelectH() возвращает найденное оптимальное значение диапазона h. В случае неудачи будет возвращено переданное в качестве параметра начальное значение h. Исходный код класса CSJPlugin размещен в файле CSJPlugin.mqh.
Необходимо пояснить некоторые особенности данной реализации.
Исходная последовательность сразу преобразуется к интервалу [0,1], а начальное значение диапазона h нормируется пропорционально масштабу преобразования исходной последовательности. К найденному в результате вычислений оптимальному значению h применяется обратная нормировка.
В конструкторе класса CSJPlugin задается eps=1e-4 - точность вычисления оценок плотности и ее производных и P_UL=500 – максимально допустимое количество внутренних итераций алгоритма. Подробнее см. в [17].
В методе SelectH() задается IMAX=20 - максимально допустимое количество итераций для Newton-Raphson метода и PREC=1e-4 – точность решения уравнения этим методом.
Традиционное использование Newton-Raphson метода предполагает необходимость расчета на каждой итерации значения самой целевой функции и ее производной в той же точке. В данном случае расчет производной был заменен на ее оценку, вычисляемую при помощи добавления небольшого приращения к значению ее аргумента.
На рисунке 2 приведен пример использования двух различных способов оценки оптимального значения диапазона h.
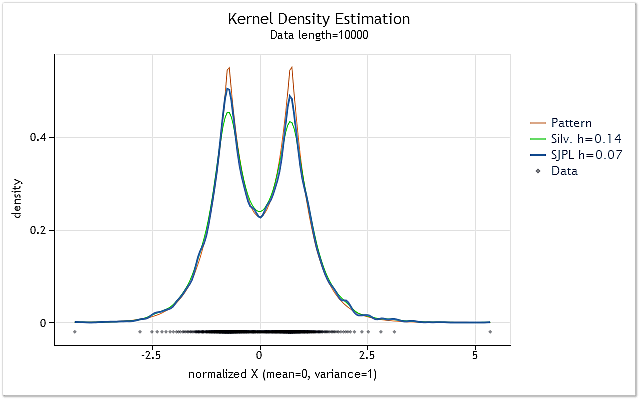
Рис. 2. Сравнение оценок оптимального значения диапазона h
На рисунке 2 представлены две оценки для случайной последовательности, истинная плотность которой показана графиком красного цвета (Pattern).
Оценки были выполнены для последовательности длиной 10000 элементов. При использовании эмпирического правила Сильвермана для этой последовательности было получено значение диапазона h=0.14, а при использовании SJPI-метода h=0.07.
Сравнивая приведенные на рисунке 2 результаты ядерной оценки плотности для этих двух значений h, нетрудно заметить, что применение SJPI-метода позволило получить по сравнению с правилом Сильвермана более привлекательную оценку h. Как видим, при h=0.07 острые вершины оказались заметно лучше проработаны, а на пологих спадах увеличения дисперсии практически не видно.
Как и ожидалось, использование SJPI-метода во многих случаях позволяет получить весьма удачные оценки диапазона h. Несмотря на то, что при создании класса CSJPlugin были использованы достаточно быстрые алгоритмы [17], оценка величины h этим методом для длинных последовательностей все же может занять слишком много времени.
Другим недостатком этого метода можно считать его склонность к завышению оценки значения h для коротких последовательностей, состоящих всего из 10-30 значений. При этом оценки SJPI-методом могут превышать оценки h, сделанные при помощи эмпирического правила Сильвермана.
Для того чтобы в какой то мере учесть эти недостатки, в дальнейшей реализации будут использоваться следующие правила:
- По умолчанию, оценкой для диапазона h будет являться оценка Сильвермана, а SJPI-метод можно будет задействовать отдельной командой;
- При использовании SJPI-метода, в качестве результирующей величины h всегда будет выбираться наименьшее из значений полученных двумя упомянутыми методами.
5. Граничный эффект
Желание использовать при оценке плотности по возможности оптимальное значение диапазона привело к созданию упомянутого достаточно громоздкого класса CSJPlugin. Но кроме проблем, связанных с определением величины диапазона и высокой ресурсоемкостью метода ядерного сглаживания, существует и еще одна проблема. Это так называемый граничный эффект.
Суть проблемы проста. Проиллюстрируем ее на примере использования ядра, определенного на отрезке [-1,1]. Такое ядро называют ядром с конечным носителем. За пределами указанного диапазона ядро принимает нулевые значения (не существует).
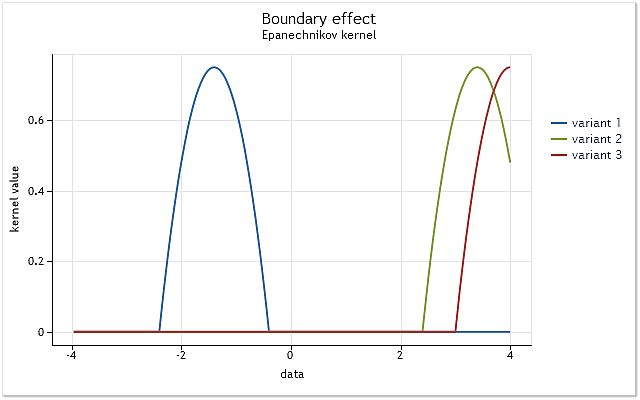
Рис. 3. Усечение ядра на границе диапазона
Как показано на рисунке 3, в первом случае ядро полностью охватывает исходные данные, лежащие в диапазоне [-1,1] относительно его центра. По мере смещения ядра (например, вправо) возникает ситуация, когда данных оказывается недостаточно для того, чтобы полностью использовать выбранную функцию ядра.
При этом ядро охватывает уже меньшее количество данных, чем в первом случае. Наихудшим вариантом является случай, когда центр ядра оказывается на границе последовательности данных. Количество данных, охваченных ядром, при этом сокращается до 50%. Такое снижение количества данных, используемых для оценки плотности, приводит к существенному смещению оценок и увеличению их дисперсии в точках, близких к границам диапазона.
На рисунке 3 приведен пример усечения на границе диапазона для ядра с конечным носителем (ядро Епанечникова). Следует заметить, что при реализации метода ядерной оценки плотности нами было использовано Гауссово ядро, определенное на бесконечном диапазоне (бесконечный носитель). Теоретически отсечка такого ядра происходит всегда. Но учитывая тот факт, что значение этого ядра для больших аргументов практически равно нулю, граничные эффекты для него проявляются так же, как и для ядер с конечным носителем.
В представленных на рисунке 1 и рисунке 2 примерах указанное явление не могло существенно повлиять на результаты оценки плотности, так как в обоих случаях оценка производилась для распределений, плотность вероятности которых спадала на границах практически до нуля.
Для того чтобы наглядно продемонстрировать влияние отсечки ядра на границах диапазона, сформируем последовательность, используя ряд положительных целых чисел X=1,2,3,4,5,6,…n. Такая последовательность имеет равномерный закон распределения плотности вероятности. То есть оценка плотности этой последовательности должна представлять собой горизонтальную прямую линию, расположенную на отличном от нуля уровне.
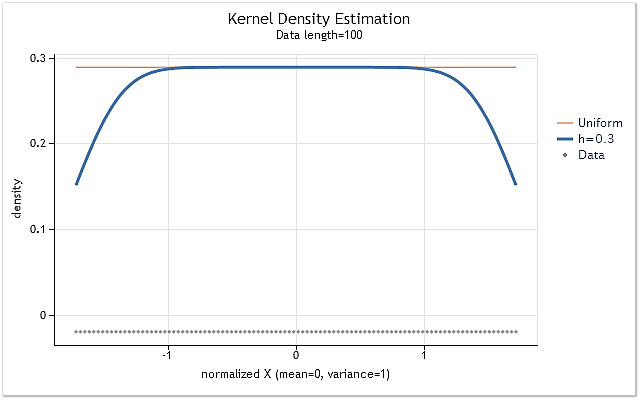
Рис. 4. Оценка плотности для последовательности с равномерным законом распределения
На рисунке 4 хорошо видно что, как и предполагалось, на границах диапазона наблюдается серьезное смещение оценок плотности. Для того чтобы в большей или меньшей степени снизить возникающее на границах смещение, используются различные методы, которые можно условно разделить на следующие группы:
- Методы отражения данных;
- Методы преобразования данных;
- Методы псевдо-данных;
- Методы граничных ядер.
Идея использования отраженных данных заключается в том, что входную последовательность искусственно увеличивают, дополняя ее данными, которые являются как бы зеркальным ее отражением по отношению к границам диапазона последовательности. После такого расширения оценку плотности производят для тех же точек, что и для исходной последовательности, но при этом в оценке уже участвуют и искусственно добавленные данные.
Методы, предполагающие преобразование данных, ориентированы на преобразование последовательности вблизи границ ее диапазона. Например, может использоваться логарифмическое или какое-либо другое преобразование, позволяющее в процессе оценки плотности как бы деформировать масштаб данных при приближении к границе диапазона.
Для искусственного расширения (дополнения) исходной последовательности могут быть использованы так называемые псевдо-данные. Это данные, которые вычисляются на основании значений исходной последовательности. Они призваны учитывать ее поведение на границах и соответствующим, оптимальным образом дополнять ее.
Большое количество работ посвящено методам граничных ядер. В этих методах ядро тем или иным способом изменяет при приближении к границе свою форму. Форма ядра изменяется таким образом, чтобы скомпенсировать возникающее на границах смещение оценок.
В публикации [18] представлены некоторые методы, призванные скомпенсировать искажения, возникающие на границах диапазона, приводится их сравнение и оценка эффективности.
В результате непродолжительных экспериментов для дальнейшего использования был выбран метод отражения данных. На выбор повлиял тот факт, что при использовании этого метода не возникает ситуаций, когда оценка плотности может принять отрицательное значение. Кроме того этот метод не требует сложных математических вычислений. При этом общее количество операций, конечно, все равно возрастает за счет необходимости производить каждую оценку по последовательности, длина которой искусственно увеличена.
Реализовать данный метод можно двумя способами. Во-первых, можно сразу дополнить исходную последовательность необходимыми данными, увеличив при этом ее размер в три раза. И далее производить оценки точно так же, как показано в представленном ранее классе CDens. Но можно и не расширять входной массив с данными, а просто определенным образом повторно выбирать из него данные. Для практической реализации был выбран второй способ.
В приведенном ранее классе CDens оценка плотности была реализована в функции void kdens(double h). Изменим эту функцию, добавив коррекцию граничных искажений.
Дополненная функция может выглядеть следующим образом.
//+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
Функция реализована с учетом того, что исходные данные в массиве X[] к моменту вызова этой функции уже отсортированы. Это позволяет легко исключить из повторной обработки два элемента последовательности, соответствующие самым крайним значениям диапазона. При реализации этой функции была предпринята попытка по возможности вынести математические операции за пределы циклов. В результате функция стала менее наглядно отражать суть используемого алгоритма.
Ранее уже упоминалось о том, что количество вычислений можно несколько сократить, если не вычислять значение ядра для больших величин аргументов, что и реализовано в приведенной функции. При этом после построения графика оцениваемой плотности, каких-либо изменений визуально заметить практически невозможно.
При использовании модифицированного варианта функции kdens() оценка плотности, показанная на рисунке 4, превращается в прямую линию, спады на границах полностью исчезают. Но такую идеальную коррекцию можно достичь только в случае, если распределение на участках вблизи границ имеет нулевой градиент, то есть представлено горизонтальной линией.
Если оцениваемая плотность распределения вблизи границы резко возрастает или спадает, то выбранный метод отражения данных будет уже не в состоянии полностью скорректировать граничный эффект. Сказанное иллюстрируется следующими рисунками.
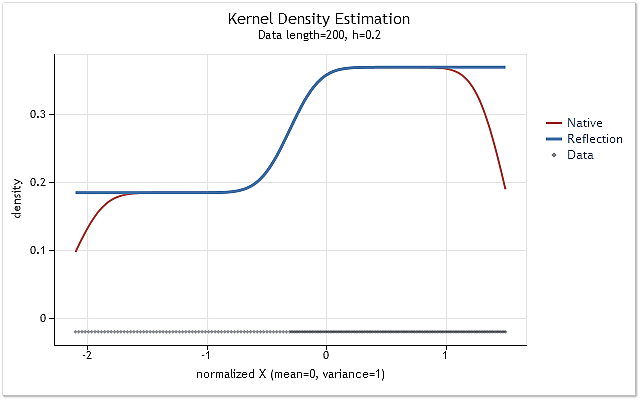
Рис. 5. Ступенчато изменяющаяся плотность вероятности
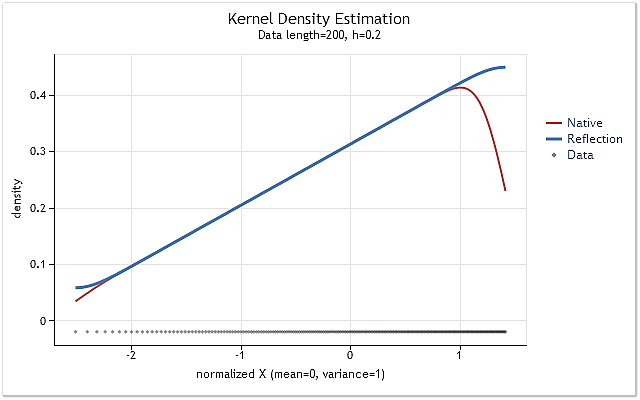
Рис. 6. Линейно возрастающая плотность вероятности
На рисунках 5 и 6 красным цветом показана оценка плотности, полученная с помощью первоначального варианта функции kdens(), а синим цветом – оценка с учетом внесенных в нее изменений, реализующих метод отражения данных. Если в случае показанном на рисунке 5 граничный эффект полностью скорректирован, то на рисунке 6 мы видим, что смещение на границах полностью не устранено. Если оцениваемая плотность возле границы резко возрастает или спадает, то она оказывается вблизи этой границы как бы несколько сглаженной.
Выбранный для корректировки граничного эффекта метод отражения данных не является самым лучшим или самым худшим из известных методов. Хотя этот метод и не может во всех случаях полностью устранить граничный эффект, он достаточно стабилен и его легко реализовать. Этот метод обеспечивает получение логичного и всегда предсказуемого результата.
6. Окончательная реализация. Класс CKDensity
Добавим в ранее созданный класс CDens возможность автоматического выбора значения диапазона h и коррекцию граничного эффекта.
Ниже приведен исходный код такого модифицированного класса.
//+------------------------------------------------------------------+ //| CKDensity.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #include "CSJPlugin.mqh" //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CKDensity:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth int Pflag; // SJ plug-in bandwidth selection flag public: void CKDensity(void); int Density(double &x[],double hh=-1); void NTpoints(int n); void PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;} private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CKDensity::CKDensity(void) { NTpoints(200); // Default number of test points Pflag=0; // Not SJ plug-in } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CKDensity::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Bandwidth selection and kernel density estimation | //+------------------------------------------------------------------+ int CKDensity::Density(double &x[],double hh=-1) { int i; double a,b,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); // Sort input data Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) a=X[0]; b=(X[N-1]-a)/(Np-1.0); for(i=0;i<Np;i++)T[i]=a+b*(double)i; // Create test points //-------------------------------- Bandwidth selection if(hh<0) { i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb if(Pflag==1) { CSJPlugin *plug=new CSJPlugin(); a=plug.SelectH(X,h); // SJ Plug-in delete plug; h=MathMin(a,h); } } else {h=hh; if(h<0.005)h=0.005;} // Manual select H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void CKDensity::kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
Основным методом этого класса является метод Density(double &x[],double hh=-1). Первым аргументом является ссылка на массив x[], в котором должна содержаться входная анализируемая последовательность. Длина входной последовательности должна быть не менее восьми элементов. Второй (необязательный) аргумент служит для принудительного задания величины диапазона h.
При этом может быть задано любое положительное число. Заданное значение h всегда будет ограничено снизу величиной 0.005. Если этот параметр имеет отрицательное значение, то величина диапазона будет выбираться автоматически. Метод Density() в случае удачного завершения возвращает ноль, а в случае аварийного завершения минус единицу.
После обращения к методу Density() и его успешного завершения массив T[] будут содержать значения тестовых точек, для которых производилась оценка плотности, а массив Y[] – содержать значения этих оценок. Массив X[] будет содержать нормированную и отсортированную входную последовательность. При этом среднее значение этой последовательности будет равно нулю, а величина стандартного отклонения равна единице.
В переменных, являющихся членами класса, будут содержаться следующие значения:
- N – длина входной последовательности;
- Np – количество тестовых точек, в которых произведена оценка плотности;
- Mean – среднее значение входной последовательности;
- Var – дисперсия входной последовательности;
- StDev – стандартное отклонение входной последовательности;
- H – значение диапазона (параметра сглаживания);
- Pflag – флаг использования SJPI-метода для определения оптимального значения диапазона h.
Метод NTpoints(int n) служит для задания количества тестовых точек, в которых будет производиться оценка плотности. Задание количества тестовых точек должно быть произведено перед обращением к основному методу Density(). Если метод NTpoints(int n) не использовать, то будет установлено принятое по умолчанию количество точек равное 200.
Метод PluginMode(int m) позволяет разрешить или запретить использование SJPI-метода для оценки оптимального значения диапазона. Если при обращении к этому методу использовать параметр равный единице, то для определения диапазона h будет задействован SJPI-метод. Если значение параметра данного метода не равно единице, то SJPI-метод использоваться не будет. Если обращения к методу PluginMode(int m) не производилось, то SJPI-метод будет по умолчанию отключен.
7. Построение графиков
В процессе написания данной статьи для построения графиков использовался метод, ранее представленный в публикации [9]. В публикации было предложено использовать заранее подготовленную HTML-страничку, включающую в себя JavaScript библиотеку highcharts [19] и полное определение всех обращений к ней. Далее MQL-программа формировала текстовый файл с предназначенными для отображения данными, который подключался к упомянутой HTML-странице.
При таком подходе, для того чтобы внести какие-либо изменения в структуру отображаемых графиков необходимо править HTML-страницу, изменяя включенный в нее JavaScript код. Для того чтобы избежать этого был разработан простейший интерфейс, позволяющий формировать обращения к методам JavaSctipt библиотеки highcharts непосредственно из MQL-программы.
При создании интерфейса задача реализации доступа ко всем возможностям библиотеки highcharts не ставилась. Были реализованы лишь возможности, позволившие при написании статьи ни разу не исправлять предварительно созданный HTML-файл.
Ниже приведен исходный код класса CLinDraw, который был использован для организации связки с методами библиотеки highcharts. Данный код не следует рассматривать как законченную программную реализацию, это, скорее всего, пример, демонстрирующий возможность создания интерфейса с графической JavaScript библиотекой.
//+------------------------------------------------------------------+ //| CLinDraw.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #import "shell32.dll" int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters, string lpDirectory,int nShowCmd); #import #import "kernel32.dll" int DeleteFileW(string lpFileName); int MoveFileW(string lpExistingFileName,string lpNewFileName); #import //+------------------------------------------------------------------+ //| type = "line","spline","scatter" | //| col = "r,g,b,y" | //| Leg = "true","false" | //| Reference: http://www.highcharts.com/ | //+------------------------------------------------------------------+ class CLinDraw:public CObject { protected: int Fhandle; // File handle int Num; // Internal number of chart line string Tit; // Title chart string SubTit; // Subtitle chart string Leg; // Legend enable/disable string Ytit; // Title Y scale string Xtit; // Title X scale string Fnam; // File name public: void CLinDraw(void); void Title(string s) { Tit=s; } void SubTitle(string s) { SubTit=s; } void Legend(string s) { Leg=s; } void YTitle(string s) { Ytit=s; } void XTitle(string s) { Xtit=s; } int AddGraph(double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double y,string type,string name,int w=0,string col=""); int LDraw(int ashow=1); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CLinDraw::CLinDraw(void) { Num=0; Tit=""; SubTit=""; Leg="true"; Ytit=""; Xtit=""; Fnam="CLinDraw.txt"; Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI); if(Fhandle<0) { Print(__FUNCTION__,": Error! FileOpen() error."); return; } FileSeek(Fhandle,0,SEEK_SET); // if file exist } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(y); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("%.5g,",y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("%.5g]},\n",y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| LDraw | //+------------------------------------------------------------------+ int CLinDraw::LDraw(int ashow=1) { int i,k; string pfnam,to,p[]; FileWriteString(Fhandle,"]});\n});"); if(Fhandle<0)return(-1); FileClose(Fhandle); pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\"+Fnam; k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("\\",0),p); to=""; for(i=0;i<k-1;i++)to+=p[i]+"\\"; to+="ChartTools\\"; // Folder name DeleteFileW(to+Fnam); MoveFileW(pfnam,to+Fnam); if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1); return(0); }
Для нормального функционирования этого класса необходима заранее подготовленная HTML-страница с подключенными JavaScript библиотеками и определяющая размер и размещение поля, предназначенного для последующего построения на нем одного или нескольких графиков. Пример реализации такой страницы можно найти в приложенных к статье файлах.
При обращении к методу AddGraph() в текстовом файле, который затем подключается к заранее созданной HTML-странице, формируется соответствующий JavaScript код. Этот код через обращение к графической библиотеке обеспечивает построение графика по данным, переданным методу AddGraph() в качестве аргумента. При повторном обращении к этому методу на поле вывода можно добавить еще один или несколько графиков.
В класс CLinDraw включено три варианта перегружаемой функции AddGraph(). Один из вариантов требует передачи ему в качестве аргумента только одного массива с отображаемыми данными. Он предназначен для построения графика последовательности с отображением по шкале X номера элемента этой последовательности.
Другой вариант получает в качестве аргумента два массива, в которых содержатся значения, отображаемые по шкале X и Y соответственно. Третий вариант позволяет для шкалы Y задавать постоянное значение. Он может быть использован для построения горизонтальной линии. Остальные аргументы у этих функций одинаковые:
- string type – тип отображаемого графика. Может принимать значения "line","spline","scatter";
- string name – имя, присваемое данному графику;
- int w=0 – толщина линии. Необязательный аргумент. Если значение равно 0 используется заданная по умолчанию толщина 2;
- string col="" – задает цвет линии и значение ее непрозрачности. Необязательный аргумент.
Метод LDraw() необходимо вызывать в последнюю очередь. Этот метод завершает вывод JavaScript кода и данных в текстовый файл, который по умолчанию создается в каталоге \MQL5\Files\. Далее этот файл перемещается в каталог, в котором расположены файлы графической библиотеки и HTML-файл.
Метод LDraw() может принимать единственный необязательный аргумент. Если значение этого аргумента не задавать или задать равным единице, то после перемещения файла с данными в соответствующий каталог произойдет вызов установленного по умолчанию WEB-браузера и отображение графика. Если задать отличное от единицы значение аргумента, то файл с данными будет так же полностью сформирован, но WEB-браузер автоматически вызван не будет.
Другие доступные методы класса CLinDraw позволяют задать заголовки графика и подписи к его осям. Более подробно вопросы, связанные с использованием библиотеки highcharts и класса CLinDraw, в данной статье рассматривать не будем. Исчерпывающую информацию по графической библиотеке highcharts можно найти по ссылке [19], а примеры ее использования для построения графиков и диаграмм в [9], [20].
Для нормального функционирования класса CLinDraw, в терминале должно быть разрешено использование внешних библиотек.
8. Пример оценки плотности и размещение файлов
В конечном итоге мы получили три класса - CKDensity, CSJPlugin и CLinDraw.
Ниже приведен исходный код примера, демонстрирующего вариант их использования.
//+------------------------------------------------------------------+ //| KDE_Example.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CKDensity.mqh" #include "ChartTools\CLinDraw.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double a; int ndata=1000; // Input data length double X[]; // Array for data double Z[]; // Array for graph of a Laplace distribution double Sc[]; // Array for scatter plot //-------------------------- Preparation of the input sequence ArrayResize(X,ndata+1); i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X); if(i!=ndata+1) { Print("Not enough historical data."); return; } for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns ArrayResize(X,ndata); //-------------------------- Kernel density estimation CKDensity *kd=new CKDensity; kd.PluginMode(1); // Enable Plug-in mode kd.Density(X); // Density estimation //-------------------------- Graph of a Laplace distribution n=kd.Np; // Number of test point ArrayResize(Z,n); for(i=0;i<n;i++) { a=MathAbs(kd.T[i]*M_SQRT2); Z[i]=0.5*MathExp(-a)*M_SQRT2; } //-------------------------- Scatter plot n=kd.N; // Data length if(n<400) { ArrayResize(Sc,n); for(i=0;i<n;i++)Sc[i]=kd.X[i]; } else // Decimation of data { ArrayResize(Sc,400); for(i=0;i<400;i++) { a=i*(n-1.0)/399.0+0.5; Sc[i]=kd.X[(int)a]; } } //-------------------------- Visualization CLinDraw *ld=new CLinDraw; ld.Title("Kernel Density Estimation"); ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H)); ld.YTitle("density"); ld.XTitle("normalized X (mean=0, variance=1)"); ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1"); ld.AddGraph(kd.T,kd.Y,"line","Estimation"); ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4"); ld.LDraw(); // With WEB-browser autostart // ld.LDraw(0); // Without autostart delete(ld); delete(kd); }
Вначале скрипта KDE_Example.mq5 подготавливаются данные, для которых будет производиться оценка функции плотности вероятности. Для этого в массив X[] копируются значения "open" текущего инструмента и текущего периода. Затем на их основе вычисляются логарифмические доходности (logarithmic return).
На следующем шаге создается экземпляр класса CKDensity. Обращение к его методу PluginMode() разрешает использование SJPI-метода для оценки диапазона h. После этого производится оценка плотности для созданной в массиве X[] последовательности. На этом процедура оценки завершается, далее следуют шаги, связанные с визуализацией полученной оценки плотности.
Для сравнения полученной оценки с каким-либо известным законом распределения в массиве Z[] формируются значения, соответствующие закону распределения Лапласа. После этого в массиве Sc[] сохраняются нормированные и отсортированные входные данные. Если длина входной последовательности превышает 400 элементов, то в массив Sc[] будут включены не все значения входной последовательности, часть из них будет отброшена. Таким образом, размер массива Sc[] никогда не будет содержать более 400 элементов.
После того как вся необходимая для отображения информация подготовлена, создается экземпляр класса CLinDraw. Далее определяются заголовки и при помощи метода AddGraph() добавляются предназначенные для отображения графики.
Первым из них следует созданный в качестве шаблона график распределения Лапласа, затем график полученной по входным данным оценки плотности. И в завершении добавляется расположенный в нижней части график, иллюстрирующий группировку исходных данных. После определения всех необходимых для отображения элементов, производится обращение к методу LDraw().
В результате получаем график, показанный на рисунке 7.
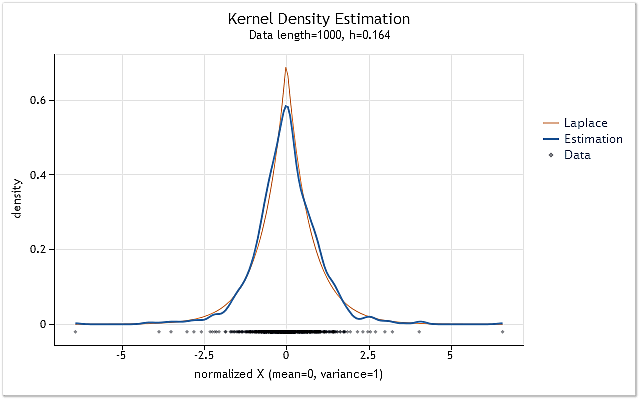
Рис. 7. Оценка плотности для логарифмических доходностей (USDJPY, Daily)
Оценка, показанная на рисунке 7, была произведена для 1000 значений логарифмических доходностей котировки USDJPY, Daily. Как видим, оценка оказалась весьма похожей на кривую, соответствующую распределению Лапласа.
Все файлы необходимые для оценки плотности и визуализации размещены в конце статьи в архиве KDEFiles.zip. Архив включает в себя следующие файлы:
- DensityEstimation\ChartTools\CLinDraw.mqh – класс взаимодействия с highcharts.js;
- DensityEstimation\ChartTools\highcharts.js - библитека Highcharts JS v2.2.0 (2012-02-16);
- DensityEstimation\ChartTools\jquery.js – библиотека jQuery v1.7.1;
- DensityEstimation\ChartTools\LinDraw.htm – предназначенная для отображения HTML-страница;
- DensityEstimation\CKDensity.mqh – класс реализующий оценку плотности;
- DensityEstimation\CSJPlugin.mqh – класс реализующий SJPI-метод оценки оптимальной величины диапазона;
- DensityEstimation\KDE_Example.mq5 – пример оценки плотности для логарифмических доходностей.
После раскрытия архива каталог DensityEstimation\ со всем его содержимым необходимо поместить в каталог Scripts (или Indicators) терминала. После этого можно сразу откомпилировать и запустить пример KDE_Example.mq5. При необходимости каталог DensityEstimation может быть переименован, на работу программы это не должно повлиять.
Следует напомнить, что для нормального функционирования класса CLinDraw, в терминале должно быть разрешено использование внешних библиотек.
Каталог DensityEstimation\ включает в себя вложенный каталог ChartTools\, в котором содержатся все компоненты, предназначенные для визуализации результатов оценки. Файлы связанные с визуализацией сгруппированы в отдельный подкаталог для того чтобы не "замусоривать" каталог DensityEstimation\, чтобы его содержимое легче воспринималось. Имя подкаталога ChartTools\ непосредственно прописано в исходных кодах, поэтому не следует его переименовывать, а в случае такой необходимости нужно будет в исходные коды внести исправления.
Ранее уже упоминалось, что в процессе визуализации создается текстовый файл, содержащий необходимую для построения графиков информацию. Этот файл первоначально создается в специально предназначенном для этого каталоге Files терминала. Но затем этот файл перемещается в упомянутый каталог ChartTools. Таким образом, ни в каталоге Files\, ни в других каталогах терминала не будет оставаться никаких следов деятельности нашего тестового примера. Поэтому для полного удаления установленных файлов данной статьи достаточно просто удалить каталог DensityEstimation вместе со всем его содержимым.
Заключение
При написании статьи в нее не были включены математические выражения, поясняющие суть того или иного метода. Сделано это было сознательно, для того чтобы попытаться облегчить процесс чтения. В случае необходимости все математические выкладки можно найти в многочисленных публикациях, на часть из них в конце статьи даны ссылки.
Приведенные в статье исходные коды никакому серьезному тестированию не подвергались, поэтому их, в первую очередь, следует рассматривать как иллюстрацию к представленному в статье материалу, а не как законченные программы.
Ссылки
- Histogram.
- Kernel density estimation.
- Kernel smoother.
- Expectation–maximization algorithm.
- А.В. Батов, В.Ю. Королев, А.Ю. Корчагин. EM-алгоритм с большим числом компонент как средство построения непараметрических оценок плотности.
- Хардле В. Прикладная непараметрическая регрессия: Пер. с англ. - М., Мир, 1993.
- Hardle W. Applied Nonparametric Regression.
- Kernel (statistics).
- Графики и диаграммы в формате HTML.
- Simon J. Sheather. (2004). Density Estimation.
- Max Kohler, Anja Schindler, Stefan Sperlich. (2011). A Review and Comparison of Bandwidth Selection Methods for Kernel Regression.
- Clive R. Loader. (1999). Bandwidth Selection: Classical or Plug-In?.
- S. J. Sheather, M. C. Jones. (1991). A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation.
- Newton's method.
- Data binning.
- Changjiang Yang, Ramani Duraiswami and Larry Davis. (2004). Efficient Kernel Machines Using the Improved Fast Gauss Transform.
- Fast optimal bandwidth estimation for univariate KDE.
- R.J. Karunamuni and T. Alberts. (2005). A Locally Adaptive Transformation Method of Boundary Correction in Kernel Density Estimation.
- Highcharts JS.
- Анализ основных характеристик временных рядов.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Создай торгового робота за 6 шагов!
Создай торгового робота за 6 шагов!
 OpenCL: Мост в параллельные миры
OpenCL: Мост в параллельные миры
 MetaTrader 5 - больше, чем можно представить!
MetaTrader 5 - больше, чем можно представить!
 Безграничные возможности с MetaTrader 5 и MQL5
Безграничные возможности с MetaTrader 5 и MQL5
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
К сожалению, в подавляющем большинстве случаев предлагаются к использованию алгоритмы, базирующиеся на МНК. Пощупать бы, например, те же сплайны, но с квантильной регрессией. Жаль, что у меня на это не хватает ни ума, ни времени.
Ага, отличия есть там по результатам (МНК и квантильную имею в виду). QR сложнее в вычислениях, например, симплекс-метод экспоненциальный, а это неприемлемо. Помнится долго искал реализации полиномиальных алгоритмов QR от внутренней точки, и нашел таки, выкладывал в форуме на четверке где-то в старых ветках. Но в плане регрессионного сплайна - не думаю, что это сильно поможет. Все таки основное отличие этих методов в степени реакции на единичные выбросы, а тут основная фишка - штраф по интегралу от второй производной, и метод регрессии существенно на результат здесь не повлияет.
upd Кстати, в упомянутой здесь ALGLIB замечательная реализация той самой идеи, которая в этой формуле с лямбдой, если ее плюс еще пару алгоритмов портируют под MQL5, то цены не будет такой библиотеке.
Выяснилось, что при использовании Internet Explorer, прикрепленный к статье пример не отображает графики. К этому сообщению прикреплен скорректированный вариант приведенного в статье примера. Данный вариант проверялся с IE-8.0, Opera 11.64, Chrome 19.0.1084.56 и Firefox 13.0 (Windows XP SP 3).
Так в чем же заключается практическая часть этой статьи с точки зрения трейдинга?
Кшиштоф
Это очень полезная и хорошая статья, спасибо, однако я не думаю, что код работает правильно даже в первом и самом простом примере.
Интересно, может ли автор или кто-то еще перепроверить код или кто-то может порекомендовать какой-нибудь код оценки плотности 1D ядра на C или MQL?