Üssel Düzeltme Kullanarak Zaman Serisi Tahmini (devamı)

Giriş

"Üssel Düzeltme Kullanarak Zaman Serisi Tahmini" [1] makalesinde, üssel düzeltme modellerinin kısa bir özeti verilmiş, model parametrelerini optimize etmek için muhtemel yaklaşımlardan biri gösterilmiş ve son olarak damping ile doğrusal büyüme modeli temelinde geliştirilen tahmin göstergesi önerilmiştir. Bu makale, bu tahmin göstergesinin doğruluğunu bir şekilde artırmaya yönelik bir girişimi temsil eder.

Döviz kurlarını tahmin etmek veya üç veya dört adım ilerisi için bile oldukça güvenilir bir tahminde bulunmak karmaşıktır. Bununla birlikte, bu serinin önceki makalesinde olduğu gibi, bu şekilde uzun vadede tatmin edici sonuçlar elde etmenin imkansız olacağının son derece farkında olarak 12 adım ilerisi için tahminler üreteceğiz. Bu nedenle, en dar güven aralıklarına sahip tahminlerin özellikle ilk birkaç adımına dikkat edilmelidir.

10 ila 12 adım ilerisine yönelik bir tahmin, esasen farklı modellerin ve tahmin yöntemlerinin davranışsal özelliklerini göstermeyi amaçlar. Her durumda, herhangi bir vade için elde edilen tahminin doğruluğu, güven aralığı sınırları kullanılarak değerlendirilebilir. Bu makale, [1] makalesinde ileri sürüldüğü gibi, esasen göstergeyi yükseltmeye yardımcı olabilecek bazı yöntemlerin gösterilmesini amaçlamaktadır.

Göstergelerin geliştirilmesinde uygulanan birkaç değişkenli bir fonksiyonun minimumunu bulmaya yönelik algoritmaya önceki makalede değinilmiştir ve bu nedenle burada tekrar tekrar anlatılmayacaktır. Makaleyi çok uzatmamak için, teorik girdiler minimumda tutulacaktır.

 

1. İlk Gösterge

IndicatorES.mq5 göstergesi ([1] makalesine bakınız), bir başlangıç noktası olarak kullanılacaktır.

Göstergenin derlenmesi için, hepsi aynı dizin içinde bulunan IndicatorES.mq5, CIndicatorES.mqh ve PowellsMethod.mqh’ye ihtiyacımız olacak. Dosyalar, makalenin sonundaki files2.zip arşivinde bulunabilir.

Bu göstergeyi geliştirirken kullanılan üssel düzleştirme modelini - dampingli doğrusal büyüme modeli - tanımlayan denklemleri yenileyelim.

Burada:

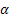• - [0,1] dizisinin seviyesi için düzleştirme parametresi;
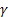• - [0,1] trendi için düzleştirme parametresi;
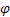•  - damping parametresi [0,1];
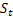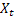• - olduktan sonra t zamanında hesaplanan dizinin düzleştirilmiş seviyesi;
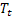• - t zamanında hesaplanan düzleştirilmiş eklemeli trend;
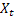• - t zamanında dizinin değeri;
  
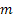• - tahminin yapıldığı gelecek adımların sayısı;
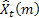• - t zamanında yapılan m adım ilerisi tahmini;
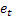• - t zamanında bir adım ilerisi tahmini hatası, .

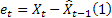Göstergenin tek girdi parametresi, model parametrelerinin optimize edileceği ve başlangıç değerlerinin (çalışma aralığı) seçileceği aralığın uzunluğunu belirleyen değerdir. Model parametrelerinin belirli bir aralıktaki en uygun değerleri belirlendikten ve gerekli hesaplamalar yapıldıktan sonra, tahmin, güven aralığı ve bir adım ilerisi tahminine karşılık gelen satır üretilir. Her yeni çubukta, parametreler optimize edilir ve tahmin yapılır.

Söz konusu gösterge yükseltileceği için, yapacağımız değişikliklerin etkisi, makalenin sonunda bulunan Files2.zip arşivinden test dizileri kullanılarak değerlendirilecektir. \Dataset2 arşiv dizini, kaydedilen EURUSD, USDCHF, USDJPY fiyat tekliflerini ve Amerikan Dolar Endeksini (DXY) içeren dosyaları içerir. Bunların her biri, M1, H1 ve D1 olarak üç zaman aralığı için sağlanmıştır. Dosyalarda kaydedilen “açık” değerler, en son değerin dosyanın sonunda olacağı şekilde yerleştirilir. Her dosya 1200 öğe içerir.

Tahmin hataları, "Ortalama Mutlak Yüzde Hata" (MAPE) katsayısı hesaplanarak tahmin edilecektir.

On iki test dizisinin her birini, her biri 80 öğe içeren 50 çakışan bölüme bölelim ve bunların her biri için MAPE değerini hesaplayalım. Bu şekilde elde edilen tahminlerin ortalaması, karşılaştırmanın yapıldığı göstergelere göre bir tahmin hata indeksi olarak kullanılacaktır. İki ve üç adım ilerisi tahmin hataları için MAPE değerleri, aynı şekilde hesaplanacaktır. Bu gibi ortalama tahminler, bundan sonra aşağıdaki gibi gösterilecektir:

• MAPE1 – bir adım ilerisi tahmin hatasının ortalama tahmini;
  
• MAPE2 – iki adım ilerisi tahmin hatasının ortalama tahmini;
  
• MAPE3 – üç adım ilerisi tahmin hatasının ortalama tahmini;
  
• MAPE1-3 – ortalama (MAPE1+MAPE2+MAPE3)/3.

MAPE değerini hesaplarken, mutlak tahmin hata değeri her adımda dizinin mevcut değerine bölünür. Sıfıra bölmekten veya bunu yaparken negatif değerler elde etmekten kaçınmak için, girdi dizilerinin bizim durumumuzda olduğu gibi yalnızca sıfır olmayan pozitif değerler alması gerekir.

İlk göstergemiz için tahmin değerleri Tablo 1'de gösterilmektedir.

	MAPE1	MAPE2	MAPE3	MAPE1-3
IndicatorES	0.2099	0.2925	0.3564	0.2863

Tablo 1. İlk gösterge tahmin hatası tahminleri

Tablo 1'de görüntülenen veri, Errors_IndicatorES.mq5 komut dosyası kullanılarak elde edilmiştir (makalenin sonunda bulunan files2.zip arşivinden alınmıştır). Komut dosyasını derlemek ve çalıştırmak için, CIndicatorES.mqh ve PowellsMethod.mqh'nin Errors_IndicatorES.mq5’le aynı dizinde yer alması ve girdi dizilerinin Files\Dataset2\ dizininde bulunması gereklidir.

Tahmin hatalarının ilk tahminlerini elde ettikten sonra, şimdi incelemekte olduğumuz göstergeyi yükseltmeye geçebiliriz.

2. Optimizasyon Kriteri

"Üssel Düzeltme Kullanarak Zaman Serisi Tahmini" makalesinde öne sürülen ilk göstergedeki model parametreleri, bir adım ilerisi tahmin hatasının karelerinin toplamı minimize edilerek belirlendi. Bir adım ilerisi tahmini için en uygun olan model parametrelerinin, daha fazla adım ilerisi tahmini için minimum hatayı vermemesi mantıklı görünmektedir. Elbette 10 ila 12 adım ilerisi tahmin hatalarını en aza indirmek istenmektedir ancak incelenen diziler için belirli aralıkta tatmin edici bir tahmin sonucu elde etmek imkansız bir görev olacaktır.

Gerçekçi olmak gerekirse, model parametrelerini optimize ederken göstergemizin ilk yükseltmesi olarak bir, iki ve üç adım ilerisi tahmin hatalarının karelerinin toplamını kullanacağız. Ortalama hata sayısının, tahminin ilk üç adımının aralığında biraz azalması beklenebilir.

Açıkçası, ilk göstergenin bu şekilde yükseltilmesi temel yapısal ilkelerini etkilemez, yalnızca parametre optimizasyon kriterini değiştirir. Bundan dolayı, iki ve üç adım ilerisi tahmin hatalarının sayısı biraz düşmesine rağmen, tahmin doğruluğunun birkaç kat artmasını bekleyemeyiz.

Tahmin sonuçlarını karşılaştırmak için, önceki makalede tanıtılan CIndicatorES sınıfına benzer CMod1 sınıfını değiştirilmiş amaç fonksiyonu func ile oluşturduk.

İlk CIndicatorES sınıfının func fonksiyonu:

double CIndicatorES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}       // Alpha  > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}       // Alpha  < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}      // Gamma  > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}       // Gamma  < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }      // Phi    > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}       // Phi    < 0.05
  sse=0; 
  for(i=0;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(Dlen*MathLog(k1*k2*k3*sse));
  }

Bazı değişikliklerden sonra, func fonksiyonu artık aşağıdaki gibi görünür

double CMod1::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,err,ae,pt,phi2,phi3,a;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;        // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}       // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}      // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}       // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }      // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}       // Phi     < 0.05
  phi2=phi+phi*phi; phi3=phi2+phi*phi*phi;
  err=0;
  for(i=0;i<Dlen-2;i++)
    {
    e=Dat[i]-(s+phi*t); err+=e*e;
    a=Dat[i+1]-(s+phi2*t); err+=a*a;
    a=Dat[i+2]-(s+phi3*t); err+=a*a;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  e=Dat[Dlen-2]-(s+phi*t); err+=e*e;
  a=Dat[Dlen-1]-(s+phi2*t); err+=a*a;
  ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
  a=Dat[Dlen-1]-(s+phi*t); err+=a*a;
  return(k1*k2*k3*err);
  }

Şimdi amaç fonksiyonunu hesaplarken, bir, iki ve üç adım ilerisi tahmin hatalarının karelerinin toplamı kullanılır.

Ayrıca, bu sınıfa dayalı olarak, yukarıda bahsi geçen Errors_IndicatorES.mq5 komut dosyasının yaptığı gibi, tahmin hatalarını tahmin etmeye izin veren Errors_Mod1.mq5 komut dosyası geliştirildi. CMod1.mqh ve Errors_Mod1.mq5, makalenin sonunda files2.zip arşivinde yer almaktadır.

Tablo 2, ilk ve yükseltilmiş sürümler için tahmin hatası tahminlerini görüntüler.

	MAPE1	MAPE2	MAPE3	MAPE1-3
IndicatorES	0.2099	0.2925	0.3564	0.2863
Mod1	0.2144	0.2898	0.3486	0.2842

Tablo 2. Tahmin hatası tahminlerinin karşılaştırması

Görülebileceği gibi, MAPE2 ve MAPE3 hata katsayıları ve MAPE1-3 ortalama değeri, aslında incelenen diziler için biraz daha düşük çıktı. O halde bu sürümü kaydedelim ve göstergemizde başka değişiklikler yapmaya devam edelim.

3. Düzeltme Sürecinde Parametrelerin Ayarlanması

Girdi dizisinin mevcut değerlerine bağlı olarak düzeltme parametrelerini değiştirme fikri yeni veya orijinal değildir ve girdi dizisinin türündeki herhangi bir değişiklik göz önüne alındığında optimal kalmaları için düzeltme katsayılarını ayarlama isteğinden kaynaklanır. Düzeltme katsayılarını ayarlamanın bazı yolları, literatürde [2], [3] açıklanmıştır.

Göstergeyi daha çok yükseltmek için, adaptif üssel düzeltme modelini kullanmanın göstergemizin tahmin doğruluğunu artırmaya izin vereceğini umarak, dinamik olarak değişen üssel düzeltme katsayısına sahip modeli kullanacağız.

Ne yazık ki, tahmin algoritmalarında kullanıldığında, adaptif yöntemlerin çoğu her zaman istenen sonuçları vermez. Uygun adaptif yöntemin seçilmesi çok zahmetli ve zaman alıcı görünebilir; bu yüzden bizim durumumuzda literatürde [4] sağlanan bulgulardan faydalanacağız ve [5] makalesinde öne sürülen "Yumuşak Geçişli Üssel Düzeltme" (STES) yaklaşımını kullanmaya çalışacağız.

Yaklaşımın özü, belirtilen makalede açık bir şekilde özetlenmiştir, dolayısıyla buraya dahil etmeyeceğiz ve adaptif düzeltme katsayısının kullanımını dikkate alarak doğrudan modelimizin denklemlerine (belirtilen makalenin başına bakınız) geçeceğiz.

 

Şimdi görebileceğimiz gibi, alfa düzeltme katsayısının değeri algoritmanın her adımında hesaplanır ve karesi alınan tahmin hatasına bağlıdır. b ve g katsayılarının değerleri, tahmin hatasının alfa değeri üzerindeki etkisini belirler. Diğer tüm yönlerden, kullanılan modelin denklemleri değişmeden kalmıştır. STES yaklaşımının kullanımına ilişkin diğer bilgiler, makalede [6] bulunabilir.

Önceki sürümlerde, verilen girdi dizisi üzerinden alfa katsayısının optimal değerini belirlememiz gerekiyorken, şimdi optimizasyona tabi olan iki adaptif katsayı (b ve g) vardır ve alfa değeri, girdi dizisini düzeltme sürecinde dinamik olarak belirlenecektir.

Bu yükseltme, CMod2 sınıfı biçiminde uygulanmaktadır. Büyük değişiklikler (önceki sefer olduğu gibi), öncelikli olarak şimdi aşağıdaki gibi görünen func fonksiyonuyla ilgiliydi.

double CMod2::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,sb,sg,k1,k2,e,err,ae,pt,phi2,phi3,a;
  
  s=p[0]; t=p[1]; gam=p[2]; phi=p[3]; sb=p[4]; sg=p[5]; k1=1; k2=1;
  if     (gam>0.95){k1+=(gam-0.95)*200; gam=0.95;}        // Gamma   > 0.95
  else if(gam<0.05){k1+=(0.05-gam)*200; gam=0.05;}        // Gamma   < 0.05
  if     (phi>1.0 ){k2+=(phi-1.0 )*200; phi=1.0; }       // Phi     > 1.0
  else if(phi<0.05){k2+=(0.05-phi)*200; phi=0.05;}        // Phi     < 0.05
  phi2=phi+phi*phi; phi3=phi2+phi*phi*phi;
  err=0;
  for(i=0;i<Dlen-2;i++)
    {
    e=Dat[i]-(s+phi*t); err+=e*e;
    a=Dat[i+1]-(s+phi2*t); err+=a*a;
    a=Dat[i+2]-(s+phi3*t); err+=a*a;
    alp=0.05+0.9/(1+MathExp(sb+sg*e*e));                  // 0.05 < Alpha < 0.95
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  e=Dat[Dlen-2]-(s+phi*t); err+=e*e;
  a=Dat[Dlen-1]-(s+phi2*t); err+=a*a;
  alp=0.05+0.9/(1+MathExp(sb+sg*e*e));                    // 0.05 < Alpha < 0.95
  ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
  a=Dat[Dlen-1]-(s+phi*t); err+=a*a;
  return(k1*k2*err);
  }

Bu fonksiyonu geliştirirken, alfa katsayısı değerini tanımlayan denklem biraz değiştirildi. Bu, bu katsayının maksimum ve minimum izin verilen değerinin sınırını sırasıyla 0,05 ve 0,95 olarak ayarlamak için yapıldı.

Tahmin hatalarını hesaplamak için, Errors_Mod2.mq5 komut dosyası daha önce yapıldığı gibi CMod2 sınıfına dayalı olarak yazıldı. CMod2.mqh ve Errors_Mod2.mq5, makalenin sonunda files2.zip arşivinde yer almaktadır.

Komut dosyası sonuçları Tablo 3'te gösterilmektedir.

	MAPE1	MAPE2	MAPE3	MAPE1-3
IndicatorES	0.2099	0.2925	0.3564	0.2863
Mod1	0.2144	0.2898	0.3486	0.2842
Mod2	0.2145	0.2832	0.3413	0.2797

Tablo 3. Tahmin hatası tahminlerinin karşılaştırması

Tablo 3'te önerildiği gibi, adaptif düzeltme katsayısının kullanılması, ortalama olarak test dizilerimiz için tahmin hatalarını biraz daha azaltmaya izin vermiştir. Böylelikle, iki yükseltmenin ardından, MAPE1-3 hata katsayısını yaklaşık olarak yüzde iki oranında azaltmayı başardık.

Oldukça mütevazi bir yükseltme sonucuna rağmen, ortaya çıkan sürümle devam edeceğiz ve diğer yükseltmeleri makalenin kapsamı dışında bırakacağız. Bir sonraki adım olarak, Box-Cox dönüşümünü kullanmayı denemek ilginç olacaktır. Bu dönüşüm, çoğunlukla ilk dizi dağılımını normal dağılıma yaklaştırmak için kullanılır.

Bizim durumumuzda, ilk diziyi dönüştürmek, tahmini hesaplamak ve tahmini ters dönüştürmek için kullanılabilir. Bunu yaparken uygulanan dönüşüm katsayısı, ortaya çıkan tahmin hatasının minimize edileceği şekilde seçilmelidir. Box-Cox dönüşümünün tahmin dizilerinde kullanıldığı bir örnek, [7] makalesinde görülebilir.

4. Tahmin Güven Aralığı

İlk IndicatorES.mq5 göstergesindeki (önceki makalede öne sürülen) tahmin güven aralığı, seçilen üssel düzeltme modeli [8] için türetilen analitik ifadelere göre hesaplanmıştır. Bizim durumumuzda yapılan değişiklikler, incelenen modelde değişikliklere yol açmıştır. Değişken düzeltme katsayısı, güven aralığının tahmini için yukarıda bahsi geçen analitik ifadenin kullanılmasını uygunsuz kılmaktadır.

Daha önce kullanılan analitik ifadelerin, tahmin hatası dağılımının simetrik ve normal olduğu varsayımına dayanarak türetilmiş olması, güven aralığı hesap yöntemini değiştirmek için ek bir gerekçe oluşturabilir. Bu gereksinimler, bizim dizi sınıfımız için karşılanmamaktadır ve tahmin hatası dağılımı normal veya simetrik olmayabilir.

İlk göstergede güven aralığını hesaplarken, bir adım ilerisi tahmin hatası varyansı, ilk olarak girdi dizisinden hesaplandı, daha sonra iki, üç ve daha fazla adım ilerisi tahmini için, elde edilen bir adım ilerisi tahmin hatası varyansının değerine dayalı olarak, analitik ifadeler kullanılarak varyans hesaplaması yapıldı.

Analitik ifadelerin kullanımından kaçınmak için, iki, üç ve daha fazla adım ilerisi tahmini için varyansın doğrudan girdi dizisinden ve bir adım ilerisi tahmini varyansından hesaplandığı basit bir yol vardır. Bununla birlikte, bu yaklaşımın önemli bir dezavantajı bulunmaktadır: Kısa girdi dizilerinde, güven aralığı tahminleri geniş bir dağılıma sahip olacaktır ve varyansın ve ortalama kare hatasının hesaplaması, hataların beklenen normalliği üzerindeki kısıtlamaları ortadan kaldırmaya izin vermeyecektir.

Bizim durumumuzda, parametrik olmayan bootstrap'in (yeniden örnekleme) kullanılması çözüm olabilir [9]. Fikrin dayanağı basitçe şu şekilde ifade edilir: İlk diziden değiştirerek rastgele bir şekilde örnekleme yapıldığı zaman (tekdüze dağıtım), bu şekilde üretilen yapay dizinin dağıtımı ilk diziyle aynı olacaktır.

N elemanlı bir girdi dizimiz olduğunu varsayalım; [0,N-1] aralığında tekdüze bir şekilde dağıtılmış sözde rastgele bir dizi üreterek ve bu değerleri ilk diziden örnekler alırken indeksler olarak kullanarak, ilkinden esasen daha fazla bir uzunluğa sahip bir yapay dizi üretebiliriz. Bununla beraber, oluşturulan dizinin dağıtımı, ilk dizininkiyle aynı (neredeyse aynı) olacaktır.

Güven aralıklarının tahmini için bootstrap prosedürü aşağıdaki gibi olabilir:

1. Değişiklik sonucu elde edilen üssel düzeltme modeli için girdi dizisinden model parametrelerinin en uygun başlangıç değerlerini, katsayılarını ve adaptif katsayılarını belirleyin. En uygun parametreler, daha önce olduğu gibi, Powell arama yöntemini kullanan algoritma kullanılarak belirlenir;
2. Belirlenen optimal model parametrelerini kullanarak, ilk dizinin üzerinden "geçin" ve bir adım ilerisi tahmin hatalarından oluşan bir dizi oluşturun. Dizi öğelerinin sayısı, girdi dizisi uzunluğuna N eşit olacaktır;
3. Hata dizisinin her öğesinden bunun ortalama değerini çıkararak hataları hizalayın;
4. Sözde rastgele dizi oluşturucuyu kullanarak, [0,N-1] aralığında indisler oluşturun ve bunları 9999 öğe uzunluğunda bir yapay hata dizisi oluşturmak için kullanın (yeniden örnekleme);
5. Yapay şekilde oluşturulmuş hata dizisinden değerleri mevcut kullanılan modeli tanımlayan denklemlere ekleyerek, sözde girdi dizisinin 9999 değerini içeren bir dizi oluşturun. Başka bir deyişle, önceden girdi dizi değerlerini model denklemlerine ekleyip bu şekilde tahmin hatası hesaplamak zorundayken, artık ters hesaplamalar yapılmaktadır. Dizinin her bir öğesi için, hata değeri girdi değerini hesaplamak amacıya eklenir. Bunun sonucunda, tahmin güven aralıklarını doğrudan tahmin etmek için yeterli uzunluğa sahipken, girdi dizisiyle aynı dağılıma sahip diziyi içeren 9999 öğeli dizi elde ederiz.

Daha sonra, oluşturulan yeterli uzunluktaki diziyi kullanarak güven aralıklarını hesaplayın. Bu amaçla, oluşturulan tahmin hata dizisi artan düzende sıralanırsa, 9999 değer içeren dizi için 249 ve 9749 indislerine sahip dizi hücrelerinin %95 güven aralığı sınırlarına karşılık gelen değerlere sahip olacağı gerçeğinden faydalanacağız [10].

Tahmin aralıklarının daha doğru bir tahminini elde etmek için dizi uzunluğu tek olmalıdır. Bizim durumumuzda, tahmin güven aralıklarının sınırları aşağıdaki gibi hesaplanmaktadır:

1. Daha önce belirlendiği gibi optimal model parametrelerini kullanarak, oluşturulan dizinin üzerinden "geçin" ve 9999 bir adım ilerisi tahmin hatasından oluşan bir dizi oluşturun;
2. Ortaya çıkan diziyi sıralayın;
3. Sıralanan hata dizisinden, %95 güven aralığının sınırlarını temsil eden 249 ve 9749 indislerine sahip değerleri seçin;
4. İki, üç ve daha fala adım ilerisi tahmin hataları için 1., 2. ve 3. adımları tekrarlayın.

Güven aralıklarını hesaplamaya yönelik bu yaklaşımın avantajları ve dezavantajları vardır.

Avantajları arasında, tahmin hatalarının dağılım türüne ilişkin varsayımların olmaması yer alır. Normal veya simetrik bir şekilde dağıtılmış olmalarına gerek yoktur. Ayrıca, bu yaklaşım kullanılan model için analitik ifadeler türetmenin imkansız olduğu durumlarda faydalı olabilir.

Gerekli olan hesaplamaların kapsamında büyük bir artış ve tahminlerin kullanılan sözde rastgele dizi oluşturucunun kalitesine bağlı olması da dezavantajları arasında sayılabilir.

Yeniden örnekleme ve kuantilleri kullanarak güven aralıklarını hesaplamaya yönelik önerilen yaklaşım oldukça ilkeldir ve bunu iyileştirmenin yolları olmalıdır. Ancak bizim durumumuzda güven aralıkları yalnızca görsel değerlendirmeye tabi olduğu için, yukarıdaki yaklaşım tarafından sağlanan doğruluğun oldukça yeterli olduğu görülebilir.

 

5. Göstergenin Değiştirilmiş Sürümü

Makaleye eklenen yükseltmeler dikkate alınarak ForecastES.mq5 göstergesi geliştirilmiştir. Yeniden örnekleme için, daha önce makalede [11] önerilen sözde rastgele dizi oluşturucuyu kullandık. Standart MathRand() oluşturucu oldukça zayıf sonuçlar verdi, bunun sebebi muhtemelen oluşturduğu değerlerin aralığının [0,32767] yeterince geniş olmamasıydı.

ForecastES.mq5 göstergesini derlerken, PowellsMethod.mqh, CForeES.mqh ve RNDXor128.mqh onunla aynı dizinde yer alacaktır. Tüm bu dosyalar fore.zip arşivinde bulunabilir.

ForecastES.mq5 göstergesi için kaynak kodu aşağıda yer almaktadır.

//+------------------------------------------------------------------+
//|                                                   ForecastES.mq5 |
//|                                          Copyright 2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright   "2012, victorg."
#property link        "https://www.mql5.com"
#property version     "1.02"
#property description "Forecasting based on the exponential smoothing."

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"           // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "ConfUp"             // Confidence interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCrimson
#property indicator_style3  STYLE_DOT
#property indicator_width3  1
#property indicator_label4  "ConfDn"             // Confidence interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCrimson
#property indicator_style4  STYLE_DOT
#property indicator_width4  1

input int nHist=80; // History bars, nHist>=24

#include  "CForeES.mqh"
#include  "RNDXor128.mqh"

#define   NFORE 12
#define   NBOOT 9999

double    Hist[],Fore[],Conf1[],Conf2[];
double    Data[],Err[],BSDat[],Damp[NFORE],BSErr[NBOOT];
int       NDat;

CForeES   Es;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   NDat=nHist; if(NDat<24)NDat=24;
   MqlRates rates[];
   CopyRates(NULL,0,0,NDat,rates);                 // Load missing data
   ArrayResize(Data,NDat);
   ArrayResize(Err,NDat);
   ArrayResize(BSDat,NBOOT+NFORE);

   SetIndexBuffer(0,Hist,INDICATOR_DATA);
   PlotIndexSetString(0,PLOT_LABEL,"History");
   SetIndexBuffer(1,Fore,INDICATOR_DATA);
   PlotIndexSetString(1,PLOT_LABEL,"Forecast");
   PlotIndexSetInteger(1,PLOT_SHIFT,NFORE);
   SetIndexBuffer(2,Conf1,INDICATOR_DATA);         // Confidence interval
   PlotIndexSetString(2,PLOT_LABEL,"ConfUp");
   PlotIndexSetInteger(2,PLOT_SHIFT,NFORE);
   SetIndexBuffer(3,Conf2,INDICATOR_DATA);         // Confidence interval
   PlotIndexSetString(3,PLOT_LABEL,"ConfDN");
   PlotIndexSetInteger(3,PLOT_SHIFT,NFORE);
   IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int  &spread[])
  {
   int i,j,k,start;
   double s,t,alp,gam,phi,sb,sg,e,f,a,a1,a2;

   if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);}
   if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar
   start=rates_total-NDat;
//-----------------------
   PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat);
   PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE);
   PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE);
   PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE);

   for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data
   Es.CalcPar(Data);                                    // Optimization of parameters
   s=Es.GetPar(0); t=Es.GetPar(1); gam=Es.GetPar(2);
   phi=Es.GetPar(3); sb=Es.GetPar(4); sg=Es.GetPar(5);
//----
   a=phi; Damp[0]=phi;
   for(j=1;j<NFORE;j++){a=a*phi; Damp[j]=Damp[j-1]+a;}  // Phi table
//----
   f=s+phi*t;
   for(i=0;i<NDat;i++) // History
     {
      e=Data[i]-f; Err[i]=e;
      alp=0.05+0.9/(1+MathExp(sb+sg*e*e));               // 0.05 < Alpha < 0.95
      a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
      f=(s+phi*t); Hist[start+i]=f;                      // History
     }
   for(j=0;j<NFORE;j++)Fore[rates_total-NFORE+j]=s+Damp[j]*t;  // Forecast
//----
   a=0;
   for(i=0;i<NDat;i++)a+=Err[i];
   a/=NDat;
   for(i=0;i<NDat;i++)Err[i]-=a;                       // alignment of the array of errors
//----
   f=Es.GetPar(0)+phi*Es.GetPar(1);
   for(i=0;i<NBOOT+NFORE;i++) // Resampling
     {
      j=(int)(NDat*Rnd.Rand_01());
      if(j>NDat-1)j=NDat-1;
      e=Err[j];
      BSDat[i]=f+e;
      alp=0.05+0.9/(1+MathExp(sb+sg*e*e));               // 0.05 < Alpha < 0.95
      a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
      f=s+phi*t;
     }
//----
   for(j=0;j<NFORE;j++) // Prediction intervals
     {
      s=Es.GetPar(0); t=Es.GetPar(1);
      f=s+phi*t;
      for(i=0,k=0;i<NBOOT;i++,k++)
        {
         BSErr[i]=BSDat[i+j]-(s+Damp[j]*t);
         e=BSDat[i]-f;
         a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
         f=(s+phi*t);
        }
      ArraySort(BSErr);
      Conf1[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[249];
      Conf2[rates_total-NFORE+j]=Fore[rates_total-NFORE+j]+BSErr[9749];
     }
   return(rates_total);
  }
//-----------------------------------------------------------------------------------

Daha iyi göstermek için, gösterge mümkün olduğunca bir düz satır kodu olarak yürütülmüştür. Kodlarken herhangi bir optimizasyon amaçlanmamıştır.

Şekil 1 ve 2, iki farklı durum için göstergenin çalışma sonuçlarını göstermektedir.

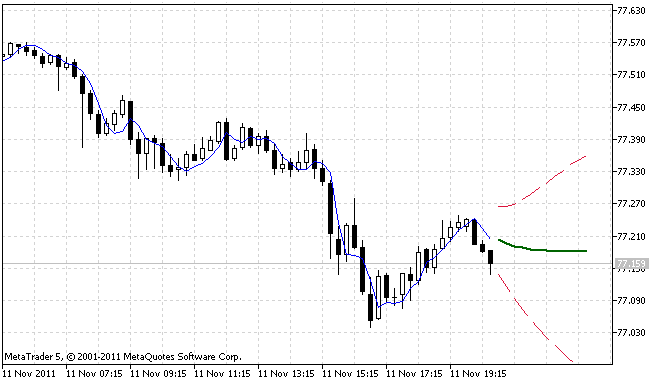
Şekil 1. ForecastES.mq5 göstergesinin birinci çalıştırma örneği

 

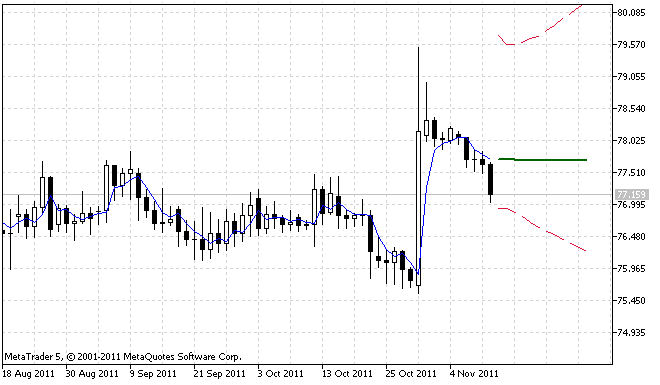
Şekil 2. ForecastES.mq5 göstergesinin ikinci çalıştırma örneği

Şekil 2, %95 tahmin güven aralığının asimetrik olduğunu açıkça göstermektedir. Bu, girdi dizisinin, tahmin hatalarının asimetrik dağılımına sebep olan kayda değer aykırı değerler içermesinden kaynaklanmaktadır.

www.mql4.com ve www.mql5.com web siteleri, daha önce ekstrapolatör göstergeleri sağlamıştır. Bunlardan birini - ar_extrapolator_of_price.mq5 - alalım ve sonuçlarını geliştirdiğimiz göstergeyi kullanarak alınan sonuçlarla karşılaştırmak için Şekil 3'te gösterildiği gibi parametre değerlerini ayarlayalım.

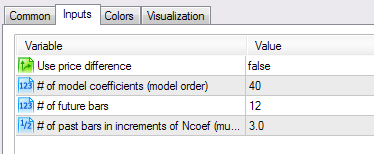
Şekil 3. ar_extrapolator_of_price.mq5 göstergesinin ayarları

Bu iki göstergenin çalışması EURUSD ve USDCHF için farklı zaman dilimlerinde görsel olarak karşılaştırıldı. Yüzeyde, her iki göstergenin tahmin yönünün çoğu durumda çakıştığı görünmektedir. Bununla birlikte, daha uzun gözlemlerde, ciddi ayrımlara rastlanabilmektedir. Bununla beraber, ar_extrapolator_of_price.mq5 her zaman daha kırık bir tahmin çizgisi üretecektir.

ForecastES.mq5 ve ar_extrapolator_of_price.mq5 göstergelerinin eşzamanlı çalışmasının bir örneği, Şekil 4'te gösterilmektedir.

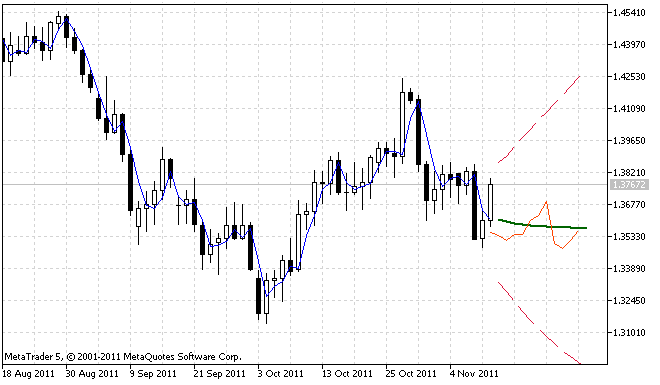
Şekil 4. Tahmin sonuçlarının karşılaştırması

ar_extrapolator_of_price.mq5 göstergesi tarafından üretilen tahmin, Şekil 4'te kesintisiz turuncu-kırmızı bir çizgi olarak görüntülenmektedir.

 

Sonuç

Bu ve önceki makaleyle ilgili sonuçların özeti:

• Zaman serisi tahmininde kullanılan üssel düzeltme modelleri tanıtıldı;
• Modellerin uygulanması için programlama çözümleri önerildi;
• Optimal başlangıç değerlerinin ve model parametrelerinin seçimine ilişkin konularda kısaca bilgi verildi;
• Powell yöntemi kullanılarak birkaç değişkenli bir fonksiyonunun minimumunu bulmak için algoritmanın bir programlama uygulaması sağlandı;
• Girdi dizisi kullanılarak tahmin modelinin parametre optimizasyonu için programlama çözümleri önerildi;
• Tahmin algoritmasını yükseltmeye ilişkin bazı basit örnekler gösterildi;
• Bootstrap ve kuantilleri kullanarak tahmin güven aralıklarını tahmin etmeye yönelik bir yöntem kısaca özetlendi;
• ForecastES.mq5 tahmin göstergesi, makalelerde açıklanan tüm yöntemleri ve algoritmaları içerecek şekilde geliştirildi;
• Bu konuyla ilgili makalelere, dergilere ve kitaplara birkaç bağlantı verildi.

Ortaya çıkan ForecastES.mq5 göstergesiyle ilgili olarak, Powell yönteminin kullanıldığı optimizasyon algoritmasının bazı durumlarda amaç fonksiyonun minimumunu belirli bir doğrulukla belirlemede başarısız olabileceği unutulmamalıdır. Bu durumda, izin verilen maksimum tekrar sayısına ulaşılacaktır ve ilgili bir mesaj günlükte görünecektir. Bununla birlikte, bu durum makalede öne sürülen algoritmaların gösterilmesi için oldukça kabul edilebilir olan gösterge kodunda herhangi bir şekilde işlenmez. Bununla birlikte, ciddi uygulamalar söz konusu olunca bu gibi durumlar bir şekilde izlenmeli ve işlenmelidir.

Tahmin göstergesini daha fazla geliştirmek ve iyileştirmek için, örneğin Akaike Bilgi Kriteri kullanılarak bunlardan birini daha seçmek için, her adımda eşzamanlı olarak birkaç farklı tahmin modelinin kullanılmasını önerebiliriz. Veya aynı türe sahip olan birkaç modelin kullanılması durumunda, bunların tahmin sonuçlarının ağırlıklı ortalama değerini hesaplamak için. Bu durumda ağırlık katsayıları, her modelin tahmin hata katsayısına dayanarak seçilebilir.

Zaman serisi tahmini konusu o kadar geniştir ki, ne yazık ki bu makaleler ilgili konuların bazılarının yüzeyine ancak dokunabilmiştir. Bu yayınların, okuyucunun dikkatini tahminle ilgili konulara ve bu alandaki gelecek çalışmalara çekmeye yardımcı olacağı umulmaktadır.

Referanslar

1. "Üssel Düzeltme Kullanarak Zaman Serisi Tahmini".
2. Yu. P. Lukashin. Adaptive Methods for Short-Term Forecasting of Time Series: Textbook. - М.: Finansy i Statistika, 2003.-416 pp.
3. S.V. Bulashev. Statistics for Traders. - М.: Kompania Sputnik +, 2003. - 245 pp.
4. Everette S. Gardner Jr., Exponential Smoothing: The State of the Art – Part II. June 3, 2005.
5. James W. Taylor, Smooth Transition Exponential Smoothing. Journal of Forecasting, 2004, Vol. 23, pp. 385-394.
6. James W. Taylor, Volatility Forecasting with Smooth Transition Exponential Smoothing. International Journal of Forecasting, 2004, Vol. 20, pp. 273-286.
7. Alysha M De Livera. Automatic Forecasting with a Modified Exponential Smoothing State Space Framework. 28 April 2010, Department of Econometrics and Business Statistics, Monash University, VIC 3800 Australia.
8. Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30 January 2003.
9. The Quantile Journal. issue No. 3, September 2007.
10. http://ru.wikipedia.org/wiki/Квантиль
11. "Zaman Serisinin Temel Özelliklerinin Analizi".