MetaTrader 5 / Статистика и анализ
English 中文 Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
Преобразование Бокса-Кокса

Преобразование Бокса-Кокса

MetaTrader 5 — Статистика и анализ | 17 января 2012, 08:01
20 409 6
Victor
Victor

Введение

С увеличением производительности персональных компьютеров у трейдеров и аналитиков рынка FOREX появляется все больше возможностей для использования развитых, сложных математических алгоритмов, которые требуют значительных вычислительных ресурсов. Но достаточность вычислительных ресурсов сама по себе не в состоянии дать ответы на интересующие трейдеров вопросы. Необходимы эффективные алгоритмы, позволяющие производить анализ предоставляемых рынком котировок.

В настоящее время в таких областях, как математическая статистика, экономика, эконометрика наработано большое количество методов, моделей и отлаженных, эффективных алгоритмов, к которым, естественно, в первую очередь и обращаются трейдеры при анализе рынка. Чаще всего это традиционные параметрические методы, которые были созданы исходя из предположения о стационарности исследуемых последовательностей и о нормальности закона их распределения.

Но ни для кого не секрет, что котировки FOREX представляют собой последовательности, которые никак нельзя отнести к разряду стационарных и имеющих нормальный закон распределения. Поэтому, формально, при анализе котировок мы не имеем права использовать "классические" параметрические методы математической статистики, эконометрики и так далее.

В статье "Бокс-Кокс преобразование и иллюзия "нормальности" макроэкономического ряда" [1] А.Н.Порунов пишет:

"Очень часто экономисту-аналитику приходится иметь дело со статистическими данными, которые по тем или иным причинам не проходят тест на нормальность. В этой ситуации есть два выхода: либо обратиться к непараметрическим методам, что весьма проблематично для экономиста, поскольку требует изрядной математической подготовки, либо воспользоваться специальными методами, позволяющими преобразовать исходную "ненормальную статистику" в "нормальную", что само по себе так же непросто".

Несмотря на то, что в приведенной цитате А.Н.Порунов упоминает экономистов-аналитиков, все сказанное в полной мере можно отнести к попыткам анализировать "ненормальные" котировки FOREX параметрическими методами математической статистики и эконометрики. Подавляющее большинство этих методов разработаны и предназначены для анализа последовательностей, имеющих нормальный закон распределения. Но зачастую, при их использовании, тот факт, что исходные данные "ненормальны" просто игнорируется. Кроме того упомянутые методы чаще всего требуют не только нормальности распределения, но и стационарности исходных последовательностей.

К таким "классическим" методам, требующим нормальности исходных данных, можно отнести регрессионный анализ, дисперсионный анализ (ANOVA) и так далее. Перечислить все параметрические методы, имеющие ограничения по нормальности закона распределения, не представляется возможным, так как это вся область, например, эконометрики, за исключением ее непараметрических методов.

Справедливости ради следует отметить, что разные "классические" параметрические методы имеют различную чувствительность к отклонению закона распределения входных данных от нормального. Поэтому, при использовании таких методов, далеко не всегда отклонение от "нормальности" приводит к катастрофическим последствиям, но, конечно, и не увеличивает точность и достоверность получаемых результатов.

Все сказанное заставляет серьезно задуматься над переходом на непараметрические методы анализа и прогнозирования котировок. Тем не менее, параметрические методы остаются весьма привлекательными. Это объясняется их широкой распространенностью и как следствие достаточным количеством информации, готовых алгоритмов и примеров по их использованию. Для того, чтобы корректно использовать эти методы, необходимо преодолеть как минимум две проблемы, связанные с исходными последовательностями – нестационарность и "ненормальность".

Если повлиять на стационарность входных последовательностей мы не можем, то попытаться приблизить их закон распределения к нормальному вполне возможно. Для решения этой задачи существуют различные преобразования, краткий обзор наиболее известных из них можно найти в публикации "The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses" [2]. Но далее, в данной статье будем рассматривать только одно из них – преобразование Бокса-Кокса (Box-Cox Transformation) [1],[2],[3].

Сразу следует подчеркнуть, что при использовании преобразования Бокса-Кокса, как, пожалуй, и любого другого преобразования, можно лишь в той или иной степени приблизить закон распределения исходной последовательности к нормальному. То есть применение данного преобразования само по себе не гарантирует получения результирующей последовательности с нормальным законом распределения.


1. Преобразование Бокса-Кокса

Для исходной последовательности X длиной N

Однопараметрическое Бокс-Кокс преобразование определяется следующим образом:


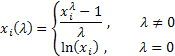
где .

Как видим, это преобразование имеет единственный параметр - лямбда. При значении лямбда равном нулю осуществляется логарифмическое преобразование входной последовательности, при значении лямбда отличном от нуля – степенное. Если параметр лямбда равен единице, то закон распределения исходной последовательности не изменяется, хотя при этом последовательность получит сдвиг за счет вычитания единицы из каждого ее значения.

В зависимости от значения лямбда, преобразование Бокса-Кокса включает в себя следующие частные случаи:


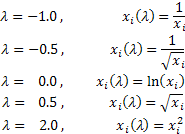
При использовании Бокс-Кокс преобразования необходимо, чтобы все значения входной последовательности были положительными и отличными от нуля. Если входная последовательность не удовлетворяет этим требованиям, то ее можно сдвинуть в положительную область на величину, гарантирующую "положительность" всех ее значений.

Остановимся пока на рассмотрении только однопараметрического Бокс-Кокс преобразования, подготавливая для него соответствующим образом входные данные. Для того, чтобы избежать во входных данных появления отрицательных или равных нулю значений, всегда будем находить минимальное значение входной последовательности и вычитать его из каждого ее элемента, дополнительно осуществляя сдвиг на небольшую величину, равную 1e-5. Такое дополнительное смещение необходимо для гарантированного сдвига последовательности в положительную область, в случае, если минимальное ее значение равно нулю.

Для последовательностей, которые содержат только положительные значения, такого сдвига можно было бы и не делать, но для того чтобы в процессе преобразования при возведении в степень снизить вероятность получения излишне больших величин, и для "положительных" последовательностей будем использовать тот же алгоритм сдвига. Таким образом, любая входная последовательность после сдвига будет располагаться в положительной области, и иметь при этом близкое к нулю минимальное значение.

На рис. 1 показано, как выглядят кривые Бокс-Кокс преобразования при различных значениях параметра лямбда. Рис. 1 заимствован из статьи "Box-Cox Transformations" [3]. Горизонтальная шкала на графике представлена в логарифмическом масштабе.

Рис. 1. Бокс-Кокс преобразование при различных значениях параметра лямбда

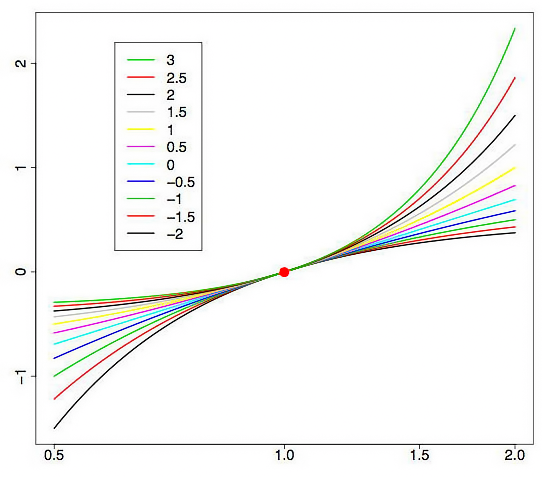
Рис. 1. Бокс-Кокс преобразование при различных значениях параметра лямбда

Как видим, при изменении параметра лямбда "хвосты" исходного распределения могут быть или "растянуты", или "поджаты". Верхняя кривая на рис. 1 соответствует значению лямбда=3, а нижняя значению лямбда=-2.

Для того чтобы в результате Бокс-Кокс преобразования закон распределения результирующий последовательности был максимально приближен к нормальному закону, необходимо выбрать оптимальное значение параметра лямбда.

Одним из способов определения оптимальной величины этого параметра является максимизация логарифма функции правдоподобия:

где

То есть необходимо выбрать такое значение параметра лямбда, при котором данная функция принимает максимальное значение.

В публикации "Box-Cox Transformations" [3] кратко рассматривается другой способ определения оптимального значения этого параметра, основанный на поиске максимальной величины коэффициента корреляции между квантилями функции нормального распределения и отсортированной преобразованной последовательностью. Наверняка можно найти и другие методы оптимизации параметра лямбда, но для начала остановим свой выбор на поиске максимума логарифма приведенной ранее функции правдоподобия.

Находить максимум логарифма функции правдоподобия можно разными способами. Например, методом простого перебора. Для этого необходимо в выбранном диапазоне, изменяя с небольшим шагом величину параметра лямбда, вычислять значение функции правдоподобия. И в качестве оптимального значения лямбда выбрать то, при котором величина функции правдоподобия окажется максимальной.

При этом величина шага будет определять точность вычисления оптимального значения параметра лямбда. Чем мельче шаг, тем выше точность, но при уменьшении шага пропорционально будет увеличиваться и требуемый объем вычислений. Для повышения эффективности вычислений могут быть использованы различные алгоритмы поиска максимума/минимума функции, генетические алгоритмы и так далее.


2. Преобразование к нормальному закону распределения

Одной из задач Бокс-Кокс преобразования, возможно основной, является приведение закона распределения входной последовательности к "нормальному" виду. Попробуем разобраться, насколько хорошо такая задача может быть решена при помощи этого преобразования.

Чтобы сильно не отвлекаться от темы данной статьи и заново не рассматривать какой-либо алгоритм поиска минимума/максимума функции, для определения оптимального значения параметра лямбда далее будем использовать рассмотренный ранее в статьях "Прогнозирование временных рядов при помощи экспоненциального сглаживания" и "Прогнозирование временных рядов при помощи экспоненциального сглаживания (окончание)" алгоритм, реализующий поиск минимума функции методом Пауэлла (Powell's method).

Для поиска оптимального значения параметра преобразования создадим класс CBoxCox, в котором в качестве целевой будет реализована упомянутая выше функция правдоподобия. При этом в качестве базового класса используем класс PowellsMethod [4], [5], реализующий непосредственно алгоритм поиска.

//+------------------------------------------------------------------+
//|                                                      CBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| Класс CBoxCox                                                    |
//+------------------------------------------------------------------+
class CBoxCox:public PowellsMethod
  {
protected:
   double            Dat[];          // Входные данные
   double            BCDat[];        // Данные Box-Cox
   int               Dlen;          // Размер данных
   double            Par[1];         // Параметры
   double            LnX;            // Сумма ln(x)
public:
   void   CBoxCox(void) { }
   void              CalcPar(double &dat[]);
   double GetPar(int n) { return(Par[n]); }
private:
   virtual double    func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CBoxCox::CalcPar(double &dat[])
  {
   int i;
   double a;
   //--- начальное значение Lambda
   Par[0]=1.0;                
   Dlen=ArraySize(dat);
   ArrayResize(Dat,Dlen);
   ArrayResize(BCDat,Dlen);
   LnX=0;
   for(i=0;i<Dlen;i++)
     {
    //--- входные данные
      a=dat[i]; Dat[i]=a;
     //--- сумма ln(x)
     LnX+=MathLog(a);        
     }
    //--- оптимизация Powell
    Optimize(Par);            
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CBoxCox::func(const double &p[])
  {
   int i;
   double a,lamb,var,mean,k,ret;

   lamb=p[0]; var=0; mean=0; k=0;
   if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;}         // Lambda >  5.0
   else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0

   //--- Lambda != 0.0
   if(lamb!=0)                                     
     {
      for(i=0;i<Dlen;i++)
        {
          //--- преобразование Box-Cox
         BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb;  
          //--- расчет среднего
         mean+=BCDat[i]/Dlen;
        }
     }
    //--- Lambda == 0.0
    else                                            
     {
      for(i=0;i<Dlen;i++)
        {
          //--- преобразование Box-Cox
         BCDat[i]=MathLog(Dat[i]);
          //--- расчет среднего
         mean+=BCDat[i]/Dlen;
        }
     }
   for(i=0;i<Dlen;i++)
     {
      a=BCDat[i]-mean;
       //--- variance
      var+=a*a/Dlen;
     }
   //--- log-likelihood
   ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX;         
   return(k+ret);
  }
//------------------------------------------------------------------------------------

Теперь, для того чтобы найти оптимальное значение параметра лямбда, достаточно обратиться к методу CalcPar данного класса, передав ему в качестве параметра ссылку на массив, содержащий входные данные. Получить значение найденной оптимальной величины параметра можно при помощи обращения к методу GetPar. Как уже упоминалось, входные данные при этом должны быть положительны.

Класс PowellsMethod реализует алгоритм поиска минимума функции многих переменных, а в нашем случае оптимизируется лишь единственный параметр. Это привело к тому, что размерность массива Par[] оказалась равной единице, то есть массив содержит только одно значение. Теоретически, в таком случае можно было бы вместо массива параметров использовать обыкновенную переменную, но это потребовало бы внесения изменений в код базового класса PowellsMethod. Можно предположить, что при компиляции исходного MQL5-кода с использованием массивов, содержащих всего один элемент, проблем не возникнет.

Необходимо обратить внимание на то, что в функции CBoxCox::func() вводится ограничение на диапазон допустимых значений параметра лямбда. В нашем случае этот диапазон ограничен значениями от -5 до 5. Это сделано для того чтобы при возведении входных данных в степень лямбда избежать получения излишне больших или излишне малых величин.

Кроме того, если в процессе оптимизации получаются слишком большие или слишком малые значения лямбда, то это может означать, что данная последовательность малопригодна для выбранного типа преобразования, поэтому, в любом случае, при определении значения лямбда выходить за какой-то разумный диапазон не стоит.


3. Случайные последовательности

Создадим тестовый скрипт, который, используя класс CBoxCox, будет производить Бокс-Кокс преобразование формируемой нами псевдослучайной последовательности.

Ниже приведен исходный код такого скрипта.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest1.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- размер данных
   n=1600;
//--- подготовка входного массива
   ArrayResize(dat,n);
//--- массив преобразованных данных
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- генерация случайной последовательности
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp();

//--- сдвиг входных данных
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- оптимизация по lambda  
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- входные данные
//--- bcdat[] <-- преобразованные данные
  }
//-----------------------------------------------------------------------------------

В приведенном скрипте в качестве входных преобразуемых данных используется псевдослучайная последовательность с экспоненциальным законом распределения. Длина последовательности задается в переменной n и в данном случае равна 1600 значениям.

Для генерации псевдослучайной последовательности используется класс RNDXor128 (George Marsaglia, Xorshift RNG), который ранее был представлен в статье "Анализ основных характеристик временных рядов" [6]. Все необходимые для компиляции скрипта BoxCoxTest1.mq5 файлы находятся в архиве Box-Cox-Tranformation_MQL5.zip. Для успешной компиляции эти файлы должны быть размещены в одном каталоге.

При выполнении приведенного скрипта производится формирование входной последовательности, ее смещение в положительную область значений и поиск оптимального значения параметра лямбда. Далее производится вывод сообщения, содержащего найденное значение лямбда и количество проходов алгоритма поиска. В результате в выходном массиве bcdat[] будет сформирована преобразованная последовательность.

Данный скрипт, в том виде как он здесь представлен, позволяет только подготовить преобразованную последовательность для дальнейшего ее использования и никаких действий над ней не производит. При написании данной статьи для оценки результатов преобразования был выбран способ анализа, описанный в статье "Анализ основных характеристик временных рядов" [6]. Используемые для этого скрипты, в целях сокращения объема публикуемых кодов, в данной статье не представлены. Далее будем приводить лишь готовые графические результаты анализа.

На рис. 2 показана гистограмма и график со шкалой нормального распределения для используемой в скрипте BoxCoxTest1.mq5 входной псевдослучайной последовательности с экспоненциальным законом распределения. Результат теста Жака-Бера JB=3241.73, p= 0.000. Как видим, входная последовательность совсем не является "нормальной" и, как и ожидалось, ее распределение похоже на экспоненциальное.

Рис. 2.

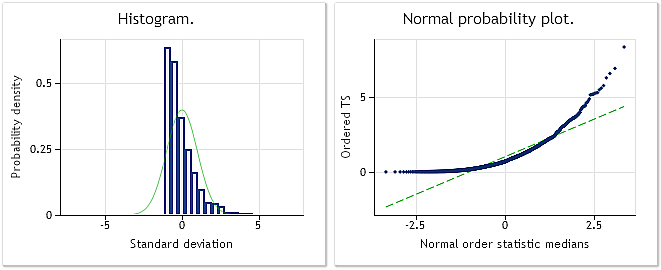
Рис. 2. Псевдослучайная последовательность с экспоненциальным законом распределения. Тест Жака-Бера JB=3241.73, р=0.000.

 Рис. 3.

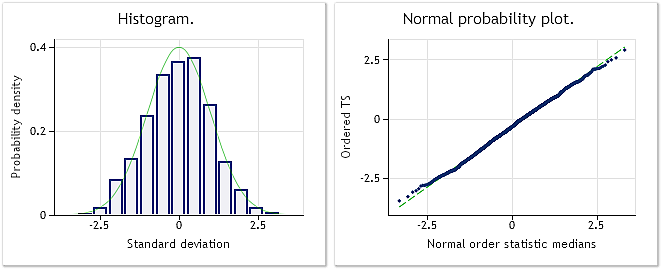
Рис. 3. Преобразованная последовательность. Параметр лямбда=0.2779, тест Жака-Бера JB=4.73, р=0.094

На рис. 3 представлен результат анализа преобразованной последовательности (скрипт BoxCoxTest1.mq5, массив bcdat[]). Закон распределения преобразованной последовательности значительно более близок к нормальному, что подтверждают и результаты теста Жака-Бера JB=4.73, p=0.094. Найденное значение параметра лямбда=0.2779.

В приведенном примере Бокс-Кокс преобразование достаточно хорошо себя проявило. На вид результирующая последовательность стала значительно ближе к "нормальной", а результат теста Жака-Бера уменьшил свое значение с JB=3241.73 до JB=4.73. Но это и не удивительно, так как выбранная нами входная последовательность заведомо неплохо подходит для данного типа преобразования.

Рассмотрим еще один пример Бокс-Кокс преобразования псевдослучайной последовательности. Учитывая, что преобразование Бокса-Кокса является степенным, создадим "удобную" для него входную последовательность. Для этого сгенерируем псевдослучайную последовательность (уже имеющую закон распределения, близкий к нормальному) и далее исказим его, возведя все ее значения в степень 0.35. Можно ожидать, что Бокс-Кокс преобразование с большой точностью вернет входной последовательности ее исходное нормальное распределение.

Ниже приведен исходный код тестового скрипта BoxCoxTest2.mq5.

Этот скрипт отличается от рассмотренного ранее скрипта только тем, что в нем генерируется другая входная последовательность.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest2.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- размер данных
   n=1600;
//--- массив входных данных
   ArrayResize(dat,n);
//--- массив преобразованных данных
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- генерация случайной последовательности
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm();

//--- сдвиг входных данных
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;
   for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35);

//--- оптимизация по lambda
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);

   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;   }
   else          { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);  }     // Lambda == 0.0

//-- dat[]   <-- входные данные
//-- bcdat[] <-- преобразованные данные
  }
//-----------------------------------------------------------------------------------

В приведенном скрипте генерируется входная псевдослучайная последовательность с нормальным законом распределения, осуществляется ее сдвиг в положительную область значений и далее все элементы этой последовательности возводятся в степень 0.35. После завершения работы скрипта массив dat[] содержит входную последовательность, а массив bcdat[] преобразованную.

На рис. 4 представлены характеристики входной последовательности, которая за счет возведения в степень 0.35 потеряла свое исходное нормальное распределение. При этом тест Жака-Бера JB=3609.29, p= 0.000.

Рис. 4.

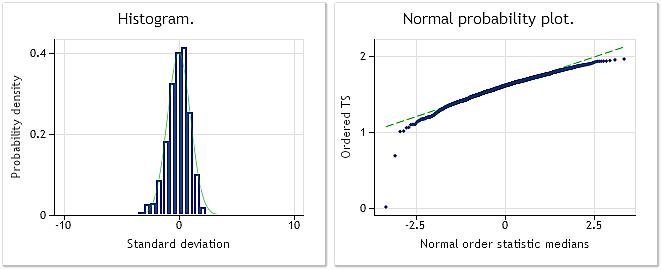
Рис. 4. Входная псевдослучайная последовательность. Тест Жака-Бера JB=3609.29, p=0.000.

Рис. 5.

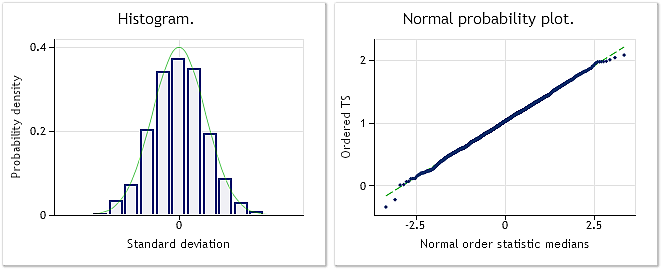
Рис. 5. Преобразованная последовательность. Параметр лямбда=2.9067, тест Жака-Бера JB=0.30, p=0.859

Как показано на рис. 5, преобразованная последовательность имеет закон распределения достаточно близкий к нормальному закону, что подтверждает и значение теста Жака-Бера JB=0.30, p=0.859.

Приведенные примеры использования Бокс-Кокс преобразования продемонстрировали очень хорошие результаты. Но не следует забывать, что в обоих случаях в качестве входных были выбраны такие последовательности, с которыми данное преобразование заведомо должно было легко справиться. Поэтому приведенные результаты можно рассматривать просто как подтверждение работоспособности созданного нами алгоритма.


4. Котировки

Убедившись в работоспособности алгоритма реализующего преобразования Бокса-Кокса, попробуем применить его к реальным котировкам FOREX, так как именно их хотелось бы привести к нормальному закону распределения.

В качестве тестовых котировок будем использовать последовательности, которые ранее были приведены в статье "Прогнозирование временных рядов при помощи экспоненциального сглаживания (окончание)" [5]. Они размещены в каталоге \Dataset2 архива Box-Cox-Tranformation_MQL5.zip. Это реальные котировки, 1200 значений которых были сохранены в соответствующие файлы. Для обеспечения доступа к этим файлам, извлеченный из архива каталог \Dataset2 необходимо скопировать в каталог \MQL5\Files терминала.

Далее условимся считать, что эти котировки не являются стационарными последовательностями. Поэтому результаты анализа не будем распространять на так называемую генеральную совокупность, а будем рассматривать их лишь как характеристики данной конкретной последовательности конечной длины.

Кроме того, следует напомнить, что в случае отсутствия стационарности, у различных фрагментов котировок одной и той же валютной пары можно обнаружить совершенно разные законы распределения.

Создадим скрипт, позволяющий считывать значения последовательности из файла и производить ее Бокс-Кокс преобразование. От приведенных ранее тестовых скриптов он будет отличаться только способом формирования входной последовательности. Ниже приведен исходный код такого скрипта, а сам скрипт BoxCoxTest3.mq5 размещен в прилагаемом архиве.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest3.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
CBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
   string fname;
//--- файл входных данных
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- чтение данных
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- размер данных
   n=ArraySize(dat);
//--- массив преобразованных данных
   ArrayResize(bcdat,n);

//--- сдвиг входных данных
   min=dat[ArrayMinimum(dat)]-1e-5;
   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- оптимизация параметра lambda
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- входные данные
//--- bcdat[] <-- преобразованные данные
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//-----------------------------------------------------------------------------------

В этом скрипте из файла с котировками, имя которого задано в переменной fname, в массив dat[] считываются все значения (в нашем случае 1200). Далее, как было описано ранее, производится сдвиг входной последовательности, поиск оптимального значения параметра и Бокс-Кокс преобразование. После выполнения скрипта результат преобразования располагается в массиве bcdat[].

Как видно из приведенного исходного кода, в скрипте для преобразования была выбрана последовательность котировок EURUSD M1. Результат анализа исходной и преобразованной последовательности показан на рис. 6 и рис. 7.

Рис. 6.

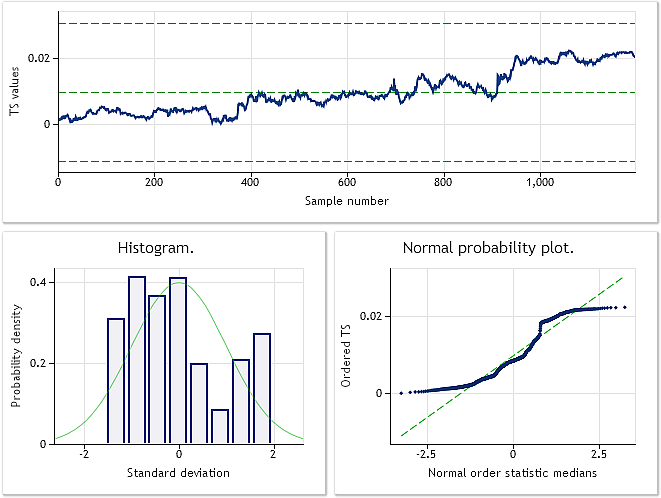
Рис. 6. Исходная последовательность EURUSD M1. Тест Жака-Бера JB=100.94, p=0.000.

Рис. 7.

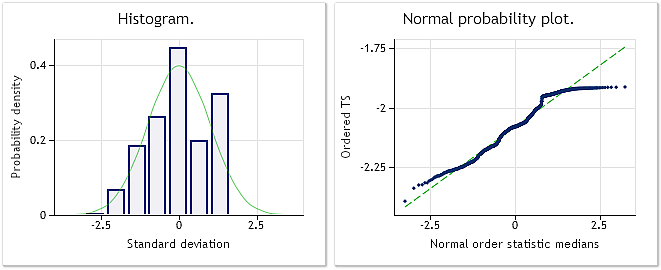
Рис. 7. Преобразованная последовательность. Параметр лямбда=0.4146, тест Жака-Бера JB=39.30, p=0.000

Судя по представленным на рис. 7 характеристикам, результат преобразования котировок EURUSD M1 оказался не таким впечатляющим, как приведенные ранее результаты преобразования псевдослучайных последовательностей. Бокс-Кокс преобразование, хотя и считается достаточно универсальным, в состоянии справится далеко не со всеми видами входных последовательностей. Например, трудно ожидать от степенного преобразования, что оно сможет превратить распределение с двумя вершинами в нормальное распределение.

Но хотя закон распределения, показанный на рис. 7, вряд ли можно считать нормальным, тем не менее, как и в прошлых примерах, мы видим значительное снижение величины теста Жака-Бера. Если для исходной последовательности JB=100.94, то после преобразования тест показал значение JB=39.30. Это говорит о том, что хотя после преобразования закон распределения и не стал нормальным, он все же в некоторой степени к нему приблизился.

Примерно такие же результаты были получены и при преобразовании различных фрагментов других котировок. Каждый раз Бокс-Кокс преобразование в большей или меньшей степени приближало закон распределения к нормальному. Хотя в результате нормальным он так и не становился.

Ряд экспериментов с преобразованием различных котировок позволяет сделать достаточно ожидаемый вывод – Бокс-Кокс преобразование в подавляющем большинстве случаев в той или иной степени позволяет приблизить закон распределения котировок FOREX к нормальному, но при этом не гарантирует достижения истиной нормальности закона распределения преобразованных данных.

Насколько целесообразно производить преобразование, которое все равно не приводит исходную последовательность к нормальной? На этот вопрос нельзя дать однозначного ответа. В каждом конкретном случае необходимо принимать индивидуальное решение о необходимости использования Бокс-Кокс преобразования. В этом случае многое будет зависеть от того, какими параметрическими методами предполагается производить анализ котировок, и насколько эти методы чувствительны к отклонению исходных данных от нормального закона распределения.


5. Снятие тренда

В верхней части рис. 6 приведен график используемой в скрипте BCTransform.mq5 исходной последовательности EURUSD M1. Нетрудно заметить, что значения этой последовательности на всем ее протяжении почти равномерно возрастают. В первом приближении можно говорить о наличии в последовательности линейного тренда. Наличие такой явной "трендовости" наводит на мысль о том, чтобы попытаться сначала исключить тренд, и лишь затем производить различного рода преобразования и анализ полученной последовательности.

Удаление тренда из входных анализируемых последовательностей, наверное, не следует считать приемом, который можно рекомендовать абсолютно для всех случаев. Но предположим, что мы собираемся производить анализ приведенной на рис. 6 последовательности с целью выявления наличия в ней периодических (или циклических) компонент. В этом случае мы, естественно, можем, определив параметры линейного тренда, вычесть его из входной последовательности.

Снятие линейного тренда не только не должно повлиять на выявление периодических компонент, но даже, в зависимости от выбранного метода анализа, может оказаться полезным и в какой- то степени сделать результаты такого анализа более точными или более достоверными.

Если мы пришли к выводу, что в каких-то случаях снятие тренда может быть полезным, то, наверное, имеет смысл посмотреть, как Бокс-Кокс преобразование справится с последовательностью после исключения из нее тренда.

В любой ситуации, при снятии тренда обязательно возникает вопрос – какую кривую лучше использовать для аппроксимации тренда? Это могут быть и прямая линия, и кривые более высокого порядка, и скользящие средние, и так далее. В данном случае, для того чтобы не отвлекаться на исследования по определению оптимальной кривой, просто остановим свой выбор, если можно так сказать, на крайнем варианте. Будем использовать вместо исходной последовательности ее приращения, то есть разности между текущим и предыдущим ее значениями.

Раз уж речь зашла о переходе на анализ приращений, то совершенно невозможно удержаться от того, чтобы не прокомментировать некоторые связанные с этим моменты.

В различных публикациях и на форумах необходимость перехода на анализ приращений иногда обосновывается таким образом, что может сложиться неверное впечатление о свойствах такого перехода. Часто переход на анализ приращений представляют как некое преобразование, которое способно превратить исходную последовательность в стационарную или нормализовать закон ее распределения. Так ли это на самом деле? Попробуем разобраться.

Начнем с того, что в основе перехода на анализ приращений лежит очень простая идея, суть которой заключается в разложении исходной последовательности на две компоненты. Продемонстрировать это можно следующим образом.

Предположим, что у нас имеется входная последовательность

И мы по тем или иным причинам решили разделить эту последовательность на тренд и остатки, которые получаются при вычитании значений тренда из элементов исходной последовательности. Предположим, что для аппроксимации тренда мы решили использовать простое скользящее среднее с периодом усреднения в два элемента последовательности.

Такое скользящее среднее находится как деленная на два сумма двух соседних элементов последовательности. Тогда остатки от вычитания этой средней из исходной последовательности будут представлять собой деленную на два разность между теми же соседними элементами.

Обозначим упомянутое выше среднее значение как S, а остатки как D. Если постоянный множитель 2 вынести для наглядности в левую часть уравнения, то получим:


В результате несложных преобразований мы разделили нашу исходную последовательность на две составляющие, одна из которых является суммой соседних значений последовательности, а другая представлена разностями. Именно эти разности мы и называли приращениями, а суммы - трендом.

В связи с этим, приращения логичнее рассматривать только как некую часть исходной последовательности. Поэтому не стоит забывать о том, что если мы переходим на анализ приращений, то другая часть последовательности, определяемая суммами, чаще всего просто отбрасывается, если, конечно, мы не анализируем ее отдельно.

Для того чтобы разобраться в том, какую же пользу мы можем извлечь при таком разделении последовательности, проще всего обратиться к спектральному методу.

Непосредственно из приведенных ранее выражений следует, что S-компонента является результатом фильтрации исходной последовательности при помощи фильтра нижних частот с импульсной характеристикой h=1,1. Соответственно D-компонента – результат фильтрации фильтром верхних частот с импульсной характеристикой h=-1,1. На рис. 8 условно показаны частотные характеристики таких фильтров.

Рис. 8.

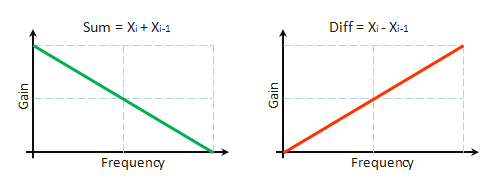
Рис. 8. Амплитудно-частотные характеристики

Предположим, что мы перешли с анализа непосредственно самой последовательности на анализ ее разностей. Чего в этом случае можно ожидать? Тут возможны различные варианты, кратко рассмотрим лишь некоторые из них.

  1. Если основная энергия исследуемого процесса сосредоточена в низкочастотной области исходной последовательности, то переход на анализ разностей просто подавит ее, усложнив или вовсе сделав невозможным дальнейшее ее исследование;
  2. Если основная энергия исследуемого процесса сосредоточена в высокочастотной области исходной последовательности, то при переходе на анализ разностей можно ожидать положительного эффекта за счет фильтрации низкочастотных мешающих составляющих. Но это лишь в том случае, если такая фильтрация существенно не повлияет на свойства исследуемого процесса;
  3. Можно упомянуть и о варианте, когда энергия исследуемого процесса равномерно распределена по всему частотному диапазону последовательности. Тогда, после перехода на анализ ее разностей, мы, скорее всего, необратимо исказим характер этого процесса, подавив низкочастотную его часть.

Рассуждая подобным образом можно сделать выводы о результатах перехода на анализ разностей и для любых других комбинаций тренда, кратковременного тренда, мешающего шума и так далее. Но ни в одном случае переход на анализ разностей не приведет к стационарному виду интересующий нас процесс и не сделает распределение этого процесса более нормальным.

На основании сказанного, наверное, можно сделать вывод о том, что при переходе на анализ разностей автоматического "улучшения" последовательности не происходит. Можно предположить, что в некоторых случаях для получения более полного представления о входной последовательности имеет смысл анализировать как непосредственно ее саму, так и разности, и суммы ее соседних значений, а окончательные выводы о свойствах этой последовательности делать на основании совместного рассмотрения всех полученных результатов.

Вернемся к непосредственной теме данной статьи и посмотрим, как поведет себя Бокс-Кокс преобразование в случае перехода на анализ приращений показанной на рис. 6 последовательности EURUSD M1. Для этого используем приведенный ранее скрипт BoxCoxTest3.mq5, в котором после считывания значений последовательности из файла, заменим сами эти значения на разности (приращения). Так как других изменений в исходный код скрипта не вносится, публиковать его не имеет смысла, просто приведем результаты анализа его работы.

Приращения EURUSD M1. Тест Жака-Бера JB=32494.8, p=0.000

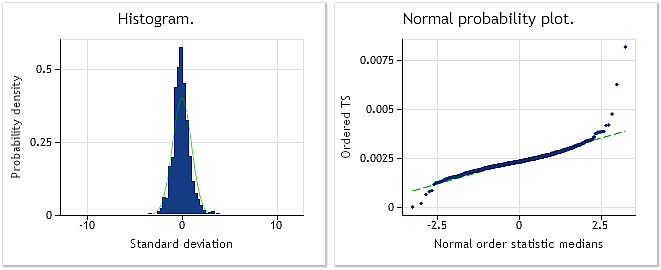
Рис. 9. Приращения EURUSD M1. Тест Жака-Бера JB=32494.8, p=0.000

Рис. 10. Преобразованная последовательность. Параметр лямбда=0.6662, тест Жака-Бера JB=10302.5, p=0.000

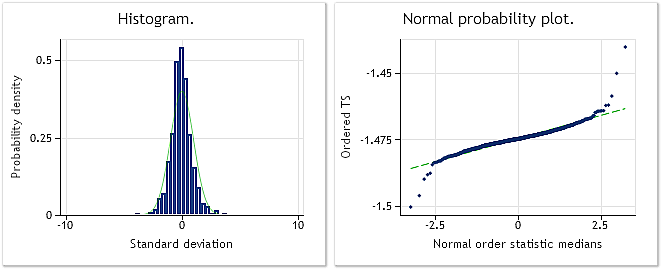
Рис. 10. Преобразованная последовательность. Параметр лямбда=0.6662, тест Жака-Бера JB=10302.5, p=0.000

На рис. 9 представлены характеристики последовательности, состоящей из приращений (разностей) EURUSD M1, а на рис. 10 представлены характеристики, полученные после ее Бокс-Кокс преобразования. Несмотря на то, что после преобразования значение теста Жака-Бера снизилось более чем в три раза с JB=32494.8 до JB=10302.5, закон распределения преобразованной последовательности все же далек от нормального.

Тем не менее, следует предостеречь от поспешных выводов о том, что Бокс-Кокс преобразование плохо справляется с преобразованием приращений. Мы рассмотрели лишь частный случай. Для других входных последовательностей, возможно, будет получен совершенно иной результат.


6. Приведенные примеры

Все приведенные ранее примеры Бокс-Кокс преобразования относятся к случаю, когда предполагается приведение закона распределения исходной последовательности к нормальному. Вернее, к закону по возможности наиболее близкому к нормальному. Как уже упоминалось в начале статьи, такое преобразование может оказаться необходимым при использовании параметрических методов анализа, которые могут быть весьма чувствительны к отклонению закона распределения исследуемой последовательности от нормального.

Представленные примеры продемонстрировали, что во всех случаях, судя по результатам теста Жака-Бера, мы действительно после преобразования получали последовательности, у которых, по сравнению с исходными, закон распределения становился более близким к нормальному. Этот факт хорошо демонстрирует действенность преобразования Бокса-Кокса и подтверждает универсальность и эффективность данного преобразования.

Но не следует переоценивать возможности Бокс-Кокс преобразования и считать, что любая входная последовательность будет обязательно преобразована в строго нормальную. Как видно из приведенных выше примеров, это далеко не так. Для реальных котировок, ни исходную, ни преобразованную последовательность, конечно, нельзя считать нормальной.

До сих пор Бокс-Кокс преобразование рассматривалось только в его более наглядной, однопараметрической форме. Это было сделано для того, чтобы облегчить и упростить первое знакомство с ним. Такой подход вполне оправдан для демонстрации возможностей этого преобразования, но в практических целях, наверное, целесообразнее использовать более общую форму его представления.


7. Общая форма Бокс-Кокс преобразования

Следует напомнить, что преобразование Бокса-Кокса применимо только к последовательностям, у которых все элементы имеют положительные и не равные нулю значения. На практике это требование легко удовлетворяется простым смещением последовательности в положительную область, однако величина смещения в пределах положительной области способна оказать непосредственное влияние на результат преобразования.

Поэтому величину смещения можно рассматривать как дополнительный параметр преобразования и оптимизировать его наряду с параметром лямбда, конечно, не допуская выхода значений последовательности в отрицательную область.

Для исходной последовательности X длиной N:

выражения, определяющие более общую форму двухпараметрического Бокс-Кокс преобразования, выглядят следующим образом:

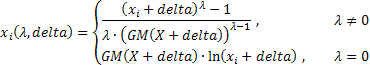
где:

;

GM() - геометрическое среднее.

Геометрическое среднее последовательности может быть вычислено следующим образом:

Как видим, в приведенных выражениях используются уже два параметра - лямбда и дельта, теперь в процессе преобразования необходимо оптимизировать одновременно оба эти параметра. Несмотря на некоторое усложнение алгоритма, введение дополнительного параметра, несомненно, способно увеличить эффективность преобразования. Кроме того, по сравнению с ранее используемым преобразованием, в выражениях появились дополнительные нормирующие множители, благодаря которым при изменении параметра лямбда результат преобразования будет сохранять свою размерность.

Дополнительную информацию по Бокс-Кокс преобразованию можно найти в [7],[8]. В литературе [8] кратко рассматриваются и некоторые другие подобного рода преобразования.

Перечислим основные особенности данной, более общей формы преобразования:

  1. Само преобразование все так же требует, чтобы входная последовательность содержала только положительные значения. Но введение дополнительного параметра delta, при выполнении определенных условий, позволяет автоматически осуществлять требуемый сдвиг последовательности;
  2. При выборе оптимального значения параметра delta его величина должна гарантировать "положительность" всех значений последовательности;
  3. Преобразование является непрерывным при изменении параметра лямбда, в том числе и возле его нулевого значения;
  4. Результат преобразования сохраняет свою размерность при изменении величины параметра лямбда.

Во всех приведенных ранее примерах при поиске оптимального значения параметра лямбда использовался критерий максимизации логарифма функции правдоподобия. Конечно, это не единственный способ оценки оптимального значения параметров преобразования.

В качестве примера можно привести способ оптимизации параметров, при котором ищется максимум коэффициента корреляции между отсортированной по возрастанию преобразованной последовательностью и последовательностью квантилей функции нормального распределения. Такой вариант уже ранее упоминался в статье. Значения квантилей функции нормального распределения могут быть вычислены согласно выражениям предложенным Филлибеном (James J. Filliben) [9].

Выражения, определяющие общую форму двухпараметрического преобразования, несомненно, являются более громоздкими по сравнению с рассмотренными ранее. Возможно поэтому, такая форма преобразования не так часто встречается в математических и статистических пакетах. Для того чтобы в случае необходимости можно было использовать Бокс-Кокс преобразование в такой более общей форме, приведенные выражения были реализованы на MQL5.

В файле CFullBoxCox.mqh содержится исходный код класса CFullBoxCox, который осуществляет поиск оптимального значения параметров преобразования. При этом процесс оптимизации основан на вычислении коэффициента корреляции, как об этом уже говорилось.

//+------------------------------------------------------------------+
//|                                                  CFullBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+

#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| Класс CFullBoxCox                                                |
//+------------------------------------------------------------------+
class CFullBoxCox:public PowellsMethod
  {
protected:
  int    Dlen;                     // размер данных
  double Dat[];                    // массив входных данных
  double Shift[];                  // массив входных данных со сдвигом
  double BCDat[];                  // преобразованные данные (Box-Cox)
  double Mean;                     // среднее значение преобразованных данных
  double Cdf[];                    // Quantile кумулятивной функции распределения
  double Scdf;                     // Square root of summ of Quantile^2
  double R;                        // коэффициент корреляции 
  double DeltaMin;                 // минимальное значение Delta
  double DeltaMax;                 // максимальное значение Delta
  double Par[2];                   // массив параметров
public:
  void   CFullBoxCox(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)           { return(Par[n]); }
private:
  double ndtri(double y0);         // функция, обратная функции нормального распределения
  virtual double func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CFullBoxCox::CalcPar(double &dat[])
  {
  int i;
  double a,max,min;
  
  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayResize(Shift,Dlen);
  ArrayResize(BCDat,Dlen);
  ArrayResize(Cdf,Dlen);
//--- копируем массив входных данных
  ArrayCopy(Dat,dat);
  
  Scdf=0;
  a=MathPow(0.5,1.0/Dlen);
  Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1];
  Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0];
  a=Dlen+0.365;
  for(i=1;i<(Dlen-1);i++)
    {
    //--- расчет Quantile кумулятивной функции распределения
    Cdf[i]=ndtri((i+0.6825)/a);
    //--- расчет суммы Quantile^2
    Scdf+=Cdf[i]*Cdf[i];
    }

//--- квадратный корень из суммы Quantile^2
  Scdf=MathSqrt(Scdf);             
  
  min=dat[0]; max=min;
  for(i=0;i<Dlen;i++)
    {
//--- копируем входные данные
    a=dat[i]; Dat[i]=a;
    if(min>a)min=a;
    if(max<a)max=a;
    }
  
//--- минимальное значение Delta
  DeltaMin=1e-5-min;
//--- максимальное значение Delta
  DeltaMax=(max-min)*200-min;
//--- начальное значение Lambda
  Par[0]=1.0;
//--- начальное значение Delta 
  Par[1]=(max-min)/2-min;
//--- оптимизация методом Powell
  Optimize(Par);             
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CFullBoxCox::func(const double &p[])
  {
  int i;
  double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret;
  
  lam=p[0]; del=p[1]; k1=0; k2=0;
  if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;}                    // Lambda >  5.0
  else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;}             // Lambda < -5.0
  if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;}    // Delta > DeltaMax
  else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin
  
  gm=0;
  for(i=0;i<Dlen;i++)
    {
    Shift[i]=Dat[i]+del;
    gm+=MathLog(Shift[i]);
    }

//--- геометрическое среднее
  gm=MathExp(gm/Dlen);
  gmpow=lam*MathPow(gm,lam-1);
  mean=0;
//--- Lambda != 0.0
   if(lam!=0)                                  
    {
    for(i=0;i<Dlen;i++)
      {
      a=(MathPow(Shift[i],lam)-1.0)/gmpow;
       //--- преобразованные данные (Box-Cox)
      BCDat[i]=a;
       //--- среднее значение
      mean+=a;
      }
    }
  //--- Lambda == 0.0
  else                                        
     {
    for(i=0;i<Dlen;i++)
      {
      a=gm*MathLog(Shift[i]);
       //--- преобразованные данные (Box-Cox)
      BCDat[i]=a;
      //--- среднее значение
      mean+=a;
      }
    }
  mean=mean/Dlen;
  //--- сортировка массива преобразованных данных
  ArraySort(BCDat);
  a=0; b=0;
  for(i=0;i<Dlen;i++)
    {
    c=(BCDat[i]-mean);
    a+=Cdf[i]*c;
    b+=c*c;
    }
  //--- коэффициент корреляции
  ret=a/(Scdf*MathSqrt(b)); 
  return(k1+k2-ret);
  }
//+------------------------------------------------------------------+
//| Функция, обратная функции нормального распределения              |
//| Prototype:                                                       |
//| Cephes Math Library Release 2.8: June, 2000                      |
//| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier           |
//+------------------------------------------------------------------+
double CFullBoxCox::ndtri(double y0)
  {
  static double s2pi =2.50662827463100050242E0; // sqrt(2pi)
  static double P0[5]={-5.99633501014107895267E1,  9.80010754185999661536E1,
                       -5.66762857469070293439E1,  1.39312609387279679503E1,
                       -1.23916583867381258016E0};
  static double Q0[8]={ 1.95448858338141759834E0,  4.67627912898881538453E0,
                        8.63602421390890590575E1, -2.25462687854119370527E2,
                        2.00260212380060660359E2, -8.20372256168333339912E1,
                        1.59056225126211695515E1, -1.18331621121330003142E0};
  static double P1[9]={ 4.05544892305962419923E0,  3.15251094599893866154E1,
                        5.71628192246421288162E1,  4.40805073893200834700E1,
                        1.46849561928858024014E1,  2.18663306850790267539E0,
                       -1.40256079171354495875E-1,-3.50424626827848203418E-2,
                       -8.57456785154685413611E-4};
  static double Q1[8]={ 1.57799883256466749731E1,  4.53907635128879210584E1,
                        4.13172038254672030440E1,  1.50425385692907503408E1,
                        2.50464946208309415979E0, -1.42182922854787788574E-1,
                       -3.80806407691578277194E-2,-9.33259480895457427372E-4};
  static double P2[9]={ 3.23774891776946035970E0,  6.91522889068984211695E0,
                        3.93881025292474443415E0,  1.33303460815807542389E0,
                        2.01485389549179081538E-1, 1.23716634817820021358E-2,
                        3.01581553508235416007E-4, 2.65806974686737550832E-6,
                        6.23974539184983293730E-9};
  static double Q2[8]={ 6.02427039364742014255E0,  3.67983563856160859403E0,
                        1.37702099489081330271E0,  2.16236993594496635890E-1,
                        1.34204006088543189037E-2, 3.28014464682127739104E-4,
                        2.89247864745380683936E-6, 6.79019408009981274425E-9};
  double x,y,z,y2,x0,x1,a,b;
  int i,code;
  if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);}
  if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);}
  code=1; y=y0;
  if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;}  // 0.135... = exp(-2)
  if(y>0.13533528323661269189)                         // 0.135... = exp(-2)
    {
    y=y-0.5; 
    y2=y*y;
    a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i];
    b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i];
    x=y+y*(y2*a/b);
    x=x*s2pi; 
    return(x);
    }
  x=MathSqrt(-2.0*MathLog(y));
  x0=x-MathLog(x)/x;
  z=1.0/x;
//--- y > exp(-32) = 1.2664165549e-14
  if(x<8.0)
    {
    a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i];
    b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i];
    x1=z*a/b;
    }
  else
    {
    a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i];
    b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i];
    x1=z*a/b;
    }
  x=x0-x1;
  if(code!=0)x=-x;
  return(x);
  }
//------------------------------------------------------------------------------------

В процессе оптимизации на диапазон изменения параметров преобразования накладываются ограничения. Величина параметра лямбда ограничена значениями 5.0 и -5.0. Ограничения для параметра дельта определяются по отношению к минимальному значению входной последовательности. Этот параметр ограничен величинами DeltaMin=(0.00001-min) и DeltaMax=(max-min)*200-min, где min и max – минимальное и максимальное значение элементов входной последовательности.

Скрипт FullBoxCoxTest.mq5 демонстрирует использование класса CFullBoxCox. Исходный код этого скрипта приведен ниже.

//+------------------------------------------------------------------+
//|                                               FullBoxCoxTest.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include  "CFullBoxCox.mqh"
CFullBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],shift[],bcdat[],lambda,delta,gm,gmpow;
   string fname;

//--- имя входного файла
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- чтение данных
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- размер данных
   n=ArraySize(dat);
//--- массив сдвинутых входных данных
   ArrayResize(shift,n);
//--- массив преобразованных данных
   ArrayResize(bcdat,n);

//--- оптимизация параметров lambda и delta
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   delta=Bc.GetPar(1);

   PrintFormat("Iterations= %i,   lambda= %.4f,   delta= %.4f",
               Bc.GetIter(),lambda,delta);
   gm=0;
   for(i=0;i<n;i++)
     {
      shift[i]=dat[i]+delta;
      gm+=MathLog(shift[i]);
     }
//--- геометрическое среднее
   gm=MathExp(gm/n);
   gmpow=lambda*MathPow(gm,lambda-1);
   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;}
   else         {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);}
//--- dat[]   <-- входные данные
//--- shift[] <-- входные данные со сдвигом
//--- bcdat[] <-- преобразованные данные
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//------------------------------------------------------------------------------------

В начале скрипта в массив dat[] из файла загружается входная последовательность, затем производится поиск оптимальных значений параметров преобразования. Далее, используя найденные параметры, производится непосредственно само преобразования. В результате массив dat[] содержит исходную последовательность, массив shift[] – сдвинутую на величину delta исходную последовательность и массив bcdat[] - содержит результат Бокс-Кокс преобразования.

Все файлы необходимые для компиляции скрипта FullBoxCoxTest.mq5 находятся в архиве Box-Cox-Tranformation_MQL5.zip.

При помощи скрипта FullBoxCoxTest.mq5 производилось преобразование используемых нами тестовых последовательностей. В результате анализа полученных данных можно сделать вывод, что данная двухпараметрическая форма преобразования по сравнению с однопараметрической формой, как и ожидалось, дает несколько лучшие результаты. Например, для последовательности EURUSD M1, результаты анализа которой представлены на рис. 6, значение теста Жака-Бера составило JB=100.94. После однопараметрического преобразования JB=39.30 (см. рис. 7), а после двухпараметрического (скрипт FullBoxCoxTest.mq5) это значение снизилось до JB=37.49.


Заключение

В данной статье рассматривались примеры, когда параметры Бокс-Кокс преобразования оптимизировались таким образом, чтобы закон распределения результирующей последовательности оказался как можно ближе к нормальному. Но на практике могут встретиться случаи, когда Бокс-Кокс преобразование целесообразно использовать несколько иным способом. Например, при прогнозировании временных последовательностей может быть использован следующий алгоритм:

  1. Выбираются предварительные значения параметров Бокс-Кокс преобразования и модели прогноза;
  2. Производится Бокс-Кокс преобразование входных данных;
  3. В соответствии с текущими параметрами осуществляется прогноз;
  4. Для результатов прогноза производится обратное Бокс-Кокс преобразование;
  5. По входной непреобразованной последовательности оценивается ошибка прогноза;
  6. Значения параметров изменяются таким образом, чтобы минимизировать ошибку прогноза и производится возврат к пункту 2.

В приведенном алгоритме параметры преобразования предполагается минимизировать так же, как и параметры прогнозной модели – по критерию минимума ошибки прогноза. В этом случае, перед Бокс-Кокс преобразованием уже не ставится задача преобразования входной последовательности к нормальному закону распределения.

Теперь необходимо преобразовать входную последовательность таким образом, чтобы в результате был получен закон распределения, обеспечивающий минимальную ошибку прогноза. В зависимости от выбранного способа прогнозирования этот закон распределения совсем не обязательно должен быть нормальным.

Непосредственно само рассматриваемое в статье Бокс-Кокс преобразование применимо только к последовательностям с положительными и не равными нулю значениями, а во всех остальных случаях требуется осуществлять сдвиг входной последовательности. Эту особенность данного преобразования можно смело отнести к его недостаткам. Но, несмотря на это, Бокс-Кокс преобразование, скорее всего, является наиболее универсальным и эффективным среди других подобного рода преобразований.


Литература

  1. А.Н. Порунов, Бокс-Кокс преобразование и иллюзия "нормальности" макроэкономического ряда. Журнал "Бизнес-Информатика" №2(12)-2010, c.3-10.
  2. Mohammad Zakir Hossain, The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses. Journal of Emerging Trends in Economics and Management Sciences (JETEMS) 2(1):32-39.
  3. Box-Cox Transformations.
  4. Статья "Прогнозирование временных рядов при помощи экспоненциального сглаживания".
  5. Статья "Прогнозирование временных рядов при помощи экспоненциального сглаживания (окончание)".
  6. Анализ основных характеристик временных рядов.
  7. Power transform.
  8. Draper N.R. and H. Smith, Applied Regression Analysis, 3rd ed., 1998, John Wiley & Sons, New York.
  9. Q-Q plot.

Прикрепленные файлы |
Загрузить ZIP
box-cox-transformation_mql5.zip (91.48 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (6)
Victor
Victor | 18 янв. 2012 в 05:22
denkir:

Victor, как вы считаете, целесообразно ли в случае плохого приближения к нормальности после БК преобразования применить это же преобразование повторно?

Я не знаю, но думаю, что повторное применение преобразования уже не даст такого сильного эффекта как первое.

Мне кажется, что подобного рода преобразования не являются идеальными. Применение такого преобразования, как впрочем, и любого другого, приводит к изменению исходных характеристик входной последовательности (наверное). И тут главное не переборщить, иначе полученная после преобразований последовательность не будет иметь ничего общего с исходной. Наверно поэтому не распространены преобразования, которые способны привести любую входную последовательность к нормальной. Но подчеркну еще раз, я всерьез над этими вопросами не задумывался.

Denis Kirichenko
Denis Kirichenko | 18 янв. 2012 в 06:51

Ясно. Да, затронутая тема довольно-таки глубока. Можно, как говорится, пилить и пилить...

Статья очень познавательна. Есть логическая связь с тем, что Вы писали ранее. Спасибо за материал.

СанСаныч Фоменко
СанСаныч Фоменко | 18 янв. 2012 в 08:27

Если говорить о трейдинге, то интерес представляет стабильность характеристик котира при движении вдоль него. Вы привели характеристики изменения после преобразования не сдвигая, а что будет с параметром БК при сдвиге на один бар вперед? Если сравнить стат характеристики, сдвигая последовательно вдоль не преобразованного котира со стат характеристиками преобразованного котира, то что мы увидим? Уменьшиться ли колебания дисперсии при сдвиге. Если уменьшается, то именно это огромный плюс для БК.
Victor
Victor | 18 янв. 2012 в 09:08
denkir:
Ясно. Да, затронутая тема довольно-таки глубока. Можно, как говорится, пилить и пилить...

Статья очень познавательна. Есть логическая связь с тем, что Вы писали ранее. Спасибо за материал.

Спасибо за оценку моего труда.

Victor
Victor | 18 янв. 2012 в 09:09
faa1947:
Если говорить о трейдинге, то интерес представляет стабильность характеристик котира при движении вдоль него. Вы привели характеристики изменения после преобразования не сдвигая, а что будет с параметром БК при сдвиге на один бар вперед? Если сравнить стат характеристики, сдвигая последовательно вдоль не преобразованного котира со стат характеристиками преобразованного котира, то что мы увидим? Уменьшиться ли колебания дисперсии при сдвиге. Если уменьшается, то именно это огромный плюс для БК.

Эта статья задумывалась как статья начального уровня, призванная в первую очередь обратить внимание читателя на особенности классических статистических методов и предоставить некие инструментальные средства для экспериментов. Ваши вопросы выходят далеко за рамки данной статьи. Ответить на них я Вам не смогу.

Трейдминатор 3: восстание торговых роботов Трейдминатор 3: восстание торговых роботов
В статье "Доктор Трейдлав..." мы остановились на том, что создали эксперт, оптимизирующий самостоятельно параметры заранее выбранной торговой системы. Было предложено создать эксперт, который не только оптимизирует параметры одной торговой системы, заложенной в основу эксперта, но делает выбор из нескольких торговых систем. Посмотрим же, что из этого может получится...
Создание советников при помощи Expert Advisor Visual Wizard Создание советников при помощи Expert Advisor Visual Wizard
Программа Expert Advisor Visual Wizard предоставляет интуитивно понятную графическую среду с полным набором готовых торговых блоков, которые позволят вам за несколько минут создавать советники. Знания программирования и языка MQL5 не требуется. Подход "click, drag and drop" позволяет вам создавать визуальные представления торговых стратегий и сигналов. Эти торговые диаграммы автоматически анализируются генератором MQL5-кода, который преобразует их в готовые к работе советники. Интерактивная графическая среда упрощает процесс проектирования и избавляет от необходимости написания кода на MQL5.
Интервью с Александром Арашкевичем (ATC 2011) Интервью с Александром Арашкевичем (ATC 2011)
Наконец улеглись страсти, мы можем перевести дух и начинать переосмысливать еще раз его результаты. И у нас есть еще один победитель Александр Арашкевич (AAA777) из Белоруссии, который получил специальный приз от Главного спонсора Automated Trading Championship 2011 - бесплатную поездку на соревнование Формулы-1 в 2012 году. Мы не могли упустить такой возможности пообщаться с ним.
Простейшие торговые системы с использованием семафорных индикаторов Простейшие торговые системы с использованием семафорных индикаторов
Если разобраться досконально в любой сложной торговой системе, то мы увидим, что в основе её лежит набор простых торговых сигналов. Поэтому начинающему разработчику торговых роботов не стоит сразу же приниматься за написание сложных алгоритмов. В статье приводится пример торговой системы, использующей для осуществления сделок семафорные индикаторы.