
Статистические оценки
Введение
В настоящее время можно часто встретить статьи и публикации на темы, связанные с эконометрикой, прогнозированием ценовых рядов, выбором и оценкой адекватности той или иной модели и так далее. При этом в большинстве случаев рассуждения строятся исходя из предположения, что читатель знаком с методами математической статистики и легко может оценить простейшие статистические параметры рассматриваемой последовательности.
Оценка статистических параметров последовательности очень важна, так как большинство математических моделей и методов строятся исходя из различного рода предположений, например, о нормальности закона распределения, или требуют знания значения дисперсии или других параметров. Таким образом, при анализе и прогнозировании временных рядов требуется простой и удобный инструмент, позволяющий быстро и наглядно производить оценку основных статистических параметров. В данной статье предпринята попытка создания такого инструмента.
В статье кратко рассматриваются простейшие статистические параметры случайной последовательности и некоторые методы ее визуального анализа. Предлагается реализация этих методов на MQL5 и способ визуализации результатов расчета при помощи программы Gnuplot. Данная статья ни в коем случае не претендует на роль учебника или справочника, поэтому в ней могут встретиться определенные вольности, допущенные по отношению к терминологии и формулировкам.
Анализ параметров по выборке
Предположим, что во времени бесконечно долго существует некий стационарный процесс, который может быть представлен последовательностью дискретных отсчетов. Эту последовательность отсчетов будем называть генеральной совокупностью. Часть отсчетов выбранных из генеральной совокупности будем называть выборкой из генеральной совокупности или просто выборкой объемом N отсчетов. Кроме того будем считать, что никакие истинные параметры генеральной совокупности нам неизвестны, поэтому их оценку будем производить по выборке конечного объема.
Исключение промахов
Прежде чем перейти к оценке статистических параметров, необходимо отметить, что точность оценки может оказаться недостаточной, если выборка содержит грубые ошибки (промахи). Влияние промахов на точность оценок особенно сильно проявляется, когда выборка имеет небольшой объем. Промахами будем считать значения, аномально отклоняющиеся от центра распределения. Такие отклонения могут быть вызваны различного рода маловероятными событиями и ошибками, возникшими при сборе статистики и формировании последовательности.
Принять решение о том, фильтровать промахи или нет, достаточно сложно, так как в большинстве случаев невозможно однозначно определить является ли данное значение промахом или принадлежит рассматриваемому процессу. Если промахи обнаружены и принято решение об их фильтрации, то возникает вопрос, как поступить с этими ошибочными значениями? Логичнее всего просто исключить их из выборки, при этом точность оценки статистических характеристик генеральной совокупности может увеличиться, но не следует забывать, что имея дело с временными последовательностями, следует с осторожностью относиться к исключению отсчетов из последовательности.
Для того чтобы иметь возможность исключать промахи из выборки или хотя бы обнаруживать их, реализуем алгоритм, рассмотренный в книге С.В. Булашева "Статистика для трейдеров".
В соответствии с этим алгоритмом, необходимо вычислить пять значений оценки центра распределения:
- Медиана (median);
- Центр 50%-ного интерквантильного промежутка (midquartile range, MQR);
- Среднее арифметическое по всей выборке (mean);
- Среднее арифметическое по 50%-ному интерквантильному промежутку (interquartile mean, IQM);
- Центр размаха (midrange) - определяется как среднее между максимальным и минимальным значением в выборке.
После этого результаты оценок центра распределения сортируются по возрастанию, и в качестве центра распределения Xcen выбирается среднее, то есть третье по счету, значение. Таким образом, выбранная оценка оказывается наименее подвержена влиянию промахов.
Далее, используя полученную оценку центра распределения Xcen, вычисляется выборочное среднеквадратичное отклонение s, эксцесс K и по эмпирической формуле находится коэффициент цензурирования:
![]()
где N – количество отсчетов в выборке (объем выборки).
Тогда значения, лежащие за пределами интервала:
![]()
будут считаться промахами и должны быть исключены из выборки.
Данный метод достаточно подробно рассмотрен в книге "Статистика для трейдеров", поэтому сразу перейдем к реализации этого алгоритма. Алгоритм, позволяющий обнаруживать и исключать промахи, реализован в виде функции erremove().
Ниже приведен скрипт, написанный для тестирования этой функции.
//---------------------------------------------------------------------------- // erremove.mq5 // Copyright 2011, MetaQuotes Software Corp. // https://www.mql5.com //---------------------------------------------------------------------------- #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #import "shell32.dll" bool ShellExecuteW(int hwnd,string lpOperation,string lpFile, string lpParameters,string lpDirectory,int nShowCmd); #import //---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[100]; double y[]; srand(1); for(i=0;i<ArraySize(dat);i++)dat[i]=rand()/16000.0; dat[25]=3; // Make Error !!! erremove(dat,y,1); } //---------------------------------------------------------------------------- int erremove(const double &x[],double &y[],int visual=1) { int i,m,n; double a[],b[5]; double dcen,kurt,sum2,sum4,gs,v,max,min; if(!ArrayIsDynamic(y)) // Error { Print("Function erremove() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function erremove() error!"); return(-1); } ArrayResize(a,n); ArrayCopy(a,x); ArraySort(a); b[0]=(a[0]+a[n-1])/2.0; // Midrange m=(n-1)/2; b[1]=a[m]; // Median if((n&0x01)==0)b[1]=(b[1]+a[m+1])/2.0; m=n/4; b[2]=(a[m]+a[n-m-1])/2.0; // Midquartile range b[3]=0; for(i=m;i<n-m;i++)b[3]+=a[i]; // Interquartile mean(IQM) b[3]=b[3]/(n-2*m); b[4]=0; for(i=0;i<n;i++)b[4]+=a[i]; // Mean b[4]=b[4]/n; ArraySort(b); dcen=b[2]; // Distribution center sum2=0; sum4=0; for(i=0;i<n;i++) { a[i]=a[i]-dcen; v=a[i]*a[i]; sum2+=v; sum4+=v*v; } if(sum2<1.e-150)kurt=1.0; kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*(n-1.0)/(n-2.0)/(n-3.0); // Kurtosis if(kurt<1.0)kurt=1.0; gs=(1.55+0.8*MathLog10((double)n/10.0)*MathSqrt(kurt-1))*MathSqrt(sum2/(n-1)); max=dcen+gs; min=dcen-gs; m=0; for(i=0;i<n;i++)if(x[i]<=max&&x[i]>=min)a[m++]=x[i]; ArrayResize(y,m); ArrayCopy(y,a,0,0,m); if(visual==1)vis(x,dcen,min,max,n-m); return(n-m); } //---------------------------------------------------------------------------- void vis(const double &x[],double dcen,double min,double max,int numerr) { int i; double d,yma,ymi; string str; yma=x[0];ymi=x[0]; for(i=0;i<ArraySize(x);i++) { if(yma<x[i])yma=x[i]; if(ymi>x[i])ymi=x[i]; } if(yma<max)yma=max; if(ymi>min)ymi=min; d=(yma-ymi)/20.0; yma+=d;ymi-=d; str="unset key\n"; str+="set title 'Sequence and error levels (number of errors = "+ (string)numerr+")' font ',10'\n"; str+="set yrange ["+(string)ymi+":"+(string)yma+"]\n"; str+="set xrange [0:"+(string)ArraySize(x)+"]\n"; str+="plot "+(string)dcen+" lt rgb 'green',"; str+=(string)min+ " lt rgb 'red',"; str+=(string)max+ " lt rgb 'red',"; str+="'-' with line lt rgb 'dark-blue'\n"; for(i=0;i<ArraySize(x);i++)str+=(string)x[i]+"\n"; str+="e\n"; if(!saveScript(str)){Print("Create script file error");return;} if(!grPlot())Print("ShellExecuteW() error"); } //---------------------------------------------------------------------------- bool grPlot() { string pnam,param; pnam="GNUPlot\\binary\\wgnuplot.exe"; param="-p MQL5\\Files\\gplot.txt"; return(ShellExecuteW(NULL,"open",pnam,param,NULL,1)); } //---------------------------------------------------------------------------- bool saveScript(string scr1="",string scr2="") { int fhandle; fhandle=FileOpen("gplot.txt",FILE_WRITE|FILE_TXT|FILE_ANSI); if(fhandle==INVALID_HANDLE)return(false); FileWriteString(fhandle,"set terminal windows enhanced size 560,420 font 8\n"); FileWriteString(fhandle,scr1); if(scr2!="")FileWriteString(fhandle,scr2); FileClose(fhandle); return(true); } //----------------------------------------------------------------------------
Рассмотрим функцию erremove(). В качестве первого параметра функции передается адрес массива x[], в котором размещены значения исследуемой выборки, объем выборки должен быть не менее четырех элементов. Предполагается, что размер массива x[] равен размеру выборки, поэтому значение объема выборки N функции не передается. Данные, находящиеся в массиве x[], в результате выполнения функции не изменяются.
Следующим параметром является адрес массива y[]. В случае успешного завершения функции в этом массиве будет расположена входная последовательность с исключенными промахами. Размер массива y[] меньше размера массива x[] на количество значений, исключенных из выборки. Массив y[] должен быть объявлен как динамический, иначе его размер в теле функции не сможет быть изменен.
Последним (необязательным) параметром является флаг, отвечающий за визуализацию результатов вычисления. Если его значение равно единице (значение по умолчанию), то перед завершением функции в отдельном окне будет построен график, отображающий входную последовательность, линию центра распределения и границы диапазона, за пределами которого значения выборки будут считаться промахами.
Способ построения графиков будет рассмотрен позже. В случае удачного завершения функция возвращает количество значений, исключенных из выборки, или -1 в случае ошибки. Если ошибочных значений (промахов) не было обнаружено, то функция вернет 0, а последовательность в массиве y[] будет дублировать содержимое массива x[].
В начале функции данные из массива x[] копируются в массив a[], сортируются по возрастанию, и вычисляются пять оценок центра распределения.
Центр размаха (midrange) определяется как деленная на два сумма значений крайних элементов отсортированного массива a[].
Медиана (median) вычисляется для нечетных объемов выборки N как:
![]()
для четных объемов выборки:
![]()
Учитывая, что индексы отсортированного массива a[] начинаются с нуля, получим:
m=(n-1)/2; median=a[m]; if((n&0x01)==0)b[1]=(median+a[m+1])/2.0;
Центр 50%-ного интерквантильного промежутка (midquartile range, MQR):
![]()
где M=N/4 (целочисленное деление).
Для отсортированного массива a[] получим:
m=n/4; MQR=(a[m]+a[n-m-1])/2.0; // Midquartile range
Среднее арифметическое по 50%-ному интерквантильному промежутку (interquartile mean, IQM). В отсортированной выборке отсекается по 25% с каждого края и для оставшихся 50% значений определяется среднее арифметическое:
![]()
где M=N/4 (целочисленное деление).
m=n/4; IQM=0; for(i=m;i<n-m;i++)IQM+=a[i]; IQM=IQM/(n-2*m); // Interquartile mean(IQM)
Среднее (mean) определяется как среднее арифметическое по всей выборке.
Каждое из найденных значений заносится в массив b[], после чего этот массив сортируется по возрастанию. В качестве центра распределения выбирается значение элемента массива b[2]. Далее, используя это значение, находятся несмещенные оценки среднеквадратичного отклонения и коэффициента эксцесса, алгоритм их вычисления будет рассмотрен позже.
По полученным оценкам определяется коэффициент цензурирования и границы интервала для обнаружения промахов (выражения были приведены ранее). В завершении производится формирование в массиве y[] последовательности с исключенными промахами и вызывается функция vis() для построения графика. Рассмотрим кратко способ визуализации, используемый при написании статьи.
Визуализация
Для отображения результатов вычислений была выбрана свободно распространяемая программа gnuplot, предназначенная для создания различных 2D и 3D графиков. Gnuplot имеет возможность выводить графики на экран (в отдельном окне) или записывать их в файл в различных графических форматах. Команды построения графиков могут исполняться из заранее подготовленного текстового файла. Официальная страница проекта gnuplot - gnuplot.sourceforge.net. Программа мультиплатформенная и распространяется в виде исходных кодов, а также уже откомпилированных под разные платформы двоичных файлов.
Примеры, написанные для данной статьи, тестировались только под Windows XP SP3 со сборкой gnuplot версии 4.2.2. Файл gp442win32.zip можно скачать по адресу http://sourceforge.net/projects/gnuplot/files/gnuplot/4.4.2/. С другими сборками и версиями программы gnuplot примеры не тестировались.
После загрузки архива gp442win32.zip его необходимо разархивировать. В результате появится каталог \gnuplot, в котором содержится сама программа, help-файл, документация и демонстрационные примеры. Для взаимодействия с программами из данной статьи каталог \gnuplot со всем его содержимым необходимо переместить в домашний каталог "MetaTrader 5".
Рисунок 1. Размещение каталога \gnuplot
После того, как каталог перемещен, можно проверить работоспособность программы gnuplot, для этого нужно запустить файл \gnuplot\binary\wgnuplot.exe и после появления приглашения "gnuplot>" набрать команду "plot sin(x)". В результате должно появиться окно с графиком функции sin(x). Также можно посмотреть поставляемые с программой демонстрационные примеры, для этого нужно выбрать пункт меню File\Demos и далее выбрать файл \gnuplot\demo\all.dem.
Теперь при запуске скрипта erremove.mq5 в отдельном окне будет построен график, показанный на рис 2:
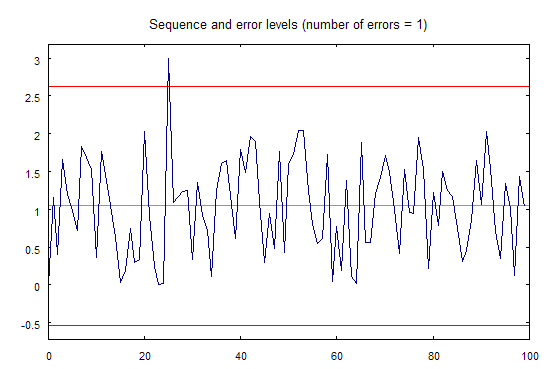
Рисунок 2. График, построенный при помощи скрипта erremove.mq5
Далее в статье лишь коротко коснемся некоторых особенностей использования gnuplot, так как информацию по этой программе и ее командам можно легко найти в документации, которая поставляется с программой, а так же на различных сайтах в сети, например, http://gnuplot.ikir.ru/.
В примерах программ, написанных для данной статьи при построении графиков, используется простейший вариант взаимодействия с gnuplot. Сначала создается текстовый файл gplot.txt, который содержит команды gnuplot и отображаемые данные. Далее вызывается программа wgnuplot.exe, в которую имя этого файла передается в качестве аргумента командной строки. Программа wgnuplot.exe вызывается функцией ShellExecuteW(), импортированной из системной библиотеки shell32.dll, поэтому в терминале должен быть разрешен импорт функций из внешних dll.
В используемой версии gnuplot построение графиков в отдельном окне возможно для двух типов терминалов: wxt и windows. Терминал wxt при построении графиков использует алгоритмы антиалиасинга и зачастую позволяет получить изображение более высокого качества, чем терминал windows. Тем не менее, при написании программ для этой статьи используется терминал windows. Это связно с тем, что если выбран терминал windows, то системный процесс, создаваемый при вызове "wgnuplot.exe -p MQL5\\Files\\gplot.txt" и открытии графического окна, будет автоматически завершен после закрытия этого окна.
Если выбрать терминал wxt, то после закрытия окна, в котором отображался график, системный процесс wgnuplot.exe автоматически не завершается. Таким образом, при выбранном терминале wxt и многократном обращении к wgnuplot.exe как указано выше в системе могут накопиться множество процессов никак себя внешне не проявляющих. При использовании вызова "wgnuplot.exe -p MQL5\\Files\\gplot.txt" с выбранным терминалом windows удается избежать открытия нежелательных дополнительных окон и появления незакрытых системных процессов.
Окно, в котором отображается график, является интерактивным и обрабатывает события мышки и клавиатуры. Чтобы получить информацию о назначенных по умолчанию горячих клавишах, нужно запустить wgnuplot.exe, после чего командой "set terminal windows" выбрать тип терминала и построить какой-нибудь график, например, командой "plot sin(x)". Если окно с графиком находится в фокусе, то нажав клавишу "h" увидим подсказку, которая будет выведена в текстовое окно wgnuplot.exe.
Оценка параметров
После краткого знакомства со способом построения графиков, вернемся к оценкам параметров распределения генеральной совокупности по ее конечной выборке. Предполагая, что никакие статистические параметры рассматриваемой генеральной совокупности заранее неизвестны, в дальнейшем будем использовать только несмещенные оценки этих параметров.
Основным параметром, характеризующим распределение последовательности, можно считать оценку математического ожидания или выборочное среднее значение (mean). Среднее значение вычисляется по формуле:
![]()
где N – число отсчетов в выборке.
Особую значимость этому параметру придает тот факт, что среднее значение является оценкой для центра распределения и используется при вычислении других параметров, связанных с центральными моментами. Кроме среднего значения в качестве статистических параметров распределения будем использовать оценку дисперсии (dispersion, variance), среднеквадратичного отклонения (standard deviation), коэффициента асимметрии (skewness) и коэффициента эксцесса (kurtosis).
![]()
где m – центральные моменты.
Центральные моменты являются числовой характеристикой распределения генеральной совокупности.
Второй, третий и четвертый выборочные центральные моменты определяются выражениями:
![]()
Но эти оценки не являются несмещенными. В данном случае следует упомянуть о k-Statistic и h-Statistic, которые при определенных условиях позволяют получить несмещенные оценки центральных моментов, поэтому их можно использовать при вычислении несмещенных оценок дисперсии, среднеквадратичного отклонения, асимметрии и эксцесса.
Следует обратить внимание на то, что четвертый центральный момент в k и h-оценках вычисляется по-разному. Это приводит к тому, что при использовании k или h, для оценки коэффициента эксцесса будут получены разные выражения. Например, в Microsoft Excel эксцесс вычисляется по формуле, соответствующей использованию k-оценок, а в книге "Статистика для трейдеров" несмещенная оценка коэффициента эксцесса вычисляется на основе h-оценок.
Остановим свой выбор на использовании h-оценок, тогда подставив их вместо m в ранее приведенные выражения, найдем интересующие нас параметры.
Дисперсия и среднеквадратичное отклонение:
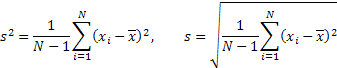
Коэффициент асимметрии:
![]()
Коэффициент эксцесса:
![]()
Найденный по приведенному выражению коэффициент эксцесса для последовательности с нормальным законом распределения будет давать значение 3.
Следует обратить внимание на то, что часто в качестве эксцесса используют величину, полученную путем вычитания тройки из найденного значения, таким образом, как бы нормируя полученное значение по отношению к нормальному закону распределения. В первом случае в иностранной литературе этот коэффициент называют "kurtosis", а во втором "excess kurtosis".
Расчет параметров по приведенным выражениям производятся в функции dStat():
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dStat(const double &x[],statParam &sP) { int i,m,n; double a,b,sum2,sum3,sum4,y[]; ZeroMemory(sP); // Reset sP n=ArraySize(x); if(n<4) // Error { Print("Function dStat() error!"); return(-1); } sP.kurt=1.0; ArrayResize(y,n); ArrayCopy(y,x); ArraySort(y); m=(n-1)/2; sP.median=y[m]; // Median if((n&0x01)==0)sP.median=(sP.median+y[m+1])/2.0; sP.mean=0; for(i=0;i<n;i++)sP.mean+=x[i]; sP.mean/=n; // Mean sum2=0;sum3=0;sum4=0; for(i=0;i<n;i++) { a=x[i]-sP.mean; b=a*a;sum2+=b; b=b*a;sum3+=b; b=b*a;sum4+=b; } if(sum2<1.e-150)return(1); sP.var=sum2/(n-1); // Variance sP.stdev=MathSqrt(sP.var); // Standard deviation sP.skew=n*sum3/(n-2)/sum2/sP.stdev; // Skewness sP.kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)* (n-1.0)/(n-2.0)/(n-3.0); // Kurtosis return(1);При вызове dStat() в функцию передается адрес массива x[], который содержит исходные данные и ссылка на структуру statParam, которая будет содержать вычисленные значения параметров. В случае ошибки, если входной массив содержит менее четырех элементов, функция возвращает -1.
Гистограмма
Кроме параметров, вычисляемых функцией dStat(), большой интерес может представлять закон распределения рассматриваемой генеральной совокупности. Для визуальной оценки закона распределения по конечной выборке можно построить гистограмму. При построении гистограммы диапазон изменения значений выборки делится на некоторое число равных интервалов и подсчитывается количество элементов, попавших в каждый из них (групповые частоты).
Далее по найденным групповым частотам строится столбиковая диаграмма, называемая гистограммой. После нормирования к ширине интервала, гистограмма будет представлять собой эмпирическую плотность распределения случайной величины. При построении гистограммы для определения оптимального количества интервалов воспользуемся эмпирическим выражением, приведенным в книге "Статистика для трейдеров":
![]()
где L – искомое количество интервалов, N – объем выборки, e – эксцесс.
Ниже приведена функция dHist(), определяющая количество интервалов, производящая подсчет количества попаданий значений в каждый из них, и производящая нормирование полученных групповых частот.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dHist(const double &x[],double &histo[],const statParam &sp) { int i,k,n,nbar; double a[],max,s,xmin; if(!ArrayIsDynamic(histo)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } nbar=(sp.kurt+1.5)*MathPow(n,0.4)/6.0; if((nbar&0x01)==0)nbar--; if(nbar<5)nbar=5; // Number of bars ArrayResize(a,n); ArrayCopy(a,x); max=0.0; for(i=0;i<n;i++) { a[i]=(a[i]-sp.mean)/sp.stdev; // Normalization if(MathAbs(a[i])>max)max=MathAbs(a[i]); } xmin=-max; s=2.0*max*n/nbar; ArrayResize(histo,nbar+2); ArrayInitialize(histo,0.0); histo[0]=0.0;histo[nbar+1]=0.0; for(i=0;i<n;i++) { k=(a[i]-xmin)/max/2.0*nbar; if(k>(nbar-1))k=nbar-1; histo[k+1]++; } for(i=0;i<nbar;i++)histo[i+1]/=s; return(1); }
На вход функции передается адрес массива x[], в котором расположена исходная последовательность, содержимое этого массива в результате выполнения функции не изменяется. Следующим параметром является ссылка на динамический массив histo[] в котором будут сохранены вычисленные значения. Количество элементов этого массива будет соответствовать количеству интервалов, используемых для вычисления, плюс два элемента.
В начало и в конец массива histo[] добавляются по одному элементу, содержащему нулевые значения. Последний параметр - это адрес, указывающий на структуру statParam, которая должна содержать заранее вычисленные значения хранящихся в ней параметров. В случае если передаваемый функции массив histo[] не является динамическим или входной массив x[] содержит менее четырех элементов, функция завершит выполнение и вернет значение -1.
Построив по вычисленным значениям гистограмму, можно, например, визуально оценить принадлежность выборки к нормальному закону распределения. Для более наглядного графического представления соответствия выборки нормальному закону распределения кроме гистограммы можно построить график со шкалой нормальной вероятности (Normal probability plot).
Normal probability plot
Основная идея при построении такого графика заключается в том, что шкала X у этого графика деформируется таким образом, что при отображении значений последовательности с нормальным распределением эти значения ложатся на одну линию. Таким образом, гипотеза нормальности может быть проверена графически. Более подробную информацию о таком типе графиков можно получить по ссылкам "Normal probability plot" или "e-Handbook of Statistical Methods".
Для вычисления значений, необходимых для построения графика нормальной вероятности используется приведенная ниже функция dRankit().
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dRankit(const double &x[],double &resp[],double &xscale[],const statParam &sp) { int i,n; double np; if(!ArrayIsDynamic(resp)||!ArrayIsDynamic(xscale)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } ArrayResize(resp,n); ArrayCopy(resp,x); ArraySort(resp); for(i=0;i<n;i++)resp[i]=(resp[i]-sp.mean)/sp.stdev; ArrayResize(xscale,n); xscale[n-1]=MathPow(0.5,1.0/n); xscale[0]=1-xscale[n-1]; np=n+0.365; for(i=1;i<(n-1);i++)xscale[i]=(i+1-0.3175)/np; for(i=0;i<n;i++)xscale[i]=ltqnorm(xscale[i]); return(1); } //---------------------------------------------------------------------------- double A1 = -3.969683028665376e+01, A2 = 2.209460984245205e+02, A3 = -2.759285104469687e+02, A4 = 1.383577518672690e+02, A5 = -3.066479806614716e+01, A6 = 2.506628277459239e+00; double B1 = -5.447609879822406e+01, B2 = 1.615858368580409e+02, B3 = -1.556989798598866e+02, B4 = 6.680131188771972e+01, B5 = -1.328068155288572e+01; double C1 = -7.784894002430293e-03, C2 = -3.223964580411365e-01, C3 = -2.400758277161838e+00, C4 = -2.549732539343734e+00, C5 = 4.374664141464968e+00, C6 = 2.938163982698783e+00; double D1 = 7.784695709041462e-03, D2 = 3.224671290700398e-01, D3 = 2.445134137142996e+00, D4 = 3.754408661907416e+00; //---------------------------------------------------------------------------- double ltqnorm(double p) { int s=1; double r,x,q=0; if(p<=0||p>=1){Print("Function ltqnorm() error!");return(0);} if((p>=0.02425)&&(p<=0.97575)) // Rational approximation for central region { q=p-0.5; r=q*q; x=(((((A1*r+A2)*r+A3)*r+A4)*r+A5)*r+A6)*q/(((((B1*r+B2)*r+B3)*r+B4)*r+B5)*r+1); return(x); } if(p<0.02425) // Rational approximation for lower region { q=sqrt(-2*log(p)); s=1; } else //if(p>0.97575) // Rational approximation for upper region { q = sqrt(-2*log(1-p)); s=-1; } x=s*(((((C1*q+C2)*q+C3)*q+C4)*q+C5)*q+C6)/((((D1*q+D2)*q+D3)*q+D4)*q+1); return(x); }
На вход функции передается адрес массива x[], в котором расположена исходная последовательность. Следующие два параметра является ссылками на выходные массивы resp[] и xscale[]. В этих массивах после выполнения функции располагаются значения, откладываемые при построении графика по шкале Y и шкале X соответственно. Далее функции передается адрес структуры statParam, в которой должны содержаться заранее вычисленные значения статистических параметров входной последовательности. В случае ошибки функция возвращает значение -1.
При формировании значений для шкалы X вызывается функция ltqnorm() которая вычисляет обратную интегральную функцию нормального распределения. Используемый для вычисления алгоритм был заимствован по ссылке "An algorithm for computing the inverse normal cumulative distribution function".
Четыре графика
Ранее была приведена функция dStat(), в которой рассчитываются значения статистических параметров. Кратко напомним их смысл.
Дисперсия (dispersion, variance) – среднее значение квадратов отклонений случайной величины от ее математического ожидания (среднего значения). Параметр, показывающий, насколько сильно случайная величина отклоняется от своего центра распределения. Чем больше значение этого параметра, тем больше отклонение.
Среднеквадратичное отклонение (standard deviation) – так как дисперсия имеет размерность квадрата случайной величины, в качестве более наглядной характеристики рассеяния часто используют среднеквадратичное отклонение, которое равно квадратному корню из дисперсии.
Коэффициент асимметрии (skewness) – если построить кривую распределения случайной величины, то коэффициент асимметрии будет показывать, насколько несимметрична относительно центра распределения кривая плотности вероятности. Если значение коэффициента асимметрии больше нуля, то кривая плотности вероятности имеет крутой левый и пологий правый спад. При отрицательном значении коэффициента асимметрии наоборот, левый спад оказывается более пологим. Когда кривая плотности вероятности симметрична относительно центра распределения, коэффициент асимметрии равен нулю.
Коэффициента эксцесса (kurtosis) – характеризует остроту пика кривой плотности вероятности и крутизну спада хвостов распределения. Чем более острым является пик кривой около центра распределения, тем большее значение принимает коэффициент эксцесса.
Несмотря на то, что перечисленные статистические параметры достаточно полно характеризуют последовательность, зачастую представление о характере последовательности проще получить по результатам оценок, представленным в графическом виде. Например, обычный график последовательности может очень хорошо дополнить впечатление, полученное при анализе статистических параметров.
Ранее в статье были приведены функции dHist() и dRankit(), позволяющие подготовить данные для построения гистограммы и графика со шкалой нормального распределения. Если одновременно с обычным графиком на одном листе отобразить и гистограмму и график нормального распределения, то дополняя друг друга, они позволят визуально буквально "на глазок" выявить основные особенности изучаемой последовательности.
К этим трем перечисленным графикам следует добавить график, при построении которого по шкале Y откладывается текущее значение последовательности, а по шкале X предыдущее. Такой график называется "Lag Plot". При сильной корреляции между соседними отсчетами значения выборки на этом графике вытягиваются в прямую линию, а при отсутствии корреляции между соседними отсчетами, например, при анализе случайной последовательности, значения будут рассеяны по всему графику.
Для быстрой предварительной оценки характера исходной последовательности предлагается построить на одном листе четыре графика и там же отобразить значения найденных статистических параметров. Эта идея не является новой, об использовании при проведении анализа четырех перечисленных графиков можно почитать по ссылке "4-Plot".
В конце статьи в разделе "Файлы" приведен скрипт s4plot.mq5, строящий на одном листе четыре упомянутых выше графика. В функции скрипта OnStart() создается массив dat[], содержащий исходную последовательность и затем поочередно вызываются функции dStat(), dHist() и dRankit() которые вычисляют все необходимые для построения графиков данные. Далее вызывается функция vis4plot(), которая на основании этих данных создает текстовый файл с командами gnuplot и вызывает саму эту программу для построения графиков в отдельном окне.
Полностью приводить в статье весь исходный текст этого скрипта не имеет смысла, так как функции dStat(), dHist() и dRankit() рассматривались ранее, а функция vis4plot() создающая последовательность команд gnuplot серьезных особенностей не имеет, а описание самих команд программы gnuplot выходит за рамки тематики данной статьи. Кроме того, для построения графиков может быть использована не программа gnuplot, а выбран какой либо другой способ.
Поэтому приведем лишь фрагмент скрипта s4plot.mq5, его функцию OnStart().
//---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[128],histo[],rankit[],xrankit[]; statParam sp; MathSrand(1); for(i=0;i<ArraySize(dat);i++) dat[i]=MathRand(); if(dStat(dat,sp)==-1)return; if(dHist(dat,histo,sp)==-1)return; if(dRankit(dat,rankit,xrankit,sp)==-1)return; vis4plot(dat,histo,rankit,xrankit,sp,6); }
В этом примере в качестве исходных данных массив dat[] при помощи вызова функции MathRand() заполняется случайной последовательностью. В результате выполнения скрипта должен получиться следующий результат:
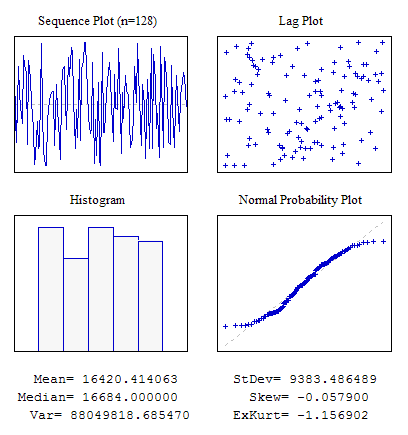
Рисунок 3. Четыре графика. Скрипт s4plot.mq5
Следует обратить внимание на последний параметр функции vis4plot(), он отвечает за то, в каком формате будут выводиться числовые значения. В данном примере значения выводятся с шестью знаками после запятой. Этот параметр аналогичен параметру, определяющему формат в функции DoubleToString().
При очень больших или очень маленьких значениях входной последовательности, для более наглядного отображения можно использовать научный формат, выбрав в качестве этого параметра, например значение -5. Для функции vis4plot() значение -5 является значением по умолчанию.
Для демонстрации того, насколько наглядно метод четырех графиков отображает особенности той или иной последовательности, нам понадобится генератор этих последовательностей.
Генератор псевдослучайной последовательности
Класс RNDXor128 предназначен для генерации псевдослучайных последовательностей.
Ниже приведен исходный текст включаемого файла с определением этого класса.
//----------------------------------------------------------------------------------- // RNDXor128.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Генерация псевдослучайных последовательностей. Используется алгоритм Xorshift RNG // (George Marsaglia) с периодом генерируемой последовательности 2**128. // uint rand_xor128() // { // static uint x=123456789,y=362436069,z=521288629,w=88675123; // uint t=(x^(x<<11));x=y;y=z;z=w; // return(w=(w^(w>>19))^(t^(t>>8))); // } // Методы: // Rand() - равномерное распределение на отрезке [0,UINT_MAX=4294967295]. // Rand_01() - равномерное распределение на отрезке [0,1]. // Rand_Norm() - нормальное распределение с нулевым средним и единичной дисперсией. // Rand_Exp() - экспоненциальное распределение с параметром 1.0. // Rand_Laplace() - распределение Лапласа параметром 1.0 // Reset() - сброс всех исходных значений в первоначальное состояние. // SRand() - установка новых исходных значений генератора. //----------------------------------------------------------------------------------- #define xor32 xx=xx^(xx<<13);xx=xx^(xx>>17);xx=xx^(xx<<5) #define xor128 t=(x^(x<<11));x=y;y=z;z=w;w=(w^(w>>19))^(t^(t>>8)) #define inidat x=123456789;y=362436069;z=521288629;w=88675123;xx=2463534242 class RNDXor128:public CObject { protected: uint x,y,z,w,xx,t; uint UINT_half; public: RNDXor128() {UINT_half=UINT_MAX>>1;inidat;}; double Rand() {xor128;return((double)w);}; int Rand(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w;} return(0);}; double Rand_01() {xor128;return((double)w/UINT_MAX);}; int Rand_01(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w/UINT_MAX;} return(0);}; double Rand_Norm() {double v1,v2,s,sln;static double ra;static uint b=0; if(b==w){b=0;return(ra);} do{ xor128;v1=(double)w/UINT_half-1.0; xor128;v2=(double)w/UINT_half-1.0; s=v1*v1+v2*v2; } while(s>=1.0||s==0.0); sln=MathLog(s);sln=MathSqrt((-sln-sln)/s); ra=v2*sln;b=w; return(v1*sln);}; int Rand_Norm(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Norm(); return(0);}; double Rand_Exp() {xor128;if(w==0)return(DBL_MAX); return(-MathLog((double)w/UINT_MAX));}; int Rand_Exp(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Exp(); return(0);}; double Rand_Laplace() {double a;xor128; a=(double)w/UINT_half; if(w>UINT_half) {a=2.0-a; if(a==0.0)return(-DBL_MAX); return(MathLog(a));} else {if(a==0.0)return(DBL_MAX); return(-MathLog(a));}}; int Rand_Laplace(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Laplace(); return(0);}; void Reset() {inidat;}; void SRand(uint seed) {int i;if(seed!=0)xx=seed; for(i=0;i<16;i++){xor32;} xor32;x=xx;xor32;y=xx; xor32;z=xx;xor32;w=xx; for(i=0;i<16;i++){xor128;}}; int SRand(uint xs,uint ys,uint zs,uint ws) {int i;if(xs==0&&ys==0&&zs==0&&ws==0)return(-1); x=xs;y=ys;z=zs;w=ws; for(i=0;i<16;i++){xor128;} return(0);}; }; //-----------------------------------------------------------------------------------
Используемый для генерации псевдослучайной последовательности алгоритм подробно описан в статье George Marsaglia "Xorshift RNGs" (смотри в конце статьи файл xorshift.zip). Описание методов класса RNDXor128 приведено в файле RNDXor128.mqh. При использовании данного класса могут быть получены последовательности с равномерным, нормальным, экспоненциальным законом распределения и распределением Лапласа (двойное экспоненциальное).
Необходимо обратить внимание на тот факт, что при создании объекта класса RNDXor128 начальные значения генерируемой последовательности устанавливаются в исходное состояние, поэтому в отличие от обращения к функции MathRand() при каждом новом запуске скрипта или индикатора, использующего RNDXor128, будет генерироваться одна и та же последовательность. Так же, как при использовании пары вызовов MathSrand() и затем MathRand().
Примеры последовательностей
Ниже в качестве примера приводятся результаты, полученные при анализе последовательностей, сильно отличающихся друг от друга по своему характеру.
Пример 1. Случайная последовательность с равномерным законом распределения.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_01(); ... }
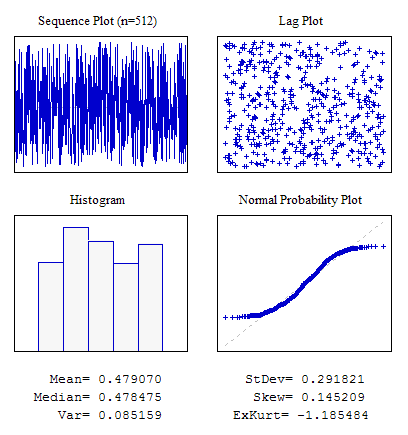
Рисунок 4. Равномерное распределение
Пример 2. Случайная последовательность с нормальным законом распределения.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Norm(); ... }
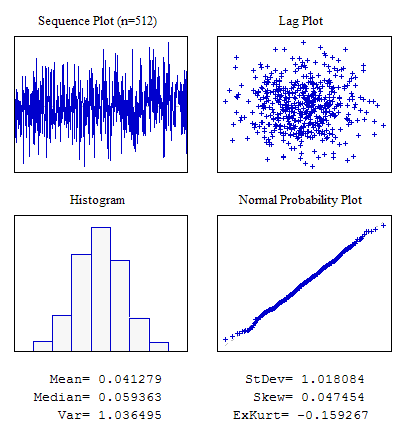
Рисунок 5. Нормальное распределение
Пример 3. Случайная последовательность с экспоненциальным законом распределения.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Exp(); ... }
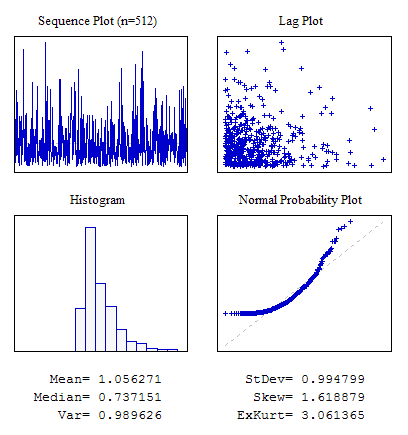
Рисунок 6. Экспоненциальное распределение
Пример 4. Случайная последовательность с распределением Лапласа.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Laplace(); ... }
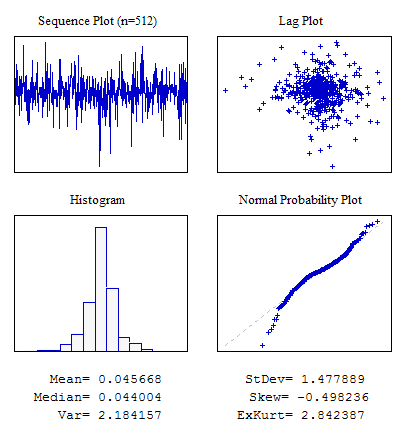
Рисунок 7. Распределение Лапласа
Пример 5. Синусоидальная последовательность.
//---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=MathSin(2*M_PI/4.37*i); ... }
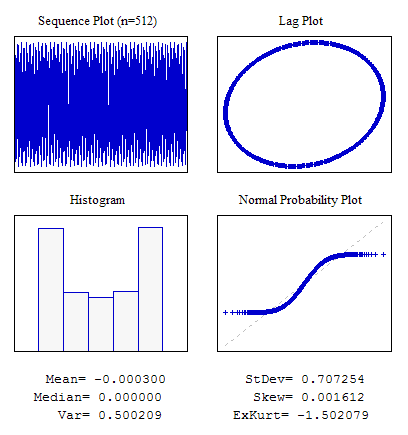
Рисунок 8. Синусоидальная последовательность
Пример 6. Последовательность с заметной корреляцией между соседними отсчетами.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512],a; for(i=0;i<ArraySize(dat);i++) {a+=Rnd.Rand_Laplace();dat[i]=a;} ... }
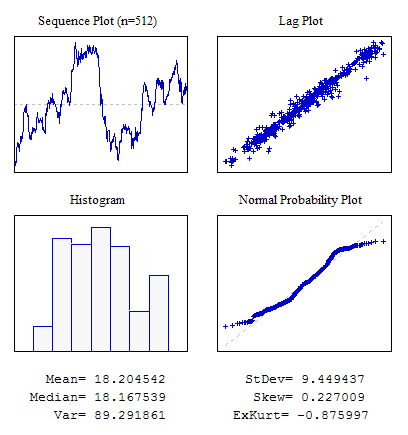
Рисунок 9. Корреляция между соседними отсчетами
Заключение
Разработка программных алгоритмов, реализующих те или иные вычисления, всегда является достаточно сложной задачей, так как должен быть учтен целый ряд требований, связанный с минимизацией ошибок, которые могут возникать в результате округления, усечения или переполнения переменных.
В процессе написания примеров для данной статьи по отношению к программным алгоритмам никакого анализа не производилось. При написании функций математические алгоритмы были реализованы, что называется "впрямую". Поэтому для использования в "серьезных" приложениях необходимо произвести анализ на предмет их устойчивости и точности.
В статье совершенно не затрагиваются вопросы, связанные с особенностями программы gnuplot. Это вызвано тем, что эти вопросы выходят за рамки тематики данной статьи. Все же хочется упомянуть о том, что gnuplot может быть адаптирован для совместного использования с MetaTrader 5. Для этого можно внести корректировки в его исходные коды и заново перекомпилировать. Кроме того, способ передачи в gnuplot команд и данных через файл, скорее всего, не является оптимальным, так как взаимодействие с gnuplot может быть организовано через программный интерфейс.
Файлы
- erremove.mq5 – пример скрипта, исключающего промахи из выборки.
- function_dstat.mq5 – функция для расчета статистических параметров.
- function_dhist.mq5 - функция для расчета значений гистограммы.
- function_drankit.mq5 – функция для расчета значений, используемых при построении графика со шкалой нормального распределения.
- s4plot.mq5 – пример скрипта, строящего на одном листе четыре графика.
- RNDXor128.mqh – класс генератора псевдослучайной последовательности.
- xorshift.zip - George Marsaglia. "Xorshift RNGs".
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Трассировка, отладка и структурный анализ кода
Трассировка, отладка и структурный анализ кода
 Использование ресурсов в MQL5
Использование ресурсов в MQL5
 Уменьшаем расход памяти на вспомогательные индикаторы
Уменьшаем расход памяти на вспомогательные индикаторы
 Реализация автоматического анализа волн Эллиотта на MQL5
Реализация автоматического анализа волн Эллиотта на MQL5
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
"Исключение промахов
Прежде чем перейти к оценке статистических параметров, необходимо отметить, что точность оценки может оказаться недостаточной, если выборка содержит грубые ошибки (промахи). Влияние промахов на точность оценок особенно сильно проявляется, когда выборка имеет небольшой объем. Промахами будем считать значения, аномально отклоняющиеся от центра распределения. Такие отклонения могут быть вызваны различного рода маловероятными событиями и ошибками, возникшими при сборе статистики и формировании последовательности.
Принять решение о том, фильтровать промахи или нет, достаточно сложно, так как в большинстве случаев невозможно однозначно определить является ли данное значение промахом или принадлежит рассматриваемому процессу. Если промахи обнаружены и принято решение об их фильтрации, то возникает вопрос, как поступить с этими ошибочными значениями? Логичнее всего просто исключить их из выборки, при этом точность оценки статистических характеристик генеральной совокупности при этом может увеличиться, но не следует забывать, что имея дело с временными последовательностями, следует с осторожностью относиться к исключению отсчетов из последовательности."
Лучше вообще этого не делать.
Да, все данные дожны пройти проверки, да, проверки должны быть автоматизированы.
Но лучше отказаться от источника данных, чем манипулировать исходными данными, вручную или автоматически.
В реальной жизни принятие или исключение из учета больших по объему рисков на основании их "малой вероятности" является причиной многих трагедий и катастроф.
Victor, вот такого рода вопрос.
Как вы полагаете, Kurtosis может быть меньше 1?
Если да, то
будет равно -1.#IND, не так ли? :-)
Отличная статья!
Victor, вот такого рода вопрос.
Как вы полагаете, Kurtosis может быть меньше 1?
Если да, то
будет равно -1.#IND, не так ли? :-)
Отличная статья!
Скорее всего, теоретически kurtosis не может быть меньше единицы. Наверное, значение равное единице получится для последовательности, состоящей из отсчетов прямой линии. Например, 1,2,3,4,5.
Может ли за счет ошибок, используемый в статье алгоритм дать значение kurtosis меньшее единицы, я не знаю. В конце статьи упоминалось, что поведение алгоритма расчетов коэффициентов не исследовалось.
Действительно при вычислении несмещенных оценок kurtosis может принимать значение меньшее единицы. Например, для входной последовательности 4,7,13,16.
Спасибо за замечание. Внесу изменения.