Знакомство с методом эмпирической модовой декомпозиции
19 003
35
Введение
Все реальные процессы, с которыми нам приходится сталкиваться на практике, являются сложными процессами, состоящими, как правило, из большого количества компонент. Например, погода. При анализе графика количества выпавших осадков мы должны помнить, что перед нами график, отражающий взаимодействие большого количества разнообразных процессов. Таких, как смена времен года, глобальные процессы потепления/похолодания, изменения в океанических течениях, динамика развития циклонов и антициклонов, количество выбросов углекислого газа в атмосферу, циклы солнечной активности и так далее. Этот список можно было бы продолжать до бесконечности.
Поэтому анализировать непосредственно такой график достаточно сложно, так как составляющие его компоненты, взаимодействуя друг с другом, маскируют и искажают те закономерности, которые мы хотели бы выявить. В этом случае возникает законное желание разделить наблюдаемый нами процесс на отдельные составляющие и анализировать каждую из компонент по отдельности. Анализируя отдельные компоненты и изучая вклад каждой из них в исследуемый процесс можно лучше понять происходящее и, например, повысить достоверность прогноза.
Не исключением является и различная получаемая нами биржевая информация, в том числе и котировки валютных пар, которые так же формируются под воздействием очень большого количества различных факторов. Поэтому вполне резонно ожидать, что предварительное разложение их на отдельные компоненты может существенно облегчить дальнейший их анализ.
Термин "декомпозиция" формально означает разделение составного процесса или составного материала на отдельные входящие в его состав компоненты. Но уже давно, в областях связанных с анализом различных процессов, анализом сигналов, анализом различного рода последовательностей и так далее, этот термин используется в более широком смысле, зачастую обозначающим разложение не на реальные исходные составляющие, а разложение на какие-то функции, которые при процессе формирования исходных данных реально не присутствовали. Эти функции как бы искусственно формируются в процессе разложения исходных данных, но, несмотря на их "искусственное" происхождение, позволяют произвести более глубокий анализ этих данных, помогая выявлять скрытые закономерности.
Подавляющее большинство методов, используемых при анализе рынка, можно явно или неявно отнести к методам выделения из анализируемого процесса тех или иных его компонент, то есть к методам декомпозиции. Кратко коснемся некоторых из них.
1. Декомпозиция
Существует большое количество используемых на практике всевозможных методов декомпозиции анализируемой последовательности. Эти методы могут основываться на различных математических или эмпирических подходах, иметь разную степень сложности и различные области применения.
Например, даже фундаментальный анализ рынка можно, хоть и некоторой натяжкой, отнести к методам декомпозиции. При таком анализе производится попытка анализировать воздействие набора исходных событий, непосредственно влияющих на состояние рынка. То есть производится неявная декомпозиция анализируемого рыночного процесса на целый ряд формирующих его событий.
Далее вопросов, связанных с фундаментальным анализом, касаться не будем. Будем считать, что какая-либо дополнительная информация об анализируемом процессе у нас отсутствует, а имеется только последовательность, отражающая поведение данного процесса.
Простейшим примером декомпозиции может служить разложение последовательности на несколько компонент при помощи привычных хорошо известных приемов. Например, на графике любой валютной пары построим MA. Затем из исходной последовательности вычтем полученную кривую. В результате будем иметь две компоненты исходной последовательности - кривую MA и остаток. Если к полученному остатку применить ту же процедуру, но с MA большего периода, то в результате получим уже три компоненты - две кривые MA и остаток от преобразования. Как видим процесс декомпозиции нетрудно организовать и подручными средствами. Весь вопрос заключается в свойствах результатов такого процесса.
Среди хорошо известных методов декомпозиции и спектрального анализа нельзя не выделить преобразование Фурье. Преобразование Фурье относится к классу ортогональных преобразований, в котором используется фиксированный базис гармонических функций. Результат преобразования Фурье можно представить как разложение исходного процесса на гармонические функции, имеющие фиксированные частоту и амплитуду. Отметим два важных для нас момента.
Во-первых, преобразование всегда производится в фиксированном, заданном заранее, базисе ортогональных функций. То есть базис преобразования не зависит от характера преобразуемой последовательности.
Во-вторых, результирующие гармонические компоненты имеют постоянные значения амплитуды и частоты. То есть их параметры неизменны на всем протяжении исходной последовательности. Это означает, что если характер исходный последовательности на рассматриваемом интервале времени изменялся, то эти изменения не будут отражены в результатах преобразования. Полученные в этом случае результаты будут отражать лишь некоторое усредненное состояние процесса, так как данное преобразование построено исходя из предположения стационарности исходных данных.
Для того чтобы избежать ограничений, связанных с нестационарностью исходной последовательности, можно от преобразования Фурье перейти к использованию вейвлет-преобразования. Вейвлет-преобразование, так же как и преобразование Фурье, производит разложение в фиксированном базисе функций. В отличие от преобразования Фурье, этот базис должен быть предварительно задан, то есть должна быть выбрана вейвлет-функция, используемая в процессе преобразования.
В отличие от преобразования Фурье, при вейвлет-преобразовании каждая найденная компонента имеет параметры, определяющие во времени ее масштаб и уровень. За счет этого решается проблема, связанная с возможной нестационарностью анализируемого процесса.
Преобразование Фурье и вейвлет-преобразование заслуженно получили широкую известность благодаря использованию в них хорошо обоснованных математических методов и наличию эффективных алгоритмов их реализации. Кроме того, оба это преобразования, как показала практика, достаточно универсальны и могут с успехом применяться в различных областях.
Но для практического использования хотелось бы иметь преобразование, не только позволяющее работать с нестационарными процессами, но и использующее адаптивный, определяемый исходными данными базис преобразования. Такое преобразование существует, перейдем к краткому его рассмотрению, обращаясь непосредственно к основной теме статьи.
2. Эмпирическая модовая декомпозиция
Эмпирическая модовая декомпозиция (Empirical Mode Decomposition, EMD) была предложена как составная часть преобразования Гильберта-Хуанга (Hilbert–Huang transform, HHT). Преобразование Гильберта-Хуанга производится как бы в два приема. Сначала при помощи алгоритма EMD находятся эмпирические моды или внутренние колебания (Intrinsic Mode Functions, IMF).
Затем на втором этапе при помощи преобразования Гильберта на их основе определяется мгновенный спектр исходной последовательности. Преобразования Гильберта-Хуанга позволяет находить мгновенный спектр нелинейных нестационарных последовательностей. Соответственно и эмпирическая модовая декомпозиция предназначена для работы с такими последовательностями.
В данной статье построение мгновенного спектра при помощи преобразования Гильберта рассматривать не будем. Остановимся только на алгоритме эмпирической модовой декомпозиции (EMD).
В отличие от упомянутого ранее преобразования Фурье и вейвлет-преобразования в процессе эмпирической модовой декомпозиции производится разложение на эмпирические моды (IMF), которые не заданы аналитически и определяются исключительно самой анализируемой последовательностью. При этом базисные функции преобразования формируются адаптивно, непосредственно из входных данных. Выделенные в процессе использования метода EMD эмпирические моды должны удовлетворять только следующим требованиям:
- Количество экстремумов эмпирической моды (сумма максимумов и минимумов) и количество пересечений нуля не должны отличаться более чем на единицу;
- В любой точке эмпирической моды среднее значение огибающих, определенных локальными максимумами и локальными минимумами, должно быть нулевым.
В процессе декомпозиции получается семейство IMF функций, упорядоченных по частоте. Каждая последующая IMF имеет более низкую частоту, чем предыдущая. Использование термина "частота" по отношению к IMF не совсем корректно, хотя, наверное, наилучшим образом подходит для определения ее характера. Дело в том, что хотя IMF и имеет колебательный характер, это колебание может быть промодулировано во времени как по частоте, так и по амплитуде.
Представить результат работы алгоритма EMD по словесному описанию достаточно сложно, поэтому перейдем к его программной реализации. Это даст возможность ближе познакомиться с особенностями работы данного алгоритма.
3. Алгоритм EMD
В основе предложенного Хуангом алгоритма лежит построение гладких огибающих по максимумам и минимумам последовательности и дальнейшее вычитание среднего этих огибающих из исходной последовательности. Для этого производится поиск максимумов и минимумов и строятся сплайны, проходящие через эти точки. Эти сплайны и образуют верхнюю и нижнюю огибающие.
Процесс построения огибающих показан на рисунке 1.
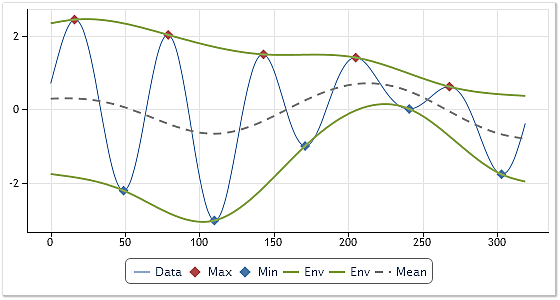
Рис. 1. Построение огибающих и средней линии
Анализируемая последовательность представлена на рисунке 1 тонкой синей линией. Максимумы и минимумы этой последовательности отмечены красным и синим цветом соответственно. Огибающие показаны зеленым цветом.
По двум огибающим вычисляется среднее значение. Это среднее показано на рисунке 1 штриховой линией. Найденное таким образом среднее значение далее вычитается из исходной последовательности.
В результате перечисленных шагов в первом приближении находится искомая эмпирическая функция. Для полноценного выделения IMF необходимо вновь найти максимумы и минимумы у этой оценки IMF, и повторить изложенные ранее действия. Этот повторяющийся процесс называется просеиванием (sifting). Процесс просеивания продолжается до тех пор, пока не будет достигнут заданный критерий его останова. Выбор критериев останова просеивания является одним из ключевых моментов, влияющих на результат декомпозиции в целом. К обсуждению этого вопроса вернемся немного позже.
Если процесс просеивания удачно завершен, то в результате мы получаем первую найденную эмпирическую функцию. Далее, для того чтобы найти следующую IMF, необходимо из исходного сигнала вычесть уже найденную IMF и снова повторить описанную процедуру. Так продолжается до тех пор, пока не будут найдены все IMF. Поиск очередной IMF обычно прекращается тогда, когда остаток имеет, например, не более двух экстремальных точек.
Как видим, описанная процедура эмпирической модовой декомпозиции базируется не на строгих математических выкладках, а полностью оправдывая свое название, действительно является эмпирической. Несмотря на простоту и ясность предложенного Хуангом описанного выше алгоритма, он содержит ряд моментов, которые можно отнести к его недостаткам.
В различных публикациях, посвященных данной теме, можно найти и подробное рассмотрение слабых сторон предложенного Хуангом алгоритма и пути его модернизации. В данной статье не будем заострять внимание на возможных вариантах модернизации данного метода, а просто попытаемся создать его программную реализацию. Особенности этой реализации будут кратко рассмотрены далее.
4. Класс CEMDecomp
Основываясь на найденных в Интернете публикациях, посвященных преобразованию Гильберта-Хуанга и эмпирической модовой декомпозиции, был создан класс CEMDecomp, реализующий алгоритм EMD. Реализованный алгоритм практически очень близок к алгоритму, первоначально предложенному Хуангом, и не содержит каких-либо серьезных модификаций.
Ниже приведен фрагмент исходного кода, содержащегося в файле CEMDecomp.mqh. Этот файл можно найти в конце статьи.
//------------------------------------------------------------------------------------ // The Empirical Mode Decomposition (EMD). //------------------------------------------------------------------------------------ class CEMDecomp:public CObject { public: int N; // Input and output data size double Mean; // Mean of input data int nIMF; // IMF counter int MaxIMF; // Maximum number of IMF int MaxIter; // Maximum number of iterations int FixedIter; // 0-variable number of sifting iterations; // 1-always ten sifting iterations. double IMFResult[]; // Result private: double X[]; double Imf[]; double XMax[]; // x of local maxima double YMax[]; // y of local maxima double XMin[]; // x of local minima double YMin[]; // y of local minima double EnvUpp[]; // Upper envelope double EnvLow[]; // Lower envelope double Eps; // Accuracy comparison of floating-point numbers double Tol; // Accuracy of calculation IMF public: void CEMDecomp(void); int Decomp(double &y[]); // Decomposition void GetIMF(double &x[], int nn); // Get IMF number nn private: int arrayprepare(void); void extrema(double &y[],int &nmax,double &xmax[],double &ymax[], int &nmin,double &xmin[],double &ymin[]); int SplineInterp(double &x[],double &y[],int n,double &x2[], double &y2[],int btype=0); };
Рассмотрим доступные (public) переменные и методы, объявленные в классе CEMDecomp.
N – Количество элементов последовательности. Значение переменной N формируется после обращения к методу Decomp() и равно длине входной последовательности. Найденные IMF будут иметь такой же размер.
Mean – Среднее значение входной последовательности. Значение формируется после обращения к методу Decomp().
nIMF – Счетчик количества IMF. После обращения к методу Decomp() содержит число найденных IMF плюс два. Таким образом, эта величина указывает, сколько компонент можно будет считать методом GetIMF(). При этом компонента с индексом 0 всегда будет содержать исходную последовательность, из которой вычтено ее среднее значение, а компонента с номером nIMF будет содержать остаток от декомпозиции.
MaxIMF – Максимально допустимое количество IMF. Разложение входной последовательности на отдельные IMF будет прекращено, если их количество достигнет значения MaxIMF. Значение этой переменной может быть задано до обращения к методу Decomp(). Значение по умолчанию равно 16.
MaxIter – Максимально допустимое количество итераций для процесса просеивания (sifting). Если количество итераций в процессе просеивания достигнет этой величины, то просеивание будет завершено независимо от того, была ли достигнута заданная точность или нет. Значение этой переменной может быть задано до обращения к методу Decomp(). Значение по умолчанию равно 2000.
FixedIter – Флаг, при помощи которого может быть задан критерий останова при просеивании. Если значение FixedIter равно нулю, то процесс просеивания для каждой из IMF будет завершаться при достижении заданной точности. Для достижения заданной точности при формировании разных IMF может потребоваться разное количество итераций. Если значение FixedIter задать равным единице, то формирование любой IMF будет происходить всегда за 10 итераций. Значение этой переменной может быть задано до обращения к методу Decomp(). Значение по умолчанию равно 0.
Decomp(double &y[]) – Основной метод класса, осуществляющий декомпозицию. В качестве входного параметра получает ссылку на массив, содержащий входные данные. При успешном завершении переменная N будет равна длине входного массива. Такой же размер будут иметь и найденные IMF. Переменная Mean будет равна среднему значению входной последовательности, а переменная nIMF равна количеству компонент, которые могут быть считаны при помощи метода GetIMF().
GetIMF(double &x[], int nn) – Служит для обеспечения доступа к результатам, полученным при помощи метода Decomp().В качестве входного параметра передается адрес массива, в который будет скопирована компонента с номером, заданным параметром nn. При этом компонента с индексом 0 всегда будет содержать исходную последовательность, из которой вычтено ее среднее значение, а компонента с номером nIMF будет содержать остаток от декомпозиции. Если длина переданного в качестве параметра массива окажется меньше длины результирующих компонент, то массив будет заполнен настолько, насколько позволит его длина.
Использование класса CEMDecomp демонстрируется следующим примером:
#include "CEMDecomp.mqh" //------------------------------------------------------------------------------------ // Script program start function //------------------------------------------------------------------------------------ void OnStart() { int n,ret; double yy[],imf2[]; n=400; // Длина входной последовательности ArrayResize(yy,n); // Массив входных данных ArrayResize(imf2,n); // Массив для считывания результата CopyOpen(_Symbol,PERIOD_CURRENT,0,n,yy); // Формирование входных данных CEMDecomp *emd=new CEMDecomp(); // Создание экземпляра класса CEMDecomp ret=emd.Decomp(yy); // Декомпозиция входной последовательности if((ret==0)&&(emd.nIMF>3)) // Если не было ошибки и было найдено // достаточное количество компонент, то emd.GetIMF(imf2,2); // копируем компоненту номер 2 в // массив imf2[]. delete(emd); // Удаление экземпляра класса CEMDecomp // Одна из найденных компонент в массиве imf2[]. } //------------------------------------------------------------------------------------
В конце статьи в архиве CEMDecomposition.zip размещен полный пример декомпозиции с отображением найденных IMF при помощи Web-интерфейса. Для запуска этого примера необходимо раскрыть указанный архив и поместить каталог \CEMDecomposition вместе со всем его содержимым в каталог \Indicators или \Scripts терминала. После этого можно откомпилировать и запустить скрипт EMDecomp_Test.mq5. Следует помнить, что в терминале при этом должно быть разрешено использование внешних библиотек.
На рисунке 2 приведен другой пример декомпозиции, здесь показано разложение котировок USDJPY, Daily с длиной последовательности 100 элементов. Как видим, в результате декомпозиции этой последовательности были найдены четыре IMF и остаток.
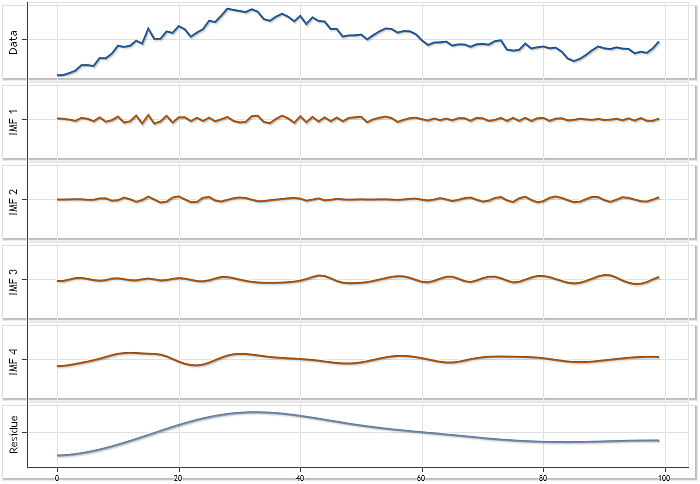
Рис. 2. Разложение последовательности USDJPY,Daily,N=100
На рисунке 2 все графики представлены в едином масштабе, что позволяет оценить вклад каждой из найденных IMF. Но при таком построении графиков недостаточно ясно видны особенности каждой из IMF. На рисунке 3 представлены те же результаты, но при этом для каждого из графиков использовался режим автоматического масштабирования.
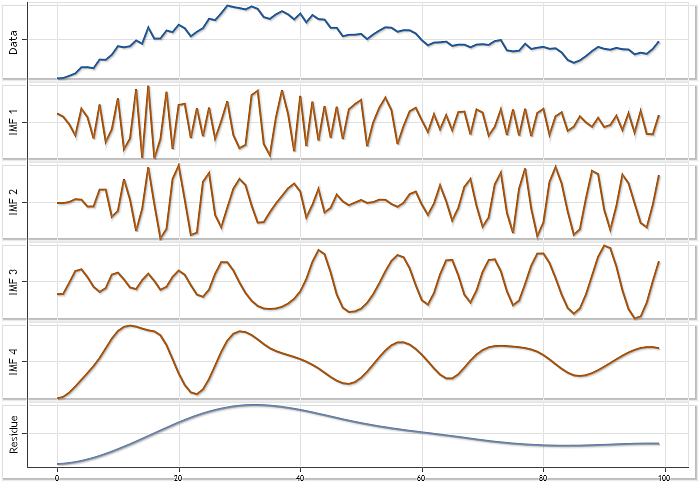
Рис. 3. Разложение последовательности USDJPY, Daily, N=100. Автомасштабирование
Хотя рисунок 3 и не отображает реального соотношения амплитуд отдельных компонент, используемый режим автоматического масштабирования позволяет более детально представить каждую из них.
5. Пояснения к данной реализации алгоритма EMD
Первое, на что хотелось бы обратить внимание, это способ определения максимумов и минимумов исходной последовательности. В данном случае речь идет о двух возможных вариантах.
На рисунке 4 показан результат работы алгоритма определения экстремумов.
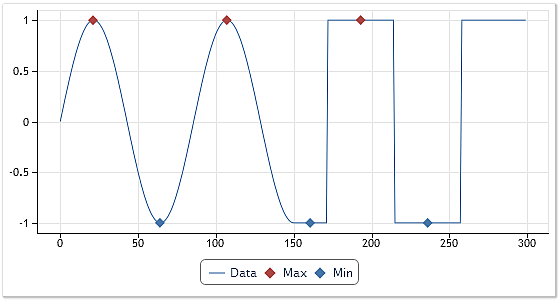
Рис. 4. Определение экстремумов. Первый вариант
Когда речь идет о поиске максимумов или минимумов функции, то чаще всего предполагается использование следующего алгоритма:
- Значение текущего элемента последовательности сравнивается с предыдущим и последующим значениями;
- Если текущее значение больше предыдущего и больше последующего, то фиксируется максимум функции;
- Если текущее значение меньше предыдущего и меньше последующего, то фиксируется минимум функции;
Для последовательностей, имеющих ярко выраженные экстремумы, определение максимумов и минимумов не представляет никакой сложности. Приведенный алгоритм прекрасно работает. Этот случай демонстрируется в первой половине показанного на рисунке 4 графика. Но такой алгоритм не будет реагировать на плоские вершины, когда соседние значения последовательности равны между собой.
Если использовать приведенный алгоритм, то последнего максимума и двух последних минимумов, показанных на рисунке 4, не было бы. С одной стороны, это был бы ожидаемый и корректный результат. Но с другой стороны, если следовать аналогии с колебательными процессами, то мы при наличии пересечений нулевой линии явно пропустили бы экстремумы. Не совсем ясно, можно ли плоские вершины последовательности прямоугольной формы или участки с одинаковыми значениями последовательности считать экстремумами?
Тем не менее, при реализации класса EMDecomp использовался несколько модернизированный, по сравнению с приведенным, алгоритм поиска экстремумов. Результат работы именно этого модернизированного алгоритма и показан на рисунке 4. Этот алгоритм принимает за экстремумы и интервалы с равными значениями последовательности, размещая экстремальные точки на середине таких интервалов.
Алгоритм поиска максимумов и минимумов, результат работы которого показан на рисунке 4, используется в классе CEMDecomp для подсчета количества экстремумов при определении момента прекращения цикла декомпозиции. Например, если получена IMF, не имеющая ни одного экстремума, то процесс декомпозиции прекращается, а такая IMF отбрасывается.
Если такой же алгоритм поиска экстремумов использовать и при построении огибающих, то в случаях, когда входная последовательность, например, имеет такую форму как на рис. 4, будут получаться огибающие в виде двух прямых параллельных линий. Далее, процедура просеивания никоим образом не сможет преобразовать исходную последовательность и эта последовательность не сможет быть разложена на составляющие.
Выходом из такой ситуации может служить использование несколько иного алгоритма поиска экстремумов, предназначенных для построения огибающих.
На рисунке 5 показан результат работы другого алгоритма определения экстремумов.
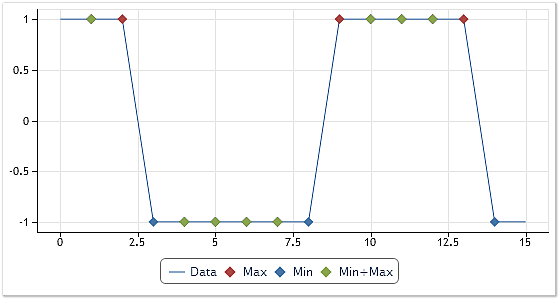
Рис. 5. Определение экстремумов. Второй вариант
Обратимся к рисунку 5. На нем в отличие от рисунка 4 зеленым цветом помечены точки, которые одновременно являются и максимумом и минимумом. Если по таким экстремумам построить огибающие, то они уже не будут прямыми параллельными линиями, и далее, в процессе просеивания, смогут быть выделены скрытые компоненты последовательности прямоугольной формы. Хорошей иллюстрацией этому является тестовый пример, размещенный в конце статьи в архиве CEMDecomposition.zip.
К сожалению, данный подход не решает всех проблем, связанных с выделением скрытых компонент. Например, для последовательности треугольной формы скрытые компоненты таким образом выделить не удастся. Этот факт можно отнести к недостаткам данной реализации алгоритма EMD. Возможно, что выходом из этой затруднительной ситуации может служить переход на использование для декомпозиции алгоритма CEEMD (The Complementary Ensemble Empirical Mode Decomposition Method) который в данной статье не рассматривается.
Кроме особенностей, связанных с реализацией алгоритмов поиска экстремумов, следует так же обратить внимание на типичную для подобного рода алгоритмов проблему граничных эффектов. Для пояснения сказанного обратимся к рис. 1. На рисунке 1 хорошо видно, что верхняя огибающая соединяет точки максимумов при помощи интерполирующей сплайн-функции.
При этом огибающая должна быть определена и для участков, расположенных как левее самой первой точки максимума, так и правее самой последней такой точки. От того, каким образом производится такое расширение огибающей, наверняка будет зависеть характер выделенных IMF вблизи их границ. Не будем вдаваться в подробности программной реализации коррекции граничных эффектов, просто акцентируем внимание читателя на этом моменте.
Далее отметим, что на характер и количество найденных IMF может и будет влиять используемый при формировании IMF выбранный метод прекращения цикла отсеивания. В классе CEMDecomp в качестве основного метода прекращения процесса отсеивания используется вычисление отношения, показывающего, насколько велико в текущей IMF оказалось изменение, определяемое последним циклом просеивания.
Если просеивание практически перестает оказывать на искомую IMF какое-либо воздействие, то процесс просеивания прекращается, и IMF считается сформированной. В конструкторе класса задается порог, по умолчанию определяющий точность формирования IMF. При заданном по умолчанию значении этого порога, количество итераций просеивания может иногда достигать 200 или даже 300. В публикациях по данной тематике многие авторы предостерегают от использования такого большого количества итераций просеивания. Тем не менее, в данной реализации алгоритма EMD, выбор пал именно на такой заданный по умолчанию порог.
Данная реализация алгоритма EMD позволяет использовать и другой критерий для прекращения циклов просеивания. Для этого перед обращением к методу Decomp() необходимо переменной FixedIter присвоить значение равное 1. В этом случае при просеивании для всех IMF всегда будут использоваться 10 итераций. Легко убедится, что при этом в процессе декомпозиции по сравнению с определенным по умолчанию методом будут получены несколько иные результаты.
6. Применение алгоритма EMD
Так как первоначально алгоритм EMD являлся составной частью преобразования Гильберта-Хуанга, то одним из примеров применения этого алгоритма, конечно, может служить вычисление мгновенного спектра последовательности. Для этого к найденным при помощи EMD модам необходимо применить преобразование Гильберта. Эта процедура в данной статье не рассматривается.
Кроме вычисления спектра, алгоритм EMD может быть использован для сглаживания последовательностей.
На рисунке 6 показан пример такого сглаживания.
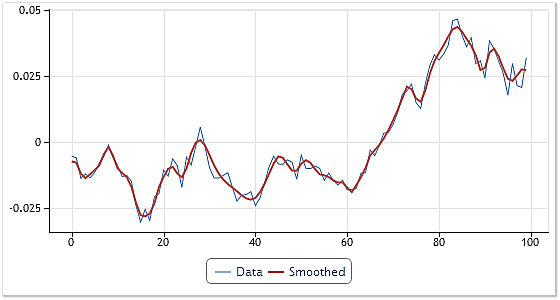
Рис. 6. Сглаживание входной последовательности
Для сглаживания был выбран произвольный фрагмент котировок USDCHF, Daily состоящий из 100 значений цен "Open". В процессе декомпозиции были получены четыре IMF и остаток. Далее были просуммированы с остатком все IMF, за исключением первой.
Таким образам, из входной последовательности была исключена самая высокочастотная из найденных составляющих. В случае, если бы при суммировании мы отбросили две первые компоненты, то результирующая кривая была бы еще более гладкой.
Другим примером использования EMD может служить формирование прогноза, который можно построить на базе выделенных из входной последовательности IMF. Для построения прогноза может быть использован любой экстраполятор, при помощи которого производится прогноз для каждой из IMF и остатка по отдельности.
Затем полученные отдельные прогнозы суммируются, формируя искомый результат прогноза для исходной последовательности. Учитывая колебательный характер отдельных IMF, можно предположить, что для прогноза целесообразно использовать экстраполяторы, учитывающие периодичность прогнозируемых последовательностей.
В данном случае рассмотрим в качестве примера результат работы более простого экстраполятора, в котором прогноз для каждой из IMF будет строиться при помощи линейной экстраполяции на 10 шагов вперед. Результат такого прогноза показан на рисунке 7.
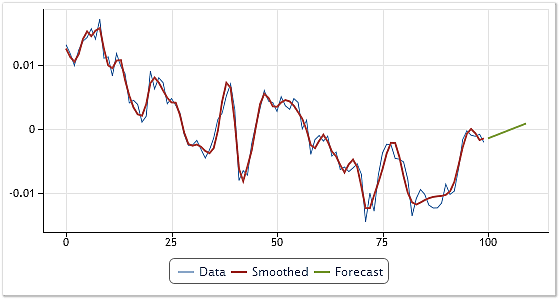
Рис. 7. Прогнозирование котировок USDCHF, H4
Необходимо отметить, что при построении прогноза одна или несколько самых высокочастотных компонент могут быть отброшены. Таким образом, может быть снижено влияние на прогноз высокочастотного шума. На рисунке 7 представлен результат прогноза, не учитывающий самую первую IMF. Прогнозирующая способность такого метода в данном случае никак не оценивалась. Подробный анализ методов прогнозирования построенных на основе эмпирической модовой декомпозиции здесь не приводится, так как эта тема выходит за рамки данной статьи.
Нельзя не упомянуть и о процедурах снятия тренда. После того как при помощи EMD получены отдельные компоненты последовательности, можно организовать достаточно гибкий алгоритм снятия тренда. За тренд можно принять остаток от декомпозиции или остаток, просуммированный с одной или несколькими последними IMF. Количество IMF, участвующих совместно с остатком в формировании трендовой линии, может варьироваться в зависимости от того, сколько низкочастотных составляющих необходимо сохранить в последовательности после снятия тренда.
Таким образом, для снятия тренда достаточно просуммировать все найденные в процессе декомпозиции IMF, за исключением одной или нескольких последних. Эту процедуру очень легко совместить со сглаживанием полученного результата, если из процесса суммирования исключить и самую высокочастотную IMF. На рисунке 8 показан пример снятия тренда, использующий описанный прием.
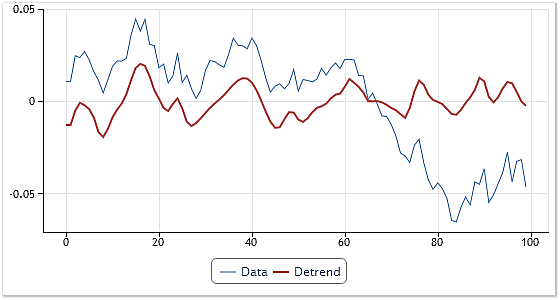
Рис. 8. Снятие тренда и сглаживание
В качестве исходных данных была взята последовательность котировок EURUSD, Daily. После декомпозиции были просуммированы все полученные компоненты, исключая остаток декомпозиции, самую последнюю и самую первую IMF. При этом произошло не только снятие тренда, но и некоторое сглаживание результирующей кривой.
Область применения метода эмпирической модовой декомпозиции, конечно, не ограничивается приведенными здесь простейшими примерами его использования. Но так как данная статья посвящена скорее вопросам реализации самого метода EMD, а не его использованию, остановимся на приведенных здесь примерах.
Дополнительной иллюстрацией работоспособности данной реализации метода EMD может служить рисунок 9, на котором представлен результат декомпозиции, полученный при использовании параметров, установленных в CEMDecomp.mqh по умолчанию. Для этого примера были использованы котировки XAUUSD, H4. Длина последовательности составляла 150 элементов.
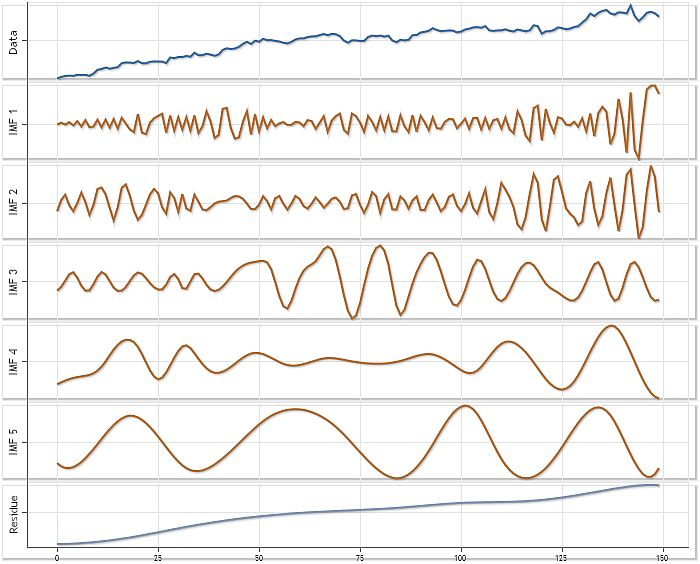
Рис. 9. Пример декомпозиции. XAUUSD, H4
На рисунке 9 для каждой из компонент был использован режим автоматического масштабирования.
Заключение
Напомним, что метод эмпирической модовой декомпозиции, также как и преобразование Гильберта-Хуанга, предназначен для анализа нелинейных нестационарных процессов. Это не означает, что этот подход не может быть использован и по отношению к линейным и стационарным последовательностям.
В начале статьи кратко упоминалось о некоторых подходах, используемых в алгоритмах декомпозиции. И говорилось, что большинство из этих алгоритмов производят разложение последовательности на составляющие, не являющиеся в действительности исходными процессами, из которых реально была сформирована исследуемая последовательность.
Это как бы синтетические компоненты, выделение которых просто помогает лучше понять структуру входной последовательности и во многих случаях позволяет упростить ее анализ. Метод EMD не является исключением. Ни в коем случае не следует считать, что полученные при помощи этого метода компоненты отражают реальные физические процессы, из которых были первоначально сформированы исходные анализируемые данные.
Что касается непосредственно самой предложенной в статье реализации, то она, возможно, потребует дополнительного тестирования и доработки. Так как вряд ли данную реализацию можно считать идеальной.
Основной целью статьи было познакомить читателя с методом EMD и некоторыми особенностями, связанными с его реализацией.
Подведем итоги.
- В статье очень кратко затрагиваются некоторые общие вопросы, связанные с декомпозицией;
- Кратко представлена суть метода эмпирической модовой декомпозиции;
- Представлен листинг и краткое описание интерфейсной части класса CEMDecomp, в котором реализован метод EMD;
- Приведен пример, демонстрирующий взаимодействие с классом CEMDecomp, обращение к его методам;
- Отмечены некоторые особенности данной реализации метода EMD;
- Приведены несколько простейших примеров использования метода EMD при анализе данных;
- В конце статьи размещен файл CEMDecomp.mqh, реализующий метод EMD и файл EMDecomposition.zip в котором содержится полный тестовый пример использования класса CEMDecomp.
Ссылки
Дополнение
Оригинальная статья была опубликована 28 июня, 2012. Данное дополнение предложено 5 июля 2012.
В качестве дополнения к статье предлагается несколько иная реализация метода EMD. Эта реализация оформлена в виде класса CEMD и размещена в конце статьи в файле CEMD_2.mqh.
MetaTrader 4 на Mac OS
Применение метода собственных координат к анализу структуры неэкстенсивных статистических распределений
Прибыльные алгоритмы на трейлинг стопах
Визуализируй стратегию в тестере MetaTrader 5
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Спасибо за статью, с удовольствием прочитал.
Несколько пунктов актуальных для любой декомпозиции (не только EMD):
По EMD:
P.S. Для сравнения функций сглаживания стоит, конечно, выработать раз и навсегда критерий эффективности сглаживания. По которому сравнить все известные функции, включая EMD.
Спасибо за статью, с удовольствием прочитал.
Спасибо за проявленный к статье интерес.
Сожалею, но вдаваться в подробности EMD я не смогу. Я хотел создать программную реализацию этого метода. Такая реализация и была выполнена, что и послужило основой для написания данной статьи. Никаких серьезных исследований не проводилось.
По EMD:
Сильно ли зависит результат EMD от типа используемой сплайн-функции?
Я не пробовал использовать другие сплайны, например четвертой степени, поэтому собственного мнения на этот счет у меня нет. Кажется, я где то встречал публикации по этому поводу, но, к сожалению, точно не помню где.
Прокомментируйте, по какой причине в EMD выбран такой критерий построения:
В любой точке эмпирической моды среднее значение огибающих, определенных локальными максимумами и локальными минимумами, должно быть нулевым.
Тут я не могу ничего прокомментировать, это надо смотреть в работах Хуанга. Это его условия.
Исследование любого метода декомпозиции требует программной реализации, так что основа в работе раскрыта почти полностью.
P.S. Странно, что ниразу нигде (в интернете) не попадались критерии сравнений различных функций. Это повод задуматься о своем велосипеде.
Прежде всего, огромное спасибо автору за статью! Интересно, понятно, лаконично. Материала как раз достаточно для того, чтобы понять: нужно это тебе или нет и принять решение, стоит ли продолжать изучать эту тему дальше или нет - этакая вводная лекция. Кроме того, автор дал базу для первоначального тестирования. За это еще одно огромное спасибо.
Теперь, обращусь к тем, кому нужно все, сразу и при этом, чтобы и пальцем не нужно было шевелить. Люди - включайте мозги и боритесь со своей ленью. Некоторые посты просто неприятно читать. Автор старался, а вы не цените.
Нельзя ли пару слов про "несколько иную реализацию EMD" во втором приложенном инклуднике . плюсы минусы отличия
большой + за статью