Гауссовcкие процессы в машинном обучении (Часть 1): Модель классификации в MQL5

Введение

Продолжаем наше знакомство с моделью машинного обучения — гауссовскими процессами (ГП). В предыдущей статье мы детально разобрали задачу регрессии, где основной целью было предсказание непрерывных значений. Сегодня нам предстоит разобраться с гораздо более сложной темой — классификацией. Её основная трудность заключается в том, что процесс вывода (inference) для классификации в гауссовских процессах не имеет аналитического решения, что требует применения приближенных методов, таких как аппроксимация Лапласа.

Для эффективного решения этой сложной задачи мы разработаем модульную библиотеку гауссовских процессов на MQL5. Такой подход позволит нам структурировать код, разделив модель ГП на независимые компоненты, и предоставит прочную основу для дальнейших улучшений и расширений. Эта библиотека станет универсальным инструментом как для задач регрессии, так и классификации.

В этой первой части статьи мы подробно разберём теорию классификации ГП, включая математику, лежащую в основе приближённых методов. Мы также представим главный класс библиотеки — GaussianProcess, который объединит все компоненты модели, и класс GPOptimizationObjective, отвечающий за связь с библиотекой оптимизации Alglib.

Классификация

Классификация — это задача машинного обучения, которая заключается в присвоении объекту одной из предопределённых категорий. Например, в финансовой сфере классификация может помочь предсказать, вырастет или упадёт цена акции на основе исторических данных.

В этой статье мы сосредоточимся на бинарной классификации, где объект относится к одному из двух классов, например, «рост» (+1) или «падение» (-1). В отличие от таких методов, как метод опорных векторов (SVM) или деревья решений, которые выдают только метку класса, ГП позволяют получить вероятностное предсказание. Например, модель может сказать, что вероятность роста акции составляет 75%. Такая информация особенно ценна в трейдинге, когда степень уверенности в прогнозе помогает принимать взвешенные решения, позволяя отсеивать неблагонадежные сигналы. 

К сожалению, решение задачи классификации с использованием ГП значительно сложнее, по сравнению с  регрессией. Это связано с типом используемого правдоподобия: 

• В регрессии, как правило, используется гауссово правдоподобие. Комбинация ГП (как априорного распределения функции) и гауссова правдоподобия позволяет получить апостериорное распределение аналитически, что упрощает все вычисления.
• Для классификации, где цели — дискретные метки классов, гауссово правдоподобие не подходит. Вместо него применяют, например,  логит-правдоподобие. Это приводит к тому, что апостериорное распределение также не является гауссовым и не имеет аналитического решения.

Как следствие, нам приходится прибегать к сложным методам приближённого вывода (approximate inference). Основная идея этих методов заключается в том, чтобы аппроксимировать истинное не-гауссово апостериорное распределение гауссовым распределением, центрированным в его моде.  В рамках данной статьи мы сосредоточимся на квадратичной аппроксимации Лапласа (Laplace Approximation), поскольку она является одним из наиболее простых и эффективных подходов для получения гауссовской аппроксимации апостериорного распределения. 

Для бинарной классификации основополагающая идея прогнозирования с помощью ГП довольно проста.  Мы начинаем с априорного распределения скрытых функций f(x). Представьте, что ГП генерирует не одну функцию, а бесконечное множество возможных функций, каждая из которых является потенциальной "скрытой" зависимостью в данных. Затем каждая из этих потенциальных реализаций скрытой функции f(x) "пропускается" через логистическую функцию (сигмоиду). Сигмоида преобразует любое вещественное число (значение f(x)) в вероятность от 0 до 1, которая и будет нашей априорной вероятностью π(x) принадлежности к классу «+1»:

Важно отметить, что π — это детерминированная функция от f, но поскольку сама f является стохастической (случайной, выборкой из ГП), то и функция π тоже становится стохастической. Эта концепция наглядно проиллюстрирована на рис. 1 и 2 для одномерного входного пространства X.

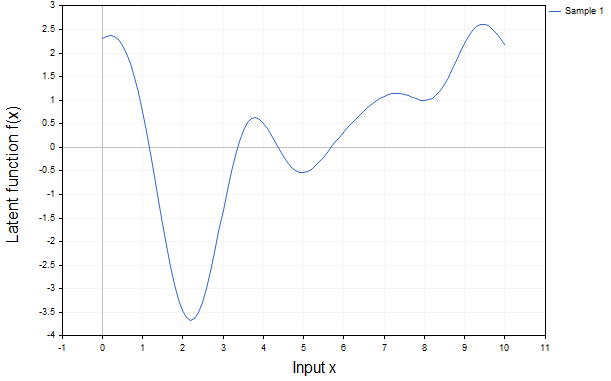
Рис.1 Реализация скрытой функции f(x)

Рис.1 показывает лишь одну возможную реализацию скрытой функции, демонстрируя типичное поведение функции, соответствующее заданным гиперпараметрам ядра.

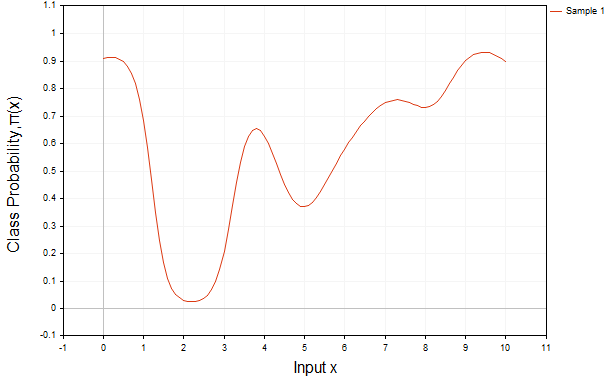
Рис.2 Та же функция, но преобразованная с помощью сигмоиды

Рис. 2 демонстрирует результат применения логистической (сигмоидной) функции к этой же функции f(x):

Таким образом, мы получаем априорное распределение вероятности принадлежности к классу  π(x)=σ (f(x)), которое на данном этапе ещё не учитывает обучающие данные y. Без наблюдений y, это априорное распределение остаётся лишь нашей исходной гипотезой, не подкреплённой эмпирическими фактами; без них модель лишена информации о том, какие из её начальных предположений были верны, а какие требуют пересмотра. 

Естественно, выбор априорных предположений существенно влияет на конечные апостериорные результаты. Это ключевая особенность байесовского подхода, поскольку именно от решения исследователя о типе ядра  зависят свойства априорного распределения функций, а следовательно, и конечная модель. 

Процесс Вывода (Inference)

Итак, чтобы делать обоснованные предсказания, нам необходимо учесть реальные обучающие данные y. Именно здесь в игру вступает процесс вывода (Inference). Его основная цель — преобразовать наши априорные убеждения в апостериорные, то есть, скорректированные с учётом наблюдаемых данных. Для классификации, этот процесс естественным образом делится на два последовательных шага.

Шаг 1: Прогнозное распределение скрытой функции f∗ 

На первом шаге мы вычисляем p(f*|X, y, x*) апостериорное распределение скрытой функции f* для новой тестовой точки x* при условии наблюдаемых тренировочных данных (X, y). Оно определяется следующим интегралом:

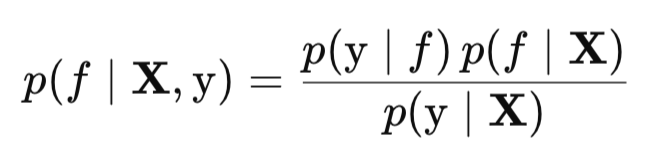
где,

• p(f*∣X, x*, f) — условное распределение скрытой функции f* в новой тестовой точке x* при условии скрытых функций f в обучающих точках X. Это распределение всегда является нормальным, поскольку ГП по определению имеет совместное нормальное распределение,
• p(f|X, y) — это апостериорное распределение скрытых функций f на тренировочных данных. Из-за нелинейной функции правдоподобия (сигмоиды) оно не является гауссовским.

Важно отметить: поскольку p(f|X, y) не является нормальным, данный интеграл не имеет аналитического решения. Это означает, что для его вычисления нам потребуются приближённые методы. 

Шаг 2: Окончательная прогнозная вероятность π*

На втором шаге мы используем это прогнозное распределение для формирования окончательного вероятностного предсказания π*— вероятности принадлежности тестовой точки x* к положительному классу (y* = +1):

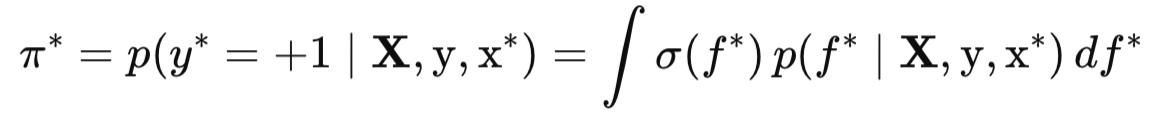
Здесь σ(f*) — это логистическая (сигмоидная) функция, которая преобразует значение скрытой функции f* в вероятность от 0 до 1. Сам же интеграл означает, что мы усредняем эти вероятности по всем возможным значениям f*, взвешенным по их апостериорному прогнозному распределению. По сути этот одномерный интеграл — это математическое ожидание функции σ(f*) относительно распределения p(f*|X, y, x*).

Опять-таки, для логит-правдоподобия этот интеграл не имеет аналитического решения. Поэтому нам и здесь потребуются приближенные методы. Забегая вперед скажем, что в нашей библиотеке GP реализовано три таких аппроксимации, что позволяет выбрать подходящий метод в зависимости от требований к точности и вычислительным затратам:

•  пробит аппроксимация,
•  численное интегрирование,
•  метод Монте-Карло.

Эти два шага, которые мы только что описали — вычисление апостериорного распределения скрытой функции и последующее интегрирование для получения прогнозной вероятности — представляют собой общую схему байесовского вывода в ГП. Именно эти два интеграла мы обязаны вычислить, чтобы получить желаемый прогноз, и оба они требуют использования приближённых методов. 

Аппроксимация Лапласа

Как мы уже выяснили, при байесовском выводе для классификации возникают неразрешимые в замкнутой форме интегралы. Аппроксимация Лапласа решает эту проблему, приближая негауссовское распределение p(f∣X, y) гауссовским распределением q(f∣X, y). Поскольку условное распределение p(f*∣X, x*, f) также является гауссовским, то и результирующее прогнозное распределение p(f*∣X, y, x*) тоже становится гауссовским. Это позволяет нам вывести аналитические формулы для среднего и дисперсии f*, что значительно упрощает дальнейшие вычисления. Таким образом, вся красота и вычислительная эффективность аппроксимации Лапласа заключается в её способности свести вычисления апостериорного распределения и предсказаний к операциям с гауссовскими распределениями.

Важно понимать, что аппроксимация Лапласа — это компромисс. Она делает неразрешимую в замкнутой форме задачу вычислительно разрешимой, но за счёт точности представления истинной формы апостериорного распределения. Качество этого нормального приближения напрямую зависит от того, насколько истинное распределение p(f∣X, y) близко к нормальному. Чем оно ближе, тем точнее будет аппроксимация, и наоборот.

Если нас интересует истинное распределение p(f*∣X, y, x*), а не его приближение, то для этого обычно применяются методы MCMC (Markov Chain Monte Carlo). Хотя метод MCMC способен предоставить более точные оценки, он является вычислительно очень затратным и сложным в реализации. MCMC можно использовать как золотой стандарт для сравнения с приближенными методами вывода.

Теперь давайте более подробно рассмотрим, что из себя представляет аппроксимация Лапласа. Эта аппроксимация строится вокруг моды (максимума) истинного апостериорного распределения p(f∣X, y). Она использует второй порядок разложения Тейлора логарифма апостериорной плотности вокруг этой моды. Математически мы аппроксимируем логарифм апостериорной плотности следующим образом:

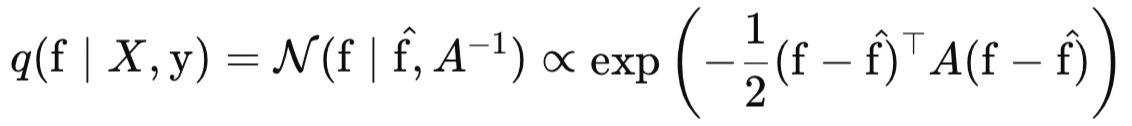
где,

• q(f∣X, y) — гауссовская аппроксимация для апостериорного распределения p(f∣X, y),
• f_hat = argmax(f) p(f|X, y) — мода апостериорного распределения,
• A = −∇∇ log p(f|X, y)|f=f_hat — гессиан отрицательного логарифма апостериорного распределения в точке моды.

В первую очередь для выполнения аппроксимации Лапласа, нам нужно найти наиболее вероятное значения скрытой функции f, то есть моду f_hat. Чтобы получить апостериор p(f∣X, y), мы используем правило Байеса. Мы уже знаем, что это правило связывает апостериорное распределение с правдоподобием p(y∣f), априором p(f∣X) и маргинальным правдоподобием p(y∣X) следующим образом:

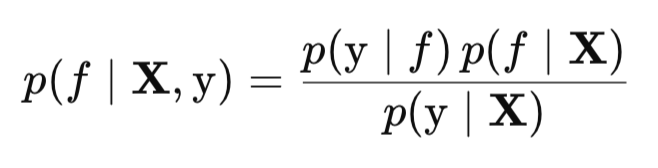
Для максимизации p(f∣X, y) по f, нам необязательно знать нормировочную константу p(y∣X), так как она не зависит от f и, следовательно, не влияет на положение максимума. Поэтому мы можем работать с ненормированным апостериорным распределением, которое пропорционально произведению правдоподобия и априора p(y∣f)p(f∣X).

Чтобы упростить вычисления и избежать численных проблем с очень малыми значениями вероятностей, мы берём логарифм от этого ненормированного апостериорного распределения. Благодаря свойству логарифмов, произведение вероятностей при этом становится суммой их логарифмов:

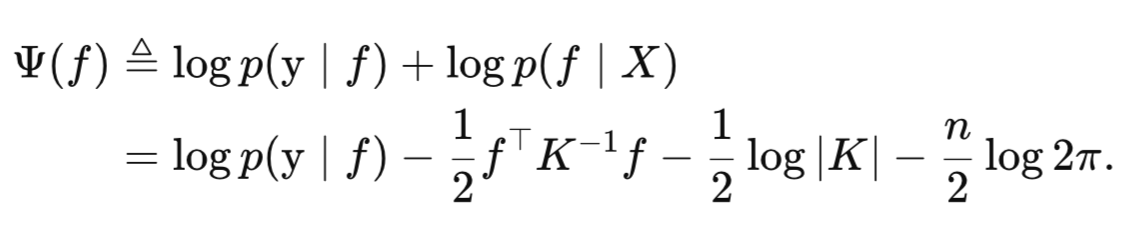
Ψ(f) является целевой функцией, которую мы будем максимизировать с помощью метода Ньютона для нахождения моды скрытой функции. Метод Ньютона требует вычисления первых и вторых производных Ψ(f) по f.

Дифференцируя данное уравнение по f, получаем:

где,

• W = −∇∇ log p(y|f) — отрицательный Гессиан логарифма правдоподобия, который является диагональной матрицей.

После того, как мы вычислили градиент и Гессиан, мы итеративно находим моду с помощью метода Ньютона:

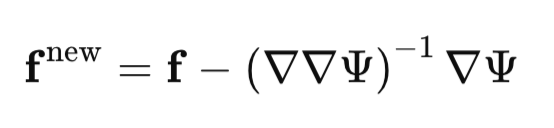
На каждой итерации метод Ньютона обновляет наше текущее предположение о моде в направлении, определённом градиентом и Гессианом, пока не будет достигнута сходимость. 

После получения моды, мы можем вычислить ковариационную матрицу аппроксимированного гауссовского распределения.  Эта матрица равна  отрицательному обратному гессиану Ψ(f) вычисленному в точке моды f_hat.

Таким образом, ковариационная матрица Σ нашей Гауссовой аппроксимации равна:

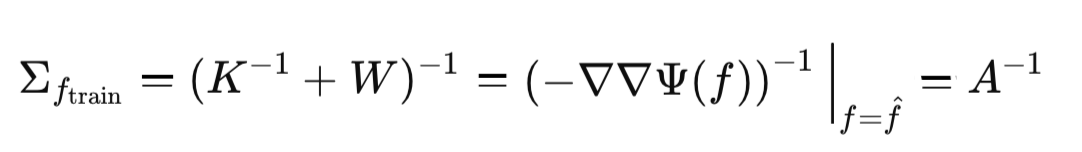
Это завершает описание первого шага Лапласовской аппроксимации — нахождения нормального приближения апостериорного распределения.

Предсказание в аппроксимации Лапласа

После получения q(f∣X, y), мы можем перейти ко второму шагу вывода — предсказанию для новых тестовых точек x∗. На этом этапе мы хотим найти прогнозное распределение p(f∗∣X, y, x∗). Благодаря Лапласовской аппроксимации, которая сделала p(f∣X, y) гауссовым (в виде q(f∣X, y)), и тому факту, что p(f∗∣X, x∗, f) также гауссово, результирующее прогнозное распределение p(f∗∣X, y, x∗) также становится гауссовым. Это позволяет нам аналитически получить его апостериорное среднее и дисперсию.

Среднее значение скрытой функции f* для новой тестовой точки x* (mu_f_star) вычисляется как:

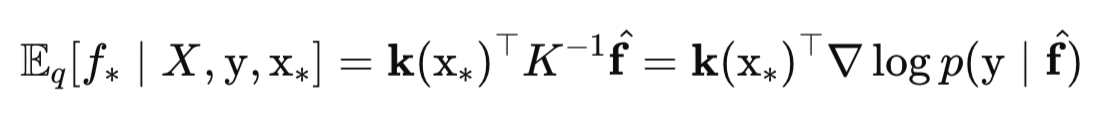
Дисперсия скрытой функции Var(f*) для новой тестовой точки x* (Sigma_f_star) вычисляется как:

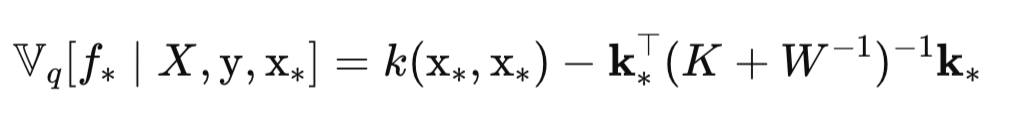
Теперь, когда у нас есть среднее и дисперсия прогнозного распределения, мы можем, наконец-то, вычислить искомую вероятность принадлежности к классу π∗: 

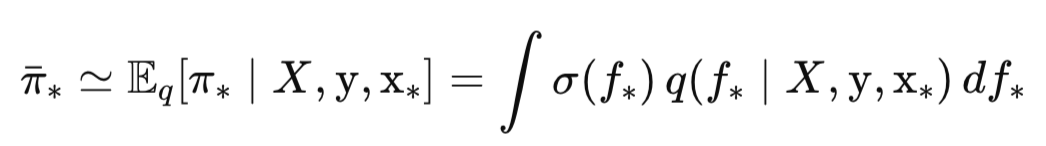
Эта формула является сердцем прогнозирования вероятностей в GP-классификаторе на основе Лапласовской аппроксимации.

Возможно вы обратили внимание, что мы не вычисляем вероятности класса просто как σ(E[f∗]), то есть подставляя апостериорное среднее для f* напрямую в сигмоидную функцию. Такой подход, известный как MAP-предсказание (Maximum A Posteriori Prediction), безусловно, имеет право на жизнь.

Однако, вычисляя MAP-прогноз σ(E[f∗]), мы игнорируем неопределенность в f*. Мы просто берём центральную точку f* (среднее значение) и преобразуем её в вероятность. Когда мы вычисляем E[σ(f*)] (что соответствует интегрированию), мы учитываем всю форму распределения f*. Это даёт нам более точную и осмысленную предсказательную вероятность, особенно когда существует значительная неопределенность в f* (т.е. большая дисперсия V[f*]), или когда распределение f* асимметрично. Этот подход называется усредненными предсказаниями (averaged predictive probability).

Понимание этой разницы имеет важное практическое значение:

• Если ваша единственная цель — получить бинарную метку класса (например, "купить" или "продать", +1 или −1), то использование более простого MAP-предсказания может быть достаточным, поскольку оно даст ту же самую метку, что и более вычислительно затратное усреднённое предсказание.
• Однако, если вам важны сами вероятности, то усреднённые предсказания (E[σ(f*)]) всё равно являются более точными, так как в полной мере учитывают неопределённость модели. 

В торговле, простая бинарная метка класса ("купить" или "продать") недостаточна. Нам нужна тонкая градация уверенности, которую предоставляют именно вероятности. Величина вероятности позволяет нам фильтровать торговые сигналы. Сигнал с вероятностью успеха 0.51 (что лишь немногим лучше случайного угадывания) будет иметь гораздо меньшую ценность, чем сигнал с вероятностью 0.60. Это позволяет трейдеру устанавливать пороговые значения для входа в сделку. Например, можно решить, что сделки будут открываться только при вероятности успеха выше 0.55 или 0.60, тем самым снижая количество ложных сигналов.

Маргинальное правдоподобие в аппроксимации Лапласа

Теперь, когда мы понимаем механизм вывода в ГП для классификации, встаёт вопрос: как настроить нашу модель для оптимальных предсказаний? Ответ кроется в маргинальном правдоподобии (Marginal Likelihood, LML). Это целевая функция, по которой мы оптимизируем гиперпараметры θ нашей модели. Без её вычисления невозможно найти наилучшие параметры, которые объясняют наши данные: 

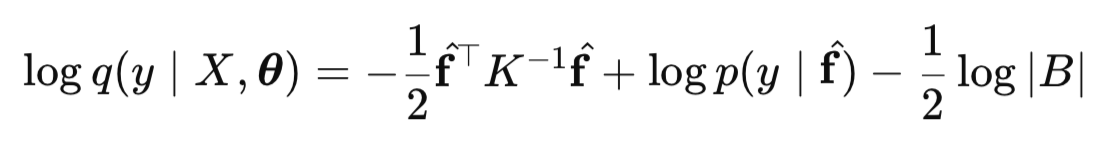
где, B

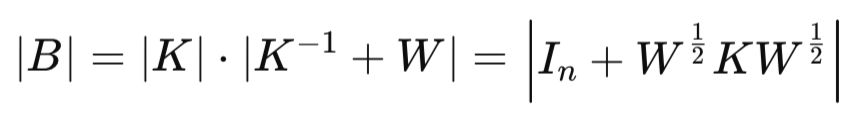
Определив целевую функцию для оптимизации, следующим важным шагом является вычисление её частных производных по гиперпараметрам θ. Это необходимо, потому что мы будем выполнять оптимизацию с использованием аналитических градиентов. Такой подход в разы ускоряет вычисления по сравнению с численными методами. Аналитические градиенты позволяют оптимизатору более эффективно и точно двигаться к минимуму целевой функции. 

Градиент LML состоит из явной и неявной части:

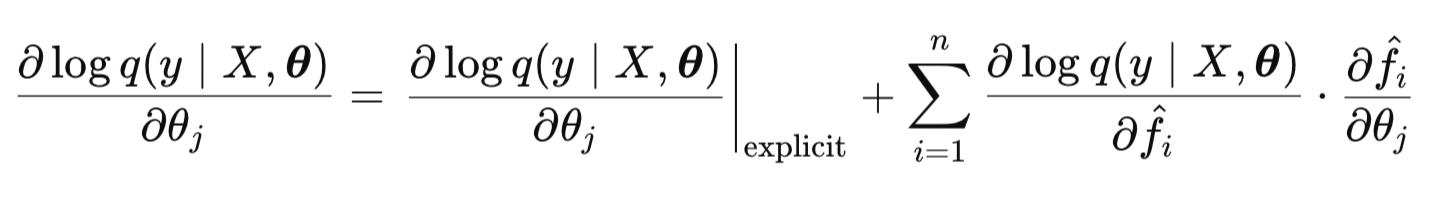
Формула для расчета явной части:

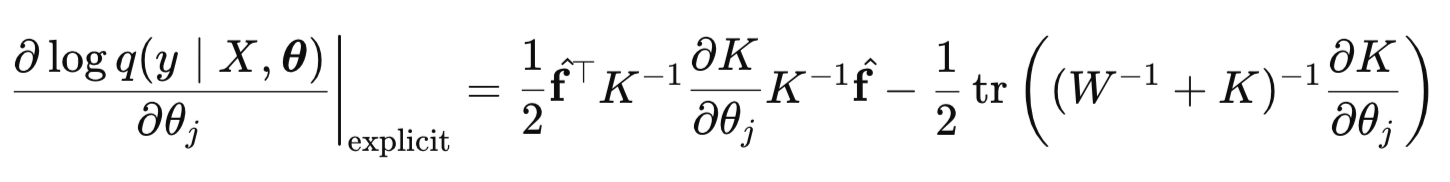
Здесь основная проблема — это вычисление производной матрицы ядра K по каждому гиперпараметру. Реализацией производных для выбранной функции ядра займемся во второй части статьи.

Неявная часть состоит из двух множителей. Первый множитель в неявной части находят по формуле:

Для вычисления данной формулы нам придется вычислить третью производную логарифма правдоподобия.

Второй множитель неявной части вычисляется следующим образом: 

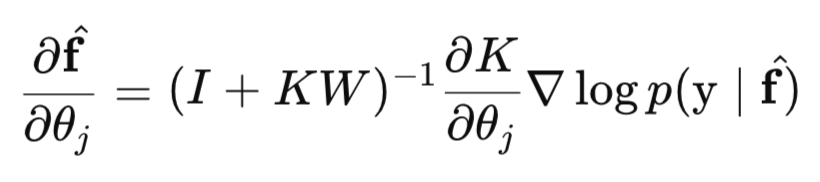
В заключение отметим, что NLML нужен не только для оценки гиперпараметров, но и для сравнения различных моделей (например, с разными типами ядер). Модели с меньшим значением NLML считаются лучшими, поскольку это означает более высокое маргинальное правдоподобие, то есть, что модель лучше объясняет наблюдаемые данные.

Кроме того ГП, используя маргинальное правдоподобие для оптимизации гиперпараметров, автоматически решают проблему баланса между подгонкой к данным и сложностью модели. NLML естественным образом штрафует слишком сложные модели, предотвращая переобучение. Благодаря этому, нет необходимости в явных критериях остановки для предотвращения переобучения, как это делается, например, при обучении нейронных сетей. Оптимизация NLML сама по себе стремится найти оптимальный баланс. Это одно из главных преимуществ байесовского подхода в гауссовских процессах.

Библиотека Гауссовских Процессов

Теперь, когда мы рассмотрели все необходимые теоретические концепции, переходим к практической реализации. Наша главная цель — создать универсальную библиотеку ГП на MQL5, которая будет служить надёжным инструментом для задач прогнозирования. Эта библиотека будет обладать модульной архитектурой, где модель ГП разбита на независимые, взаимозаменяемые компоненты, что позволит легко расширить ее возможности и обеспечить простоту обслуживания. Она будет разрабатываться с учётом следующих ключевых функциональных особенностей:

• Гибкость при выборе ядра: возможность легко подключать существующие ковариационные ядра, а также создавать их комбинации (SumKernel, ProductKernel) для моделирования более сложных зависимостей;
• Поддержка различных функций правдоподобия;
• Поддержка различных методов вывода апостериорного распределения для задач классификации и регрессии;
• Многофункциональность: библиотека должна быть универсальной, что позволит решать как задачи регрессии, так и бинарной классификации;
• Оптимизация гиперпараметров: использование аналитических градиентов для повышения скорости и точности процесса обучения. Интеграция с библиотекой Alglib должна обеспечить эффективную оптимизацию гиперпараметров модели.

Рассмотрим более подробно структуру библиотеки. Она состоит из шести основных компонентов, каждый из которых реализует конкретную функциональность:

• Класс GaussianProcess: это центральный узел библиотеки, который управляет всем жизненным циклом модели ГП — от инициализации и оптимизации гиперпараметров до выполнения предсказаний на новых данных.

• Класс GPOptimizationObjective: этот вспомогательный класс служит "мостиком" между  нашей библиотеки и библиотекой оптимизации Alglib. Он адаптирует целевую функцию и её градиент к формату, требуемому Alglib (через наследование от CNDimensional_Grad).

• Интерфейс IKernel: определяет набор методов для различных ковариационных функций (ядер). Включает такие реализации, как RBFKernel, LinearKernel, PeriodicKernel, а также их комбинации (SumKernel, ProductKernel).

• Интерфейс ILikelihood: определяет набор методов для функций правдоподобия. Реализации включают GaussianLikelihood для регрессии и LogitLikelihood для бинарной классификации.

• Интерфейс IInference: предоставляет методы для вывода апостериорного распределения скрытой функции ГП. На данный момент реализован  ExactInference  и LaplaceInference.

• Вспомогательные структуры и утилиты (StructUtils.mqh): набор общих перечислений, структур данных (для результатов инференса и предсказаний) и функций, необходимых для работы с данными, матрицами и графиками для визуализации результатов.

Благодаря такой модульной структуре и строго определённым интерфейсам, мы сможем легко добавлять новые ядра, методы вывода и функции правдоподобия, что позволит легко развивать библиотеку  в будущем. 

Класс GaussianProcess

Класс GaussianProcess — это центральный класс библиотеки. Он инкапсулирует всю логику, необходимую для построения, обучения и прогнозирования модели ГП. Разработанный по принципу композиции, GaussianProcess не содержит функционал ядер, правдоподобия или инференса напрямую. Вместо этого, он объединяет эти компоненты, используя три основных интерфейса:

• ядро (IKernel),
• функцию правдоподобия (ILikelihood),
• метод инференса (IInference).

Благодаря этому, можно гибко адаптировать модель ГП под различные задачи прогнозирования без изменения основного класса GaussianProcess.

//+------------------------------------------------------------------+
//| Класс Гауссовского Процесса                                      |
//+------------------------------------------------------------------+
class GaussianProcess
{
private:
    IKernel*      m_kernel;       // указатель на выбранное ядро
    ILikelihood*  m_likelihood;   // указатель на выбранную функцию правдоподобия
    IInference*   m_inference;    // указатель на выбранный метод инференса
    matrix        m_X_train;      // Тренировочные входные данные Nxd
    vector        m_y_train;      // Тренировочные целевые данные Nx1

    GPInferenceResult m_last_inference_result; // Структура сохраняющая последние результаты инференса
    
    int m_last_termination_type;  // Код завершения операции оптимизации
    int m_last_iterations_count;  // Количество итераций выполненных оптимизатором
    double m_last_nlml_value;     // Итоговое значение NLML после оптимизации
    
private:
    // Вспомогательная функция для численного интегрирования 
    double CalculateNumericalProbability(double mu_f_star, double sigma_f_star_diag, LogitLikelihood *likelihood);

public:
    // Конструктор класса 
    GaussianProcess(IKernel* kernel, ILikelihood* likelihood, IInference* inference,
    const matrix &X_train, const vector &y_train);
    // Статический метод для создания обьекта GaussianProcess с проверкой входных параметров
    static GaussianProcess* Create(IKernel* kernel, ILikelihood* likelihood, IInference* inference,
    const matrix &X_train, const vector &y_train);
    
    // Деструктор
    ~GaussianProcess();
    
    // --- Методы для получения состояния модели ---
    // Возвращает результаты последней операции инференса
    GPInferenceResult GetLastInferenceResult() const;
    // Возвращает тип завершения последней оптимизации гиперпараметров
    int GetLastTerminationType() const;
    // Возвращает количество итераций, выполненных при последней оптимизации гиперпараметров
    int GetLastIterationsCount() const;
    // Возвращает значение отрицательного логарифма маргинального правдоподобия после оптимизации
    double GetLastNLML() const;
    // Возвращает указатель на используемое ядро
    IKernel* GetKernel() const;
    // Возвращает текущие значения всех оптимизируемых гиперпараметров.
    vector GetCurrentHyperparameters();
  
    // --- Методы обучения и настройки ---
    // Запускает полный процесс обучения модели, включая оптимизацию гиперпараметров
    bool Fit();
    // Выполняет одиночный шаг инференса без оптимизации гиперпараметров
    bool PerformInference();
    // Устанавливает тренировочные данные для модели 
    void SetTrainingData(const matrix& X, const vector& y);
    // Устанавливает заданные гиперпараметры для ядра и функции правдоподобия
    void SetHyperparameters(const vector &params);
    // Метод, вызываемый оптимизатором для вычисления целевой функции (NLML)
    double CalculateNLMLObjective(const vector &hyperparameters);
    
    // --- Метод выполняет прогноз для новых тестовых данных
    // Параметр predictmode определяет метод расчета вероятностей для классификации (PROBIT, NUM_INTEGR, MONTE_CARLO)
    bool Predict(const matrix &X_test, GPPredictionResult &result, PredictMode mode = PROBIT);
    
    // --- Вспомогательные методы ---
    // Статический метод для генерации выборок из априорного ГП
    static bool SamplePriorGP(const matrix &x, IKernel* kernel, int num_samples, matrix &f_samples,
                              bool plot_samples = false, int plot_display_seconds = 10);
    //--- Метод для вывода в журнал итоговых значений гиперпараметров
    void PrintOptimizedKernelParameters();  
};

Рассмотрим основные методы класса:

Для создания экземпляра класса предусмотрено два основных способа:

• Метод Create: используйте данный метод для безопасного создания объекта GaussianProcess. Этот метод выполняет необходимые проверки входных данных (X_train, y_train, указатели на интерфейсы) и возвращает указатель на объект или NULL в случае ошибки.

//+------------------------------------------------------------------+
//| Метод Create                                                     |
//+------------------------------------------------------------------+
GaussianProcess* GaussianProcess::Create(IKernel* kernel, ILikelihood* likelihood, IInference* inference,
const matrix &X_train, const vector &y_train)
{
    // 1. Проверка на NULL-указатели
    if (kernel == NULL || likelihood == NULL || inference == NULL) {
        Print("ERROR: Kernel, Likelihood, or Inference pointer is NULL");
        return NULL;
    } 
    // 2. Проверка корректности входных данных X_train и y_train 
    if (X_train.Rows() == 0 || y_train.Size() == 0 || X_train.Rows() != y_train.Size()) {
    Print("ERROR: Invalid training data dimensions");
    return NULL;
    }
    // 3. Проверка совместимости likelihood и inference
    string likelihood_name = likelihood.GetName();
    string inference_name  = inference.GetName();   
    if (inference_name == "ExactInference" && likelihood_name != "GaussianLikelihood") {
        Print("ERROR: ExactInference supports only GaussianLikelihood!");
        delete kernel; delete likelihood; delete inference;
        return NULL;
    }    
    // 4. Если все проверки пройдены, создаем объект
    GaussianProcess* gp_model = new GaussianProcess(kernel, likelihood, inference,X_train, y_train);
    if (gp_model == NULL) {
        Print("ERROR: Failed to create GaussianProcess object");
        delete kernel; delete likelihood; delete inference;
        return NULL;
    }    
    return gp_model;
}

• Конструктор класса: предоставляет прямой способ инициализации, без каких-либо проверок данных. Если вы уверены в своих данных, можно создавать объект через конструктор.

//+------------------------------------------------------------------+
//| Конструктор класса GaussianProcess                               |
//+------------------------------------------------------------------+
GaussianProcess::GaussianProcess(IKernel* kernel, ILikelihood* likelihood, IInference* inference,
const matrix &X_train, const vector &y_train) :
    m_kernel(kernel),
    m_likelihood(likelihood),
    m_inference(inference),
    m_X_train(X_train), 
    m_y_train(y_train), 
    m_last_termination_type(0),
    m_last_iterations_count(0),
    m_last_nlml_value(0.0){ }

• Метод Fit(): запускает полный процесс обучения модели. В рамках этого метода происходит оптимизация гиперпараметров ядра и функции правдоподобия с использованием оптимизатора MinBleic, который минимизирует отрицательное логарифмическое маргинальное правдоподобие (NLML).

//+------------------------------------------------------------------+
//| Метод для обучения модели                                        |
//+------------------------------------------------------------------+
bool GaussianProcess::Fit()
{
    // Создаем обьект GPOptimizationObjective, передавая ему указатель на текущий объект GaussianProcess
    // Этот указатель попадает в приватное поле класса m_gp с помощью которого мы вызываем метод
    // CalculateNLMLObjective,чтобы получить значение NLML для текущего набора гиперпараметров
    GPOptimizationObjective objective_func(GetPointer(this));
    CNDimensional_Rep frep; 
    CObject Obj;
    vector initial_hyperparams = GetCurrentHyperparameters(); // Получаем стартовые значения гиперпараметров
    double theta[];
    ArrayResize(theta, (int)initial_hyperparams.Size()); 
    VectorToArray(initial_hyperparams,theta);
    int num_params = (int)initial_hyperparams.Size();
    double s[];
    double bndl[];
    double bndu[];
    ArrayResize(s, num_params);
    ArrayResize(bndl, num_params);
    ArrayResize(bndu, num_params);

    int param_idx = 0; 
    IKernel* kernels_to_process[]; // массив указателей на интерфейс IKernel
    
    // Логика получения ядер для установки границ 
    // Этот блок кода определяет, с каким типом ядра мы имеем дело,
    // и заполняет массив kernels_to_process соответствующими указателями:
    if (dynamic_cast<SumKernel*>(m_kernel) != NULL) {          // Проверяем, является ли текущее ядро m_kernel обьектом SumKernel 
        SumKernel* sum_k = dynamic_cast<SumKernel*>(m_kernel); // Если да, то приводим тип m_kernel к типу SumKernel*, 
        sum_k.GetKernels(kernels_to_process); // и вызываем метод GetKernels(), который заполняет массив kernels_to_process всеми ядрами, входящими в сумму
    } else if (dynamic_cast<ProductKernel*>(m_kernel) != NULL) { // Аналогичная логика, если ядро является обьектом ProductKernel
        ProductKernel* prod_k = dynamic_cast<ProductKernel*>(m_kernel);
        prod_k.GetKernels(kernels_to_process);
    } else {
        ArrayResize(kernels_to_process,1); // Если ядро не является ни суммой, ни произведением (т.е. это не композитное ядро), 
        kernels_to_process[0] = m_kernel; // то массив kernels_to_process просто содержит указатель на m_kernel.
    }

   // Этот цикл проходит по каждому базовому ядру, найденному в массиве kernels_to_process,
   // и устанавливает для его гиперпараметров начальный масштаб s, нижнюю bndl и верхнюю bndl границу
    for(int i = 0; i < ArraySize(kernels_to_process); i++) {
        IKernel* current_k = kernels_to_process[i];
            string kernel_name = current_k.GetName();   
            if (kernel_name == "RBFKernel") {
                if (param_idx + 2 <= num_params) {    
                    s[param_idx] = 1.0; bndl[param_idx] = 1e-3; bndu[param_idx] = 1e3; param_idx++;    
                    s[param_idx] = 1.0; bndl[param_idx] = 1e-3; bndu[param_idx] = 1e3; param_idx++;    
                } 
            } else if (kernel_name == "LinearKernel") {
                if (param_idx + 1 <= num_params) {
                    s[param_idx] = 1.0; bndl[param_idx] = 1e-3; bndu[param_idx] = 1e3; param_idx++;    
                } 
            } else if (kernel_name == "PeriodicKernel") {
                if (param_idx + 3 <= num_params) {
                    s[param_idx] = 1.0; bndl[param_idx] = 1e-3; bndu[param_idx] = 1e3; param_idx++;    
                    s[param_idx] = 1.0; bndl[param_idx] = 1e-3; bndu[param_idx] = 1e3; param_idx++;    
                    s[param_idx] = 1.0; bndl[param_idx] = 1e-3; bndu[param_idx] = 1e3; param_idx++;    
                } 
            }           
    }
    
// --- Добавляем границы и масштабы для параметров правдоподобия (если они есть) ---
// LogitLikelihood не имеет гиперпараметров, поэтому для него этот блок будет пропущен
// GaussianLikelihood имеет 1 параметр (sigma)
if (m_likelihood.GetNumHyperparameters() > 0) {
    if (param_idx + m_likelihood.GetNumHyperparameters() <= num_params) {
        s[param_idx] = 1.0;           // Масштаб
        bndl[param_idx] = 1e-10;      // Нижняя граница 
        bndu[param_idx] = 1e3;        // Верхняя граница
        param_idx++;
    } 
}
    CMinBLEICStateShell state;
    CMinBLEICReportShell rep; // объект, который будет содержать отчёт о результатах оптимизации
    //-----------------------  критерии остановки оптимизатора
    double epsg = 0.0001;     //Точность по градиенту (0 означает, что остановка по градиенту отключена)
    double epsf = 0.0000;     //Точность по значению функции    
    double epsw = 0.0000;     //Точность по параметрам 
    //-------------------------   
    double epso = 0.00001;    //Параметры для внешних  условий сходимости в BLEIC
    double epsi = 0.00001;    //Параметры для внутренних условий сходимости в BLEIC
    CAlglib::MinBLEICCreate(theta, state);       // инициализация оптимизатора. Она создаёт начальное состояние state для MinBLEIC, используя начальные значения гиперпараметров из массива theta  
    CAlglib::MinBLEICSetBC(state, bndl, bndu);   // Устанавливает нижние (bndl) и верхние (bndu) границы для каждого параметра
    CAlglib::MinBLEICSetScale(state, s);         //Устанавливает масштабы (s) для каждого параметра. Это может помочь оптимизатору эффективнее работать с параметрами разных порядков величины.
    CAlglib::MinBLEICSetInnerCond(state,epsg,epsf,epsw);    
    CAlglib::MinBLEICSetOuterCond(state, epso, epsi);    
    CAlglib::MinBLEICOptimize(state, objective_func, frep, 0, Obj); // запускаем процесс оптимизации    
    CAlglib::MinBLEICResults(state, theta, rep); // отчет оптимизации
    
    m_last_termination_type = rep.GetTerminationType();
    m_last_iterations_count = rep.GetInnerIterationsCount();
    m_last_nlml_value = objective_func.GetNLML(); // Получаем финальное NLML
//------------------------------------------------------------------------------------    
//    TerminationType field contains completion code, which can be:
//-8     internal integrity control detected    infinite    or    NAN    values    in
//     function/gradient. Abnormal termination signalled.
//-3     inconsistent constraints. Feasible point is
//     either nonexistent or too hard to find. Try to
//     restart optimizer with better initial approximation
// 1     relative function improvement is no more than EpsF.
// 2     relative step is no more than EpsX.
// 4     gradient norm is no more than EpsG
// 5     MaxIts steps was taken
// 7     stopping conditions are too stringent,
//     further improvement is impossible,
//     X contains best point found so far.
// 8     terminated by user who called minbleicrequesttermination(). X contains
//     point which was "current accepted" when    termination    request    was
//     submitted.
//-------------------------------------------------------------------------------------  
// Определяем успешность оптимизации на основе TerminationType
    bool success = true;     
    if (m_last_termination_type < 0)
    {
        Print("Ошибка: Оптимизация GP завершилась неудачно. Тип завершения: ", m_last_termination_type);
        success = false;
    } 
    // Обновляем гиперпараметры модели после оптимизации
    vector optimized_hyperparams;
    optimized_hyperparams.Assign(theta);
    SetHyperparameters(optimized_hyperparams);   
    return success;     
}

Внутри метода Fit() мы подготавливаем всё необходимое для эффективной работы оптимизатора.

Создаётся специальный объект objective_func (GPOptimizationObjective), который представляет целевую функцию NLML и её аналитический градиент в формате, понятном для Alglib. В его конструктор передаётся указатель на текущий объект GaussianProcess, (это необходимо для вызова метода CalculateNLMLObjective).

Далее получаем текущие значения всех гиперпараметров модели в массив гиперпараметров theta. Эти значения (полученные из ядра и функции правдоподобия) будут служить начальной точкой для поиска оптимума. Для каждого гиперпараметра задаются масштабы (s), нижние (bndl) и верхние (bndu) границы. Границы предотвращают поиск решений в некорректных или бессмысленных областях (например, отрицательные длины масштаба или дисперсии). Масштабирование используется оптимизатором для нормализации параметров, что повышает стабильность и скорость сходимости, особенно при сильно различающихся порядках величин параметров. По умолчанию s = 1.0

Далее объявляем массив указателей kernels_to_process на интерфейс Ikernel. Он будет использоваться для хранения списка всех базовых ядер, гиперпараметры которых нужно оптимизировать. Если у нас простое ядро (не составное), то в этом массиве будет только один элемент – указатель на это ядро. Если же это SumKernel или ProductKernel, то в нём будут храниться указатели на все ядра, входящие в состав этой композиции.

Далее с помощью оператора dynamic_cast проверяем, является ли текущее ядро m_kernel, (которое является полем класса GaussianProcess и указывает на выбранное пользователем ядро) экземпляром SumKernel или ProductKernel. Если да, то происходит приведение типа к SumKernel или ProductKernel, и вызывается метод GetKernels(), который заполняет массив kernels_to_process всеми ядрами, входящими в сумму или произведение ядер. Если ядро не является ни суммой, ни произведением (т.е. это обычное ядро, например, RBFKernel), то массив kernels_to_process просто содержит указатель на само m_kernel.

После чего, в цикле проходим по каждому базовому ядру, найденному в kernels_to_process, и устанавливаем для его гиперпараметров масштаб s, и границы bndl и bndu.

Наконец, после всех гиперпараметров ядра, обрабатываются гиперпараметры функции правдоподобия. У гауссовского правдоподобия один параметр, у логит-правдоподобия параметров нет. После подготовки всех параметров, запускается процесс оптимизации.

• Метод CalculateNLMLObjective() выступает в роли связующего звена между основным классом GaussianProcess и внешним оптимизатором Alglib. Это именно та целевая функция, которую оптимизатор MinBleic постоянно вызывает (через класс GPOptimizationObjective) для оценки текущих значений гиперпараметров. Его основная задача — вернуть значение NLML для заданного набора гиперпараметров.

//+-------------------------------------------------------------------+
//| Метод, который будет вызываться оптимизатором для вычисления NLML |
//+-------------------------------------------------------------------+
double GaussianProcess::CalculateNLMLObjective(const vector &hyperparameters)
{
    //  Устанавливаем все гиперпараметры (ядра и правдоподобия)
    SetHyperparameters(hyperparameters);    
    //  Вызываем инференс, который вычислит NLML
    m_inference.Infer(m_X_train, m_y_train, m_kernel, m_likelihood,m_last_inference_result);
    if (!m_last_inference_result.success) {    
        Print("Ошибка Инференса !");
        return DBL_MAX;    
    }    
    return m_last_inference_result.nlml_value;
}

На каждой итерации оптимизатор MinBleic предлагает новый набор гиперпараметров. Первым делом CalculateNLMLObjective() берет этот набор (hyperparameters) и использует метод SetHyperparameters() для обновления соответствующих параметров внутри объектов ядра (m_kernel) и функции правдоподобия (m_likelihood). Это очень важно, поскольку все последующие вычисления NLML должны основываться на этих актуальных значениях гиперпараметров.

После того, как гиперпараметры обновлены, метод вызывает Infer() у объекта инференса (m_inference). Это основной шаг, где происходят все сложные математические вычисления, направленные на оценку апостериорного распределения.

Результаты инференса, включая значение NLML и его градиенты (которые будут использоваться функцией Grad), сохраняются в приватном поле класса m_last_inference_result.

Если инференс успешен, метод возвращает значение NLML.

• Метод  GaussianProcess::SetHyperparameters(const vector &params) отвечает за распределение и установку оптимизированных значений гиперпараметров ядра и функции правдоподобия. 

//+------------------------------------------------------------------+    
//| Метод для установки гиперпараметров                              |
//+------------------------------------------------------------------+
void GaussianProcess::SetHyperparameters(const vector &params)
{
//+------------------------------------------------------------------+    
//Это вызов полиморфного метода SetHyperparameters у объекта, на который указывает m_kernel.
//Поскольку m_kernel является указателем базового типа (IKernel*), вызов SetHyperparameters
//будет перенаправлен на конкретную реализацию этого метода в производном классе ядра,
//к которому относится m_kernel.Например,если m_kernel на самом деле  указывает на объект
//RBFKernel,будет вызвана RBFKernel::SetHyperparameters(params).Если это SumKernel, 
//будет вызван метод SumKernel::SetHyperparameters(params), и так далее.    
//+------------------------------------------------------------------+
    int kernel_params_count = m_kernel.GetNumHyperparameters();
    int likelihood_params_count = m_likelihood.GetNumHyperparameters();
    // Устанавливаем параметры ядра
    vector kernel_hps(kernel_params_count);
    for(int i = 0; i < kernel_params_count; i++) {
        kernel_hps[i] = params[i];
    }
    m_kernel.SetHyperparameters(kernel_hps);    
    // Устанавливаем параметры правдоподобия
    vector likelihood_hps(likelihood_params_count);
    for(int i = 0; i < likelihood_params_count; i++) {
        likelihood_hps[i] = params[kernel_params_count + i];
    }
    m_likelihood.SetHyperparameters(likelihood_hps);
}

Вектор params содержит все гиперпараметры модели ГП в фиксированном порядке: сначала идут все гиперпараметры ядра (или ядер, если это составное ядро), а затем — параметры функции правдоподобия. Ключевая особенность этого метода — использование полиморфизма. Один и тот же вызов m_kernel.SetHyperparameters() ведет себя по-разному в зависимости от фактического типа объекта, на который указывает m_kernel во время выполнения программы. 

• Метод Predict(). Это то, ради чего, по сути, строится модель: получение предсказаний на новых данных. 

//+------------------------------------------------------------------+
//| Метод предсказания для регрессии и классификации                 |
//+------------------------------------------------------------------+    
bool GaussianProcess::Predict(const matrix &X_test, GPPredictionResult &result,PredictMode predict_mode)
{     
    // 1. Проверка, что модель была обучена
    if (!m_last_inference_result.success) {
        Print("Error: Predict - Inference results not available");
        return false;
    }
    // 1.1 Проверка совпадения количества признаков
    if (X_test.Cols() != m_X_train.Cols()) {
        Print("Error: Predict - Number of features in X_test  must match X_train ");
        return false;
    }

    int N_train = (int)m_X_train.Rows();
    int N_test = (int)X_test.Rows();

    // 2. K_s и K_ss вычисляются независимо от типа инференса/правдоподобия
    matrix K_s = m_kernel.Compute(m_X_train, X_test);            
    matrix K_ss = m_kernel.Compute(X_test, X_test);
    
    // --- 3. Логика для расчета mu_f_star и Sigma_f_star (общая для обоих типов задач) ---
    //------------------------- Алгоритм 2.1 GPML----------------------------------------
    if (m_inference.GetName() == "ExactInference") {
        // Для ExactInference
        matrix L_K_noisy = m_last_inference_result.L_K_noisy;
        vector alpha = m_last_inference_result.alpha;
        
        result.mu_f_star = K_s.Transpose() @ alpha;            

        matrix V(N_train, N_test);    
        if (!L_K_noisy.LinearEquationsSolution(K_s, V)) {
            Print("Error: Predict (Exact) - LinearEquationsSolution failed");
            return false;        
        }          
        result.Sigma_f_star = K_ss - V.Transpose() @ V;

    } else if (m_inference.GetName() == "LaplaceInference") {
    //------------------------- Алгоритм 3.2 GPML ----------------------------------------
        matrix W = -1 * m_last_inference_result.H;    
        matrix L_B = m_last_inference_result.L_B;    
        matrix sW = m_last_inference_result.sW;        
        vector f_hat = m_last_inference_result.mu_f_train;    
        vector grad_f_hat = m_likelihood.LogLikelihoodGradient(f_hat, m_y_train);
        // Eq[f*∣X,y,x*]=k(x*)^T K^−1 f_hat = k(x*)^T ∇log p(y∣f_hat) 
        result.mu_f_star = K_s.Transpose() @ grad_f_hat;
        
        matrix SwKs = sW @ K_s;
        matrix V(N_train, N_test);    
        if (!L_B.LinearEquationsSolution(SwKs, V)) {
            Print("Error: Predict (Laplace) - LinearEquationsSolution failed");
            return false;
        }
        // Vq[f*|X, y,x*] = Kss - Ks^T(K + W^-1)^-1 Ks
        result.Sigma_f_star = K_ss - V.Transpose() @ V;
    }    
    
    // --- 4. Логика, специфичная для типа правдоподобия (Likelihood) ---
if (m_likelihood.GetName() == "GaussianLikelihood") {
    // --- 4.1. Регрессия (GaussianLikelihood) ---
    double noise_variance = 0.0;
    vector likelihood_params = m_likelihood.GetHyperparameters();
    if (likelihood_params.Size() > 0) {
        noise_variance = likelihood_params[0] * likelihood_params[0];
    }    
    result.Sigma_y_star = result.Sigma_f_star + matrix::Identity(N_test, N_test) * noise_variance;
    result.mu_y_star = result.mu_f_star; // Для гауссовского правдоподобия mu_y_star = mu_f_star

    } else if (m_likelihood.GetName() == "LogitLikelihood") {
        // --- 4.2. Классификация (LogitLikelihood) ---
          // Убедимся, что m_likelihood является LogitLikelihood для доступа к методу sigmoid
        LogitLikelihood *logit = dynamic_cast<LogitLikelihood*>(m_likelihood);
        if (logit == NULL) {
            Print("Error: Failed to cast m_likelihood to LogitLikelihood in Predict");
            return false;
        }
        
        result.predicted_probabilities.Resize(N_test);
        result.predicted_labels.Resize(N_test);
        double mc_samples_array[]; 
 
        for (int i = 0; i < N_test; i++) {
            double mu_f_star_i = result.mu_f_star[i];  //среднее апостериорного распределения q(f*|X,y,x*)
            double sigma_f_star_diag_i = result.Sigma_f_star[i, i]; // дисперсия апостериорного распределения q(f*|X,y,x*)
    //------------------- 1)Пробит-аппроксимация (Probit Approximation)----------------------
            if (predict_mode == PROBIT) {
                double k_i = 1.0 / MathSqrt(1.0 + M_PI / 8.0 * sigma_f_star_diag_i);
                result.predicted_probabilities[i] = logit.sigmoid(mu_f_star_i * k_i);}
    // ----------------- 2) Численное интегрирование ---------------------------------------
            else if (predict_mode == NUM_INTEGR) {  
                result.predicted_probabilities[i] = CalculateNumericalProbability(
                    mu_f_star_i,
                    sigma_f_star_diag_i,
                    logit
                );} 
   // ----------------------3) Метод Монте Карло ---------------------------------------              
            else if (predict_mode == MONTE_CARLO) {      
                // Количество сэмплов для Монте-Карло
                int num_samples = 10000;                
                ArrayResize(mc_samples_array, num_samples); 
                double std_dev_f_star_i = MathSqrt(sigma_f_star_diag_i);
                // Генерируем num_samples значений из N(mu_f_star_i, std_dev_f_star_i)             
                MathRandomNormal(mu_f_star_i, std_dev_f_star_i, num_samples, mc_samples_array);
                double sum_sigmoid_samples = 0.0;
                for (int s = 0; s < num_samples; s++) {
                    sum_sigmoid_samples += logit.sigmoid(mc_samples_array[s]);
                }
            //Чтобы получить ожидаемую вероятность  p(y*=+1|X,y,x*)
            //мы вычисляем среднее арифметическое всех полученных значений σ(f_sample*). 
            //По закону больших чисел, когда num_samples достаточно велико, 
            //это среднее будет хорошей аппроксимацией истинного значения интеграла     
                result.predicted_probabilities[i] = sum_sigmoid_samples / num_samples;
            }    
            // Предсказанные метки (+1 или -1)
            result.predicted_labels[i] = (result.predicted_probabilities[i] >= 0.5) ? 1.0 : -1.0;
        }
    }
    return true;    
    }

Результаты предсказаний (среднее, дисперсия, вероятности, метки классов) записываются в структуру GPPredictionResult.

В первую очередь вычисляем матрицы K* и K**. Эти матрицы являются основой для предсказаний в ГП. Они необходимы для вычисления среднего и дисперсии скрытой функции f* в новых тестовых точках. Логика здесь зависит от того, какой метод инференса (ExactInference или LaplaceInference) был использован во время обучения, поскольку они предоставляют разные компоненты для формул предсказания (Алгоритм 2.1 для Exact, Алгоритм 3.2 для Laplace из книги GPML Рассмусена и Уильямса).

Если использовался точный инференс (ExactInference), извлекаются заранее вычисленные L_K_noisy и alpha. Если использовалась аппроксимация Лапласа (LaplaceInference), извлекаются W, L_B, sW и f_hat (мода). В обоих случаях, результатом являются среднее значения (mu_f_star) и ковариационная матрица (Sigma_f_star) скрытой функции для каждой тестовой точки.

Как мы уже обсуждали в теоретической части статьи, существует проблема вычисления интеграла для получения вероятности класса. Поэтому используются аппроксимации:

• predict_mode == PROBIT (Пробит-аппроксимация):

Это часто используемая быстрая аппроксимация. Она заменяет сигмоидную функцию кумулятивной функцией распределения нормального распределения, которая похожа по форме. Это позволяет вычислить интеграл аналитически.

• predict_mode == NUM_INTEGR (Численное интегрирование):

В этом режиме вызывается вспомогательная функция CalculateNumericalProbability. Она численно аппроксимирует интеграл, разбивая диапазон f* на дискретные интервалы и суммируя значения. Это может быть точнее, но медленнее. 

• predict_mode == MONTE_CARLO (Метод Монте-Карло):

Это стохастический метод. Генерируется большое количество случайных сэмплов (выборок) f* из апостериорного распределения q(f*∣X, y, x*). Для каждого сэмпла f* вычисляется sigma(f*).

Среднее арифметическое всех этих значений sigma(f*) является аппроксимацией искомой вероятности p(y*=+1|X, y, x*). Это самый вычислительно затратный метод. Для генерации выборок из нормального распределения используется функция из стандартной библиотеки MathRandomNormal.

На основе вычисленных вероятностей, для каждого из вышеперечисленных методов аппроксимации принимается решение о предсказанной метке класса. Если вероятность принадлежности к классу +1 больше или равна 0.5, то предсказывается +1, иначе -1.

Класс GPOptimizationObjective

//+------------------------------------------------------------------+
//| Класс для целевой функции оптимизатора Alglib                    |
//+------------------------------------------------------------------+
class GPOptimizationObjective : public CNDimensional_Grad
{
private:  
    GaussianProcess* m_gp; // указатель на объект GaussianProcess
    double nlml;           // Отрицательное логарифмическое правдоподобие
public:
    // Конструктор 
    GPOptimizationObjective(GaussianProcess* gp_instance) : m_gp(gp_instance), nlml(0.0) {}
    double GetNLML() { return nlml; }
    ~GPOptimizationObjective() {}

    // Метод Grad, который будет вызван оптимизатором
    virtual void Grad(CRowDouble &w, double &func,CRowDouble &grad, CObject &obj) override {     
        // Преобразуем CRowDouble в vector для передачи в GP
        vector hyperparameters(w.Size());
        for(int i = 0; i < (int)w.Size(); i++) { 
           hyperparameters[i] = w[i];        
        }
        
        // Вызываем метод GP для вычисления NLML
        func = m_gp.CalculateNLMLObjective(hyperparameters);
        nlml = func; 
        
         GPInferenceResult current_result = m_gp.GetLastInferenceResult(); 
        if (!current_result.success ) {
            Print("Warning: GPOptimizationObjective::Grad - Gradient calculation failed");
            for(int i = 0; i < (int)w.Size(); i++) {
                grad.Set(i, DBL_MAX); 
            }
            return;
        }            
        // Заполняем grad элементами из current_result.nlml_gradient
        for(int i = 0; i < (int)w.Size(); i++) {
        grad.Set(i, current_result.nlml_gradient[i]);
        }       
    }      
};

Данный класс  является связующим звеном между нашим классом GaussianProcess и внешней библиотекой оптимизации Alglib (в частности, оптимизатором MinBLEIC).

Alglib требует, чтобы целевая функция, которую он оптимизирует, соответствовала определённому интерфейсу. Именно для этого и нужен GPOptimizationObjective. Он наследуется от CNDimensional_Grad — базового класса Alglib, который определяет этот интерфейс. Этот базовый класс предоставляет виртуальные методы, которые класс  GPOptimizationObjective должен реализовать. Эти методы позволяют оптимизаторам Alglib работать с любой целевой функцией, при условии, что она предоставляет как значение функции, так и её градиент. 

Приватный член GaussianProcess* m_gp содержит указатель на наш объект GaussianProcess. Это позволяет классу GPOptimizationObjective вызывать метод CalculateNLMLObjective для выполнения необходимых вычислений. 

Метод Grad() — это самая важная часть этого класса. Он переопределяет виртуальный метод из CNDimensional_Grad и будет вызываться оптимизатором Alglib на каждой итерации. Функция Grad() получает от Alglib текущий вектор гиперпараметров w, и должна вернуть значение целевой функции func и вектор её градиентов grad. 

Заключение

Подведем промежуточные итоги.

В первой части статьи мы заложили прочную теоретическую основу для понимания модели классификации ГП. Мы детально рассмотрели принципы работы ГП для бинарной классификации и метод аппроксимации Лапласа. Этот метод критически важен, так как делает задачу классификации практически решаемой и вычислительно эффективной для нужд онлайн-торговли, в отличие от точного, но невероятно затратного метода MCMC.

Разобравшись с теоретическими построениями, мы приступили к практической реализации, спроектировав и описав два ключевых класса нашей библиотеки ГП:

• GaussianProcess: главный класс, инкапсулирующий всю логику построения, обучения и предсказания модели ГП,
• GPOptimizationObjective: действующий как посредник, подготавливая целевую функцию и её градиент в формате, необходимом библиотеке Alglib для оптимизации гиперпараметров.

Во второй части мы завершим реализацию библиотеки, предоставив:

• подробное описание и код реализации ключевых интерфейсов: IKernel (для различных ядер), IInference (для методов вывода) и ILikelihood (для функций правдоподобия);
• примеры работы библиотеки на синтетических данных для наглядной демонстрации её возможностей;
• практическое применение в трейдинге: разработаем индикаторы для классификации и регрессии на базе нашей библиотеки, показав, как ГП могут быть использованы для принятия торговых решений.