Критерий независимости Гильберта-Шмидта (HSIC)

Введение

Основная задача трейдера при работе с котировками финансовых инструментов — создание торговой системы (советника) с положительным математическим ожиданием. При проектировании таких систем часто предполагается, что в данных, используемых для обучения и последующей торговли, присутствуют скрытые зависимости. Однако, вопрос о статистической проверке этого предположения обычно не рассматривается. Считается, что косвенный ответ можно получить через результаты тестирования на вневыборочных данных (out-of-sample).

Между тем, статистически обоснованный ответ на вопрос о наличии связи между признаками и целевой переменной имеет ключевое значение. Положительный ответ дает уверенность в целесообразности использования предсказательных моделей, тогда как отрицательный заставляет задуматься: что именно пытается предсказать алгоритм?

В математической статистике на вопрос о наличии, либо отсутствии, вероятностной связи между случайными величинами отвечают критерии независимости. Одним из таких критериев является статистический тест HSIC — мощный непараметрический метод, разработанный в 2005 году статистиком Артуром Греттоном.

В отличие от коэффициента корреляции, который выявляет только линейные связи, HSIC способен обнаруживать как линейные, так и нелинейные зависимости. Благодаря этому, он широко применяется в машинном обучении для выбора признаков, анализа причинно-следственных отношений и других задач. В этой статье мы разберем принцип работы HSIC и реализуем его в среде MQL5.

Что такое HSIC

HSIC — это мера зависимости между двумя случайными величинами X и Y, основанная на ядерном подходе. Метод использует математическую "магию" ядерных функций (например, гауссовской (рис.1)), которые преобразуют данные в специальное пространство RKHS (Reproducing Kernel Hilbert Spaces), где зависимости становится легче обнаружить.

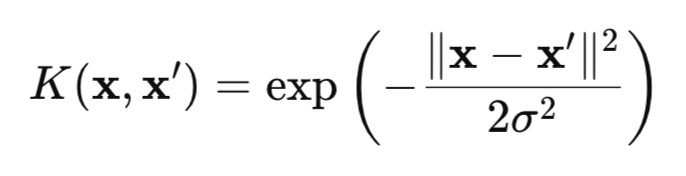
Рис.1 Гауссовское ядро (RBF-ядро)

где:

• x, x' – векторы (точки) наблюдений,
• ||   ||² – квадрат евклидовой нормы,
• σ — ширина ядра.

Существует множество ядер, которые можно использовать для теста HSIC, таких, как ядра для категориальных данных или ядро Лапласа. Однако в данной статье, мы сконцентрируем наше внимание на гауссовском ядре, поскольку оно универсально и обладает свойством характеристичности. Это свойство позволяет выявлять любые зависимости в данных, делая гауссовское ядро особенно эффективным.

Классический HSIC тестирует парную независимость между двумя случайными величинами X и Y, проверяя выполняется ли условие P(X,Y) = P(X)P(Y). Для этого, HSIC анализирует отклонение совместного распределения от произведения маргинальных распределений, используя ядерные матрицы (это таблица, где каждый элемент отражает сходство между парами точек данных, вычисленное с помощью ядерной функции).

Важное преимущество HSIC заключается в его способности работать с данными любой размерности: скалярными, векторными или их комбинациями. Это особенно ценно в задачах, где явное построение многомерных совместных распределений P(X,Y) является сложным из-за высокой размерности данных.

С математической точки зрения критерий HSIC определяется, как квадрат нормы Гильберта-Шмидта оператора кросс-ковариации в RKHS:

где:

• K(X,X') – ядерная функция для случайной величины X,
• L(Y,Y') – ядерная функция для случайной величины Y,
• ||  ||HS  - норма Гильберта-Шмидта.

Здесь уместно сравнить HSIC с обычной ковариацией. Классическая ковариация измеряет линейную связь между величинами X и Y в их исходном пространстве, тогда как HSIC работает с отображениями X и Y в воспроизводящее ядерное гильбертово пространство (RKHS), то есть, в пространство функций, что позволяет преобразовать данные для выявления сложных нелинейных зависимостей.

На практике вычисление нормы Гильберта-Шмидта напрямую не требуется. Вместо этого HSIC оценивается через эмпирическую статистику, которая опирается на ядерные матрицы, построенные для выборки данных:

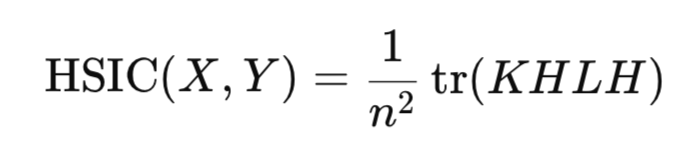
где:

• K,L – матрицы ядра n*n,
• H – центрирующая матрица n*n (I -1/n11^T),
• tr() – след матрицы,
• n – количество наблюдений.

Подобно коэффициенту корреляции, HSIC оценивает наличие зависимости между случайными величинами X и Y, используя выборочную статистику, без необходимости построения распределений этих величин.

Статистика HSIC всегда неотрицательна:

• значение HSIC > 0 указывает на наличие зависимости,
• тогда как HSIC = 0 свидетельствует о независимости данных.

Проверка значимости HSIC

Однако, для надежных выводов недостаточно вычислить статистику — необходимо подтвердить ее статистическую значимость, чтобы исключить случайный результат. Для статистики HSIC нет точной аналитической формы распределения при нулевой гипотезе. То есть мы не можем просто воспользоваться, например, нормальным распределением и быстро и легко без вычислительных затрат получить критическое значение или p-value. Для решения этой проблемы применяются два основных подхода:

• перестановочный тест,
• гамма-аппроксимация.

Перестановочный тест является основным и наиболее точным методом оценки распределения HSIC при H0. Его цель разрушить любую зависимость между X и Y, c помощью случайной перестановки индексов одной из переменных или перемешивания полученной матрицы ядра этой переменной. Для того чтобы получить точный результат, приходится выполнять довольно много таких перестановок (около 1000). Поэтому перестановочный тест довольно затратный, так как требуется вычисление HSIC для каждой такой перестановки.

Главное преимущество перестановочного теста состоит в том, что он не требует какого-либо предположения о форме распределения данных, вместо этого, он опирается на эмпирическое распределение статистики, полученное путём перестановок. Далее эмпирическое распределение HSIC используется для получения оценки p-value. 

Для ускорения вычислений статистики применяется гамма-аппроксимация. В этом подходе статистика HSIC масштабируется с учетом размера выборки(n*HSIC), а параметры гамма-распределения оцениваются по выборочным моментам HSIC (среднему и дисперсии). Этот метод значительно быстрее перестановочного теста, но его точность может быть ниже для малых выборок. Существуют и другие методы оценки распределения HSIC под нулевой гипотезой независимости, но они сложны в реализации и редко используются на практике, поэтому в данной статье они не рассматриваются.

Реализация HSIC Permutation в MQL5

Перестановочный тест реализован в функции hsic_test.

//+------------------------------------------------------------------+
//| Функция для перестановочного теста                               |
//+------------------------------------------------------------------+
vector hsic_test(matrix &X,matrix &Y,const double alpha,bool Bootstrap = false,int n_permutations=1000)
{
vector ret = vector::Zeros(3);
int n = (int)X.Rows(); 

matrix K =  RBF_kernel(X); // матрица ядра для X
matrix L =  RBF_kernel(Y); // матрица ядра для Y
matrix H = matrix::Eye(n, n) - matrix::Ones(n, n)/n; // Центрирующая матрица
//--------------------------------------

// Kc центрированная ядерная матрица К
   matrix Kc(n, n);
   if(!Kc.GeMM(H, K, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Kc = H * K");
      return ret;
   }
   if(!Kc.GeMM(Kc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Kc * H");
      return ret;
   }
   Kc = Kc.Transpose();
   double coef = 1/pow(n,2);

// Вычисляем наблюдаемое значение статистики HSIC
   double  hsic_obs = compute_hsic(L,Kc,coef);
   ret[0]= hsic_obs;

  //------------ Перестановочный тест ------------------------------------
  if (Bootstrap == true){ 
    vector hsic_perms = vector::Zeros(n_permutations);   
    for ( int i = 0; i<n_permutations; i++)
    {        
        ShuffleMatrix(L); // Перемешиваем матрицу
        hsic_perms[i] = compute_hsic(L,Kc,coef);
    }
    
    int count = 0;
for(int i = 0; i < n_permutations; i++)
{
   if(hsic_perms[i] >= hsic_obs)
      count++;
}
   // Вычисляем p-value
double p_value = (n_permutations > 0) ? (double)count / n_permutations : 0.0;
    ret[1] = p_value; 
  
  // Вычисляем критическое значение
  double hsic_sort[];
  VectortoArray(hsic_perms,hsic_sort);
  ArraySort(hsic_sort);
  double CV = hsic_sort[(int)round((1-alpha)*n_permutations)];
    ret[2] = CV; 
    }
 //----------------------------------------------------------------------------------   
  return ret;  
}

• Функция принимает два набора данных X и Y (это матрицы размером n*d, где n это количество наблюдений, а d – размерность данных),

• параметр alpha задает уровень значимости (это ошибка I рода, то есть вероятность отклонить нулевую гипотезу, когда она на самом деле верна),

• параметр Bootstrap (если true, считаем тест с перестановками для получения p-value, иначе — только расчет статистики),

• n_permutations –количество случайных перестановок,

• функция возвращает вектор, содержащий наблюдаемое значение HSIC, p_value и критическое значение статистики для выбранного уровня alpha.

Вычисление матрицы гауссовского ядра выполняется в функции  RBF_kernel.

//+------------------------------------------------------------------+
//| Гауссовское ядро                                                 |
//+------------------------------------------------------------------+ 
matrix RBF_kernel(const matrix &X) {
   int n = (int)X.Rows();
   
   // Вычисляем матрицу расстояний через скалярное произведение
   matrix XX(n, n); 
   if(!XX.GeMM(X, X.Transpose(), 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить XX = X * X^T");    
   }
   
 matrix diag(n,1);
 diag.Col(XX.Diag(),0);  // вектор диагональных элементов
 //  квадраты расстояний
 matrix D_sq = matrix::Ones(n, 1).MatMul(diag.Transpose()) + diag.MatMul(matrix::Ones(1, n)) - 2*XX;
   
   // Вычисляем sigma на первых n_sigma строках
   int n_sigma = MathMin(n, 100);
   int num_elements = (n_sigma * (n_sigma - 1)) / 2;
   vector upper_tri(num_elements);
   int idx = 0;
   for(int i = 0; i < n_sigma; i++) {
      for(int j = i + 1; j < n_sigma; j++) {
         upper_tri[idx] = D_sq[i, j]; 
         idx++;
      }
   }
  double sigma = MathSqrt(0.5 * upper_tri.Median());
   
   return MathExp((-1* D_sq) / (2 * sigma*sigma)); 
}

Функция рассчитывает квадрат расстояний между точками данных, ширину ядра сигма и возвращает искомую матрицу ядра размером n*n.

Для эффективного расчета квадратов расстояния, используется матричная форма вместо обычного цикла:

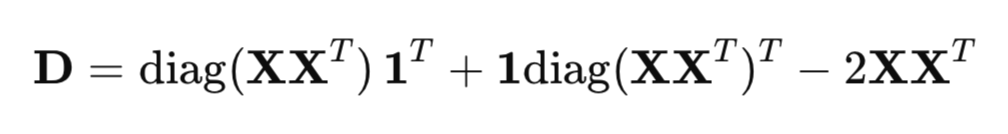
где:

• XX^T - матрица Грама (матрица скалярнях произведений),
• diag(XX^T ) - вектор диагональных элементов,
• 1 - вектор из единиц.

Параметр сигма в гауссовском ядре определяет ширину ядра и существенно влияет на чувствительность HSIC к обнаружению зависимостей в данных. Параметр сигма определяет масштаб сходства: большие значения сигма делают ядро более широким (точки, находящиеся дальше друг от друга, всё ещё считаются похожими), а малые значения — более узким (только очень близкие точки считаются похожими).

Один из распространенных методов выбора сигма — использование следующей медианной эвристики:

Коэффициент 0,5 берется для того, чтобы знаменатель RBF ядра был равен медиане квадратов евклидовых расстояний между точками данных, что обеспечивает адаптивную оценку, учитывающую масштаб данных. 

Переменная n_sigma = MathMin (n, 100) ограничивает количество данных для расчета сигма до 100. Это сделано для того, чтобы снизить вычислительные затраты при больших выборках, при этом сохраняя репрезентативность для оценки сигма.  В вектор upper_tri копируются квадраты евклидовых расстояний, используя только верхний треугольник матрицы расстояний (без диагонали, i=j), чтобы избежать дублирования и нулевых расстояний.

Функция для расчета статистики HSIC  compute_hsic.

//+------------------------------------------------------------------+
//| Функция для вычисления HSIC                                      |
//+------------------------------------------------------------------+
double compute_hsic(const matrix &L, const matrix& Kc, const double coef){
matrix KcL= Kc*L;               
return coef*KcL.Sum();
}

После вычисления наблюдаемой статистики HSIC, проводится перестановочный тест для проверки её статистической значимости. Функция ShuffleMatrix (matrix &m) реализует эту перестановку для ядерной матрицы L, соответствующей переменной Y. Статистически, разницы нет, перемешивать L или K, так как HSIC симметричен относительно X и Y, что даёт эквивалентные результаты в перестановочном тесте для HSIC. Перемешивание же самой переменной Y и последующий пересчет для нее матрицы L для каждой перестановки является неэффективным.

//+------------------------------------------------------------------+
//| Функция для перемешивания данных матрицы                         |
//+------------------------------------------------------------------+
void ShuffleMatrix(matrix &m)
{
   int rows = (int)m.Rows();
   int cols = (int)m.Cols();
   
   if (rows != cols) {
   Print("Ошибка: Матрица должна быть квадратной");
}  
   int perm[];
   GeneratePermutation(rows, perm);  // Генерация случайной перестановки индексов
   matrix temp = m;  
   // Перестановка строк и столбцов
   for(int i = 0; i < rows; i++)
   {
      for(int j = 0; j < cols; j++)
      {
         m[i,j] = temp[perm[i], perm[j]];
      }
   }
}

Генерация случайных индексов выполняется с помощью функции GeneratePermutation.

//+------------------------------------------------------------------+
//| Функция для создания случайной перестановки индексов             |
//+------------------------------------------------------------------+ 
void GeneratePermutation(int size, int &perm[])
{
   MathSequence(0,size,1,perm);
   
   // Алгоритм Фишера-Йетса для перестановки
   for(int i = size - 1; i > 0; i--)
   {
      // Генерация случайного индекса от 0 до i
      int j = (int)(MathRand() / 32768.0 * (i + 1)); 
      int temp = perm[i];
      perm[i] = perm[j];
      perm[j] = temp;
   }
}

После многократной перестановки ядерной матрицы L, с помощью функции ShuffleMatrix формируется эмпирическое распределение статистики HSIC под нулевой гипотезой независимости. P-value определяется как доля перестановочных значений HSIC, превышающих или равных наблюдаемой статистике. Если p-value меньше уровня значимости alpha, нулевая гипотеза независимости отвергается.

Критическое значение выбирается как квантиль эмпирического распределения на уровне 1−alpha, то есть, значение, выше которого находится alpha⋅100% перестановочных расчетов HSIC.

Реализация HSIC Gamma

За расчет Гамма-аппроксимации отвечает функция hsic_Gamma_test.

//+------------------------------------------------------------------+
//| Функция для Гамма-аппроксимации HSIC                             |
//+------------------------------------------------------------------+
double hsic_Gamma_test(matrix &X, matrix &Y, double &CV, double & pvalue)
{
int n = (int)X.Rows(); 

matrix K =  RBF_kernel(X); // матрица ядра для X
matrix L =  RBF_kernel(Y); // матрица ядра для Y
matrix H = matrix::Eye(n, n) - matrix::Ones(n, n)/n; // Центрирующая матрица

   matrix Kc(n, n); // Вычисляем центрированную матрицу ядра X  
   if(!Kc.GeMM(H, K, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Kc = H * K");
      return 0;
   }
   if(!Kc.GeMM(Kc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Kc * H");
      return 0;
   }   
   matrix KcT = Kc.Transpose();
     
   matrix Lc(n, n);  // Вычисляем центрированную матрицу ядра Y 
   if(!Lc.GeMM(H, L, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Lc = H * L");
      return 0;
   }
   
   if(!Lc.GeMM(Lc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Lc * H");
      return 0;
      }
              
   double m = (double)n; 
   double coef = 1/m;
   
// Вычисляем наблюдаемое значение HSIC
matrix KcLc;
double  hsic_obs = compute_hsic_Gamma(Lc,KcT,coef,KcLc); // n*HSIC

   matrix varHSIC_m = KcLc*KcLc;
   varHSIC_m = (1.0/36.0)*varHSIC_m;  
   double  varHSIC = 1/(m)/(m-1) * (varHSIC_m.Sum() - varHSIC_m.Trace() );
   varHSIC = 72*(m-4)*(m-5)/m/(m-1)/(m-2)/(m-3)  *  varHSIC; // Дисперсия HSIC
   
   matrix KD;
   KD.Diag(K.Diag(),0);
   matrix LD;
   LD.Diag(L.Diag(),0);
   K = K-KD;   
   L = L-LD;  
   matrix one = matrix::Ones(n,1);
   matrix a = 1/m/(m-1)*one.Transpose();
   matrix muX;
   muX.GeMM(a,K.MatMul(one),1,0);
   matrix  muY;
   muY.GeMM(a,L.MatMul(one),1,0);
   double mHSIC  = 1/m * ( 1 +muX[0,0]*muY[0,0]  - muX[0,0] - muY[0,0] ) ; // математическое ожидание HSIC

//параметры Гамма распределения
 double alphaG = mHSIC*mHSIC / varHSIC;
 double beta = varHSIC*m / mHSIC;   
 
 int err;
 CV = MathQuantileGamma(1-alpha_,alphaG,beta,err);  // Critical value
 pvalue = 1 - MathCumulativeDistributionGamma(hsic_obs,alphaG,beta,err); // p-value 
 //----------------------------------------------------------------------------------   
  return hsic_obs;  
}

Здесь мы вычисляем статистику HSIC, масштабируемую на размер выборки n (n*HSIC), которой приближенно соответствует гамма-распределение с параметрами формы (alpha) и масштаба (beta). Данные параметры определяются на основе математического ожидания и дисперсии статистики HSIC.

Проверка на синтетических данных

Для оценки способности HSIC выявлять нелинейные зависимости, смоделируем эксперимент, типичный для задач трейдинга. Рассмотрим два признака X={X 1 ,X 2 }, которые нелинейно связаны со скалярной целевой переменной Y, но не имеют с ней линейной корреляции (рис. 2). Такая ситуация отражает реальную задачу, с которой сталкивается трейдер: проверить, оказывают ли отобранные признаки влияние на прогнозируемую переменную, прежде, чем использовать их в торговой системе.

Сгенерируем данные следующим образом:

Y = X1^2 * cos(pi * X2) + Noise

где:

• X1 и X2 - независимые и одинаково распределенные равномерные величины [-5,5],
• Noise – гауссовский шум,
• Y - целевая переменная, связанная с X1 и X2нелинейной зависимостью.

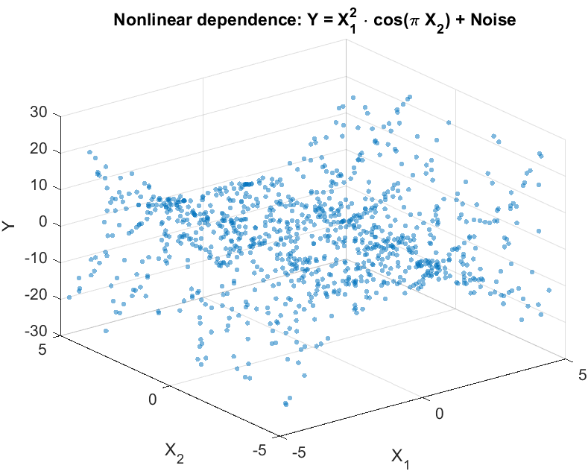
Рис.2 Гистограмма рассеяния для целевой переменной Y и признаков X

Цель эксперимента — проверить гипотезу независимости в форме:

P(X1,X2,Y) = P(X1,X2)P(Y),

то есть определить, влияют ли оба признака совместно на целевую переменную или между ними никакой связи нет.

В реальных задачах, где число признаков может быть большим, HSIC позволяет гибко проверять зависимости: как для отдельных признаков (например, X1 или X2 с Y), так и для произвольных подгрупп данных. Это делает метод полезным для выбора информативных признаков, например, путем ранжирования их по p-value, чтобы отобрать наиболее значимые для построения торговой системы.

На рис.3 представлены результаты теста HSIC с помощью Гамма-аппроксимации. Полученное значение HSIC, и соответствующее ему p-value, и критическое значение подтверждают статистически значимую нелинейную зависимость между X и Y. Это демонстрирует способность HSIC эффективно выявлять сложные связи в данных, что особенно важно для анализа биржевых котировок, где признаки часто имеют нелинейное влияние на прогнозируемую переменную. Для сравнения, коэффициент корреляции, рассчитанный для X1, X2 и Y оказался близким к нулю, не обнаруживая линейной связи.

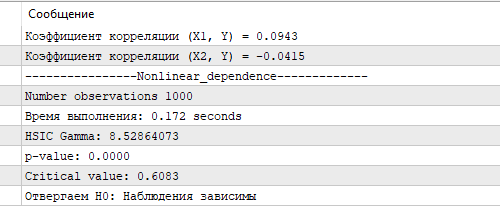
Рис.3 Результаты теста HSIC, гамма-аппроксимация

Точный перестановочный тест HSIC, выполненный на выборке того же размера, занял 8,5 секунд на довольно скромном по нынешним меркам компьютере автора (4 ядерный Ryzen 3). Тем не менее, время расчета гамма-аппроксимации выполняется значительно быстрее, что делает ее предпочтительным выбором в задачах, где важна скорость вычислений, например, при анализе больших объемов финансовых данных в реальном времени. Гамма-аппроксимация, несмотря на возможные неточности при малых выборках, обеспечивает баланс между скоростью и точностью, что делает её ценным инструментом для реализации HSIC в торговых алгоритмах на MQL5.

Заключение

В данной статье мы рассмотрели HSIC (Hilbert-Schmidt Independence Criterion) — мощный непараметрический метод для оценки зависимости между случайными величинами. HSIC использует ядерный подход, что позволяет выявлять сложные нелинейные зависимости, без необходимости явного моделирования совместных распределений.

Основные преимущества HSIC:

• работает со скалярными и векторными данными любой размерности,
• улавливает сложные нелинейные зависимости,
• относительно прост в реализации

Однако, у метода есть и ограничения:

• чувствительность к выбору параметра ширины ядра σ,
• зависимость от размера выборки: на малых выборках перестановочный тест может быть менее мощным, а на больших — вычисление ядерных матриц K и L довольно затратно по времени,
• HSIC указывает только на наличие зависимости, но не характеризует ее силу, в отличие от коэффициента корреляции.

В статье мы продемонстрировали применение HSIC на синтетических данных с нелинейной зависимостью, подтвердив его способность обнаруживать связи, недоступные традиционным методам, таким как корреляция Пирсона. Реализация HSIC в MQL5 показала его практическую применимость для выбора информативных признаков в разработке торговых систем.

Мы рассмотрели базовую версию метода с гауссовским ядром, но HSIC имеет более широкие возможности, включая работу с категориальными данными и тестирование условной независимости. Эти направления открывают перспективы для дальнейших исследований и применения метода в задачах трейдинга, машинного обучения и анализа данных.