Гауссовcкие процессы в машинном обучении (Часть 2): Реализация и тестирование модели классификации в MQL5
58
0
Введение
В предыдущей статье мы познакомились с теоретическими основами байесовской модели машинного обучения — Гауссовскими Процессами, а также приступили к созданию библиотеки ГП в MQL5, описав два ключевых класса: GaussianProcess и GPOptimizationObjective.
Сегодня мы завершим построение библиотеки, подробно рассмотрев реализацию ключевых интерфейсов: IKernel, ILikelihood и IInference. После этого мы протестируем библиотеку на синтетических данных и напишем индикаторы для классификации и регрессии, демонстрирующие её работу в онлайн-режиме — с переобучением модели на каждом новом баре.
Интерфейс IKernel
Интерфейс IKernel, который вы найдёте в файле Kernels.mqh, — это основа для создания ковариационных ядер в нашей библиотеке. Он делает систему гибкой и легко расширяемой: вы можете добавлять новые виды ядер или их комбинации, не меняя при этом главную структуру кода.
interface IKernel { // Вычисляет ковариационную матрицу между двумя наборами данных virtual matrix Compute(const matrix &X1, const matrix &X2) = 0; // Вычисляет производную ковариационной матрицы по заданному гиперпараметру // param_index: индекс гиперпараметра, по которому берется производная (начиная с 0) virtual matrix ComputeDerivative(int param_index) = 0; // Возвращает текущие значения всех гиперпараметров ядра virtual vector GetHyperparameters() const = 0; // Устанавливает новые значения гиперпараметров ядра virtual void SetHyperparameters(const vector ¶ms) = 0; // Возвращает количество гиперпараметров ядра virtual int GetNumHyperparameters() const = 0; // Возвращает строковое имя ядра virtual string GetName() const = 0; };
Интерфейс определяет два наиболее важных метода, которые лежат в основе работы любого ядра:
- Compute(const matrix &X1, const matrix &X2) — вычисляет ковариационную матрицу K между двумя наборами данных.
- ComputeDerivative(int param_index) — вычисляет производную ковариационной матрицы по одному из гиперпараметров ядра. param_index указывает индекс гиперпараметра, по которому берется производная.
Класс RBFKernel (Радиально-базисное ядро)
RBFKernel, также известное как гауссовское или квадратично-экспоненциальное ядро, является одним из наиболее часто используемых ковариационных ядер. Оно характеризуется двумя гиперпараметрами: дисперсией сигнала σ_f (амплитуда) и масштабом длины l (length), определяющим гладкость функции.
//+------------------------------------------------------------------+ //| Класс RBF ядра | //+------------------------------------------------------------------+ class RBFKernel : public IKernel { private: double length; double sigma_f; int n; // Количество строк в X1; int m; // Количество строк в X2; matrix m_K; matrix m_D_sq; // матрица квадратов расстояний ||x_i - x_j||^2 public: //Конструктор RBFKernel(double ls, double sf) : length(ls), sigma_f(sf) {} //Деструктор ~RBFKernel() {} matrix Compute(const matrix &X1, const matrix &X2) override { n = (int)X1.Rows(); m = (int)X2.Rows(); matrix XX(n, m); if (!XX.GeMM(X1, X2.Transpose(), 1.0, 0.0)) { Print("Ошибка: Не удалось вычислить XX = X * X^T"); return matrix::Zeros(n, m); } matrix diag1(n, 1); matrix X1_sq = X1 @ X1.Transpose(); diag1.Col(X1_sq.Diag(), 0); matrix diag2(m, 1); matrix X2_sq = X2 @ X2.Transpose(); diag2.Col(X2_sq.Diag(), 0); m_D_sq = matrix::Ones(n, 1) @ diag2.Transpose() + diag1 @ matrix::Ones(1, m) - 2 * XX; m_K = sigma_f * sigma_f * MathExp((-1 * m_D_sq) / (2 * length * length)); return m_K; } matrix ComputeDerivative(int param_index) override { matrix dK(n, m); switch (param_index) { case 0: { dK = (2.0 / sigma_f) * m_K; break; } case 1: { dK = m_K * (m_D_sq / (length * length * length)); break; } } return dK; } vector GetHyperparameters() const override { vector params(2); params[0] = sigma_f; params[1] = length; return params; } void SetHyperparameters(const vector ¶ms) override { if (params.Size() == 2) { sigma_f = params[0]; length = params[1]; } } int GetNumHyperparameters() const override { return 2; } string GetName() const override { return "RBFKernel"; } };
К счастью, для RBF ядра производные находятся легко:
Производная по sigma_f:
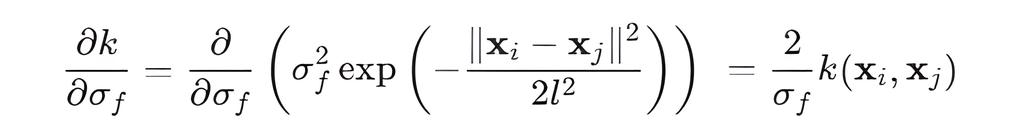
- Производная по l:
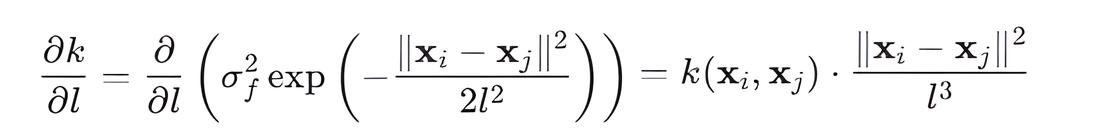
Для параметра length мы выполняем поэлементное умножение матрицы K на (D_sq / length^3), D_sq — матрица квадратов евклидовых расстояний.
Класс LinearKernel (Линейное ядро)
LinearKernel — это простое ковариационное ядро, предполагающее линейную зависимость между точками данных. Оно часто применяется, когда ожидается, что функция может быть аппроксимирована линейной моделью, или как компонент в более сложных составных ядрах.
Линейное ядро имеет один гиперпараметр: дисперсия сигнала σ_l.
//+------------------------------------------------------------------+ //| Класс для линейного ядра | //+------------------------------------------------------------------+ class LinearKernel : public IKernel { private: double sigma_l; int n; int m; matrix m_K; public: //Конструктор LinearKernel(double sl): sigma_l(sl){} //Деструктор ~LinearKernel() {} matrix Compute(const matrix &X1, const matrix &X2) override { n = (int)X1.Rows(); m = (int)X2.Rows(); m_K.GeMM(X1, X2.Transpose(), sigma_l * sigma_l, 0.0); return m_K; } matrix ComputeDerivative(int param_index) override { matrix dK(n, m); switch (param_index) { case 0: { // Производная по sigma_l dK = (2.0 / sigma_l) * m_K; break; } } return dK; } vector GetHyperparameters() const override { vector params(1); params[0] = sigma_l; return params; } void SetHyperparameters(const vector ¶ms) override { if (params.Size() == 1) { sigma_l = params[0]; } } int GetNumHyperparameters() const override { return 1; } string GetName() const override { return "LinearKernel"; } };
Метод ComputeDerivative(int param_index):
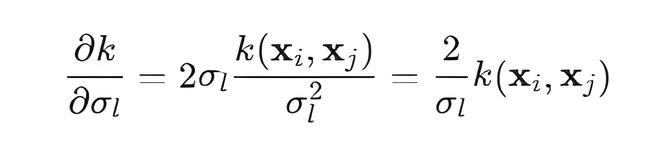
Класс PeriodicKernel (Периодическое ядро)
PeriodicKernel используется для моделирования данных с повторяющимися паттернами или сезонностью, позволяя улавливать циклические зависимости.
//+------------------------------------------------------------------+ //| Класс для периодического ядра | //+------------------------------------------------------------------+ class PeriodicKernel : public IKernel { private: double sigma_f; // Дисперсия сигнала (амплитуда колебаний) double length; // Длина масштаба (гладкость колебаний) double period; // Период колебаний int n; // Количество строк в X1 int m; // Количество строк в X2 matrix m_K; // Ковариационная матрица matrix m_D; // Матрица D (сумма производных по d [2 * sin^2(M_PI*distance/period] ) matrix m_distance_dim[]; // Массив матриц разностей по каждому измерению |x_i_k - x_j_k| int m_d_cols; // Количество измерений(признаков) (X.Cols()) public: //Конструктор PeriodicKernel(double ls, double sf, double p) : sigma_f(sf), length(ls), period(p){} //Деструктор ~PeriodicKernel() {} matrix Compute(const matrix &X1, const matrix &X2) override { n = (int)X1.Rows(); m = (int)X2.Rows(); int d = (int)X1.Cols(); m_d_cols = d; m_D = matrix::Zeros(n, m); ArrayResize(m_distance_dim, d); for (int k = 0; k < d; k++) { vector x1_k = X1.Col(k); vector x2_k = X2.Col(k); // Создаем матрицу, где каждая колонка - это вектор x1_k // (n x 1) * (1 x m) = (n x m) matrix x1_k_copy = x1_k.Outer(vector::Ones(m)) ; // Создаем матрицу, где каждая строка - это транспонированный вектор x2_k // (n x 1) * (1 x m) = (n x m) matrix x2_k_copy = vector::Ones(n).Outer(x2_k); // Вычисляем матрицу всех попарных абсолютных разностей между элементами векторов x1_k и x2_k matrix distance = MathAbs(x1_k_copy - x2_k_copy); m_distance_dim[k] = distance; // Кешируем distance для каждого измерения(признака) matrix sin_term = MathSin(M_PI * distance / period); sin_term = 2.0 * sin_term * sin_term; // 2 * sin^2(u) m_D += sin_term; // Суммируем поэлементно } // Вычисляем матрицу K m_K = sigma_f * sigma_f * MathExp(-1 * m_D / (length * length)); return m_K; } matrix ComputeDerivative( int param_index) override { matrix dK(n, m); switch (param_index) { case 0: { // Производная по sigma_f // dK/d(sigma_f) = (2 / sigma_f) * K dK = (2.0 / sigma_f) * m_K; break; } case 1: { // Производная по length // dK/d(length) = K * (2 * D / length^3) dK = m_K * ( 2.0 * m_D / (length * length * length) ); break; } case 2: { // Производная по period // dK/d(period) = K * (-1/l^2) * dD/d(period) // dD/d(period) = Sum{k=1:d} (2 * pi * (x_ik - x_jk) / period^2) * sin(2*pi*(x_ik - x_jk)/period) matrix dD_dp = matrix::Zeros(n, m); for (int k = 0; k < m_d_cols; k++) { // Цикл по каждому измерению (колонке) данных matrix distance_k = m_distance_dim[k]; // матрица абсолютных разностей для k-го измерения matrix u = M_PI * distance_k / period; // Вычисление аргумента u_k = pi * |x_ik - x_jk| / period matrix sin_2u = MathSin(2.0 * u); // Вычисление sin(2 * u_k) // Используем уже вычисленное u для расчета // -pi * |x_ik - x_jk| / period^2 matrix second_term = (-1*u) / period; // Накопление dD/d(period) для текущего измерения dD_dp += 2.0 * sin_2u * second_term; } // объединение всех частей производной // dK = K * (-1/length^2) * dD_dp dK = m_K * (-1.0 / (length * length)) * dD_dp; break; } } return dK; } vector GetHyperparameters() const override { vector params(3); params[0] = sigma_f; params[1] = length; params[2] = period; return params; } void SetHyperparameters(const vector ¶ms) override { if (params.Size() == 3) { sigma_f = params[0]; length = params[1]; period = params[2]; } } int GetNumHyperparameters() const override { return 3; } string GetName() const override { return "PeriodicKernel"; } };
Производная периодического ядра по параметру period:
Вычисление производной по параметру периода является наиболее сложным, так как period находится внутри тригонометрической функции, которая, в свою очередь, является частью экспоненты.
Формула производной основана на цепном правиле, где K зависит от D, а D зависит от period через синусоидальные члены. Реализация ComputeDerivative итеративно вычисляет составляющую dD_dp для каждого измерения, а затем вычисляет итоговую производную:
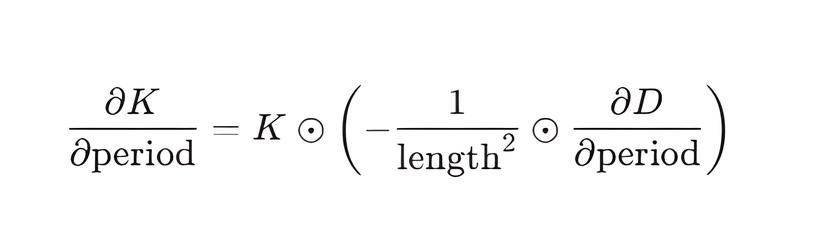
Где dD_dp рассчитывается как сумма производных 2 * sin^2(M_PI*distance/period) по всем измерениям(признакам).
Композитные Ядра
Гауссовские процессы позволяют комбинировать простые ковариационные ядра для создания более сложных моделей, способных описывать различные аспекты данных (например, тренд, периодичность, шум). Эта функциональность реализована через два композитных ядра:
- SumKernel — объединяет несколько ядер путём суммирования их ковариационных матриц.
- ProductKernel — объединяет ядра путём поэлементного умножения их ковариационных матриц.
Оба класса управляют гиперпараметрами своих дочерних ядер, собирая их в один общий вектор для оптимизации и затем распределяя обратно.
Класс SumKernel
//+------------------------------------------------------------------+ //| Класс для суммы ядер | //+------------------------------------------------------------------+ class SumKernel : public IKernel { private: IKernel* kernels[]; public: // Конструктор SumKernel(IKernel* &input_kernels[]) { ArrayResize(kernels, ArraySize(input_kernels)); ArrayCopy(kernels, input_kernels); } //Деструктор ~SumKernel() { for (int i = 0; i < ArraySize(kernels); i++) { if (kernels[i] != NULL) { delete kernels[i]; } } ArrayFree(kernels); } matrix Compute(const matrix &X1, const matrix &X2) override { int n = (int)X1.Rows(); int m = (int)X2.Rows(); matrix sum = matrix::Zeros(n,m); for (int i = 0; i < ArraySize(kernels); i++) { sum += kernels[i].Compute(X1, X2); // Суммируем матрицы от каждого дочернего ядра } return sum; } matrix ComputeDerivative(int param_index) override { int current_param_offset = 0; // Начинаем со смещения 0 для первого ядра for (int i = 0; i < ArraySize(kernels); i++) { // Получаем количество гиперпараметров текущего дочернего ядра int num_params_current_kernel = kernels[i].GetNumHyperparameters(); // Проверяем, принадлежит ли глобальный param_index текущему дочернему ядру // param_index должен быть: // - больше или равен текущему смещению // - строго меньше, чем текущее смещение + количество параметров текущего ядра if (param_index >= current_param_offset && param_index < current_param_offset + num_params_current_kernel) { // Если param_index принадлежит этому ядру, вычисляем его локальный индекс int local_param_index = param_index - current_param_offset; // Вызываем ComputeDerivative для найденного дочернего ядра и // передаем ему локальный индекс. // Поскольку производная суммы ядер по параметру одного ядра равна производной // этого конкретного ядра по этому параметру, мы можем сразу вернуть результат return kernels[i].ComputeDerivative(local_param_index); } // Если param_index не принадлежит текущему ядру, // увеличиваем смещение для проверки следующего ядра current_param_offset += num_params_current_kernel; } Print("Error: SumKernel::ComputeDerivative - Parameter index ", param_index, " out of bounds"); return matrix::Zeros(1, 1); } //+-------------------------------------------------------------------+ //| Функция возвращает значения всех гиперпараметров составного ядра | //+-------------------------------------------------------------------+ vector GetHyperparameters() const override { vector all_params(GetNumHyperparameters()); int current_idx = 0; for (int i = 0; i < ArraySize(kernels); i++) { // Получаем значения параметров текущего дочернего ядра vector kernel_params = kernels[i].GetHyperparameters(); for (int j = 0; j < (int)kernel_params.Size(); j++) { // Копируем параметры в общий вектор all_params[current_idx + j] = kernel_params[j]; } // Обновляем смещение для следующего ядра current_idx += (int)kernel_params.Size(); } return all_params; } //+----------------------------------------------------------------------+ //|Функция принимает вектор значений всех гиперпараметров, разбирает | //|его на соответствующие части и присваивает их каждому дочернему ядру | //+----------------------------------------------------------------------+ void SetHyperparameters(const vector ¶ms) override { int current_idx = 0; for (int i = 0; i < ArraySize(kernels); i++) { // Получаем количество гиперпараметров текущего дочернего ядра int num_params = kernels[i].GetNumHyperparameters(); vector sub_params(num_params); // Копируем соответствующие параметры из общего вектора for (int j = 0; j < num_params; j++) { sub_params[j] = params[current_idx + j]; } // Вызываем метод SetHyperparameters() на текущем дочернем ядре, // передавая ему только его собственные параметры, собранные в векторе sub_params kernels[i].SetHyperparameters(sub_params); current_idx += num_params; } } //+---------------------------------------------------------------------------------+ //| Возвращает общее количество гиперпараметров для всего составного ядра SumKernel | | //+---------------------------------------------------------------------------------+ int GetNumHyperparameters() const override { int total_params = 0; for (int i = 0; i < ArraySize(kernels); i++) { total_params += kernels[i].GetNumHyperparameters(); } return total_params; } string GetName() const override { string name = "Sum("; for (int i = 0; i < ArraySize(kernels); i++) { name += kernels[i].GetName(); if (i < ArraySize(kernels) - 1) name += ","; } name += ")"; return name; } //+------------------------------------------------------------------+ //| Предоставляет внешний доступ к списку дочерних ядер | //+------------------------------------------------------------------+ void GetKernels(IKernel* &output_kernels[]) const { // Копируем указатели из внутреннего массива kernels в переданный // внешний массив output_kernels. Это обеспечивает доступ к дочерним // ядрам в методе GaussianProcess::Fit(), где требуется пройтись // в цикле по всем элементарным ядрам для установки границ оптимизации // их гиперпараметров. ArrayCopy(output_kernels, kernels); } };
- Метод Compute — вычисляет итоговую ковариационную матрицу K как простую сумму ковариационных матриц, возвращаемых каждым дочерним ядром. Здесь работает принцип полиморфизма: несмотря на то, что массив kernels хранит указатели базового типа IKernel*, вызов kernels[i].Compute(X1, X2) фактически вызывает специфическую реализацию Compute для каждого конкретного дочернего ядра. Это позволяет SumKernel работать с любыми ядрами, унаследованными от IKernel.
- Метод ComputeDerivative — производная ковариационной функции суммы ядер по конкретному гиперпараметру равна производной ковариационной функции только того дочернего ядра, которому принадлежит данный гиперпараметр. Это означает, что ComputeDerivative находит соответствующее дочернее ядро по param_index и возвращает производную только от него. Производные по параметрам других дочерних ядер считаются равными нулю.
Класс ProductKernel
//+------------------------------------------------------------------+ //| Класс для произведения ядер | //+------------------------------------------------------------------+ class ProductKernel : public IKernel { private: IKernel* kernels[]; matrix m_X1; matrix m_X2; int n; int m; public: // Конструктор: копирует указатели на дочерние ядра ProductKernel(IKernel* &input_kernels[]) { ArrayResize(kernels, ArraySize(input_kernels)); ArrayCopy(kernels, input_kernels); } // Деструктор ~ProductKernel() { for (int i = 0; i < ArraySize(kernels); i++) { if (kernels[i] != NULL){ delete kernels[i]; } } ArrayFree(kernels); } matrix Compute(const matrix &X1, const matrix &X2) override { n = (int)X1.Rows(); m = (int)X2.Rows(); m_X1 = X1; m_X2 = X2; matrix product = matrix:: Ones(n,m); for (int i = 0; i < ArraySize(kernels); i++) { // Полиморфизм: вызываем метод Compute() каждого дочернего ядра, // независимо от его конкретного типа, и поэлементно умножаем результат product *= kernels[i].Compute(X1, X2); } return product; } matrix ComputeDerivative(int param_index) override { matrix dK_prod(n, m); // Итоговая матрица производной int current_param_offset = 0; int target_kernel_idx = -1; // Индекс ядра, которому принадлежит гиперпараметр int local_param_index = -1; // Локальный индекс гиперпараметра в этом ядре // Шаг 1: Находим ядро и локальный индекс гиперпараметра for (int i = 0; i < ArraySize(kernels); i++) { int num_params_current_kernel = kernels[i].GetNumHyperparameters(); if (param_index >= current_param_offset && param_index < current_param_offset + num_params_current_kernel) { target_kernel_idx = i; local_param_index = param_index - current_param_offset; break; } current_param_offset += num_params_current_kernel; } if (target_kernel_idx == -1) { Print("Error: ProductKernel::ComputeDerivative - Parameter index ", param_index, " out of bounds"); return matrix::Zeros(1, 1); } // Шаг 2: Вычисляем dK_k / d_theta_j для целевого ядра matrix dK_target_kernel = kernels[target_kernel_idx].ComputeDerivative(local_param_index); // Шаг 3: Вычисляем произведение K_m для всех остальных ядер (m != k) matrix other_kernels_product = matrix::Ones(n, m); for (int i = 0; i < ArraySize(kernels); i++) { if (i != target_kernel_idx) { // Пропускаем целевое ядро other_kernels_product = other_kernels_product * kernels[i].Compute(m_X1, m_X2); } } // Шаг 4: Поэлементно перемножаем результаты dK_prod = dK_target_kernel * other_kernels_product; return dK_prod; } // Собирает значения гиперпараметров всех дочерних ядер в один вектор vector GetHyperparameters() const override { vector all_params(GetNumHyperparameters()); int current_idx = 0; for (int i = 0; i < ArraySize(kernels); i++) { vector kernel_params = kernels[i].GetHyperparameters(); for (int j = 0; j < (int)kernel_params.Size(); j++) { all_params[current_idx + j] = kernel_params[j]; } current_idx += (int)kernel_params.Size(); } return all_params; } void SetHyperparameters(const vector ¶ms) override { int current_idx = 0; for (int i = 0; i < ArraySize(kernels); i++) { int num_params_kernel = kernels[i].GetNumHyperparameters(); vector sub_params(num_params_kernel); for (int j = 0; j < num_params_kernel; j++) { sub_params[j] = params[current_idx + j]; } kernels[i].SetHyperparameters(sub_params); current_idx += num_params_kernel; } } int GetNumHyperparameters() const override { int total_params = 0; for (int i = 0; i < ArraySize(kernels); i++) { total_params += kernels[i].GetNumHyperparameters(); } return total_params; } string GetName() const override { string name = "Prod("; for (int i = 0; i < ArraySize(kernels); i++) { name += kernels[i].GetName(); if (i < ArraySize(kernels) - 1) name += "*"; } name += ")"; return name; } //+------------------------------------------------------------------+ //| Предоставляет внешний доступ к списку дочерних ядер | //+------------------------------------------------------------------+ void GetKernels(IKernel* &output_kernels[]) const { ArrayCopy(output_kernels, kernels); } };
- Метод Compute: вычисляет итоговую ковариационную матрицу K как поэлементное произведение ковариационных матриц, возвращаемых каждым дочерним ядром. Как и в SumKernel, здесь используется полиморфизм для вызова метода Compute соответствующего дочернего ядра.
- Метод ComputeDerivative : для вычисления производной K по гиперпараметру, принадлежащему конкретному дочернему ядру K_p, ProductKernel применяет правило произведения (правило Лейбница). Производная K по данному параметру равна произведению производной матрицы K_p по этому параметру на поэлементное произведение ковариационных матриц всех остальных дочерних ядер, взятых без производной:
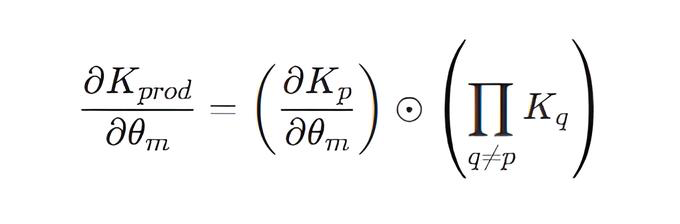
Интерфейс ILikelihood
Интерфейс ILikelihood определяет, как должна работать любая функция правдоподобия в нашей библиотеке. Он позволяет нам работать с разными видами данных — будь то непрерывные значения (как в регрессии) или дискретные категории (как в классификации).
//+------------------------------------------------------------------+ //|Интерфейс для функций правдоподобия | //+------------------------------------------------------------------+ interface ILikelihood { // Вычисляет логарифм правдоподобия p(y|f) для скрытых значений f и наблюдаемых y virtual double LogLikelihood(const vector &f, const vector &y) = 0; //----------------------------- Производные логарифма правдоподобия по f ----------------- // Вычисляет вектор первой производной логарифма правдоподобия по f (dlp/df) virtual vector LogLikelihoodGradient(const vector &f, const vector &y) = 0; // Вычисляет матрицу второй производной (Гессиан) логарифма правдоподобия по f (d^2lp/df df^T) virtual matrix LogLikelihoodHessian(const vector &f, const vector &y) = 0; // Вычисляет вектор третьей производной логарифма правдоподобия по f (d^3lp/df^3) virtual vector LogLikelihoodThirdDerivative(const vector &f, const vector &y) = 0; //----------------------------- Производные логарифма правдоподобия по параметрам ----------------- // Первая производная логарифма правдоподобия по j-му гиперпараметру правдоподобия. virtual double LogLikelihoodGradientParam(const vector &f, const vector &y, int param_index) = 0; // Производная Гессиана логарифма правдоподобия по j-му гиперпараметру правдоподобия. virtual matrix LogLikelihoodHessianDerivative(const vector &f, const vector &y, int param_index) = 0; // Возвращает имя функции правдоподобия virtual string GetName() const = 0; // Возвращает текущие значения гиперпараметров правдоподобия virtual vector GetHyperparameters() const = 0; // Устанавливает новые значения гиперпараметров правдоподобия virtual void SetHyperparameters(const vector ¶ms) = 0; // Возвращает количество гиперпараметров правдоподобия virtual int GetNumHyperparameters() const = 0; };
Класс GaussianLikelihood
GaussianLikelihood реализует функцию правдоподобия для задач регрессии, предполагая нормальный шум в наблюдаемых данных.
//+------------------------------------------------------------------+ //| Класс Гауссовского правдоподобия (для задач регрессии) | //+------------------------------------------------------------------+ class GaussianLikelihood : public ILikelihood { private: double m_noise_sigma; // Параметр шума (стандартное отклонение) public: // Конструктор GaussianLikelihood(double initial_noise_sigma) : m_noise_sigma(initial_noise_sigma) {} // Возвращает текущее значения гиперпараметра vector GetHyperparameters() const override { vector params(1); params[0] = m_noise_sigma; return params; } // Устанавливает новое значения гиперпараметра void SetHyperparameters(const vector ¶ms) override { if (params.Size() == 1) { m_noise_sigma = params[0]; } } // Возвращает количество гиперпараметров int GetNumHyperparameters() const override { return 1; } // Вычисляет логарифм правдоподобия log p(y|f) для гауссовского распределения double LogLikelihood(const vector &f, const vector &y) override { int n = (int)y.Size(); double noise_variance = m_noise_sigma * m_noise_sigma; vector residual = y - f; // Формула логарифма плотности многомерного нормального распределения return -0.5 / noise_variance * (residual @ residual) - 0.5 * n * MathLog(2 * M_PI * noise_variance); } //------------------ Производные по f ----------------------- // Вычисляет вектор первой производной логарифма правдоподобия по f (dlp/df) vector LogLikelihoodGradient(const vector &f, const vector &y) override { // d(log p(y|f))/df = (y - f) / sigma^2 return (y - f) / (m_noise_sigma * m_noise_sigma); } // Вычисляет матрицу второй производной (Гессиан) логарифма правдоподобия по f (d^2lp/dfdf^T) matrix LogLikelihoodHessian(const vector &f, const vector &y) override { // d^2(log p(y|f))/dfdf^T = -1/sigma^2 * I int n = (int)y.Size(); return matrix::Identity(n, n) * (-1.0 / (m_noise_sigma * m_noise_sigma)); } // Вычисляет вектор третьей производной логарифма правдоподобия по f vector LogLikelihoodThirdDerivative(const vector &f, const vector &y) override { // Для Гауссовского правдоподобия d^3(log p(y|f))/df^3 = 0 return vector::Zeros((int)y.Size()); } // ------------------------------ Производные по параметру ----------------------------------- // // Вычисляет первую производную логарифма правдоподобия по j-му гиперпараметру правдоподобия virtual double LogLikelihoodGradientParam(const vector &f, const vector &y, int param_index) override { // Гауссовское правдоподобие имеет только 1 гиперпараметр: m_noise_sigma (индекс 0) if (param_index == 0) { // Формула для d(log p(y|f))/d(sigma_n): // = (y-f)^T(y-f) / sigma_n^3 - N / sigma_n vector y_minus_f = y - f; double sn3 = m_noise_sigma * m_noise_sigma * m_noise_sigma; double term1 = (y_minus_f @ y_minus_f) / sn3; double term2 = y.Size() / m_noise_sigma; // N / sigma_n return term1 - term2; } else { return 0.0; } } // Вычисляет производную Гессиана логарифма правдоподобия по j-му гиперпараметру правдоподобия matrix LogLikelihoodHessianDerivative(const vector &f, const vector &y, int param_index) override { int n = (int)y.Size(); if (param_index == 0) { // Производная Hessian по m_noise_sigma: d/d(sigma_n) [-1/sigma_n^2 * I] = (2/sigma_n^3) * I double derivative_coeff = 2.0 / (m_noise_sigma * m_noise_sigma * m_noise_sigma); return matrix::Identity(n, n) * derivative_coeff; } else { return matrix::Zeros(n, n); } } string GetName() const override { return "GaussianLikelihood"; } };
Ключевые методы:
- Конструктор GaussianLikelihood — инициализирует единственный гиперпараметр — стандартное отклонение шума.
- LogLikelihood() — вычисляет логарифм правдоподобия p(y∣f) для плотности вероятности многомерного нормального распределения:
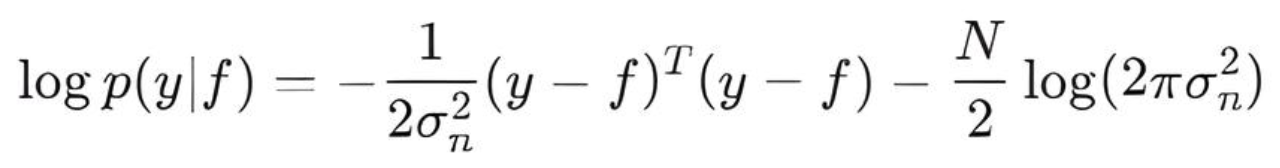
- LogLikelihoodGradient() — вычисляет первую производную логарифма правдоподобия по скрытым значениям f. Это вектор, где каждый элемент равен:
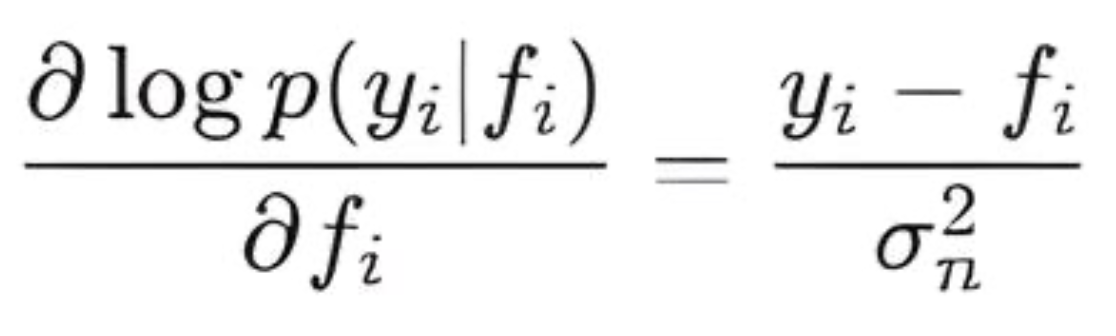
- LogLikelihoodHessian() — вычисляет вторую производную (Гессиан) логарифма правдоподобия по f. Для Гауссовского правдоподобия Гессиан является диагональной матрицей:
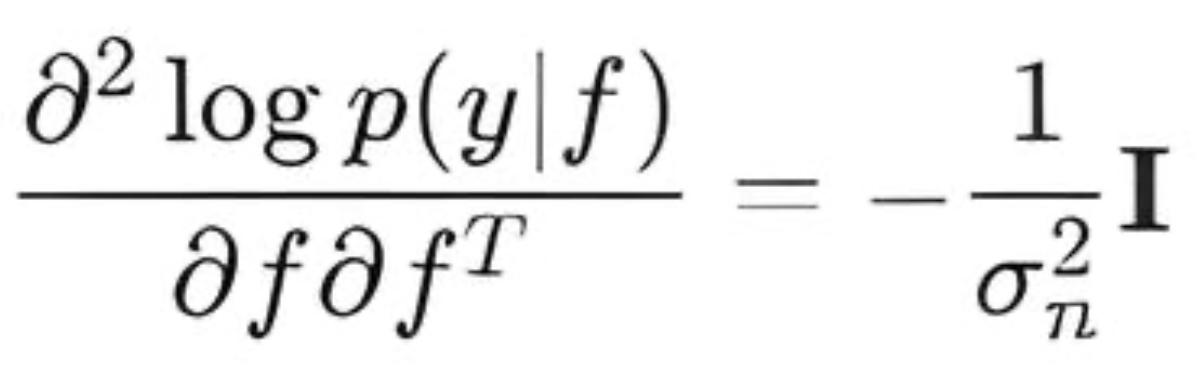
- LogLikelihoodThirdDerivative() — вычисляет третью производную. Для Гауссовского правдоподобия все производные выше второй равны нулю
- LogLikelihoodGradientParam() — вычисляет первую производную логарифма правдоподобия по гиперпараметру m_noise_sigma:
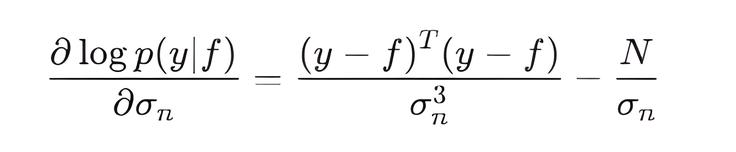
- LogLikelihoodHessianDerivative() — вычисляет производную Гессиана логарифма правдоподобия по гиперпараметру m_noise_sigma:
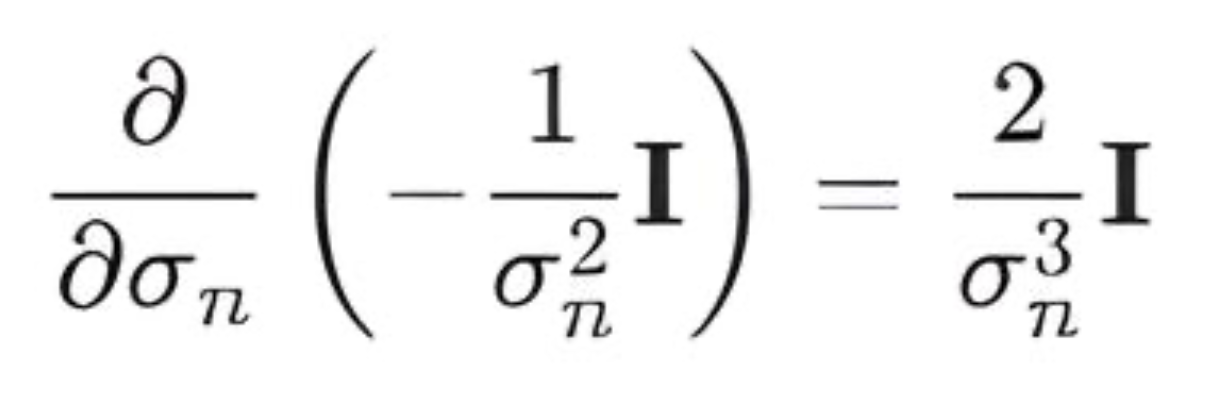
Класс LogitLikelihood
LogitLikelihood используется для бинарной классификации, где наблюдаемые целевые значения y принимают значения {−1,+1}. Оно связывает скрытую функцию f с вероятностью принадлежности к классу через сигмоидную функцию.
В реализации LogitLikelihood предусмотрены вспомогательные функции sigmoid() и Softplus() с проверками на большие/малые входные значения.
//+------------------------------------------------------------------+ //| Класс для Логит-правдоподобия (y {-1, +1}) | //+------------------------------------------------------------------+ class LogitLikelihood : public ILikelihood { public: // logit_sigmoid(x) = 1 / (1 + exp(-x)) double sigmoid(double x) const { if (x > 100.0) return 1.0; // Избегаем появления NaN if (x < -100.0) return 0.0; return 1.0 / (1.0 + MathExp(-x)); } // Функция Softplus log(1 + exp(x)) double Softplus(double x) const { if (x > 100.0) return x; // Для очень больших x, log(1 + exp(x)) ~ x if (x < -100.0) return MathExp(x); // Для очень маленьких x, log(1 + exp(x)) ~ exp(x) return MathLog(1.0 + MathExp(x)); } public: // Конструктор (логит-правдоподобие не имеет собственных гиперпараметров) LogitLikelihood() {} vector GetHyperparameters() const override { return vector::Zeros(0); } void SetHyperparameters(const vector ¶ms) override {} // Возвращает количество гиперпараметров правдоподобия int GetNumHyperparameters() const override { return 0; } // --- Вычисляет логарифм правдоподобия: log p(y|f) --- // Формула: sum_i (-log(1 + exp(-y_i * f_i))) double LogLikelihood(const vector &f, const vector &y) override { int n = (int)y.Size(); double total_log_likelihood = 0.0; for (int i = 0; i < n; i++) { total_log_likelihood += -Softplus(-y[i] * f[i]); } return total_log_likelihood; } // Вычисляет градиент логарифма правдоподобия по f // Формула: d(log p(y_i|f_i))/df_i = y_i * sigma(-y_i * f_i) vector LogLikelihoodGradient(const vector &f, const vector &y) override { int n = (int)y.Size(); vector grad(n); for (int i = 0; i < n; i++) { grad[i] = y[i] * sigmoid(-y[i] * f[i]); // grad[i] = y[i] * (1 - sigmoid(y[i] * f[i])); эквивалентно } return grad; } // Вычисляет Гессиан логарифма правдоподобия по f (диагональная матрица H) // Формула: d^2(log p(y_i|f_i))/df_i^2 = -sigma(y_i*f_i)(1 - sigma(y_i*f_i)) matrix LogLikelihoodHessian(const vector &f, const vector &y) override { int n = (int)y.Size(); matrix H = matrix::Identity(n, n); for (int i = 0; i < n; i++) { double sig = sigmoid(y[i] * f[i]); H[i][i] = -1*sig * (1.0 - sig); } return H; } // Вычисляет третью производную логарифма правдоподобия по f // Формула: d^3(log p(y_i|f_i))/df_i^3 = y_i * sigma(-y_i f_i) * (1 - sigma(-y_i f_i)) * (1 - 2*sigma(-y_i f_i)) vector LogLikelihoodThirdDerivative(const vector &f, const vector &y) override { int n = (int)y.Size(); vector third_deriv(n); for (int i = 0; i < n; i++) { double sig_neg_yf = sigmoid(-y[i] * f[i]); third_deriv[i] = y[i] * sig_neg_yf * (1.0 - sig_neg_yf) * (1.0 - 2.0 * sig_neg_yf); // эквивалентно // double sig_yf = sigmoid(y[i] * f[i]); // third_deriv[i] = -y[i] * sig_yf * (1.0 - sig_yf) * (1.0 - 2.0 * sig_yf); } return third_deriv; } // LogitLikelihood не имеет гиперпараметров virtual double LogLikelihoodGradientParam(const vector &f, const vector &y, int param_index) override { return 0.0; } // LogitLikelihood не имеет гиперпараметров matrix LogLikelihoodHessianDerivative(const vector &f_latent, const vector &y, int param_index) override { int n = (int)y.Size(); return matrix::Zeros(n, n); } string GetName() const override { return "LogitLikelihood"; } };
Ключевые методы:
- LogLikelihood() — вычисляет логарифм правдоподобия logp(y∣f). Для бинарной классификации с y {−1,+1} это сумма логарифмов бинарного кросс-энтропийного правдоподобия:
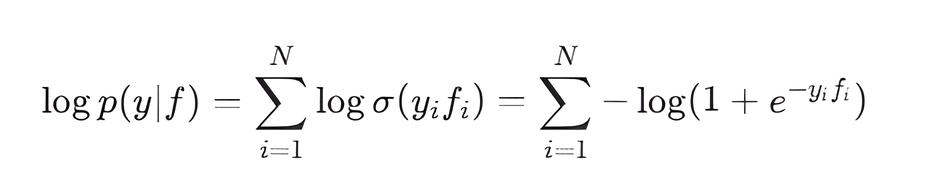
- LogLikelihoodGradient() — вычисляет первую производную логарифма правдоподобия по f. Каждый элемент вектора градиента равен:
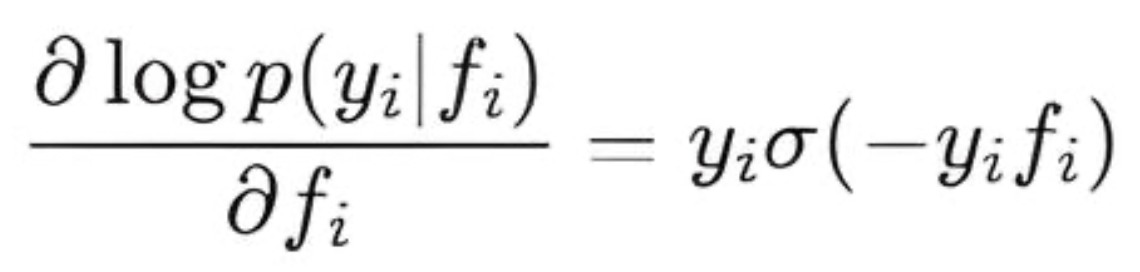
- LogLikelihoodHessian() — вычисляет вторую производную (Гессиан) логарифма правдоподобия по f. Для LogitLikelihood Гессиан является диагональной матрицей, где диагональные элементы равны:
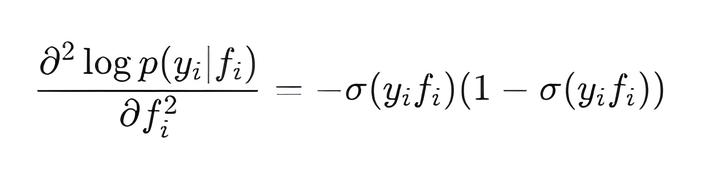
- LogLikelihoodThirdDerivative() — вычисляет третью производную логарифма правдоподобия по f. Каждый элемент вектора равен:
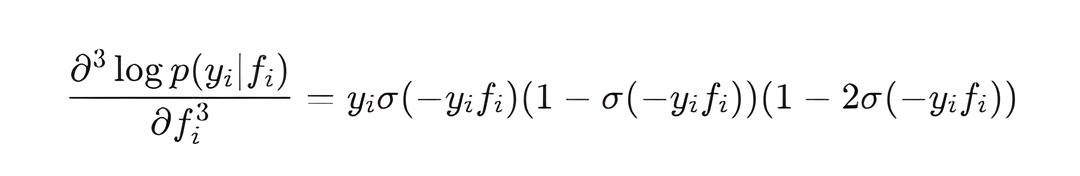
Вспомогательные функции и структуры
Файл StructUtils.mqh содержит набор перечислений, структур данных и функций, которые облегчают работу с ГП.
enum PredictMode { PROBIT = 0, // Probit Approximation NUM_INTEGR = 1, // Numerical integration MONTE_CARLO = 2 // Monte Carlo }; //--- Структура для результатов предсказания struct GPPredictionResult { vector mu_f_star; // Апостериорное среднее для скрытой функции f* на новых данных matrix Sigma_f_star; // Апостериорная ковариация для скрытой функции f* на новых данных // Поля только для регрессии (GaussianLikelihood) vector mu_y_star; // Апостериорное среднее наблюдений y* matrix Sigma_y_star; // Апостериорная ковариация наблюдений y* // Поля только для классификации (LogitLikelihood, ProbitLikelihood и т.д.) vector predicted_probabilities; // Вероятности p(y*=+1 | X*, D) vector predicted_labels; // Предсказанные метки y* (+1 или -1) }; // Структура для результата инференса struct GPInferenceResult { double nlml_value; // Отрицательный логарифм маргинального правдоподобия vector nlml_gradient; // Градиент NLML по гиперпараметрам ядра и правдоподобия // Результаты инференса на обучающих данных: vector mu_f_train; // Апостериорное среднее скрытой функции f на обучающих данных matrix Sigma_f_train; // Апостериорная ковариация скрытой функции f на обучающих данных (K^−1+W)^−1 matrix L_K_noisy; // Разложение Холецкого K_noisy = cholesky(K + s2n*I) matrix L_B; // Разложение Холецкого B = I + W^0.5 @ K @ W^0.5 matrix sW; // sW = W^0.5; vector sW_diag; // диагональ sW matrix sW_K; // sW @ K vector alpha; // (K_noisy)^-1 * y matrix H; // Гессиан логарифма правдоподобия d^2 log p(y|f)/df^2 (для LaplaceInference) bool success; // Флаг успешности функции инференса };
- Перечисление PredictMode определяет различные режимы для выполнения предсказаний в модели классификации.
- Структура GPInferenceResult используется для хранения всех ключевых результатов, полученных в процессе инференса.
- Структура GPPredictionResult предназначена для хранения всех результатов, полученных после выполнения предсказания на новых (тестовых) данных (X_test)
- DiagonalTrace
//+-------------------------------------------------------------------+ //| Вычисляет след произведения двух матриц, используя только | //| диагональные элементы итоговой матрицы | //+-------------------------------------------------------------------+ double DiagonalTrace(const matrix &A, const matrix &B) { ulong m = A.Rows(); ulong n = A.Cols(); ulong n_b = B.Rows(); ulong p = B.Cols(); // Находим минимальный размер для диагонали ulong k = MathMin(m, p); double tr = 0.0; for(ulong i = 0; i < k; i++) { // Скалярное произведение i-й строки A и i-го столбца B tr += A.Row(i)@B.Col(i); } return tr; }
Вычисляет след произведения двух матриц A и B (Tr(A @ B)) без необходимости формирования всей матрицы произведения. Она делает это, суммируя скалярные произведения строк матрицы A и соответствующих столбцов матрицы B. Это позволяет значительно снизить вычислительные затраты по сравнению с полным умножением матриц.
- cho_solve (обёртка OpenBLAS LinearEquationsSolutionTriangular)
//+------------------------------------------------------------------+ //| Решает систему A*X = B, используя разложение Холецкого A = LL^T | //| Параметры: | //| c: Нижняя треугольная матрица L из разложения Холецкого | //| b: правая часть системы (матрица) | //| Возвращает: матрица X - решение системы | //+------------------------------------------------------------------+ matrix cho_solve(const matrix &c, const matrix &b) { // Проверка, является ли матрица 'c' нижней треугольной if (!c.IsLowerTriangular()) { Print("Error: cho_solve - Input matrix 'c' is not lower triangular."); return matrix::Zeros(c.Rows(), b.Cols()); } // Шаг 1: Решаем L * Y = B // Y - промежуточная матрица, результат решения L^-1 * B matrix Y; if (!c.LinearEquationsSolutionTriangular(EQUATIONSFORM_N, b, Y)) { PrintFormat("Error: cho_solve- LinearEquationsSolutionTriangular L * Y = B failed. Error Code: %d", GetLastError()); return matrix::Zeros(c.Rows(), b.Cols()); } // Шаг 2: Решаем L^T * X = Y // X - решение системы L^T * X = Y, что эквивалентно (L^T)^-1 * Y matrix X; if (!c.LinearEquationsSolutionTriangular(EQUATIONSFORM_T, Y, X)) { PrintFormat("Error: cho_solve- LinearEquationsSolutionTriangular L^T * X = Y failed. Error Code: %d", GetLastError()); return matrix::Zeros(c.Rows(), b.Cols()); } return X; } //+------------------------------------------------------------------+ //| Решает систему Ax = b, используя разложение Холецкого A = LL^T | //| Параметры: | //| c: Нижняя треугольная матрица L из разложения Холецкого | //| b: правая часть системы (вектор) | //| Возвращает: вектор x - решение системы | //+------------------------------------------------------------------+ vector cho_solve(const matrix &c, const vector &b) { // Проверка, является ли матрица c нижней треугольной if (!c.IsLowerTriangular()) { Print("Error: cho_solve - Input matrix 'c' is not lower triangular"); return vector::Zeros(c.Rows()); } // Шаг 1: Решаем L * y = b // y - промежуточный вектор, результат решения L^-1 * b vector y; if (!c.LinearEquationsSolutionTriangular(EQUATIONSFORM_N, b, y)) { PrintFormat("Error: cho_solve- LinearEquationsSolutionTriangular L * y = b failed. Error Code: %d", GetLastError()); return vector::Zeros(c.Rows()); } // Шаг 2: Решаем L^T * x = y // x - конечное решение системы L^T * x = y, что эквивалентно (L^T)^-1 * y vector x; if (!c.LinearEquationsSolutionTriangular(EQUATIONSFORM_T, y, x)) { PrintFormat("Error: cho_solve- LinearEquationsSolutionTriangular L^T * x = y failed. Error Code: %d", GetLastError()); return vector::Zeros(c.Rows()); } return x; }
Функция cho_solve — предназначена для эффективного решения систем линейных уравнений Ax=b (или AX=B для матричного B), где матрица A получена из её разложения Холецкого A=LL^T. Здесь L — нижняя треугольная матрица.
Прямое вычисление A^−1 (A.Inv()) требует много ресурсов и может быть численно нестабильным. Разложение Холецкого, напротив, предлагает значительно более эффективный и надёжный подход.
Внутри cho_solve выполняются две основные операции:
- Прямое замещение: решается система LY=B (или Ly=b), где L – это входная матрица c, а Y (или y) – промежуточный результат. Поскольку L является треугольной матрицей, это решение является относительно быстрым.
- Обратное замещение: затем решается система L^TX=Y (или L^Tx=y), где L^T – это транспонированная матрица L. Это также эффективно, поскольку L^T является верхней треугольной матрицей.
Эти операции реализуются с помощью функций LinearEquationsSolutionTriangular из высокопроизводительной библиотеки линейной алгебры OpenBLAS. Это обеспечивает значительное ускорение вычислений, что делает их незаменимыми для ресурсоёмких моделей машинного обучения, таких как Гауссовские процессы.
Интерфейс IInference
interface IInference { // Этот метод выполняет инференс (вывод апостериорного распределения f) // и возвращает компоненты, необходимые для NLML и предсказания virtual void Infer(const matrix &X, const vector &y, IKernel *kernel, ILikelihood *likelihood,GPInferenceResult &result) = 0; virtual string GetName() const = 0; };
Интерфейс позволяет переключаться между различными методами вывода, такими как точный инференс для гауссовского правдоподобия и приближенные методы для не-гауссовых случаев, без изменения основной логики GaussianProcess.
Метод Infer является центральным в этом интерфейсе. Он выполняет вывод апостериорного распределения скрытой функции f и возвращает компоненты, необходимые для дальнейших расчетов (NLML и предсказания). Принимает следующие аргументы:
- X — матрица обучающих признаков,
- y — вектор обучающих меток,
- kernel — указатель на объект Ikernel,
- likelihood — указатель на объект ILikelihood,
- result — ссылка на структуру GPInferenceResult, которая используется для хранения всех результатов инференса, включая:
- отрицательный логарифм маргинального правдоподобия (NLML), необходимый для оптимизации гиперпараметров,
- вектор градиентов NLML по всем гиперпараметрам ядра и правдоподобия,
- вспомогательные матрицы и векторы: (L_K_noisy, L_B, sW, mu_f_train, Sigma_f_train, alpha)используемые для вычисления градиентов NLML и последующего предсказания новых данных.
Класс ExactInference
//+------------------------------------------------------------------+ //| ExactInference Только для гауссовского правдоподобия | //+------------------------------------------------------------------+ class ExactInference : public IInference { public: ExactInference() {} void Infer(const matrix &X, const vector &y, IKernel *kernel, ILikelihood *likelihood,GPInferenceResult &result) override { if(likelihood.GetName() != "GaussianLikelihood") { Print("ExactInference supports only GaussianLikelihood"); result.nlml_value = DBL_MAX; return; } result.success = false; int n = (int)y.Size(); // Вычисление K с текущими параметрами ядра matrix K = kernel.Compute(X, X); // Получаем дисперсию шума vector likelihood_params = likelihood.GetHyperparameters(); double sigma = likelihood_params[0]; double variance = sigma * sigma; double jitter = 1e-6; matrix K_noisy = K + matrix::Identity(n, n) * (variance + jitter); if(!K_noisy.Cholesky(result.L_K_noisy)) { PrintFormat("Error: Cholesky decomposition failed. Error Code: %d",GetLastError()); result.nlml_value = DBL_MAX; return; } //------------- Algorithm 2.1 GPML --------------------------- //Вычисляем alpha (K_noisy^-1 * y) - O(N^2) result.alpha = cho_solve(result.L_K_noisy, y); //+------------------------------------------------------------------+ //| NLML = 0.5y^T(K+σ^2*I)^-1*y + 0.5*log|K+σ^2*I| +n/2*Log(2π) | //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| NLML = 0.5y^T*alpha + 0.5*log|K+σ^2*I| +n/2*Log(2π) | //+------------------------------------------------------------------+ // --- Вычисляем первое слагаемое в формуле NLML : double data_term = 0.5 * (y @ result.alpha); // --- Вычисляем второе слагаемое: 1/2 * log|K + sigma^2*I| = sum(log(L_ii)) double log_det = MathLog(result.L_K_noisy.Diag()).Sum(); // --- Вычисляем третье слагаемое: n/2 * log(2π) double const_term = 0.5 * n * MathLog(2 * M_PI); //--- NLML result.nlml_value = data_term + log_det + const_term; // -------------------- Вычисления градиентов NLML -------------------------------------- result.nlml_gradient.Resize(kernel.GetNumHyperparameters() + likelihood.GetNumHyperparameters()); int current_grad_idx = 0; // Вычисление (K_noisy^-1) matrix K_noisy_inv = cho_solve(result.L_K_noisy, matrix::Identity(n, n)); // 1. Градиенты по гиперпараметрам ядра vector kernel_hyperparams = kernel.GetHyperparameters(); // Вычисляем aatK_noisy_inv один раз до цикла - O(N^2) matrix aatK_noisy_inv = result.alpha.Outer(result.alpha) - K_noisy_inv; matrix dK_dtheta; for(int i = 0; i < (int)kernel_hyperparams.Size(); i++) { dK_dtheta = kernel.ComputeDerivative(i); // O(N^2) result.nlml_gradient[current_grad_idx] = -0.5 * DiagonalTrace(aatK_noisy_inv, dK_dtheta); current_grad_idx++; } // 2. Градиент по гиперпараметру шума // dNLML/d(sigma^2) = 0.5 * (trace(K_noisy^-1) - alpha^T * alpha ) double dNLML_d_sigma2n = 0.5 * (K_noisy_inv.Trace() - result.alpha @ result.alpha); result.nlml_gradient[current_grad_idx] = dNLML_d_sigma2n * (2.0 * sigma); result.success = true; } string GetName() const override { return "ExactInference"; } };
Класс ExactInference предназначен для выполнения точного вывода в ГП и применим только при использовании гауссовского правдоподобия. Основное внимание в его реализации уделено эффективному вычислению NLML и его аналитических градиентов. Аналитические градиенты, вычисляемые напрямую по формулам, обеспечивают более высокую точность и значительно ускоряют процесс оптимизации по сравнению с численными методами.
Алгоритм инференса состоит из нескольких ключевых шагов:
- Формирование ковариационной матрицы Knoisy: cначала вычисляется матрица ковариации ядра K для обучающих данных. Затем к диагональным элементам K добавляется дисперсия шума (variance = sigma * sigma) и небольшое положительное значение jitter (1e-6). Это формирует матрицу Knoisy;
- Вычисление вектора αlpha;
- Расчет отрицательного логарифма маргинального правдоподобия (NLML);
- Вычисление градиентов NLML для оптимизации.
Для вычисления необходимых градиентов и самого NLML требуются обратная матрица ковариации (K+σ2*I)^−1 и вектор α=(K+σ2*I)^−1 * y.
Функция cho_solve помогает рассчитать эти переменные максимально быстро.
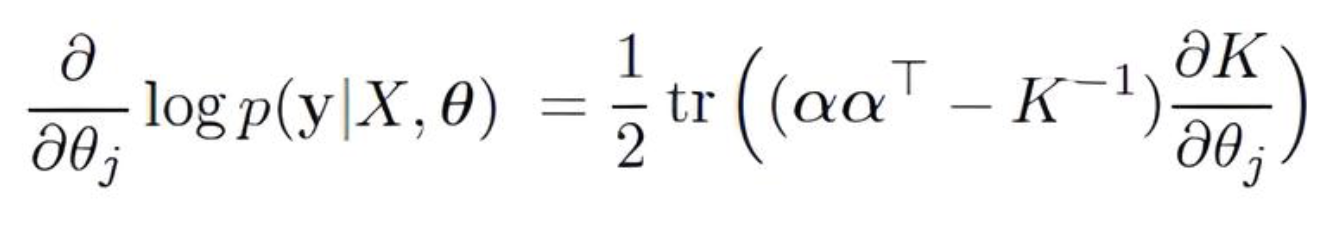
Класс LaplaceInference
LaplaceInference реализует Лапласовское приближение — метод приближённого вывода, применимый как к задачам регрессии, так и классификации в ГП.
//+------------------------------------------------------------------+ //| LaplaceInference | //+------------------------------------------------------------------+ class LaplaceInference : public IInference { private: int m_max_iterations; double m_tolerance; public: LaplaceInference(int max_iter = 100, double tolerance = 1e-10) : m_max_iterations(max_iter), m_tolerance(tolerance) {} void Infer(const matrix &X_train, const vector &y, IKernel *kernel, ILikelihood *likelihood, GPInferenceResult &result) override { result.success = false; int n = (int)y.Size(); // Вычисление K matrix K = kernel.Compute(X_train, X_train); double jitter = 1e-6; K = K + matrix::Identity(n, n) * jitter; vector f = (result.mu_f_train.Size() == n) ? result.mu_f_train : vector::Zeros(n); bool converged = false; matrix W(n, n); // W := -Hessian matrix L_B(n, n); // L := cholesky(I + W^0.5*K*W^0.5), B = I + W^0.5*K*W^0.5 vector b(n); // b := Wf + grad loglike p(y|f) vector a(n); // a := b - W^0.5*L^T\(L\(W^0.5*K*b)) matrix sW = matrix::Zeros(n, n); // W^0.5 vector sW_diag(n); // вектор для хранения диагональных элементов sqrt(W) double prev_lml_value = -DBL_MAX; // Для критерия сходимости по LML double current_lml_value = -DBL_MAX; int iter; // --- Шаг 1: Нахождение моды f_hat методом Ньютона (Согласно Алгоритму 3.1 GPML) --- for(iter = 0; iter < m_max_iterations; iter++) { // 1. W := - Hessian (диагональная матрица) W = -1 * likelihood.LogLikelihoodHessian(f, y); // Вычисление sW_diag_vector (корень из W) sW_diag = MathSqrt(W.Diag()); // 2. L_B := cholesky(I + W^0.5*K*W^0.5) // Вычисляем sW_K = sW * K result.sW_K.Resize(n, n); for(int i = 0; i < n; i++) { result.sW_K.Row(sW_diag[i] * K.Row(i),i); // K[i,:] * sW_diag_vector[i] } // Вычисляем B = I + sW_K * sW matrix temp_sWKsW(n, n); for(int j = 0; j < n; j++) { temp_sWKsW.Col(result.sW_K.Col(j)*sW_diag[j],j) ; // sW_K[:,j] * sW_diag_vector[j] } matrix B = matrix::Identity(n, n) + temp_sWKsW; if(!B.Cholesky(L_B)) { PrintFormat("Error:Cholesky decomposition of B failed. Error Code: %d", GetLastError()); result.nlml_value = DBL_MAX; return; } result.L_B = L_B; // Сохраняем для использования в прогнозах // 3. b := W*f + grad loglike p(y|f) b = W.Diag() * f + likelihood.LogLikelihoodGradient(f, y); // 4. a := b - W^0.5*L_B^T\(L_B\(W^0.5*K*b)) a = b - sW_diag*cho_solve(L_B,result.sW_K @ b); // 5. f := K * a (новый ньютоновский шаг) f = K @ a; // --- Вычисление текущего NLML для критерия сходимости --- double log_likelihood_at_f = likelihood.LogLikelihood(f, y); double sum_log_diag_L_B = MathLog(L_B.Diag()).Sum(); current_lml_value = -0.5 * a @ f + log_likelihood_at_f - sum_log_diag_L_B; result.nlml_value = -current_lml_value; // 6. Проверка сходимости double lml_change = current_lml_value - prev_lml_value; // PrintFormat("Iter %d: LML = %g, delta LML = %g",iter, current_lml_value, lml_change); // Проверка сходимости по LML if((lml_change < m_tolerance)) { // PrintFormat("Converged at iter %d: LML = %g, delta LML = %g",iter, current_lml_value, lml_change); converged = true; break; } prev_lml_value = current_lml_value; } if(!converged) { PrintFormat("Warning: Newton algorithm didn't converge at iteration %d. Final LML: %g (delta: %g, tolerance: %g)", iter, current_lml_value, (current_lml_value - prev_lml_value), m_tolerance); } //---Сохраняем в структуру GPInferenceResult result.mu_f_train = f; // Апостериорное среднее скрытой функции в обучающих точках result.H = likelihood.LogLikelihoodHessian(f, y); // Гессиан в точке f_hat // --- Вычисления аналитических градиентов NLML Алгоритм 5.1 GPML --- result.nlml_gradient.Resize(kernel.GetNumHyperparameters() + likelihood.GetNumHyperparameters()); int current_grad_idx = 0; // ============================================================================== // 1. Градиенты по гиперпараметрам ЯДРА // ============================================================================== // Вычисление R := W^0.5*L_B^-T*(L_B^-1*W^0.5) result.sW.Diag(sW_diag); matrix R(n,n); matrix cs = cho_solve(L_B,result.sW); for(int i = 0; i < n; i++) { R.Row(sW_diag[i] * cs.Row(i),i); } // Вычисление C := L_B^-1 * W^0.5 * K // Для этого решаем линейное уравнение: L_B * C = sW * K относительно C matrix C; if(!L_B.LinearEquationsSolutionTriangular(EQUATIONSFORM_N,result.sW_K, C)) { PrintFormat("Error: LinearEquationsSolutionTriangular L_B * C = W^0.5 * K.Error Code: %d", GetLastError()); result.nlml_value = DBL_MAX; return; } // Вычисление A = Sigma_f_train = (K^−1+W)^−1 = K - C^T @ C // Sigma_f_train - апостериорная ковариационная матрица скрытой функции f на обучающих данных matrix CTC = C.Transpose() @ C; result.Sigma_f_train = K - CTC; //------------------- grad NLML = -(s1 + s2^T*s3) // Вычисление s2 (первая неявная часть) // s2 := -0.5 * diag( diag(K) - diag(C^T*C) ) * ThirdDerivative loglike по f vector third_deriv = likelihood.LogLikelihoodThirdDerivative(f, y); //matrix diag; //diag.Diag(K.Diag() - CTC.Diag()); //vector s2 = -0.5 * diag @ third_deriv; vector s2 = -0.5 * (result.Sigma_f_train.Diag() * third_deriv); // Предварительно вычислим градиент логарифма правдоподобия vector log_lik_gradient = likelihood.LogLikelihoodGradient(f, y); int num_kernel_hyperparameters = kernel.GetNumHyperparameters(); for(int j = 0; j < num_kernel_hyperparameters; j++) { // C2 := dK_dtheta_j (производная матрицы ядра по текущему гиперпараметру) matrix dK_dtheta_j = kernel.ComputeDerivative(j); ///------------------------------------------------------------------------------------- // s1 := 0.5*a^T*C2*a - 0.5 *trace (R*C2) // явная часть производной double s1_term1 = 0.5 * (a @(dK_dtheta_j @ a)); // 0.5 * a^T * dK_dtheta_j * a // matrix R_dK_dtheta_j = R @ dK_dtheta_j; // double s1_term2 = -0.5 * R_dK_dtheta_j.Trace(); // -0.5 * trace(R * dK_dtheta_j) double s1_term2 = -0.5 * DiagonalTrace(R,dK_dtheta_j); // более эффективный вариант double s1_explicit_part = s1_term1 + s1_term2; ///-------------------------------------------------------------------------------------- // b := C2 * grad loglike vector b = dK_dtheta_j @ log_lik_gradient; // s3 := b - K * R * b // вторая неявная часть vector s3 = b - K @(R @ b); double implicit_part = s2 @ s3; // неявная часть производной // NLML result.nlml_gradient[current_grad_idx] = -(s1_explicit_part + implicit_part); current_grad_idx++; } // ============================================================================== // 2. Градиент по гиперпараметрам ПРАВДОПОДОБИЯ dLogLikelihood/d(param_j) // ============================================================================== if(likelihood.GetNumHyperparameters() > 0) { vector likelihood_hyperparams = likelihood.GetHyperparameters(); for(int j = 0; j < (int)likelihood_hyperparams.Size(); j++) { // Term 1: Производная log p(y|f*) по sigma double dlogpy_d_param_j = likelihood.LogLikelihoodGradientParam(f, y, j); // (метод возвращает dHessian/d(param_j) = d^3(log p)/d(param_j)d(f)^2) matrix dH_param_j = likelihood.LogLikelihoodHessianDerivative(f, y, j); // Преобразуем dH_d_param_j в dW_d_param_j (где W = -H) matrix dW_d_param_j = -1.0 * dH_param_j; double term2_lik = -0.5*DiagonalTrace(result.Sigma_f_train,dW_d_param_j); result.nlml_gradient[current_grad_idx] = -(dlogpy_d_param_j + term2_lik); current_grad_idx++; } } result.success = true; } string GetName() const override { return "LaplaceInference"; }
Конструктор LaplaceInference(int max_iter = 100, double tolerance = 1e-10): конструктор класса позволяет инициализировать параметры итерационного метода Ньютона, который используется для поиска моды апостериорного распределения.
- max_iter — максимальное количество итераций, после которых алгоритм остановится, даже если сходимость не достигнута.
- tolerance — уровень сходимости. Алгоритм прекратит итерации, если изменение значения NLML между последовательными шагами станет меньше этого порога.
Метод Infer реализует два ключевых алгоритма из книги "Gaussian Processes for Machine Learning" (GPML):
- Алгоритм 3.1 поиск моды апостериорного распределения и вычисления NLML,
- Алгоритм 5.1 вычисление градиентов NLML по гиперпараметрам.
Рис.1. Алгоритм 3.1для поиска моды f_hat и LML
- Процесс начинается с вычисления ковариационной матрицы ядра K. Для ускоренной и более стабильной сходимости, в качестве начального приближения f используется результат mu_f_train из предыдущей итерации оптимизации гиперпараметров, вместо того чтобы каждый раз начинать с нулевого вектора.
- Используя метод Ньютона, f_hat итерационно обновляется.
- Вычисление NLML: После сходимости моды f (когда изменение LML становится меньше m_tolerance), передаем значение NLML оптимизатору.
Рис.2. Алгоритм 5.1 Вычисление градиентов LML
- Градиенты по гиперпараметрам ядра включают вычисление вспомогательных матриц R и C. Матрица R вычисляется с использованием cho_solve, а матрица C — с помощью LinearEquationsSolutionTriangular.
- Вычисляется апостериорная ковариационная матрица скрытой функции на обучающих данных Σf_train = K−C^TC.
- Градиент для каждого гиперпараметра ядра (dK_dtheta_j) складывается из явной части (s1) и неявных частей (s2, s3). Вычисление s1оптимизировано за счёт использования DiagonalTrace, а s3 также включает cho_solve для решения систем.
- Градиенты по гиперпараметрам правдоподобия вычисляются с использованием производных логарифмического правдоподобия и его Гессиана по соответствующим гиперпараметрам. Для этого используются методы LogLikelihoodGradientParam и LogLikelihoodHessianDerivative объекта likelihood.
Теперь, когда у нас есть все базовые строительные блоки (ядра, правдоподобия, методы инференса), переходим к демонстрации работы библиотеки.
Тестирование библиотеки на синтетических данных
Скрипт Gpsynthetic.mq5 поможет нам протестировать нашу библиотеку на простых синтетических данных. Это позволит убедиться в работоспособности и корректности реализованных методов.
// --- Подключаем библиотеку GP --- #include <GP/GP.mqh> enum IntervalType { INTERVAL_F = 0, // Доверительный интервал скрытой функции f* INTERVAL_Y = 1 // Доверительный интервал наблюдений y* }; enum Type_inference { Exact = 0, // Exact Inference Laplace = 1 // Laplace Inference }; enum Type_Data { Regression = 0, // Regression Classification = 1 // Classification }; //--- Входные параметры input IntervalType interval_type = INTERVAL_F; // Тип интервала для отображения input Type_Data DataType = Classification; input Type_inference inf = Laplace ; // Тип инференса //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string InpFileName1; string InpFileName2; string InpFileName3; string InpFileName4; if(DataType == Regression) { // Данные для регрессии InpFileName1 = "Data_Regression/X_train.csv"; InpFileName2 = "Data_Regression/Y_train.csv"; InpFileName3 = "Data_Regression/X_test.csv"; InpFileName4 = "Data_Regression/Y_test.csv"; } else { InpFileName1 = "Data_Classification/X.csv"; // 200 InpFileName2 = "Data_Classification/y.csv"; InpFileName3 = "Data_Classification/X_star.csv"; InpFileName4 = "Data_Classification/y_star.csv"; } //----------- Dataset matrix x_train, y_train, x_test, y_test; CSVtoMatrix(InpFileName1,x_train); CSVtoMatrix(InpFileName2,y_train); CSVtoMatrix(InpFileName3,x_test); CSVtoMatrix(InpFileName4,y_test); // Создаем векторы меток из матриц vector y_train_ = y_train.Col(0); vector y_test_ = y_test.Col(0); //--- 1. Создание объектов ядер IKernel* rbf = new RBFKernel(1,1); // IKernel* linear = new LinearKernel(1.0); // IKernel* periodic = new PeriodicKernel(1.0, 1.0, 5.8); //--- 2. Комбинация ядер (создание составного ядра) // IKernel* functional_kernels_array[] = {rbf, linear, periodic}; // SumKernel* combined_functional_kernel = new SumKernel(functional_kernels_array); //--- 3. Создание объекта правдоподобия ILikelihood* likelihood = NULL; // Объявляем указатель базового типа if(DataType == Regression) { likelihood = new GaussianLikelihood(1); // Присваиваем объект } if(DataType == Classification) { likelihood = new LogitLikelihood(); } //--- 4. Создание объекта инференса IInference* inference; // Объявляем указатель на интерфейс // Выбираем тип инференса: if(inf == Exact) { inference = new ExactInference(); } else { inference = new LaplaceInference(100, 1e-10); } //--- 5. Создание экземпляра модели Гауссовского Процесса CREATE_GP_MODEL(gp_model, rbf, likelihood, inference,x_train, y_train_); // CREATE_GP_MODEL(gp_model, combined_functional_kernel, likelihood, inference,x_train, y_train_); //-------------------------------------------------- ulong start_time_fit = GetMicrosecondCount(); //--- 6. Оптимизация гиперпараметров gp_model.Fit(); ulong end_time_fit = GetMicrosecondCount(); double elapsed_time_ms = (end_time_fit - start_time_fit) / 1000.0; Print(inference.GetName()); Print("Время выполнения Fit: ", StringFormat("%.3f", elapsed_time_ms), " мс"); gp_model.PrintOptimizedKernelParameters(); //--- 7. Предсказание для тестовых точек GPPredictionResult gp_predictions; // создаем структуру куда будут записаны результаты предсказаний ulong start_time_predict = GetMicrosecondCount(); gp_model.Predict(x_test, gp_predictions,PROBIT); // MONTE_CARLO,NUM_INTEGR,PROBIT ulong end_time_predict = GetMicrosecondCount(); elapsed_time_ms = (end_time_predict - start_time_predict) / 1000.0; Print("Время выполнения Predict: ", StringFormat("%.3f", elapsed_time_ms), " мс"); // --- 8. Результаты Классификации if(DataType == Classification) { DisplayClassificationResults(gp_predictions, y_test_); } //--- 9. Результаты Регрессии if(DataType == Regression) { VisualizeGP(x_train, y_train, x_test, y_test_, gp_predictions, gp_model, 15); } //--- 10. Освобождение памяти delete gp_model; }
В зависимости от выбранного DataType (регрессия или классификация), скрипт определяет пути к CSV-файлам с обучающими и тестовыми данными. Предполагается, что эти файлы находятся в папках Data_Regression или Data_Classification в разделе Files.
Далее создаются объекты ядер. Для построения более сложной ковариационной функции можно использовать комбинированные ядра, такие как SumKernel или ProductKernel.
Затем создается объект функции правдоподобия (ILikelihood) в зависимости от выбранного DataType, а также объект инференса (IInference).
С помощью макроса CREATE_GP_MODEL (или аналогичного конструктора) создается модель ГП, связывающая выбранное ядро, функцию правдоподобия и метод инференса с обучающими данными.
Метод gp_model.Fit(int maxiter = 20) запускает процесс обучения модели. В методе появился новый параметр отвечающий за установку максимального количества итераций maxiter.
После завершения обучения, метод gp_model.Predict() используется для выполнения предсказаний на новых (тестовых) данных x_test. Результаты предсказаний (средние значения, ковариации, вероятности/метки) сохраняются в структуре GPPredictionResult.
Для классификации можно выбрать режим предсказания (PROBIT, NUM_INTEGR, MONTE_CARLO).
Затем скрипт выводит результаты предсказания:
- для классификации — вызывается функция DisplayClassificationResults(), которая рассчитывает метрику точности и предсказанные вероятности;
- для регрессии — функция VisualizeGP() отвечает за отрисовку результатов.
Для регрессии используются синтетические данные, сгенерированные функцией y = sin(x) + 0.5 * x + noise(sigma = 0.1). На этой задаче подробно останавливаться не будем, так как мы ее рассматривали в статье посвященной регрессии. Просто обратите внимание насколько улучшилось время обучения, благодаря тому, что мы перешли на использование аналитических градиентов и методов из библиотеки OpenBLAS.
Для бинарной классификации применяются данные, представляющие собой задачу XOR(исключающее ИЛИ). Это классическая задача в машинном обучении, которая демонстрирует ограничение линейных моделей и необходимость использования нелинейных подходов таких как ГП.
Вспомним, что XOR — это логическая операция, которая принимает два бинарных входа (0 или 1) и возвращает 1, если ровно один из входов равен 1 и 0 в противном случае. Таблица истинности XOR:
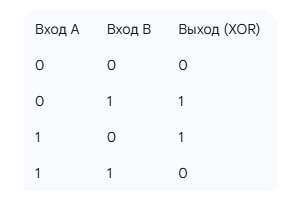
Задача бинарной классификации XOR заключается в том, чтобы построить модель, которая на основе двух входов (A, B) предсказывает их XOR-выход (0 и 1). Но так как наша модель работает только с метками «+1» и «-1», то мы заменим метку «0» на «-1».
Данные для задачи XOR генерируются следующим образом. Создаются двухмерные входные точки X (X=[x1,x2]), которые случайно распределены в некотором диапазоне (например, [−4,4] по каждой оси). Метки y для этих точек определяются на основе логики XOR:
- Если x1 и x2 имеют одинаковые знаки (оба положительны или оба отрицательны), то их произведение x1⋅x2 будет положительным. В этом случае метка присваивается +1.
- Если x1 и x2 имеют разные знаки (один положителен, другой отрицателен), то их произведение x1⋅x2 будет отрицательным. В этом случае метка присваивается −1.
Таким образом, точки (+,+) и (−,−) относятся к классу +1, а точки (+,−) и (−,+) — к классу −1. Для данной задачи будем использовать только RBF-ядро, так как оно отлично справляется с нелинейными зависимостями, позволяя Гауссовским процессам эффективно разделять такие классы.
В ходе тестирования я использовал 200 наблюдений для обучения и 100 новых точек для проверки точности. Точность предсказания составила 98%, что демонстрирует высокую эффективность ГП в решении нелинейных задач классификации.
Индикатор GPRegressor: Регрессия на время с помощью ГП
Индикатор является примером динамического прогнозирования финансовых временных рядов с учётом неопределённости. Используя скользящее окно для формирования обучающей выборки и постоянное переобучение модели, он реализует принцип адаптации к изменяющимся рыночным условиям.
//+------------------------------------------------------------------+ //| GPRegressor.mq5 | //| Eugene | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Eugene" #property link "https://www.mql5.com" #property version "1.00" // --- Подключаем библиотеку GP --- #include <GP/GP.mqh> #property indicator_chart_window #property indicator_buffers 3 #property indicator_plots 2 // plot Predicted mean #property indicator_label1 "Predicted mean" #property indicator_type1 DRAW_LINE #property indicator_color1 clrBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 2 //--- plot Confidence interval #property indicator_label2 "Confidence interval" #property indicator_type2 DRAW_FILLING #property indicator_color2 clrLightGray #property indicator_width2 1 //--- Входные параметры input int WindowLength = 10; // Длина окна для обучения модели input int calculate_bars = 100; // Глубина истории для расчета input double zscore = 1.96; // z-значение для интервала (1.96 = 95%) input bool ShowRMSE = false; // Показывать метрику RMSE //--- Переменные-буферы для отрисовки double ExtPredictionBuffer[]; // Буфер для предсказанных значений double ExtUpperBandBuffer[]; // Буфер для верхней границы доверительного интервала double ExtLowerBandBuffer[]; // Буфер для нижней границы //--- Глобальные объекты GaussianProcess* g_gp_model = NULL; IKernel* g_kernel = NULL; ILikelihood* g_likelihood = NULL; IInference* g_inference = NULL; //--- Глобальная матрица для временных индексов X_train matrix g_X_train; //--- Глобальные переменные для накопления данных для RMSE vector gp_pred; vector naive_pred; vector y_true; // Флаг, указывающий, был ли RMSE уже рассчитан (для однократного расчета) bool rmse_calculated = false; string comment; double gp_rmse,naive_rmse; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { if(Bars(Symbol(), Period()) < WindowLength + calculate_bars) { PrintFormat("Ошибка: недостаточно баров для вычислений. Требуется минимум %d. Доступно: %d", WindowLength + calculate_bars, Bars(Symbol(), Period())); return(INIT_FAILED); } rmse_calculated = false; // Сбрасываем флаг при инициализации/переинициализации //--- Инициализируем глобальные векторы для RMSE gp_pred.Resize(calculate_bars-1); naive_pred.Resize(calculate_bars-1); y_true.Resize(calculate_bars-1); //--- indicator buffers mapping SetIndexBuffer(0, ExtPredictionBuffer, INDICATOR_DATA); SetIndexBuffer(1, ExtUpperBandBuffer, INDICATOR_DATA); SetIndexBuffer(2, ExtLowerBandBuffer, INDICATOR_DATA); //--- Создаем объекты ядра, правдоподобия и метода инференса g_kernel = new RBFKernel(1.0, 1.0); if(g_kernel == NULL) { Print("Failed to create RBFKernel object"); return(INIT_FAILED); } g_likelihood = new GaussianLikelihood(0.1); if(g_likelihood == NULL) { Print("Failed to create GaussianLikelihood object"); delete g_kernel; return(INIT_FAILED); } g_inference = new ExactInference(); if(g_inference == NULL) { Print("Failed to create ExactInference object"); delete g_kernel; delete g_likelihood; return(INIT_FAILED); } //--- Инициализируем матрицу признаков X_train (один признак - время) g_X_train = matrix::Zeros(WindowLength, 1); for(int i = 0; i < WindowLength; i++) { g_X_train[i][0] = (double)(i + 1); // X = [1, 2, ..., WindowLength] } //--- Создаем объект GaussianProcess // Передаем g_X_train и пустой y_train vector initial_y_train = vector::Zeros(WindowLength); g_gp_model = new GaussianProcess(g_kernel, g_likelihood, g_inference, g_X_train, initial_y_train); if(g_gp_model == NULL) { Print("Failed to create GaussianProcess object"); delete g_kernel; delete g_likelihood; delete g_inference; return(INIT_FAILED); } return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnCalculate(const int32_t rates_total, const int32_t prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int32_t &spread[]) { // Проверка на достаточное количество баров if(rates_total < WindowLength) { Print("Ошибка: недостаточно баров для вычислений. Требуется минимум ", WindowLength, ", доступно: ", rates_total); return(0); } int start; if(prev_calculated == 0) { // Определяем, откуда начинать расчет. // calculate_bars - это глубина истории для расчета. // MathMax(WindowLength, ...) гарантирует, что начнем не раньше, чем есть полное окно данных. start = MathMax(WindowLength, rates_total - calculate_bars); // Инициализируем все буферы значением EMPTY_VALUE ArrayInitialize(ExtPredictionBuffer, EMPTY_VALUE); ArrayInitialize(ExtUpperBandBuffer, EMPTY_VALUE); ArrayInitialize(ExtLowerBandBuffer, EMPTY_VALUE); // Устанавливаем начало отрисовки буферов PlotIndexSetInteger(0, PLOT_DRAW_BEGIN, start); PlotIndexSetInteger(1, PLOT_DRAW_BEGIN, start); PlotIndexSetInteger(2, PLOT_DRAW_BEGIN, start); } else { if(time[rates_total - 1] == time[prev_calculated - 1]) { // Это означает, что новый бар НЕ появился. // Мы находимся на том же баре, просто пришли новые тики. return(rates_total); } // Если время последнего бара изменилось, значит, появился новый закрытый бар. // Начинаем расчет с prev_calculated, чтобы обработать все новые бары. start = prev_calculated; } for(int i = start; i < rates_total && !IsStopped(); i++) { // Проверка достаточности баров для формирования окна if(i < WindowLength) { Print("Ошибка: недостаточно баров для формирования окна на баре ", i, ". Требуется: ", WindowLength, ", доступно: ", i); ExtPredictionBuffer[i] = EMPTY_VALUE; ExtUpperBandBuffer[i] = EMPTY_VALUE; ExtLowerBandBuffer[i] = EMPTY_VALUE; continue; // Пропускаем этот бар } // Формирование вектора y из close[i-1], close[i-2], ..., close[i-WindowLength] // close[i-1] - самый новый бар в окне // close[i-WindowLength] - самый старый бар в окне vector y(WindowLength); for(int j = 0; j < WindowLength; j++) { y[WindowLength - 1 - j] = close[i - 1 - j]; } //Print(" y = ", y[WindowLength-1]); // Самый новый бар в окне данных //--- Стандартизация данных double mu_raw = y.Mean(); // Print("mu_raw = ", mu_raw); double sigma_raw = y.Std(); // Print("sigma_raw = ", sigma_raw); vector y_standardized = (y - mu_raw) / sigma_raw; //--- Устанавливаем обучающие данные g_gp_model.SetTrainingData(g_X_train, y_standardized); //--- Сброс начальных гиперпараметров перед Fit() vector initial_params(3); initial_params[0] = 1.0; // sigma_f (RBFKernel) initial_params[1] = 1.0; // length_scale (RBFKernel) initial_params[2] = 0.1; // sigma_n (GaussianLikelihood) g_gp_model.SetHyperparameters(initial_params); // vector params = g_gp_model.GetCurrentHyperparameters(); // Print(params); // ulong start_time_fit = GetMicrosecondCount(); //--- Обучаем модель if(!g_gp_model.Fit()) { Print("Ошибка: не удалось оптимизировать гиперпараметры GP для бара ", i); ExtPredictionBuffer[i] = EMPTY_VALUE; ExtUpperBandBuffer[i] = EMPTY_VALUE; ExtLowerBandBuffer[i] = EMPTY_VALUE; continue; // Пропускаем текущий бар } //ulong end_time_fit = GetMicrosecondCount(); // double elapsed_time_ms = (end_time_fit - start_time_fit) / 1000.0; //Print("Время выполнения Fit: ", StringFormat("%.3f", elapsed_time_ms), " мс"); vector params = g_gp_model.GetCurrentHyperparameters(); double sigma_f = params[0]; // sigma_f (RBFKernel) double length_scale = params[1]; // length_scale (RBFKernel) double sigma_n = params[2]; // sigma_n (GaussianLikelihood) // --- Создаем точку для прогноза (X_star) // Предсказываем значение для следующего шага после WindowLength matrix X_star = matrix::Zeros(1, 1); X_star[0][0] = (double)(WindowLength + 1); // --- Выполняем предсказание GPPredictionResult gp_predictions; if(!g_gp_model.Predict(X_star, gp_predictions)) { Print("Ошибка: не удалось получить прогноз от GP-модели для бара ", i); ExtPredictionBuffer[i] = EMPTY_VALUE; ExtUpperBandBuffer[i] = EMPTY_VALUE; ExtLowerBandBuffer[i] = EMPTY_VALUE; continue; } // --- double predicted_mean_st = gp_predictions.mu_f_star[0]; // --- Выполняем обратное преобразование предсказанного среднего значения // обратно в исходную ценовую шкалу double predicted_mean = predicted_mean_st * sigma_raw + mu_raw; double sigma_f_star = gp_predictions.Sigma_f_star[0,0]; // дисперсия (Σ) сигнала f* double predicted_variance_st = gp_predictions.Sigma_y_star[0,0]; // дисперсия(Σ) наблюдения y* // --- Выполняем обратное преобразование дисперсии // Дисперсия масштабируется квадратом стандартного отклонения (sigma_raw) данных, // которые были использованы для стандартизации. double predicted_variance = predicted_variance_st * sigma_raw * sigma_raw; // Расчет спрогнозированного доверительного интервала double std_predict = MathSqrt(predicted_variance); double upper_bound = predicted_mean + zscore * std_predict; double lower_bound = predicted_mean - zscore * std_predict; // --- Сохраняем результаты в буферы индикатора для отрисовки ExtPredictionBuffer[i] = predicted_mean; ExtUpperBandBuffer[i] = upper_bound; ExtLowerBandBuffer[i] = lower_bound; comment = StringFormat("GP Regressor | Mean=%.5f | Upper=%.5f | Lower=%.5f |\n", predicted_mean, upper_bound, lower_bound); comment+= StringFormat("Sigma_f = %.5f | Length_Scale = %.5f | Sigma_n = %.5f\n",sigma_f,length_scale,sigma_n); comment+= StringFormat("mu f* = %.5f | Σ y* = %.5f | Σ f*= %.5f",predicted_mean_st,predicted_variance_st,sigma_f_star); Comment(comment); // Отладочный вывод Print("Прогноз для бара ", i, ": Mean=", DoubleToString(predicted_mean, Digits()), " Upper=", DoubleToString(upper_bound, Digits()), " Lower=", DoubleToString(lower_bound, Digits())); } // --- Расчет RMSE для оценки эффективности прогнозной модели ГП по сравнению с простым "наивным" прогнозом if(ShowRMSE && !rmse_calculated) { vector returns(calculate_bars-1); for(int j=0; j <calculate_bars-1;j++) { // истинное значение y_true[j] = close[rates_total - calculate_bars + j]; //Print("y_true[j]", y_true[j] ); // GP прогноз: gp_pred[j] = ExtPredictionBuffer[rates_total-calculate_bars + j]; //Print("gp_pred[j]", gp_pred[j] ); // "Наивный" прогноз (цена завтра = цена сегодня): naive_pred[j] = close[rates_total - calculate_bars + j-1]; // Print("naive_pred[j]", naive_pred[j] ); returns[j] = close[rates_total - calculate_bars + j] - close[rates_total - calculate_bars + j-1]; } gp_rmse=gp_pred.RegressionMetric(y_true,REGRESSION_RMSE); naive_rmse=naive_pred.RegressionMetric(y_true,REGRESSION_RMSE); double std_returns = returns.Std(); // стандартное отклонение приращений Close comment = comment + StringFormat("\nRMSE GP: %.5f | RMSE Naive: %.5f | StdDev Returns Close: %.5f ", gp_rmse, naive_rmse, std_returns); rmse_calculated = true; } Comment(comment); //--- Возвращаем rates_total для следующего вызова return(rates_total); } //+------------------------------------------------------------------+ //| Custom indicator deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Очищаем комментарий на графике Comment(""); //--- Освобождаем выделенную память для объекта GP if(g_gp_model != NULL) { delete g_gp_model; } } //+------------------------------------------------------------------+
Входные параметры:
- WindowLength — длина окна данных (в барах) для обучения GP-модели.
- calculate_bars — глубина истории для расчета и отрисовки индикатора.
- zscore — количество стандартных отклонений для построения доверительного интервала (например, 1.96 для 95%).
- ShowRMSE — флаг для отображения среднеквадратичной ошибки (RMSE) прогноза.
Инициализация (OnInit):
- Глобальные объекты. Создаются и инициализируются глобальные объекты ядра (RBFKernel), функции правдоподобия (GaussianLikelihood) и метода инференса (ExactInference).
- Признаки X_train. GPRegressor реализует регрессию на время, используя индексы времени (от 1 до WindowLength) внутри обучающего окна как входные признаки X.
- Модель GaussianProcess. Инициализируется объект g_gp_model с указанными компонентами, при этом y_train изначально пустой и будет заполняться динамически.
Основной цикл расчета (OnCalculate):
- Формирование данных: на каждом баре извлекается WindowLength последних цен закрытия для формирования вектора y.
- Стандартизация данных: y стандартизируется (приводится к нулевому среднему и единичной дисперсии), для численной стабильности работы ГП.
- Обновление и обучение модели:
- Гиперпараметры сбрасываются к начальным значениям перед каждым обучением (g_gp_model.SetHyperparameters)
- Модель GP обучается на текущем окне стандартизированных цен g_gp_model.Fit().
- Предсказание: для прогноза следующего бара создается точка X_star с временным индексом WindowLength + 1. Метод g_gp_model.Predict() выполняет предсказание, возвращая среднее (mu_f_star) и дисперсию (Sigma_y_star) для стандартизированных данных.
- Дестандартизация: предсказанные среднее и дисперсия преобразуются обратно в исходную ценовую шкалу с помощью среднего (mu_raw) и стандартного отклонения (sigma_raw) текущего окна.
- Доверительный интервал: верхняя и нижняя границы интервала рассчитываются на основе преобразованного среднего и стандартного отклонения с использованием заданного пользователем значения количества стандартных отклонений zscore.
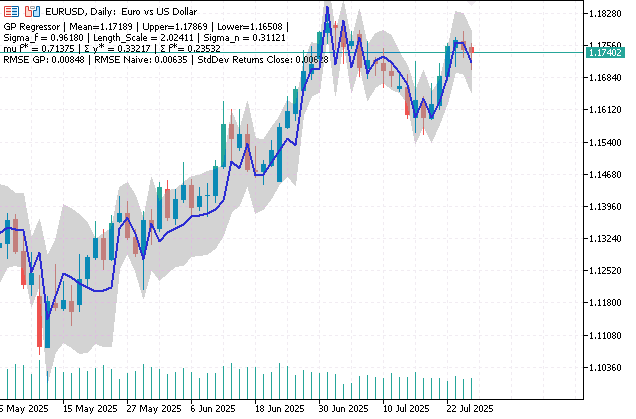
Рис.3. Прогноз регрессионной модели и 95% доверительный интервал
Расчет метрики RMSE:
Индикатор однократно, по запросу пользователя, выводит статистику RMSE для прогнозов модели ГП и "наивного" прогноза (где цена завтра = цена сегодня) для последних calculate_bars. Она помогает объективно оценить текущую эффективность модели.
Например, типичные показатели для EURUSD на минутном таймфреме могут быть: RMSE GP (0.00032) | RMSE Naive (0.00029), а стандартное отклонение приращений цен закрытия (StdDev Returns Close) — 0.00029.
Тот факт, что RMSE GP выше RMSE Naive, указывает на худшую производительность модели ГП по сравнению с простым "наивным" прогнозом на данном анализируемом периоде. Более того, равенство RMSE Naive и StdDev Returns Close является характерным признаком случайного блуждания, когда будущие изменения цены не зависят от прошлых, а текущее значение является лучшим прогнозом.
Отсюда можем сделать вывод, что на данном участке временного ряда либо отсутствуют прогнозируемые закономерности, либо текущая конфигурация модели ГП (использующая только время как признак) пока не способна извлечь полезную информацию для превосходства над наивным прогнозом.
Индикатор GPClassifier: классификация на основе Гауссовских Процессов
Индикатор GPClassifier демонстрирует процесс создания, обучения и прогнозирования модели ГП в задаче бинарной классификации. В качестве признаков используются приращения цен закрытия, которые считаются в скользящем окне исторических данных. С помощью функции NormalizeData выполняется нормализация матрицы признаков для стабилизации обучения модели.
//+------------------------------------------------------------------+ //| GPClassifier.mq5 | //| Eugene | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Eugene" #property link "https://www.mql5.com" #property version "1.00" // --- Подключаем библиотеку GP --- #include <GP/GP.mqh> #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 2 // plot для предсказанного класса "+1" (стрелки вверх) #property indicator_label1 "Predicted Class +1" #property indicator_type1 DRAW_ARROW #property indicator_color1 clrGreen #property indicator_width1 1 // plot для предсказанного класса "-1" (стрелки вниз) #property indicator_label2 "Predicted Class -1" #property indicator_type2 DRAW_ARROW #property indicator_color2 clrBlack #property indicator_width2 1 //--- Входные параметры input int WindowLength = 10; // Длина окна для обучения модели GP input int NumLags = 1; // Количество признаков input int calculate_bars = 100; // Глубина истории для расчета input double ProbabilityThreshold = 0.5; // Порог вероятности input int ArrowShiftPx = 10; // Смещение стрелок в пикселях input bool ShowACCURACY = false; // Показывать точность на графике //--- Переменные-буферы для отрисовки double ExtClassUpBuffer[]; // Буфер для отображения стрелок UP double ExtClassDownBuffer[]; // Буфер для отображения стрелок DOWN double ExtPredictedClassBuffer[]; // Буфер для хранения предсказанных меток класса double ExtPredictedProbabilityBuffer[]; // Буфер для хранения предсказанных вероятностей //--- Глобальные объекты гауссовского процесса GaussianProcess* g_gp_model = NULL; IKernel* g_kernel = NULL; ILikelihood* g_likelihood = NULL; IInference* g_inference = NULL; //--- Глобальные переменные для метрик классификации bool accuracy_calculated = false; vector gp_pred,naive_pred,y_true,gp_accuracy,naive_accuracy; string comment; int currentsize; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { accuracy_calculated = false; // Сбрасываем флаг при инициализации/переинициализации //--- Инициализируем глобальные векторы для Accuracy gp_pred.Resize(0); naive_pred.Resize(0); y_true.Resize(0); gp_accuracy.Resize(1); naive_accuracy.Resize(1); currentsize = 0; //--- indicator buffers mapping SetIndexBuffer(0, ExtClassUpBuffer, INDICATOR_DATA); // Для стрелок вверх SetIndexBuffer(1, ExtClassDownBuffer, INDICATOR_DATA); // Для стрелок вниз SetIndexBuffer(2, ExtPredictedClassBuffer, INDICATOR_CALCULATIONS); // для хранения предсказанных меток SetIndexBuffer(3, ExtPredictedProbabilityBuffer, INDICATOR_CALCULATIONS); // для хранения вероятностей // --- Устанавливаем символы стрелок PlotIndexSetInteger(0, PLOT_ARROW, 225); // Стрелка вверх для буфера 0 PlotIndexSetInteger(1, PLOT_ARROW, 226); // Стрелка вниз для буфера 1 // --- Устанавливаем смещение стрелок в пикселях --- // Для стрелок вверх (буфер 0), используем отрицательное смещение, чтобы они были над High PlotIndexSetInteger(0, PLOT_ARROW_SHIFT, -ArrowShiftPx); // отрицательное = вверх // Для стрелок вниз (буфер 1), используем положительное смещение, чтобы они были ниже Low PlotIndexSetInteger(1, PLOT_ARROW_SHIFT, ArrowShiftPx); // положительное = вниз // Добавляем проверку на соотношение NumLags и WindowLength if(NumLags <= 0) { Print("Ошибка: NumLags должен быть положительным числом"); return(INIT_FAILED); } if(NumLags >= WindowLength) { Print("Ошибка: NumLags (", NumLags, ") не может быть больше или равен WindowLength (", WindowLength, ")."); return(INIT_FAILED); } //--- Создаем объекты ядра, правдоподобия и метода инференса g_kernel = new RBFKernel(1.0, 1.0); if(g_kernel == NULL) { Print("Failed to create RBFKernel object"); return(INIT_FAILED); } g_likelihood = new LogitLikelihood(); if(g_likelihood == NULL) { Print("Failed to create LogitLikelihood object"); delete g_kernel; return(INIT_FAILED); } g_inference = new LaplaceInference(); if(g_inference == NULL) { Print("Failed to create ExactInference object"); delete g_kernel; delete g_likelihood; return(INIT_FAILED); } // --- Создаем модель GaussianProcess // Передаем пустые матрицы для X_train и y_train. // Они будут переопределяться в OnCalculate. g_gp_model = new GaussianProcess(g_kernel, g_likelihood, g_inference,matrix::Zeros(1,1), vector::Zeros(1)); if(g_gp_model == NULL) { Print("Failed to create GaussianProcess object"); delete g_kernel; delete g_likelihood; delete g_inference; return(INIT_FAILED); } return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int32_t rates_total, const int32_t prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int32_t &spread[]) { // Проверка на достаточное количество баров if(rates_total < WindowLength + NumLags + 1) { Print("Ошибка: недостаточно баров для вычислений. Требуется минимум ", WindowLength + NumLags + 1, ", доступно: ", rates_total); return(0); } int start; if(prev_calculated == 0) { start = MathMax(WindowLength + NumLags + 1, rates_total - calculate_bars); // Инициализируем все буферы EMPTY_VALUE ArrayInitialize(ExtClassUpBuffer, EMPTY_VALUE); ArrayInitialize(ExtClassDownBuffer, EMPTY_VALUE); // Количество начальных баров без отрисовки и значений в DataWindow PlotIndexSetInteger(0, PLOT_DRAW_BEGIN, start); PlotIndexSetInteger(1, PLOT_DRAW_BEGIN, start); } else { if(time[rates_total - 1] == time[prev_calculated - 1]) { return(rates_total); } start = prev_calculated; } // --- Главный цикл расчета прогнозов for(int i = start; i < rates_total && !IsStopped(); i++) { // Проверка достаточности баров для формирования окна X и y if(i < WindowLength + NumLags + 1) { ExtClassUpBuffer[i] = EMPTY_VALUE; ExtClassDownBuffer[i] = EMPTY_VALUE; continue; } // --- Шаг 1: Формирование обучающих данных (X_train и y_train) matrix X_train = matrix::Zeros(WindowLength, NumLags); vector y_train = vector::Zeros(WindowLength); for(int j = 0; j < WindowLength; j++) { // Расчет индекса бара в массиве close для текущего наблюдения в окне. int idx = i - WindowLength + j; // Формирование признаков (лагов) для текущего наблюдения (строки X_train[j]) for(int lag_idx = 0; lag_idx < NumLags; lag_idx++) { // Пример: // lag_idx = 0: (close[idx - 1] - close[idx - 2]) - приращение предыдущего бара // lag_idx = 1: (close[idx - 2] - close[idx - 3]) - приращение позапрошлого бара X_train[j,lag_idx] = close[idx - 1 - lag_idx] - close[idx - 2 - lag_idx]; } // Y_train[j]: Бинарная метка для приращения цены на баре idx. if(close[idx] - close[idx - 1] > 0) { y_train[j] = 1; // Цена выросла } else { y_train[j] = -1; // Цена упала или осталась неизменной } } // Print(y_train); // --- Нормализация X_train matrix X_train_norm; vector out_mean; vector out_std; if(!NormalizeData(X_train,X_train_norm,out_mean,out_std)) { Print("Ошибка: не удалось нормализовать матрицу признаков ", i); continue; } // --- Шаг 2: Подаем данные в GP-модель g_gp_model.SetTrainingData(X_train_norm, y_train); // Сброс начальных гиперпараметров перед каждым обучением Fit() vector initial_params(2); initial_params[0] = 1.0; // sigma_f (RBFKernel) initial_params[1] = 1.0; // length_scale (RBFKernel) g_gp_model.SetHyperparameters(initial_params); // --- Шаг 3: Обучаем модель // ulong start_time_fit = GetMicrosecondCount(); if(!g_gp_model.Fit()) { Print("Ошибка: не удалось оптимизировать гиперпараметры GP для бара ", i); ExtClassUpBuffer[i] = EMPTY_VALUE; ExtClassDownBuffer[i] = EMPTY_VALUE; continue; } // ulong end_time_fit = GetMicrosecondCount(); // double elapsed_time_ms = (end_time_fit - start_time_fit) / 1000.0; // Print("Время выполнения Fit: ", StringFormat("%.3f", elapsed_time_ms), " мс"); // --- Шаг 4: Создаем точку для прогноза X_star // X_star - это приращения цен предыдущих NumLags закрытых баров, // используемые для предсказания движения текущего бара (бара i). matrix X_star = matrix::Zeros(1, NumLags); for(int lag_idx = 0; lag_idx < NumLags; lag_idx++) { X_star[0][lag_idx] = close[i - 1 - lag_idx] - close[i - 2 - lag_idx]; } // X_star также должен быть нормализован, используя те же средние и стандартные отклонения, // что и для соответствующих столбцов X_train. for(int lag_idx = 0; lag_idx < NumLags; lag_idx++) { X_star[0][lag_idx] = (X_star[0][lag_idx] - out_mean[lag_idx]) / out_std[lag_idx]; } // --- Шаг 5: Выполняем предсказание GPPredictionResult gp_predictions; if(!g_gp_model.Predict(X_star, gp_predictions)) { Print("Ошибка: не удалось получить прогноз от GP-модели для бара ", i); ExtClassUpBuffer[i] = EMPTY_VALUE; ExtClassDownBuffer[i] = EMPTY_VALUE; continue; } double predicted_probability = gp_predictions.predicted_probabilities[0]; // Вероятность для единственной тестовой точки int predicted_class = (int)gp_predictions.predicted_labels[0]; // Метка (+1 или -1) // --- Шаг 6: Сохраняем результаты в буферы индикатора для отрисовки ExtClassUpBuffer[i] = EMPTY_VALUE; ExtClassDownBuffer[i] = EMPTY_VALUE; ExtPredictedClassBuffer[i] = predicted_class; ExtPredictedProbabilityBuffer[i] = predicted_probability; // Добавляем вывод вероятности и количество признаков (лагов) в комментарий на график comment = StringFormat("GP Classifier (Lags: %d) | Probability(UP) = %.10f", NumLags, predicted_probability); Comment(comment); // Если прогнозируемый класс - "+1" и вероятность выше заданного порога if(predicted_class == 1 && predicted_probability > ProbabilityThreshold) { ExtClassUpBuffer[i] = high[i]; } // Если прогнозируемый класс - "-1" и вероятность падения выше заданного порога else if(predicted_class == -1 && (1.0 - predicted_probability) > ProbabilityThreshold) { ExtClassDownBuffer[i] = low[i]; } Print("Прогноз для бара ", i, ": Probability(UP)=" + DoubleToString(predicted_probability, 10) + ", Predicted Class=" + IntegerToString(predicted_class), " time: ", time[i]); } // --- Расчет точности классификации для оценки эффективности прогнозной модели ГП по сравнению //с "наивным" прогнозом. if(ShowACCURACY && !accuracy_calculated) { for(int j=0; j <calculate_bars-1;j++) { // индекс до текущего бара int bar_idx = rates_total - calculate_bars + j; if(ExtClassUpBuffer[bar_idx]!= EMPTY_VALUE || ExtClassDownBuffer[bar_idx] != EMPTY_VALUE) { currentsize = (int)gp_pred.Size(); currentsize++; gp_pred.Resize(currentsize,100); naive_pred.Resize(currentsize,100); y_true.Resize(currentsize,100); // Истинная метка: считаем до текущего бара if(close[bar_idx] - close[bar_idx - 1] > 0) { y_true[currentsize-1] = 1; // Цена выросла } else { y_true[currentsize-1] = -1; // Цена упала или осталась неизменной } // Print("y_true", y_true[currentsize-1] ); // Прогноз GP: считаем до текущего бара gp_pred[currentsize-1] = ExtPredictedClassBuffer[bar_idx]; // Print(" gp_pred", gp_pred[currentsize-1]); // "Наивный" прогноз: метка бара "на завтра" равна метке "сегодня" if(close[bar_idx - 1] - close[bar_idx - 2] > 0) { naive_pred[currentsize-1] = 1; } else { naive_pred[currentsize-1] = -1; } } } if(!(int)gp_pred.Size()==0) { gp_accuracy=gp_pred.ClassificationMetric(y_true,CLASSIFICATION_ACCURACY); naive_accuracy=naive_pred.ClassificationMetric(y_true,CLASSIFICATION_ACCURACY); comment += StringFormat("\nGP Accuracy: %.2f %% | Naive Accuracy: %.2f %%", gp_accuracy[0], naive_accuracy[0]); comment += StringFormat("\nNumber of Filtered Signals: %d", (int)gp_pred.Size()); } else { comment += StringFormat("\n No Signals for ProbabilityThreshold: %.4f ", ProbabilityThreshold); } accuracy_calculated = true; } Comment(comment); //--- Возвращаем rates_total для следующего вызова return(rates_total); } //+------------------------------------------------------------------+ //| Custom indicator deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { // Очищаем комментарий на графике при удалении индикатора Comment(""); if(g_gp_model != NULL) { delete g_gp_model; } }
Входные параметры:
- WindowLength — длина окна данных для обучения модели. Количество наблюдений в обучающей выборке.
- NumLags — количество лагов (приращений цен). Например, если NumLags = 1, признаком будет только приращение цены на предыдущем баре. Если NumLags = 3, признаками будут приращения цены на трех предыдущих барах и т.д.
- calculate_bars — определяет количество последних баров на графике, для которых будет выполняться расчет и отрисовка индикатора.
- ProbabilityThreshold — порог вероятности. Индикатор отображает сигналы стрелками вверх/вниз, если предсказанная вероятность движения цены в соответствующем направлении превышает этот порог.
- ArrowShiftPx —смещение стрелок в пикселях от экстремумов бара.
- ShowACCURACY — флаг для отображения метрик точности классификации на графике
OnInit() — инициализация GP-Модели:
- Создаем ядро RBF, функцию правдоподобия и метод инференса:
- g_kernel = new RBFKernel(1.0, 1.0)
- g_likelihood = new LogitLikelihood()
- g_inference = new LaplaceInference()
- Создаем модель GaussianProcess:
- g_gp_model = new GaussianProcess(g_kernel, g_likelihood, g_inference, matrix::Zeros(1,1), vector::Zeros(1));
- Объект g_gp_model создается с пустыми начальными матрицами для обучающих данных X_train и y_train. Эти данные будут динамически заполняться и обновляться на каждом баре в функции OnCalculate.
OnCalculate() — основной цикл расчета:
1. Проверка на достаточное количество баров: перед началом расчетов убеждаемся, что на графике достаточно баров для формирования обучающего окна, учитывая WindowLength, NumLags и один бар для прогнозируемой метки.
2. Формирование обучающих данных (X_train и y_train):
- Признаки X_train — на каждом шаге в скользящем окне формируется матрица признаков X_train. Каждая строка — это наблюдение, столбцы — приращения цен (лаги) за предыдущие NumLags баров.
- Метки y_train — бинарные метки, указывающие на направление движения цены следующего бара: «1» (цена выросла) или «-1» (цена упала или не изменилась).
3. Нормализация X_train — матрица признаков стандартизируется для численной стабильности. Средние значения (out_mean) и стандартные отклонения (out_std), полученные на этом этапе, сохраняются для нормализации точки прогноза.
4. Обновление и обучение GP-модели:
- g_gp_model.SetTrainingData(X_train_stdard, y_train) — обучающие данные обновляются на каждом баре.
- g_gp_model.SetHyperparameters(initial_params) — гиперпараметры ядра сбрасываются и заново оптимизируются для каждого нового бара
- g_gp_model.Fit() — запускаем процесс обучения на текущем окне стандартизированных данных.
5.Создание и нормализация новой точки для прогноза (X_star): нормализуется с использованием векторов out_mean и out_std.
6.Выполнение предсказания: метод g_gp_model.Predict(X_star, gp_predictions) возвращает предсказанную вероятность движения вверх (predicted_probabilities[0]) и бинарную метку (predicted_labels[0]).
7.Отрисовка и вывод: в зависимости от predicted_class и ProbabilityThreshold, на графике рисуется стрелка вверх или стрелка вниз. Информация о вероятности прогноза и предсказанном классе выводится в комментарии на график и журнал.
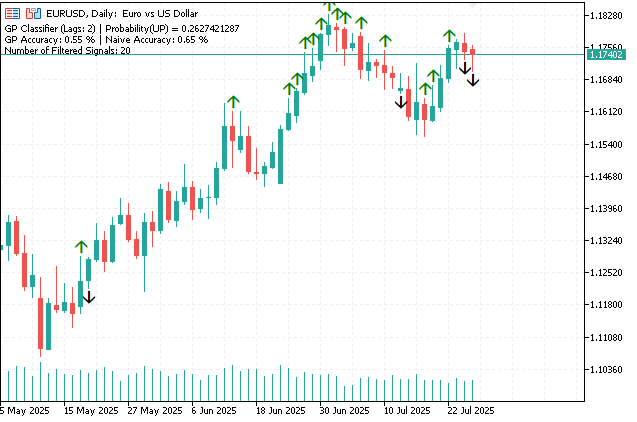
Рис.4. Результат предсказания индикатора GP Classifier (RBF-ядро)
Расчет метрик точности (ShowACCURACY)
При включении параметра ShowACCURACY индикатор выполняет однократный расчет точности классификации для последних calculate_bars, сравнивая прогнозы модели ГП с "наивным" прогнозом.
Истинные метки (y_true) определяются как фактическое направление движения цены. Прогноз ГП (gp_pred) - это метки, предсказанные моделью ГП. "Наивный" прогноз (naive_pred) предполагает, что направление следующего движения цены будет таким же, как и предыдущее движение (например, если цена выросла на предыдущем баре, наивный прогноз — рост).
Сравниваются метрики CLASSIFICATION_ACCURACY для обеих моделей (gp_accuracy и naive_accuracy), и результаты выводятся в комментарий на графике. Это позволяет объективно оценить эффективность модели ГП относительно простого бенчмарка.
Заключение
Сегодня мы завершили рассмотрение модели классификации Гауссовских процессов. После подробного рассмотрения теоретических построений нам удалось создать базовую версию библиотеки, позволяющую решать как задачи регрессии, так и классификации. Тестирование на синтетических данных подтвердило корректность работы реализованных компонентов библиотеки, включая эффективное применение аналитических градиентов и использование высокопроизводительной библиотеки OpenBLAS для численной стабильности и скорости.
Индикаторы GPRegressor и GPClassifier продемонстрировали практические возможности применения ГП для динамического прогнозирования финансовых временных рядов в реальном времени, а такие метрики, как RMSE (для регрессии) и Accuracy (для классификации), позволили объективно оценить эффективность модели.
Тем не менее, реализация библиотеки далека от своего идеала. Несмотря на все приложенные усилия, скорость её работы уступает признанным решениям, например таким как scikit-learn. Отчасти это связано с тем, что мы использовали не самый быстрый оптимизатор MinBleic.
Поэтому дальнейшее улучшение библиотеки может быть связано с:
- использованием более производительного градиентного оптимизатора. В частности, нам потребуется быстрый алгоритм L-BFGS, который значительно превосходит текущий в эффективности для задач с большим числом гиперпараметров;
- более робастной реализации метода Ньютона для Лапласовской аппроксимации. Добавление линейного поиска позволит более эффективно и надёжно находить моду апостериорного распределения, улучшая сходимость итоговой оптимизации;
- реализацией разреженных методов. В отличие от текущей работы с полными матрицами, использование разреженных представлений позволит библиотеке обучаться на значительно больших объёмах данных, открывая новые возможности для масштабирования и применения ГП.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | GPClassifier.mq5 | Индикатор | Прогнозирует цену и доверительный интервал на один шаг вперед (онлайн обучение) |
| 2 | GPRegressor.mq5 | Индикатор | Прогнозирует цену и доверительный интервал на один шаг вперед (онлайн обучение) |
| 3 | GPsynthetic.mq5 | Скрипт | Проверка модели ГП на синтетических данных |
| 4 | GP.mqh | Библиотека класса | Класс GaussianProcess, объединяющий ядро, функцию правдоподобия и метод инференса, класс GPOptimizationObjective отвечающий за оптимизацию |
| 5 | Inference.mqh | Библиотека класса | Интерфейс IInference и его реализации, определяющие методы вывода |
| 6 | Kernels.mqh | Библиотека класса | Интерфейс IKernel и реализации ковариационных ядер |
| 7 | Likelihoods.mqh | Библиотека класса | Интерфейс ILikelihood и реализации функций правдоподобия |
| 8 | StructUtils.mqh | Библиотека класса | Вспомогательные функции и структуры данных |
| 9 | DataRegression | CSV | Данные для скрипта GPsynthetic.mq5 |
| 10 | DataClassification | CSV | Данные для скрипта GPsynthetic.mq5 |
Прикрепленные файлы |
MQL5.zip
(53.23 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Перейти к обсуждению на форуме трейдеров
Автоматизация торговых стратегий с помощью MQL5 (Часть 2): Система прорыва Кумо с Ichimoku и Awesome Oscillator
В этой статье мы создаем советник, который автоматизирует стратегию прорыв Кумо (Kumo Breakout) с использованием индикатора Ichimoku Kinko Hyo и Awesome Oscillator. Мы рассмотрим инициализацию хэндлов индикаторов, обнаружение условий прорыва и автоматизацию входов и выходов из сделок. Кроме того, мы внедрим трейлинг-стопы и логику управления позициями для повышения производительности советника и его адаптивности к рыночным условиям.
Нейросети в трейдинге: Декомпозиция вместо масштабирования (SSCNN)
В данной статье мы начинаем знакомство с фреймворком SSCNN — современным архитектурным решением для анализа временных рядов, сочетающим в себе точность, структурированность и высокую вычислительную эффективность. Мы последовательно рассмотрим его теоретические аспекты, обратим внимание на ключевые отличия от предшественников и начнем практическую реализацию базовых компонентов в среде MQL5.
Моделирование рынка (Часть 01): Кросс-ордеры (I)
Сегодня мы начнем второй этап, на котором рассмотрим вопрос о системе репликации/моделирования рынка. Для начала мы покажем возможное решение для кросс-ордеров. Я покажу решение, но оно еще не окончательное, это будет вариант решения проблемы, решить которую предстоит в ближайшем будущем.
Интеграция MQL5 с пакетами обработки данных (Часть 4): Обработка больших данных
В статье рассматриваются передовые методы интеграции MQL5 с мощными инструментами обработки данных, а также уделяется внимание эффективной обработке больших данных для улучшения торгового анализа и принятия решений.
Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь