Гауссовcкие процессы в машинном обучении: регрессионная модель в MQL5

Введение

Гауссовские процессы (ГП) представляют собой инструмент байесовского моделирования, широко используемый в машинном обучении для задач регрессии и классификации. В отличие от множества традиционных моделей, предоставляющих только точечные прогнозы, ГП формируют полное вероятностное распределение для предсказываемых значений. Это позволяет не только получать точечные предсказания, но и важную оценку неопределённости этих прогнозов, выраженную через доверительные интервалы. Это является отличительной особенностью байесовского подхода, когда объединяют априорные знания с наблюдаемыми данными, для получения прогнозного распределения.

ГП относятся к классу ядерных методов, использующих ковариационные функции (или ядра) для моделирования зависимостей между данными. Благодаря возможности комбинирования различных ядер (например, путем сложения или умножения), достигается определенная гибкость в описании возможных прогнозных функций. Каждое ядро при этом обладает своими гиперпараметрами, которые необходимо оптимизировать для достижения максимальной точности модели.

В данной статье мы подробно разберем процесс прогнозирования с помощью регрессионной модели на основе гауссовских процессов, наглядно продемонстрировав, как ГП позволяют не только строить точные прогнозы, но и всесторонне оценивать их неопределённость.

Что такое гауссовский процесс

С вероятностной точки зрения, гауссовский процесс — это случайный процесс, который описывает распределение вероятностей над функциями. В отличие от обычного нормального распределения, которое описывает одну случайную величину, ГП определяет бесконечный набор случайных величин, любое конечное подмножество которых подчиняется многомерному нормальному распределению.

В машинном обучении ГП относятся к непараметрическим моделям, которые не требуют заранее заданной формы функции (например, линейную или полиномиальную, как в классической регрессии). Вместо этого, ГП моделирует скрытую функцию f(x), которая, как предполагается, отображает истинные зависимости в данных. Однако сама функция f(x) непосредственно не наблюдаема, нам доступны лишь её значения с шумом в заданных точках x. В основе модели ГП лежит предположение о нормальности распределения этой неизвестной функции f(x):

f (x)~ N( μ, Σ),

где:

• f(x) — скрытая (латентная) функция, значения которой в наблюдаемых точках мы хотим смоделировать,
•  μ — вектор средних значений, зависящий от априорной функции среднего (часто принимается нулевым для простоты),
•  Σ — ковариационная матрица, элементы которой определяются ковариационной функцией (или ядром) K(x, x'), задающей степень корреляции между точками  x и  x'.

Ключевая идея ГП заключается в моделировании распределения функций через ковариационную структуру, заданную ядром, которое, в свою очередь, определяет различные свойства функций, такие как их гладкость, периодичность, нестационарность и т.д.

Основная цель ГП — восстановить  латентную функцию f(x) на основе конечного набора данных D=(X,y), где X – набор признаков, а y - зашумленные наблюдения.

Байесовский подход в ГП

Гауссовские процессы используют байесовский подход к статистическому выводу, который объединяет априорные знания с наблюдаемыми данными для построения вероятностных прогнозов. Это отличает ГП от многих других методов машинного обучения (таких, например, как нейронные сети или SVM), позволяя не только предсказывать значения, но и оценивать их неопределенность. В основе этого подхода лежит теорема Байеса:

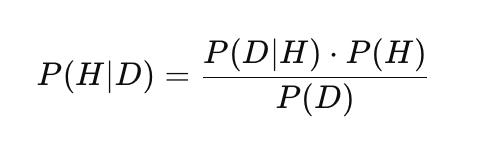
где:

• P(H) — априорная вероятность: начальная вероятность гипотезы H, отражающая  предварительные знания или предположения до наблюдения данных,
• P(D|H) — правдоподобие: вероятность наблюдать данные D, если гипотеза H верна,
• P(H|D) — апостериорная вероятность: вероятность гипотезы H после наблюдения данных D,
• P(D) — маргинальная вероятность данных (нормализующая константа), обеспечивающая корректность апостериорного распределения.

В контексте ГП байесовский подход применяется следующим образом. Гипотеза H трактуется, как распределение над функциями f(x), из которых могла быть сгенерирована наша выборка данных, а данные D — это обучающий датасет (X, y).

Таким образом, теорема Байеса в ГП принимает вид:

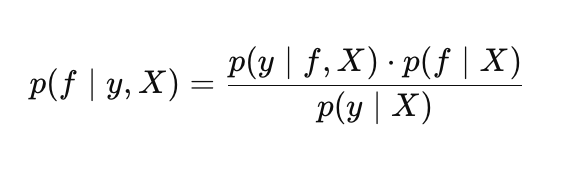
где:

• p(f |X) — априорное распределение над функциями f,
• p(y |f, X) — правдоподобие,
• p(f |y, X) — апостериорное распределение над функциями f ,
• p(y |X) — маргинальное правдоподобие (evidence). Используется для оптимизации гиперпараметров гауссовского процесса.

В ГП, поскольку как априорное распределение функций, так и правдоподобие являются гауссовскими, апостериорное распределение также является гауссовским процессом, но уже с обновленными функциями среднего и ковариации, которые включают информацию, извлеченную из данных. Это происходит, благодаря математическому свойству сопряженности гауссовских распределений, что делает вывод формулы для предсказаний относительно простым.

Априорное распределение

Априорное распределение описывает наши начальные предположения о возможных функциях до того, как мы увидим данные. По сути, априорное распределение — это множество возможных функций, из которых ГП выберет наиболее подходящие на основе обучающих данных. Ядро играет ключевую роль, задавая свойства этих функций. Существует множество видов ядер, каждое из которых подходит для разных типов данных, например:

RBF (гауссовское ядро): моделирует гладкие нелинейные функции:

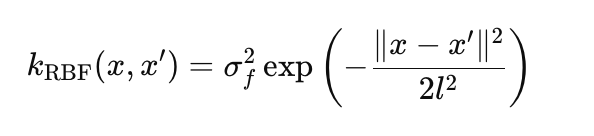
где:

• σ_f  — амплитуда, задает масштаб вариаций (в коде params.rbf.sigma_f),
• l — длина масштаба (length scale), контролирует скорость затухания корреляции (params.rbf.length),
• ∥x−x′∥ — евклидово расстояние между точками x и x'.

Линейное ядро: моделирует линейные зависимости:

• x*x' — скалярное произведение двух векторов,
• σ_l — масштаб линейного тренда (params.linear.sigma_l)

Периодическое ядро: улавливает циклические паттерны:

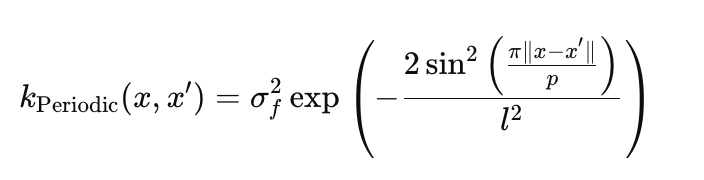
• σ_f  — амплитуда, задает масштаб колебаний (params.periodic.sigma_f),
• l — длина масштаба, контролирует гладкость колебаний (params.periodic.length),
• p — период, определяет частоту повторений (params.periodic.period).

Для наглядной демонстрации априорного распределения, рассмотрим выборки функций f(x), сгенерированные с использованием различных ядер. На рис.1 показаны выборки из априорного распределения с RBF ядром. Траектории представляют собой гладкие нелинейные функции, которые варьируются в зависимости от параметров ядра.

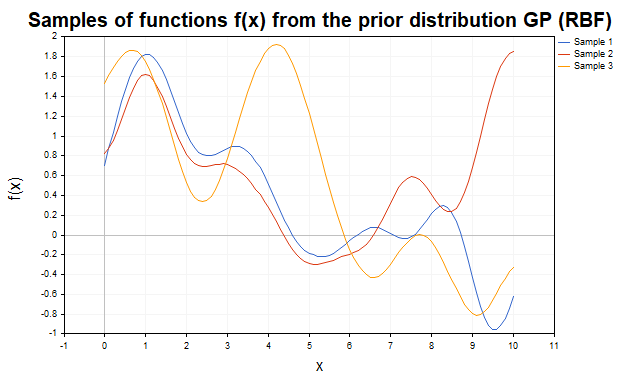
Рис.1 Выборки функций f из априорного распределения ГП (RBF-ядро)

На (рис.2) показаны выборки из априорного распределения с линейным ядром. Траектории представляют собой прямые линии с различными наклонами, что отражает способность ядра моделировать линейные тренды.

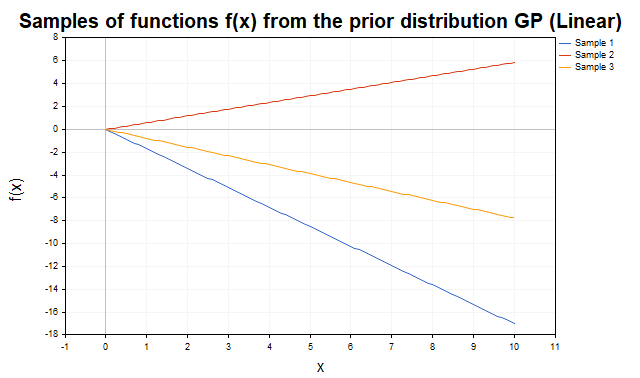
Рис.2  Выборки функций f из априорного распределения ГП (линейное ядро)

Рис.3 демонстрирует выборки с периодическим ядром. Траектории представляют собой циклические функции с периодом p, что делает ядро идеальным для моделирования периодических компонент.

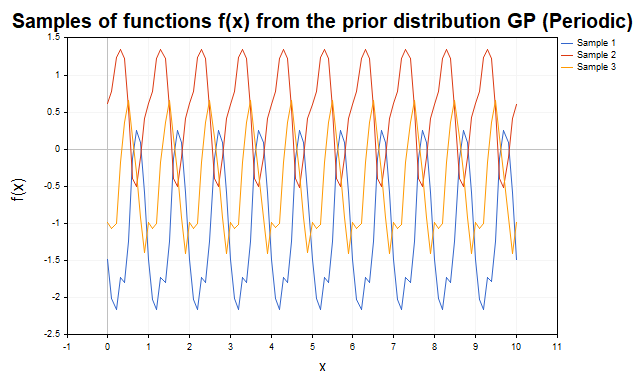
Рис.3 Выборки функций f из априорного распределения ГП (периодическое ядро)

На рис.4 показаны траектории хорошо известного винеровского процесса с ковариационной функцией K(x,x') = min(x, x'). 

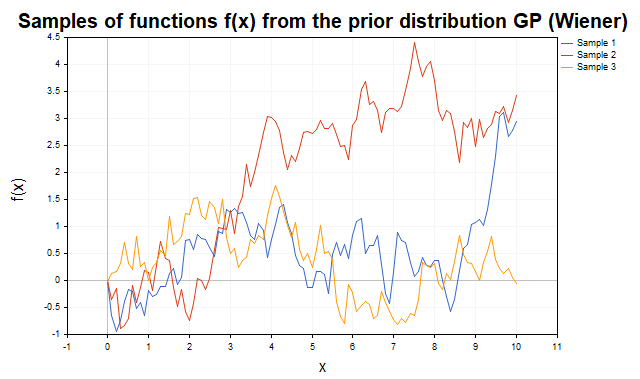
Рис.4 Выборки функций f из априорного распределения ГП с ковариационной функцией винеровского процесса

Гибкость ГП достигается за счет возможности комбинировать ядра (путем их сложения или умножения), что позволяет моделировать функции с разнообразными свойствами, такими как сочетание линейных и нелинейных трендов, периодических колебаний и т.д. Выборки были сгенерированы с использованием скрипта SamplesPrior.

Правдоподобие

В Гауссовских процессах правдоподобие p(y |f, X) описывает вероятность наблюдать данные y при условии конкретной функции f из априорного распределения и данных X. Оно играет ключевую роль в байесовском выводе, связывая априорное распределение над функциями с наблюдаемыми данными. Для набора данных, правдоподобие задаётся многомерным нормальным распределением:

где:

• f(x) — вектор значений скрытой функции в точках X,
• σy^2 — дисперсия шума,
• ∥y−f(x)∥^2 — квадрат евклидовой нормы разности между наблюдаемыми данными и значениями функции f.

Эта формула показывает, что правдоподобие тем выше, чем ближе значения функции f к наблюдаемым данным y.

Апостериорное распределение

Апостериорное распределение — это результат байесовского обновления априорного распределения с учетом наблюдаемых данных и правдоподобия. Оно описывает вероятность значений скрытой функции f(x) в новых тестовых точках X*. Это распределение характеризуется обновлённым средним μ*, представляющим прогноз, и ковариационной матрицей Σ*, описывающей неопределённость прогнозов.

Таким образом, априорное распределение задает множество функций, правдоподобие "взвешивает" их на основе данных, а апостериорное распределение предоставляет наиболее вероятную функцию с оценкой неопределенности.

Регрессия ГП с гауссовским правдоподобием

Гауссовские процессы, в сочетании с гауссовским шумом наблюдений, позволяют решать задачу регрессии в аналитической форме, используя методы линейной алгебры. Это значительно упрощает вычисления и избавляет от необходимости применять сложные численные методы. ГП подходят для моделирования как зашумлённых, так и незашумленных данных.  Рассмотрим  сначала идеализированный случай, когда целевые значения y являются незашумленными истинными значениями функции, то есть когда y = f(x) (сценарий интерполяции).

Случай без шума: интерполяция 

Предположим, у нас есть набор данных D = {(xn, yn) : n = 1 : N}, где yn = f(xn) — это точное незашумленное наблюдение функции f, вычисленной в точке xn. Наша задача — предсказать значения функции f* для тестового набора X* размером N*×d.

Для обучающих точек X и тестовых точек X*, совместное априорное распределение значений функции f и f* является многомерным нормальным распределением:

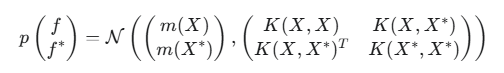
где:

• f — вектор истинных значений скрытой функции в обучающих  точках,
• f* — вектор истинных  значений скрытой функции в тестовых  точках,
• m(X) — вектор средних  значений функции для обучающих точек (вектор нулей для упрощения),
• m(X*) — вектор средних  значений функции для тестовых точек (вектор нулей для упрощения),
• K(X,X) — ковариационная матрица NxN между всеми парами обучающих точек ,
• K(X,X*) — ковариационная матрица NxN* между обучающими и тестовыми точками,
• K(X*,X*) — ковариационная матрица  N*xN* между всеми парами тестовых точек
• N — количество входных точек данных,
• N* — количество тестовых точек данных,
• d — размерность входных данных ( количество признаков).

Поскольку наблюдения y в данном случае точно соответствуют f (y=f), то есть правдоподобие является дельта-функцией, мы можем сразу перейти к условному распределению f* при условии y. В силу свойств условных распределений многомерного нормального распределения, апостериорное распределение для f* при условии наблюдаемых данных y имеет вид:

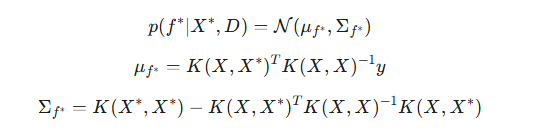
где:

• μf* — апостериорное среднее, наилучшее предсказания значений скрытой функции f* в новых(тестовых) точках, исходя из обучающих данных,
• Σf* — апостериорная ковариационная матрица для тестовых точек. Количественно выражает неопределенность в предсказании скрытой функции f*.

Случай с шумом: регрессия

В реальных задачах данные y обычно содержат непредсказуемый шум: y=f(X)+ϵ, где ϵ∼N(0,σ^2) — гауссовский шум. В этом случае, ГП не интерполирует обучающие данные точно (т.е., не проходит строго через каждую точку), а вместо этого, сглаживает их, учитывая предполагаемый уровень шума. Апостериорное распределение для зашумленных данных модифицируется, путём добавления дисперсии шума к диагональным элементам ковариационной матрицы обучающих данных:

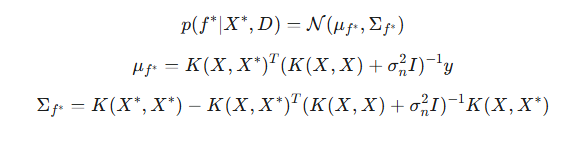
Параметр шума σ​ является гиперпараметром модели и оптимизируется вместе с параметрами ядра. 

Очень важный момент: с добавлением шума, мы получаем возможность предсказывать доверительные интервалы не только для скрытой функции f*, но и для новых наблюдений y*. В отличие от случая без шума, где предсказательные распределения для f* и y* совпадали, теперь эти распределения отличаются. Главное различие кроется в их ковариационных матрицах. Ковариация Σf* отражает неопределённость самой скрытой функции в тестовых точках. Ковариация Σy*, включает в себя неопределённость скрытой функции, плюс дисперсию шума наблюдений.

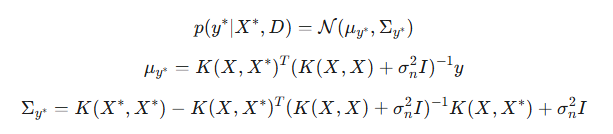
• μy* — апостериорное среднее для нового наблюдения y*. Оно совпадает с μf*, поскольку ожидаемое значение шума равно нулю,
• Σy* — апостериорная ковариация для нового наблюдения y*.  

Поэтому, если нас интересуют доверительные интервалы для новых наблюдений y*, а не для новых значений латентной функции f*, мы должны использовать эту формулу.

Чтобы наглядно показать, как гауссовские процессы адаптируются к данным, рассмотрим визуализацию выборок функций f, сгенерированных из апостериорного распределения в случае отсутствия шума. На рис.5 представлены три функции f, построенные после наблюдения пяти обучающих точек с использование RBF-ядра.

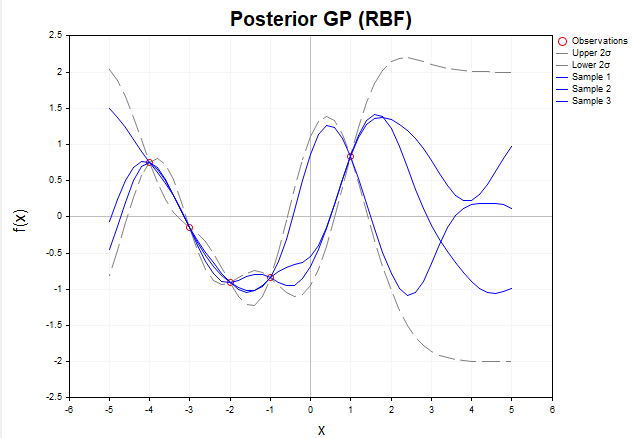
Рис.5 Выборки функций f из апостериорного распределения  (RBF-ядро, без шума)

До наблюдения каких-либо данных, априорное распределение, заданное ГП, описывает бесконечное множество функций. После того, как мы добавляем обучающие данные, апостериорное распределение ограничивает это множество, оставляя только функции, которые точно проходят через наблюдаемые точки. Иными словами, оно фокусируется исключительно на тех функциях, которые точно интерполируют данные. 

В обучающих точках X дисперсия (диагональные элементы апостериорной ковариационной матрицы Σ*) равна нулю, что означает полное отсутствие неопределенности в этих точках: все функции, сэмплированные из апостериорного распределения, гарантированно проходят точно через обучающие точки. Вне обучающих точек функции могут варьироваться, отражая неопределенность модели в областях, где данные отсутствуют. Однако, их поведение по-прежнему определяются структурой выбранного ядра, в данном случае — RBF.

Теперь рассмотрим график выборок функций f из апостериорного распределения, когда наблюдаемые данные y содержат гауссовский шум. (рис.6)

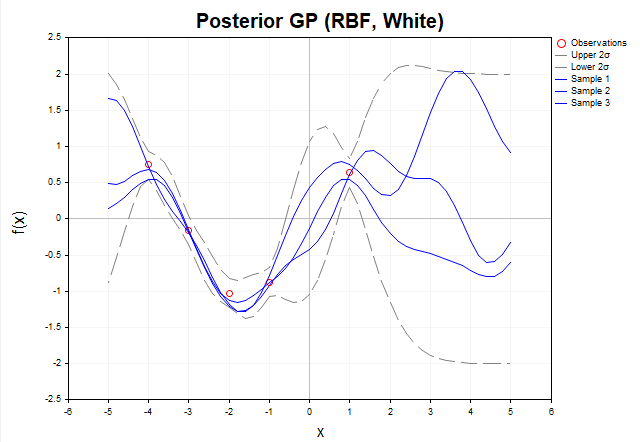
Рис. 6 Выборки функций f из апостериорного распределения  (RBF-ядро, с шумом)

При наличии шума, апостериорные функции не обязаны точно проходить через наблюдаемые данные y. Это означает, что множество возможных функций, которые могут объяснить данные, становится шире, так как они могут отклоняться от наблюдаемых значений в пределах шума. Серые пунктирные линии обозначают доверительные интервалы в пределах 2 сигма, охватывающие около 95% вероятности апостериорного распределения f*. В областях, удалённых от обучающих данных, неопределённость возрастает ещё больше, и доверительные интервалы становятся значительно шире, показывая снижение уверенности модели в этих областях. Важно отметить: серые пунктирные линии обозначают доверительные интервалы именно для скрытой функции f*, а не для новых наблюдений y*. 

Оптимизация гиперпараметров гауссовского процесса

Эффективность модели гауссовских процессов в значительной степени зависит от оптимального выбора ее гиперпараметров, что позволяет модели подстраиватся под данные, максимизируя её способность объяснять наблюдаемые зависимости. К таким гиперпараметрам относятся парметры ядра и дисперсия шума. В ГП оптимизация проводится с помощью минимизации отрицательного логарифмического маргинального правдоподобия (NLML):

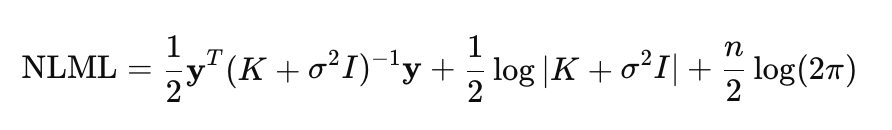
Прямое вычисление (K+σ^2*I)^−1 * y вычислительно затратно для больших n, так как требует обращения матрицы размером n×n. Поэтому, чтобы сделать вычисления более эффективными и устойчивыми, используется разложение Холецкого. С учетом этого разложения формула NLML переписывается как:

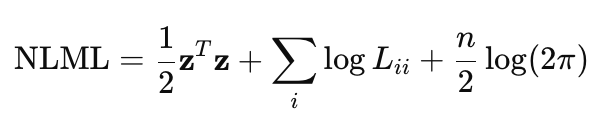
• z — вектор, получаемый при решении системы линейных уравнений с использованием разложения Холецкого,    z=L^−1*y
• L — нижняя треугольная матрица из разложения Холецкого K+σ^2*I = LL^T

Данная формула реализована в функции NegativeLogMarginalLikelihood.

//+------------------------------------------------------------------+
//| Вычисление отрицательного логарифмического правдоподобия         |
//+------------------------------------------------------------------+
double NegativeLogMarginalLikelihood(const matrix &x, const matrix &y, int &kernel_list[], KernelParams &params)
{
   int n = (int)x.Rows();

   //--- Вычисляем ковариационную матрицу K
   matrix K = ComputeKernelMatrix(x, x, kernel_list, params);
   
   //--- Добавляем дисперсию белого шума, если выбран KERNEL_WHITE 
    double white_noise_variance = 0.0;
    for (int i = 0; i < ArraySize(kernel_list); i++)
    {
        if (kernel_list[i] == KERNEL_WHITE)
        {
            white_noise_variance = params.white.sigma * params.white.sigma;
            break; 
        }
    }
   // Добавление небольшого джиттера предотвращает проблемы,
   // если матрица K оказывается сингулярной или близкой к сингулярной 
   // из-за особенностей вычислений или выбранного ядра
    double jitter = 1e-6;
    K += matrix::Identity(n, n) * (white_noise_variance + jitter);
     
   // ---Выполняем разложение Холецкого: K + sigma^2*I = L * L^T
   matrix L;
   if (!K.Cholesky(L))
   {
      Print("Ошибка: Разложение Холецкого не удалось");
      return DBL_MAX;
   }

  //--- Решаем линейную систему L * z = y для нахождения z = L^(-1) * y
   vector z = L.LstSq(y.Col(0));
   if (z.Size() == 0)
   {
      Print("Ошибка: Не удалось решить систему L * z = y");
      return DBL_MAX;
   }

   //--- Вычисляем первое слагаемое в формуле NLML : 
   // 1/2 * y^T * (K + sigma^2*I)^-1 * y = 1/2 * z^T * z
    double data_term = 0.5 * z @ z; // Скалярное произведение z^T * z   

   //--- Вычисляем второе слагаемое: 1/2 * log|K + sigma^2*I| = sum(log(L_ii))
   vector diag = L.Diag();
   double log_det = 0.0;
   for (int i = 0; i < n; i++)
      log_det += MathLog(diag[i]); // суммируем логарифмы диагональных элементов L
  
   //--- Вычисляем третье слагаемое: n/2 * log(2π)
   double const_term = 0.5 * n * MathLog(2 * M_PI);

   return data_term + log_det + const_term;
   
}

Ковариационная матрица K вычисляется с помощью функции ComputeKernelMatrix, которая суммирует вклады от всех выбранных ядер (например, RBF, Linear, Periodic и т.д.).

//+------------------------------------------------------------------+
//| Вычисление ковариационной матрицы                                |
//+------------------------------------------------------------------+
matrix ComputeKernelMatrix(const matrix &X1, const matrix &X2, int &kernel_list[], KernelParams &params)
{
   matrix K  = matrix::Zeros(X1.Rows(), X2.Rows());
   for (int i = 0; i < ArraySize(kernel_list); i++)
   {
      switch (kernel_list[i])
      {
         case KERNEL_RBF:
            K += RBF_kernel(X1, X2, params.rbf.sigma_f, params.rbf.length);
            break;
         case KERNEL_LINEAR:
            K += Linear_kernel(X1, X2, params.linear.sigma_l);
            break;
         case KERNEL_PERIODIC:
            K += Periodic_kernel(X1, X2, params.periodic.sigma_f, params.periodic.length, params.periodic.period);
            break;
         case KERNEL_WHITE:
            // WhiteKernel добавляется отдельно в виде sigma^2 * I
            break;
      }
   }
   return K;
}

NLML используется как целевая функция для оптимизации гиперпараметров в функции OptimizeGP. Оптимизация проводится с помощью метода BLEIC из библиотеки ALGLIB. 

//+------------------------------------------------------------------+
//| Оптимизация гиперпараметров гауссовского процесса                |
//+------------------------------------------------------------------+
KernelParams OptimizeGP(int &kernel_list[], matrix &x_train, matrix &y_train)
{
   double w[]; //Массив начальных значений гиперпараметров
   double s[]; //Массив масштабов для гиперпараметров, используемых для нормализации в оптимизации
   double bndl[], bndu[]; // Массивы нижних и верхних границ для каждого гиперпараметра    
   CObject Obj;
   CNDimensional_GP ffunc(kernel_list, x_train, y_train);// Объект класса, реализующего целевую функцию NLML
   CNDimensional_Rep frep; // Объект для хранения отчета об оптимизации 
   
   // Инициализация параметров
   InitializeKernelParams(kernel_list, w, s, bndl, bndu);
   /*
   Подсчитывается общее количество параметров (num_params) в зависимости от типов ядер в kernel_list.
   Задает начальные значения параметров w,масштаб и границы для параметров  
   */

   CMinBLEICStateShell state;
   CMinBLEICReportShell rep; //Объект для хранения результатов оптимизации.

   double epsg = 0;  //Точность по градиенту (0 означает, что остановка по градиенту отключена)
   double epsf = 0.0001; //Точность по значению функции 
   double epsw = 0; // точность по параметрам 
   double diffstep = 0.0001; // Шаг для численного вычисления производных.
   double epso = 0.00001; // Параметры для внешних и внутренних условий сходимости в BLEIC
   double epsi = 0.00001;

   CAlglib::MinBLEICCreateF(w, diffstep, state); // Создает объект оптимизации BLEIC с начальными параметрами w и шагом для численных производных diffstep
   CAlglib::MinBLEICSetBC(state, bndl, bndu); //Устанавливает границы параметров (bndl, bndu).
   CAlglib::MinBLEICSetScale(state, s); //Устанавливает масштабы параметров (s).
   CAlglib::MinBLEICSetInnerCond(state, epsg, epsf, epsw); 
   CAlglib::MinBLEICSetOuterCond(state, epso, epsi);
   CAlglib::MinBLEICOptimize(state, ffunc, frep, 0, Obj);
   CAlglib::MinBLEICResults(state, w, rep);
   Print("TerminationType =", rep.GetTerminationType()); // Код завершения оптимизации
   /*
                * -8    internal integrity control  detected  infinite or
                        NAN   values   in   function/gradient.   Abnormal
                        termination signalled.
                * -3   inconsistent constraints. Feasible point is
                       either nonexistent or too hard to find. Try to
                       restart optimizer with better initial approximation
                *  1   relative function improvement is no more than EpsF.
                *  2   scaled step is no more than EpsX.
                *  4   scaled gradient norm is no more than EpsG.
                *  5   MaxIts steps was taken
                *  8   terminated by user who called minbleicrequesttermination().
                       X contains point which was "current accepted"  when
                       termination request was submitted.   
   */
   Print("IterationsCount =", rep.GetInnerIterationsCount()); // Количество итераций

   Print("Parameters:");
   PrintKernelParams(w, kernel_list); // Выводит оптимизированные параметры в журнал
   Print("NLML = ", ffunc.GetNLML()); // финальное значение NLML для оптимальных параметров

   KernelParams optimized_params;    
   CRowDouble parameters = w;   
   //определяем правильное распределение параметров по ядрам
   ExtractKernelParams(parameters, kernel_list, optimized_params); 

   return optimized_params;
}

Регрессия ГП в MQL5

Для иллюстрации возможностей регрессионной модели на основе гауссовского процесса, рассмотрим пример, использующий синтетические данные. Реализация представлена в скрипте GP_Regressor, который демонстрирует процесс создания, обучения и тестирования модели.

Генерация данных осуществляется с помощью функции Dataset, которая формирует матрицы синтетических данных для обучения и тестирования. Датасет состоит из 100 точек, равномерно распределенных в диапазоне [−5,5], и представляет собой функцию y=sin⁡(x)+0.5x с добавленным гауссовским шумом. Такой подход позволяет имитировать реальные данные, содержащие как линейный тренд, так и периодическую компоненту, с учетом  неопределенности.

Для построения регрессионной модели, необходимо определить список ядер, формирующих ковариационную функцию. Каждое ядро вносит уникальный вклад в ковариационную матрицу K, определяя характер зависимостей, которые модель способна улавливать. Настройка списка ядер осуществляется функцией SetKernelList, которая формирует массив kernel_list на основе входного параметра kernel_combination (тип enum KernelCombination). Поддерживаются следующие комбинации:

• COMBINATION_1: [RBF, Linear, White] (3 ядра),
• COMBINATION_2: [RBF, Linear, Periodic, White] (4 ядра),
• COMBINATION_3: [RBF, White] (2 ядра).

Гибкость выбора комбинации ядер позволяет адаптировать модель к различным типам данных, будь то линейные тренды, периодические колебания или сложные нелинейные зависимости.
После выбора ядер выполняется оптимизация гиперпараметров модели с помощью функции OptimizeGP. Эта функция минимизирует отрицательное логарифмическое правдоподобие (NLML), возвращая структуру KernelParams, содержащую оптимальные параметры для каждого ядра, такие как амплитуда (σ_f), длина масштаба (l) или период (p).

После того, как оптимальные параметры найдены, переходим к прогнозу c помощью функции Predict.

//+------------------------------------------------------------------------+
//| Предсказание гауссовского апостериорного распределения для новых точек |    
//+------------------------------------------------------------------------+
GPPredictionResult Predict(const matrix &x_train, const matrix &y_train, const matrix &x_test, 
             int &kernel_list[], KernelParams &params)
{
  GPPredictionResult result; 

   //  Вычисляет ковариационную матрицу K для обучающих точек
   matrix K = ComputeKernelMatrix(x_train, x_train, kernel_list, params); 
   // Получаем дисперсию шума наблюдений
    double observation_noise_variance = 0.0;
    for (int i = 0; i < ArraySize(kernel_list); i++)
    {
        if (kernel_list[i] == KERNEL_WHITE)
        {
            observation_noise_variance = params.white.sigma * params.white.sigma;
            break;
        }
    }
   
   // Формируем матрицу шума для обучающих данных: K + sigma_n^2 * I
   matrix K_noisy_train = K + matrix::Identity((int)x_train.Rows(), (int)x_train.Rows()) * observation_noise_variance;  
   // Вычисляет кросс-ковариационную матрицу K* между обучающими и тестовыми точками   
   matrix K_star = ComputeKernelMatrix(x_train, x_test, kernel_list, params);
   // Вычисление апостериорного среднего
   matrix inv_term = K_noisy_train.Inv(); 
   result.mu_f_star = K_star.Transpose() @ (inv_term @ y_train); // Совпадает с mu_y_star
     
   // Вычисление апостериорной ковариационной матрицы для скрытой функции (Sigma_f_star)
    matrix K_star_star = ComputeKernelMatrix(x_test, x_test, kernel_list, params);
    result.Sigma_f_star = K_star_star - K_star.Transpose() @ (inv_term @ K_star);
    
   // Вычисление апостериорной ковариационной матрицы для нового наблюдения (Sigma_y_star)
   // Sigma_y_star = Sigma_f_star + sigma_n^2 * I
    result.Sigma_y_star = result.Sigma_f_star + matrix::Identity((int)x_test.Rows(), (int)x_test.Rows()) * observation_noise_variance;

    return result;
   
}

Функция Predict — это ключевой элемент реализации модели ГП, поскольку она не просто возвращает предсказанные значения, а предоставляет полную информацию об апостериорном распределении в тестовых точках. Функция возвращает структуру GPPredictionResult которая содержит:

• апостериорное среднее для латентной функции f* (μf* = μy*),
• апостериорную ковариационную матрицу Σf* для латентной функции f*,
• апостериорную ковариационную матрицу Σy* для новых наблюдаемых значений y*. Эта матрица включает в себя как неопределенность латентной функции, так и дисперсию шума наблюдений (σ^2), которая определяется в ходе оптимизации параметра ядра WhiteKernel.

Теперь посмотрим на результаты прогноза для различных комбинаций ядер. Для начала попробуем предсказать нашу функцию только с помощью RBF-ядра предполагая, что в данных присутствует шум (рис.7).

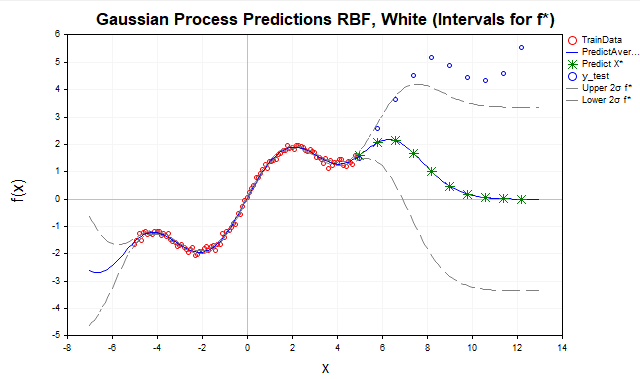
Рис.7 Прогноз с помощью RBF ядра

• Красные точки — обучающие данные (TrainData),
• Синяя линия — предсказанное среднее,
• Зеленые звездочки — предсказание для тестовых точек (X*),
• Синие точки — тестовые данные вне диапазона обучения,
• Серые пунктирные линии — доверительные интервалы (± 2 сигма для f* или y*)

Здесь мы видим, что при удалении тестовых точек от диапазона обучающих данных [-5,5], предсказания стремятся к априорному среднему ГП, которое обычно принимают равное нулю. Это происходит, поскольку вдали от обучающих данных ковариации K* (между новыми точками x* и обучающими точками х) для RBF ядра экспоненциально уменьшаются до нуля. Поэтому RBF-ядро лучше подходит для интерполяции данных, но для экстраполяции его применение ограничено из-за быстрого затухания корреляций.

 Для улучшения экстраполяции добавим линейное ядро (рис.8).

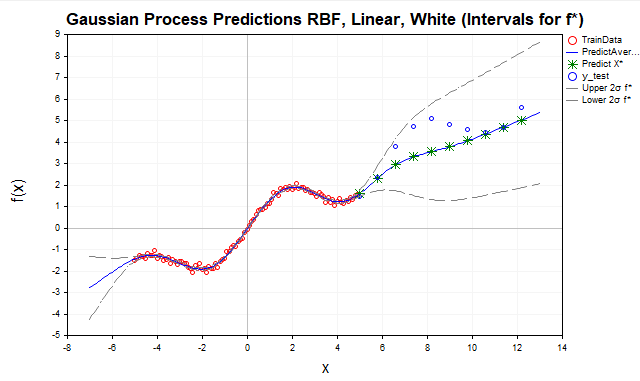
Рис.8 Прогноз с помощью суммы RBF и линейного ядра, f* интервалы

Линейное ядро моделирует линейные зависимости, что делает его подходящим для экстраполяции, особенно если данные имеют линейный или почти линейный тренд, как в нашем примере с функцией y=sin⁡(x)+0.5x. Включение линейного ядра позволило улучшить предсказания вне диапазона обучающих данных, уловив линейную компоненту (0.5x). Однако, как видно на графике, модель все еще не полностью отражает структуру данных, упуская их периодическую составляющую.

Для моделирования сезонных или циклических колебаний, таких как sin⁡(x) в наших данных, используется периодическое ядро (рис.9).

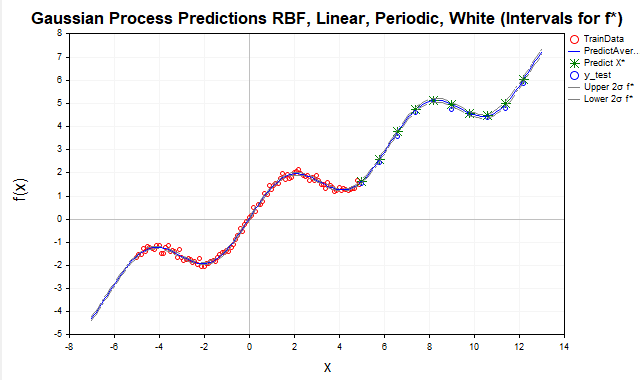
Рис.9 Прогноз с помощью суммы RBF, периодического и линейного ядра, f* интервалы

После добавления периодического ядра, модель достигла практически идеального прогноза, поскольку ей удалось уловить все существенные зависимости, присутствующие в данных. В результате, доверительные интервалы для f* (скрытой функции) практически сливаются с апостериорным средним. Для наблюдаемых значений y*, напротив, доверительные интервалы значительно шире, что логично, поскольку они учитывают дисперсию шума наблюдений, как показано на рис.10.

Рис.10 Прогноз с помощью суммы RBF, периодического и линейного ядра, y* интервалы

Важное замечание о предсказаниях в ГП. Без должного учёта дисперсии шума можно ошибочно интерпретировать доверительные интервалы для f*(x), как предсказательные интервалы для y*. Для получения корректных предсказательных интервалов для y*, необходимо явно включить дисперсию шума в ковариационную матрицу, что и реализовано в функции Predict.

Заключение

В данной статье мы подробно рассмотрели основы гауссовских процессов на примере задачи регрессии. Мы изучили ключевые компоненты ГП: априорное распределение, правдоподобие и апостериорное распределение, обеспечивающее полноценные вероятностные прогнозы с количественной оценкой неопределенности. Мы реализовали основные ядерные функции такие как RBF, Linear и Periodic, хотя их конечно значительно больше.

Особое внимание было уделено оптимизации гиперпараметров, что является критически важным для адаптации ГП к конкретным данным. Мы показали, что эта оптимизация осуществляется путём минимизации отрицательного логарифмического маргинального правдоподобия (NLML), где для повышения вычислительной эффективности и численной стабильности применяется разложение Холецкого. В реализованной модели в качестве оптимизатора использовался градиентный метод BLEIC из библиотеки ALGLIB.

Данная статья сосредоточена на базовых принципах ГП, и ряд продвинутых тем остался за её пределами. К ним относятся, например, применение аналитических выражений для градиентов NLML, которое способно значительно повысить эффективность оптимизации, а также использование разреженных аппроксимаций, критически важных для обработки больших объемов данных. Эти направления открывают перспективы для дальнейших исследований модели ГП.

#	Имя	Тип	Описание
1	GP_Samples_Prior.mq5	Script	Демонстрация выборок из априорного распределения
2	GP_Samples_Posterior.mq5	Script	Демонстрация выборок из апостериорного распределения
3	GP_Regressor	Script	Построение регрессионной модели