Интеграция скрытых марковских моделей в MetaTrader 5

Введение

Одной из основных характеристик финансовых временных рядов является то, что они обладают памятью. В контексте анализа временных рядов память относится к структуре зависимостей внутри данных, где прошлые значения влияют на текущие и будущие значения. Понимание структуры памяти помогает выбрать подходящую модель для временного ряда. В этой статье мы рассмотрим другой тип памяти: тип, который принимает форму скрытой марковской модели (Hidden Markov Mode, HMM). Мы рассмотрим основы HMM и покажем, как создать HMM с помощью модуля Python hmmlearn. Наконец, мы представим код на Python и MQL5, который позволяет экспортировать HMM для использования в программах MetaTrader 5.

Определение скрытых марковских моделей

Скрытые марковские модели — это мощный статистический инструмент, используемый для моделирования временных рядов данных, где моделируемая система характеризуется ненаблюдаемыми (скрытыми) состояниями. Фундаментальная предпосылка HMM заключается в том, что вероятность нахождения в заданном состоянии в определенный момент времени зависит от состояния процесса в предыдущем временном интервале. Эта зависимость представляет собой память HMM.

В контексте финансовых временных рядов состояния могут отражать тенденцию ряда к росту, к снижению или колебания в определенном диапазоне. Любой, кто пользовался финансовыми индикаторами, знаком с эффектом пилы, вызванным шумом, присущим финансовым временным рядам. HMM позволяет отфильтровывать эти ложные сигналы, давая более четкое представление об основных трендах.

Для построения HMM нам нужны наблюдения, которые охватывают всю совокупность поведения, определяющего процесс. Эта выборка данных используется для изучения параметров соответствующей HMM. Она будет состоять из различных характеристик моделируемого процесса. Например, если бы мы изучали цены закрытия финансового актива, мы могли бы также включить другие аспекты, связанные с ценой закрытия, например, различные индикаторы, которые в идеале помогают определить скрытые состояния, которые нас интересуют.

Обучение параметров модели проводится исходя из предположения, что моделируемый ряд всегда будет находиться в одном из двух или более состояний. Состояния имеют обозначения от 0 до S-1. Для этих состояний мы должны назначить набор вероятностей, которые отражают правдоподобие (likelihood) переключения процесса из одного состояния в другое. Эти вероятности обычно называют матрицей перехода. Первое наблюдение имеет особый набор начальных вероятностей нахождения в каждом возможном состоянии. Если наблюдение находится в определенном состоянии, ожидается, что оно будет следовать определенному распределению, связанному с этим состоянием.

Таким образом, HMM полностью определяется четырьмя свойствами:

• Число предполагаемых состояний
• Начальные вероятности нахождения первого наблюдения в любом из состояний
• Матрица переходов вероятностей
• Функции плотности вероятности для каждого состояния.
  

В начале у нас есть наблюдения и предполагаемое число состояний. Мы хотим найти параметры HMM, соответствующие имеющемуся у нас набору данных. Это делается путем наблюдения за правдоподобием с использованием статистического метода, называемого оценкой максимального правдоподобия. В нашем случае оценка максимального правдоподобия представляет собой поиск свойств модели, которые с наибольшей вероятностью соответствуют нашим выборкам данных. Поиск происходит путем расчета правдоподобия того, что каждый образец будет находиться в определенном состоянии в определенное время. Расчет производится с помощью прямого и обратного алгоритмов, которые проходят по всем образцам вперед и назад во времени соответственно.

Прямой алгоритм

Мы начинаем с первого наблюдения в нашем наборе данных, а затем вычисляем правдоподобия для последующих выборок. Для первой выборки мы используем начальные вероятности состояний, которые в настоящее время считаются тестовыми параметрами для кандидата в HMM. Если о моделируемом процессе ничего не известно, вполне приемлемо установить все начальные вероятности состояний равными 1/S, где S - общее число предполагаемых состояний. Применяя теорему Байеса, получаем следующее общее уравнение:

где lk - правдоподобие того, что образец в момент времени t будет находиться в состоянии i, а p - вероятность того, что образец будет находиться в состоянии i в момент времени t с учетом выборок вплоть до момента времени t. O - это отдельная выборка, отдельная строка в наборе данных.

Правдоподобие первой выборки рассчитывается по правилу условной вероятности, P(A) = P(A|B)P(B). Таким образом, для первой выборки правдоподобие нахождения в состоянии i вычисляется путем умножения начальной вероятности нахождения в состоянии i на функцию плотности вероятности первой выборки.

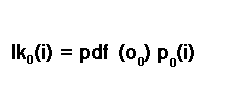
Это еще один тестовый параметр кандидата в HMM. В литературе его иногда называют вероятностью эмиссии. Более подробно вероятности эмиссии будут рассмотрены ниже. А пока просто помните, что на данном этапе это еще один тестовый параметр. Мы не уверены в текущем состоянии. Мы должны учитывать возможность того, что можем оказаться в любом из возможных состояний. В результате окончательное начальное правдоподобие представляет собой сумму всех правдоподобий всех возможных состояний.

 

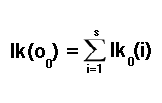
Чтобы рассчитать правдоподобия последующих наблюдений, нам необходимо рассмотреть возможность перехода в определенное состояние из любого из возможных состояний в предыдущем временном интервале. Здесь вступают в силу вероятности перехода, которые на данном этапе являются еще одним тестовым параметром. Вероятность достижения определенного состояния в следующем временном интервале, учитывая, что мы вычислили вероятность для текущего, оценивается путем умножения текущей известной вероятности состояния на соответствующую вероятность перехода.

Сейчас самое подходящее время поговорить о вероятностях перехода или матрице перехода.

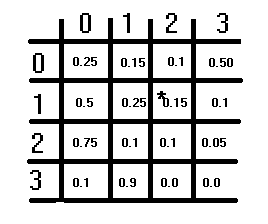
На рисунке выше показана гипотетическая матрица перехода. Она имеет структуру S×S, где S — число предполагаемых состояний. Каждый элемент представляет собой вероятность, а сумма вероятностей в каждой строке должна равняться 1. Это условие не распространяется на столбцы. Чтобы получить соответствующую вероятность перехода из одного состояния в другое, сначала обращаются к строкам, а затем к столбцам. Текущее состояние, из которого выполняется переключение, соответствует индексу строки, а состояние, в которое выполняется переключение, соответствует индексу столбца. Значение этих индексов представляет собой соответствующую вероятность перехода. Диагональ матрицы отображает вероятности того, что состояние не изменится.

Возвращаясь к задаче расчета правдоподобий для остальных наблюдений в выбранной нами выборке данных, мы умножали вероятность состояния на вероятность перехода. Однако, чтобы получить полную картину, мы должны рассмотреть возможность перехода в любое из возможных состояний. Мы делаем это, суммируя все возможности в соответствии со следующим уравнением:

            

На этом расчет индивидуальных правдоподобий для каждой выборки в нашем наборе данных завершен. Эти отдельные правдоподобия можно объединить путем умножения, чтобы получить правдоподобие для всего набора данных. Описанное выше вычисление называется прямым алгоритмом из-за временной прямой рекурсии метода.

Обратный алгоритм

Также можно рассчитать индивидуальные правдоподобия, перемещаясь назад по времени, начиная с последней выборки данных и заканчивая первой. Начнем с установки правдоподобия для всех состояний на уровне 1 для последней выборки данных. Для каждой выборки данных, если она находится в определенном состоянии, мы вычисляем правдоподобие последующего набора выборок, учитывая, что мы можем перейти в любое из состояний. Мы делаем это, вычисляя взвешенную сумму правдоподобий каждого состояния: вероятность нахождения в этом состоянии, умноженную на функцию плотности вероятности нахождения образца в том же состоянии. Результат этого расчета затем корректируется с использованием вероятности перехода из текущего состояния в следующее в качестве весового коэффициента. Всё это показано в формуле ниже:

Функции плотности вероятности

В обсуждениях прямого и обратного алгоритмов упоминались функции плотности вероятности (probability density functions, PDF) в качестве параметров HMM. Как упоминалось ранее, параметры PDF модели HMM обычно называются вероятностями эмиссии. Их называют вероятностями, когда моделируемые данные состоят из дискретных или категориальных значений. При работе с непрерывными переменными мы используем PDF.

В этой статье мы демонстрируем HMM, которые моделируют наборы данных непрерывных переменных, следующие многомерному нормальному распределению. Можно реализовать и другие распределения. Модуль Python, который мы рассмотрим позже, имеет реализации HMM для различных распределений моделируемых данных. В более широком смысле параметры предполагаемого распределения становятся одним из параметров HMM. В случае многомерного нормального распределения его параметрами являются средние значения и ковариации.

Алгоритм Баума-Велша

Алгоритм Баума-Велша - метод максимизации ожиданий, используемый для проверки различных параметров кандидатов на роль HMM с целью выбора оптимального варианта. Максимизируемое значение в этой процедуре оптимизации — это правдоподобие для всего набора данных образцов. Алгоритм Баума-Велша известен своей эффективностью и надежностью, но у него есть свои недостатки. Одним из существенных недостатков является его невыпуклость. Невыпуклые функции по отношению к оптимизации — это функции с многочисленными локальными минимумами или максимумами.

Это означает, что при достижении сходимости глобальный максимум или минимум пространства параметров может быть не найден. Функция в принципе не гарантирует сходимости в оптимальной точке. Лучший способ смягчить этот недостаток — пробовать параметры, которые имеют большое правдоподобие по сравнению с другими в пространстве параметров. Для этого нам пришлось бы перебрать множество случайных значений параметров, чтобы найти наилучшее начальное пространство параметров, с которого можно было бы начать оптимизацию.

Расчет вероятностей состояний

Получив оптимальную модель HMM и ее параметры, мы можем использовать ее для расчета вероятностей состояний для невидимых выборок данных. Результатом такого расчета будет набор вероятностей, по одной для каждого состояния, указывающих вероятность нахождения в каждом состоянии. Отдельные правдоподобия из прямого алгоритма умножаются на правдоподобия из обратного алгоритма, в результате чего получается правдоподобие определенного состояния. Согласно правилу Байеса, вероятность того, что наблюдение находится в определенном состоянии, рассчитывается как:

Расчет вероятностей состояний с использованием алгоритма Витерби

Помимо вероятностей состояний, мы также можем сделать вывод о вероятном состоянии, в котором находится наблюдение, используя алгоритм Витерби. Расчет начинается с первого наблюдения, вероятности состояний которого вычисляются с использованием начальных вероятностей состояний, умноженных на вероятности эмиссии.

Для каждого наблюдения со второго по последнее вероятность каждого состояния рассчитывается с использованием вероятности предыдущего состояния, соответствующей вероятности перехода и вероятности его эмиссии. Наиболее вероятным будет состояние с наибольшей вероятностью.

Мы рассмотрели все компоненты скрытой марковской модели. Теперь перейдем к его практической реализации. Начнем с рассмотрения реализации HMM на языке Python, представленной в пакете hmmlearn. Мы обсудим использование реализации гауссовой HMM в hmmlearn, а затем перейдем к коду MQL5, чтобы продемонстрировать, как интегрировать модель, обученную на Python с помощью hmmlearn, в приложения MetaTrader 5.

Пакет hmmlearn для Python

Библиотека hmmlearn на Python предоставляет инструменты для работы со скрытыми марковскими моделями. Инструменты для обучения HMM находятся в пространстве имен 'hmm'. Внутри 'hmm' объявлено несколько специальных классов для работы с процессами разных дистрибутивов. А именно:

• MultinomialHMM: Модели HMM, где наблюдения дискретны и следуют полиномиальному распределению.
• GMMHMM: Модели HMM, в которых наблюдения генерируются из совокупности гауссовых распределений.
• PoissonHMM: Модели HMM, в которых предполагается, что наблюдения следуют распределению Пуассона.
• Наконец, у нас есть класс GaussianHMM, который обрабатывает наборы данных, которые, как правило, следуют многомерному гауссовскому (нормальному) распределению. Это класс, который мы продемонстрируем и модель которого мы свяжем с MetaTrader 5.

Для установки пакета используйте следующую команду:

pip install hmmlearn

После установки пакета вы можете импортировать класс GaussianHMM, используя следующий оператор импорта:

from hmmlearn.hmm import GaussianHMM

В качестве альтернативы вы можете импортировать модуль hmm, который содержит все перечисленные выше классы, а также другие полезные утилиты. Если используется этот метод, то имена классов должны начинаться с префикса hmm, например:

from hmmlearn import hmm

Вы можете инициализировать объект GaussianHMM несколькими параметрами:

model = GaussianHMM(n_components=3, covariance_type='diag', n_iter=100, tol=0.01)

где:

• n_components - количество состояний в модели
• covariance_type - тип используемых параметров ковариации (spherical, diag, full, tied). Используемый тип ковариации связан с особенностями набора данных. Сферическую (spherical) ковариацию следует выбирать, если признаки или переменные в моделируемом наборе данных имеют схожую дисперсию и не имеют возможности корреляции. В противном случае, если переменные имеют контрастные дисперсии, наилучшим вариантом будет выбор диагонального типа ковариации (diag). Если переменные коррелируют, то следует выбрать либо полный, либо связанный тип ковариации. Выбор полной (full) ковариации обеспечивает наибольшую гибкость, но может быть сопряжен с большими вычислительными затратами. Это самый безопасный выбор, ограничивающий количество предположений относительно моделируемого процесса. Связанная (tied) ковариация предполагает, что состояния имеют схожую ковариационную структуру. Это немного эффективнее по сравнению с полной ковариацией
• n_iter - максимальное количество итераций, выполняемых во время обучения
• tol - порог конвергенции.

Чтобы изучить все параметры, определяющие модель, вы можете обратиться к документации по библиотеке hmmlearn. В документации содержится подробная информация о различных параметрах и их использовании. Вы можете получить к ней доступ онлайн на официальном сайте библиотеки hmmlearn или посмотреть документацию, входящей в комплект установки библиотеки, с помощью встроенной справочной утилиты Python.

help(GaussianHMM)

Для обучения модели вызываем метод fit(). В качестве входных данных ожидается как минимум один двумерный массив.

model.fit(data)

После завершения обучения мы можем получить скрытые состояния набора данных, вызвав predict() или decode(). Оба ожидают двумерный массив с тем же количеством признаков, что и набор данных, используемый для обучения модели. Метод predict() возвращает массив вычисленных скрытых состояний, а decode() - логарифмическое правдоподобие вместе с массивом скрытых состояний, заключенным в кортеж.

Вызов score_samples() возвращает логарифмическое правдоподобие, а также вероятности состояний для набора данных, предоставленного в качестве входных данных. Опять же, данные должны иметь то же количество признаков, что и данные, используемые для обучения модели.

Экспорт скрытой марковской модели

Экспорт модели, обученной на Python с использованием пакета hmmlearn, для использования в MetaTrader 5 включает реализацию двух пользовательских компонентов:

• Компонент Python: этот компонент отвечает за сохранение параметров обученной модели в формате, читаемом из приложения MetaTrader. Он включает экспорт параметров модели в формат файла, который может быть проанализирован приложениями MetaTrader 5.
• Компонент MQL5: Содержит код, написанный на языке MQL5. Этот компонент должен включать функционал для чтения параметров HMM, экспортируемых компонентом Python. Кроме того, необходимо реализовать прямой, обратный алгоритмы и алгоритм Витерби для расчета скрытых состояний и вероятностей состояний для набора данных на основе указанной HMM.
  

Реализация этих компонентов требует тщательного рассмотрения форматов сериализации данных, операций ввода и вывода файлов, а также алгоритмических реализаций как на Python, так и на MQL5. Для точного переноса обученной модели и выполнения задач вывода в MetaTrader 5 крайне важно обеспечить совместимость между реализациями Python и MQL5.

Пакет hmmlearn позволяет сохранить обученную HMM с помощью модуля pickle. Проблема в том, что после pickle с файлами нелегко работать вне Python. Поэтому лучшим вариантом будет использование формата json. Параметр HMM будет записан в структурированный файл JSON, который можно прочитать с помощью кода MQL5. Этот функционал реализована в функции Python ниже.

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

Эта функция принимает в качестве входных данных экземпляр класса GaussianHMM и имя файла и записывает параметры HMM в файл JSON в структурированном формате, который можно прочитать с помощью кода MQL5.

В коде MQL5 функционал для чтения моделей HMM, сохраненных в формате JSON, заключен в hmmlearn.mqh. Файл содержит определение класса HMM.

//+------------------------------------------------------------------+
//|                                                     hmmlearn.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Alglib\dataanalysis.mqh>
#include<Math\Stat\Uniform.mqh>
#include<Math\Stat\Math.mqh>
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>

//+------------------------------------------------------------------+
//|Markov model estimation method                                    |
//+------------------------------------------------------------------+
enum ENUM_HMM_METHOD
  {
   MODE_LOG=0,
   MODE_SCALING
  };
//+------------------------------------------------------------------+
//| state sequence decoding algorithm                                |
//+------------------------------------------------------------------+
enum ENUM_DECODE_METHOD
  {
   MODE_VITERBI=0,
   MODE_MAP
  };
//+------------------------------------------------------------------+
//| Hidden Markov Model class                                        |
//+------------------------------------------------------------------+
class HMM
  {
private:
   ulong m_samples ;       // Number of cases in dataset
   ulong m_vars ;        // Number of variables in each case
   ulong m_states ;      // Number of states
   vector            m_initprobs;   // vector of probability that first case is in each state
   matrix            m_transition;  // probability matrix
   matrix m_means ;                 //state means
   matrix m_covars[] ;              // covariances
   matrix densities ;              // probability densities
   matrix alpha ;       // result of forward algorithm
   matrix beta ;        // result of backward algorithm
   matrix m_stateprobs ; // probabilities of state
   double likelihood ;  //  log likelihood
   matrix            trial_transition;
   bool              trained;
   double            m_mincovar;
   ENUM_HMM_METHOD   m_hmm_mode;
   ENUM_DECODE_METHOD m_decode_mode;
   //+------------------------------------------------------------------+
   //| normalize array so sum(exp(a)) == 1                              |
   //+------------------------------------------------------------------+
   matrix            log_normalize(matrix &in)
     {
      matrix out;
      if(in.Cols()==1)
         out = matrix::Zeros(in.Rows(), in.Cols());
      else
         out = logsumexp(in);
      return in-out;
     }
   //+------------------------------------------------------------------+
   //| log of the sum of exponentials of input elements                 |
   //+------------------------------------------------------------------+
   matrix            logsumexp(matrix &in)
     {
      matrix out;

      vector amax = in.Max(1);

      for(ulong i = 0; i<amax.Size(); i++)
         if(fpclassify(MathAbs(amax[i])) == FP_INFINITE)
            amax[i] = 0.0;

      matrix ama(amax.Size(),in.Cols());
      for(ulong i=0; i<ama.Cols();i++)
         ama.Col(amax,i);

      matrix tmp = exp(in - ama);

      vector s = tmp.Sum(1);

      out.Init(s.Size(),in.Cols());
      for(ulong i=0; i<out.Cols();i++)
         out.Col(log(s),i);

      out+=ama;

      return out;
     }

   //+------------------------------------------------------------------+
   //| normarlize vector                                                |
   //+------------------------------------------------------------------+
   vector            normalize_vector(vector &in)
     {
      double sum = in.Sum();
      return in/sum;
     }
   //+------------------------------------------------------------------+
   //|  normalize matrix                                                |
   //+------------------------------------------------------------------+
   matrix            normalize_matrix(matrix &in)
     {
      vector sum = in.Sum(1);

      for(ulong i = 0; i<sum.Size(); i++)
         if(sum[i] == 0.0)
            sum[i] = 1.0;

      matrix n;
      n.Init(sum.Size(), in.Cols());
      for(ulong i =0; i<n.Cols(); i++)
         n.Col(sum,i);

      return in/n;
     }
   //+------------------------------------------------------------------+
   //|   Set up model from JSON object                                  |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      if(jsonmodel["implementation"].ToStr() == "log")
         m_hmm_mode = MODE_LOG;
      else
         m_hmm_mode = MODE_SCALING;

      if(jsonmodel["algorithm"].ToStr() == "Viterbi")
         m_decode_mode = MODE_VITERBI;
      else
         m_decode_mode = MODE_MAP;

      m_states = (ulong)jsonmodel["numstates"].ToInt();
      m_vars = (ulong)jsonmodel["numvars"].ToInt();


      if(!m_initprobs.Resize(m_states) || !m_means.Resize(m_states,m_vars) ||
         !m_transition.Resize(m_states,m_states) || ArrayResize(m_covars,int(m_states))!=int(m_states))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(uint i = 0; i<m_covars.Size(); i++)
        {
         if(!m_covars[i].Resize(m_vars,m_vars))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

         for(int k = 0; k<int(m_covars[i].Rows()); k++)
            for(int j = 0; j<int(m_covars[i].Cols()); j++)
               m_covars[i][k][j] = jsonmodel["covars"][i][k][j].ToDbl();
        }

      for(int i =0; i<int(m_initprobs.Size()); i++)
        {
         m_initprobs[i] = jsonmodel["initprobs"][i].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_vars); j++)
            m_means[i][j] = jsonmodel["means"][i][j].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_states); j++)
            m_transition[i][j] = jsonmodel["transitions"][i][j].ToDbl();
        }

      return true;
     }

   //+------------------------------------------------------------------+
   //|  Multivariate Normal Density function                            |
   //+------------------------------------------------------------------+
   double            mv_normal(ulong nv,vector &x, vector &mean, matrix &in_covar)
     {
      matrix cv_chol;
      vector vc = x-mean;

      if(!in_covar.Cholesky(cv_chol))
        {
         matrix ncov = in_covar+(m_mincovar*matrix::Eye(nv,nv));
         if(!ncov.Cholesky(cv_chol))
           {
            Print(__FUNCTION__,": covars matrix might not be symmetric positive-definite, error ", GetLastError());
            return EMPTY_VALUE;
           }
        }

      double cv_log_det = 2.0 * (MathLog(cv_chol.Diag())).Sum();
      vector cv_sol = cv_chol.Solve(vc);

      return -0.5*((nv*log(2.0 * M_PI)) + (pow(cv_sol,2.0)).Sum() + cv_log_det);

     }


   //+------------------------------------------------------------------+
   //|logadd exp                                                        |
   //+------------------------------------------------------------------+
   double            logaddexp(double a, double b)
     {
      return a==-DBL_MIN?b:b==-DBL_MIN?a:MathMax(a,b)+log1p(exp(-1.0*MathAbs(b-a)));
     }
   //+------------------------------------------------------------------+
   //| scaled trans calculation                                         |
   //+------------------------------------------------------------------+
   matrix            compute_scaling_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logdens = exp(dens).Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Resize(nc,nc);
      out.Fill(0.0);

      for(ulong t =0; t<ns-1; t++)
        {
         for(ulong i = 0; i<nc; i++)
           {
            for(ulong j = 0; j<nc; j++)
              {
               out[i][j] += alf[t][i] * trans[i][j] * logdens[t+1][j]*bta[t+1][j];
              }
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| log trans calculation                                            |
   //+------------------------------------------------------------------+
   matrix            compute_log_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      vector row = alf.Row(ns-1);
      double logprob = (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);

      matrix out;
      out.Init(nc,nc);

      out.Fill(-DBL_MIN);

      for(ulong t = 0 ; t<ns-1; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               double vl = alf[t][i] + logtrans[i][j]+ logdens[t+1][j]+bta[t+1][j] - logprob;
               out[i][j] = logaddexp(out[i][j], vl);
              }
           }
        }

      return out;

     }
   //+------------------------------------------------------------------+
   //| forward scaling                                                  |
   //+------------------------------------------------------------------+
   double            forwardscaling(vector &startp, matrix &trans, matrix &dens,matrix &out, vector&outt)
     {
      double minsum = 1.e-300;
      vector gstartp = startp;
      matrix gtrans = trans;
      matrix gdens = exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      if(outt.Size()!=ns)
         outt.Resize(ns);

      out.Fill(0.0);

      double logprob = 0.0;

      for(ulong i = 0; i<nc; i++)
         out[0][i] = gstartp[i]*gdens[0][i];

      double sum  = (out.Row(0)).Sum();

      if(sum<minsum)
         Print("WARNING: forward pass failed with underflow consider using log implementation ");

      double scale = outt[0] = 1.0/sum;
      logprob -= log(scale);

      for(ulong i=0; i<nc; i++)
         out[0][i] *=scale;

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j=0; j<nc; j++)
           {
            for(ulong i=0; i<nc; i++)
              {
               out[t][j]+=out[t-1][i] * gtrans[i][j];
              }
            out[t][j]*=gdens[t][j];
           }
         sum = (out.Row(t)).Sum();
         if(sum<minsum)
            Print("WARNING: forward pass failed with underflow consider using log implementation ");

         scale = outt[t] = 1.0/sum;
         logprob -= log(scale);
         for(ulong j = 0; j<nc; j++)
            out[t][j] *= scale;

        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //|backward scaling                                                  |
   //+------------------------------------------------------------------+
   matrix            backwardscaling(vector &startp, matrix &trans, matrix &dens,vector &scaling)
     {
      vector gstartp = startp;
      vector scaled = scaling;
      matrix gtrans = trans;
      matrix gdens =  exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      matrix out;
      out.Init(ns,nc);

      out.Fill(0.0);
      for(ulong i = 0; i<nc; i++)
         out[ns-1][i] = scaling[ns-1];

      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i=0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               out[t][i]+=(gtrans[i][j]*gdens[t+1][j]*out[t+1][j]);
              }
            out[t][i]*=scaling[t];
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| forward log                                                      |
   //+------------------------------------------------------------------+
   double            forwardlog(vector &startp, matrix &trans, matrix &dens,matrix &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j =0; j<nc; j++)
           {
            for(ulong i =0; i<nc; i++)
              {
               buf[i] = out[t-1][i] + logtrans[i][j];
              }
            out[t][j] = logdens[t][j] + (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }

      vector row = out.Row(ns-1);

      return (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);
     }
   //+------------------------------------------------------------------+
   //|  backwardlog                                                     |
   //+------------------------------------------------------------------+
   matrix            backwardlog(vector &startp, matrix &trans, matrix &dens)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Init(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[ns-1][i] = 0.0;

      for(long t = long(ns-2); t>=0; t--)
        {
         for(long i =0; i<long(nc); i++)
           {
            for(long j =0; j<long(nc); j++)
              {
               buf[j] = logdens[t+1][j] + out[t+1][j] + logtrans[i][j];
              }
            out[t][i] = (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities scaling                    |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_scaling(matrix &alf, matrix &bta)
     {
      return normalize_matrix(alf*bta);
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities log                        |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_log(matrix &alf, matrix &bta)
     {
      return exp(log_normalize(alf+bta));
     }
   //+------------------------------------------------------------------+
   //|calculate the probability of a state                              |
   //+------------------------------------------------------------------+
   double            compute_posteriors(matrix &data, matrix &result, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix alfa,bt,dens;
      double logp=0.0;
      dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      if(use_log == MODE_LOG)
        {
         logp = forwardlog(m_initprobs,m_transition,dens,alfa);
         bt = backwardlog(m_initprobs,m_transition,dens);
         result = compute_posteriors_log(alfa,bt);
        }
      else
        {
         vector scaling_factors;
         logp = forwardscaling(m_initprobs,m_transition,dens,alfa,scaling_factors);
         bt = backwardscaling(m_initprobs,m_transition,dens,scaling_factors);
         result = compute_posteriors_scaling(alfa,bt);
        }
      return logp;
     }
   //+------------------------------------------------------------------+
   //| map  implementation                                              |
   //+------------------------------------------------------------------+
   double            map(matrix &data,vector &out, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix posteriors;
      double lp = compute_posteriors(data,posteriors,use_log);
      lp = (posteriors.Max(1)).Sum();
      out = posteriors.ArgMax(1);
      return lp;
     }
   //+------------------------------------------------------------------+
   //| viterbi implementation                                           |
   //+------------------------------------------------------------------+
   double            viterbi(vector &startp, matrix &trans, matrix &dens, vector &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      double logprob = 0;
      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Size()<ns)
         out.Resize(ns);

      matrix vit(ns,nc);
      for(ulong i = 0; i<nc; i++)
         vit[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t = 1; t<ns; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            double max = -DBL_MIN;
            for(ulong j = 0; j<nc; j++)
              {
               max = MathMax(max,vit[t-1][j]+logtrans[j][i]);
              }
            vit[t][i] = max+logdens[t][i];
           }
        }
      out[ns-1] = (double)(vit.Row(ns-1)).ArgMax();
      double prev = out[ns-1];
      logprob = vit[ns-1][long(prev)];
      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i =0; i<nc; i++)
           {
            prev = ((vit[t][i]+logtrans[i][long(prev)])>=-DBL_MIN && i>=0)?double(i):double(0);
           }
         out[t] = prev;
        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //| Calculate the probability density function                       |
   //+------------------------------------------------------------------+
   matrix              find_densities(ulong variables,ulong states,matrix &mdata,matrix &the_means, matrix &covs[])
     {
      matrix out;
      out.Resize(states,mdata.Rows());

      for(ulong state=0 ; state<states ; state++)
        {
         for(ulong i=0 ; i<mdata.Rows() ; i++)
            out[state][i] = mv_normal(variables, mdata.Row(i), the_means.Row(state), covs[state]) ;
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| Forward algorithm                                                |
   //+------------------------------------------------------------------+

   double            forward(matrix &_transitions)
     {
      double sum, denom, log_likelihood;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         alpha[0][i] = m_initprobs[i] * densities[i][0] ;
         denom += alpha[0][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         alpha[0][i] /= denom ;


      for(ulong t=1 ; t<m_samples ; t++)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            ulong trans_ptr = i;
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
              {
               sum += alpha[t-1][j] * _transitions.Flat(trans_ptr);
               trans_ptr += m_states ;
              }
            alpha[t][i] = sum * densities[i][t] ;
            denom += alpha[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            alpha[t][i] /= denom ;
        }

      return log_likelihood ;

     }
   //+------------------------------------------------------------------+
   //| Backward algorithm                                               |
   //+------------------------------------------------------------------+
   double            backward(void)
     {
      double sum, denom, log_likelihood ;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         beta[(m_samples-1)][i] = 1.0 ;
         denom += beta[(m_samples-1)][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         beta[(m_samples-1)][i] /= denom ;

      for(long t=long(m_samples-2) ; t>=0 ; t--)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
               sum += m_transition[i][j] * densities[j][t+1] * beta[(t+1)][j] ;
            beta[t][i] = sum ;
            denom += beta[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            beta[t][i] /= denom ;
        }

      sum = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
         sum += m_initprobs[i] * densities[i][0] * beta[0][i] ;

      return log(sum) + log_likelihood ;
     }

public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     HMM(void)
     {
      trained =false;

      m_hmm_mode = MODE_LOG;
      m_decode_mode = MODE_VITERBI;
      m_mincovar = 1.e-7;
     }
   //+------------------------------------------------------------------+
   //| desctructor                                                      |
   //+------------------------------------------------------------------+

                    ~HMM(void)
     {

     }

   //+------------------------------------------------------------------+
   //| Load model data from regular file                                |
   //+------------------------------------------------------------------+
   bool               load(string file_name)
     {
      trained = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         trained = fromJSON(js);
        }
      return trained;
     }
   //+------------------------------------------------------------------+
   //|Predict the state given arbitrary input variables                 |
   //+------------------------------------------------------------------+

   matrix            predict_state_probs(matrix &inputs)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         matrix::Zeros(1, m_states);
        }

      matrix probs;
      compute_posteriors(inputs,probs,m_hmm_mode);

      return probs;
     }
   //+------------------------------------------------------------------+
   //|Predict the state sequence of arbitrary input variables           |
   //+------------------------------------------------------------------+
   vector            predict_state_sequence(matrix &inputs, ENUM_DECODE_METHOD decoder=WRONG_VALUE)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         vector::Zeros(1);
        }

      vector seq = vector::Zeros(inputs.Rows());
      ENUM_DECODE_METHOD decm;
      if(decoder!=WRONG_VALUE)
         decm = decoder;
      else
         decm = m_decode_mode;

      switch(decm)
        {
         case MODE_VITERBI:
           {
            matrix d = find_densities(m_vars,m_states,inputs,m_means,m_covars);
            viterbi(m_initprobs,m_transition,d,seq);
            break;
           }
         case MODE_MAP:
           {
            map(inputs,seq,m_hmm_mode);
            break;
           }
        }

      return seq;
     }
   //+------------------------------------------------------------------+
   //| get the loglikelihood of the model                               |
   //+------------------------------------------------------------------+

   double            get_likelihood(matrix &data)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return EMPTY_VALUE;
        }

      matrix dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      matrix alfa;
      vector sc;

      switch(m_hmm_mode)
        {
         case MODE_LOG:
            likelihood = forwardlog(m_initprobs,m_transition,dens,alfa);
            break;
         case MODE_SCALING:
            likelihood = forwardscaling(m_initprobs,m_transition,dens,alfa,sc);
            break;
        }

      return likelihood;
     }
   //+------------------------------------------------------------------+
   //| get the initial state probabilities of the model                 |
   //+------------------------------------------------------------------+

   vector            get_init_probs(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return vector::Zeros(1);
        }
      return m_initprobs;
     }
   //+------------------------------------------------------------------+
   //| get the probability transition matrix                            |
   //+------------------------------------------------------------------+

   matrix            get_transition_matrix(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_transition;
     }
   //+------------------------------------------------------------------+
   //|get the state means matrix                                        |
   //+------------------------------------------------------------------+

   matrix            get_means(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_means;
     }

   //+------------------------------------------------------------------+
   //| get the covariance matrix for a particular state                 |
   //+------------------------------------------------------------------+

   matrix            get_covar_matrix_for_state_at(ulong state_index)
     {
      if(!trained || state_index>m_states)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_covars[state_index];
     }
   //+------------------------------------------------------------------+
   //|  get the number of features for the model                        |
   //+------------------------------------------------------------------+
   ulong             get_num_features(void)
     {
      return m_vars;
     }
  };


//+------------------------------------------------------------------+

После создания экземпляра класса HMM мы вызываем метод load() с определенным именем файла.

//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }

Если параметры модели успешно прочитаны, метод вернет true.

После загрузки модели мы можем получить скрытые состояния и вероятности состояний для определенного набора наблюдений. Однако важно отметить, что реализация всех алгоритмов, описанных ранее в тексте, несколько отличается. Вместо необработанных правдоподобий код использует логарифм необработанных значений для обеспечения числовой стабильности. Таким образом, вместо обычных правдоподобий мы имеем логарифмические правдоподобия. Это также означает, что везде, где требуется умножение, нам придется использовать сложение, поскольку мы имеем дело с логарифмом значений.

Метод HMM get_likelihood() возвращает логарифмическое правдоподобие для набора наблюдений на основе загруженных параметров модели. Он рассчитывается с использованием прямого алгоритма. Метод predict_state_probs() рассчитывает вероятности состояний для каждого наблюдения, предоставленного в качестве входного параметра. Этот метод возвращает матрицу, в которой каждая строка представляет вероятности состояний для наблюдения.

С другой стороны, метод predict_state_sequence() возвращает вектор, представляющий состояние для каждого образца, который был предоставлен в качестве входного параметра. По умолчанию он использует алгоритм Витерби для расчета наиболее вероятной последовательности состояний. Однако можно также выбрать простую технику map, имитирующую поведение метода decode() в GaussianHMM.

Класс HMM предоставляет методы-получатели для извлечения параметров загруженной модели:

• get_means() - возвращает матрицу средних значений, используемых для определения плотностей вероятностей
• get_covar_matrix_for_state_at() - получает полную ковариационную матрицу для определенного состояния
• get_transition_matrix() - возвращает вероятности перехода в виде матрицы
• get_init_probs() - возвращает вектор вероятностей начального состояния модели
• get_num_features() - возвращает беззнаковое значение long, представляющее количество переменных, ожидаемых в качестве входных параметров для модели. Это означает, что любая матрица, предоставленная в качестве входного параметра для predict_state_probs(), predict_state_sequence() и get_likelihood(), должна иметь указанное количество столбцов и не менее двух строк.

Скрипт saveHMM.py обучает HMM на основе случайного набора данных. Он включает определение функции hmm2json(), которая отвечает за сохранение окончательных параметров модели в файле json. Данные состоят из 10 строк и 5 столбцов. Создается экземпляр класса GaussianHMM, и HMM обучается на случайных данных. После подбора модели вызывается hmm2json() для сохранения параметров модели в файле JSON. Затем выводятся логарифмическое правдоподобие, скрытые состояния и вероятности состояний.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
from hmmlearn import hmm
import numpy as np
import pandas as pd
import json 


assumed_states = 2 #number of states of process
maxhmm_iters = 10000 #maximum number of iterations for optimization procedure

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 
#dataset to train model on    
dataset = np.array([[0.56807844,0.67179966,0.13639585,0.15092627,0.17708295],
                   [0.62290044,0.15188847,0.91947761,0.29483647,0.34073613],
                   [0.47687505,0.06388765,0.20589139,0.16474974,0.64383775],
                   [0.25606858,0.50927144,0.49009671,0.0284832,0.37357852],
                   [0.95855305,0.93687549,0.88496015,0.48772751,0.10256193],
                   [0.36752403,0.5283874 ,0.52245909,0.77968798,0.88154157],
                   [0.35161822,0.50672902,0.7722671,0.56911901,0.98874104],
                   [0.20354888,0.82106204,0.60828044,0.13380222,0.4181293,],
                   [0.43461371,0.60170739,0.56270993,0.46426138,0.53733481],
                   [0.51646574,0.54536398,0.03818231,0.32574409,0.95260478]])  
#instantiate an HMM and train on dataset
model = hmm.GaussianHMM(assumed_states,n_iter=maxhmm_iters,covariance_type='full',random_state=125, verbose=True).fit(dataset)  
#save the model to the common folder of Metatrader 5 install
hmm2json(model,r'C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\Common\Files\exampleHMM.json')
#get the state probabilities and log likelihood
result = model.score_samples(dataset)
print("log_likelihood " ,result[0]) #print the loglikelihood
print("state sequence ", model.decode(dataset)[1]) #print the state sequence of dataset
print("state probs ", result[1]) #print the state probabilities 

Соответствующий скрипт MetaTrader 5 testHMM.mq5 предназначен для загрузки json-файла, созданного saveHMM.py. Идея состоит в том, чтобы воспроизвести логарифмическое правдоподобие, скрытые состояния и вероятности состояний, выведенные saveHMM.py.

//+------------------------------------------------------------------+
//|                                                      TestHMM.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<hmmlearn.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- random dataset equal to that used in corresponding python script saveHMM.py
   matrix dataset =
     {
        {0.56807844,0.67179966,0.13639585,0.15092627,0.17708295},
        {0.62290044,0.15188847,0.91947761,0.29483647,0.34073613},
        {0.47687505,0.06388765,0.20589139,0.16474974,0.64383775},
        {0.25606858,0.50927144,0.49009671,0.0284832,0.37357852},
        {0.95855305,0.93687549,0.88496015,0.48772751,0.10256193},
        {0.36752403,0.5283874,0.52245909,0.77968798,0.88154157},
        {0.35161822,0.50672902,0.7722671,0.56911901,0.98874104},
        {0.20354888,0.82106204,0.60828044,0.13380222,0.4181293},
        {0.43461371,0.60170739,0.56270993,0.46426138,0.53733481},
        {0.51646574,0.54536398,0.03818231,0.32574409,0.95260478}
     };
//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }
//--get the log likelihood of the model
   double lk = hmm.get_likelihood(dataset);
   Print("LL ", lk);
//-- get the state probabilities for a dataset
   matrix probs = hmm.predict_state_probs(dataset);
   Print("state probs ", probs);
//---get the hidden states for the provided dataset
   vector stateseq = hmm.predict_state_sequence(dataset);
   Print("state seq ", stateseq);
  }
//+------------------------------------------------------------------+

Результаты выполнения обоих скриптов показаны ниже.

Результат saveHMM.py.

KO      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   log_likelihood  47.90226114316213
IJ      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state sequence  [0 1 1 1 1 0 0 1 0 0]
ED      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state probs  [[1.00000000e+000 1.32203104e-033]
RM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JR      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
RH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
LS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 5.32945369e-123]
EH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 8.00195599e-030]
RN      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
HS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 1.04574121e-027]
RD      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [9.99999902e-001 9.75116254e-008]]

Содержимое сохраненного файла JSON.

{"numstates":2,"numvars":5,"algorithm":"viterbi","implementation":"log","initprobs":[1.0,8.297061845628157e-28],"means":[[0.44766002665812865,0.5707974904960126,0.406402863181157,0.4579477485782787,0.7074610252191268],[0.5035892002511225,0.4965970189510691,0.6217412486192438,0.22191983002481444,0.375768737249644]],"transitions":[[0.4999999756220927,0.5000000243779074],[0.39999999999999913,0.6000000000000008]],"covars":[[[0.009010166768420797,0.0059122234200326374,-0.018865453701221935,-0.014521967883281419,-0.015149047353550696],[0.0059122234200326374,0.0055414217505728725,-0.0062874071503534424,-0.007643976931274206,-0.016093347935464856],[-0.018865453701221935,-0.0062874071503534424,0.0780495488091017,0.044115693492388836,0.031892068460887116],[-0.014521967883281419,-0.007643976931274206,0.044115693492388836,0.04753113728071052,0.045326684356283],[-0.015149047353550696,-0.016093347935464856,0.031892068460887116,0.045326684356283,0.0979523557527634]],[[0.07664631322010616,0.01605057520615223,0.042602194598462206,0.043095659393111246,-0.02756159799208612],[0.01605057520615223,0.12306893856632573,0.03943267795353822,0.019117932498522734,-0.04009804834113386],[0.042602194598462206,0.03943267795353822,0.07167474799610704,0.030420143149584727,-0.03682040884824712],[0.043095659393111246,0.019117932498522734,0.030420143149584727,0.026884283954788642,-0.01676189860422705],[-0.02756159799208612,-0.04009804834113386,-0.03682040884824712,-0.01676189860422705,0.03190589647162701]]]}

Результат testHMM.mq5.

HD      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   LL 47.90226114316213
EO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state probs [[1,1.322031040402482e-33]
KP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KF      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KM      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
EJ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,5.329453688054051e-123]
IP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,8.00195599043147e-30]
KG      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
ES      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,1.045741207369424e-27]
RQ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0.999999902488374,9.751162535898832e-08]]
QH      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state seq [0,1,1,1,1,0,0,1,0,0]

Заключение

Модели HMM представляют собой мощные статистические инструменты для моделирования и анализа последовательных данных. Их способность улавливать скрытые состояния, лежащие в основе наблюдаемых последовательностей, делает их ценными для задач, связанных с временными рядами, например, финансовыми данными. Несмотря на свои сильные стороны, HMM не лишены ограничений. Они опираются на предположение Маркова первого порядка, которое может оказаться слишком упрощенным для сложных зависимостей. Вычислительные требования к обучению и выводу, особенно для больших пространств состояний, а также потенциальная возможность переобучения представляют собой существенные проблемы. Более того, выбор оптимального количества состояний и инициализация параметров модели требуют тщательного рассмотрения и могут повлиять на производительность. Тем не менее, HMM остаются основополагающим методом моделирования последовательностей, предлагая надежную основу для многих практических приложений. Благодаря постоянному совершенствованию и гибридным подходам, объединяющим HMM с более гибкими моделями, их полезность продолжает расти. Понимание возможностей и ограничений HMM имеет важное значение для эффективного использования их потенциала в развитии автоматизированной торговли.

Весь код, описанный в статье, приложен ниже. Каждый из файлов исходного кода описан в таблице.

Файл	Описание
Mql5\Python\script\saveHMM.py	Демонстрирует обучение и сохранение скрытой марковской модели, содержит определение функции hmm2json()
Mql5\include\hmmlearn.mqh	Содержит определение класса HMM, позволяющего импортировать HMM, обученные на Python, для использования в MQL5
Mql5\script\testHMM.mq5	Скрипт MetaTrader 5, демонстрирующий загрузку сохраненного HMM