Возможности Мастера MQL5, которые вам нужно знать (Часть 34): Эмбеддинг цены с нетрадиционной RBM

Введение

Мы продолжаем серию статей, посвященную различным торговым настройкам и идеям, реализованным в среде быстрой разработки и прототипирования MetaTrade 5 в Мастере MQL5. Статьи направлены на изучение идей, которые могут быть не столь распространены, но могут дать преимущество заинтересованному трейдеру в зависимости от того, как он решит их использовать. В этой серии мы больше занимаемся исследованием, чем практикой с учетом того, что доступные рабочие торговые идеи имеют тенденцию слишком положительно коррелировать друг с другом.

Конечно, хорошо, когда тренд преимущественно бычий и всё идет вверх. Однако, диверсификация — это то, что смягчит просадки, когда тренды меняются на противоположные. Найти ценные бумаги с обратной корреляцией гораздо сложнее чем кажется. Вот почему пользовательские входы и выходы из сделок могут быть лучшим решением, чем простое следование общепринятым настройкам. В статье рассматриваются ограниченные машины Больцмана (Restricted Boltzmann Machines, RBM) в сочетании с обратным распространением (Backpropagation) в противоположность традиционным реализациям на основе выборки Гиббса (Gibbs Sampling) и контрастивной дивергенции (Contrastive Divergence, CD).

В середине 1980-х годов (около 1986 года, когда появились RBM под названием Harmonium) вычислительные затраты на реализацию обратного распространения в машинах Больцмана были просто невозможны. Повышенная сложность машин Больцмана в чистом виде заключается в том, что они, в отличие от RBM, не используют двудольный график (bi-partite graph), располагая внутринейронные связи в пределах слоя. Эти сложности приводят к тому, что даже более простая реализация машин Больцмана, такая как RBM, полагается на вероятностные модели на основе энергии(energy-based models, EBM) в тонкой настройке параметров (весов и смещений) сети, не занимаясь обработкой каждого параметра за раз, как это практикуется в других нейронных сетях и в обратном распространении.

Согласно Deep-AI:

Контрастивная дивергенция решает вычислительную задачу, поставленную статистической суммой (partition function) в моделях на основе энергии. Ключевой момент, лежащий в основе контрастной дивергенции, заключается в том, что эти модели можно обучать без необходимости вычисления полной функции распределения. Вместо этого CD фокусируется на настройке параметров модели таким образом, чтобы вероятность наблюдаемых данных увеличивалась, а вероятность выборок, сгенерированных моделью, уменьшалась. 

CD выполняет выборку Гиббса, начиная с обучающих данных, чтобы создать выборки, которые модель считает вероятными. Затем она использует эти образцы для оценки градиента логарифмического правдоподобия обучающих данных по отношению к параметрам модели. Градиент используется для обновления параметров в направлении, улучшающем представление данных моделью.

Таким образом, выборка Гиббса и CD позволили избежать вычислений для каждой вероятности. Но вернемся в современность. Теперь обратное распространение ошибки, безусловно, может быть приемлемым вариантом, особенно если учесть, что большую часть рабочей нагрузки ИИ теперь несут не центральные, а графические процессоры. Такой выбор оборудования при работе с сетями типа машины Больцмана (например, RBM) имеет ключевое значение, поскольку, хотя они имеют всего два слоя, эти слои, как правило, очень глубокие, и поэтому необходимо правильно продумать, как будут регулироваться веса каждого нейрона.

Итак, что же на самом деле представляют собой RBM, учитывая ограничение в два слоя? Если коротко, это классификаторы, которые уменьшают размерность входных данных, чтобы выявить скрытые свойства данных в меньшем количестве размерностей, чем входные данные. Если дать более подробное определение, это генеративные стохастические нейронные сети, обученные без учителя для изучения распределения вероятностей входных данных. Результаты входных данных, которые регистрируются в скрытом слое сети, затем могут использоваться при классификации, кластеризации или в качестве входных данных для другой сети.

В этой статье мы используем последний вариант, принимая значения скрытого слоя нашей RBM в качестве входных данных для многослойного перцептрона. Общая структура статьи будет соответствовать формату, к которому мы привыкли на протяжении всей этой серии.

Эмбеддинг цены

Эмбеддинг цены (Price-Embedding) в контексте статьи понимается как процесс, очень похожий на векторное представление слов (word embedding). Как вы, возможно, знаете, это предварительный шаг к преобразованию сетей больших языковых моделей. Векторное представление слов, которое можно определить как нумерацию слов, в сочетании с самовниманием (self-attention) помогает преобразовать большую часть письменного материала, доступного в Интернете, в формат, понятный нейронным сетям. Мы также следуем этому подходу, предполагая, что по умолчанию данные о ценах на ценные бумаги (даже если они числовые) не могут быть легко "поняты" нейронными сетями с самого начала. Наш подход заключается в использовании RBM, обученной методом обратного распространения.

Итак, преобразование слов в числа — это не просто присвоение числа слову или букве, а сложный процесс, требующий самовнимания. Я полагаю, что отсюда можно провести параллели с RBM, если рассмотреть их конструкцию двудольного графа.

источник

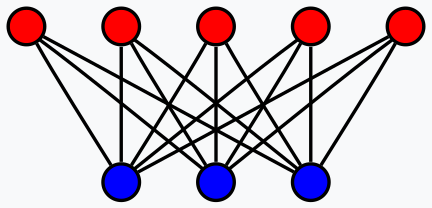
Хотя в слое RBM нет прямых связей между нейронами, эти связи, которые могут быть ключевыми для захвата компонента самовнимания любых входных данных, осуществляются через скрытый слой. Согласно этому тезису, скрытый слой регистрирует не только то, как каждый нейрон может быть перерисован, но и то, каково значение его связей с другими нейронами.

Как всегда, в случае с трейдингом преимущества эмбеддинга цены могут быть подтверждены только результатами торговли. Мы собираемся перейти к первой части этого процесса, однако стоит подчеркнуть, что масштаб вознаграждений, которые мы получаем от эмбеддинга слова в число, нельзя сравнивать с тем, которые мы рассматриваем при эмбеддинге числа в число, потому что то, что мы здесь делаем, далеко не столь трансформационно. Теперь давайте рассмотрим, как реконструировать RBM с помощью обратного распространения.

Ограниченные машины Больцмана (RBM)

RBM работают в двух циклах, которые часто называют положительной фазой и отрицательной фазой. Как уже упоминалось, они часто обучаются без учителя (хотя есть исключения). Это по сути означает, что при запуске и прохождении обучения мы не знаем, какими должны быть скрытые свойства каждой протестированной точки данных. Обучающие данные не имеют меток (или целевых значений).

Таким образом, RBM ведет подсчет очков, восстанавливая значения скрытого слоя так, чтобы они соответствовали значениям входного слоя в отрицательной фазе. Положительная фаза похожа на прямое распространение обычного многослойного перцептрона и передает значения в скрытый слой. Эти значения скрытого слоя и являются нашей целью, поскольку они представляют собой представление входных данных с уменьшенной размерностью, которое отражает искомые нами свойства.

При распространении к скрытому слою (положительная фаза) используется матрица весов, как и в нейронных сетях. Однако особенностью RBM является то, что в отрицательной фазе для реконструкции входных данных используются те же веса. Как уже упоминалось, эта реконструкция представляет собой способ обучения RBM без учителя или подсчет очков, а поскольку мы реализуем обратное распространение, входные данные фактически служат меткой (или целью) для себя.

Я утверждаю, что это все еще обучение без учителя, поскольку для обучения этой RBM не требуется никаких дополнительных данных, кроме входных данных обучения. В случаях, когда обучение с учителем проводилось с RBM, использовались метки идеальных значений скрытого слоя, а это не входит в цели нашей статьи. Итак, для начала нам необходимо реконструировать типичные функции RBM положительной и отрицательной фазы. Это выглядит следующим образом:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::GetPositive(void)
{  vector _positive = weights[0].MatMul(inputs), _output;
   _positive += biases[0];
   _positive.Activation(_output, THIS.activation);
   output = _output;
}

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::GetNegative(void)
{  vector _negative = output.MatMul(weights[0]), _output;
   _negative += biases[1];
   _negative.Activation(_output, THIS.activation);
   label = _output;
}

Наш MQL5-класс, C_u_rbm, наследуется от другого класса - Cmlp, который мы использовали в предыдущих статьях. Несмотря на то, что C_u_rbm наследуется от Cmlp, его необходимо настроить, чтобы обеспечить наличие необходимого количества слоев и выполнение соответствующих шагов проверки. Создадим класс, как указано в его интерфейсе:

#include <My\Cmlp-.mqh>
//+------------------------------------------------------------------+
//| Unconventional RBM that uses:                                    |
//| reconstruction-error instead of free-energy                      |
//| and back-propagation instead of contrastive divergence           |
//+------------------------------------------------------------------+
class C_u_rbm : public Cmlp
{
protected:

public:
   void              GetPositive();
   void              GetNegative();
   
   void              BackPropagate(double LearningRate = 0.1);

   double            Get(ENUM_REGRESSION_METRIC R)
   {                 return(label.RegressionMetric(inputs, R));
   }

   void              C_u_rbm(Smlp &MLP) : Cmlp(MLP)
   {  validated = false;
      int _layers =    ArraySize(MLP.arch);
      if(_layers == 2 && MLP.arch[0] > MLP.arch[1])
      {  ArrayResize(biases, _layers);
         //
         ArrayResize(gradients, _layers);
         ArrayResize(gradients_1st_moment, _layers);
         ArrayResize(gradients_2nd_moment, _layers);
         ArrayResize(sum_gradients, _layers);
         ArrayResize(sum_gradients_update, _layers);
         //
         ArrayResize(deltas, _layers);
         ArrayResize(deltas_1st_moment, _layers);
         ArrayResize(deltas_2nd_moment, _layers);
         ArrayResize(sum_deltas, _layers);
         ArrayResize(sum_deltas_update, _layers);
         //
         hidden_layers = 0;
         bool _norm_validated = true;
         for(int i = 0; i < _layers; i++)
         {  int _rows = MLP.arch[_layers - 1 - i], _columns = MLP.arch[i];
            //
            biases[i].Init(_rows);
            biases[i].Fill(MLP.initial_bias);
            //
            gradients[i].Init(_rows, _columns);
            gradients[i].Fill(0.0);
            //
            gradients_1st_moment[i].Init(_rows, _columns);
            gradients_1st_moment[i].Fill(0.0);
            gradients_2nd_moment[i].Init(_rows, _columns);
            gradients_2nd_moment[i].Fill(0.0);
            //
            sum_gradients[i].Init(_rows, _columns);
            sum_gradients[i].Fill(0.0);
            sum_gradients_update[i].Init(_rows, _columns);
            sum_gradients_update[i].Fill(0.0);
            //
            deltas[i].Init(_rows);
            deltas[i].Fill(0.0);
            deltas_1st_moment[i].Init(_rows);
            deltas_1st_moment[i].Fill(0.0);
            deltas_2nd_moment[i].Init(_rows);
            deltas_2nd_moment[i].Fill(0.0);
            sum_deltas[i].Init(_rows);
            sum_deltas[i].Fill(0.0);
            sum_deltas_update[i].Init(_rows);
            sum_deltas_update[i].Fill(0.0);
         }
         validated = true;
      }
      else
      {  printf(__FUNCSIG__ +
                " invalid network arch! Settings size is: %i, Max layer size is: %i, Min layer size is: %i, and activation is %s ",
                _layers, MLP.arch[ArrayMaximum(MLP.arch)], MLP.arch[ArrayMinimum(MLP.arch)], EnumToString(MLP.activation)
               );
      }
   };
   void              ~C_u_rbm(void) { };
};

При настройке конструктора для нашего класса мы опустили массив матриц весов, поскольку его размер всегда равен общему числу слоев минус один. Таким образом, конструктор имеет дело с отличиями: во-первых, у нас есть два вектора смещения, хотя слоев всего два. Это означает, что у нас также будет два дельта-вектора, по одному для каждого вектора смещения. Еще одна необходимая настройка касается количества градиентных матриц. Несмотря на то, что у нас есть только одна матрица весов, у нас есть две матрицы градиента, поскольку наше обратное распространение будет выполняться для двух циклов тестирования: положительной фазы и отрицательной фазы.

Это также подразумевает, что наша единая матрица весов обновляется дважды при каждом обратном распространении. Как всегда, обратное распространение включает в себя вычисление дельт, затем градиентов, а затем обновление весов и смещений с использованием этих значений. Выполняем обратное распространение следующим образом:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::BackPropagate(double LearningRate = 0.1)
{  
//COMPUTE DELTAS
   vector _loss = label.LossGradient(inputs, THIS.loss);
   //
   vector _negative = output.MatMul(weights[0]), _negative_derivative;
   _negative.Derivative(_negative_derivative, THIS.activation);
   deltas[1] = Hadamard(_loss, _negative_derivative);
   //
   vector _positive = weights[0].MatMul(inputs), _positive_derivative;
   _positive.Derivative(_positive_derivative, THIS.activation);
   matrix _weights;
   _weights.Copy(weights[0]);
   _weights.Transpose();
   vector _product = _weights.MatMul(deltas[1]);
   deltas[0] = Hadamard(_product, _positive_derivative);
//COMPUTE GRADIENTS
   gradients[0] = TransposeCol(deltas[0]).MatMul(TransposeRow(inputs));
   gradients[1] = TransposeCol(deltas[1]).MatMul(TransposeRow(output));
   
// UPDATE WEIGHTS AND BIASES
   for(int h = 1; h >= 0;  h--)
   {  matrix _gradients;
      _gradients.Copy(gradients[h]);
      if(h == 1)
      {  _gradients = _gradients.Transpose();
      }
      weights[0] -= LearningRate * _gradients;
      biases[h] -= LearningRate * deltas[h];
   }
}

Таким образом, функция суммирует наш класс, который наследуется от Cmlp, при этом все непереопределенные функции базового класса все еще действуют. Почему у нас есть два вектора смещения, два дельта-вектора, две матрицы градиентов и только одна матрица весов находится в положительной фазе? Мы впервые сталкиваемся с матрицей весов, и ее произведение необходимо прибавить к первому вектору смещения. Произведение также подразумевает необходимость захвата градиентной матрицы для правильного обновления весов по нему. На втором этапе тот же процесс повторяется, но, как уже упоминалось, ключевым отличием является то, что мы используем те же веса, что и в положительном этапе.

Несмотря на использование тех же весов, к произведению второй фазы добавляется новый (другой) вектор смещения, и это приводит к нашей реконструкции входных данных. Разница между этими реконструированными данными и исходными входными данными затем определяет наши дельты. Именно это и используется в обратном распространении.

RBM в классе пользовательских сигналов

Чтобы создать пользовательский класс сигналов, нам потребуется сослаться на наш пользовательский класс RBM, созданный выше, в новом экземпляре пользовательского класса сигналов, который мы собираем в виде советника с помощью Мастера MQL5. Руководства для новичков можно найти здесь и здесь. После настройки наша торговая система будет готова наполовину, поскольку, как упоминалось во введении, у нас есть значения входных данных скрытого слоя RBM, которые служат входными данными для другой нейронной сети в форме многослойного перцептрона (MLP). Функция, выполняемая RBM, заключается в том, чтобы встроить изменения цен в целях выявления их эквивалента в меньшем измерении. В целях нашего тестирования RBM представляет собой сеть 8-4, где числа представляют собой размеры видимых и скрытых слоев. Задача RBM, по моему мнению, больше склоняется к классификации, чем к регрессии, и поэтому функция потерь и активация будут представлять собой категориальную перекрестную энтропию (categorical cross entropy) и soft-sign. Их все еще можно настроить так, чтобы они работали в качестве классификаторов, как мы рассматривали в недавних статьях, однако мы используем эти настройки как константы, и их нельзя оптимизировать.

Функции, выполняемые RBM, как уже упоминалось, больше соответствуют эмбеддингу (внедрению), и поэтому ответственная функция в нашем пользовательском классе сигналов называется Embedder. Ее исходный код представлен ниже:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalEmbedding::Embedder(vector &Extraction)
{  m_learning.rate = m_learning_rate;
   for(int i = 1; i <= m_epochs; i++)
   {  U_RBM.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old, _out, _out_new, _out_old;
         if
         (
         _in_new.Init(__RBM_VISIBLE) && 
         _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __RBM_VISIBLE) && 
         _in_new.Size() == __RBM_VISIBLE &&
         _in_old.Init(__RBM_VISIBLE) && 
         _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS + 1, __RBM_VISIBLE) && 
         _in_old.Size() == __RBM_VISIBLE
         &&
         _out_new.Init(__MLP_OUTPUTS) &&
         _out_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_OUTPUTS) &&
         _out_new.Size() == __MLP_OUTPUTS &&
         _out_old.Init(__MLP_OUTPUTS) &&
         _out_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __MLP_OUTPUTS) &&
         _out_old.Size() == __MLP_OUTPUTS
         )
         {  _in = _in_new - _in_old;
            _out = _out_new - _out_old;
            U_RBM.Set(_in);
            U_RBM.GetPositive();
            U_RBM.GetNegative();
            U_RBM.BackPropagate(m_learning.rate);
            Extraction = Extractor(U_RBM.output, _out, ii > 0);
         }
      }
   }
}

Наша подготовка данных очень похожа на ту, что мы использовали в предыдущих статьях. В большинстве советников, которые кодируются вручную, а не с помощью Мастера MQL5, необходимо предпринять дополнительные шаги, чтобы гарантировать, что запрашиваемые советником ценовые данные действительно доступны на сервере брокера, прежде чем будут выполнены вычисления сигналов. Обычно при сборке в Мастере их можно избежать, однако в нашем случае мы просто используем условие if, чтобы гарантировать, что искомые данные действительно скопированы в необходимые векторы.

При копировании данных в векторы также важно помнить, что данные не сортируются как ряд, то есть наивысший индекс в копируемом векторе имеет самое последнее значение. Подробнее об этом можно почитать здесь. Поскольку у нас есть цепочечная структура, в которой RBM предоставляет входные данные для многослойного перцептрона (MLP), мы решили обучать две сети практически одновременно. В каждой точке обучающего набора RBM мы обучаем RBM, а затем - MLP. Это отличается от первоначального завершения сеанса обучения RBM перед обучением MLP.

Конечно, читатель может внести изменения в эту схему, учитывая, что полный исходный код приложен внизу, однако мы приняли ее, поскольку она может быть более эффективной, учитывая необходимость обучения двух сетей для наших целей тестирования. Учитывая почти одновременное обучение, нам необходимо получать входные данные RBM и метки MLP одновременно. Именно поэтому наши условия if очень длинные.

Интеграция RBM с MLP

Таким образом, в процессе обучения мы обновляем веса RBM, что позволяет нам обрабатывать больше входных данных и получать их скрытые значения (распределение вероятностей). Это распределение вероятностей (не необработанные предыдущие изменения цен), которое мы называем эмбеддингом цен, затем передается в MLP. Эмбеддинг используется в функции Extractor, которая просто передает эмбеддинг цен, предоставленный RBM, через MLP. По мере передачи данных он также обучает MLP, если указана метка (целевое значение). Поскольку обучение проводится до последних изменений цен, для которых не существует меток, нам необходимо это отслеживать. Трекер — это третий входной параметр в функции Extractor, представляющий собой логическое значение Train. По умолчанию оно равно true, однако как только мы достигаем конца обучающего набора и у нас нет метки, ему присваивается значение false. Код функции Extractor представлен ниже:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CSignalEmbedding::Extractor(vector &Embedding, vector &Labels, bool Train = true)
{  vector _extraction;
   _extraction.Init(MLP.output.Size());
   m_learning.rate = m_learning_rate;
   for(int i = 1; i <= m_epochs; i++)
   {  MLP.LearningType(m_learning, i);
      MLP.Set(Embedding);
      MLP.Forward();
      _extraction = MLP.output;
      if(Train)
      {  MLP.Get(Labels);
         MLP.Backward(m_learning, i);
      }
   }
   return(_extraction);
}

Он возвращает вектор, который мы называем _extraction, но в нашем случае нас интересует только одно значение — следующее изменение цены, так что на самом деле это вектор одного размера. В то время как RBM структурирован как классификатор с помощью своей функции активации и функции потерь, MLP, вероятно, должен работать лучше, если будет структурирован как регрессор. Это связано с его уникальным плавающим выходом данных, который может быть отрицательным. В качестве регрессора мы используем активацию soft-sign, а в качестве функции потерь — Хубера. Причины указывались в предыдущих статьях, в частности здесь.

Как RBM, так и MLP не настроены должным образом на оптимальную производительность, поскольку, например, они используют одинаковые начальные веса и смещения, а обучение происходит одновременно, что по сути означает, что для обучения обеих сетей используется один сеанс обучения. Альтернативой является проведение обучающих сессий разного масштаба для RBM и MLP, где обучение MLP проводится только после завершения обучения RBM. Кроме того, скорость обучения фиксирована для обеих сетей, а различные форматы, включающие адаптивное обучение, не использовались. Многие из этих дополнительных настроек оставлены на усмотрение читателя.

Тестирование на истории и оптимизация

Мы проводим оптимизацию за 2023 год для пары GBPUSD на дневном таймфрейме, одновременно стремясь к идеальным начальным весам и смещениям сети. Напомню, что у нас есть один входной параметр для обоих этих значений в двух сетях, что не обязательно идеально. Кроме того, мы ищем пороговые значения открытия и закрытия для функций LongCondition и ShortCondition нашего пользовательского класса сигналов, а также уровень тейк-профита в пунктах. Мы провели несколько неполных прогонов и получили следующие результаты:

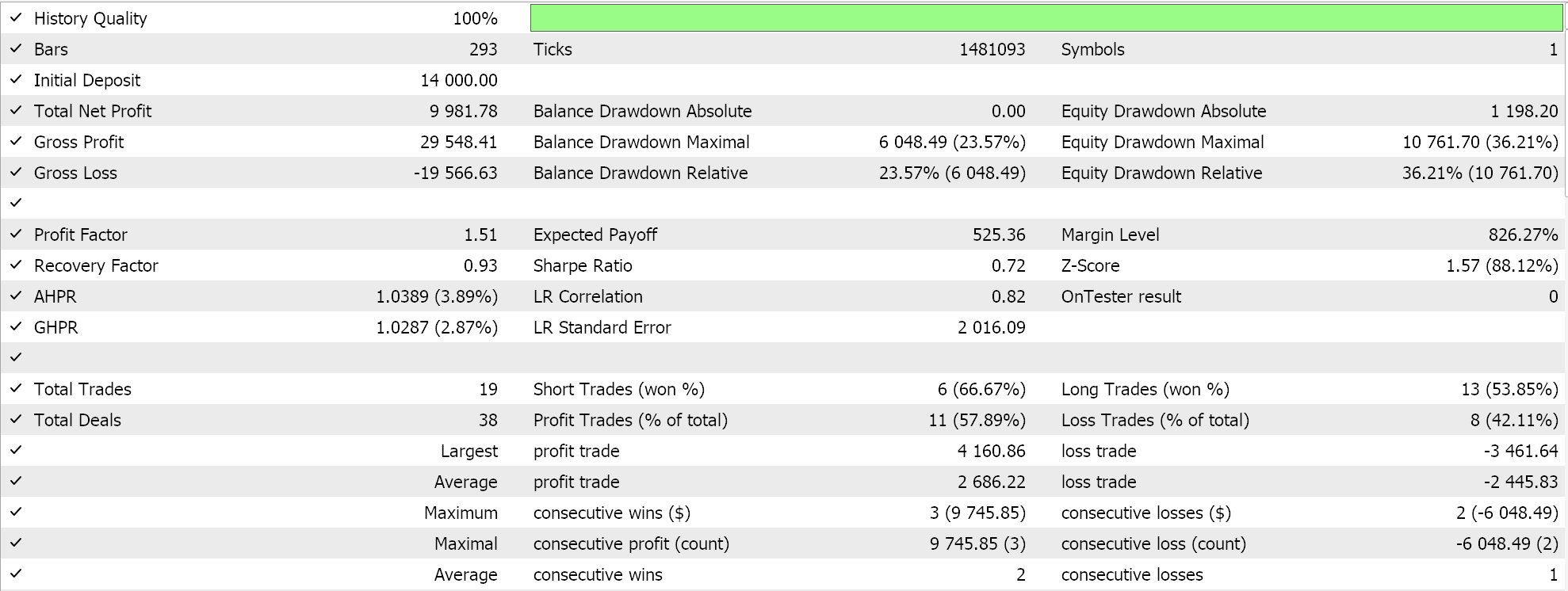
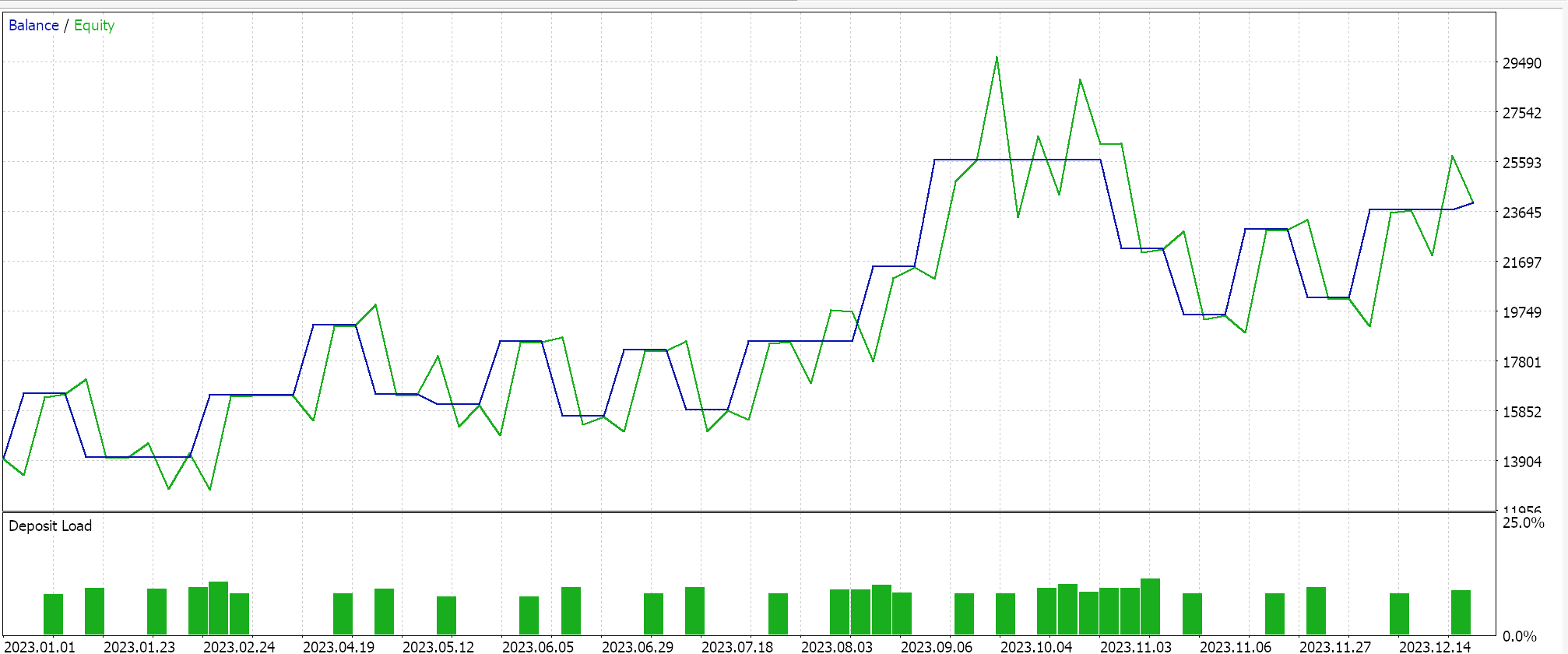
Наш советник, собранный в Мастере, может торговать, однако, как это всегда бывает, необходимо больше проверок, включая тестирование на более длительных исторических периодах и последующие форвард-тесты. Также стоит отметить, что поскольку это сигнал на основе нейронной сети, пользователь всегда должен предусматривать сохранение весов и смещений сети (здесь их две).

Заключение

Мы предоставили RBM в качестве ценового "эмбеддера" для MLP с его оптимизированными торговыми результатами за один год, но как можно оценить эффективность "ценового эмбеддинга" в контексте, в котором оно используется в этой статье? Короткий ответ таков: в этом нам поможет еще один чистый сигнал MLP, который принимает в качестве входных данных необработанные предыдущие изменения цен и также обучен, как MLP из этой статьи, прогнозировать следующее изменение цен. Настройка также относительно проста, поскольку классы привязки для MLP аналогичны тем, что мы использовали, поэтому можно легко получить сравнительные результаты.

Мы также добавили RBM, который подключается к MLP, а не наоборот. Я считаю, что это лучший способ совместной работы этих двух типов нейронных сетей (классификатора и регрессора). Регрессоры часто, хотя и не всегда, выводят единственное значение с плавающей точкой (которое может быть отрицательным), и при учете "классифицированных" входных данных такое сопряжение может быть оправдано. В дальнейшем эту компоновку можно будет расширить не путем наложения RBM друг на друга, поскольку они используют глубину, а путем их параллельного расположения в качестве входов для сетей регрессоров, ориентированных на трансформеры. Я считаю, что классификаторы с их глубиной лучше подходят для "специализации", чем сети регрессоров.

В заключение отмечу, что мы попытались классифицировать изменения цен в качестве "эмбеддинга цен", однако при поиске данных "эмбеддинга цен" в MLP можно также учитывать различные финансовые данные и временные ряды. К ним могут относиться свечные модели, значения ценовых индикаторов, данные экономических новостей и т. д. Предполагаю, что производительность и результаты тестирования в каждом случае будут существенно различаться, поэтому читателю предстоит самостоятельно найти и внедрить то, что лучше всего будет соответствовать его взгляду на рынки.