Возможности Мастера MQL5, которые вам нужно знать (Часть 31): Выбор функции потерь

Введение

Мастер MQL5 может стать испытательным полигоном для самых разных идей. Часть из них мы уже рассмотрели в этой серии. Время от времени мы сталкиваемся с пользовательскими сигналами, который можно реализовать несколькими способами. Мы рассмотрели такой вариант в двух статьях о темпах обучения, а также в предыдущей статье о пакетной нормализации. Как уже обсуждалось, каждый из этих аспектов машинного обучения представляет собой более одного потенциального пользовательского сигнала. То же самое касается и функции потерь в силу наличия нескольких форматов.

Не существует единого метода сравнения результата тестового прогона с целевым значением. В ENUM_LOSS_FUNCTION доступны 14 перечислений, и этот список не исчерпывающий. Означает ли это, что каждый из них предлагает свой собственный подход к машинному обучению? Возможно, нет, но суть в том, что существуют различия, которые часто требуют тщательно выбирать функцию потерь в зависимости от характера сети или алгоритма, который вы обучаете.

Однако помимо функции потерь можно рассмотреть возможность использования ENUM_REGRESSION_METRIC. Но такой подход, больше связанный со статистикой, здесь неуместен, поскольку он лучше подходит в качестве метрики для оценки производительности алгоритма машинного обучения после самого обучения. Поэтому этот перечень метрик будет очень полезен особенно в случаях, когда конечный результат имеет более одного измерения. Однако в этой статье основное внимание уделяется целевой функции.

И выбор подходящей меры потерь имеет решающее значение, поскольку в принципе нейронные сети (наш алгоритм машинного обучения для этой статьи) могут попадать в категорию регрессоров (в отличие от классификаторов), или они могут использоваться в обучении с учителем (в отличие от тех, что используются в обучении без учителя). Кроме того, такие парадигмы как обучение с подкреплением могут потребовать многогранный подход к использованию и применению функции потерь.

Таким образом, функции потерь можно применять различными способами не только потому, что существует множество форматов, но и потому, что существует множество "задач" (типов нейронных сетей), которые необходимо решить. При решении этих проблем или в процессе обучения функция потерь в первую очередь количественно определяет, насколько далеки тестируемые параметры от предполагаемого целевого значения (обучение с учителем).

В случае с функцией потерь всегда интуитивно понятно, что она предназначена для обучения с учителем. При этом вопрос об идеальной функции потерь для обучения без учителя может показаться некорректным. Тем не менее, даже в неконтролируемых условиях, таких как карты Кохонена или кластеризация, всегда существует необходимость в стандартизированной метрике при измерении пробелов или расстояний в многомерных данных, и функция потерь могла бы заполнить этот пробел.

Обзор функций потерь

Итак, MQL5 предлагает до 14 различных методов количественной оценки функции потерь, и мы рассмотрим все из них, прежде чем рассматривать примеры применения. Для наших целей потеря используется для обозначения градиента потерь, и ожидаемыми выходными данными являются векторы, а не скалярные значения. Кроме того, код MQL5, реализующий эти формулы, не будет передан, поскольку ВСЕ они запускаются из встроенных векторных функций. Ниже приведен простой скрипт для тестирования различных функций потерь:

#property  script_show_inputs
input ENUM_LOSS_FUNCTION __loss = LOSS_HUBER;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
      vector _a = {1.0, 2.0, 4.0};
      vector _b = {4.0, 12.0, 36.0 };
      
      vector _loss = _a.LossGradient(_b,__loss); 
      
      printf(__FUNCSIG__+" for: "+EnumToString(__loss));
      Print(" loss gradient is: ",_loss);
      PrintFormat(" while loss is: %.5f. ",_a.Loss(_b,__loss));
  }
//+------------------------------------------------------------------+

Во-первых, среднеквадратическая ошибка потери (loss-mean-squared-error, MSE). Это широко используемая функция потерь, цель которой — измерить квадрат разницы между прогнозируемыми и целевыми значениями, тем самым определяя величину ошибки. Это гарантирует, что ошибка всегда положительна (упор делается на величину), и существенно "наказывает" большие ошибки из-за возведения в квадрат. Интерпретация также становится более плавной, поскольку ошибка всегда находится в квадратах единиц целевой переменной. Формула представлена ниже:

где

• n — размерность целевой и сравниваемой переменной. Обычно эти переменные имеют векторный формат.
• i — внутренний индекс в векторном пространстве
• y^ — выходной или прогнозируемый вектор
• y — целевой вектор

Его плюсами могут быть чувствительность к большим ошибкам и хорошая приспособляемость к методам оптимизации градиентного спуска благодаря плавному градиенту. Минусом является чувствительность к выбросам.

Следующая функция - средняя абсолютная ошибка потери (loss-mean-absolute-error). Это, как и MSE выше, еще одна распространенная функция потерь, которая, как и MSE, фокусируется на ошибке величины без учета направления. Отличие от MSE заключается в том, что он не придает дополнительного веса большим значениям, поскольку не применяется возведение в квадрат. Поскольку возведение в квадрат не используется, единицы погрешности соответствуют единицам целевого вектора, и поэтому интерпретация более проста, чем при использовании MSE. Его формула, аналогичная той, что мы имеем выше, имеет следующий вид:

где

• n, i, y и y^ представляют те же значения, что и в MSE выше

Основными преимуществами являются меньшая чувствительность к выбросам и большим ошибкам, поскольку не выполняется возведение в квадрат, а также простота поддержания целевых единиц, что облегчает интерпретацию. Однако его градиентное поведение не такое плавное, как у MSE, поскольку при дифференцировании выходной сигнал равен либо +1,0, либо -1,0, либо нулю. Чередование этих значений не способствует тому, чтобы процесс обучения сходился так же гладко, как при использовании MSE. Это может стать проблемой, особенно в регрессионных средах. Кроме того, отношение ко всем ошибкам как к равным в некоторой степени препятствует процессу конвергенции.

Это приводит нас к категориальной перекрестной энтропии (categorical cross entropy). Это позволяет измерить в строго многомерном пространстве разницу между прогнозируемым и фактическим распределением вероятностей. Таким образом, хотя мы используем MAE и MSE в качестве векторных выходных данных в алгоритме функции потерь MQL5 (поскольку индивидуальные различия не суммируются), они легко могут быть скалярами, как показывают их формулы. С другой стороны, категориальная перекрестная энтропия (Categorical Cross Entropy, CCE) всегда выдает многомерный результат. Формула имеет вид:

где

• N — число классов или размер вектора точек данных
• y — фактическое или целевое значение
• p — прогнозируемое или сетевое выходное значение
• log — натуральный логарифм

CCE по своей сути является классификатором, а не регрессором, и особенно подходит в случаях, когда для категоризации набора данных при обучении используется более одного класса. Основные области применения этого метода — графика и обработка изображений, но, конечно, это не мешает нам искать способы его применения для трейдеров. Однако следует отметить, что CCE лучше всего работает в паре с активацией таким образом, что все они в сумме дают единицу. Метод хорошо подходит для поиска распределений вероятностей анализируемых классов для заданной точки данных. Логарифмический компонент "наказывает" уверенные, но неверные прогнозы сильнее, чем менее уверенные предсказания, и это в первую очередь связано с практикой прямого кодирования. Целевые или истинные значения всегда нормализуются таким образом, что только правильному классу присваивается полный вес (обычно 1,0), а всем остальным присваивается ноль. CCE обеспечивает плавные градиенты во время оптимизации и способствует тому, чтобы модели были уверены в своих прогнозах из-за штрафного эффекта, описанного выше в случае неверных прогнозов. При обучении среди несбалансированной численности популяции в разных классах можно применять корректировки весов, чтобы выровнять условия работы. Однако существует опасность переобучения при наличии слишком большого количества классов, поэтому необходимо соблюдать осторожность при определении количества классов, которые должна оценивать модель.

Следующий метод - бинарная перекрестная энтропия (binary cross entropy, BCE), родственный CCE. Он также количественно определяет разрыв между прогнозом и целью в двухклассовых условиях, в отличие от CCE, который более эффективен при работе с несколькими классами. Его выходной сигнал находится в диапазоне от 0,0 до 1,0 и определяется следующей формулой:

где

• N, как и в других функциях потерь выше, — это размер выборки.
• y — прогнозируемое значение
• p — это предсказание
• log — натуральный логарифм

В случае BCE два рассматриваемых класса часто именуются положительным классом и отрицательным классом. Таким образом, по сути, выход BCE всегда понимается как предоставление вероятности в той степени, в которой точка данных находится в положительном классе, и это значение находится в диапазоне 0,0 – 1,0 с подходящей парной функцией активации, являющейся жесткой сигмоидальной функцией. Векторный вывод функций активации MQL5, встроенных в векторный тип данных, выводит вектор, который должен включать 2 вероятности для положительного и отрицательного класса.

Расстояние Кульбака — Лейблера (Kullback Liebler Divergence) — еще один интересный алгоритм функции потерь, похожий на методы векторного зазора, которые мы рассмотрели выше. Его формула имеет вид:

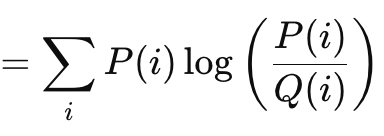
где

• P — прогнозируемая вероятность
• Q — фактическая вероятность

Его выходные данные варьируются от 0, что указывает на отсутствие расхождения, до бесконечности. Эти положительные значения являются четким индикатором того, насколько далек прогноз от "истины". Как показано в приведенной выше формуле, суммирование имеет значение только при расчете скалярного выходного сигнала. Встроенная векторная реализация метода в MQL5 обеспечивает векторный вывод, который более удобен и необходим для вычисления дельт и, в конечном итоге, градиентов при выполнении обратного распространения. Расстояние Кульбака — Лейблера основано на теории информации и нашло применение в обучении с подкреплением, учитывая его ловкость, а также в вариационных автокодировщиках. Его недостатками являются асимметрия, чувствительность к нулевым значениям и трудности в интерпретации, учитывая несвязанный характер его выходных данных. Нулевая чувствительность важна, поскольку если одному классу присвоена вероятность, равная нулю, то другой автоматически имеет бесконечное значение, но асимметрия не только затрудняет правильную интерпретацию заданной вероятности, но и затрудняет трансферное обучение (transfer learning). (Вероятность P при условии K не обратна вероятности K при условии P). Суммы прямых и обратных вероятностей не являются предопределенным значением. Иногда это бесконечность, иногда — нет.

Это приводит нас к косинусному коэффициенту (cosine similarity), который, в отличие от рассмотренных нами до сих пор мер векторного разрыва, учитывает направление. Его формула имеет следующий вид:

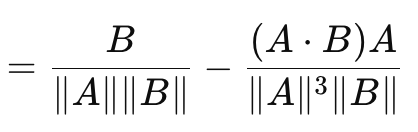
где

• A.B — скалярное произведение двух векторов
• ||A|| и ||B|| — их величины или нормы

Приведенная выше формула относится к градиенту потерь относительно вектора A. Формула относительно вектора B является отдельной обратной формулой и при суммировании с косинусом A и B не дает фиксированной или произвольной константы. В связи с этим косинусный коэффициент не является истинной метрикой, поскольку не удовлетворяет треугольнику неравенства (triangle of inequality). (Косинусный коэффициент A и B плюс косинусный коэффициент B и C не всегда больше или равен косинусному коэффициенту A и C). Его преимуществом является масштабная инвариантность (scale invariance), поскольку выдаваемое им значение не зависит от величины рассматриваемых векторов, что может быть важно, когда первостепенное значение имеет направление, а не величина. Кроме того, он требует меньших вычислительных ресурсов, чем другие методы, что является ключевым фактором при работе с очень глубокими сетями или трансформерами, или и тем, и другим! Метод нашел широкое применение для многомерных данных, таких как текстовые вставки больших языковых моделей, где выведенное направление (смысл?) является более релевантной метрикой, чем отдельные величины каждого векторного значения. Его минусы в том, что он не подходит для всех задач, особенно в ситуациях, когда важна величина векторов при обучении. Кроме того, в случае, если один из векторов имеет нулевую норму (где все значения равны нулю), то косинусный коэффициент будет неопределенным. Наконец, уже упомянутая невозможность использования в качестве метрики из-за невыполнения правила треугольника неравенства. Примеры того, где это имеет решающее значение, могут быть немного странными, но они включают в себя: геометрическое глубокое обучение, нейронные сети на основе графов и сравнительные потери в сиамских сетях. В каждом из этих случаев использования величина важнее направления. Однако при применении косинусного сходства в MQL5 важно отметить, что используется и возвращается именно косинусная близость, поскольку это более актуально для машинного обучения. Это эквивалент расстояния косинуса угла, и он получается путем вычитания косинусного подобия из единицы.

Функция градиента потерь Пуассона (Poisson loss-gradient function) подходит для моделирования счетных или дискретных данных. Это похоже на то, как если бы упомянутые выше функции потерь были реализованы с помощью встроенных функций векторного типа данных. Его формула имеет вид:

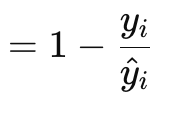
где

• y — целевое значение вектора (по индексу i)
• y^ — прогнозируемое значение

Значения градиента возвращаются в векторном формате, поскольку он гораздо лучше подходит для обратного распространения. Они также являются производными первого порядка исходной скалярной функции Пуассона, возвращающей формулу:

где

• компоненты совпадают с составом формулы градиента

Тип дискретных данных, которые трейдеры могут передавать нейронной сети в этом случае, может включать типы ценовых баров или информацию о том, были ли предыдущие бары бычьими, медвежьими или флетовыми. Однако варианты ее использования охватывают сценарии подсчета данных, так, например, нейронную сеть, которая берет различные паттерны ценовых баров свечей, взятые из недавней истории, можно обучить возвращать количество свечей определенного типа, которое следует ожидать из стандартной выборки, скажем, из 10 будущих ценовых баров. Его коэффициенты легко интерпретировать, поскольку они представляют собой логарифмические отношения скоростей, и они хорошо согласуются с регрессией Пуассона, что означает, что анализ после обучения можно легко выполнить с помощью регрессии Пуассона. Это также гарантирует, что прогнозы подсчетов всегда будут положительными (неотрицательными). К минусам относится предположение о дисперсии, при котором всегда предполагается, что среднее значение и дисперсия имеют одинаковые или почти близкие значения. Если это явно не так, то функция потерь не будет работать должным образом. Она чувствительна к выбросам, особенно с большим количеством входных данных. Использование натурального логарифма может привести к получению NaN или недействительных результатов. Кроме того, его применение ограничено положительными исчисляемыми данными, то есть его нельзя использовать в случаях, когда необходимы непрерывные отрицательные прогнозы, например, при прогнозировании изменений цен.

Функция градиента-потери Хубера (Huber gradient-loss function) завершает наш обзор возможностей MQL5 в отношении векторного типа данных. Есть и другие классы, которые мы не рассматривали, например: логарифм гиперболического косинуса (logarithm of hyperbolic cosine), категориальный шарнир (categorical hinge), квадратичный шарнир (squared hinge), шарнир (hinge), среднеквадратичная логарифмическая ошибка (mean-squared logarithmic error) и средняя абсолютная процентная ошибка (mean absolute percentage error). Они не влияют на то, является ли нейронная сеть регрессором или классификатором, что в свою очередь важно для нас, поэтому мы их игнорируем. Однако Huber loss вычисляется по формуле:

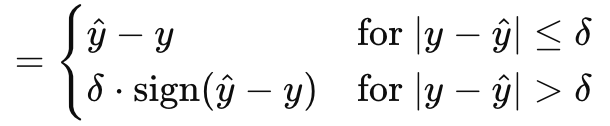
где

• y^ — прогнозируемое значение
• y — цель
• Дельта — это входное значение потерь, при котором зависимость меняется с линейной на квадратичную.

Градиент, как и исходный Huber-loss можно рассчитать одним из двух способов в зависимости от того, как истинное или целевое значение сравнивается с прогнозом. Это частично линейная и частично квадратичная функция, которая отображает разницу между целевыми и прогнозируемыми значениями при корректировке входных параметров. Она преобладает в робастной регрессии (robust regression), поскольку сочетает в себе лучшее из MAE и MSE и менее чувствительна к выбросам, но при этом более стабильна, чем MAE, при небольших ошибках. Будучи полностью дифференцируемой, она идеально подходит для градиентного спуска и легко адаптируется благодаря дельте, где меньшая дельта действует как MAE, а большие дельты действуют скорее как MSE. Это позволяет контролировать баланс между надежностью и чувствительностью. С другой стороны, хотя Huber-loss относительно более сложен, вычисление и определение идеальной дельты часто является довольно сложным занятием. Учитывая это, реализация средствами языка MQL5 не раскрывает, как вычисляется значение дельта для встроенных функций Huber-loss и градиента Huber-loss. Хотя его можно сочетать с различными функциями активации, линейная активация часто рекомендуется как более подходящая.

Функции потерь для моделей регрессии

Итак, какой из этих алгоритмов потерь лучше всего подойдет для регрессионных сетей? Ответ: MSE, MAE и Huber-Loss. Регрессионные сети характеризуются своей целью прогнозирования непрерывных числовых значений, а не категориальных меток или дискретных данных. Это означает, что выходной слой этих сетей обычно выдает действительные числа, которые могут охватывать широкий диапазон. Природа задач регрессии требует минимизации необходимости измерения широкомасштабных отклонений между прогнозируемыми и истинными значениями при их оптимизации, в отличие от сетей классификации, где выходных данных, которые необходимо перечислить, часто немного, и их количество известно заранее.

Это приводит нас к MSE. Как отмечено выше, он имеет большие квадратичные штрафы за большие ошибки, что сразу подразумевает, что он направляет градиентный спуск и оптимизацию к более узким отклонениям, что важно для эффективной работы регрессионных сетей. Кроме того, гладкость и простота дифференциации делают его естественным для непрерывных данных, обрабатываемых регрессионными сетями.

Регрессионные сети также сильно подвержены выбросам, поэтому необходима функция потерь, которая достаточно надежна для обработки этих выбросов. Это MAE. В отличие от MSE, которая налагает квадратичные штрафы на свои ошибки, MAE налагает линейные штрафы, и это делает его менее чувствительным к выбросам по сравнению с MSE. Кроме того, его мера погрешности представляет собой надежную среднюю погрешность, которая может быть полезна в зашумленных данных.

Наконец, утверждается, что регрессионные сети, в дополнение к вышесказанному, нуждаются в механизме баланса или компромисса между чувствительностью к небольшим ошибкам и надежностью. Это два свойства, которые обеспечивает функция Huber-loss, и, кроме того, они обеспечивают гладкость, которая помогает в дифференциации на протяжении всего процесса оптимизации.

Если все три "идеальные" функции потерь обнулены, то какую идеальную палитру функций активации следует учитывать при их использовании в регрессионной сети? Официально рекомендации касаются линейной и тождественной активации (identity activation), причем последняя подразумевает сохранение величины выходных данных сети для того, чтобы охватить как можно большую часть изменчивости данных. Основными аргументами в пользу этих двух подходов являются несвязанный характер их выходных данных, гарантирующий отсутствие потерь данных в ходе процессов прямой передачи данных и обучения сети. Лично я сторонник ограниченных выходных данных, поэтому я бы предпочел использовать Soft-Sign и TANH, поскольку они охватывают как отрицательные, так и положительные действительные числа, но они ограничены диапазоном от -1,0 до +1,0. Я думаю, что ограниченные выходы важны, потому что они позволяют избежать проблем с взрывными и исчезающими градиентами во время обратного распространения, что является основным источником сложностей.

Функции потерь для моделей классификации

А как насчет классификационных нейронных сетей? Как обстоит дело с выбором функций потери и активации? Что ж, процесс принятия нами решения здесь не сильно отличается: по сути, мы смотрим на ключевые характеристики сети, и они определяют наш выбор.

Сети классификации предназначены для прогнозирования отдельных меток классов из пула предопределенных возможных категорий. Эти сети выводят вероятности, указывающие на вероятность каждого класса, при этом главная цель состоит в том, чтобы максимизировать точность этих прогнозов за счет минимизации потерь. Таким образом, выбор функции потерь играет ключевую роль в обучении сети различать и идентифицировать классы. На основании этих ключевых особенностей был достигнут консенсус относительно категориальной перекрестной энтропии и двоичной перекрестной энтропии как двух ключевых функций потерь, наиболее подходящих для сетей классификации из MQL5-перечисления.

BCE классифицирует данные по двум возможным категориям, однако количество прогнозов, которые необходимо сделать, часто может превышать два, а размер пакета (batch) определяет норму вектора градиента. Таким образом, значение в каждом индексе вектора градиента будет частичной производной функции потерь BCE, как указано выше в общей формуле, и эти значения будут использоваться в обратном распространении. Однако выходные значения сети будут вероятностями для положительного класса, как упоминалось выше, и они будут для каждого прогнозируемого значения в выходном векторе.

BCE подходит для сетей классификации, поскольку вероятности легко интерпретируются, так как указывают на положительный класс. Он чувствителен к различным вероятностям каждого выходного значения, поскольку фокусируется на максимизации логарифмического правдоподобия правильных классов пакета. Поскольку его можно дифференцировать не как константу, а как переменную, это значительно облегчает плавное и эффективное вычисление градиента при обратном распространении.

CCE расширяет BCE, позволяя классифицировать более 2 категорий, а норма или размер выходного вектора всегда представляет собой число классов, для каждого из которых задана вероятность. Это отличается от BCE, где мы могли делать прогнозы, скажем, для 5 значений, и все значения для каждого из них были либо истинными, либо ложными. В CCE размер выходных данных имеет префикс, соответствующий номеру класса. Как упоминалось ранее, прямое кодирование полезно для нормализации целевых векторов до измерения пробелов в прогнозе.

Идеальной формой активации для сопряжения, следовательно, была бы любая функция, которая выходит за пределы диапазона от 0,0 до +1,0. Сюда входят Soft-Max, Sigmoid и Hard Sigmoid.

Тестирование

Мы проведем 2 набора тестов: один - для регрессивного MLP и один - для классификатора. Целью тестирования является демонстрация реализации на языке MQL5 и в виде советника идей функции потерь и активации. Представленные результаты тестирования не являются призывом для развертывания и использования прилагаемого кода на реальных счетах. Мы призываем читателей провести собственное тестирование на реальных тиковых данных своего брокера в течение длительных периодов времени, если они сочтут торговую систему подходящей. Развертывание в реальных условиях, как всегда, должно быть идеальным только после проведения перекрестной проверки или прямого тестирования, дающих удовлетворительные результаты.

Итак, мы будем тестировать GBPCHF на дневном таймфрейме за 2023 год. Чтобы получить регрессивную сеть, мы обратимся к классу Cmlp, который мы представили в предыдущей статье, и поскольку нашими входными данными будут проценты изменения цены (а не пункты), мы можем протестировать ее с активацией TANH и функцией Huber loss, чтобы увидеть, насколько пригодной для торговли может быть наша система. Пользовательские условия позиций на покупку и продажу реализованы в MQL5 следующим образом:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalRegr::LongCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] > 0.0)
   {  result = int(round(100.0*(fabs(_out[0])/(fabs(_out[0])+fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))))));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalRegr::ShortCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] < 0.0)
   {  result = int(round(100.0*(fabs(_out[0])/(fabs(_out[0])+fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))))));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}

Мы также проводим одновременное тестирование советника на исторических данных с обучением сет на каждом новом ценовом баре. Это еще одно ключевое решение, которое можно легко изменить, если обучение проводится раз в 6 месяцев или в течение другого заранее определенного более длительного периода, чтобы избежать переобучения сети для краткосрочных действий. Эта регрессорная сеть имеет располагает тремя слоями 4-7-1 (где числа представляют размеры слоев), что подразумевает, что в качестве входных данных используются 4 последних изменения цен, а единственным выходным значением является следующее изменение цены.

Проведение тестовых запусков GBPCHF на 2023 год ежедневно дает нам следующий отчет:

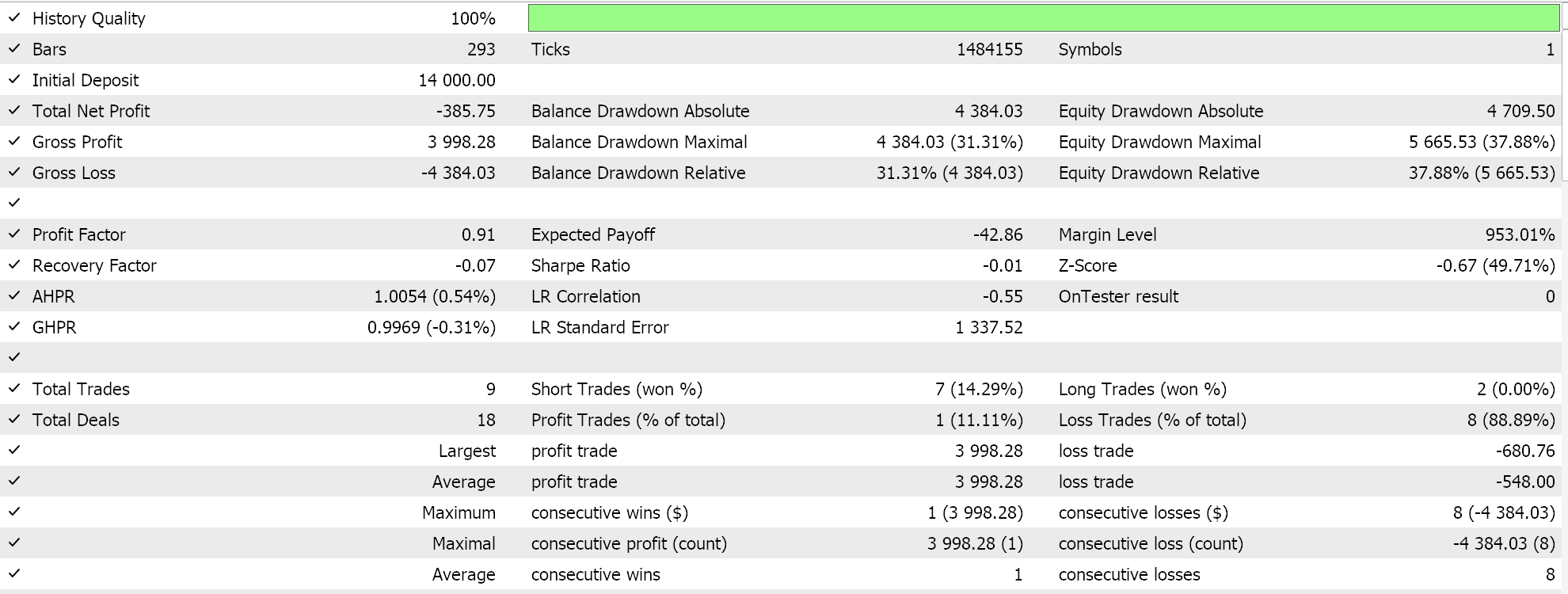
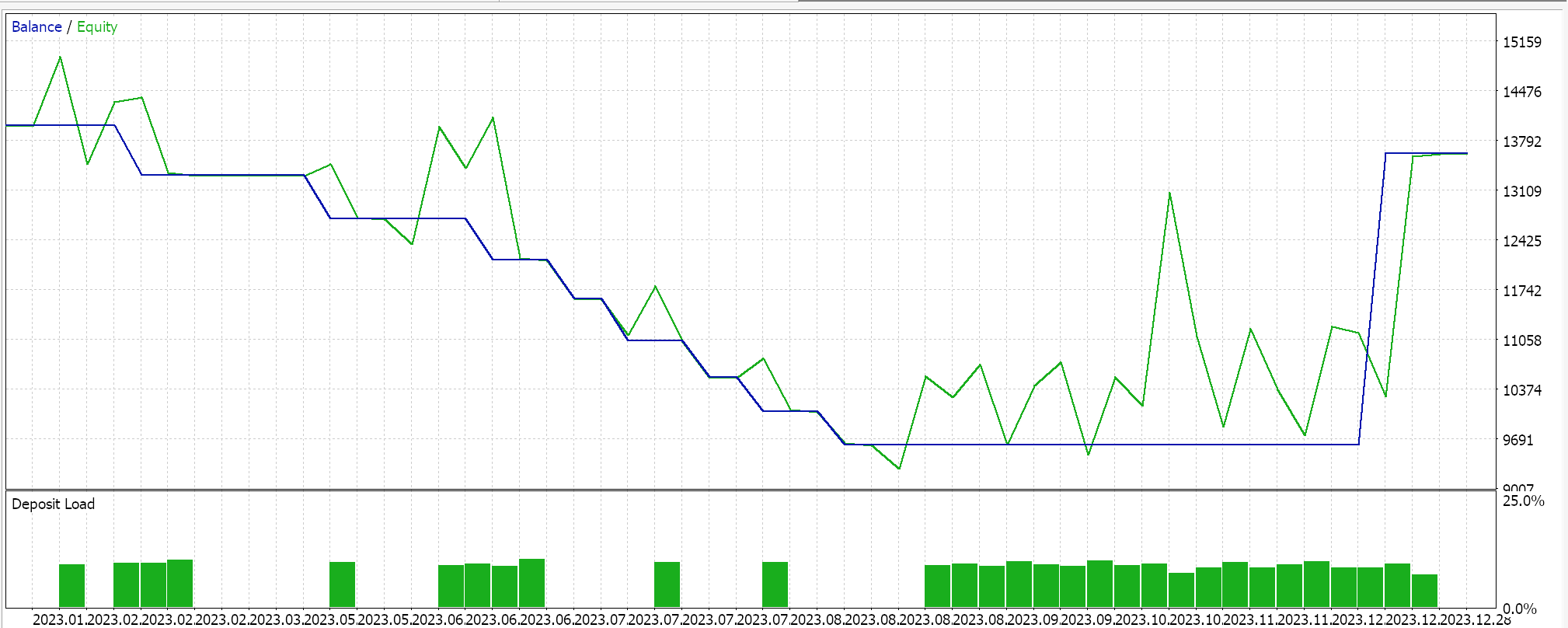
Для сети классификатора мы по-прежнему используем класс Cmlp в качестве базы, а нашими входными данными будут классификации последних трех ценовых точек. Они передаются в простую сеть MLP 3-6-3, также состоящую только из 3 слоев, где (поскольку мы рассматриваем 3 возможные классификации, а наша функция потерь — CCE) конечный выходной слой также должен иметь размер 3, чтобы он служил распределением вероятностей. Генерация условий на покупку и продажу реализована в MQL5 следующим образом:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalClas::LongCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[2] > _out[1] && _out[2] > _out[0])
   {  result = int(round(100.0 * _out[2]));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[2],  result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalClas::ShortCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] > _out[1] && _out[0] > _out[2])
   {  result = int(round(100.0 * _out[0]));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}

Аналогичные тестовые прогоны для советника классификатора дают нам следующие результаты:

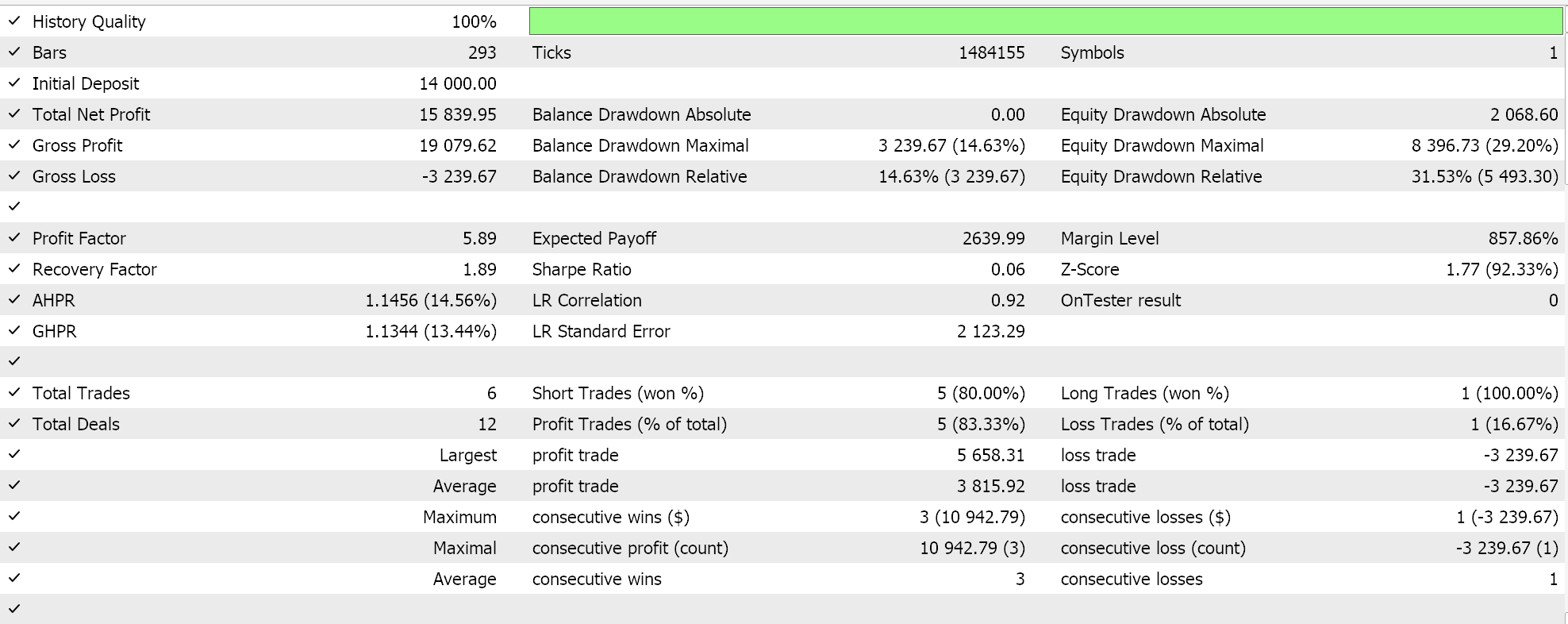
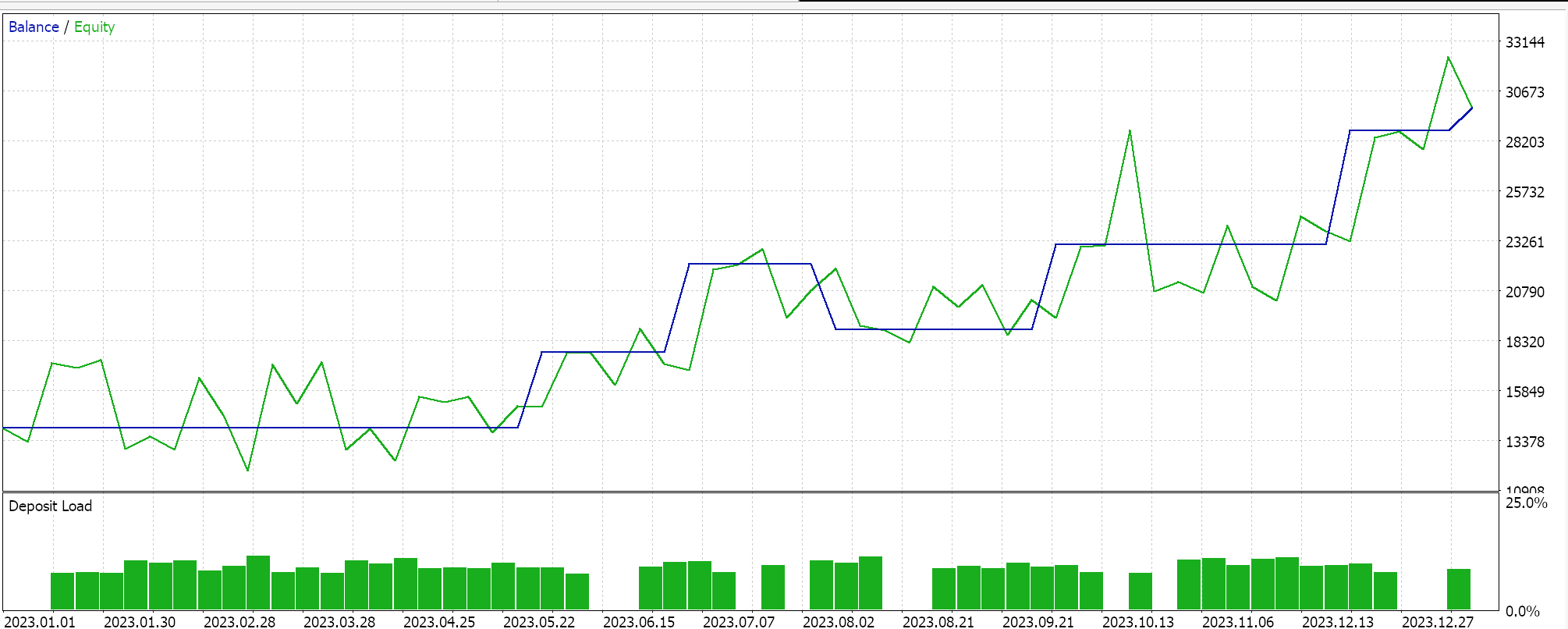
Приложенный код используется при сборке советников с помощью Мастера. Подробности можно найти здесь и здесь.

Заключение

Мы рассмотрели возможные функции потерь, доступные в MQL5 при разработке алгоритмов машинного обучения, таких как нейронные сети. Количество функций велико, однако мы выделили несколько ключевых, которые хорошо работают с определенными функциями активации, рассмотренными в предыдущих статьях, уделив особое внимание предотвращению взрывного роста/исчезновения градиентов и эффективности. Многие из доступных функций потерь не обязательно подойдут для типичных сетей регрессии и классификации не только потому, что их выходные данные не связаны, но и потому, что они не отвечают основным требованиям к характеристикам этих сетей, поэтому мы рассмотрели далеко не все функции потерь.