您应当知道的 MQL5 向导技术（第 34 部分）：采用非常规 RBM 进行价格嵌入
61
0
概述
我们继续本系列，探索各种交易设置和思路，这要归功于 MetaTrade-5 的快速开发和原型设计环境，以及 MQL5 向导。原则上，这些文章旨在探讨交易者如何通过探索可能不那么常见的想法来令自己领先一筹，并且能够为感兴趣的交易者带来优势，具体取决于他选择如何利用它们。故此，我们于此进行探索，不一定用得上，原因在于领衔是众多交易思路起作用，且倾向彼此之间过于正相关。
当趋势看涨，且每个关口都一路绿灯时，这确实超级棒，不过，正如大家所同意的那样，当趋势逆转时，多元化可以减轻回撤，但简单地找到负相关的证券比纸上谈兵要困难得多。这就是为什么对于而言，入场交易和离场都要很具体，比之简单地依赖常用设置，这样做是更好的避难所。就此，本文着眼于使用反向传播实现时的受限玻尔兹曼机（RBM），而非它们的传统吉布斯（Gibbs）采样和对比散度实现。
有种论调，即最初使用这些方式的原因是因为在 80 年代中期（大约 1986 年，当时 RBM 曾以 Harmonium 的名义引入），在玻尔兹曼机中实现计算反向传播的成本是根本不可行的。玻尔兹曼机，RBM 顾名知义，其甚至更复杂，因为它们不像 RBM 那样使用二分图，而代之于层内由内部神经元连接。这些连接复杂性致使像 RBM 这样的玻尔兹曼机器的简单实现，也偏向于依赖概率能量基础模型（EBMs）来优调网络参数（权重和乖离），而非像其它神经网络和反向传播那样，每个参数逐次处理或处置。
据 Deep-AI：
对比散度解决了基于能量的模型中分区函数带来的计算挑战。对比散度背后的关键见解，是其可在无需完整计算分割函数的情况下训练这些模型。代之，CD 专注调整模型参数，如此观察到数据的概率增加，而模型生成的样本概率降低。
为达此目的，对比散度一开始就从训练数据的吉布斯采样过程执行，以便生成模型认可的样本。它之后用这些样本来估算训练数据相对于模型参数的对数似然的梯度。该梯度在改进模型的数据表示时为更新参数导向。
故此，为了避免计算每个概率，吉布斯采样和对比散度显然是一个有意义的福音。快进到今天，当遇到同样的问题时，反向传播肯定是一个可行的选项，尤其是考虑到大部分 AI 工作负载不再由 CPU 承担，但显然 GPU 正在加速承担这些任务时。在处理类似玻尔兹曼机的网络（如 RBM）时，这种硬件选择是关键，因为即使它们仅有 2 层，这些层往往非常深，故要考虑如何相应调整每个神经元的权重。
那么，给定 2 层限制的 RBM 到底是什么呢？简短的回答是一个分类器，它降低了其输入数据的维度，以此在比输入更少的维度中揭示数据的隐藏属性。这是一个过于简化的定义，好比会有人提到它们是在无监督设定下训练生成式随机神经网络，用来学习其输入数据的概率分布。从输入数据中发现的，记录在网络隐藏层中的结果可以用于分类、聚类、或作为另一个网络的输入。
至于本文，我们将利用后者，将 RBM 隐藏层值作为多层感知器的输入。文章的整体结构，原则上将遵循我们在本系列中习惯的格式。
价格嵌入
在本文的上下文中，价格嵌入的用法非常类似于单词嵌入的过程；正如一些读者可能知道的那样，这是转换大型语言模型网络的先决条件。单词嵌入，可定义为单词的编号，当与自注意配对时，有助于将在线可用的许多书面材料转换为神经网络可以理解的格式。我们同样借鉴了这种方式，假设默认情况下，神经网络无法轻易地“理解”证券价格数据（即使是数字）。我们令其更易于理解的方式是用反向传播训练的 RBM。
现在，单词到编号的转换不仅仅是为单词或字母分配一个数字，而是一个复杂的过程，如上所述，它涉及自我注意。与其并列，我相信，当人们研究二分图设计时，能够当成 RBM。
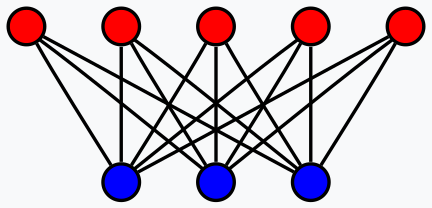
虽然 RBM 的一层内没有直接的神经元到神经元连接，但这些可能是捕获任意输入数据的自我注意分量的关键，是经由隐藏层。配上这些，隐藏层不仅记录了每个神经元可以重绘为什么，还记录了其与其它神经元的关系的重要性。
如常，就交易者而言，证据就在布丁中，因此这种价格嵌入的益处只能通过交易结果来证明。我们将进入这个过程的第一部分，但值得强调的是，从单词到数字嵌入获得的奖励规模无法与我们在数字到数字嵌入中所看到的奖励规模相提并论，这是因为我们在这里所做的并无那么具有变换性。据其，现在我们来研究如何配以反向传播来重造 RBM。
受限玻尔兹曼机（RBM）
RBM 以两个周期运行，通常称为正相位和负相位。如前所述，它们通常是无监督的（尽管已经实现了一些有监督的版本），这意味着本质上当我们开始并完成训练过程时，我们并不知晓每个测试数据点的隐藏属性应该是什么。训练数据没有标签（或目标值）。
RBM 保持分数的方式，是重建隐藏层值，以此匹配负相位中的输入层值。故此，有 2 个相位，类似于常规 MLP 的正向传播的正相位为隐藏层提供数值。这些隐藏层值是我们的意向，在于它们是捕获我们所寻求属性的输入数据降维表示。
在朝着隐藏层（正相位）传播时，与神经网络中的情况一样，使用权重矩阵；然而，RBM 的特别之处在于，在负相位，相同的权重用来重造输入数据。这种重造,如前所述，RBM 如何在无监督的情况下训练或保持分数，并且由于我们正在实现反向传播，故输入数据充当其自身的实际标签（或目标）。
我维持这仍然是无监督的看法，因为训练这个 RBM 不需要训练输入数据之外的其它数据。在依据 RBM 执行监督训练的实例中，采用理想隐藏层的标签值，而这并非我们在此所做的。故此，首先，我们需要重建正相位和负相位的典型 RBM 函数。如下所示：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void C_u_rbm::GetPositive(void) { vector _positive = weights[0].MatMul(inputs), _output; _positive += biases[0]; _positive.Activation(_output, THIS.activation); output = _output; }
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void C_u_rbm::GetNegative(void) { vector _negative = output.MatMul(weights[0]), _output; _negative += biases[1]; _negative.Activation(_output, THIS.activation); label = _output; }
我们的 MQL5 类 'C_u_rbm' 继承自我们在最近文章中一直在使用的另一个类 'Cmlp'。即使 “C_u_rbm” 继承自 “Cmlp”，也需要对其进行定制，以确保拥有相应数量的层，并涵盖相关的验证步骤。我们如下执行该类的构造，其接口如所示：
#include <My\Cmlp-.mqh> //+------------------------------------------------------------------+ //| Unconventional RBM that uses: | //| reconstruction-error instead of free-energy | //| and back-propagation instead of contrastive divergence | //+------------------------------------------------------------------+ class C_u_rbm : public Cmlp { protected: public: void GetPositive(); void GetNegative(); void BackPropagate(double LearningRate = 0.1); double Get(ENUM_REGRESSION_METRIC R) { return(label.RegressionMetric(inputs, R)); } void C_u_rbm(Smlp &MLP) : Cmlp(MLP) { validated = false; int _layers = ArraySize(MLP.arch); if(_layers == 2 && MLP.arch[0] > MLP.arch[1]) { ArrayResize(biases, _layers); // ArrayResize(gradients, _layers); ArrayResize(gradients_1st_moment, _layers); ArrayResize(gradients_2nd_moment, _layers); ArrayResize(sum_gradients, _layers); ArrayResize(sum_gradients_update, _layers); // ArrayResize(deltas, _layers); ArrayResize(deltas_1st_moment, _layers); ArrayResize(deltas_2nd_moment, _layers); ArrayResize(sum_deltas, _layers); ArrayResize(sum_deltas_update, _layers); // hidden_layers = 0; bool _norm_validated = true; for(int i = 0; i < _layers; i++) { int _rows = MLP.arch[_layers - 1 - i], _columns = MLP.arch[i]; // biases[i].Init(_rows); biases[i].Fill(MLP.initial_bias); // gradients[i].Init(_rows, _columns); gradients[i].Fill(0.0); // gradients_1st_moment[i].Init(_rows, _columns); gradients_1st_moment[i].Fill(0.0); gradients_2nd_moment[i].Init(_rows, _columns); gradients_2nd_moment[i].Fill(0.0); // sum_gradients[i].Init(_rows, _columns); sum_gradients[i].Fill(0.0); sum_gradients_update[i].Init(_rows, _columns); sum_gradients_update[i].Fill(0.0); // deltas[i].Init(_rows); deltas[i].Fill(0.0); deltas_1st_moment[i].Init(_rows); deltas_1st_moment[i].Fill(0.0); deltas_2nd_moment[i].Init(_rows); deltas_2nd_moment[i].Fill(0.0); sum_deltas[i].Init(_rows); sum_deltas[i].Fill(0.0); sum_deltas_update[i].Init(_rows); sum_deltas_update[i].Fill(0.0); } validated = true; } else { printf(__FUNCSIG__ + " invalid network arch! Settings size is: %i, Max layer size is: %i, Min layer size is: %i, and activation is %s ", _layers, MLP.arch[ArrayMaximum(MLP.arch)], MLP.arch[ArrayMinimum(MLP.arch)], EnumToString(MLP.activation) ); } }; void ~C_u_rbm(void) { }; };
在为我们的类自定义构造函数时，我们省略了权重矩阵数组，因为它的大小始终是层的总数减 1，这就是我们在这里看到的。因此，构造函数处置处不同的内容，首先，即使层只有两个，我们也有两个乖离向量。这意味着我们也将有两个增量向量，每个乖离向量一个。另一个必要的自定义是梯度矩阵数量。尽管只有一个权重矩阵，但我们有两个梯度矩阵，因为我们的反向传播将针对两个测试周期；正相位和负相位。
这也意味着我们的单一权重矩阵在每次反向传播中更新两次。如常，反向传播涉及计算增量，然后是梯度，然后是这些数值的权重和偏差更新。我们按如下方式执行反向传播：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void C_u_rbm::BackPropagate(double LearningRate = 0.1) { //COMPUTE DELTAS vector _loss = label.LossGradient(inputs, THIS.loss); // vector _negative = output.MatMul(weights[0]), _negative_derivative; _negative.Derivative(_negative_derivative, THIS.activation); deltas[1] = Hadamard(_loss, _negative_derivative); // vector _positive = weights[0].MatMul(inputs), _positive_derivative; _positive.Derivative(_positive_derivative, THIS.activation); matrix _weights; _weights.Copy(weights[0]); _weights.Transpose(); vector _product = _weights.MatMul(deltas[1]); deltas[0] = Hadamard(_product, _positive_derivative); //COMPUTE GRADIENTS gradients[0] = TransposeCol(deltas[0]).MatMul(TransposeRow(inputs)); gradients[1] = TransposeCol(deltas[1]).MatMul(TransposeRow(output)); // UPDATE WEIGHTS AND BIASES for(int h = 1; h >= 0; h--) { matrix _gradients; _gradients.Copy(gradients[h]); if(h == 1) { _gradients = _gradients.Transpose(); } weights[0] -= LearningRate * _gradients; biases[h] -= LearningRate * deltas[h]; } }
因此，该函数汇总了从 'Cmlp' 继承的类，而基类的所有非覆盖函数仍然有效。只是为了澄清为什么我们有两个乖离向量、两个增量向量、两个梯度矩阵、和一个权重矩阵在正相位上，我们第一次遇到权重矩阵，并且它的乘积需要添加到第一个乖离向量之中。该乘积还意味着需要捕获梯度矩阵，以便正确更新该乘积的权重。在第二阶段，会重复相同过程，但关键区别在于，如前所述，我们用到正相位的相同权重。
尽管使用相同权重，但一个新的（不同的）乖离向量被添加到第二阶段的乘积之中，而该导致我们对输入数据的重建。然后，这个重建的数据和原始输入数据之间的差异就是我们定义的增量，并将其馈送到反向传播之中。
自定义信号类中的 RBM
为了构建自定义信号类，我们需要在自定义信号类的新实例中引用上面创建的自定义 RBM 类，我们通过 MQL5 向导将其组装到智能交易系统之中。这里和这里有为新读者准备的指南。一旦我们引用并设置它，我们将得到交易系统的半成品，因为正如引言中提到的，我们将其输入数据的 RBM 隐藏层数值以多层感知器（MLP）的形式当作另一个神经网络的输入。RBM 执行的功能是嵌入价格变化，以便在更小维度中隐藏它们的等价物。在我们的测试中，我们的 RBM 是一个 8-4 网络，其中数字是可见层和隐藏层的大小。以我之见，RBM 任务更倾向于分类而不是回归，因此损失函数和激活将是分类交叉熵和 soft-sign。正如我们在最近的文章中讲述的那样，这些仍然可以调整为可起作用分类器，不过我们把这些设置当作常量，并且它们不可优化。
如前所述，RBM 执行的函数与嵌入更一致，由此负责在我们的自定义信号类中执行该任务的函数名为 'Embedder'。其源代码分享如下：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalEmbedding::Embedder(vector &Extraction) { m_learning.rate = m_learning_rate; for(int i = 1; i <= m_epochs; i++) { U_RBM.LearningType(m_learning, i); for(int ii = m_train_set; ii >= 0; ii--) { vector _in, _in_new, _in_old, _out, _out_new, _out_old; if ( _in_new.Init(__RBM_VISIBLE) && _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __RBM_VISIBLE) && _in_new.Size() == __RBM_VISIBLE && _in_old.Init(__RBM_VISIBLE) && _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS + 1, __RBM_VISIBLE) && _in_old.Size() == __RBM_VISIBLE && _out_new.Init(__MLP_OUTPUTS) && _out_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_OUTPUTS) && _out_new.Size() == __MLP_OUTPUTS && _out_old.Init(__MLP_OUTPUTS) && _out_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __MLP_OUTPUTS) && _out_old.Size() == __MLP_OUTPUTS ) { _in = _in_new - _in_old; _out = _out_new - _out_old; U_RBM.Set(_in); U_RBM.GetPositive(); U_RBM.GetNegative(); U_RBM.BackPropagate(m_learning.rate); Extraction = Extractor(U_RBM.output, _out, ii > 0); } } } }
我们的数据准备与过去文章中行事非常相似。在大多数手工编码而不是通过 MQL5 向导编码的智能系统中，需要采取额外的步骤来确保在计算信号之前，智能系统查询的价格数据在交易商的服务器上真实可用。通常，当向导组装智能系统时，能够略过这一点，在我们的例子中，我们只是使用 if 子句来确保我们寻求的数据实际上被复制到我们预期的向量当中。
将数据复制到向量时，重点要记住，数据不会将其按序列排序，这意味着复制到向量中的最高索引含有最新值。关于这个主题此处还有更多内容。因为我们有一个链式排布，RBM 为 MLP 提供输入，所以我们选择几乎同时训练两个网络，在 RBM 训练集的每个点上，我们训练 RBM，随后训练 MLP 来跟进。这与在训练 MLP 之前先穷尽 RBM 的训练会话期有所不同。
鉴于完整的源代码附在底部，读者当然可以修改这种排布，不过我们采用它，是出于我们的测试目的，需要训练两个网络，这样可以更有效。由于几乎同时进行训练，我们需要同时获取 RBM 输入和 MLP 标签，这就是为什么我们的 if 子句非常冗长的原因。
RBM 与 MLP 集成
那么，通过训练过程，我们更新了 RBM 权重，这令我们能够处理更多的输入数据，并获取其隐藏值（也就是它的概率分布）。然后，我们称之为价格嵌入的概率分布被投喂到 MLP，而非原始的先验价格变化。这种嵌入是在 'Extractor' 函数中使用，它简单地转发由 MLP 经 RBM 提供的价格嵌入。当它投喂时，如果提供了标签（目标值），它还会训练 MLP。因为训练是按照最近的价格变化执行，所以它们不应成为标签，故我们需要持续跟踪这一点。跟踪器是 'Extractor' 函数中的第三个输入参数，即布尔值 'Train'。默认情况下，它是 true，若一旦我们到达训练集的末尾，并且没有标签，它就会被赋值 false。'Extractor' 函数的代码分享如下：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ vector CSignalEmbedding::Extractor(vector &Embedding, vector &Labels, bool Train = true) { vector _extraction; _extraction.Init(MLP.output.Size()); m_learning.rate = m_learning_rate; for(int i = 1; i <= m_epochs; i++) { MLP.LearningType(m_learning, i); MLP.Set(Embedding); MLP.Forward(); _extraction = MLP.output; if(Train) { MLP.Get(Labels); MLP.Backward(m_learning, i); } } return(_extraction); }
它返回一个我们称为 '_extraction' 的向量，但在我们的例子中，我们只对一个值感兴趣，即下一次价格变化，故它实际上是一个大小的向量。虽然 RBM 的结构类似于分类器，其激活函数和损失函数，但 MLP 在结构上像回归器一样时可能应该会更好。这是因为它的奇异浮点数据输出可以是负数。作为回归器，我们使用 soft-sign 激活，损失函数是 Huber。在处理回归器网络时的这个原因，在最近的文章中有所介绍，例如这里，因故新读者可以看一下。
RBM 和 MLP 两者都未经适当调整，以实现最优性能，因为，举例来说，它们使用相同的初始权重和乖离，而且训练是并发的，这意味着本质上一个训练会话期用于训练两个网络。替代方案包括为 RBM 和 MLP 提供不同规模的训练会话期，其中 MLP 训练仅在 RBM 训练完成后进行。此外，两种网络的学习率都是固定的，并且尚未利用包含自适应学习的不同格式。许多这些额外的调整，以及更多内容留给读者去验证。
回测和优化
我们依据 GBPUSD 货币对，2023 年的日线时间帧进行了优化，同时寻求理想的初始网络权重和乖离。回想一下，对于这两个网络的两个值，我们只有一个输入参数，这不一定是理想的。此外，我们正在寻求自定义信号类的 'LongCondition' 和 'ShortCondition' 函数的开盘和收盘阈值，以及以点数为单位的止盈位。我们执行了一些并不详尽的运行，从中，我们得到了以下结果：
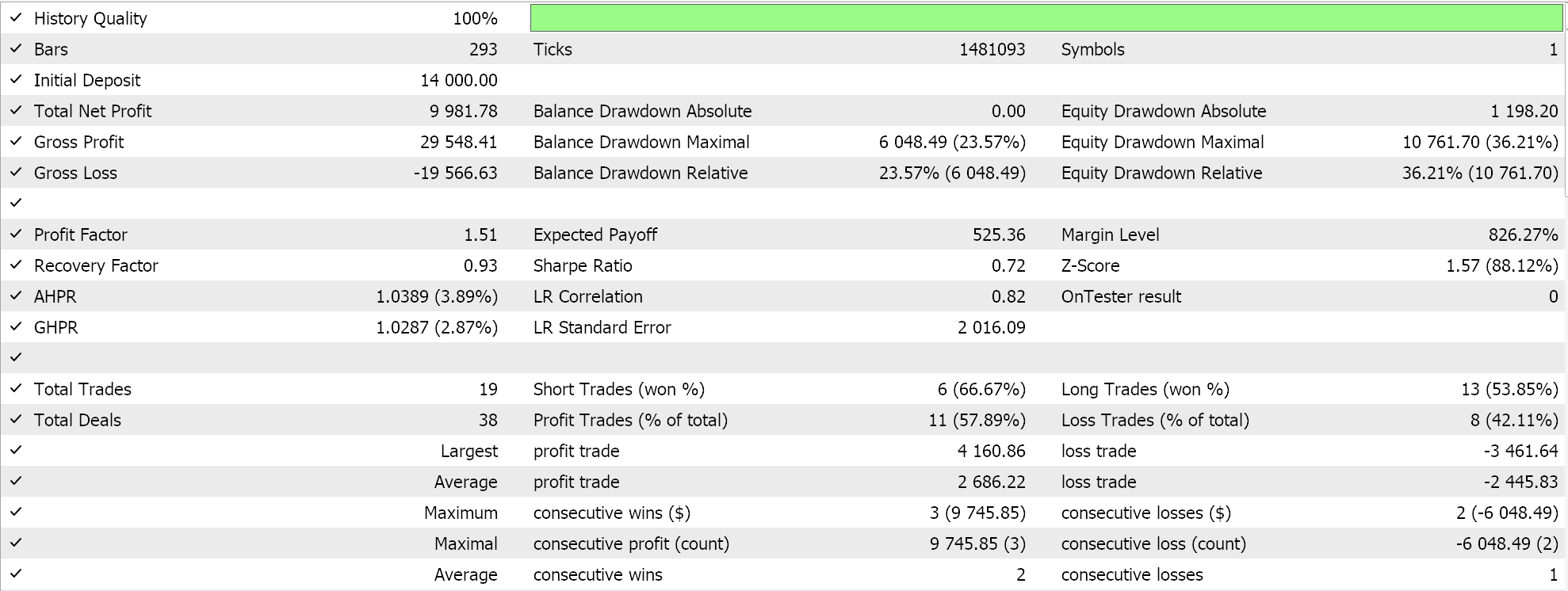
我们的向导组装的智能系统能够交易，不过一如既往，在较长的历史记录中进行测试，以及前向游走测试通验，以跟进优化，还需要更加努力。另外，值得一提的是，这是一个基于神经网络的信号，用户应该始终计划网络（这里有 2 个）权重和偏差的记录和保存。
结束语
我们已经提供了 RBM 作为 MLP 的价格嵌入器，并在一年内优化了交易结果，但如何据本文中所用的上下文来衡量“价格嵌入”的有效性？好吧，简短的回答是，如果我们有另一个纯粹的 MLP 信号，它以原始的先验价格变化作为输入，并且也像本文的 MLP 一样i二手训练，来预测下一个价格变化。设置它也相对容易，因为 MLP 的锚点类与我们一直所用的类似，因此很容易获得比较结果。
我们还配对了一个 RBM，它投喂到 MLP 之中，而非绕路而行。我觉得这样的方式，令这两种类型的神经网络（分类器和回归器）协同工作更佳。回归器通常（但并非总是）输出单个浮点值（可以是负数），并通过采用“分类”输入，这种配对可能是合理的。展望未来，这种排布可以扩展，并非通过堆叠 RBM，因为它们只利用了深度，但把它们并行排列作为变换器提示回归器网络的输入。我觉得拥有深度的分类器，比回归器网络更适合“专业化”。
此外，作为一条最后备注，我们已简单地视察了将价格变化归类为“价格嵌入”，不过在为 MLP 寻找“价格嵌入”数据时，也可以参考不同的财经数据和时间序列。这些可能包括蜡烛图价格形态、价格指标值、经济日历新闻数据、等等。正如人们所期望的那样，其中每一种的性能和测试结果必然会有很大差异，如此需由读者找到，并定制最符合他们观察市场的方式和方法。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/15652
大气云模型优化（ACMO）：理论
新手在交易中的10个基本错误
使用PSAR、Heiken Ashi和深度学习进行交易
