Características del Wizard MQL5 que debe conocer (Parte 34): Incorporación de precios con un RBM no convencional

Introducción

Continuamos con esta serie que explora diversas configuraciones e ideas comerciales gracias al entorno de creación de prototipos y desarrollo rápido de MetaTrader 5 con el asistente MQL5 (MQL5 Wizard). Estos artículos, en principio, buscan explorar de qué otra manera los traders pueden diferenciarse del resto al explorar ideas que pueden no ser tan comunes y que podrían brindar una ventaja al trader interesado, dependiendo de cómo elija explotarlas. Entonces, aquí nos dedicamos a explorar, no necesariamente a explotar, y la razón por la cual una ventaja es tan importante es que muchas ideas comerciales funcionales que están disponibles tienden a correlacionarse demasiado positivamente entre sí.

Esto está muy bien cuando las tendencias son alcistas y todo el mundo está en verde, sin embargo, como muchos estarían de acuerdo, la diversificación es lo que mitigaría las caídas cuando las tendencias se invierten y, sin embargo, simplemente encontrar valores inversamente correlacionados es mucho más difícil de lo que parece sobre el papel. Por eso, las entradas y salidas de operaciones específicas de un operador pueden ser un mejor refugio que confiar simplemente en las configuraciones más comunes. Con eso, este artículo examina las Máquinas de Boltzmann Restringidas (RBMs) cuando se implementan con Retropropagación en contraposición a sus implementaciones tradicionales de Muestreo de Gibbs y Divergencia Contrastiva.

Se argumenta que la razón por la que se utilizaron estos enfoques al principio fue porque a mediados de los años 80 (alrededor de 1986, cuando se introdujeron las RBMs bajo el nombre de Harmonium) los costes de computación de la implementación de la propagación hacia atrás en las máquinas de Boltzmann, simplemente no era factible. Las máquinas de Boltzmann, de las que las RBMs reciben su nombre, son aún más complejas, ya que no utilizan un grafo bipartito como las RBMs, sino que tienen conexiones intra neuronales dentro de una capa. Estas complejidades de conexión son las que predisponen incluso a una implementación más simple de las Máquinas de Boltzmann como las RBMs a confiar en Modelos Basados en Energía (Energy Based Models, EBMs) probabilísticos en el ajuste fino de los parámetros (pesos y sesgos) de la red en lugar de tener que procesar o tratar con cada parámetro a la vez como es práctica con otras redes neuronales y en retropropagación.

Según Deep-AI:

La divergencia contrastiva aborda el reto computacional que plantea la función de partición en los modelos basados en la energía. La idea clave de la divergencia contrastiva es que es posible entrenar estos modelos sin tener que calcular la función de partición completa. En cambio, la divergencia contrastiva se centra en ajustar los parámetros del modelo para que aumente la probabilidad de los datos observados mientras disminuye la probabilidad de las muestras generadas por el modelo. 

Para lograrlo, la divergencia contrastiva realiza un procedimiento de muestreo de Gibbs a partir de los datos de entrenamiento para producir muestras que el modelo considera probables. Luego utiliza estas muestras para estimar el gradiente de la verosimilitud logarítmica de los datos de entrenamiento con respecto a los parámetros del modelo. Este gradiente se utiliza para actualizar los parámetros en una dirección que mejora la representación de los datos del modelo.

Así pues, para evitar realizar cálculos para cada probabilidad, el muestreo de Gibbs y la divergencia contrastiva fueron una ventaja que claramente tenía sentido. Avanzamos rápidamente hasta hoy y cuando nos enfrentamos a los mismos problemas, la retropropagación ciertamente puede ser una opción factible, especialmente cuando se considera que la mayor parte de la carga de trabajo de la IA ya no la soportan las CPU, sino que las GPU están asumiendo significativamente estas tareas y a un ritmo acelerado. Esta elección de hardware al manejar redes tipo máquina de Boltzmann (como RBM) es clave porque si bien sólo tienen 2 capas, estas capas tienden a ser muy profundas y por lo tanto se debe considerar adecuadamente cómo se ajustan los pesos de cada neurona.

Entonces, ¿qué son realmente los RBM dado el límite de 2 capas? La respuesta corta es un clasificador, que reduce las dimensiones de sus datos de entrada para revelar propiedades ocultas de los datos en menos dimensiones que la entrada. Esta es una definición demasiado simplificada, ya que alguien más diligente mencionaría que son redes neuronales estocásticas generativas entrenadas en entornos no supervisados para aprender la distribución de probabilidad de sus datos de entrada. Los resultados de los datos de entrada, que se registran en la capa oculta de la red, se pueden utilizar luego en la clasificación, la agrupación o como entrada para otra red.

En este artículo, explotamos esto último, tomando los valores de la capa oculta de nuestros RBM como entrada para un perceptrón multicapa. La estructura general del artículo seguirá en principio el formato al que estamos acostumbrados a lo largo de esta serie.

Incorporación de precios

En el contexto de este artículo, la incrustación de precios se utiliza como un proceso muy similar a Word embedding o encaje léxico; y esto, como algunos lectores pueden saber, es el paso previo para transformar redes de modelos lingüísticos grandes. La incrustación de palabras, que puede definirse como la numeración de palabras, cuando se combina con Atención ayuda a convertir gran parte del material escrito que está disponible en línea en un formato que las redes neuronales pueden entender. También nos inspiramos en este planteamiento al presumir que, por defecto, las redes neuronales no pueden «comprender» fácilmente los datos sobre las cotizaciones de los valores (aunque sean numéricos). Y nuestro enfoque para hacer esto más comprensible es utilizar un RBM entrenado por retropropagación.

Ahora bien, la conversión de palabras en números no consiste simplemente en asignar un número a una palabra o letra, sino que es un proceso intrincado que implica autoatención, como ya se ha mencionado anteriormente. Creo que se pueden establecer paralelismos con los RBM si se tiene en cuenta su diseño gráfico bipartito.

Fuente

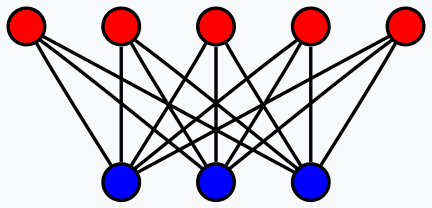
Si bien no hay conexiones directas de neurona a neurona dentro de una capa de un RBM, estas conexiones, que podrían ser clave para capturar el componente de autoatención de cualquier dato de entrada, se realizan a través de la capa oculta. Con esta tesis, la capa oculta no solo registra cómo podría redibujarse cada neurona, sino también cuál es el significado de sus relaciones con las otras neuronas.

Como siempre, en lo que respecta a los traders, la prueba está en el pudín y, por lo tanto, los beneficios de esta incorporación de precios solo se pueden demostrar con los resultados comerciales. Y vamos a llegar a la primera parte de este proceso, sin embargo, podría valer la pena resaltar que la escala de recompensas que uno obtiene de la incrustación de palabra a número no se puede comparar con las que estamos viendo en la incrustación de número a número, esto se debe a que lo que estamos haciendo aquí no es tan transformacional. Con esto, consideremos ahora cómo reconstruimos un RBM con retropropagación.

Máquinas de Boltzmann restringidas (RBM)

Los RBM funcionan en dos ciclos que suelen denominarse fase positiva y fase negativa. Como ya se ha mencionado, a menudo son sin supervisión (aunque se han implementado algunas versiones supervisadas) y esto significa inherentemente que, a medida que comenzamos y avanzamos en el proceso de entrenamiento, no sabemos cuáles deberían ser las propiedades ocultas de cada punto de datos probado. Los datos de entrenamiento no tienen etiquetas (ni valores objetivo).

Por lo tanto, la forma en que los RBM mantienen la puntuación es reconstruyendo los valores de la capa oculta para que coincidan con los valores de la capa de entrada en la fase negativa. Entonces, hay dos fases: la fase positiva, que es similar a la propagación hacia adelante de un MLP regular, proporciona valores a la capa oculta. Estos valores de capa oculta son nuestro objetivo, ya que son una representación de dimensionalidad reducida de los datos de entrada que capturan las propiedades que buscamos.

Al propagarse hacia la capa oculta (la fase positiva), se utiliza una matriz de pesos como es el caso en las redes neuronales; sin embargo, lo que hace que los RBM sean especiales es que en la fase negativa, se utilizan los mismos pesos para reconstruir los datos de entrada. Esta reconstrucción, como se mencionó, es la forma en que el RBM se entrena sin supervisión o lleva la cuenta y, dado que estamos implementando la retropropagación, los datos de entrada sirven como etiqueta de facto (o destino) para sí mismos.

Sostengo que esto sigue siendo no supervisado porque no se requieren datos adicionales, aparte de los de entrada de entrenamiento, para entrenar este RBM. En los casos en que se realizó entrenamiento supervisado con RBM, se usaron etiquetas de valores ideales de la capa oculta, y eso no es lo que estamos haciendo aquí. Entonces, para comenzar, necesitaríamos reconstruir las funciones RBM típicas de fase positiva y fase negativa. Esto es lo siguiente:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::GetPositive(void)
{  vector _positive = weights[0].MatMul(inputs), _output;
   _positive += biases[0];
   _positive.Activation(_output, THIS.activation);
   output = _output;
}

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::GetNegative(void)
{  vector _negative = output.MatMul(weights[0]), _output;
   _negative += biases[1];
   _negative.Activation(_output, THIS.activation);
   label = _output;
}

Nuestra clase MQL5 de esta, 'C_u_rbm' hereda de otra clase 'Cmlp' que hemos estado usando en artículos recientes. La construcción de 'C_u_rbm', aunque hereda de 'Cmlp', debe personalizarse para garantizar que se implemente la cantidad adecuada de capas y se cubran los pasos de validación relevantes. Realizamos la construcción de esta clase de la siguiente manera, tal y como se indica en su interfaz:

#include <My\Cmlp-.mqh>
//+------------------------------------------------------------------+
//| Unconventional RBM that uses:                                    |
//| reconstruction-error instead of free-energy                      |
//| and back-propagation instead of contrastive divergence           |
//+------------------------------------------------------------------+
class C_u_rbm : public Cmlp
{
protected:

public:
   void              GetPositive();
   void              GetNegative();
   
   void              BackPropagate(double LearningRate = 0.1);

   double            Get(ENUM_REGRESSION_METRIC R)
   {                 return(label.RegressionMetric(inputs, R));
   }

   void              C_u_rbm(Smlp &MLP) : Cmlp(MLP)
   {  validated = false;
      int _layers =    ArraySize(MLP.arch);
      if(_layers == 2 && MLP.arch[0] > MLP.arch[1])
      {  ArrayResize(biases, _layers);
         //
         ArrayResize(gradients, _layers);
         ArrayResize(gradients_1st_moment, _layers);
         ArrayResize(gradients_2nd_moment, _layers);
         ArrayResize(sum_gradients, _layers);
         ArrayResize(sum_gradients_update, _layers);
         //
         ArrayResize(deltas, _layers);
         ArrayResize(deltas_1st_moment, _layers);
         ArrayResize(deltas_2nd_moment, _layers);
         ArrayResize(sum_deltas, _layers);
         ArrayResize(sum_deltas_update, _layers);
         //
         hidden_layers = 0;
         bool _norm_validated = true;
         for(int i = 0; i < _layers; i++)
         {  int _rows = MLP.arch[_layers - 1 - i], _columns = MLP.arch[i];
            //
            biases[i].Init(_rows);
            biases[i].Fill(MLP.initial_bias);
            //
            gradients[i].Init(_rows, _columns);
            gradients[i].Fill(0.0);
            //
            gradients_1st_moment[i].Init(_rows, _columns);
            gradients_1st_moment[i].Fill(0.0);
            gradients_2nd_moment[i].Init(_rows, _columns);
            gradients_2nd_moment[i].Fill(0.0);
            //
            sum_gradients[i].Init(_rows, _columns);
            sum_gradients[i].Fill(0.0);
            sum_gradients_update[i].Init(_rows, _columns);
            sum_gradients_update[i].Fill(0.0);
            //
            deltas[i].Init(_rows);
            deltas[i].Fill(0.0);
            deltas_1st_moment[i].Init(_rows);
            deltas_1st_moment[i].Fill(0.0);
            deltas_2nd_moment[i].Init(_rows);
            deltas_2nd_moment[i].Fill(0.0);
            sum_deltas[i].Init(_rows);
            sum_deltas[i].Fill(0.0);
            sum_deltas_update[i].Init(_rows);
            sum_deltas_update[i].Fill(0.0);
         }
         validated = true;
      }
      else
      {  printf(__FUNCSIG__ +
                " invalid network arch! Settings size is: %i, Max layer size is: %i, Min layer size is: %i, and activation is %s ",
                _layers, MLP.arch[ArrayMaximum(MLP.arch)], MLP.arch[ArrayMinimum(MLP.arch)], EnumToString(MLP.activation)
               );
      }
   };
   void              ~C_u_rbm(void) { };
};

Al personalizar el constructor para nuestra clase, omitimos la matriz de pesos porque su tamaño es siempre el número total de capas menos uno, y eso es lo que tenemos aquí. Por lo tanto, el constructor se ocupó de lo que es diferente: en primer lugar, tenemos dos vectores de polarización aunque las capas son solo dos. Esto implica que también tendremos dos vectores delta, uno para cada vector de polarización. Otra personalización necesaria está en el número de matrices de gradiente. A pesar de tener solo una matriz de pesos, tenemos dos matrices de gradiente porque nuestra retropropagación será para los dos ciclos de prueba; la fase positiva y la fase negativa.

Esto también implica que nuestra única matriz de pesos se actualiza dos veces en cada retropropagación. Como siempre, la retropropagación implica calcular los deltas, luego los gradientes y luego la actualización de los pesos y sesgos con estos valores. Realizamos nuestra retropropagación de la siguiente manera:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::BackPropagate(double LearningRate = 0.1)
{  
//COMPUTE DELTAS
   vector _loss = label.LossGradient(inputs, THIS.loss);
   //
   vector _negative = output.MatMul(weights[0]), _negative_derivative;
   _negative.Derivative(_negative_derivative, THIS.activation);
   deltas[1] = Hadamard(_loss, _negative_derivative);
   //
   vector _positive = weights[0].MatMul(inputs), _positive_derivative;
   _positive.Derivative(_positive_derivative, THIS.activation);
   matrix _weights;
   _weights.Copy(weights[0]);
   _weights.Transpose();
   vector _product = _weights.MatMul(deltas[1]);
   deltas[0] = Hadamard(_product, _positive_derivative);
//COMPUTE GRADIENTS
   gradients[0] = TransposeCol(deltas[0]).MatMul(TransposeRow(inputs));
   gradients[1] = TransposeCol(deltas[1]).MatMul(TransposeRow(output));
   
// UPDATE WEIGHTS AND BIASES
   for(int h = 1; h >= 0;  h--)
   {  matrix _gradients;
      _gradients.Copy(gradients[h]);
      if(h == 1)
      {  _gradients = _gradients.Transpose();
      }
      weights[0] -= LearningRate * _gradients;
      biases[h] -= LearningRate * deltas[h];
   }
}

Por lo tanto, esta función resume nuestra clase que hereda de 'Cmlp' con todas las funciones no anuladas de la clase base aún en efecto. Solo para aclarar por qué tenemos dos vectores de sesgo, dos vectores delta, dos matrices de gradientes y solo una matriz de pesos está en la fase positiva, encontramos la matriz de pesos por primera vez y el producto de esa debe agregarse al primer vector de sesgo. Este producto también implica que se debe capturar una matriz de gradiente para actualizar adecuadamente los pesos de este producto. Durante la segunda fase se repite el mismo proceso con la diferencia clave de que, como ya se mencionó, utilizamos los mismos pesos de la fase positiva.

Sin embargo, a pesar de utilizar los mismos pesos, se agrega un nuevo vector de sesgo (diferente) al producto de la segunda fase y esto produce nuestra reconstrucción de los datos de entrada. La diferencia entre estos datos reconstruidos y los datos de entrada originales define entonces nuestros deltas, y esto alimenta la retropropagación.

RBM en la clase de señal personalizada

Para crear la clase de señal personalizada, necesitaremos hacer referencia a nuestra clase RBM personalizada creada anteriormente en una nueva instancia de una clase de señal personalizada que ensamblamos en un Asesor Experto a través del asistente MQL5. Hay guías aquí y aquí sobre esto para los lectores que sean nuevos. Y una vez que lo referenciamos y lo configuramos, tendríamos solo la mitad de nuestro sistema comercial porque, como se mencionó en la introducción, tenemos los valores de la capa oculta de RBM de sus datos de entrada que sirven como entrada a otra red neuronal en forma de un perceptrón multicapa (Multi-Layer Perceptron, MLP). La función que cumple el RBM es incorporar los cambios de precios para desenmascarar su equivalente en una dimensión menor. Para nuestras pruebas, nuestro RBM es una red 8-4, donde los números son los tamaños de las capas visibles y ocultas. En mi opinión, la tarea RBM se inclina más hacia la clasificación que hacia la regresión y, por lo tanto, la función de pérdida y la activación serán de entropía cruzada categórica y de signo suave. Estos aún podrían ajustarse para que funcionen como clasificadores, como cubrimos en artículos recientes, sin embargo, estamos usando estas configuraciones como constantes y no son optimizables.

Las funciones realizadas por el RBM como se mencionó están más alineadas con la incrustación y, por lo tanto, la función responsable de realizar esto en nuestra clase de señal personalizada se denomina "Embedder". Su código fuente se comparte a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalEmbedding::Embedder(vector &Extraction)
{  m_learning.rate = m_learning_rate;
   for(int i = 1; i <= m_epochs; i++)
   {  U_RBM.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old, _out, _out_new, _out_old;
         if
         (
         _in_new.Init(__RBM_VISIBLE) && 
         _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __RBM_VISIBLE) && 
         _in_new.Size() == __RBM_VISIBLE &&
         _in_old.Init(__RBM_VISIBLE) && 
         _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS + 1, __RBM_VISIBLE) && 
         _in_old.Size() == __RBM_VISIBLE
         &&
         _out_new.Init(__MLP_OUTPUTS) &&
         _out_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_OUTPUTS) &&
         _out_new.Size() == __MLP_OUTPUTS &&
         _out_old.Init(__MLP_OUTPUTS) &&
         _out_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __MLP_OUTPUTS) &&
         _out_old.Size() == __MLP_OUTPUTS
         )
         {  _in = _in_new - _in_old;
            _out = _out_new - _out_old;
            U_RBM.Set(_in);
            U_RBM.GetPositive();
            U_RBM.GetNegative();
            U_RBM.BackPropagate(m_learning.rate);
            Extraction = Extractor(U_RBM.output, _out, ii > 0);
         }
      }
   }
}

Nuestra preparación de datos es muy similar a la que tuvimos en artículos anteriores. En la mayoría de los Asesores Expertos que se codifican manualmente y no a través del asistente MQL5, se deben tomar medidas adicionales para garantizar que los datos de precios consultados por el Asesor Experto estén realmente disponibles en el servidor del bróker antes de que se realicen los cálculos de la señal. Generalmente, cuando un asistente ensambla el Asesor Experto, esto se puede omitir, aunque en nuestro caso simplemente usamos la cláusula 'if' para garantizar que los datos que buscamos realmente se copien en los vectores deseados.

Al copiar datos a vectores, también es importante tener en cuenta que los datos no se ordenan como una serie, lo que implica que el índice más alto del vector copiado tiene el valor más reciente. Hay más aquí sobre este tema. Debido a que tenemos un arreglo en cadena donde el RBM proporciona entrada al MLP, hemos elegido entrenar las dos redes casi simultáneamente, donde en cada punto en el conjunto de entrenamiento del RBM entrenamos el RBM y luego continuamos esto entrenando también el MLP. Esto es diferente a agotar primero la sesión de entrenamiento del RBM antes de entrenar al MLP.

Esta disposición es ciertamente modificable por el lector dado que la fuente completa se adjunta en la parte inferior, sin embargo, la adoptamos porque podría ser más eficiente dada la necesidad de entrenar dos redes, para nuestros propósitos de prueba. Dado el entrenamiento casi concurrente, necesitamos obtener la entrada RBM y las etiquetas MLP al mismo tiempo, y es por eso que nuestras cláusulas 'if' son muy largas.

Integración del RBM con un MLP

Entonces, a través del proceso de entrenamiento, actualizamos los pesos RBM, lo que nos permite procesar más datos de entrada y obtener sus valores ocultos (también conocidos como su distribución de probabilidad). Esta distribución de probabilidad, a la que nos referimos como incorporación de precios, se introduce entonces en el MLP, y no los cambios de precios previos sin procesar. El uso de esta incrustación se realiza en la función 'Extractor', que simplemente alimenta la incrustación de precios proporcionada por el RBM a través del MLP. A medida que avanza, también entrena el MLP si se proporciona una etiqueta (valor objetivo). Dado que el entrenamiento se realiza hasta los cambios de precios más recientes, para los cuales no habría etiquetas, necesitamos realizar un seguimiento de esto. El rastreador es el tercer parámetro de entrada en la función 'Extractor' que es el booleano 'Train'. De forma predeterminada, es verdadero; sin embargo, una vez que llegamos al final del conjunto de entrenamiento y no tenemos etiqueta, se asigna a falso. El código para la función 'Extractor' se comparte a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CSignalEmbedding::Extractor(vector &Embedding, vector &Labels, bool Train = true)
{  vector _extraction;
   _extraction.Init(MLP.output.Size());
   m_learning.rate = m_learning_rate;
   for(int i = 1; i <= m_epochs; i++)
   {  MLP.LearningType(m_learning, i);
      MLP.Set(Embedding);
      MLP.Forward();
      _extraction = MLP.output;
      if(Train)
      {  MLP.Get(Labels);
         MLP.Backward(m_learning, i);
      }
   }
   return(_extraction);
}

Devuelve un vector que llamamos '_extraction' pero en nuestro caso solo nos interesa un valor, el próximo cambio de precio, por lo que realmente es un vector de tamaño único. Si bien el RBM está estructurado como un clasificador por su función de activación y función de pérdida, el MLP probablemente debería funcionar mejor cuando está estructurado como un regresor. Esto se debe a su salida de datos flotantes singular que puede ser negativa. Como regresor utilizamos activación de signo suave y la función de pérdida es Huber. Las razones de esto cuando se trata de redes de regresores se trataron en artículos recientes como aquí, así que los nuevos lectores pueden echarle un vistazo.

Tanto el RBM como el MLP no están ajustados correctamente para un rendimiento óptimo porque, por ejemplo, utilizan pesos y sesgos iniciales idénticos y, además, el entrenamiento es concurrente, lo que esencialmente significa que se utiliza una sesión de entrenamiento para entrenar ambas redes. Las alternativas a esto incluyen tener sesiones de capacitación de diferentes tamaños para el RBM y el MLP, donde la capacitación de MLP solo se realiza una vez que se completa la capacitación de RBM. Además, la tasa de aprendizaje es fija para ambas redes y no se han explotado los diferentes formatos que incluyen aprendizaje adaptativo. Muchos de estos ajustes adicionales y más quedan a criterio del lector.

Pruebas retrospectivas y optimización

Realizamos una optimización durante el año 2023 para el par GBPUSD en el marco temporal diario mientras buscamos los pesos y sesgos iniciales ideales de la red. Recordemos que tenemos un único parámetro de entrada para ambos valores de las dos redes, lo que no es necesariamente ideal. Además, buscamos los umbrales de apertura y cierre para las funciones 'LongCondition' y 'ShortCondition' de nuestra clase de señal personalizada, además de un nivel de toma de ganancias en puntos. Realizamos algunas ejecuciones que no son exhaustivas y de ellas obtenemos los siguientes resultados:

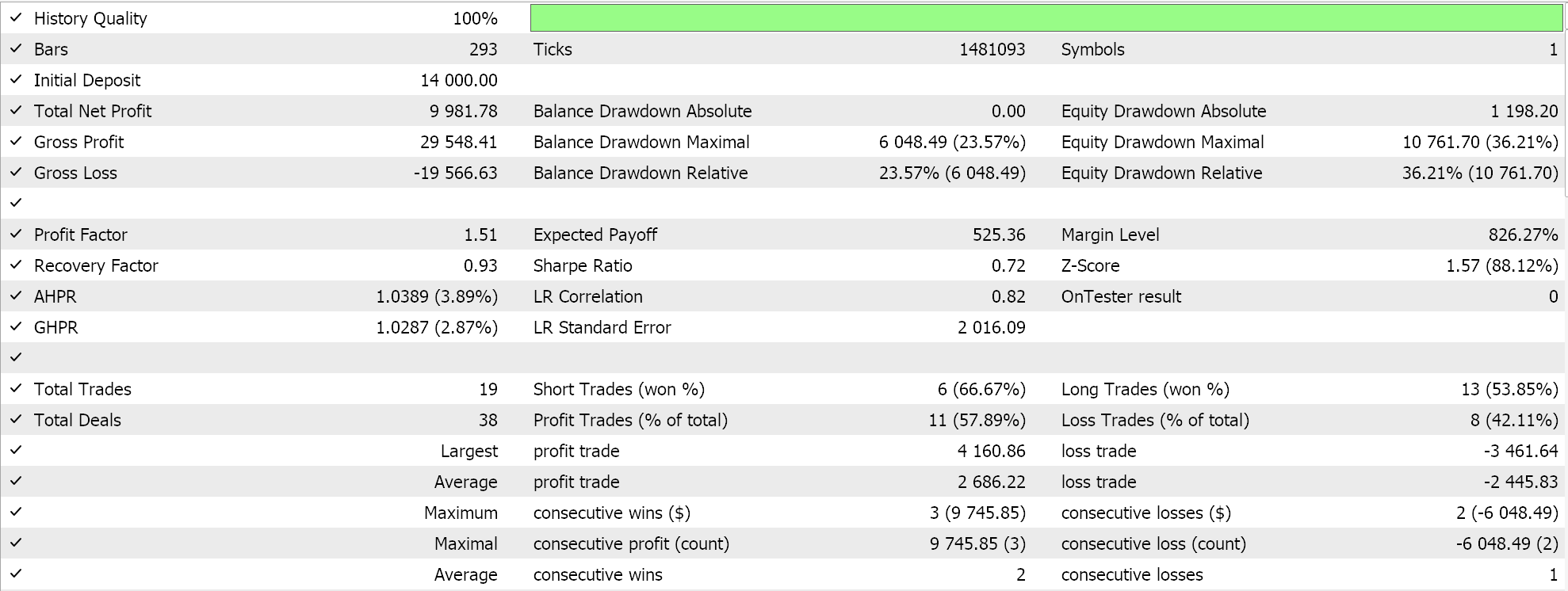
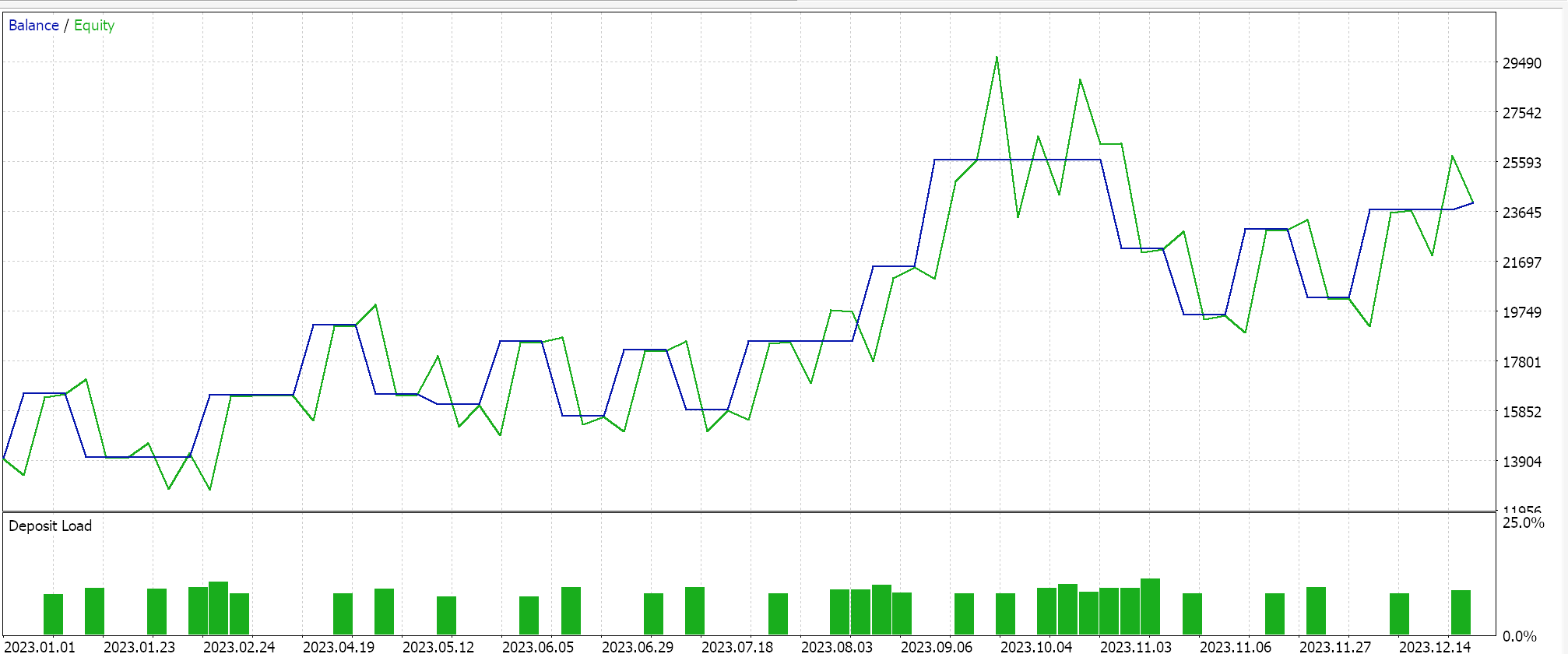
Nuestro Asesor Experto ensamblado por un mago puede operar, sin embargo, como siempre sucede, es necesaria mayor diligencia en cuanto a realizar pruebas durante períodos de historial más largos y realizar un seguimiento de las optimizaciones con pruebas de recorrido hacia adelante. Además, vale la pena mencionar que, al ser una señal basada en una red neuronal, el registro y el almacenamiento de los pesos y sesgos de la red (aquí hay 2) es algo que el usuario siempre debe planificar.

Conclusión

Hemos proporcionado un RBM como un incorporador de precios a un MLP con sus resultados comerciales optimizados durante un solo año, pero ¿cómo se podría medir la eficacia de la "integración de precios" en el contexto en el que se utiliza en este artículo? Bueno, la respuesta corta es si tenemos otra señal puramente MLP que toma como entradas los cambios de precios anteriores y también está entrenada como el MLP de este artículo para proyectar el próximo cambio de precio. Configurar esto también es relativamente fácil porque las clases de anclaje para MLP son similares a las que hemos estado usando, por lo que se pueden obtener fácilmente resultados comparativos.

También hemos emparejado un RBM que alimenta un MLP y no al revés. Considero que ésta es una mejor manera para que estos dos tipos de redes neuronales trabajen juntos (un clasificador y un regresor). Los regresores a menudo, pero no siempre, generan un único valor de punto flotante (que puede ser negativo) y, al tomar entradas "clasificadas", este emparejamiento podría justificarse. En el futuro, este arreglo se puede ampliar, no apilando los RBM, ya que explotan la profundidad, sino alineándolos en paralelo como entradas a redes regresoras con señales de transformador. Considero que los clasificadores con su profundidad están mejor diseñados para la "especialización" que las redes regresoras.

Además, como nota final, simplemente hemos tratado de clasificar los cambios de precios como "incrustación de precios", sin embargo, también se pueden considerar diferentes datos financieros y series de tiempo cuando se buscan datos de "incrustación de precios" en un MLP. Estos podrían incluir patrones de precios de velas, valores de indicadores de precios, datos de noticias del calendario económico, etc. El rendimiento y los resultados de las pruebas de cada uno de ellos seguramente variarán mucho, como era de esperar, por lo que es responsabilidad del lector encontrar y personalizar lo que funcione mejor con su forma de ver los mercados.