知っておくべきMQL5ウィザードのテクニック（第34回）：非従来型RBMによる価格の埋め込み

はじめに

この記事では、MQL5ウィザードを用いたMetaTrader 5の迅速な開発とプロトタイピング環境を活かし、様々な取引のセットアップやアイデアを探求します。本連載は、原則として、トレーダーがどのようにして群れから際立つことができるかを探ることを目的としており、あまり一般的でないアイデアを探求することで、興味のあるトレーダーに優位性をもたらす可能性があることを示しています。それは、トレーダーがそれらをどのように活用するかによります。そのため、ここでは必ずしも活用するのではなく、探索することに重点が置かれています。優位性が非常に重要である理由は、多くの有効な取引アイデアが互いに非常に強い相関関係を持つ傾向があるためです。

これは、トレンドが強気で誰もが利益を上げているときには素晴らしいことですが、トレンドが反転した際にドローダウンを緩和するには分散化が効果的です。しかし、単純に逆相関のある証券を見つけることは、理論上は簡単でも、実際にははるかに難しいのです。だからこそ、一般的に使用されているセットアップに単に依存するのではなく、トレーダー特有の取引エントリとエグジットがより良い選択肢となり得るのです。この記事では、Restricted Boltzmann Machines(RBM) （英語）をバックプロパゲーションを使用して実装した場合と、ギブスサンプリングとContrastive Divergenceの従来の実装比較していきます。

そもそもこれらのアプローチが使用された理由は、80年代半ば（RBMが「ハーモニウム」として紹介された1986年頃）には、ボルツマンマシンでバックプロパゲーションを実装するための計算コストが実現不可能だったからだとされています。RBMの名前の由来であるボルツマンマシンは、RBMのような2部グラフを使用せず、層内のニューロン間に接続があるため、さらに複雑です。これらの接続の複雑さは、RBMのようなボルツマンマシンの単純な実装でさえ、他のニューラルネットワークやバックプロパゲーションが行うように、一度に各パラメータを処理するのではなく、ネットワークのパラメータ（重みとバイアス）を微調整する際に確率的エネルギーベースモデル（EBM）（英語）に依存するように導いています。

Deep-AI:

Contrastive Divergenceは、は、エネルギーベースのモデルにおける分配関数によって引き起こされる計算上の課題に対処します。Contrastive Divergenceの重要な洞察は、完全なパーティション関数を計算することなく、これらのモデルを訓練することができるという点です。具体的には、CDはモデルによって生成されたサンプルの確率が減少する一方で、観測データの確率が増加するように、モデルのパラメータを調整することに焦点を当てます。 

この目的を達成するために、Contrastive Divergenceは、訓練データから始まるギブスサンプリング手順を実行し、モデルが高い確率を持つと考えるサンプルを生成します。そして、これらのサンプルを用いて、モデルパラメータに対する学習データの対数尤度の勾配を推定します。この勾配は、モデルのデータ表現を改善する方向にパラメータを更新するために使用されます。

確率ごとの計算を避けるために、ギブスサンプリングとContrastive Divergenceは明らかに理にかなった方法です。バックプロパゲーションは確かに実現可能な選択肢ですが、特にAIの作業負荷がCPUからGPUへとシフトしていることを考えると、さらにその重要性が増します。ボルツマンマシンのようなネットワーク（例えばRBM）を扱う場合、このハードウェアの選択が非常に重要です。なぜなら、たとえ層が2つだけであっても、これらの層は非常に深くなる傾向があり、各ニューロンの重みをどのように調整するかを適切に考慮する必要があるからです。

では、2層という制限を考慮すると、RBMとは一体何なのでしょうか。要するに、入力データの次元を減らし、入力よりも少ない次元のデータに隠れた特性を明らかにする分類器です。これは単純化しすぎた定義であり、より正確に言えば、教師なし設定で入力データの確率分布を学習するように訓練された生成的確率ニューラルネットワークと言えるでしょう。入力データから得られた知見は、ネットワークの隠れ層に記録され、分類、クラスタリング、または別のネットワークへの入力として使用することができます。

この記事では後者のアプローチを利用し、RBMの隠れ層の値を多層パーセプトロンの入力とします。本稿の全体的な構成は、原則としてこの連載でお馴染みの形式を踏襲します。

価格の埋め込み

価格の埋め込みは、この記事の文脈では、単語の埋め込みと非常に似たプロセスとして使用されています。ご存知の読者もいるかもしれませんが、これは大規模言語モデルのTransformerネットワークにおける前提ステップです。単語の埋め込みは、アテンションと組み合わせることで、単語のナンバーフィケーションとして定義でき、オンラインで利用可能な多くの文章をニューラルネットワークが理解できる形式に変換するのに役立ちます。同様に、私たちはデフォルトで、証券価格データは（たとえ数値であっても）ニューラルネットワークが簡単に「理解」できるものではないと仮定しています。このアプローチから得られる洞察を基に、バックプロパゲーションで学習させたRBMを使うことで、価格データをより理解しやすくする方法を模索しています。

さて、単語から数字への変換は、単に単語や文字に数字を割り当てることではなく、前述のように自己注意を伴う複雑なプロセスです。これに基づき、RBMの2分割グラフの設計を考慮すると、RBMとの類似性を見出すことができると考えています。

出典

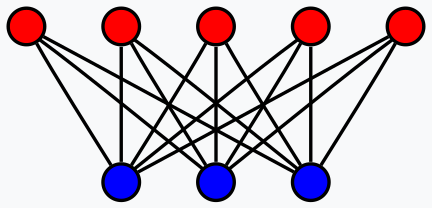
RBMの1つの層内には、ニューロン同士の直接的な結合は存在しませんが、入力データの自己注意成分を捉えるために重要なこれらの結合は、隠れ層を通じておこなわれます。この記事では、隠れ層が各ニューロンの変換だけでなく、他のニューロンとの関係がどのような意味を持つかも記録します。

いつものように、トレーダーにとっては「論より証拠」であり、この価格埋め込みの利点は取引結果によってのみ証明されるものです。そして、私たちはこのプロセスの初期段階に到達していますが、単語から数字への埋め込みで得られる報酬の規模は、数字から数字への埋め込みで見られるものと比較できないことを強調する価値があるかもしれません。これは、ここで行っていることがそれほど変革的ではないからです。それでは、バックプロパゲーションを使ってRBMを再構成する方法を考えてみましょう。

制限ボルツマンマシン(RBM)

RBMは、「正相」と「負相」と呼ばれる2つのサイクルで動作します。すでに述べたように、これらのサイクルは、通常は教師なし学習で実装されるため、学習プロセスの中で、各データポイントが持つ隠れた特性を直接的には知ることができません。すなわち、訓練データにはラベル（目標値）が存在しないということです。

この状況下でRBMがスコアを維持する方法は、負相で入力層の値に一致するよう隠れ層の値を再構成することにあります。2つの相で成り立っており、正相は通常のMLP（多層パーセプトロン）の順伝播に似たプロセスで隠れ層に値を供給します。隠れ層で得られるこれらの値は、入力データの次元を縮小した表現であり、隠された特性を捕らえるものとして、私たちの目的そのものです。

隠れ層（正のフェーズ）に向かって伝播する際には、ニューラルネットワークの場合と同様に重みの行列が使用されます。ただし、RBM が特別なのは、負のフェーズでは、同じ重みを使用して入力データを再構築することです。この再構築こそが、RBMが教師なしで学習をおこない、スコアを維持する方法であり、バックプロパゲーションを実装することで、入力データが事実上のラベル（または目標）として機能します。

このRBMを訓練するために訓練入力データ以外の追加データは必要ないため、これはまだ教師なし学習であると私は主張します。RBMが教師あり学習に使用される場合、理想的な隠れ層の値に基づくラベルが用いられますが、本記事の例では教師なしで進めます。そのため、まずは正相と負相の典型的なRBM関数を再構築することが必要です。具体的には以下の通りです。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::GetPositive(void)
{  vector _positive = weights[0].MatMul(inputs), _output;
   _positive += biases[0];
   _positive.Activation(_output, THIS.activation);
   output = _output;
}

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::GetNegative(void)
{  vector _negative = output.MatMul(weights[0]), _output;
   _negative += biases[1];
   _negative.Activation(_output, THIS.activation);
   label = _output;
}

今回紹介するMQL5のクラス「C_u_rbm」は、最近の記事で使用している別のクラス「Cmlp」を継承しています。C_u_rbmはCmlpを基盤としているものの、適切な層数の配置や関連する検証ステップがきちんとカバーされるよう、C_u_rbmの構築をカスタマイズする必要があります。このクラスの構成は、そのインターフェイスに示されているように、次のようにおこないます。

#include <My\Cmlp-.mqh>
//+------------------------------------------------------------------+
//| Unconventional RBM that uses:                                    |
//| reconstruction-error instead of free-energy                      |
//| and back-propagation instead of contrastive divergence           |
//+------------------------------------------------------------------+
class C_u_rbm : public Cmlp
{
protected:

public:
   void              GetPositive();
   void              GetNegative();
   
   void              BackPropagate(double LearningRate = 0.1);

   double            Get(ENUM_REGRESSION_METRIC R)
   {                 return(label.RegressionMetric(inputs, R));
   }

   void              C_u_rbm(Smlp &MLP) : Cmlp(MLP)
   {  validated = false;
      int _layers =    ArraySize(MLP.arch);
      if(_layers == 2 && MLP.arch[0] > MLP.arch[1])
      {  ArrayResize(biases, _layers);
         //
         ArrayResize(gradients, _layers);
         ArrayResize(gradients_1st_moment, _layers);
         ArrayResize(gradients_2nd_moment, _layers);
         ArrayResize(sum_gradients, _layers);
         ArrayResize(sum_gradients_update, _layers);
         //
         ArrayResize(deltas, _layers);
         ArrayResize(deltas_1st_moment, _layers);
         ArrayResize(deltas_2nd_moment, _layers);
         ArrayResize(sum_deltas, _layers);
         ArrayResize(sum_deltas_update, _layers);
         //
         hidden_layers = 0;
         bool _norm_validated = true;
         for(int i = 0; i < _layers; i++)
         {  int _rows = MLP.arch[_layers - 1 - i], _columns = MLP.arch[i];
            //
            biases[i].Init(_rows);
            biases[i].Fill(MLP.initial_bias);
            //
            gradients[i].Init(_rows, _columns);
            gradients[i].Fill(0.0);
            //
            gradients_1st_moment[i].Init(_rows, _columns);
            gradients_1st_moment[i].Fill(0.0);
            gradients_2nd_moment[i].Init(_rows, _columns);
            gradients_2nd_moment[i].Fill(0.0);
            //
            sum_gradients[i].Init(_rows, _columns);
            sum_gradients[i].Fill(0.0);
            sum_gradients_update[i].Init(_rows, _columns);
            sum_gradients_update[i].Fill(0.0);
            //
            deltas[i].Init(_rows);
            deltas[i].Fill(0.0);
            deltas_1st_moment[i].Init(_rows);
            deltas_1st_moment[i].Fill(0.0);
            deltas_2nd_moment[i].Init(_rows);
            deltas_2nd_moment[i].Fill(0.0);
            sum_deltas[i].Init(_rows);
            sum_deltas[i].Fill(0.0);
            sum_deltas_update[i].Init(_rows);
            sum_deltas_update[i].Fill(0.0);
         }
         validated = true;
      }
      else
      {  printf(__FUNCSIG__ +
                " invalid network arch! Settings size is: %i, Max layer size is: %i, Min layer size is: %i, and activation is %s ",
                _layers, MLP.arch[ArrayMaximum(MLP.arch)], MLP.arch[ArrayMinimum(MLP.arch)], EnumToString(MLP.activation)
               );
      }
   };
   void              ~C_u_rbm(void) { };
};

クラスのコンストラクタをカスタマイズする際、重みの行列配列は省略しました。これは、重み行列のサイズが層の総数から常に1を引いた値で決まるため、そのサイズを直接利用することで効率化できるためです。また、コンストラクタでは、2層のみで構成されるにもかかわらず、バイアスベクトルが2つ存在することに注意しました。これにより、各バイアスベクトルごとに1つのデルタベクトルが必要となり、2つのデルタベクトルが構成されます。さらに重要なカスタマイズとして、勾配行列の数を指定しました。重み行列は1つだけですが、バックプロパゲーションにおいて正相と負相の2つのサイクルでテストするため、勾配行列は2つ準備します。

これにより、バックプロパゲーションの際、重み行列が毎回2回更新されることになります。いつものように、バックプロパゲーションでは、デルタを計算し、次に勾配を計算し、これらの値で重みとバイアスを更新します。バックプロパゲーションは次のようにおこないます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void C_u_rbm::BackPropagate(double LearningRate = 0.1)
{  
//COMPUTE DELTAS
   vector _loss = label.LossGradient(inputs, THIS.loss);
   //
   vector _negative = output.MatMul(weights[0]), _negative_derivative;
   _negative.Derivative(_negative_derivative, THIS.activation);
   deltas[1] = Hadamard(_loss, _negative_derivative);
   //
   vector _positive = weights[0].MatMul(inputs), _positive_derivative;
   _positive.Derivative(_positive_derivative, THIS.activation);
   matrix _weights;
   _weights.Copy(weights[0]);
   _weights.Transpose();
   vector _product = _weights.MatMul(deltas[1]);
   deltas[0] = Hadamard(_product, _positive_derivative);
//COMPUTE GRADIENTS
   gradients[0] = TransposeCol(deltas[0]).MatMul(TransposeRow(inputs));
   gradients[1] = TransposeCol(deltas[1]).MatMul(TransposeRow(output));
   
// UPDATE WEIGHTS AND BIASES
   for(int h = 1; h >= 0;  h--)
   {  matrix _gradients;
      _gradients.Copy(gradients[h]);
      if(h == 1)
      {  _gradients = _gradients.Transpose();
      }
      weights[0] -= LearningRate * _gradients;
      biases[h] -= LearningRate * deltas[h];
   }
}

この関数では、Cmlpクラスを継承し、基本クラスでオーバーライドされていない関数が全て有効な状態を維持しています。この実装において、なぜ2つのバイアスベクトル、2つのデルタベクトル、2つの勾配行列が必要であり、重み行列が1つしかないのかを説明します。正相で初めて重み行列に遭遇し、その積を最初のバイアスベクトルに加える必要があるからです。この積はまた、この積の重みを適切に更新するために、勾配行列を捕捉する必要があることを意味します。第2相では、同じプロセスが繰り返されますが、重要な違いは、すでに述べたように、正相と同じ重みを使用することです。

しかし、同じ重みを使用しているにもかかわらず、新しい（異なる）バイアスベクトルが第2相の積に追加され、これによって入力データの再構成がおこなわれます。この再構築されたデータと元の入力データとの差分がデルタとなり、これがバックプロパゲーションに入力されます。

カスタムシグナルクラスのRBM

カスタムシグナルクラスを構築するには、MQL5ウィザードを使用し、EAに組み込むカスタムシグナルクラスの新しいインスタンスで、先述のカスタムRBMクラスを参照する必要があります。初心者の読者のために、詳細なガイドはこちらとこちらで確認できます。これらを参照し、設定を完了すると、取引システムの半分が完成します。これは、冒頭で述べたように、入力データのRBM隠し層の値が、多層パーセプトロン(MLP)の形式で他のニューラルネットワークの入力として機能するためです。RBMの機能は、価格変動を小次元の埋め込みで表現することにあります。テスト設定では、RBMは8-4構造（可視層と隠れ層のサイズがそれぞれ8と4）となります。私見では、RBMのタスクは回帰よりも分類に重きを置いており、損失関数には多クラス交差エントロピー、活性化関数にはソフトサインを使用しています。これらは、以前の記事で触れたように、分類器としての調整も可能ですが、今回はこれらの設定を定数として扱い、最適化はおこないません。

上記のように、RBMによって行われる機能は埋め込みに近いため、カスタムシグナルクラス内での埋め込み処理をおこなう関数にはEmbedderという名前を付けています。ソースコードを以下に掲載します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalEmbedding::Embedder(vector &Extraction)
{  m_learning.rate = m_learning_rate;
   for(int i = 1; i <= m_epochs; i++)
   {  U_RBM.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_new, _in_old, _out, _out_new, _out_old;
         if
         (
         _in_new.Init(__RBM_VISIBLE) && 
         _in_new.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __RBM_VISIBLE) && 
         _in_new.Size() == __RBM_VISIBLE &&
         _in_old.Init(__RBM_VISIBLE) && 
         _in_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS + 1, __RBM_VISIBLE) && 
         _in_old.Size() == __RBM_VISIBLE
         &&
         _out_new.Init(__MLP_OUTPUTS) &&
         _out_new.CopyRates(m_symbol.Name(), m_period, 8, ii, __MLP_OUTPUTS) &&
         _out_new.Size() == __MLP_OUTPUTS &&
         _out_old.Init(__MLP_OUTPUTS) &&
         _out_old.CopyRates(m_symbol.Name(), m_period, 8, ii + __MLP_OUTPUTS, __MLP_OUTPUTS) &&
         _out_old.Size() == __MLP_OUTPUTS
         )
         {  _in = _in_new - _in_old;
            _out = _out_new - _out_old;
            U_RBM.Set(_in);
            U_RBM.GetPositive();
            U_RBM.GetNegative();
            U_RBM.BackPropagate(m_learning.rate);
            Extraction = Extractor(U_RBM.output, _out, ii > 0);
         }
      }
   }
}

データ準備は、過去の記事で取り上げた手法に非常によく似ています。通常、MQL5ウィザードによって自動生成されたEAではなく手動でコーディングされたEAでは、シグナル計算が行われる前に、必要とする価格データがブローカーのサーバー上で確実に利用できるように、追加のステップを実行する必要があります。ウィザードでEAを生成する場合、この手順は省略されることが一般的ですが、今回のケースでは、データが意図した通りのベクトルに正しくコピーされているかを確認するためにif文を用いています。

また、データをベクトルにコピーする際、データがそのまま直列に並ぶわけではなく、コピーされたベクトルの最も高いインデックスが最新の値を保持することに注意が必要です。この点については、より詳しい情報がこちらにあります。今回は、RBMがMLPに対して入力データを提供する構成であるため、2つのネットワークをほぼ同時に訓練する手法を採用しました。具体的には、RBMの訓練セット内の各データポイントに対して、まずRBMを訓練し、その後すぐにMLPの訓練もおこなう、という流れです。これは、すべてのRBM訓練セッションを完了してからMLPを訓練する方法とは異なります。

この配置は、完全なソースコードが下部に掲載されているので、読者の皆さんが独自に修正することも可能です。しかし、テストの目的で2つのネットワークを効率よく訓練する必要性を考慮すると、この同時並行的な訓練の方法が有効だと判断しました。この構成を採用することで、RBMの入力とMLPのラベルを同時に取得する必要が生じるため、 if文が非常に長くなっているのです。

RBMとMLPの統合

RBMの学習プロセスにおいて、重みを更新しながら順次多くの入力データを処理し、その隠れ層の出力（確率分布）を取得することができます。この確率分布は「価格埋め込み」とも呼ばれ、生の価格変動データの代わりにMLPに入力されます。この「価格埋め込み」は、Extractor関数を通じてMLPに供給され、MLPが最終的な予測出力を生成します。Extractor関数では、RBMが提供する「価格埋め込み」をMLPに通すだけでなく、必要に応じてラベル（目標値）を用いてMLPの訓練もおこないます。訓練は、通常ラベルが付与されていない最新の価格変動データに至るまで進むため、ラベルの有無を追跡する必要があります。これにはExtractor関数の3番目の入力パラメータであるTrainフラグを用います。このフラグはデフォルトでtrueに設定されていますが、訓練セットが終了してラベルがない場合はfalseに設定します。Extractor関数のコードを以下に示します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CSignalEmbedding::Extractor(vector &Embedding, vector &Labels, bool Train = true)
{  vector _extraction;
   _extraction.Init(MLP.output.Size());
   m_learning.rate = m_learning_rate;
   for(int i = 1; i <= m_epochs; i++)
   {  MLP.LearningType(m_learning, i);
      MLP.Set(Embedding);
      MLP.Forward();
      _extraction = MLP.output;
      if(Train)
      {  MLP.Get(Labels);
         MLP.Backward(m_learning, i);
      }
   }
   return(_extraction);
}

これは「_extraction」と呼ばれるベクトルを返しますが、私たちの関心は次の価格変動という1つの値に限られているため、実際には1サイズのベクトルになります。RBMは活性化関数と損失関数によって分類器のような構造を持っていますが、MLPはおそらく回帰のような構造の方が効果的に機能します。これは、特異なフローティングデータ出力が負になる可能性があるためです。回帰としてソフトサイン活性化関数を使用し、損失関数はHuberを選択します。回帰ネットワークに関するこのような理由については最近の記事でも取り上げているため、新しい読者はそちらをご覧ください。

RBMとMLPの両方が最適なパフォーマンスを発揮していない理由は、同一の初期重みとバイアスを使用していること、さらに訓練が同時進行していることです。これは、基本的に1回の訓練セッションで両方のネットワークを訓練していることを意味します。この代替案としては、RBMとMLPで異なる規模の訓練セッションを設け、RBMの訓練が完了してからMLPの訓練をおこなう方法があります。さらに、学習率はどちらのネットワークでも固定であり、適応学習を含むさまざまな手法は利用されていません。これらの追加調整などは、読者のチェックに委ねられています。

バックテストと最適化

理想的な初期ネットワークの重みとバイアスを求めるために、GBPUSDペアについて日足時間枠で2023年の最適化をおこないます。思い出していただきたいのは、2つのネットワークへの入力パラメータがそれぞれ1つであり、これは必ずしも理想的な設定ではないという点です。さらに、カスタムシグナルクラスのLongConditionとShortCondition関数における始値と終値のしきい値、そしてポイント単位でのテイクぷプロフィットレベルも求めています。これまでにいくつかの実行をおこない、その結果は以下のようになりました。

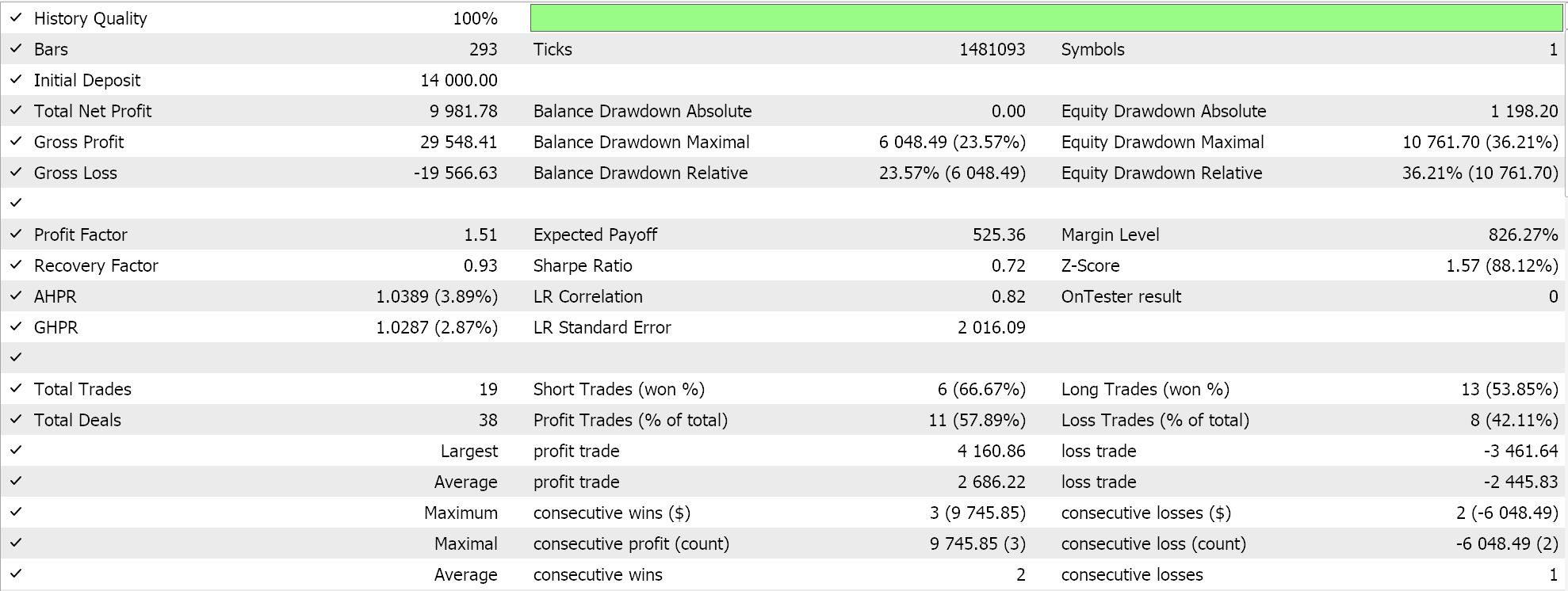
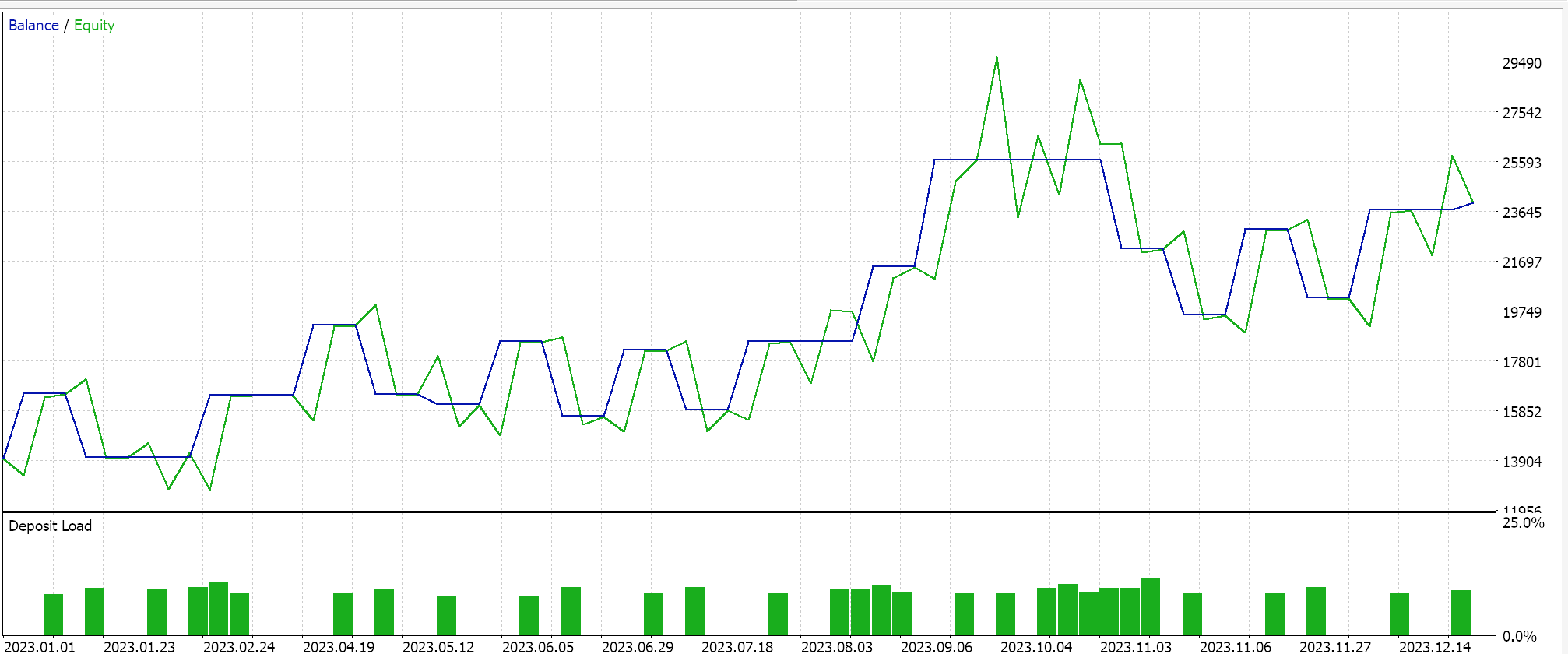
ウィザードが組み立てたEAは取引可能ですが、より長い期間の履歴をテストし、フォワードウォークテストで最適化をフォローアップすることが重要です。そのためには、常により多くの勤勉さが求められます。また、ニューラルネットワークベースのシグナルを使用しているため、ネットワーク（ここでは2つあります）の重みとバイアスの記録と保存は、ユーザーが常に計画すべき重要な要素です。

結論

MLPへの価格埋め込みとしてRBMを使用し、その1年間の最適化された取引結果を提供しましたが、この記事で述べられた文脈の中で「価格埋め込み」の有効性をどのように測定できるのでしょうか。要するに、以前の生の価格変動を入力として、次の価格変動を予測するために訓練された別の純粋なMLPシグナルが必要です。これを用意するのは比較的簡単でしょう。MLPのアンカークラスはこれまで使用してきたものと似ているため、比較結果を容易に得ることができるからです。

また、MLPに供給するRBMをペアリングしましたが、その逆の構成はおこなっていません。この2つのタイプのニューラルネットワーク（分類器と回帰器）が一緒に機能するためには、このアプローチが有効だと感じています。回帰は、常にではありませんが、1つの浮動小数点値（負の値もあり得る）を出力することが多く、「分類された」入力を取り込むことでこのペアの正当性を支持できます。RBMは深さを利用するため、RBMを積み重ねるのではなく、Transformerによってキューイングされた回帰ネットワークの入力として並列に配置することで、この配置を拡張できます。深層分類器は回帰ネットワークよりも「特殊化」に適していると考えています。

最後に、MLPへの「価格埋め込み」データを求める際、価格変動を単に「価格埋め込み」として分類するだけでなく、異なる財務データや時系列データも考慮することができます。これには、ローソク足の価格パターン、価格指標の値、経済カレンダーのニュースデータなどが含まれます。それぞれのパフォーマンスやテスト結果は、予想通り大きく異なるはずですので、読者は自身の市場観に最も適したものを見つけ、カスタマイズすることが求められます。