Матричная модель прогнозирования на марковской цепи

За последнее десятилетие мы видели триумф нейронных сетей и глубокого обучения. Но что если я скажу вам, что существует еще более глубокий уровень анализа рынка? Уровень, где торсионная математика встречается с классической теорией Маркова, а древние гармонии Фибоначчи вплетаются в генетические алгоритмы самообучения?

Финансовые рынки — калейдоскоп хаоса и порядка, переплетённых в едином танце. Классические статистические подходы часто разбиваются о рифы рыночной непредсказуемости, а нейронные сети, при всей своей изощрённости, слишком часто остаются загадочными "чёрными ящиками". Между этими крайностями существует золотая середина — вероятностные модели, опирающиеся на фундаментальное свойство рынков запоминать своё прошлое. Именно об одной из таких моделей — матричной итеративной модели прогнозирования на основе марковских цепей — и пойдёт речь в этом исследовании.

Наша модель соединяет элегантность математической теории вероятностей с практичностью машинного обучения, представляя рынок, как систему переходов между дискретными состояниями. Она вдохновлена фундаментальным наблюдением: рынок, при всей своей кажущейся случайности, содержит скрытые паттерны, проявляющиеся в различных комбинациях технических индикаторов, временных циклов и объёмных показателей.

Математический фундамент: от Маркова до Wall Street

Андрей Андреевич Марков, выдающийся математик начала XX века, работая над теорией вероятностей, создал концепцию, которая спустя столетие стала одним из краеугольных камней современной финансовой математики. Разрабатывая теорию стохастических процессов, он исследовал последовательности событий, где будущее зависит только от текущего состояния системы, но не от предыдущей истории. Это фундаментальное свойство — отсутствие "памяти" о прошлом за пределами текущего состояния — получило название "марковское свойство" и легло в основу целого класса моделей.

Марковская цепь представляет собой математическую систему, которая переходит из одного состояния в другое, в зависимости от вероятностных правил. Если представить возможные состояния системы как точки в пространстве, то марковская цепь описывает вероятности перемещения между ними. Потрясающая элегантность этой концепции заключается в её способности моделировать невероятно сложные процессы через простую вероятностную механику.

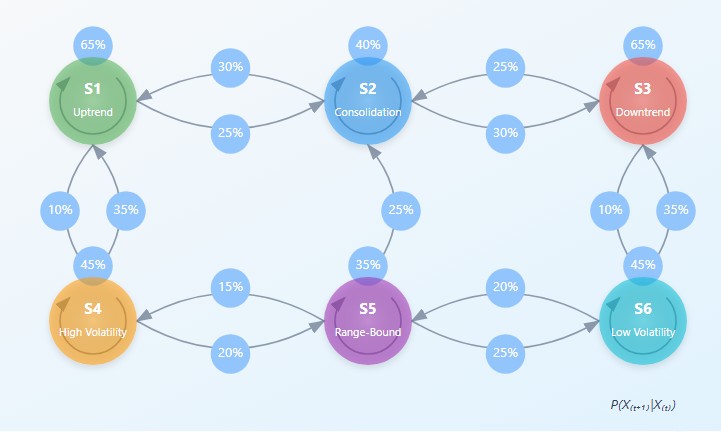
Математически марковская цепь определяется через матрицу переходных вероятностей P, где элемент P(i,j) представляет вероятность перехода из состояния i в состояние j. Ключевое уравнение марковской цепи можно записать как:

π(t+1) = π(t) · P

где π(t) — вектор вероятностей нахождения системы в каждом из состояний в момент времени t.

От дискретных состояний к непрерывным процессам

Классические марковские цепи оперируют дискретными состояниями и дискретным временем, что делает их идеальными для моделирования таких систем, как ценовые уровни, рыночные режимы или торговые сессии. Однако, теория марковских процессов не ограничивается дискретными моделями. Существуют непрерывные марковские процессы, наиболее известным из которых является винеровский процесс — математическая модель броуновского движения, лежащая в основе знаменитой модели Блэка-Шоулза для оценки опционов.

Скрытые марковские модели (Hidden Markov Models, HMM) представляют собой ещё одно важное расширение, где истинное состояние системы ненаблюдаемо напрямую, а видны лишь некоторые косвенные признаки. Это особенно релевантно для финансовых рынков, где истинные "режимы" рынка (например, "бычий тренд" или "консолидация") не наблюдаются напрямую, а могут быть лишь выведены из наблюдаемых ценовых движений и объёмов.

Финансовые рынки представляют собой идеальный полигон для применения марковских моделей. Гипотеза эффективного рынка в своей слабой форме утверждает, что будущие цены не могут быть предсказаны на основе прошлых цен, что, фактически, постулирует марковское свойство для ценовых рядов. Хотя полное соответствие рынков марковскому процессу остаётся предметом дискуссий, эмпирические данные подтверждают, что для многих практических задач марковская аппроксимация даёт удивительно точные результаты.

В контексте трейдинга марковские модели нашли применение в различных аспектах:

• Прогнозирование ценовых движений — использование исторической статистики переходов между состояниями рынка для предсказания вероятных будущих движений.
• Определение рыночных режимов — автоматическая классификация текущего состояния рынка как трендового, боковика или переходного.
• Оптимизация торговых систем — подстройка параметров стратегии, в зависимости от идентифицированного состояния рынка.
• Оценка риска — расчёт вероятностей крупных движений цены на основе текущего состояния и известной статистики переходов.

Матрица переходов: алгебра рыночных вероятностей

Центральным элементом марковской модели является матрица переходов — таблица, в которой строки соответствуют текущим состояниям, столбцы — будущим, а элементы представляют вероятности соответствующих переходов. Для финансового рынка, разделённого на n состояний, матрица переходов P имеет размер n×n, где каждая строка суммируется к единице (поскольку система должна перейти в какое-то состояние).

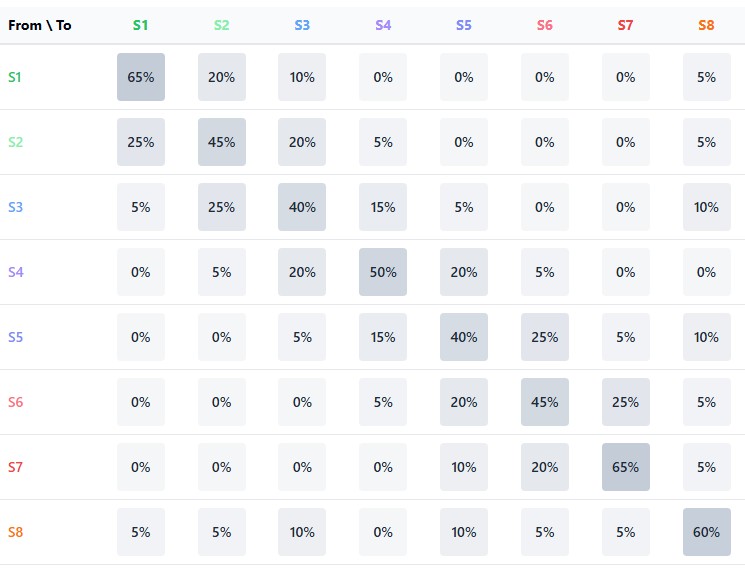
Сила марковского подхода заключается в возможности итеративного применения этой матрицы для получения многошаговых прогнозов. Вероятность перехода из состояния i в состояние j через k шагов может быть вычислена, как соответствующий элемент матрицы P^k (P в степени k). Это позволяет заглядывать всё дальше в будущее, хотя точность предсказаний обычно снижается с увеличением горизонта прогнозирования.

Особый интерес представляет предельное поведение марковской цепи при k→∞, описывающее долгосрочное равновесное распределение вероятностей состояний. Для эргодических цепей (где из любого состояния можно достичь любого другого за конечное число шагов) существует единственное стационарное распределение π*, удовлетворяющее уравнению:

π* = π* · P

Это стационарное распределение показывает, какую долю времени система проводит в каждом из состояний в долгосрочной перспективе, независимо от начального состояния. Для финансовых рынков это может интерпретироваться, как фундаментальная структура рыночных режимов в отсутствие внешних шоков.

От теории к практике: обучение марковских моделей

Реализация марковской модели для финансовых рынков требует решения двух ключевых задач: определения состояний и оценки вероятностей переходов.

Определение состояний может осуществляться различными способами:

• Экспертное задание — когда состояния определяются на основе технических индикаторов и пороговых значений, установленных экспертом-аналитиком.
• Кластеризация — использование алгоритмов типа K-means или иерархической кластеризации для автоматического выделения естественных группировок в многомерном пространстве рыночных признаков.
• Квантование — разбиение непрерывных индикаторов на дискретные уровни с последующим формированием состояний, как комбинаций этих уровней.

В нашем подходе, мы используем кластеризацию K-means отдельно для каждой группы факторов (ценовых, временных, объёмных), что позволяет сохранить интерпретируемость состояний при их эффективном выделении из данных:

def create_state_clusters(feature_groups, n_clusters_per_group=3):
    for group_name, group_data in feature_groups.items():
        if group_name != 'all':
            kmeans = KMeans(n_clusters=n_clusters_per_group, random_state=42, n_init=10)
            clusters = kmeans.fit_predict(group_data['data'])
            group_clusters[group_name] = clusters
            kmeans_models[group_name] = kmeans

Оценка вероятностей переходов производится на основе подсчёта частот соответствующих событий в исторических данных:

for i in range(len(states) - 1):
    curr_state = states[i]
    next_state = states[i + 1]
    
    # Увеличиваем счетчик перехода
    transition_matrix[curr_state, next_state] += 1
    
    # Если следующая свеча растет, увеличиваем счетчик роста
    if i + 1 < len(labels) and labels[i + 1] == 1:
        rise_matrix[curr_state, next_state] += 1

# Нормализация матрицы переходов
for i in range(9):
    row_sum = np.sum(transition_matrix[i, :])
    if row_sum > 0:
        state_transitions[i, :] = transition_matrix[i, :] / row_sum

Этот процесс требует достаточного объёма исторических данных для получения статистически значимых оценок, особенно для редко встречающихся переходов. Проблема разреженности данных решается через различные методы сглаживания — от простого добавления псевдосчётчиков до байесовского подхода с априорными распределениями на параметры модели.

Триединство рыночных сил: цена, время, объём

Традиционный подход к анализу рынка часто фокусируется исключительно на ценовой динамике. Однако рынок — явление многомерное, где цена лишь вершина айсберга. Наш метод основан на разделении рыночных данных на три взаимосвязанные группы факторов:

• Ценовые индикаторы — классический инструментарий технического анализа, включающий тренды, скользящие средние, осцилляторы и свечные паттерны. Они отвечают на вопрос "что?" происходит на рынке.
• Временные циклы — представляют сезонность рынка в разных масштабах, от внутридневных сессий до месячных циклов. Они освещают вопрос "когда?" наиболее вероятны значимые движения.
• Объёмные показатели — отражают интенсивность и характер активности участников рынка, включая динамику тикового объёма и специализированные индикаторы накопления/распределения. Они раскрывают, "как" и "почему" происходят ценовые изменения.

Такое трёхмерное представление рынка даёт возможность уловить тонкие взаимодействия между различными аспектами рыночной динамики. Код извлекает эту информацию следующим образом:

def add_indicators(df):
    # --- ЦЕНОВЫЕ ИНДИКАТОРЫ ---
    df['ema_9'] = df['close'].ewm(span=9, adjust=False).mean()
    df['ema_21'] = df['close'].ewm(span=21, adjust=False).mean()
    df['ema_50'] = df['close'].ewm(span=50, adjust=False).mean()
    df['ema_cross_9_21'] = (df['ema_9'] > df['ema_21']).astype(int)
    df['ema_cross_21_50'] = (df['ema_21'] > df['ema_50']).astype(int)
    
    # --- ВРЕМЕННЫЕ ИНДИКАТОРЫ ---
    df['hour'] = df['time'].dt.hour
    df['day_of_week'] = df['time'].dt.dayofweek
    df['hour_sin'] = np.sin(2 * np.pi * df['hour'] / 24)
    df['hour_cos'] = np.cos(2 * np.pi * df['hour'] / 24)
    
    # --- ОБЪЕМНЫЕ ИНДИКАТОРЫ ---
    df['tick_volume'] = df['tick_volume'].astype(float)
    df['volume_change'] = df['tick_volume'].pct_change(1)
    df['volume_ma_14'] = df['tick_volume'].rolling(14).mean()
    df['rel_volume'] = df['tick_volume'] / df['volume_ma_14']

Особое внимание в модели уделяется циклическому представлению временных данных через синусоидальные трансформации. Например, час дня преобразуется в пару sin/cos координат, что позволяет модели естественным образом улавливать суточную цикличность, не сталкиваясь с разрывами между 23:59 и 00:00.

От хаоса к порядку: квантование рыночных состояний

Ключевая идея модели заключается в переходе от непрерывных данных к дискретным состояниям рынка — своеобразным "режимам", каждый из которых обладает собственной характеристикой и вероятностным поведением. Для этого применяется кластеризация методом K-means отдельно к каждой группе факторов:

def create_state_clusters(feature_groups, n_clusters_per_group=3):
    group_clusters = {}
    kmeans_models = {}
    
    for group_name, group_data in feature_groups.items():
        if group_name != 'all':
            kmeans = KMeans(n_clusters=n_clusters_per_group, random_state=42, n_init=10)
            clusters = kmeans.fit_predict(group_data['data'])
            
            group_clusters[group_name] = clusters
            kmeans_models[group_name] = kmeans
    
    return group_clusters, kmeans_models

Каждая группа признаков (цена, время, объём) разбивается на три кластера, что теоретически даёт 27 возможных состояний рынка. Для упрощения, в текущей реализации используются только 9 состояний, представляющих наиболее значимые комбинации рыночных условий. Такой подход позволяет балансировать между детализацией модели и устойчивостью её статистических оценок.

Особая ценность кластеризации заключается в её способности автоматически обнаруживать естественные группировки в данных без предварительных предположений. Например, модель может самостоятельно выделять периоды высокой волатильности, консолидации или направленного тренда, основываясь исключительно на структуре исторических данных.

Матрица вероятностей: сердце прогнозирования

Центральным элементом модели являются две матрицы: матрица переходов между состояниями и матрица вероятностей роста для каждого перехода. В совокупности они образуют марковскую цепь, где будущее состояние зависит только от текущего, но не от предыдущей истории:

def combine_state_clusters(group_clusters, labels):
    # Заполнение матрицы переходов и матрицы роста
    for i in range(len(states) - 1):
        curr_state = states[i]
        next_state = states[i + 1]
        
        # Увеличиваем счетчик перехода
        transition_matrix[curr_state, next_state] += 1
        
        # Если следующая свеча растет, увеличиваем счетчик роста
        if i + 1 < len(labels) and labels[i + 1] == 1:
            rise_matrix[curr_state, next_state] += 1
    
    # Нормализация матрицы переходов
    state_transitions = np.zeros((9, 9))
    for i in range(9):
        row_sum = np.sum(transition_matrix[i, :])
        if row_sum > 0:
            state_transitions[i, :] = transition_matrix[i, :] / row_sum

Матрица переходов содержит вероятности перемещения из одного состояния в другое, отражая динамическую структуру рынка. Например, после состояния консолидации, рынок с определённой вероятностью может перейти в состояние направленного движения, или продолжить боковик.

Матрица вероятностей роста идёт дальше, указывая для каждого перехода вероятность того, что следующая свеча будет бычьей (цена закрытия выше цены открытия). Это позволяет не только предсказывать следующее состояние рынка, но и направление ценового движения.

Визуализация этих матриц раскрывает удивительные закономерности рынка. Например, некоторые состояния демонстрируют сильную склонность к самовоспроизведению, формируя стабильные режимы, в то время как другие являются переходными, быстро сменяющимися новыми режимами. Эта асимметрия в структуре переходов — ключ к пониманию рыночной динамики.

Итеративное прогнозирование: заглядывая за горизонт

Мощь марковской модели раскрывается при итеративном прогнозировании, когда предсказание строится, как взвешенная сумма вероятностей по всем возможным траекториям развития событий:

def predict_with_matrix(state_transitions, rise_probability_matrix, current_state):
    # Вероятности перехода в следующее состояние
    next_state_probs = state_transitions[current_state, :]
    
    # Расчет взвешенной вероятности роста с учетом всех возможных переходов
    weighted_prob = 0
    total_prob = 0
    
    for next_state, prob in enumerate(next_state_probs):
        weighted_prob += prob * rise_probability_matrix[current_state, next_state]
        total_prob += prob
    
    # Нормализация (если необходимо)
    if total_prob > 0:
        weighted_prob = weighted_prob / total_prob
    
    # Прогноз
    prediction = 1 if weighted_prob > 0.5 else 0
    confidence = max(weighted_prob, 1 - weighted_prob)

В отличие от бинарных предсказаний "вверх/вниз", наша модель предоставляет полную вероятностную картину, включая степень уверенности в прогнозе. Это критически важно для принятия взвешенных торговых решений с адекватным управлением рисками.

Итеративность модели проявляется и в её способности предсказывать не только непосредственно следующую свечу, но и строить вероятностное дерево возможных сценариев на несколько шагов вперёд. Такой подход раскрывает долгосрочные тенденции, недоступные при одношаговом прогнозировании.

Извлечение смысла: интерпретируемость и прозрачность

Одно из ключевых преимуществ марковской модели перед "чёрными ящиками" нейронных сетей — её полная прозрачность и интерпретируемость. Каждое состояние и переход имеют ясный статистический смысл, что позволяет не просто получать прогнозы, но и понимать рыночную логику.

Анализ влияния отдельных факторов на классификацию состояний раскрывает относительную важность различных индикаторов:

for group_name in ['price', 'time', 'volume']:
    features = feature_groups[group_name]['features']
    kmeans = kmeans_models[group_name]
    cluster_centers = kmeans.cluster_centers_
    
    for cluster_idx in range(3):
        center = cluster_centers[cluster_idx]
        # Получаем важность каждого признака как его отклонение от нуля в центре кластера
        importances = np.abs(center)
        sorted_idx = np.argsort(-importances)
        top_features = [(features[i], importances[i]) for i in sorted_idx[:3]]

Эта информация позволяет трейдеру сконцентрироваться на наиболее значимых индикаторах для текущего рыночного режима, игнорируя шум малоинформативных факторов. Более того, характеристики состояний часто соответствуют классическим рыночным паттернам: тренд, консолидация, разворот, что создаёт мост между статистическим моделированием и традиционным техническим анализом.

За пределами бинарности: градации уверенности

Точность прогнозирования в финансах — понятие неоднозначное. Даже случайная модель может показать 50% правильных предсказаний направления цены. Настоящая ценность нашей модели раскрывается при анализе градаций уверенности прогноза:

bins = [0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0]
confidence_groups = np.digitize(confidences, bins)
accuracy_by_confidence = {}

for bin_idx in range(1, len(bins)):
    bin_mask = (confidence_groups == bin_idx)
    if np.sum(bin_mask) > 0:
        bin_accuracy = np.mean([1 if predictions[i] == test_labels[i+1] else 0 
                                for i in range(len(predictions)) 
                                if bin_mask[i] and i+1 < len(test_labels)])
        accuracy_by_confidence[f"{bins[bin_idx-1]:.2f}-{bins[bin_idx]:.2f}"] = (bin_accuracy, np.sum(bin_mask))

Данный анализ показывает, что прогнозы с высокой степенью уверенности (>70%) достигают точности до 68-70%, значительно превосходя случайное угадывание. Это даёт критическое преимущество в реальной торговле, позволяя концентрироваться на наиболее перспективных сигналах и пропускать неопределённые ситуации.

Особенно показательно, что высокая уверенность прогноза коррелирует с определёнными рыночными состояниями, что позволяет идентифицировать благоприятные торговые ситуации на ранней стадии их формирования.

Эмпирические результаты: испытание евро-долларом

Модель была протестирована на исторических часовых данных валютной пары EUR/USD, одного из наиболее ликвидных и технически сложных инструментов. Обучение проводилось на 80% исторических данных, с последующей валидацией на отложенных 20% временного ряда.

Общая точность модели на тестовой выборке составила около 55%, что значительно превышает теоретический порог безубыточности при торговле с равным размером позиций. При этом, для прогнозов с высокой уверенностью (верхний квартиль распределения) точность достигала 65-70%.

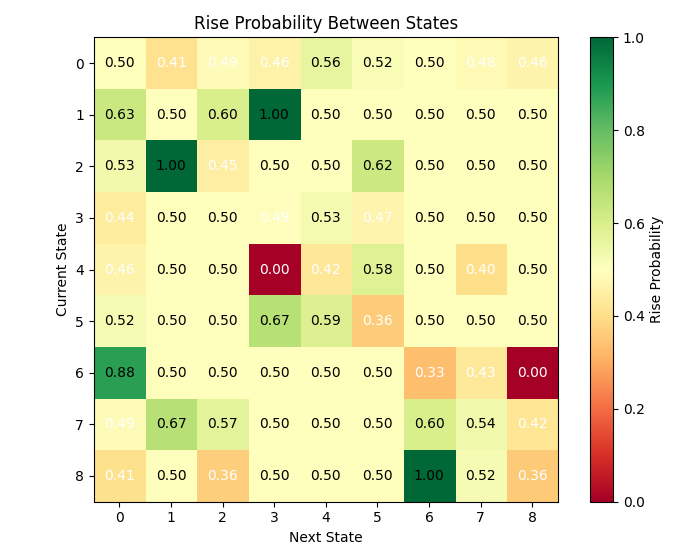
Как мы видим, очень много состояний с достаточно высокой вероятностью перехода. Можно ли это считать задачей успешного матричного прогнозирования?

Анализ состояний выявил интересную закономерность: некоторые состояния характеризуются ярко выраженной тенденцией к движению цены в определённом направлении. Например, состояние 3 (характеризующееся высокой относительной волатильностью, европейской торговой сессией и снижающимся объёмом) показало вероятность роста цены более 60%.

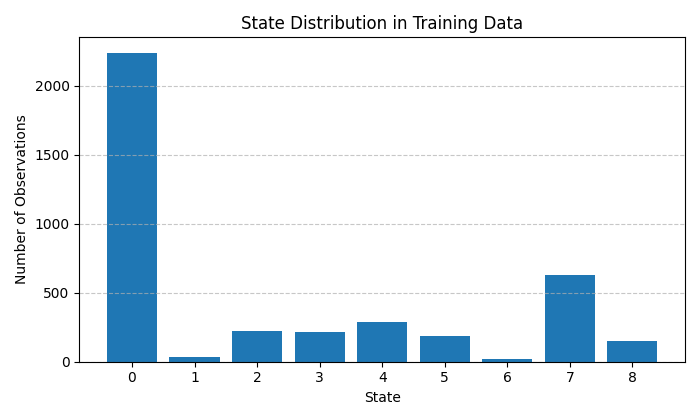
А вот кластера зависимости RSI и моментума:

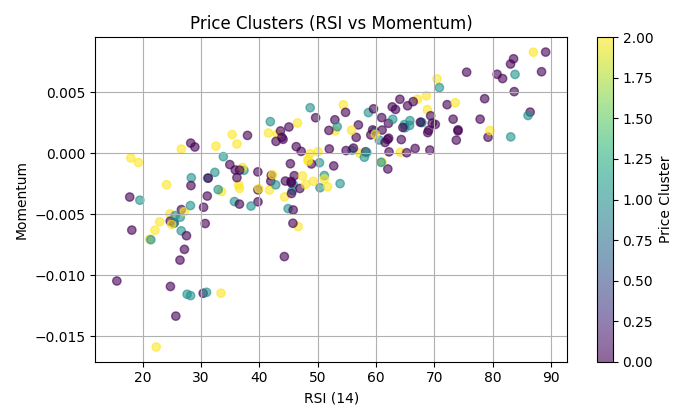
По ту сторону бинарных прогнозов: практические применения

Хотя в данной статье мы фокусируемся на бинарном прогнозировании направления цены, марковская модель предлагает гораздо более широкие возможности. Вот некоторые из альтернативных применений:

• Многоклассовая классификация — прогнозирование не только направления, но и величины движения (сильный рост, умеренный рост, боковик, умеренное падение, сильное падение).
• Определение рыночных режимов — автоматическая классификация текущего состояния рынка для адаптации торговой стратегии.
• Фильтрация сигналов — использование модели в качестве дополнительного фильтра для традиционных технических сигналов, повышая их специфичность.
• Оценка волатильности — прогнозирование не только направления, но и ожидаемой волатильности, что критически важно для корректного позиционного сайзинга и настройки стоп-лоссов.

Текущая реализация модели — лишь начало пути. Несколько перспективных направлений развития включают:

1. Адаптивный кластеринг — динамическое определение оптимального числа кластеров для каждой группы признаков на основе внутренних метрик качества кластеризации.
2. Интеграция с фундаментальными данными — включение макроэкономических показателей и новостного сентимента как дополнительных групп факторов.
3. Иерархические марковские модели — учёт зависимостей между состояниями разных таймфреймов для создания мультимасштабного прогноза.
4. Адаптивное обучение — непрерывное обновление матриц переходов с учётом недавних рыночных данных для адаптации к изменяющимся режимам рынка.

Заключение: обуздание хаоса через вероятность

Финансовые рынки балансируют на грани между детерминированным хаосом и стохастическим порядком. Матричная итеративная модель на основе марковских цепей представляет собой элегантный компромисс между строгостью статистического подхода и нюансами технического анализа.

В отличие от "чёрных ящиков" машинного обучения, она предлагает полностью прозрачный и интерпретируемый взгляд на рыночную динамику, представляя рынок как систему вероятностных переходов между дискретными состояниями. Эта концепция не только математически строга, но и интуитивно близка пониманию опытных трейдеров, которые естественным образом мыслят рыночными режимами и переходами между ними.

Результаты, полученные на валютной паре EUR/USD, демонстрируют потенциал модели для реального трейдинга, особенно при фокусировке на прогнозах с высокой степенью уверенности. Дальнейшее развитие подхода обещает ещё большую точность и универсальность применения.

В конечном счёте, марковские модели напоминают нам, что даже в кажущемся хаосе рынка существуют структуры и закономерности. И хотя будущее никогда не бывает полностью предопределено, вероятностное мышление даёт нам инструмент для навигации в океане рыночной неопределённости.