Возможности Мастера MQL5, которые вам нужно знать (Часть 30): Пакетная нормализация в машинном обучении

Введение

Пакетная нормализация (batch normalization) - форма стандартизации данных перед их передачей слоям нейронной сети, улучшающая производительность сетей. Однако единого мнения на счет причин такого улучшения нет. В оригинальной статье по этой теме в качестве причины назван внутренний ковариационный сдвиг (internal covariate shift), что можно понимать как смягчение последствий дисбаланса входных данных «вышестоящих слоев» от каскадного воздействия на нижестоящие слои. В более поздней статье утверждается, что улучшение эмпирических показателей обусловлено сглаживанием, поскольку внутрислойные градиенты имеют меньшую изменчивость с учетом нормализации.

С точки зрения трейдера, интерес к вопросу, ПОЧЕМУ пакетная нормализация влияет на производительность нейронной сети, является веской причиной для разработки и тестирования систем, использующих ее. Это наша ближайшая задача. Мы рассмотрим три основные формы пакетной нормализации, а именно стандартное масштабирование (Standard-Scaling), масштабирование признаков (Feature-Scaling) и робастное масштабирование (Robust-Scaling). Каждый из них представляет собой очень простой алгоритм. Мы проведем тесты с советниками, использующими каждый из них, а в качестве контроля мы также проведем тесты с советниками, которые не используют пакетную нормализацию. Таким образом наша статья вернется к формату, который мы использовали до последних двух статей (о темпах обучения): у нас будут описания всех трех нормализаций, затем отчеты о тестировании с контролем и, наконец, заключение.

Статья, как и все остальные в этой серии, фокусируется на тестировании новых идей с использованием советников, собранных в Мастере. Необходимую вводную информацию можно получить здесь и здесь. Эти две статьи содержат некоторые рекомендации по использованию кода, прикрепленного в конце статьи. В этой статье мы используем довольно много пользовательских перечислений данных в качестве оптимизируемых входных параметров. Встроенные перечисления MQL5 можно объявить в заголовке пользовательского файла сигнала, и они будут автоматически указаны в качестве входных данных и инициализированы как часть фильтра сигнала. Однако если перечисления являются пользовательскими, то размещение их в заголовке сделает файл невидимым (или нераспознаваемым) в Мастере MQL5, что означает, что вы не сможете выполнить сборку в Мастере. На данный момент мы можем обойти эту проблему, исключив их из заголовка класса пользовательского сигнала, но при этом объявив параметры и их функции назначения внутри класса сигнала, как это всегда бывает с любым входным параметром. После завершения сборки Мастера мы вручную вносим изменения в список входных параметров, а также инициализируем класс сигнала для добавления этого пользовательского перечисления параметров.

Я нашел способ обойти эту проблему, который, по-моему, включал объявление перечислений в самом классе сигнала, но я не помню подробностей, поэтому нам придется ограничиться редактированием вручную. В нашем тестовом советнике имеются пользовательские перечисления для типа темпа обучения, типа адаптивного темпа обучения и, что наиболее важно для этой статьи, перечисление для типов нормализации. Код последнего представлен ниже:

enum Enormalize
{  NORMALIZE_NONE = -1,
   NORMALIZE_ROBUST = 0,
   NORMALIZE_FEATURE = 1,
   NORMALIZE_STANDARD = 2,
};

Чтобы использовать и оптимизировать это перечисление в советнике, нам потребуется вручную добавить параметры перечисления в качестве входных данных следующим образом:

....

input ENUM_ACTIVATION_FUNCTION Signal_CMLP_ActivationType = AF_SIGMOID;  // CMLP(30,6,0.05,10,0.1,2,...) Activation Type
input Enormalize Signal_CMLP_NormalizeType   = NORMALIZE_FEATURE; // CMLP(30,6,0.05,10,0.1,2,...) Batch Normalisation Type
input Elearning Signal_CMLP_LearningType   = LEARNING_ADAPTIVE; // CMLP(30,6,0.05,10,0.1,2,...) Learning Type
input Eadaptive Signal_CMLP_AdaptiveType   = ADAPTIVE_GRADIENT; // CMLP(30,6,0.05,10,0.1,2,...) Adaptive Type

...

Кроме того, нам необходимо добавить объявленные параметры в экземпляр пользовательского сигнала, который инициализируется как filter0. Это делается так:

...

   filter0.ActivationType(Signal_CMLP_ActivationType);
   filter0.NormalizeType(Signal_CMLP_NormalizeType);
   filter0.LearningType(Signal_CMLP_LearningType);
   filter0.AdaptiveType(Signal_CMLP_AdaptiveType);

...

После этого собранный в Мастере советник можно использовать в обычном режиме с нашим пользовательским классом сигналов. Мы ознакомились с тремя форматами нормализации, которые мы будем учитывать с помощью пользовательского перечисления. Давайте сделаем краткий обзор предмета, прежде чем более подробно рассмотреть каждый из типов пакетного перечисления, после чего рассмотрим общую реализацию в пользовательском классе сигнала.

Аргументы в пользу пакетной нормализации в нейронных сетях

Большинство преимуществ пакетной нормализации можно найти в оригинальной статье 2015 года. Поскольку сейчас ведутся споры о том, как достичь эмпирических результатов, эти первоначальные аргументы не обязательно будут иметь тот же вес, что и в начале. Тем не менее, мы представляем их здесь, по крайней мере, в качестве введения в тему. Пакетная нормализация рекламируется как способ стабилизации процесса обучения за счет уменьшения вышеупомянутого внутреннего ковариационного сдвига. Это повышает скорость сходимости, поскольку активации на каждом уровне "более стандартны". Кроме того, он снижает чувствительность к весам инициализации, используемым в сети перед обучением. Начальные веса, как правило, оказывают непропорционально большое влияние не только на конечные веса, но и на продолжительность процесса тренировки.

Кроме того, пакетная нормализация действует как регуляризатор, делая сеть менее чувствительной к весам некоторых нейронов. Она также позволяет обучать глубокие нейронные сети, уменьшая проблемы исчезающего градиента. Она разделяет зависимости слоев, делает процесс обучения инвариантным к изменениям масштаба входных признаков, улучшает обобщение модели, облегчает обучение партий разного размера и хорошо подготовлена к экспериментам с различными графиками темпа обучения. Это некоторые из известных преимуществ пакетной нормализации. Давайте теперь рассмотрим каждый тип.

Масштабирование признаков

Эта форма нормализации преобразует все данные в векторе на слое в диапазон от 0,0 до +1,0. Формула для каждого значения в векторе следующая:

где

• x' — нормализованное значение
• x — исходное денормализованное значение
• min(x) — функция, возвращающая минимум вектора
• max(x) — максимум вектора

Реализация этого очень простого алгоритма на языке MQL5 выглядит следующим образом:

//+------------------------------------------------------------------+
//| Function to apply Feature-Scaling
//+------------------------------------------------------------------+
void Cnormalize::FeatureScaling(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Max() - _copy.Min() > 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min());
      }
   }
}

При выборе алгоритма нормализации важным фактором является тип активации, который будет использоваться на каждом уровне. Это связано с тем, что не все функции активации выводят свои результаты в одном и том же диапазоне. Ниже приведена таблица различных функций активации, доступных как перечисление в MQL5 и соответствующие им диапазоны выходных данных:

Функция активации нейрона	Диапазон выходного значения
Экспоненциальная линейная единица (Exponential Linear Unit, ELU)		(-1, ∞)
Экспоненциал (Exp)		(0, ∞)
Линейная единица ошибки Гаусса (Gaussian Error Linear Unit, GELU)		(-∞, ∞)
Жесткий сигмоид (Hard Sigmoid)		[0, 1]
Линейная зависимость (linear)		(-∞, ∞)
Линейный выпрямитель с "утечкой" (Leaky Rectified Linear Unit, Leaky ReLU)		(-∞, ∞)
Усеченное линейное преобразование (Rectified Linear Unit, ReLU)		[0, ∞)
Масштабированная экспоненциальная линейная функция (Scaled Exponential Linear Unit, SELU)		(-∞, ∞)
Сигмоид (Sigmoid)		(0, 1)
Softmax		(0, 1), в сумме дает 1
Softplus		(0, ∞)
Softsign		(-1, 1)
Swish		(-∞, ∞)
Гиперболический тангенс (Hyperbolic Tangent, Tanh)		(-1, 1)
Пороговый линейный выпрямитель (Thresholded ReLU)		{0} ∪ [θ, ∞), где θ > 0

Как видно, у нас есть только 3 функции активации, которые обеспечивают выходные данные в диапазоне, аналогичном алгоритму пакетной нормализации масштабирования признаков. Это сигмоид, жесткий сигмоид и Softmax. Все остальное находится вне диапазона. Это соответствие выходных диапазонов имеет жизненно важное значение, если сетям необходимо избежать проблемы исчезающего градиента, которая часто возникает во время обучения.

Активация жесткого сигмоида представляет собой простую аппроксимацию сигмовидной функции, которая определяется следующим уравнением:

Таким образом, независимо от того, какие входные данные у нас есть для x, выходные данные будут находиться в диапазоне от 0,0 до +1,0. Такое соответствие масштабированию функций обеспечивает последовательные и интерпретируемые активации. Кроме того, жесткий сигмоид эффективен с вычислительной точки зрения и поэтому подходит для больших и очень глубоких сетей, таких как трансформеры.

Сигмоид, возможно, является самой популярной из всех активаций, поскольку он минимизирует проблемы взрывного роста градиентов посредством контролируемого по диапазону выходного значения, которому все еще удается поддерживать некоторую степень изменчивости, в отличие, скажем, от жесткого сигмоида, описанного выше. Его уравнение выглядит так:

где

• e - постоянная Эйлера
• x — нормализованное значение

Гладкость отображения хорошо согласуется с нормализованным диапазоном масштабирования признаков. Кроме того, это позволяет избежать проблем с насыщением градиента, поскольку выходные значения 0,0 или 1,0 встречаются редко.

Активация Softmax нормализует класс (или, скажем, вектор данных) таким образом, что все его значения не только находятся в диапазоне от 0,0 до 1,0, но, кроме того, эти нормализованные значения при суммировании дают в сумме 1,0. Соответствующее уравнение приведено ниже:

где

• z i - i-й элемент входного вектора Z
• K - размер вектора Z
• e - постоянная Эйлера

Softmax обычно используется при многоклассовой классификации или сравнении точек данных, имеющих более одного измерения. Выходные данные подразумевают распределение вероятностей, при котором ни один из выходных данных не доминирует непропорционально над другими, создавая своего рода равные условия. Кроме того, суммирование до единицы гарантирует отсутствие больших чисел, которые могут создать проблемы с вычислениями в глубоких сетях или трансформерах.

Таким образом, жесткий сигмоид, сигмоид и Softmax — это три подходящих алгоритма функции активации для нормализации масштабирования признаков, поскольку выходные данные всех трех, как правило, совпадают с выходными данными пакетной нормализации. Реализация этих алгоритмов в MQL5 действительно проста, поскольку все алгоритмы активации и их соответствующие производные доступны из встроенных функций векторного типа данных. Примерами являются функции Forward() и Backward(), которые являются частью класса Cmlp, приложенного к этой статье. В качестве альтернативы также доступны официальные рекомендации для функций Activation и Derivative.

Реализация алгоритма масштабирования признаков уже была рассмотрена выше. Это простая функция, которая проверяет деление на ноль, гарантируя, что максимальные и минимальные значения в векторе не совпадают. Функции масштабирования очень просты, и это важно для минимизации вычислений, учитывая, что многие сети могут быть очень глубокими и иметь формат трансформера.

Робастное масштабирование

Эта форма нормализации обеспечивает немного большую свободу действий при выводе данных, давая значения, которые в определенных условиях немного выходят за пределы -1,0 и +1,0, но в большинстве случаев все данные часто находятся в диапазоне от -1,0 до +1,0. Исключения из этого правила встречаются часто. Они происходят в случаях, когда присутствуют выбросы, расстояние между которыми и медианой настолько велико, что превышает межквартильный диапазон. Уравнение выглядит так:

где:

• x — исходное значение
• median(x) — медиана вектора или класса
• IQR(x) — 75-^й процентиль минус 25-^й процентиль класса.

Хотя робастное масштабирование менее чувствительно к выбросам, чем масштабирование признаков, оно не игнорирует их. Фактически, выбросы, которые сильно отличаются от медианы, как правило, дают нормализованные значения, величина которых превышает единицу. Кроме того, в общем случае, если наблюдается высокая изменчивость данных (диапазон от максимального до минимального значения) по сравнению с межквартильным размахом; другими словами, ситуация, когда данные преимущественно сосредоточены вокруг медианы, но с постепенно уменьшающимся числом по направлению к крайним значениям, так что крайние значения не обязательно являются выбросами. В этих случаях значения, близкие к экстремальным, также будут иметь нормализации с величинами больше единицы.

Из приведенной выше таблицы диапазонов выходных значений активации становится ясно, что идеальным выбором функций активации для сопряжения с робастным масштабированием будет активация Softsign или TANH. Это связано с тем, что их выходные данные, хотя и немного ограничены диапазоном от -1,0 до +1,0, учитывая возможные существенные эффекты масштабирования, о которых мы упоминали выше, являются наилучшим соответствием среди всех других активаций. Однако еще важнее то, что эти выходы активации не производят никаких бесконечных значений, поэтому риск исчезновения и взрыва градиентов значительно снижается.

Softsign рассчитывается довольно просто:

где

• x — точка данных в классе или векторе
• |x| — величина этих данных

Согласно его формуле, его чистый x, или данные в нормализованном векторе, в идеале должны быть с плавающей точкой и, вероятно, иметь величину в диапазоне от 0,0 до 2,0. По мере того, как значения x увеличиваются от 2,0, изменчивость и, следовательно, интерпретация нормализованных данных будут затруднены. Это указывает на насыщение нормализованных значений вдали от нуля, но плавный переход возле нулевого значения. Симметрия и центрирование значений вокруг нуля хорошо согласуются с надежным масштабированием. Кроме того, было замечено, что градиенты от Softsign не исчезают так легко, как градиенты от других функций активации, таких как сигмоид. Это может быть очень полезно при проведении обширного обучения на больших наборах данных.

Активация TANH — это еще один эффективный алгоритм с диапазоном от -1,0 до +1,0. Его уравнение выглядит так:

где

• x — точка данных внутри класса или вектора
• e - постоянная Эйлера

Алгоритм TANH по форме очень похож на сигмоид, с очевидным отличием в том, что он центрирован вокруг 0,0, тогда как сигмоид центрирован вокруг 0,5. Сообщается также, что алгоритм обеспечивает более плавный градиент, чем сигмоид. Как мы видели выше, диапазон знака, как и в случае с Softsign, делает его еще одним идеальным кандидатом для работы с робастным масштабированием. Данные с высоким уровнем шума или наборы данных со множеством выбросов, которые с точки зрения трейдера могут включать ценовые буферы очень волатильных ценных бумаг, являются идеальными наборами данных для использования с робастным масштабированием и активацией TANH. Это обусловлено его способностью обрабатывать наборы данных разного масштаба.

Реализация в MQL5, как мы уже говорили, довольно проста - под стать описанным выше функциям активации для масштабирования признаков. Векторный тип данных имеет встроенные функции Activation и Derivative, которые выводят результаты в любой вектор, который также служит входными данными. Как я уже говорил, подробности можно найти здесь и здесь.

Робастный алгоритм масштабирования реализован в классе нормализации на языке MQL5 следующим образом:

//+------------------------------------------------------------------+
//| Function to apply Robust-Scaling
//+------------------------------------------------------------------+
void Cnormalize::RobustScaling(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Percentile(75) - _copy.Percentile(25) > 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Median()) / (_copy.Percentile(75) - _copy.Percentile(25));
      }
   }
}

Как и в алгоритме масштабирования признаков, описанном выше, проверка на наличие делений на ноль выполняется в межквартильном диапазоне. Это еще один простой, но эффективный алгоритм по причинам, указанным выше.

Z-оценка

Вероятно, наиболее популярный алгоритм нормализации. На странице в Википедии о пакетной нормализации это единственная используемая функция нормализации. Она включает преобразование класса или вектора данных таким образом, чтобы их среднее значение было равно 0, а стандартное отклонение — 1. Это явно отличается от масштабирования признаков и робастного масштабирования, которые мы рассматривали выше, где в центре внимания был диапазон выходных данных. Уравнение выглядит следующим образом:

где

• Z — нормализованное значение
• μ — среднее значение
• σ — стандартное отклонение

Из этого уравнения мы можем видеть, что выходные данные имеют неограниченный диапазон, так что возможные выходы могут охватывать диапазон от минус бесконечности до плюс бесконечности. На первый взгляд, это тревожный сигнал, поскольку "взрывающиеся" градиенты могут быстро стать проблемой, особенно если используемые функции активации также имеют несвязанные выходы. Однако выходные данные центрируются около нуля, что хорошо для стабилизации процесса обучения сетей, использующих градиентный спуск. Алгоритм очень эффективен при работе с нормально распределенными данными, поскольку обеспечивает равномерный вклад точек входных данных в процесс обучения.

У него также есть недостатки, главными из которых являются чувствительность к выбросам, предположение о гауссовском распределении данных и, как уже говорилось, несвязанный вывод. Реализация z-оценки в MQL5 может быть достигнута следующим образом:

//+------------------------------------------------------------------+
//| Function to apply Standard-Score
//+------------------------------------------------------------------+
void Cnormalize::StandardScore(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Std() != 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Mean()) / _copy.Std();
      }
   }
}

Интересно, что эта функция пока не входит в число стандартных функций MQL5. Чтобы избежать деления на ноль для всех этих трех функций нормализации, вместо проверки на нулевой знаменатель также принято добавлять небольшое ненулевое double-значение внизу, которое часто называют эпсилон. Однако эта практика, если ее применять с масштабированием признаков или робастным масштабированием, может привести к очень большим нормализованным значениям в случае, если предполагаемый знаменатель равен нулю.

Нормализующий трансформер

После того как входные данные слоя были нормализованы с помощью масштабирования признаков, робастного масштабирования или z-оценки, выходные данные этой нормализации подаются в трансформер пакетной нормализации. Это также относительно простая функция, которая определяется следующим уравнением:

где

• y - выходное значение в векторе с индексом i
• x — это ранее нормализованная точка данных с индексом i
• Gamma и Beta — оптимизируемые параметры с плавающей точкой.

Написание кода не займет много времени:

//+------------------------------------------------------------------+
//| Batch Normalizing Transform
//+------------------------------------------------------------------+
void Cnormalize::Transform(Enormalize Type, vector &Output, vector &BatchTransform, vector &Beta, vector &Gamma)
{  if(Type != NORMALIZE_NONE)
   {  if(Type == NORMALIZE_STANDARD)
      {  StandardScore(Output);
      }
      else if(Type == NORMALIZE_FEATURE)
      {  FeatureScaling(Output);
      }
      else if(Type == NORMALIZE_ROBUST)
      {  RobustScaling(Output);
      }
      //Transformer
      BatchTransform.Init(Output.Size());
      BatchTransform.Fill(0.0);
      for(int i = 0; i < int(Output.Size()); i++)
      {  BatchTransform[i] = (Gamma[i] * Output[i]) + Beta[i];
      }
   }
}

Есть пять аргументов в пользу проведения нормализации с помощью трансформера. Во-первых, он восстанавливает репрезентативную способность исходных ненормализованных данных за счет обеспечения гибкости и повторной калибровки. Гибкость, поскольку после преобразования выходные данные не обязательно могут находиться в оптимальном состоянии для облегчения обучения сети. Например, при использовании стандартной нормализации оценок выходные данные каждого вектора всегда имеют среднее значение 0 и стандартное отклонение 1. Этот и другие подобные случаи могут оказаться слишком экстремальными для эффективного обучения сети. Вот почему введение обучаемых/оптимизируемых параметров бета и гамма может помочь перекалибровать эти наборы данных в оптимальную форму для обучения.

Во-вторых, в случаях, когда исходная функция нормализации имеет потенциально несвязанные выходные данные (как, например, та же z-оценка), этот преобразователь нормализации может помочь предотвратить исчезновение и "взрыв" градиентов. Этого можно достичь путем тонкой настройки беты и гаммы. В-третьих, утверждается, что трансформер сохраняет дисперсию для эффективного обучения посредством масштабирования дисперсии. Параметр gamma может регулировать дисперсию нормализованных выходных данных, поскольку он является прямым множителем. Благодаря возможности корректировать дисперсию процесс обучения можно точно настроить в соответствии с архитектурой сети.

Кроме того, трансформер может улучшить динамику обучения сети, позволяя ей адаптироваться к данным, что часто приводит к улучшению сходимости. Оптимизируемые параметры beta и gamma снова направляют этот процесс таким образом, что данные масштабируются для лучшего использования настроек количества и размера слоев сети, в результате чего для достижения идеальных результатов требуется меньше эпох обучения. Считается, что регуляризация путем масштабирования и сдвига выходных нормализованных данных работает подобно регуляризации с выпадением данных. Регуляризация призвана подтолкнуть сеть к изучению большего количества базовых закономерностей в наборе данных и меньшего количества шума, поэтому параметры beta и gamma, которые являются векторными параметрами, уникальны для каждого слоя. Такая настройка на основе параметров, помимо регуляризации сети, также позволяет лучше реализовать ковариационный сдвиг, о котором мы говорили во введении, благодаря специфическому для параметров действию beta и gamma.

Результаты тестирования стратегии

Для тестирования мы используем символ EURJPY на дневном таймфрейме за 2023 год. Нормализация z-оценки не обязательно имеет функцию активации соответствия, поскольку она выполняется с несвязанными данными. Можно использовать связанные функции активации, упомянутые в этой статье, однако их тестирование остается за читателем. Для наших целей мы тестируем только нормализацию робастного масштабирования и нормализацию масштабирования признаков. Мы объединили их с активацией Softsign и сигмоида соответственно.

При масштабировании признаков мы получили следующие результаты:

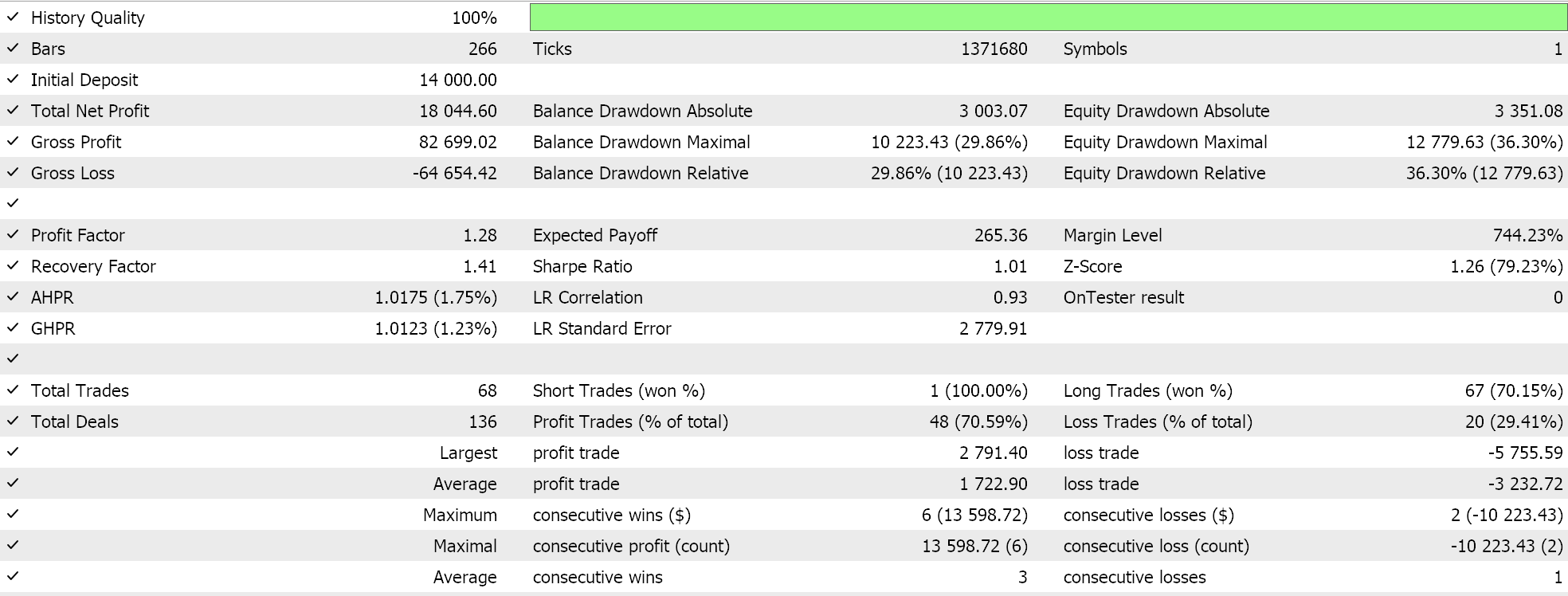
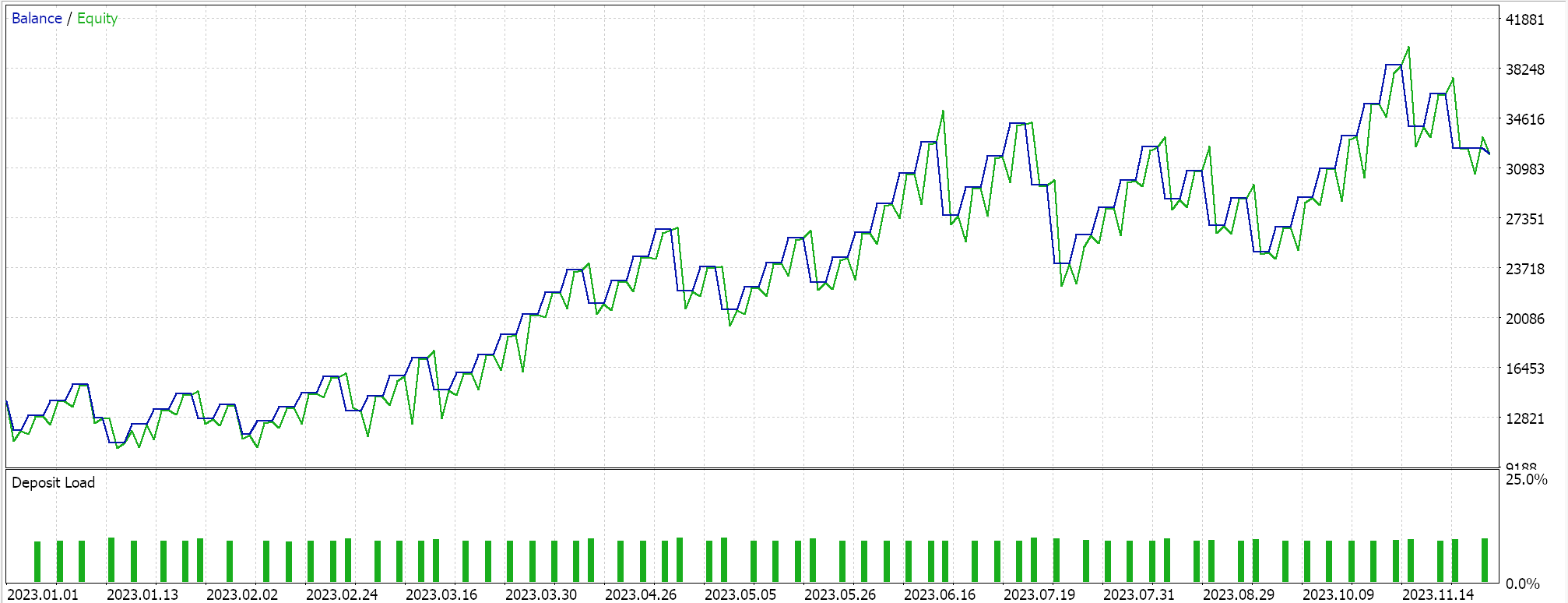
Результаты робастного масштабирования:

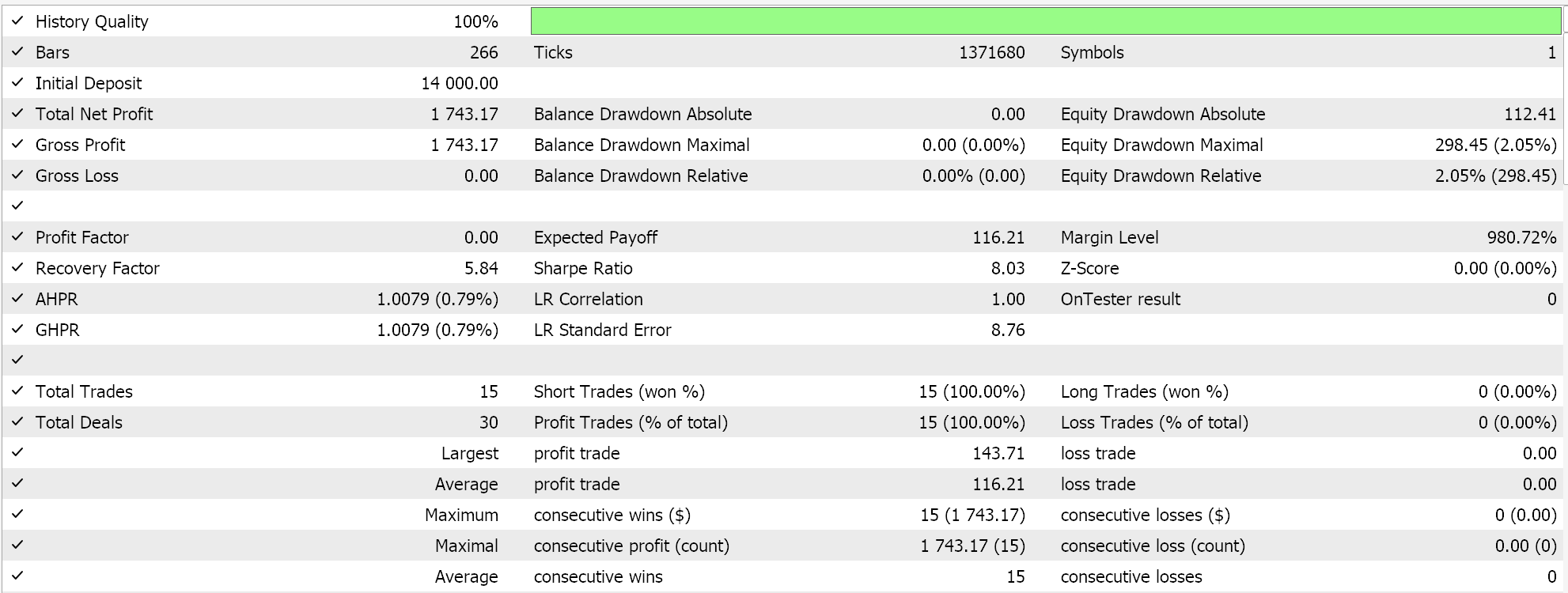
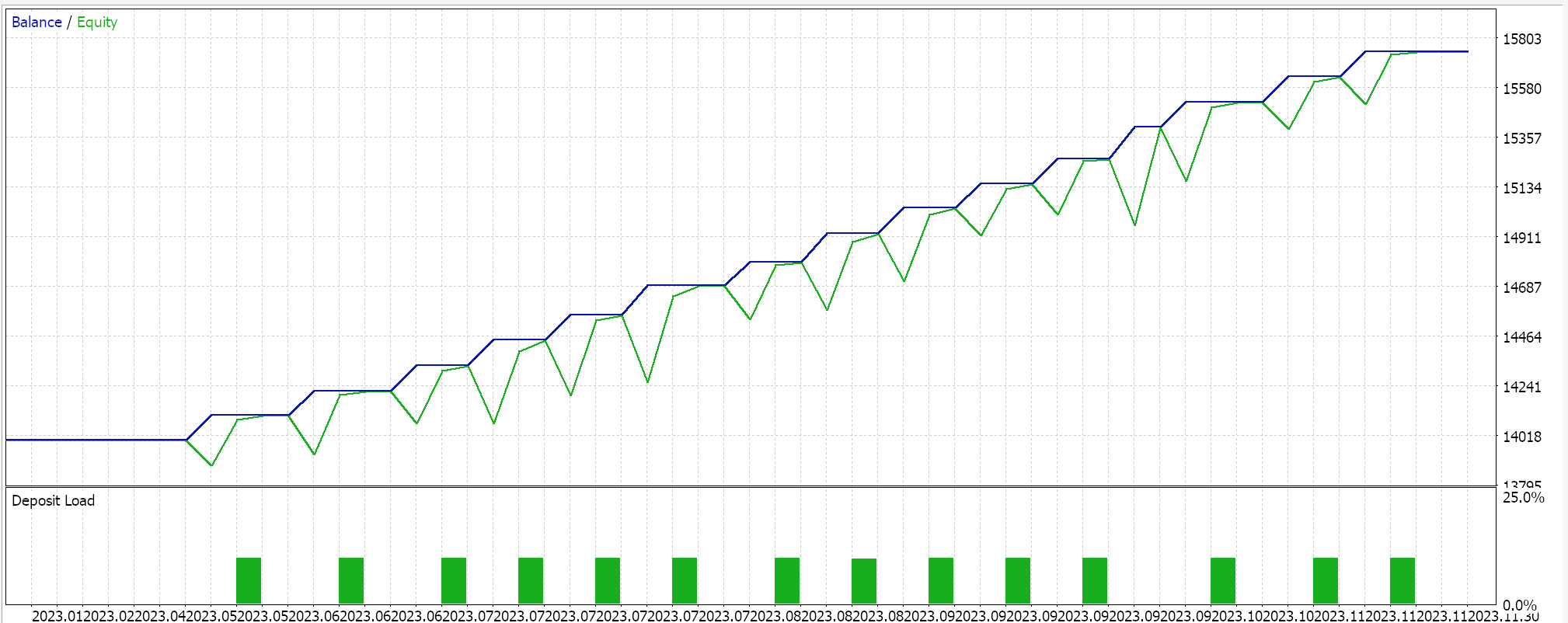
В качестве контроля проведем тестирование советника, работающим с идентичными настройками, но без нормализации. Результаты ниже:

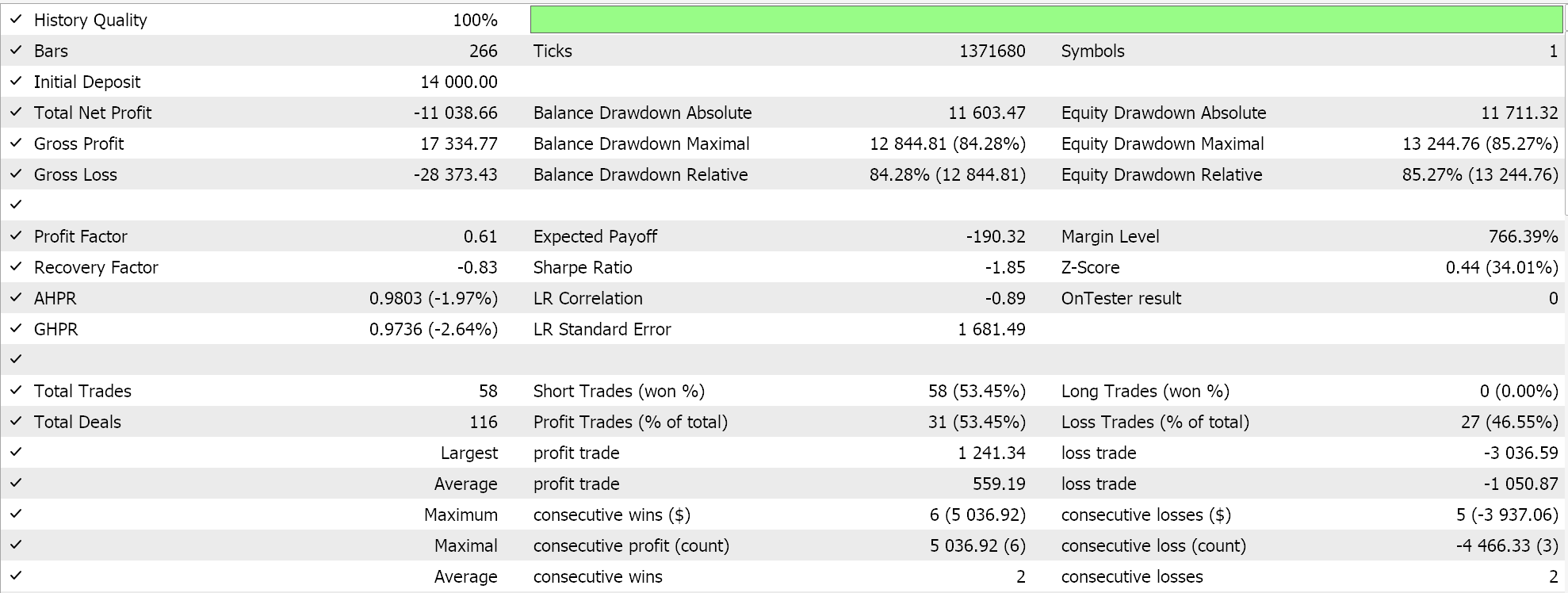
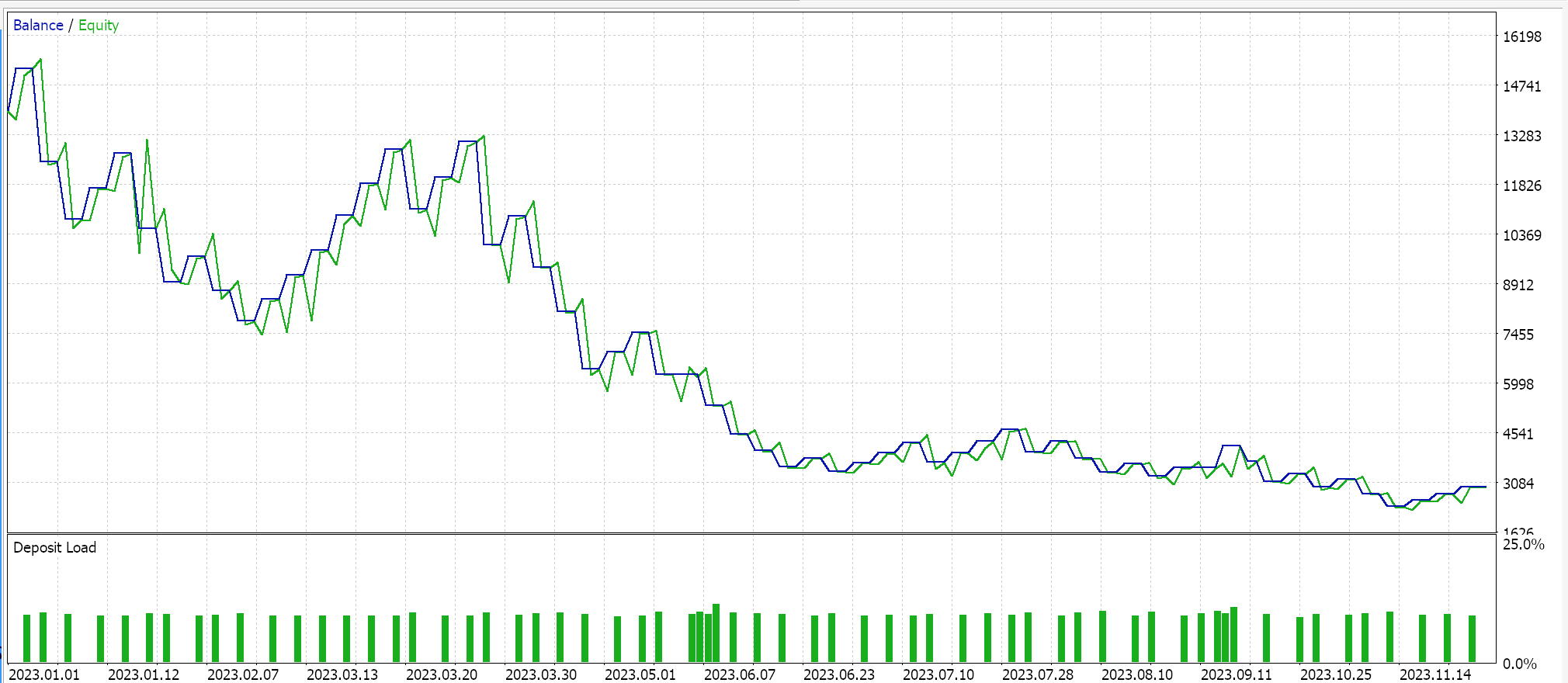
Заключение

Пакетная нормализация требует большого количества параметров и, следовательно, больших вычислительных затрат. При выборе алгоритмов нормализации необходимо проявлять особую осторожность, и хотя z-оценка очень популярна, она имеет несвязанные выходные данные, что может привести к очень большим градиентам, которые затрудняют сходимость и замедляют весь процесс обучения. Однако если использовать альтернативные алгоритмы нормализации, имеющие связанные выходные данные, такие как масштабирование признаков или робастное масштабирование, и объединить их с соответствующими функциями активации, имеющими аналогичные связанные выходные данные, то процесс обучения можно ускорить. К сожалению, скорость здесь является ключевым фактором, поскольку, как уже упоминалось, пакетная нормализация включает в себя множество параметров и требует больших вычислительных ресурсов, поэтому необходимо проявлять особую осторожность при сопряжении алгоритмов нормализации с функциями активации, а также иметь оптимальные уровни и размеры сети.