Funcionalidades do Assistente MQL5 que você precisa conhecer (Parte 30): Normalização em Lote no Aprendizado de Máquina

Introdução

A normalização em lote (batch normalization) é uma forma de padronização dos dados antes de serem processados pelas camadas da rede neural, melhorando o seu desempenho. No entanto, não há consenso sobre as razões exatas desse aprimoramento. O artigo original sobre o tema aponta o  deslocamento covariante interno (internal covariate shift) como causa, interpretado como a redução dos efeitos negativos do desequilíbrio dos dados de entrada das "camadas superiores" sobre as camadas inferiores devido ao impacto em cascata. Em um estudo posterior, argumenta-se que a melhoria empírica se deve ao efeito de suavização, pois os gradientes dentro das camadas apresentam menor variabilidade ao considerar a normalização.

Do ponto de vista de um trader, entender POR QUE a normalização em lote afeta o desempenho da rede neural é um motivo válido para desenvolver e testar sistemas que a utilizam. Essa será nossa tarefa principal. Analisaremos três formas principais de normalização em lote: Standard-Scaling, Feature-Scaling e Robust-Scaling. Cada uma delas é um algoritmo bastante simples. Conduziremos testes com EAs que utilizam cada uma dessas normalizações e, como controle, realizaremos testes com EAs que não utilizam a normalização em lote. Dessa forma, retomaremos o formato que empregamos antes dos dois últimos artigos (sobre taxas de aprendizado): primeiro, apresentaremos as três normalizações, depois os relatórios de testes com controle e, por fim, a conclusão.

Assim como todos os outros desta série, o artigo foca no teste de novas ideias utilizando EAs construídos no Assistente. As informações introdutórias necessárias podem ser encontradas aqui e aqui. Esses dois artigos contêm algumas recomendações sobre o uso do código anexado ao final. Nesta análise, utilizamos um número considerável de enumerações personalizadas de dados como parâmetros de entrada otimizáveis. As enumerações nativas do MQL5 podem ser declaradas no cabeçalho do arquivo de sinal personalizado e serão listadas automaticamente como entradas, sendo inicializadas como parte do filtro de sinal. No entanto, se as enumerações forem personalizadas, colocá-las no cabeçalho tornará o arquivo invisível (ou não reconhecível) no Assistente MQL5, impedindo sua montagem. No momento, podemos contornar esse problema excluindo as enumerações do cabeçalho da classe de sinal personalizada, mas declarando os parâmetros e suas respectivas funções dentro da própria classe de sinal, como é comum para qualquer parâmetro de entrada. Após a montagem no Assistente, realizamos manualmente alterações na lista de parâmetros de entrada e inicializamos a classe de sinal para adicionar essa enumeração personalizada de parâmetros.

Descobri uma possível solução para essa limitação, que, se não me falha a memória, envolvia declarar as enumerações dentro da própria classe de sinal. No entanto, não me recordo dos detalhes exatos, então, por enquanto, teremos que nos limitar à edição manual. Em nosso EA de teste, temos enumerações personalizadas para os tipos de taxa de aprendizado, taxa de aprendizado adaptativa e, o mais relevante para este artigo, a enumeração dos tipos de normalização. O código desta última é apresentado a seguir:

enum Enormalize
{  NORMALIZE_NONE = -1,
   NORMALIZE_ROBUST = 0,
   NORMALIZE_FEATURE = 1,
   NORMALIZE_STANDARD = 2,
};

Para usar e otimizar essa enumeração no EA, precisaremos adicioná-la manualmente como parâmetro de entrada da seguinte forma:

....

input ENUM_ACTIVATION_FUNCTION Signal_CMLP_ActivationType = AF_SIGMOID;  // CMLP(30,6,0.05,10,0.1,2,...) Activation Type
input Enormalize Signal_CMLP_NormalizeType   = NORMALIZE_FEATURE; // CMLP(30,6,0.05,10,0.1,2,...) Batch Normalisation Type
input Elearning Signal_CMLP_LearningType   = LEARNING_ADAPTIVE; // CMLP(30,6,0.05,10,0.1,2,...) Learning Type
input Eadaptive Signal_CMLP_AdaptiveType   = ADAPTIVE_GRADIENT; // CMLP(30,6,0.05,10,0.1,2,...) Adaptive Type

...

Além disso, devemos incluir os parâmetros declarados na instância do sinal personalizado, que é inicializada como filter0. Isso é feito da seguinte maneira:

...

   filter0.ActivationType(Signal_CMLP_ActivationType);
   filter0.NormalizeType(Signal_CMLP_NormalizeType);
   filter0.LearningType(Signal_CMLP_LearningType);
   filter0.AdaptiveType(Signal_CMLP_AdaptiveType);

...

Após essas etapas, o EA montado no Assistente poderá ser utilizado normalmente com nossa classe de sinais personalizada. Já examinamos os três formatos de normalização que serão considerados por meio da enumeração personalizada. Antes de explorarmos cada um dos tipos de normalização em lote em mais detalhes, faremos uma breve revisão do tema e, em seguida, analisaremos sua implementação geral na classe de sinal personalizada.

Argumentos a favor da normalização em lote em redes neurais

A maioria dos benefícios da normalização em lote pode ser encontrada no artigo original de 2015. Como atualmente há debates sobre a obtenção dos resultados empíricos, esses argumentos iniciais podem não ter o mesmo peso que antes. Ainda assim, apresentamos esses pontos aqui como uma introdução ao tema. A normalização em lote é promovida como um método para estabilizar o processo de aprendizado, reduzindo o deslocamento covariante interno mencionado anteriormente. Isso acelera a convergência, pois as ativações em cada nível se tornam “mais padronizadas”. Além disso, reduz a sensibilidade aos pesos de inicialização usados na rede antes do treinamento. Os pesos iniciais geralmente exercem uma influência desproporcionalmente grande não apenas sobre os pesos finais, mas também sobre a duração do processo de treinamento.

Além disso, a normalização em lote atua como um regularizador, tornando a rede menos sensível aos pesos de alguns neurônios. Ela também permite o treinamento de redes neurais profundas, reduzindo problemas relacionados ao desaparecimento do gradiente. Esse método desacopla as dependências entre camadas, torna o processo de aprendizado invariante a mudanças na escala das características de entrada, melhora a capacidade de generalização do modelo, facilita o treinamento em lotes de tamanhos variados e é adequado para experimentos com diferentes cronogramas de taxas de aprendizado. Esses são alguns dos benefícios conhecidos da normalização em lote. Agora, vamos examinar cada tipo de normalização.

Escalonamento de características

Este tipo de normalização transforma todos os dados dentro de um vetor na camada, ajustando-os para o intervalo de 0,0 a +1,0. A fórmula aplicada a cada valor do vetor é a seguinte:

onde

• x' é o valor normalizado
• x é o valor original (não normalizado)
• min(x) é a função que retorna o menor valor do vetor
• max(x) é a função que retorna o maior valor do vetor

A implementação desse algoritmo simples na linguagem MQL5 é a seguinte:

//+------------------------------------------------------------------+
//| Function to apply Feature-Scaling
//+------------------------------------------------------------------+
void Cnormalize::FeatureScaling(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Max() - _copy.Min() > 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min());
      }
   }
}

Ao escolher um algoritmo de normalização, é fundamental considerar o tipo de ativação que será utilizado em cada nível. Isso ocorre porque nem todas as funções de ativação produzem saídas dentro do mesmo intervalo. Abaixo, apresentamos uma tabela com diferentes funções de ativação disponíveis no MQL5, juntamente com seus respectivos intervalos de saída:

Função de ativação do neurônio	Intervalo da saída
Exponential Linear Unit (ELU)		(-1, ∞)
Exponencial (Exp)		(0, ∞)
Gaussian Error Linear Unit (GELU)		(-∞, ∞)
Hard Sigmoid		[0, 1]
Linear		(-∞, ∞)
Leaky Rectified Linear Unit (Leaky ReLU)		(-∞, ∞)
Rectified Linear Unit (ReLU)		[0, ∞)
Scaled Exponential Linear Unit (SELU)		(-∞, ∞)
Sigmoid		(0, 1)
Softmax		(0, 1), soma total igual a 1
Softplus		(0, ∞)
Softsign		(-1, 1)
Swish		(-∞, ∞)
Hyperbolic Tangent (Tanh)		(-1, 1)
Thresholded ReLU		{0} ∪ [θ, ∞), onde θ > 0

Como podemos ver, apenas três funções de ativação geram saídas dentro do mesmo intervalo do algoritmo de normalização por escalonamento de características: Sigmoide, Hard Sigmoid e Softmax. Todas as demais estão fora desse intervalo. Essa correspondência entre os intervalos de saída é essencial para evitar problemas como o desaparecimento do gradiente, que ocorre frequentemente durante o treinamento.

A ativação Hard Sigmoid é uma aproximação simplificada da função sigmoide, definida pela seguinte equação:

Assim, independentemente dos valores de entrada x, as saídas sempre estarão dentro do intervalo de 0,0 a +1,0. Esse mapeamento coerente entre funções de escalonamento garante ativações consistentes e interpretáveis. Além disso, o Hard Sigmoid é computacionalmente eficiente, tornando-se uma boa opção para redes muito profundas, como os transformers.

A função sigmoide é provavelmente a ativação mais popular, pois minimiza o problema do crescimento explosivo do gradiente ao manter os valores de saída controlados dentro do intervalo, sem, no entanto, perder a variabilidade. Isso a diferencia do Hard Sigmoid, por exemplo, que é mais rígido. Sua equação é a seguinte:

onde

• e é a constante de Euler
• x é o valor normalizado

A suavidade dessa função se alinha bem com a normalização por escalonamento de características. Além disso, ela evita problemas de saturação do gradiente, pois os valores 0,0 ou 1,0 são menos frequentes.

A ativação Softmax normaliza um conjunto de valores (ou seja, um vetor de dados) de modo que todos os seus elementos estejam no intervalo de 0,0 a 1,0 e, além disso, a soma de todos os valores do vetor seja igual a 1,0. Sua equação é:

onde

• zᵢ é o i-ésimo elemento do vetor de entrada Z
• K é o tamanho do vetor Z
• e é a constante de Euler

O Softmax é amplamente utilizado em classificação multiclasse ou comparação de pontos de dados em múltiplas dimensões. A saída desse método representa uma distribuição de probabilidades, garantindo que nenhum valor domine excessivamente os demais. Isso evita distorções e assegura que os números não sejam excessivamente grandes, o que poderia gerar problemas computacionais em redes profundas ou transformers.

Assim, Hard Sigmoid, Sigmoid e Softmax são os três algoritmos de ativação adequados para a normalização por escalonamento de características, pois suas saídas geralmente coincidem com as saídas da normalização em lote. A implementação desses algoritmos no MQL5 é bastante simples, uma vez que todas as funções de ativação e suas derivadas estão disponíveis nas funções nativas para tipos de dados vetoriais. Os exemplos incluem as funções Forward() e Backward(), que fazem parte da classe Cmlp, anexada a este artigo. Como alternativa, também há diretrizes oficiais disponíveis para as funções Activation e Derivative.

A implementação do algoritmo de escalonamento de características já foi discutida anteriormente. Trata-se de uma função simples que verifica a ocorrência de divisão por zero, garantindo que os valores máximo e mínimo do vetor não sejam iguais. As funções de escalonamento são extremamente simples, o que é fundamental para minimizar os cálculos, especialmente considerando que muitas redes podem ser muito profundas e ter arquitetura baseada em transformers.

Escalonamento robusto

Esse tipo de normalização oferece um pouco mais de flexibilidade na saída dos dados, permitindo valores que, sob certas condições, extrapolam ligeiramente os limites de -1,0 a +1,0. No entanto, na maioria dos casos, os dados permanecem dentro desse intervalo. As exceções ocorrem frequentemente quando há valores atípicos, onde a distância entre esses valores e a mediana é tão grande que excede o intervalo interquartil (IQR). A equação utilizada é:

onde:

• x é o valor original
• median(x) é a mediana do vetor ou classe
• IQR(x) representa o 75^º percentil menos o 25^º percentil da classe

Embora o escalonamento robusto seja menos sensível a valores atípicos do que o escalonamento de características, ele não os ignora completamente. Na prática, valores extremos que se afastam muito da mediana tendem a gerar valores normalizados com magnitude superior a 1,0. Além disso, em situações nas quais há alta variabilidade dos dados (ou seja, um grande intervalo entre o valor mínimo e o máximo) em comparação com o intervalo interquartil, ocorre um fenômeno interessante: os dados tendem a se concentrar próximos à mediana, mas com uma distribuição gradativa em direção aos valores extremos, sem que esses valores necessariamente sejam outliers. Nesses casos, os valores próximos às extremidades também podem resultar em normalizações com magnitudes superiores a 1,0.

A partir da tabela de intervalos de saída das ativações, fica claro que as melhores escolhas de funções de ativação para combinar com o escalonamento robusto são a Softsign e a TANH. Isso ocorre porque, embora geralmente limitados ao intervalo -1,0 a +1,0, seus valores de saída lidam bem com os efeitos de escalonamento mencionados anteriormente. Além disso, um fator ainda mais importante é que essas funções não produzem valores infinitos, reduzindo significativamente o risco de desaparecimento ou explosão do gradiente.

A função Softsign é calculada de maneira bastante simples:

onde

• x é um ponto de dado dentro da classe ou vetor
• |x| representa o valor absoluto desses dados

Segundo essa fórmula, o valor normalizado de x no vetor tende a ser um número flutuante e, idealmente, varia entre 0,0 e 2,0. No entanto, conforme x aumenta além de 2,0, a variabilidade diminui, tornando os dados normalizados menos interpretáveis. Isso sugere que os valores normalizados tendem a se estabilizar longe do zero, mas mantêm uma transição suave perto desse valor. A simetria e o centramento dos valores em torno de zero fazem com que essa ativação seja bem compatível com o escalonamento robusto. Além disso, observou-se que os gradientes do Softsign não desaparecem tão rapidamente quanto os de outras funções, como o Sigmoide. Isso pode ser muito útil em treinamentos extensivos com grandes conjuntos de dados.

A ativação TANH é outro algoritmo eficaz, também definido no intervalo -1,0 a +1,0. Sua equação é a seguinte:

onde

• x representa um ponto de dado dentro da classe ou vetor
• e é a constante de Euler

O TANH tem uma forma muito semelhante à do Sigmoide, com a principal diferença de que ele é centralizado em torno de 0,0, enquanto o Sigmoide é centralizado em torno de 0,5. Além disso, é relatado que o TANH fornece um gradiente mais suave do que o Sigmoide. Como vimos anteriormente, sua faixa de valores o torna um candidato ideal para trabalhar com o escalonamento robusto, assim como no caso do Softsign. Conjuntos de dados com muito ruído ou repletos de valores atípicos, que podem incluir movimentos extremos de preços de ativos altamente voláteis para um trader, são particularmente adequados para essa abordagem. Isso se deve à capacidade do TANH de lidar bem com dados distribuídos em múltiplas escalas.

A implementação dessas funções no MQL5 é bastante simples, assim como as funções de ativação usadas no escalonamento de características. O tipo de dado vetorial conta com funções Activation e Derivative embutidas, que podem operar diretamente sobre vetores de entrada e saída. Como mencionado anteriormente, mais detalhes podem ser encontrados aqui e aqui.

O algoritmo de escalonamento robusto é implementado dentro da classe de normalização no MQL5 da seguinte maneira:

//+------------------------------------------------------------------+
//| Function to apply Robust-Scaling
//+------------------------------------------------------------------+
void Cnormalize::RobustScaling(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Percentile(75) - _copy.Percentile(25) > 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Median()) / (_copy.Percentile(75) - _copy.Percentile(25));
      }
   }
}

Assim como no escalonamento de características, descrito anteriormente, há uma verificação para evitar divisões por zero dentro do intervalo interquartil. Esse é mais um algoritmo simples, mas altamente eficaz, por todas as razões discutidas anteriormente.

Z-score (Z-avaliação)

Provavelmente o algoritmo de normalização mais popular. Na página da Wikipédia sobre normalização em lote, essa é a única função de normalização mencionada. O Z-score transforma um conjunto de dados (classe ou vetor) para que sua média seja igual a 0 e seu desvio padrão seja 1. Isso a diferencia das técnicas de escalonamento de características e escalonamento robusto, que se concentram no intervalo dos valores de saída. A equação utilizada é:

onde

• Z é o valor normalizado
• μ representa a média
• σ é o desvio padrão

Com essa fórmula, podemos ver que os valores normalizados têm um intervalo ilimitado, ou seja, podem variar de -∞ a +∞. A princípio, isso pode parecer um problema, pois pode levar a explosões de gradiente, especialmente se as funções de ativação também tiverem saídas descontroladas. No entanto, o Z-score centraliza os dados em torno de zero, o que estabiliza o processo de aprendizado em redes que utilizam descida do gradiente. Esse método é altamente eficaz para dados com distribuição normal, pois garante uma contribuição uniforme de cada ponto de entrada no processo de aprendizado.

Ele também tem desvantagens, sendo as principais a sensibilidade a valores atípicos (outliers), a suposição de que os dados seguem uma distribuição gaussiana e, como mencionado acima, a produção de saídas sem restrição. A implementação do Z-score no MQL5 pode ser feita da seguinte forma:

//+------------------------------------------------------------------+
//| Function to apply Standard-Score
//+------------------------------------------------------------------+
void Cnormalize::StandardScore(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Std() != 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Mean()) / _copy.Std();
      }
   }
}

Curiosamente, essa função ainda não está incluída nas funções padrão do MQL5. Para evitar divisões por zero em qualquer um dos três métodos de normalização, uma prática comum é adicionar um pequeno valor double não nulo ao denominador – esse valor é chamado de epsilon. Entretanto, ao aplicar essa técnica ao escalonamento de características ou ao escalonamento robusto, pode-se gerar valores normalizados excessivamente grandes se o denominador for próximo de zero.

Transformador normalizador

Após a normalização dos dados de entrada do layer usando escalonamento de características, escalonamento robusto ou Z-score, os valores normalizados são alimentados no transformador de normalização em lote. Este é um processo relativamente simples, definido pela seguinte equação:

onde

• y é o valor de saída no vetor com índice i
• x é o ponto de dado previamente normalizado com índice i
• Gamma e Beta são parâmetros otimizáveis de ponto flutuante

A implementação desse código é bastante rápida:

//+------------------------------------------------------------------+
//| Batch Normalizing Transform
//+------------------------------------------------------------------+
void Cnormalize::Transform(Enormalize Type, vector &Output, vector &BatchTransform, vector &Beta, vector &Gamma)
{  if(Type != NORMALIZE_NONE)
   {  if(Type == NORMALIZE_STANDARD)
      {  StandardScore(Output);
      }
      else if(Type == NORMALIZE_FEATURE)
      {  FeatureScaling(Output);
      }
      else if(Type == NORMALIZE_ROBUST)
      {  RobustScaling(Output);
      }
      //Transformer
      BatchTransform.Init(Output.Size());
      BatchTransform.Fill(0.0);
      for(int i = 0; i < int(Output.Size()); i++)
      {  BatchTransform[i] = (Gamma[i] * Output[i]) + Beta[i];
      }
   }
}

Há cinco argumentos principais a favor do uso de um transformador normalizador. Primeiro, ele restaura a capacidade representativa dos dados originais não normalizados, garantindo flexibilidade e recalibração. Essa flexibilidade é crucial porque, após a normalização, os dados de saída podem não estar na forma ideal para o aprendizado da rede. Por exemplo, ao usar a normalização padrão (Z-score), os valores normalizados de cada vetor sempre terão média zero e desvio padrão igual a 1. No entanto, essa padronização excessiva pode comprometer a eficiência do aprendizado. Por isso, a introdução de parâmetros treináveis (Beta e Gamma) permite recalibrar os dados, ajustando-os para um formato mais adequado ao treinamento.

Segundo, em casos onde a função de normalização original gera saídas não correlacionadas – como no caso do Z-score – o transformador normalizador pode ajudar a prevenir o desaparecimento e a explosão de gradientes. Isso é possível graças ao ajuste fino dos parâmetros Beta e Gamma. Terceiro, afirma-se que o transformador mantém a variância necessária para um aprendizado eficiente por meio do escalonamento da dispersão. O parâmetro Gamma atua como um fator de escala direto, permitindo regular a variância dos valores normalizados. Essa capacidade de ajustar a dispersão possibilita a calibração do processo de aprendizado de acordo com a arquitetura da rede.

Além disso, o transformador pode melhorar a dinâmica do aprendizado da rede, pois permite que ela se adapte aos dados de maneira mais eficiente. Isso geralmente leva a uma melhor convergência, exigindo menos épocas de treinamento para alcançar resultados ideais. Os parâmetros Beta e Gamma, que são otimizáveis, direcionam esse ajuste, escalonando os dados de forma que a rede utilize melhor a quantidade e o tamanho das camadas, acelerando o treinamento. Por fim, acredita-se que a regularização proporcionada pelo escalonamento e deslocamento dos dados normalizados funcione de maneira semelhante ao Dropout. O objetivo da regularização é forçar a rede a aprender padrões subjacentes nos dados em vez de simplesmente capturar o ruído do conjunto de treinamento. Os parâmetros Beta e Gamma, sendo vetoriais e específicos de cada camada, não apenas ajudam na regularização da rede, mas também permitem um controle mais refinado do deslocamento covariante interno (discutido na introdução). Isso ocorre porque Beta e Gamma atuam de forma específica para cada camada, otimizando a normalização conforme as necessidades do modelo.

Resultados do teste da estratégia

Para os testes, utilizamos o par EURJPY no timeframe diário ao longo do ano 2023. A normalização por Z-score não possui uma função de ativação correspondente, pois opera sobre dados não correlacionados. É possível usar funções de ativação compatíveis, conforme discutido anteriormente, porém, a validação dessas combinações fica a critério do leitor. Para os nossos testes, focamos apenas em normalização por escalonamento robusto e normalização por escalonamento de características. Nós as combinamos com a ativação Softsign e Sigmoid, respectivamente.

Os resultados obtidos com o escalonamento de características foram os seguintes:

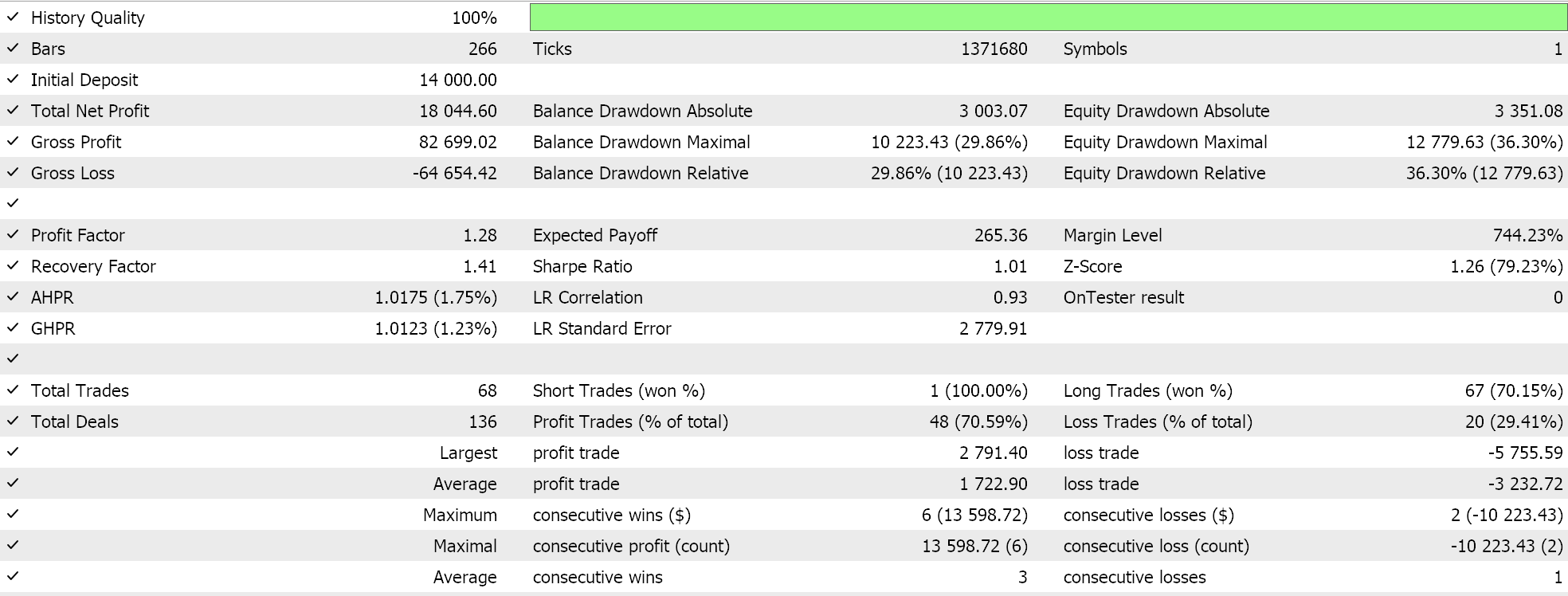
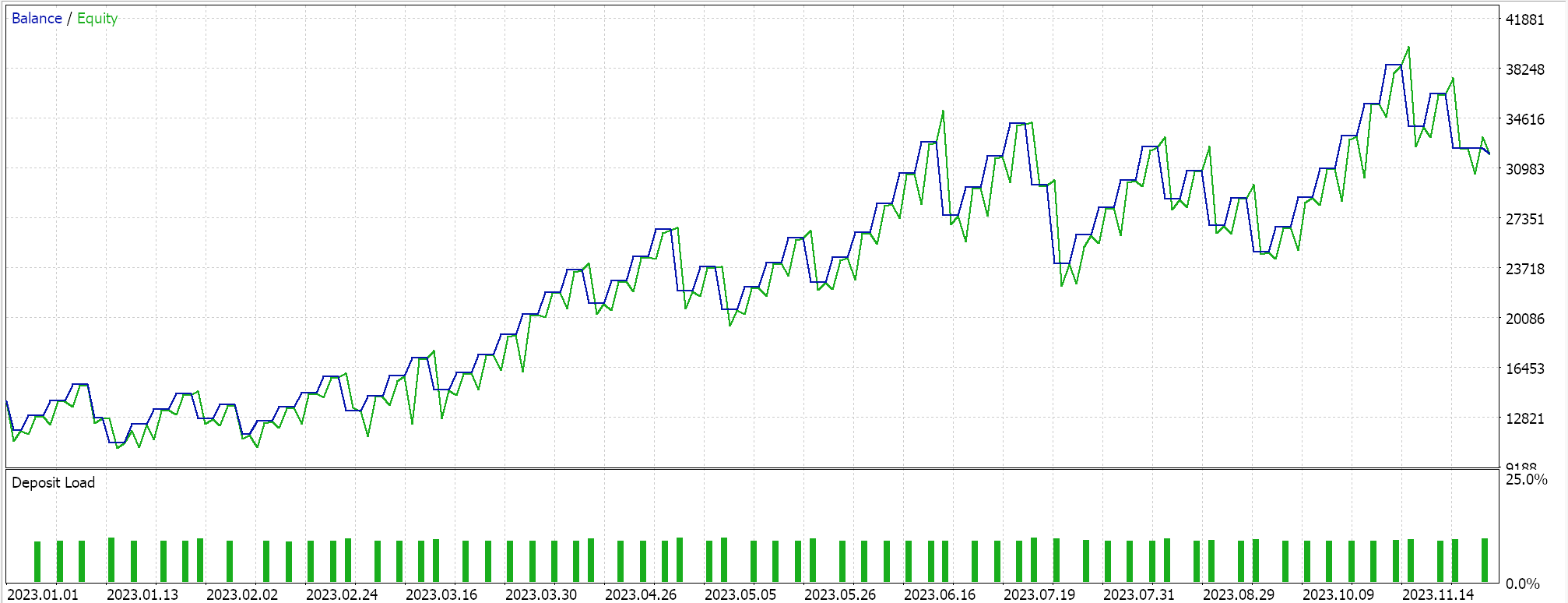
Os resultados obtidos com o escalonamento robusto foram os seguintes:

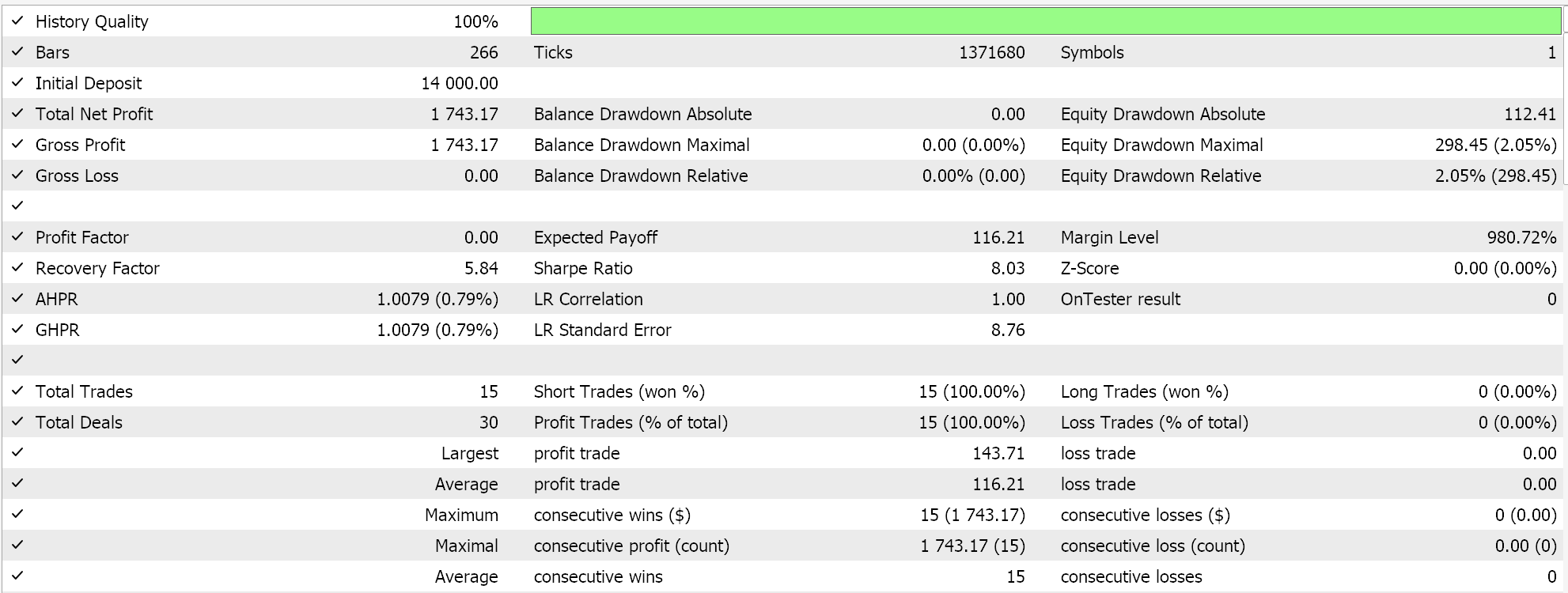
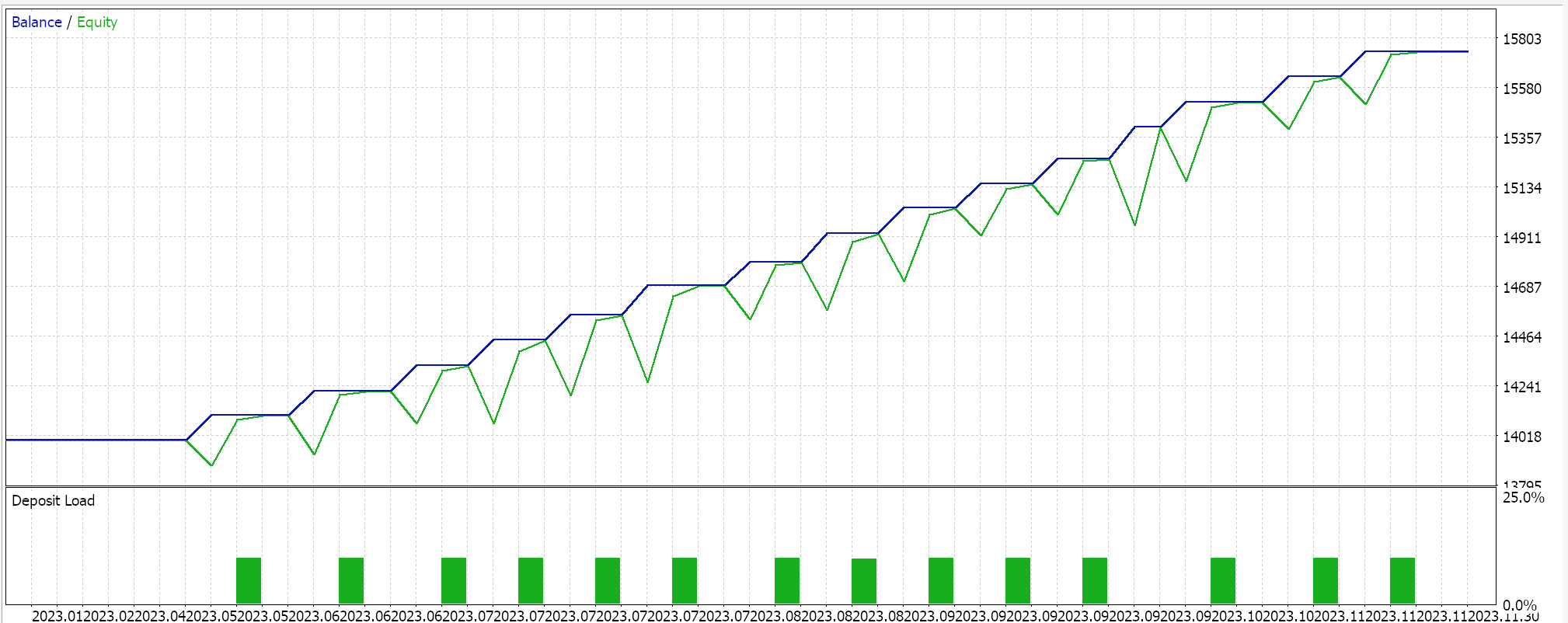
Como controle, realizamos um teste adicional com um EA idêntico, mas sem qualquer normalização. Os resultados foram:

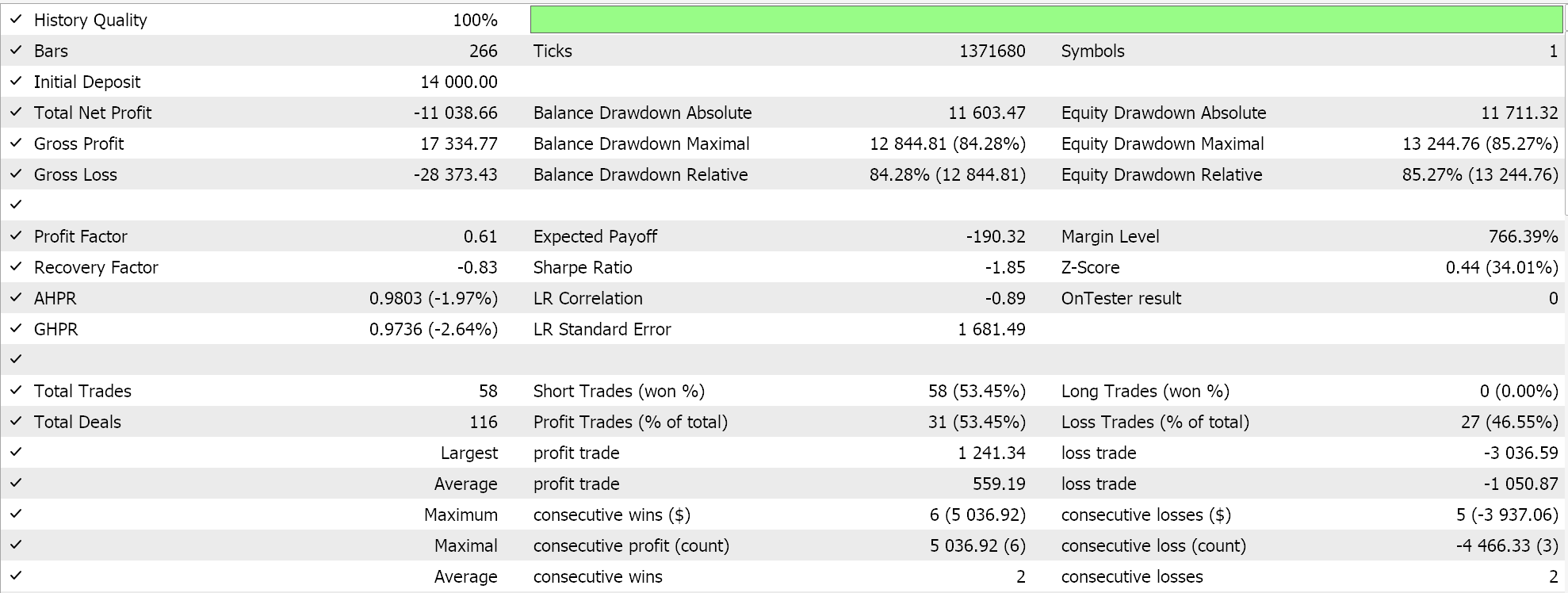
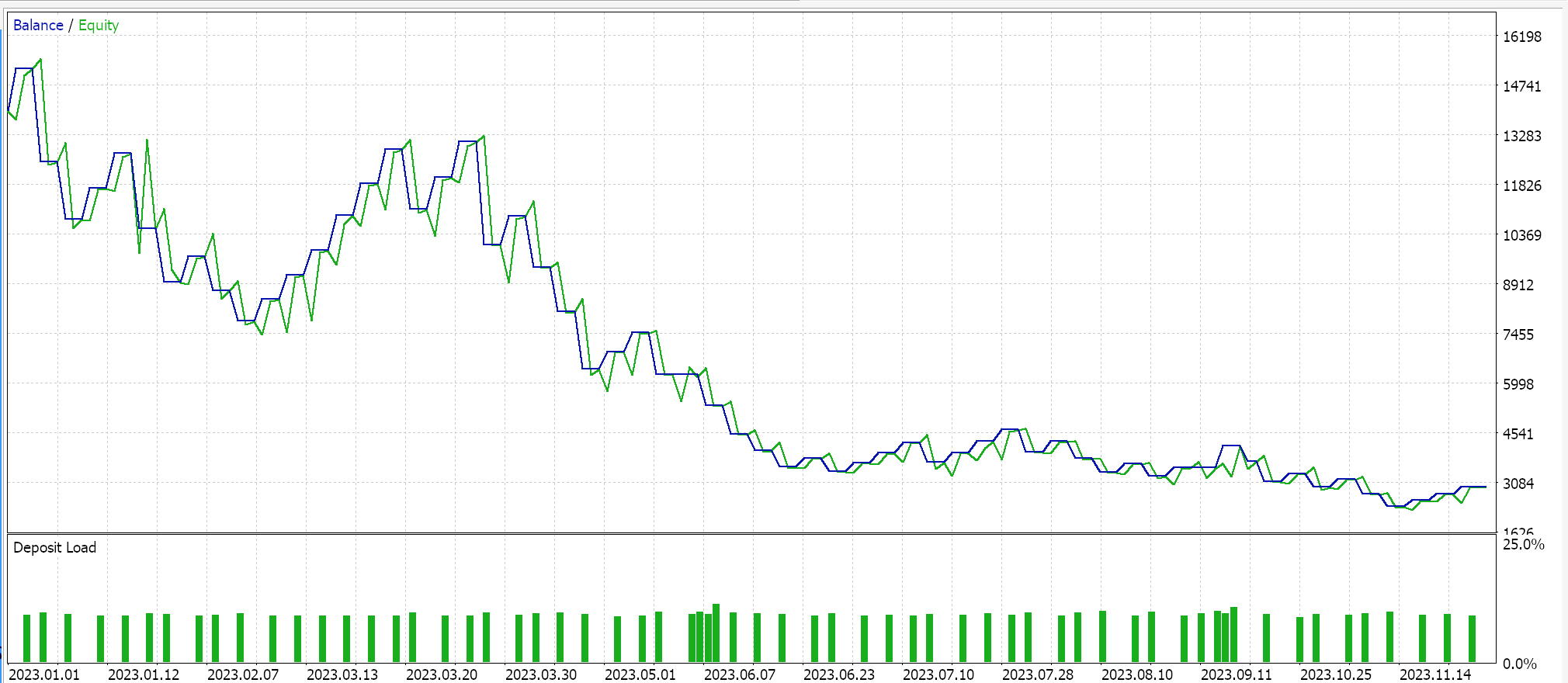
Considerações finais

A normalização em lote exige um grande número de parâmetros, o que acarreta altos custos computacionais. A escolha do algoritmo de normalização deve ser feita com muito cuidado. Embora o Z-score seja um método bastante popular, seus valores de saída não correlacionados podem gerar gradientes muito grandes, dificultando a convergência e tornando o processo de aprendizado mais lento. Por outro lado, ao optar por algoritmos de normalização alternativos, que possuem saídas correlacionadas – como o escalonamento de características ou o escalonamento robusto – e combiná-los com funções de ativação adequadas, que possuem intervalos de saída semelhantes, o processo de aprendizado pode ser acelerado. Entretanto, a velocidade é um fator crítico nesse contexto. Como mencionado anteriormente, a normalização em lote envolve múltiplos parâmetros e exige um alto poder computacional. Portanto, é essencial selecionar cuidadosamente os algoritmos de normalização e as funções de ativação, além de ajustar corretamente os níveis e o tamanho da rede neural para obter desempenho ideal.