知っておくべきMQL5ウィザードのテクニック（第30回）：機械学習におけるバッチ正規化のスポットライト

はじめに

バッチ正規化(Batch Normalization)（英語）は、ニューラルネットワークの各層にデータを供給する前に、データを標準化する手法です。この手法は、ネットワークのパフォーマンスを向上させることが知られていますが、その理由については様々な意見があります。このトピックに関する元の論文では、内部共変量シフト(Internal Covariate Shift)（英語）が原因とされています。これは、上流の層からの入力データの変動が、下流の層に連鎖的な影響を及ぼさないようにするための対策と理解できます。この最近の研究では、正規化により層内の勾配の変動が小さくなることで、経験的な性能の向上がもたらされると主張されています。

トレーダーの視点から見ると、バッチ正規化がニューラルネットワークのパフォーマンスにどのように影響するかを理解することは、システムを開発・テストする上で非常に重要です。バッチ正規化には、主に以下の3つの形式があります。 標準得点、特徴量スケーリング(Feature Scaling)（英語）、ロバスト-スケーリング(Robust Scaling)（英語）です。それぞれの形式は非常にシンプルなアルゴリズムであり、これらを使用したEAでテストを行い、コントロールとしてバッチ正規化を使用しないEAでも比較をおこないます。この記事では、前回の投稿（学習率に関するもの）で使用した形式に戻り、3つの正規化手法についての説明、同じ正規化手法に基づくテストレポート、そして最後に結論を述べます。

また、本連載の他の記事と同様に、新しいアイデアをテストするためにウィザードで構築されたEAを使用することに焦点を当てています。このプロセスに関する詳細は、こちらとこちらの記事でご確認いただけます。これらの2つの記事は、この記事の最後に添付されているコードの使用方法についての手引きを提供しています。今回の作品では、かなりの数のカスタム列挙データを最適化可能な入力として使用しています。MQL5に組み込まれた列挙型は、カスタムシグナルファイルのヘッダーで宣言でき、自動的に入力として表示され、シグナルフィルターの一部として初期化されます。しかし、カスタム列挙をヘッダーに配置すると、MQL5ウィザードでファイルが認識されなくなり、ウィザードのアセンブリを実行できなくなります。この問題の回避策として、カスタムシグナルクラスのヘッダーからパラメータを省略し、他の入力パラメータと同様に、パラメータとその割り当て関数をシグナルクラス内で宣言することが挙げられます。ウィザードの組み立てが完了したら、入力パラメータのリストと、このカスタム列挙パラメータを追加するためのシグナルクラスの初期化を手動で変更します。

私が見つけたハックは、シグナルクラス自体で列挙を宣言することでしたが、詳細は忘れてしまったため、この手動編集で妥協するしかありません。私たちのテスト用EAは、学習率タイプ、適応学習レートタイプ、そしてこの記事で最も重要な正規化タイプの列挙をカスタムしています。後者のコードを以下に示します。

enum Enormalize
{  NORMALIZE_NONE = -1,
   NORMALIZE_ROBUST = 0,
   NORMALIZE_FEATURE = 1,
   NORMALIZE_STANDARD = 2,
};

EA内でこの列挙を使用し最適化するには、以下のように列挙パラメータを入力として手動で追加する必要があります。

....

input ENUM_ACTIVATION_FUNCTION Signal_CMLP_ActivationType = AF_SIGMOID;  // CMLP(30,6,0.05,10,0.1,2,...) Activation Type
input Enormalize Signal_CMLP_NormalizeType   = NORMALIZE_FEATURE; // CMLP(30,6,0.05,10,0.1,2,...) Batch Normalisation Type
input Elearning Signal_CMLP_LearningType   = LEARNING_ADAPTIVE; // CMLP(30,6,0.05,10,0.1,2,...) Learning Type
input Eadaptive Signal_CMLP_AdaptiveType   = ADAPTIVE_GRADIENT; // CMLP(30,6,0.05,10,0.1,2,...) Adaptive Type

...

さらに、filter0として初期化されているカスタムシグナルのインスタンスに、宣言されたパラメータを追加する必要があります。これは次のようにおこなわれます。

...

   filter0.ActivationType(Signal_CMLP_ActivationType);
   filter0.NormalizeType(Signal_CMLP_NormalizeType);
   filter0.LearningType(Signal_CMLP_LearningType);
   filter0.AdaptiveType(Signal_CMLP_AdaptiveType);

...

これが完了すると、ウィザードで組み立てたEAをカスタムシグナルクラスで普通に使用できるようになります。ここで、上記のカスタム列挙型を通じて検討する3つの正規化の形式を紹介しましたが、次にそれぞれのバッチ列挙型について詳しく見ていく前に、このテーマについて簡単に概観し、その後、カスタムシグナルクラスにおける全体的な実装について考察していきましょう。

ニューラルネットワークにおけるバッチ正規化の議論

バッチ正規化のメリットについての議論は、公式には現在でも2015年に発表された論文でおこなわれた議論を中心に展開されています。この論文では、バッチ正規化がどのように機能するかについての経験的な結果が提示されていますが、現在ではその結果の解釈や意義について議論が交わされています。したがって、当初の主張が必ずしも同じ重みを持つわけではありません。それでも、少なくとも入門編として以下のポイントを紹介します。バッチ正規化は、前述の内部共変量シフトを軽減することにより、訓練プロセスの安定性を向上させるとされています。各層での活性化が「より標準的」になるため、収束速度が向上します。また、ネットワークの初期化時に使用される重みの感度を低下させる効果もあります。初期重みは最終的な重みに不釣り合いな影響を与えるだけでなく、訓練プロセスにかかる時間にも影響を及ぼす傾向があります。

さらに、バッチ正規化は一部のニューロンの重みの影響を受けにくくすることで、正則化の役割を果たします。また、消失勾配の問題を軽減し、ディープニューラルネットワークの訓練を可能にします。層間の依存関係を切り離し、入力特徴のスケールの変化に対して学習プロセスを不変に保つことにより、モデルの汎化能力を強化し、異なるバッチサイズでの訓練を容易にします。さらに、様々な学習率スケジュールを試すのにも適しています。これらはバッチ正規化の利点の一部ですが、次にそれぞれのタイプについて考えてみましょう。

特徴量スケーリング

特徴量スケーリングは、ある層のベクトル内のすべてのデータを0.0から+1.0の範囲に変換するプロセスです。ベクトル内の各値の計算式は以下の通りです。

ここで

• x'は正規化された値
• xは非正規化元の値
• min(x)はベクトルの最小値を返す関数
• max(x)はベクトルの最大値を返す関数

この非常に単純なアルゴリズムは、MQL5では次のように簡単に実装できます。

//+------------------------------------------------------------------+
//| Function to apply Feature-Scaling
//+------------------------------------------------------------------+
void Cnormalize::FeatureScaling(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Max() - _copy.Min() > 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min());
      }
   }
}

正規化アルゴリズムを選択する際には、各層で使用する活性化関数のタイプが常に重要な考慮事項となります。これは、すべての活性化関数が同じ範囲で出力を生成するわけではないためです。以下は、MQL5で列挙体として利用できるさまざまな活性化関数と、それぞれの出力範囲の表です。

活性化関数	出力範囲
指数線形ユニット(ELU: Exponential Linear Unit)		(-1, ∞)
指数(Exp: Exponential)		(0, ∞)
ガウス誤差線形ユニット(GELU: Gaussian Error Linear Unit)		(-∞, ∞)
ハードシグモイド(Hard Sigmoid)		[0, 1]
線形回帰(Linear)		(-∞, ∞)
リーキー整流線形ユニット(Leaky ReLU: Leaky Rectified Linear Unit)		(-∞, ∞)
整流線形ユニット(ReLU: Rectified Linear Unit)		[0, ∞)
指数線形単位(SELU: Scaled Exponential Linear Unit)		(-∞, ∞)
シグモイド(Sigmoid)		(0, 1)
ソフトマックス(Softmax)		(0, 1)、和は1
ソフトプラス(Softplus)		(0, ∞)
ソフトサイン(Softsign)		(-1, 1)
スウィッシュ(Swish)		(-∞, ∞)
双曲線タンジェント (Tanh)		(-1, 1)
閾値整流線形ユニット(Thresholded ReLU: Thresholded Rectified Linear Unit)		{0}∪ [θ, ∞]、ここでθ > 0

明らかなように、特徴量スケーリングのバッチ正規化アルゴリズムと同様の範囲内で出力を提供する活性化関数はハードシグモイド、シグモイド、ソフトマックスの3つしかありません。それ以外は範囲外です。ネットワークの訓練中に頻繁に発生する勾配消失/爆発問題を回避するには、この出力範囲の一致が不可欠です。

ハードシグモイド活性化は、次の式で定義されるシグモイド関数の単純な近似です。

つまり、入力 x がどのような値であっても、出力は0.0から+1.0の範囲に収まります。このように特徴量スケーリングに合わせることで、一貫性のある解釈可能な活性化が実現します。さらに、ハードシグモイドは計算効率が高いため、Transformerのような大規模で非常に深いネットワークに適しています。

シグモイド活性化関数は、ハードシグモイド活性化とは異なり、ある程度の可変性を維持しつつ、範囲制御された出力によって勾配が爆発する問題を最小化します。このため、シグモイド関数はすべての活性化関数の中で最も人気があります。以下に、その方程式を示します。

ここで

• eはオイラー定数
• xは正規化された値

そのマッピングの滑らかさは、正規化された特徴スケールの範囲とよく一致しています。さらに、出力値が0.0や1.0になることはまれであるため、勾配の飽和の問題を回避することができます。

ソフトマックス活性化関数は、クラス（またはデータのベクトル）を正規化し、すべての出力値が0.0から1.0の範囲に収まるだけでなく、これらの正規化された値の合計が1.0になるようにします。以下に、ソフトマックス関数を導出する方程式を示します。

ここで

• z iは入力ベクトルZのi番目の要素です。
• KはZのベクトルサイズ
• eはオイラー定数

ソフトマックス関数は通常、多クラス分類や2次元以上のデータポイントの比較に使用されます。出力は確率分布を表し、1つの出力が他の出力を不当に支配することがなく、一種の公平な土俵を作り出します。さらに、出力の合計を1にすることで、非常に深いネットワークやTransformerにおいて、下流の計算で問題を引き起こす可能性のある大きな数値が存在しないことを保証します。

つまり、ハードシグモイド、シグモイド、ソフトマックスの3つの活性化関数は、特徴スケーリング正規化に適したアルゴリズムです。すべての活性化アルゴリズムとそれぞれの導関数は、ベクトルデータ型の組み込み関数からアクセスできるため、MQL5でこれらのアルゴリズムを実装するのは非常に簡単です。その具体例として、この記事に添付されている「Cmlp」クラスの一部である「Forward()」および「Backward()」関数があります。また、活性化関数とその導関数に関しては、公式ガイダンスも提供されています。

特徴量スケーリングアルゴリズムの実装については、前述の通りです。 これは、ベクトルの最大値と最小値が異なることを確認することで、ゼロ除算を防ぐシンプルな関数です。このスケーリング関数は非常にシンプルであり、多くのネットワークが非常に深く、Transformer形式であることを考慮すると、計算量を最小限に抑えることが重要です。

ロバストスケーリング

この正規化手法では、特定の条件下で-1.0や+1.0をわずかに超える値を出力することで、出力に少し余裕を持たせていますが、ほとんどの場合、すべてのデータは-1.0と+1.0の間に収まります。このような例外は、中央値からの距離が非常に大きく、四分位範囲を超える異常値が存在する場合によく見られます。この方程式は以下の通りです。

ここで

• xは元の値
• median(x)はベクトルまたはクラスの中央値
• IQR(x)は75パーセンタイルから25パーセンタイルを引いた値

ロバストスケーリングは、特徴量スケーリングよりも外れ値の影響を受けにくいですが、外れ値を無視するわけではありません。実際、中央値から大きく離れた外れ値は、正規化された値が1を超える傾向があります。一般的に、四分位範囲と比較してデータのばらつき、つまり最大値から最小値までの範囲が大きい場合が該当します。これは、データが中央値を中心に分布しているものの、極端な値が必ずしも外れ値ではない状況を意味します。このような場合、極値に近いデータは1以上の正規化値を持つことがあるのです。

活性化出力範囲に関する上記の表から、ロバストスケーリングと組み合わせるのに理想的な活性化関数は、ソフトサイン活性化またはTANH活性化であることが明らかです。これは、ロバストスケーリングによる異常値の影響を考慮すると、出力が-1.0から+1.0の範囲に少し制限されるにもかかわらず、他のすべての活性化関数と最も適合するためです。さらに重要なのは、これらの活性化関数が生成する出力が無限の値にならないため、勾配が消失したり爆発したりするリスクが大幅に軽減されることです。

ソフトサインは非常にシンプルな方程式で定義されます。

ここで

• xはクラスまたはベクトルのデータ点
• |x|はこのデータの大きさ

式から明らかなように、x、つまり正規化ベクトル内のデータは、理想的には浮動小数点型で、通常は0.0から2.0の範囲にあるべきです。しかし、xの値が2.0を超えてスケールアップすると、ばらつきが大きくなり、正規化されたデータの解釈が妨げられます。これは、正規化された値がゼロから離れると飽和し、ゼロ値付近では滑らかに変化することを示しています。対称性とゼロを中心とした値は、ロバストスケーリングと非常に良く一致しています。さらに、ソフトサインからの勾配は、一般的に使用されるシグモイド活性化などの他の活性化関数からの勾配よりも消えにくいことが観察されています。これは、大規模なデータセットを用いて訓練を行う際に非常に有益です。

TANH（双曲線正接）活性化関数は、-1.0から+1.0の範囲で出力を生成するため、ロバストスケーリングと組み合わせるのに適しています。以下にその方程式を示します。

ここで

• xはクラスまたはベクトル内のデータ点
• eはオイラー定数

TANHアルゴリズムはシグモイドと非常によく似ていますが、シグモイドが0.5を中心とするのに対し、TANHは0.0を中心とする点が明らかに異なります。また、シグモイド関数よりも滑らかな勾配が得られると言われています。ソフトサインと同様、符号の範囲が広いため、上で見たようにロバストスケーリングに最適な候補となります。ノイズの多いデータや外れ値の多いデータセット（トレーダーの観点からは、ボラティリティの非常に高い証券の価格バッファなど）はすべて、ロバストスケーリングとTANHの活性化で使用するのに理想的なデータセットです。これは、さまざまなスケールのデータセットを扱う能力に起因します。

MQL5での実装は、上記の特徴量スケーリングのための3つの活性化関数で述べたようにシームレスです。ベクトルデータ型には、活性化関数と微分関数が組み込まれており、入力となるベクトルに対して結果を出力します。上記したように、その概要はこちらとこちらで概要されています。

ロバストスケーリングアルゴリズムは、MQL5のnormalizeクラスに以下のように実装されています。

//+------------------------------------------------------------------+
//| Function to apply Robust-Scaling
//+------------------------------------------------------------------+
void Cnormalize::RobustScaling(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Percentile(75) - _copy.Percentile(25) > 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Median()) / (_copy.Percentile(75) - _copy.Percentile(25));
      }
   }
}

上記の特徴量スケーリングアルゴリズムと同様に、四分位範囲を用いてゼロ除算のチェックが行われます。これもまた単純なアルゴリズムで、上で強調した効率上の理由からです。

標準得点

標準得点は、一般的にZスコアとして知られており、最も広く使用される正規化アルゴリズムの一つです。ウィキペディアのバッチ正規化では ページでは、正規化関数として唯一取り上げられています。標準得点は、データのクラスまたはベクトルを、平均が0で標準偏差が1になるように変換するプロセスです。これは、出力データの範囲に焦点を当てた、前述の特徴量スケーリングやロバストスケーリングとは明らかに異なります。その方程式は以下の通りです。

ここで

• Zは正規化された値
• μは平均
• σは標準偏差

したがって、この式から、出力がマイナス無限大からプラス無限大に及ぶ可能性があることがわかります。この広範な出力範囲は注意が必要であり、特に爆発的な勾配が問題になる可能性があります。特に、標準得点と組み合わせて使用される活性化関数が未結合の出力を持つ場合は、その影響が顕著になります。標準得点は、勾配降下法を用いたネットワークの学習プロセスを安定化させるのに適しています。また、正規分布に従うデータを扱う際には、入力データ点が学習プロセスに均等に寄与することを保証するため、非常に効果的です。

短所もありますが、その代表的なものは外れ値に対する敏感さ、データのガウス分布の推定の必要性、そして前述の通り非拘束出力がある点ですMQL5では、標準得点は以下のようにして実装できます。

//+------------------------------------------------------------------+
//| Function to apply Standard-Score
//+------------------------------------------------------------------+
void Cnormalize::StandardScore(vector &Data)
{  vector _copy;
   _copy.Copy(Data);
   if(_copy.Std() != 0.0)
   {  for (int i = 0; i < int(Data.Size()); i++)
      {  Data[i] = (_copy[i] - _copy.Mean()) / _copy.Std();
      }
   }
}

興味深いことに、これはMQL5の関数の中ではまだ標準的な機能ではありません。これら3つの正規化関数すべてにおいてゼロ除算を避けるために、分母がゼロかどうかをチェックするのではなく、イプシロンと呼ばれる小さな非ゼロの値を下部に加えることも一般的です。しかし、特徴量スケーリングやロバストスケーリングにおいては、分母がゼロの場合、正規化された値が非常に大きくなってしまいます。

正規化Transformer

層の入力データが特徴スケーリング、ロバストスケーリング、標準得点のいずれかによって正規化されると、これらの正規化からの出力はバッチ正規化Transformerに供給されます。また、次の式で定義される比較的単純な関数でもあります。

ここで

• yはインデックスiのベクトルの出力
• xはインデックスiにおける以前に正規化されたデータ点
• γとβは最適化可能な浮動小数点パラメータ

MQL5では以下のようにコーディングできます。

//+------------------------------------------------------------------+
//| Batch Normalizing Transform
//+------------------------------------------------------------------+
void Cnormalize::Transform(Enormalize Type, vector &Output, vector &BatchTransform, vector &Beta, vector &Gamma)
{  if(Type != NORMALIZE_NONE)
   {  if(Type == NORMALIZE_STANDARD)
      {  StandardScore(Output);
      }
      else if(Type == NORMALIZE_FEATURE)
      {  FeatureScaling(Output);
      }
      else if(Type == NORMALIZE_ROBUST)
      {  RobustScaling(Output);
      }
      //Transformer
      BatchTransform.Init(Output.Size());
      BatchTransform.Fill(0.0);
      for(int i = 0; i < int(Output.Size()); i++)
      {  BatchTransform[i] = (Gamma[i] * Output[i]) + Beta[i];
      }
   }
}

正規化出力をこのTransformerにかける論拠は主に5つあります。まず、柔軟性と再キャリブレーションを導入することで、正規化されていない元のデータの代表力を回復させます。変換後の出力データは、ネットワークの学習を促進するために必ずしも最適な状態にあるとは限りません。たとえば、標準得点正規化を使用すると、各ベクトルの出力データは常に平均0、標準偏差1になります。このようなケースや類似のケースは、ネットワークを効果的に訓練するには極端すぎるかもしれません。そのため、学習可能/最適化可能なパラメータβとγを導入することで、このデータセットを訓練に最適な形に再調整することができます。

第2に、標準得点のように、初期正規化関数が潜在的に非拘束出力を持つ場合、この正規化Transformerは勾配の消失や爆発を回避するのに役立ちます。これは、βとγを微調整することで実現されます。第3に、Transformerは分散スケーリングを通じて効果的な学習のための分散を維持することが主張されます。γパラメータは直接的な倍数であるため、正規化出力の分散を調整することが可能です。この分散を調整する能力により、学習プロセスをネットワークのアーキテクチャに合わせて微調整できます。

さらに、Transformerは、ネットワークをデータに適応させることで、ネットワークの学習ダイナミクスを向上させることができます。最適化可能なβとγパラメータは、ネットワークの層数やサイズの設定に応じてデータがスケーリングされるように、再びこのプロセスをガイドします。最終的には、理想的な結果を達成するために必要な訓練エポックが少なくなります。最後に、正規化されたデータの出力をスケーリングしてシフトすることによる正則化が、ドロップアウト正則化のように機能することが主張されます。正則化は、ネットワークがデータセットの根本的なパターンをより多く学習し、ノイズをより少なく学習するように誘導することを意図しているため、ベクトルパラメータであるβとγは各層に固有です。このパラメータベースのカスタマイズは、ネットワークの正則化に加えて、導入部で触れた共変量シフトの実現をより効果的に行うことができます。これは、βとγのパラメータ固有の作用によるものです。

ストラテジーテストの結果

テストには、2023年の日足時間枠で銘柄EURJPYを使用します。標準的なスコア正規化は、非結合データであるため、必ずしも適切な活性化関数を持ちません。この記事で紹介した束縛活性化関数を使うこともできますが、そのテストは読者に委ねられます。ここでは、ロバストスケーリング正規化と特徴量スケーリング正規化のみをテストします。それぞれ、ソフトサインとシグモイド活性化とペアにしました。

特徴量スケーリングについては、以下のような結果となりました。

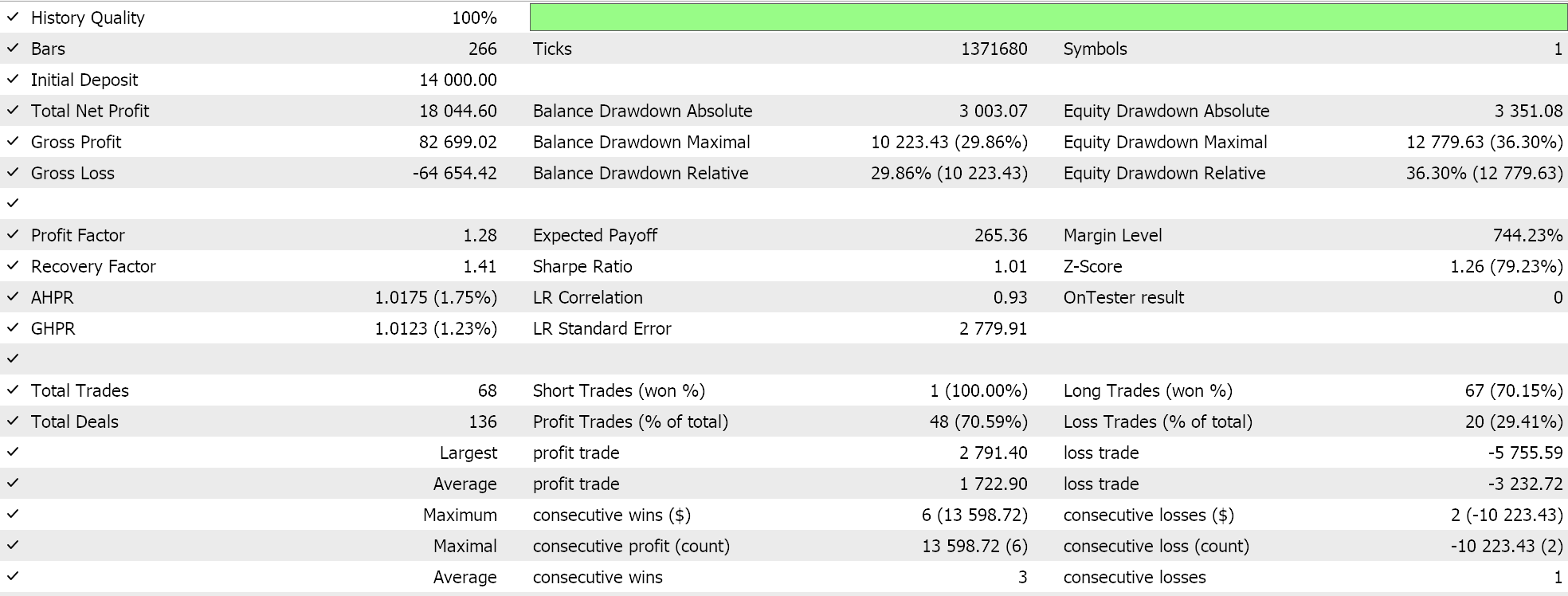
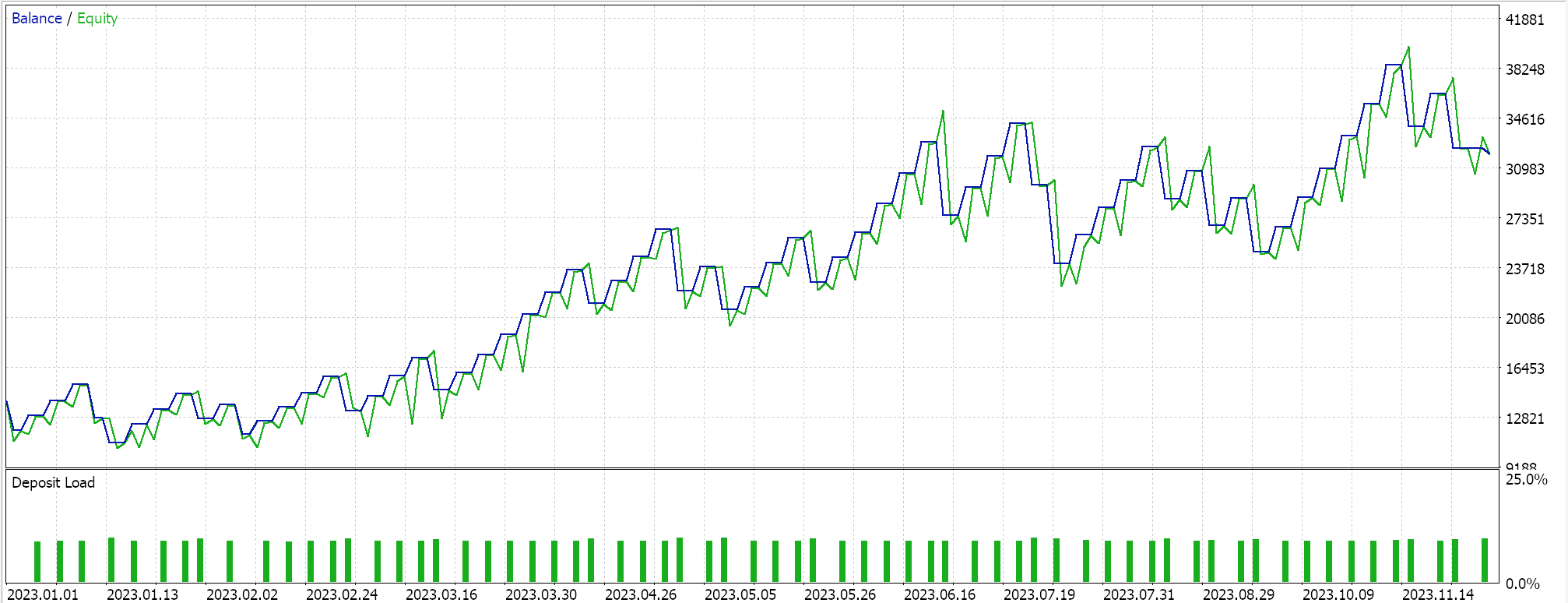
ロバストなスケーリングについては、以下のような結果となりました。

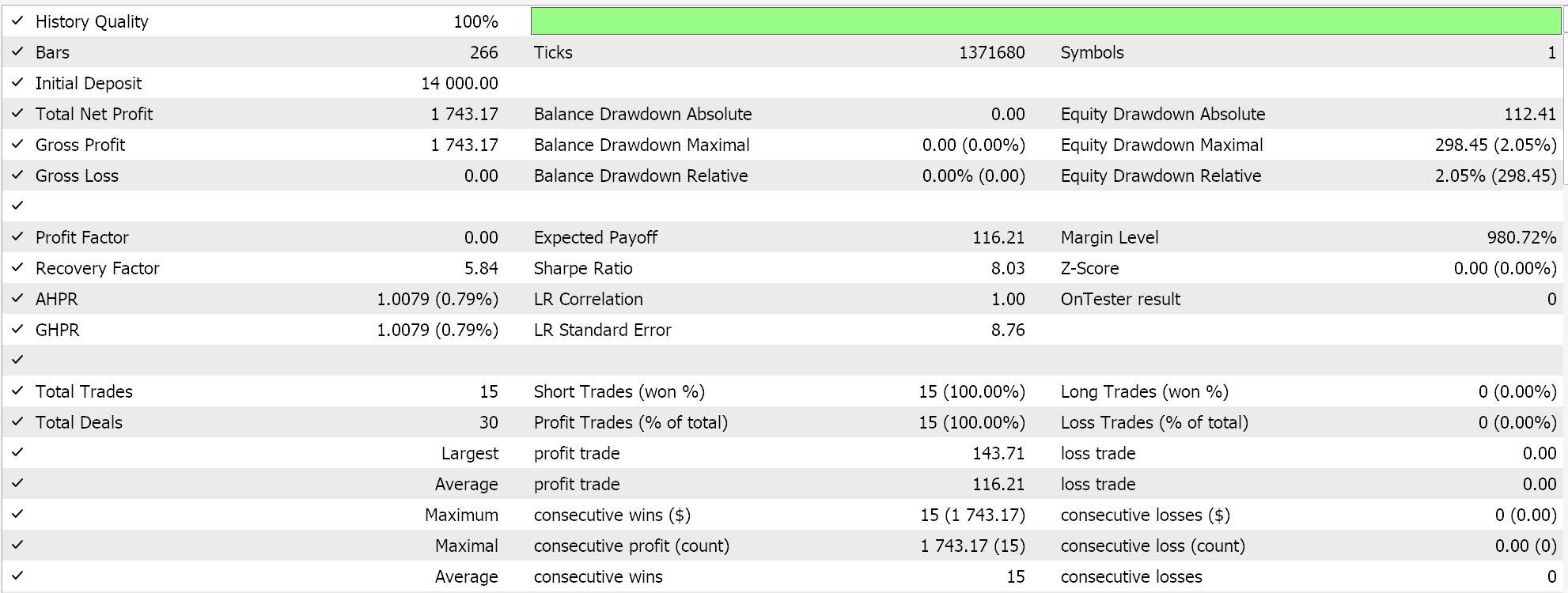
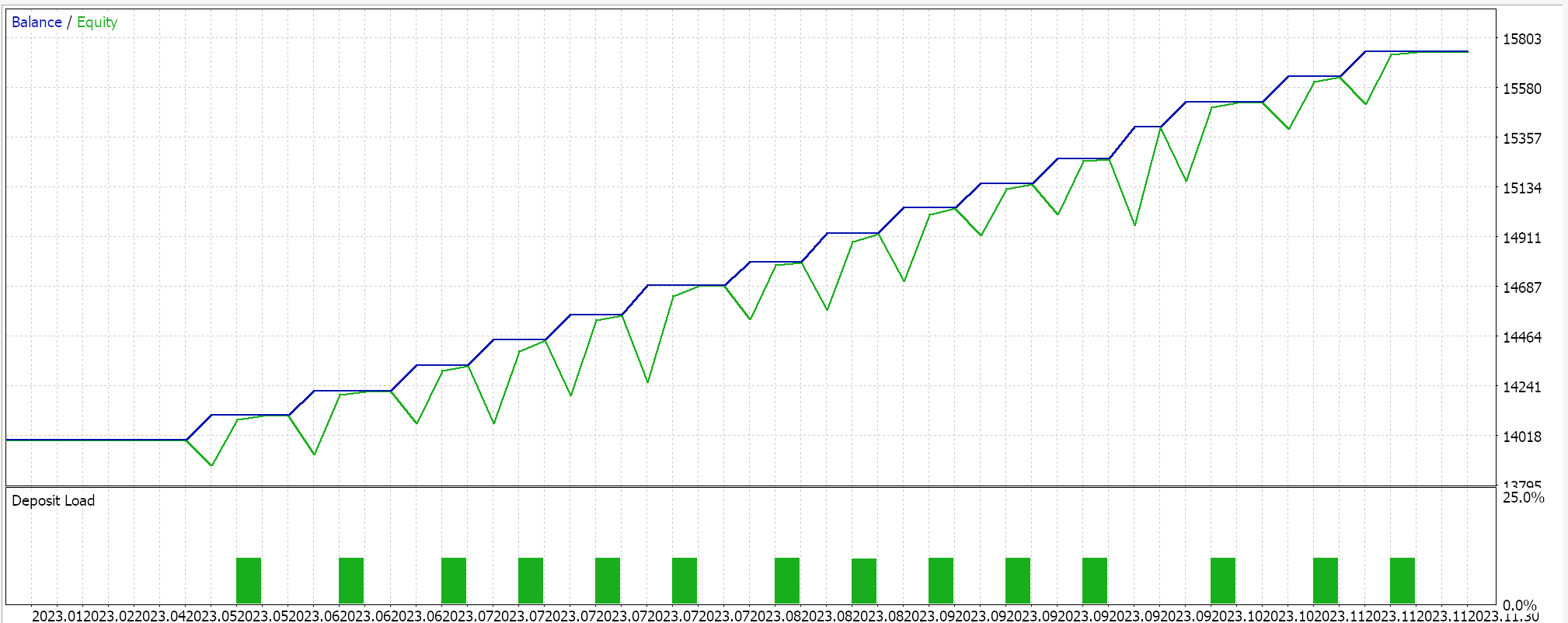
コントロールとして、EAで同じ設定をおこない、正規化をおこなわずにテストをおこないます。以下はその結果です。

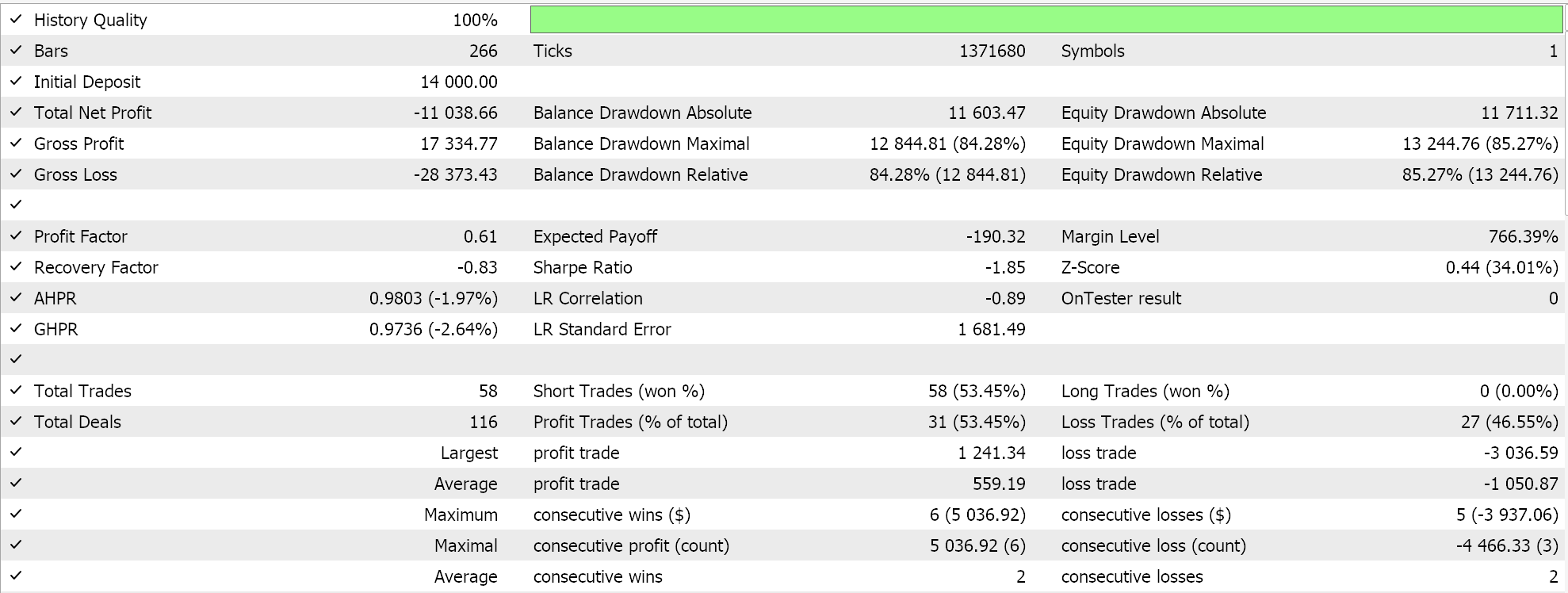
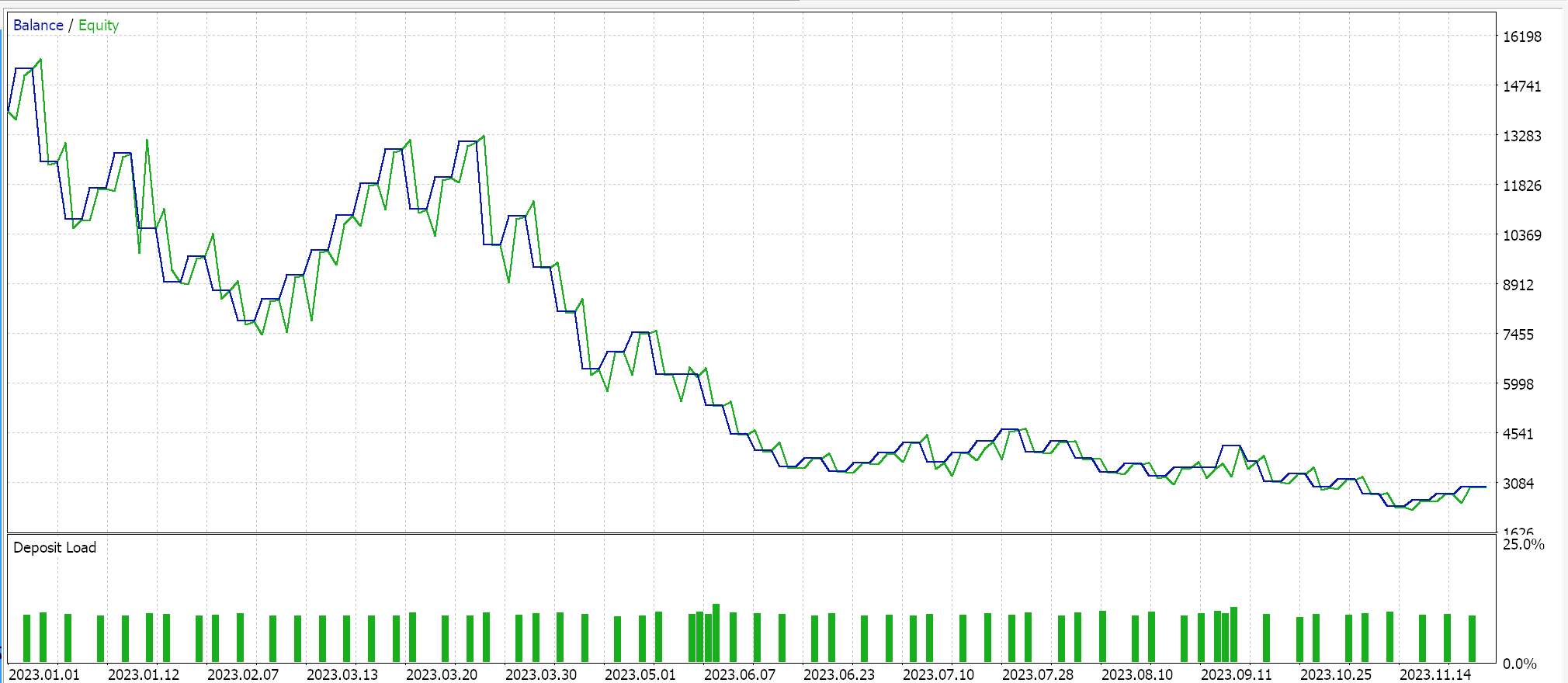
結論

主な発見を要約すると、バッチ正規化はパラメータが多く、そのため計算コストが高いということです。使用する正規化アルゴリズムを選択する際には、特に注意を払う必要があります。標準得点は非常に人気があり一般的ですが、勾配が非常に大きくなり、収束を妨げ、学習プロセス全体を遅らせる可能性があります。しかし、特徴量スケーリングやロバストスケーリングのような境界出力を持つ別の正規化アルゴリズムを使用し、これらを同様の境界出力を持つそれぞれの活性化関数と組み合わせれば訓練プロセスを加速することができます。なぜなら、バッチ正規化には多くのパラメータが含まれ、計算負荷が高いからです。したがって、正規化アルゴリズムと活性化関数の組み合わせには細心の注意を払い、最適なネットワーク層とサイズを設定する必要があります。