Integración de modelos ocultos de Márkov en MetaTrader 5

Introducción

Es bien sabido que una de las características fundamentales de las series temporales financieras es que presentan memoria. En el contexto del análisis de series temporales, la memoria se refiere a la estructura de dependencia dentro de los datos, en la que los valores pasados influyen en los valores actuales y futuros. Comprender la estructura de la memoria ayuda a elegir el modelo adecuado para las series temporales. En este artículo, hablamos de un tipo diferente de memoria: la que adopta la forma de un Modelo oculto de Márkov. Exploraremos los fundamentos de los modelos ocultos de Márkov y demostraremos cómo construir un HMM (Hidden Markov Model) utilizando el módulo 'hmmlearn' de Python. Por último, presentaremos un código en Python y MQL5 que permite exportar los HMMs para utilizarlos en programas de MetaTrader 5.

Comprender los modelos ocultos de Márkov

Los modelos ocultos de Márkov son una potente herramienta estadística utilizada para modelar datos de series temporales, en los que el sistema modelado se caracteriza por estados no observables (ocultos). Una premisa fundamental de los modelos ocultos de Márkov es que la probabilidad de estar en un estado determinado en un momento concreto depende del estado del proceso en el intervalo de tiempo anterior. Esta dependencia representa la memoria de un HMM.

En el contexto de las series temporales financieras, los estados podrían representar si una serie tiende al alza, tiende a la baja u oscila dentro de un rango específico. Cualquiera que haya utilizado algún indicador financiero está familiarizado con el efecto «whipsaw» (sierra de látigo) causado por el ruido inherente a las series temporales financieras. Se puede emplear un HMM para filtrar estas señales falsas, proporcionando una comprensión más clara de las tendencias subyacentes.

Para construir un HMM, necesitamos observaciones que capten la totalidad del comportamiento que define el proceso. Esta muestra de datos se utiliza para aprender los parámetros del HMM apropiado. Este conjunto de datos estaría formado por diversas características del proceso que se está modelando. Por ejemplo, si estuviéramos estudiando los precios de cierre de un activo financiero, también podríamos incluir otros aspectos relacionados con el precio de cierre, como diversos indicadores que, idealmente, ayuden a definir los estados ocultos que nos interesan.

El proceso de aprendizaje de los parámetros del modelo se lleva a cabo bajo el supuesto de que la serie que se está modelando estará siempre en uno de dos o más estados. Los estados se etiquetan simplemente de 0 a S-1. Para estos estados, debemos asignar un conjunto de probabilidades que capturen la probabilidad de que el proceso cambie de un estado a otro. Estas probabilidades suelen denominarse matriz de transición. La primera observación tiene un conjunto especial de probabilidades iniciales de estar en cada estado posible. Si una observación se encuentra en un estado concreto, se espera que siga una distribución específica asociada a ese estado.

Por lo tanto, un HMM se define completamente por cuatro propiedades:

• El número de estados que debe asumir.
• Las probabilidades iniciales de que la primera observación se encuentre en cualquiera de los estados.
• La matriz de transición de probabilidades.
• Las funciones de densidad de probabilidad para cada estado.
  

Al principio, tenemos las observaciones y el número supuesto de estados. Queremos encontrar los parámetros de un HMM que se ajusten al conjunto de datos que tenemos ante nosotros. Esto se hace observando la probabilidad mediante una técnica estadística llamada estimación de máxima verosimilitud. En este contexto, la estimación de máxima verosimilitud es el proceso de búsqueda de las propiedades del modelo que corresponden con mayor probabilidad a nuestras muestras de datos. Esto se consigue calculando la probabilidad de que cada muestra se encuentre en un estado concreto en un momento específico. Para ello se utilizan los algoritmos de avance y retroceso, que recorren todas las muestras, hacia delante y hacia atrás en el tiempo, respectivamente.

El algoritmo de avance

Comenzamos con la primera observación de nuestro conjunto de datos antes de calcular las probabilidades para las muestras posteriores. Para la primera muestra, utilizamos las probabilidades de estado iniciales, que, en este momento, se consideran parámetros de prueba para un HMM candidato. Si no se sabe nada del proceso que se está modelando, es perfectamente aceptable fijar todas las probabilidades de estado iniciales en 1/S, donde S representa el número total de estados supuestos. Aplicando el teorema de Bayes tenemos la siguiente ecuación general:

Donde «lk» es la probabilidad de que una muestra en el momento «t» esté en el estado «i», y «p» es la probabilidad de estar en el estado «i» en el momento «t» dadas las muestras hasta el momento «t». «O» es una muestra individual, una única fila en el conjunto de datos.

La probabilidad de la primera muestra se calcula según la regla de probabilidad condicional, P(A) = P(A|B)P(B). Por lo tanto, para la primera muestra, la probabilidad de estar en el estado i se calcula multiplicando la probabilidad inicial de estar en el estado i por la función de densidad de probabilidad de la primera muestra.

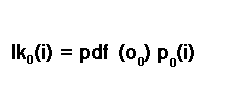
Se trata de otro parámetro de prueba del HMM candidato. En la literatura, a veces se denomina probabilidad de emisión. Entraremos en más detalle sobre las probabilidades de emisión más adelante en el texto. Por ahora, basta con ser conscientes de que se trata de otro parámetro de prueba en esta fase. Tenemos que tener en cuenta la posibilidad de que podamos estar en cualquiera de todos los estados posibles. El resultado es que la probabilidad inicial final es la suma de todas las probabilidades de todos los estados posibles.

 

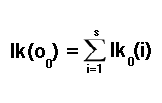
Para calcular las probabilidades de las observaciones posteriores, tenemos que considerar la posibilidad de transición a un estado concreto desde cualquiera de los estados posibles en la franja horaria anterior. Aquí es donde entran en juego las probabilidades de transición, que es otro parámetro de prueba en este punto. La probabilidad de llegar a un estado específico en la siguiente franja horaria, dado que hemos calculado la probabilidad para la franja horaria actual, se estima multiplicando la probabilidad de estado conocida actualmente por la probabilidad de transición correspondiente.

Este es tan buen momento como cualquier otro para hablar de las probabilidades de transición o de la matriz de transición.

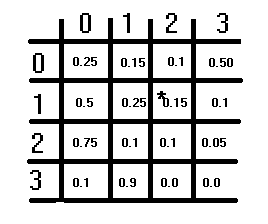
La ilustración anterior muestra una matriz de transición hipotética. Tiene una estructura S×S, siendo S el número de estados supuestos. Cada elemento representa una probabilidad, y las probabilidades de cada fila deben sumar 1. Esta condición no se aplica a las columnas. Para obtener la probabilidad de transición correspondiente al cambio de un estado a otro, se consultan primero las filas y luego las columnas. El estado actual desde el que se cambia corresponde al índice de fila, y el estado al que se cambia corresponde al índice de columna. El valor de estos índices es la probabilidad de transición correspondiente. La diagonal de la matriz representa las probabilidades de que el estado no cambie.

Volviendo a la tarea de calcular probabilidades para el resto de las observaciones en nuestra muestra de datos elegida, estábamos multiplicando una probabilidad de estado por una probabilidad de transición. Sin embargo, para obtener el panorama completo, debemos considerar la posibilidad de pasar a cualquiera de todos los estados posibles. Lo hacemos sumando todas las posibilidades, de acuerdo con la siguiente ecuación:

            

Con esto concluye el cálculo de probabilidades individuales para cada muestra en nuestro conjunto de datos. Estas probabilidades individuales se pueden combinar mediante la multiplicación para obtener la probabilidad de todo el conjunto de datos. El cálculo que acabamos de describir se llama algoritmo de avance, debido a la recursión temporal hacia adelante del método. Esto contrasta con el algoritmo inverso, que discutiremos en la siguiente sección.

El algoritmo inverso

También es posible calcular las probabilidades individuales de movimiento hacia atrás en el tiempo, desde la última muestra de datos hasta la primera. Comenzamos estableciendo la probabilidad para todos los estados en 1 para la última muestra de datos. Para cada muestra de datos, si se encuentra en un estado específico, calculamos la probabilidad del conjunto de muestras posterior, considerando que podemos realizar la transición a cualquiera de los estados. Hacemos esto calculando la suma ponderada de las probabilidades de cada estado: la probabilidad de estar en ese estado multiplicada por la función de densidad de probabilidad de que la muestra esté en el mismo estado. El resultado de este cálculo se ajusta luego utilizando la probabilidad de transición del estado actual al siguiente como factor de ponderación. Todo esto está resumido en la siguiente fórmula:

Las funciones de densidad de probabilidad

En las discusiones sobre los algoritmos de avance y retroceso, se mencionó la función de densidad de probabilidad (PDF, Probability Density Function) como parámetros de un HMM. Entonces surge una pregunta: ¿Qué distribución estamos asumiendo? Como se mencionó anteriormente, los parámetros PDF de un HMM generalmente se denominan probabilidades de emisión. Se denominan probabilidades cuando los datos que se modelan consisten en valores discretos o categóricos. Cuando trabajamos con variables continuas, utilizamos la función de densidad de probabilidad.

En este texto, demostramos los HMM que modelan conjuntos de datos de variables continuas que siguen una distribución normal multivariante. Es posible implementar otras distribuciones; de hecho, el módulo de Python que veremos más adelante tiene implementaciones de HMM para diferentes distribuciones de los datos que se modelan. Por extensión, los parámetros de la distribución asumida se convierten en uno de los parámetros del HMM. En el caso de la distribución normal multivariante, sus parámetros son las medias y las covarianzas.

El algoritmo de Baum-Welch

El algoritmo de Baum-Welch es una técnica de maximización de expectativas que se utiliza para probar diferentes parámetros de los HMM candidatos hasta llegar al óptimo. El valor que se maximiza en este procedimiento de optimización es la probabilidad para todo el conjunto de datos de muestras. El algoritmo Baum-Welch es conocido por ser eficiente y fiable, pero tiene sus defectos. Un inconveniente evidente es su naturaleza no convexa. Las funciones no convexas en relación con la optimización son funciones con numerosos mínimos o máximos locales.

Esto significa que cuando se alcanza la convergencia, puede que no se haya encontrado el máximo o el mínimo global del espacio de parámetros. Básicamente, no se garantiza que la función converja en el punto óptimo. La mejor manera de mitigar este fallo es probar parámetros que tengan una gran probabilidad en comparación con otros del espacio de parámetros. Para ello, tendríamos que probar numerosos valores aleatorios de los parámetros para encontrar el mejor espacio inicial de parámetros desde el que iniciar el proceso de optimización.

Cálculo de las probabilidades de estado

Una vez que tenemos el HMM óptimo y sus parámetros, podemos utilizarlo para calcular las probabilidades de estado de las muestras de datos no vistas. El resultado de dicho cálculo sería un conjunto de probabilidades, una para cada estado, que indicaría la probabilidad de estar en cada estado. Las probabilidades individuales del algoritmo hacia delante se multiplican por las probabilidades del algoritmo hacia atrás, lo que da como resultado la probabilidad de un estado concreto. Según la regla de Bayes, la probabilidad de que una observación se encuentre en un estado determinado, se calcula como:

Cálculo de las probabilidades de estado mediante el algoritmo de Viterbi

Además de las probabilidades de estado, también podemos inferir el estado probable en el que se encuentra una observación utilizando el algoritmo de Viterbi. El cálculo comienza a partir de la primera observación, cuyas probabilidades de estado se calculan utilizando las probabilidades de estado iniciales multiplicadas por las probabilidades de emisión.

Para cada observación, de la segunda a la última, se calcula la probabilidad de cada estado utilizando la probabilidad del estado anterior, la probabilidad de transición correspondiente y su probabilidad de emisión. El estado más probable será el de mayor probabilidad.

Hemos examinado todos los componentes de un modelo oculto de Márkov. A continuación nos adentramos en su aplicación práctica. Comenzamos examinando una implementación de los HMM basada en Python proporcionada en el paquete 'hmmlearn'. Discutiremos el uso de la implementación del HMM gaussiano de 'hmmlearn' antes de pasar al código MQL5 para demostrar cómo integrar un modelo entrenado en Python utilizando 'hmmlearn' en aplicaciones MetaTrader 5.

El paquete 'hmmlearn' de Python

La biblioteca 'hmmlearn' de Python proporciona herramientas para trabajar con modelos de Márkov ocultos. Las herramientas para entrenar HMMs se encuentran en el espacio de nombres `hmm`. Dentro de `hmm`, se declaran varias clases especiales para trabajar con procesos de diferentes distribuciones. Concretamente:

• MultinomialHMM: Modela los HMM en los que las observaciones son discretas y siguen una distribución multinomial.
• GMMHMM: Modela los HMM en los que las observaciones se generan a partir de una mezcla de distribuciones gaussianas.
• PoissonHMM: Modela los HMM en los que se supone que las observaciones siguen una distribución de Poisson.
• Por último, tenemos la clase 'GaussianHMM' que maneja conjuntos de datos que tienden a seguir una distribución multivariante gaussiana (normal). Esta es la clase que demostraremos y cuyo modelo resultante vincularemos con MetaTrader 5.

Para instalar el paquete, puede utilizar la siguiente orden:

pip install hmmlearn

Después de instalar el paquete, puede importar la clase `GaussianHMM` utilizando la siguiente sentencia 'import':

from hmmlearn.hmm import GaussianHMM

Como alternativa, puede importar el módulo `hmm`, que contiene todas las clases enumeradas anteriormente junto con otras utilidades útiles. Si se utiliza este método, los nombres de las clases deberán ir precedidos de `hmm`, de la siguiente manera:

from hmmlearn import hmm

Puede inicializar un objeto GaussianHMM con varios parámetros:

model = GaussianHMM(n_components=3, covariance_type='diag', n_iter=100, tol=0.01)

Donde:

• "n_components": Número de estados en el modelo.
• "covariance_type": Tipo de parámetros de covarianza a utilizar ('spherical', 'diag', 'full', 'tied'). El tipo de covarianza utilizado está relacionado con las características del conjunto de datos. Debe elegirse una covarianza esférica si las características o variables del conjunto de datos que se está modelando tienen una varianza similar sin posibilidad de estar correlacionadas. De lo contrario, si las variables tienen varianzas contrastantes, la mejor opción es elegir un tipo de covarianza diagonal. Si las variables están correlacionadas, entonces se debe elegir un tipo de covarianza completa o vinculada. Seleccionar la covarianza completa proporciona la mayor flexibilidad pero también puede ser computacionalmente costoso. Es la opción más segura que limita el número de suposiciones realizadas sobre el proceso que se está modelando. La covarianza vinculada supone además que los estados comparten una estructura de covarianza similar. Es un poco más eficiente en relación con la covarianza completa.
• "n_iter": Número máximo de iteraciones a realizar durante el entrenamiento.
• "tol": Umbral de convergencia.

Para explorar todos los parámetros que especifican un modelo, puede consultar la documentación de la biblioteca 'hmmlearn'. Esta documentación proporciona información detallada sobre los distintos parámetros y su uso. Puedes acceder a él en línea en la biblioteca de 'hmmlearn' en el sitio web oficial, o a través de la documentación incluida con la instalación de la biblioteca, a través de la utilidad de ayuda incorporada en Python.

Ayuda (GaussianHMM)

Para entrenar un modelo, llamamos al método «fit()». Espera al menos una matriz bidimensional como entrada.

model.fit(data)

Una vez completado el entrenamiento, podemos obtener los estados ocultos de un conjunto de datos llamando a «predict()» o a «decode()». Ambos esperan una matriz bidimensional con el mismo número de características que el conjunto de datos utilizado para entrenar el modelo. El método «predict()» devuelve una matriz de estados ocultos calculados, mientras que «decode()» devuelve el log de verosimilitud junto con la matriz de estados ocultos encerrada en una tupla.

Al llamar a "score_samples()" se devuelve la probabilidad logarítmica así como las probabilidades de estado para el conjunto de datos proporcionado como entrada. Nuevamente, los datos deben tener la misma cantidad de características que los datos utilizados para entrenar el modelo.

Exportación de un modelo oculto de Márkov

Exportar un modelo entrenado en Python utilizando el paquete 'hmmlearn' para su uso en MetaTrader 5 implica implementar dos componentes personalizados:

• Componente Python: Este componente se encarga de guardar los parámetros de un modelo entrenado en un formato legible desde una aplicación MetaTrader. Se trata de exportar los parámetros del modelo a un formato de archivo que pueda ser analizado por las aplicaciones de MetaTrader 5.
• Componente MQL5: El componente MQL5 comprende código escrito en MQL5. Este componente debe incluir la funcionalidad para leer los parámetros HMM exportados por el componente Python. Además, necesita implementar los algoritmos de avance, retroceso y Viterbi para calcular los estados ocultos y las probabilidades de estado de un conjunto de datos basado en un HMM especificado.
  

La implementación de estos componentes implica una cuidadosa consideración de los formatos de serialización de datos, las operaciones de entrada y salida de archivos y las implementaciones algorítmicas tanto en Python como en MQL5. Es esencial garantizar la compatibilidad entre las implementaciones de Python y MQL5 para transferir con precisión el modelo entrenado y realizar tareas de inferencia en MetaTrader 5.

El paquete 'hmmlearn' proporciona la capacidad de guardar un HMM entrenado utilizando el módulo 'pickle'. El problema es que no es fácil trabajar con archivos encurtidos fuera de Python. Entonces, una mejor opción sería utilizar el formato JSON. El parámetro HMM se escribirá en un archivo JSON estructurado que se puede leer mediante código MQL5. Esta funcionalidad se implementa en la función de Python a continuación:

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

Esta función toma una instancia de la clase GaussianHMM y un nombre de archivo como entrada, y escribe los parámetros HMM en un archivo JSON en un formato estructurado que puede leerse usando código MQL5.

En el código MQL5, la funcionalidad para leer modelos HMM guardados en formato JSON está incluida en 'hmmlearn.mqh'. El archivo incluye la definición de la clase HMM.

//+------------------------------------------------------------------+
//|                                                     hmmlearn.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Alglib\dataanalysis.mqh>
#include<Math\Stat\Uniform.mqh>
#include<Math\Stat\Math.mqh>
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>

//+------------------------------------------------------------------+
//|Markov model estimation method                                    |
//+------------------------------------------------------------------+
enum ENUM_HMM_METHOD
  {
   MODE_LOG=0,
   MODE_SCALING
  };
//+------------------------------------------------------------------+
//| state sequence decoding algorithm                                |
//+------------------------------------------------------------------+
enum ENUM_DECODE_METHOD
  {
   MODE_VITERBI=0,
   MODE_MAP
  };
//+------------------------------------------------------------------+
//| Hidden Markov Model class                                        |
//+------------------------------------------------------------------+
class HMM
  {
private:
   ulong m_samples ;       // Number of cases in dataset
   ulong m_vars ;        // Number of variables in each case
   ulong m_states ;      // Number of states
   vector            m_initprobs;   // vector of probability that first case is in each state
   matrix            m_transition;  // probability matrix
   matrix m_means ;                 //state means
   matrix m_covars[] ;              // covariances
   matrix densities ;              // probability densities
   matrix alpha ;       // result of forward algorithm
   matrix beta ;        // result of backward algorithm
   matrix m_stateprobs ; // probabilities of state
   double likelihood ;  //  log likelihood
   matrix            trial_transition;
   bool              trained;
   double            m_mincovar;
   ENUM_HMM_METHOD   m_hmm_mode;
   ENUM_DECODE_METHOD m_decode_mode;
   //+------------------------------------------------------------------+
   //| normalize array so sum(exp(a)) == 1                              |
   //+------------------------------------------------------------------+
   matrix            log_normalize(matrix &in)
     {
      matrix out;
      if(in.Cols()==1)
         out = matrix::Zeros(in.Rows(), in.Cols());
      else
         out = logsumexp(in);
      return in-out;
     }
   //+------------------------------------------------------------------+
   //| log of the sum of exponentials of input elements                 |
   //+------------------------------------------------------------------+
   matrix            logsumexp(matrix &in)
     {
      matrix out;

      vector amax = in.Max(1);

      for(ulong i = 0; i<amax.Size(); i++)
         if(fpclassify(MathAbs(amax[i])) == FP_INFINITE)
            amax[i] = 0.0;

      matrix ama(amax.Size(),in.Cols());
      for(ulong i=0; i<ama.Cols();i++)
         ama.Col(amax,i);

      matrix tmp = exp(in - ama);

      vector s = tmp.Sum(1);

      out.Init(s.Size(),in.Cols());
      for(ulong i=0; i<out.Cols();i++)
         out.Col(log(s),i);

      out+=ama;

      return out;
     }

   //+------------------------------------------------------------------+
   //| normarlize vector                                                |
   //+------------------------------------------------------------------+
   vector            normalize_vector(vector &in)
     {
      double sum = in.Sum();
      return in/sum;
     }
   //+------------------------------------------------------------------+
   //|  normalize matrix                                                |
   //+------------------------------------------------------------------+
   matrix            normalize_matrix(matrix &in)
     {
      vector sum = in.Sum(1);

      for(ulong i = 0; i<sum.Size(); i++)
         if(sum[i] == 0.0)
            sum[i] = 1.0;

      matrix n;
      n.Init(sum.Size(), in.Cols());
      for(ulong i =0; i<n.Cols(); i++)
         n.Col(sum,i);

      return in/n;
     }
   //+------------------------------------------------------------------+
   //|   Set up model from JSON object                                  |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      if(jsonmodel["implementation"].ToStr() == "log")
         m_hmm_mode = MODE_LOG;
      else
         m_hmm_mode = MODE_SCALING;

      if(jsonmodel["algorithm"].ToStr() == "Viterbi")
         m_decode_mode = MODE_VITERBI;
      else
         m_decode_mode = MODE_MAP;

      m_states = (ulong)jsonmodel["numstates"].ToInt();
      m_vars = (ulong)jsonmodel["numvars"].ToInt();


      if(!m_initprobs.Resize(m_states) || !m_means.Resize(m_states,m_vars) ||
         !m_transition.Resize(m_states,m_states) || ArrayResize(m_covars,int(m_states))!=int(m_states))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(uint i = 0; i<m_covars.Size(); i++)
        {
         if(!m_covars[i].Resize(m_vars,m_vars))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

         for(int k = 0; k<int(m_covars[i].Rows()); k++)
            for(int j = 0; j<int(m_covars[i].Cols()); j++)
               m_covars[i][k][j] = jsonmodel["covars"][i][k][j].ToDbl();
        }

      for(int i =0; i<int(m_initprobs.Size()); i++)
        {
         m_initprobs[i] = jsonmodel["initprobs"][i].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_vars); j++)
            m_means[i][j] = jsonmodel["means"][i][j].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_states); j++)
            m_transition[i][j] = jsonmodel["transitions"][i][j].ToDbl();
        }

      return true;
     }

   //+------------------------------------------------------------------+
   //|  Multivariate Normal Density function                            |
   //+------------------------------------------------------------------+
   double            mv_normal(ulong nv,vector &x, vector &mean, matrix &in_covar)
     {
      matrix cv_chol;
      vector vc = x-mean;

      if(!in_covar.Cholesky(cv_chol))
        {
         matrix ncov = in_covar+(m_mincovar*matrix::Eye(nv,nv));
         if(!ncov.Cholesky(cv_chol))
           {
            Print(__FUNCTION__,": covars matrix might not be symmetric positive-definite, error ", GetLastError());
            return EMPTY_VALUE;
           }
        }

      double cv_log_det = 2.0 * (MathLog(cv_chol.Diag())).Sum();
      vector cv_sol = cv_chol.Solve(vc);

      return -0.5*((nv*log(2.0 * M_PI)) + (pow(cv_sol,2.0)).Sum() + cv_log_det);

     }


   //+------------------------------------------------------------------+
   //|logadd exp                                                        |
   //+------------------------------------------------------------------+
   double            logaddexp(double a, double b)
     {
      return a==-DBL_MIN?b:b==-DBL_MIN?a:MathMax(a,b)+log1p(exp(-1.0*MathAbs(b-a)));
     }
   //+------------------------------------------------------------------+
   //| scaled trans calculation                                         |
   //+------------------------------------------------------------------+
   matrix            compute_scaling_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logdens = exp(dens).Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Resize(nc,nc);
      out.Fill(0.0);

      for(ulong t =0; t<ns-1; t++)
        {
         for(ulong i = 0; i<nc; i++)
           {
            for(ulong j = 0; j<nc; j++)
              {
               out[i][j] += alf[t][i] * trans[i][j] * logdens[t+1][j]*bta[t+1][j];
              }
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| log trans calculation                                            |
   //+------------------------------------------------------------------+
   matrix            compute_log_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      vector row = alf.Row(ns-1);
      double logprob = (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);

      matrix out;
      out.Init(nc,nc);

      out.Fill(-DBL_MIN);

      for(ulong t = 0 ; t<ns-1; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               double vl = alf[t][i] + logtrans[i][j]+ logdens[t+1][j]+bta[t+1][j] - logprob;
               out[i][j] = logaddexp(out[i][j], vl);
              }
           }
        }

      return out;

     }
   //+------------------------------------------------------------------+
   //| forward scaling                                                  |
   //+------------------------------------------------------------------+
   double            forwardscaling(vector &startp, matrix &trans, matrix &dens,matrix &out, vector&outt)
     {
      double minsum = 1.e-300;
      vector gstartp = startp;
      matrix gtrans = trans;
      matrix gdens = exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      if(outt.Size()!=ns)
         outt.Resize(ns);

      out.Fill(0.0);

      double logprob = 0.0;

      for(ulong i = 0; i<nc; i++)
         out[0][i] = gstartp[i]*gdens[0][i];

      double sum  = (out.Row(0)).Sum();

      if(sum<minsum)
         Print("WARNING: forward pass failed with underflow consider using log implementation ");

      double scale = outt[0] = 1.0/sum;
      logprob -= log(scale);

      for(ulong i=0; i<nc; i++)
         out[0][i] *=scale;

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j=0; j<nc; j++)
           {
            for(ulong i=0; i<nc; i++)
              {
               out[t][j]+=out[t-1][i] * gtrans[i][j];
              }
            out[t][j]*=gdens[t][j];
           }
         sum = (out.Row(t)).Sum();
         if(sum<minsum)
            Print("WARNING: forward pass failed with underflow consider using log implementation ");

         scale = outt[t] = 1.0/sum;
         logprob -= log(scale);
         for(ulong j = 0; j<nc; j++)
            out[t][j] *= scale;

        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //|backward scaling                                                  |
   //+------------------------------------------------------------------+
   matrix            backwardscaling(vector &startp, matrix &trans, matrix &dens,vector &scaling)
     {
      vector gstartp = startp;
      vector scaled = scaling;
      matrix gtrans = trans;
      matrix gdens =  exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      matrix out;
      out.Init(ns,nc);

      out.Fill(0.0);
      for(ulong i = 0; i<nc; i++)
         out[ns-1][i] = scaling[ns-1];

      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i=0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               out[t][i]+=(gtrans[i][j]*gdens[t+1][j]*out[t+1][j]);
              }
            out[t][i]*=scaling[t];
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| forward log                                                      |
   //+------------------------------------------------------------------+
   double            forwardlog(vector &startp, matrix &trans, matrix &dens,matrix &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j =0; j<nc; j++)
           {
            for(ulong i =0; i<nc; i++)
              {
               buf[i] = out[t-1][i] + logtrans[i][j];
              }
            out[t][j] = logdens[t][j] + (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }

      vector row = out.Row(ns-1);

      return (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);
     }
   //+------------------------------------------------------------------+
   //|  backwardlog                                                     |
   //+------------------------------------------------------------------+
   matrix            backwardlog(vector &startp, matrix &trans, matrix &dens)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Init(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[ns-1][i] = 0.0;

      for(long t = long(ns-2); t>=0; t--)
        {
         for(long i =0; i<long(nc); i++)
           {
            for(long j =0; j<long(nc); j++)
              {
               buf[j] = logdens[t+1][j] + out[t+1][j] + logtrans[i][j];
              }
            out[t][i] = (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities scaling                    |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_scaling(matrix &alf, matrix &bta)
     {
      return normalize_matrix(alf*bta);
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities log                        |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_log(matrix &alf, matrix &bta)
     {
      return exp(log_normalize(alf+bta));
     }
   //+------------------------------------------------------------------+
   //|calculate the probability of a state                              |
   //+------------------------------------------------------------------+
   double            compute_posteriors(matrix &data, matrix &result, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix alfa,bt,dens;
      double logp=0.0;
      dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      if(use_log == MODE_LOG)
        {
         logp = forwardlog(m_initprobs,m_transition,dens,alfa);
         bt = backwardlog(m_initprobs,m_transition,dens);
         result = compute_posteriors_log(alfa,bt);
        }
      else
        {
         vector scaling_factors;
         logp = forwardscaling(m_initprobs,m_transition,dens,alfa,scaling_factors);
         bt = backwardscaling(m_initprobs,m_transition,dens,scaling_factors);
         result = compute_posteriors_scaling(alfa,bt);
        }
      return logp;
     }
   //+------------------------------------------------------------------+
   //| map  implementation                                              |
   //+------------------------------------------------------------------+
   double            map(matrix &data,vector &out, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix posteriors;
      double lp = compute_posteriors(data,posteriors,use_log);
      lp = (posteriors.Max(1)).Sum();
      out = posteriors.ArgMax(1);
      return lp;
     }
   //+------------------------------------------------------------------+
   //| viterbi implementation                                           |
   //+------------------------------------------------------------------+
   double            viterbi(vector &startp, matrix &trans, matrix &dens, vector &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      double logprob = 0;
      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Size()<ns)
         out.Resize(ns);

      matrix vit(ns,nc);
      for(ulong i = 0; i<nc; i++)
         vit[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t = 1; t<ns; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            double max = -DBL_MIN;
            for(ulong j = 0; j<nc; j++)
              {
               max = MathMax(max,vit[t-1][j]+logtrans[j][i]);
              }
            vit[t][i] = max+logdens[t][i];
           }
        }
      out[ns-1] = (double)(vit.Row(ns-1)).ArgMax();
      double prev = out[ns-1];
      logprob = vit[ns-1][long(prev)];
      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i =0; i<nc; i++)
           {
            prev = ((vit[t][i]+logtrans[i][long(prev)])>=-DBL_MIN && i>=0)?double(i):double(0);
           }
         out[t] = prev;
        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //| Calculate the probability density function                       |
   //+------------------------------------------------------------------+
   matrix              find_densities(ulong variables,ulong states,matrix &mdata,matrix &the_means, matrix &covs[])
     {
      matrix out;
      out.Resize(states,mdata.Rows());

      for(ulong state=0 ; state<states ; state++)
        {
         for(ulong i=0 ; i<mdata.Rows() ; i++)
            out[state][i] = mv_normal(variables, mdata.Row(i), the_means.Row(state), covs[state]) ;
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| Forward algorithm                                                |
   //+------------------------------------------------------------------+

   double            forward(matrix &_transitions)
     {
      double sum, denom, log_likelihood;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         alpha[0][i] = m_initprobs[i] * densities[i][0] ;
         denom += alpha[0][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         alpha[0][i] /= denom ;


      for(ulong t=1 ; t<m_samples ; t++)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            ulong trans_ptr = i;
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
              {
               sum += alpha[t-1][j] * _transitions.Flat(trans_ptr);
               trans_ptr += m_states ;
              }
            alpha[t][i] = sum * densities[i][t] ;
            denom += alpha[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            alpha[t][i] /= denom ;
        }

      return log_likelihood ;

     }
   //+------------------------------------------------------------------+
   //| Backward algorithm                                               |
   //+------------------------------------------------------------------+
   double            backward(void)
     {
      double sum, denom, log_likelihood ;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         beta[(m_samples-1)][i] = 1.0 ;
         denom += beta[(m_samples-1)][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         beta[(m_samples-1)][i] /= denom ;

      for(long t=long(m_samples-2) ; t>=0 ; t--)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
               sum += m_transition[i][j] * densities[j][t+1] * beta[(t+1)][j] ;
            beta[t][i] = sum ;
            denom += beta[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            beta[t][i] /= denom ;
        }

      sum = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
         sum += m_initprobs[i] * densities[i][0] * beta[0][i] ;

      return log(sum) + log_likelihood ;
     }

public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     HMM(void)
     {
      trained =false;

      m_hmm_mode = MODE_LOG;
      m_decode_mode = MODE_VITERBI;
      m_mincovar = 1.e-7;
     }
   //+------------------------------------------------------------------+
   //| desctructor                                                      |
   //+------------------------------------------------------------------+

                    ~HMM(void)
     {

     }

   //+------------------------------------------------------------------+
   //| Load model data from regular file                                |
   //+------------------------------------------------------------------+
   bool               load(string file_name)
     {
      trained = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         trained = fromJSON(js);
        }
      return trained;
     }
   //+------------------------------------------------------------------+
   //|Predict the state given arbitrary input variables                 |
   //+------------------------------------------------------------------+

   matrix            predict_state_probs(matrix &inputs)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         matrix::Zeros(1, m_states);
        }

      matrix probs;
      compute_posteriors(inputs,probs,m_hmm_mode);

      return probs;
     }
   //+------------------------------------------------------------------+
   //|Predict the state sequence of arbitrary input variables           |
   //+------------------------------------------------------------------+
   vector            predict_state_sequence(matrix &inputs, ENUM_DECODE_METHOD decoder=WRONG_VALUE)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         vector::Zeros(1);
        }

      vector seq = vector::Zeros(inputs.Rows());
      ENUM_DECODE_METHOD decm;
      if(decoder!=WRONG_VALUE)
         decm = decoder;
      else
         decm = m_decode_mode;

      switch(decm)
        {
         case MODE_VITERBI:
           {
            matrix d = find_densities(m_vars,m_states,inputs,m_means,m_covars);
            viterbi(m_initprobs,m_transition,d,seq);
            break;
           }
         case MODE_MAP:
           {
            map(inputs,seq,m_hmm_mode);
            break;
           }
        }

      return seq;
     }
   //+------------------------------------------------------------------+
   //| get the loglikelihood of the model                             |
   //+------------------------------------------------------------------+

   double            get_likelihood(matrix &data)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return EMPTY_VALUE;
        }

      matrix dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      matrix alfa;
      vector sc;

      switch(m_hmm_mode)
        {
         case MODE_LOG:
            likelihood = forwardlog(m_initprobs,m_transition,dens,alfa);
            break;
         case MODE_SCALING:
            likelihood = forwardscaling(m_initprobs,m_transition,dens,alfa,sc);
            break;
        }

      return likelihood;
     }
   //+------------------------------------------------------------------+
   //| get the initial state probabilities of the model          |
   //+------------------------------------------------------------------+

   vector            get_init_probs(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return vector::Zeros(1);
        }
      return m_initprobs;
     }
   //+------------------------------------------------------------------+
   //| get the probability transition matrix                            |
   //+------------------------------------------------------------------+

   matrix            get_transition_matrix(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_transition;
     }
   //+------------------------------------------------------------------+
   //|get the state means matrix                                        |
   //+------------------------------------------------------------------+

   matrix            get_means(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_means;
     }

   //+------------------------------------------------------------------+
   //| get the covariance matrix for a particular state                 |
   //+------------------------------------------------------------------+

   matrix            get_covar_matrix_for_state_at(ulong state_index)
     {
      if(!trained || state_index>m_states)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_covars[state_index];
     }
   //+------------------------------------------------------------------+
   //|  get the number of features for the model                |
   //+------------------------------------------------------------------+
   ulong             get_num_features(void)
     {
      return m_vars;
     }
  };


//+------------------------------------------------------------------+

Después de crear una instancia de la clase HMM, llamaríamos al método "load()" con un nombre de archivo específico.

//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }

Si los parámetros del modelo se leen correctamente, el método devolverá verdadero.

Una vez cargado un modelo, podemos obtener los estados ocultos y las probabilidades de estado para un conjunto particular de observaciones. Sin embargo, es importante tener en cuenta que la implementación de todos los algoritmos descritos anteriormente en el texto es ligeramente diferente. En lugar de probabilidades brutas, el código utiliza el logaritmo de los valores brutos para garantizar la estabilidad numérica. Por lo tanto, tenemos log-verosimilitudes en lugar de probabilidades. Esto también significa que dondequiera que se requiera multiplicación, tenemos que usar la suma, ya que estamos tratando con el logaritmo de los valores.

El método HMM `get_likelihood()` devuelve la probabilidad logarítmica de un conjunto de observaciones en función de los parámetros del modelo cargados. Se calcula utilizando el algoritmo de avance. El método "predict_state_probs()" calcula las probabilidades de estado para cada observación proporcionada como entrada. Este método devuelve una matriz donde cada fila representa las probabilidades de estado para una observación.

Por otro lado, el método "predict_state_sequence()" devuelve un vector que representa el estado de cada muestra proporcionada como entrada. De forma predeterminada, utiliza el algoritmo de Viterbi para calcular la secuencia de estados más probable. Sin embargo, también es posible seleccionar la técnica simple "map", imitando el comportamiento del método "decode()" de GaussianHMM.

La clase "HMM" proporciona métodos getter para extraer los parámetros de un modelo cargado:

• "get_means()": Devuelve la matriz de medias utilizada para determinar las densidades de probabilidad.
• "get_covar_matrix_for_state_at()": Obtiene la matriz de covarianza completa para un estado concreto.
• "get_transition_matrix()": Devuelve las probabilidades de transición en forma de matriz.
• "get_init_probs()": Devuelve un vector de las probabilidades de estado iniciales del modelo.
• "get_num_features()": Devuelve un valor unsigned long que representa el número de variables previstas como entrada para el modelo. Esto significa que para cualquier matriz suministrada como entrada a "predict_state_probs()", "predict_state_sequence()" y "get_likelihood()", debe tener esta cantidad de columnas y al menos 2 filas.

El script 'saveHMM.py' entrena un HMM basado en un conjunto de datos aleatorio. Incluye la definición de la función "hmm2json()" que es responsable de guardar los parámetros del modelo final en un archivo JSON. Los datos constan de 10 filas y 5 columnas. Se crea una instancia de la clase GaussianHMM y se entrena el HMM con los datos aleatorios. Después de ajustar un modo, se llama a "hmm2json()" para guardar los parámetros del modelo en un archivo JSON. Luego se imprimen la probabilidad logarítmica, los estados ocultos y las probabilidades de estado.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
from hmmlearn import hmm
import numpy as np
import pandas as pd
import json 


assumed_states = 2 #number of states of process
maxhmm_iters = 10000 #maximum number of iterations for optimization procedure

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 
#dataset to train model on    
dataset = np.array([[0.56807844,0.67179966,0.13639585,0.15092627,0.17708295],
                   [0.62290044,0.15188847,0.91947761,0.29483647,0.34073613],
                   [0.47687505,0.06388765,0.20589139,0.16474974,0.64383775],
                   [0.25606858,0.50927144,0.49009671,0.0284832,0.37357852],
                   [0.95855305,0.93687549,0.88496015,0.48772751,0.10256193],
                   [0.36752403,0.5283874 ,0.52245909,0.77968798,0.88154157],
                   [0.35161822,0.50672902,0.7722671,0.56911901,0.98874104],
                   [0.20354888,0.82106204,0.60828044,0.13380222,0.4181293,],
                   [0.43461371,0.60170739,0.56270993,0.46426138,0.53733481],
                   [0.51646574,0.54536398,0.03818231,0.32574409,0.95260478]])  
#instantiate an HMM and train on dataset
model = hmm.GaussianHMM(assumed_states,n_iter=maxhmm_iters,covariance_type='full',random_state=125, verbose=True).fit(dataset)  
#save the model to the common folder of Metatrader 5 install
hmm2json(model,r'C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\Common\Files\exampleHMM.json')
#get the state probabilities and log likelihood
result = model.score_samples(dataset)
print("log_likelihood " ,result[0]) #print the loglikelihood
print("state sequence ", model.decode(dataset)[1]) #print the state sequence of dataset
print("state probs ", result[1]) #print the state probabilities 

El script MetaTrader 5 correspondiente 'testHMM.mq5' está diseñado para cargar el archivo JSON creado por 'saveHMM.py'. La idea es reproducir la probabilidad logarítmica, los estados ocultos y las probabilidades de estado generadas por 'saveHMM.py'.

//+------------------------------------------------------------------+
//|                                                      TestHMM.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<hmmlearn.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- random dataset equal to that used in corresponding python script saveHMM.py
   matrix dataset =
     {
        {0.56807844,0.67179966,0.13639585,0.15092627,0.17708295},
        {0.62290044,0.15188847,0.91947761,0.29483647,0.34073613},
        {0.47687505,0.06388765,0.20589139,0.16474974,0.64383775},
        {0.25606858,0.50927144,0.49009671,0.0284832,0.37357852},
        {0.95855305,0.93687549,0.88496015,0.48772751,0.10256193},
        {0.36752403,0.5283874,0.52245909,0.77968798,0.88154157},
        {0.35161822,0.50672902,0.7722671,0.56911901,0.98874104},
        {0.20354888,0.82106204,0.60828044,0.13380222,0.4181293},
        {0.43461371,0.60170739,0.56270993,0.46426138,0.53733481},
        {0.51646574,0.54536398,0.03818231,0.32574409,0.95260478}
     };
//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }
//--get the log likelihood of the model
   double lk = hmm.get_likelihood(dataset);
   Print("LL ", lk);
//-- get the state probabilities for a dataset
   matrix probs = hmm.predict_state_probs(dataset);
   Print("state probs ", probs);
//---get the hidden states for the provided dataset
   vector stateseq = hmm.predict_state_sequence(dataset);
   Print("state seq ", stateseq);
  }
//+------------------------------------------------------------------+

Los resultados de ejecutar ambos scripts se muestran a continuación.

Resultado de 'saveHMM.py':

KO      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   log_likelihood  47.90226114316213
IJ      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state sequence  [0 1 1 1 1 0 0 1 0 0]
ED      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state probs  [[1.00000000e+000 1.32203104e-033]
RM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JR      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
RH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
LS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 5.32945369e-123]
EH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 8.00195599e-030]
RN      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
HS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 1.04574121e-027]
RD      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [9.99999902e-001 9.75116254e-008]]

El contenido del archivo JSON guardado.

{"numstates":2,"numvars":5,"algorithm":"viterbi","implementation":"log","initprobs":[1.0,8.297061845628157e-28],"means":[[0.44766002665812865,0.5707974904960126,0.406402863181157,0.4579477485782787,0.7074610252191268],[0.5035892002511225,0.4965970189510691,0.6217412486192438,0.22191983002481444,0.375768737249644]],"transitions":[[0.4999999756220927,0.5000000243779074],[0.39999999999999913,0.6000000000000008]],"covars":[[[0.009010166768420797,0.0059122234200326374,-0.018865453701221935,-0.014521967883281419,-0.015149047353550696],[0.0059122234200326374,0.0055414217505728725,-0.0062874071503534424,-0.007643976931274206,-0.016093347935464856],[-0.018865453701221935,-0.0062874071503534424,0.0780495488091017,0.044115693492388836,0.031892068460887116],[-0.014521967883281419,-0.007643976931274206,0.044115693492388836,0.04753113728071052,0.045326684356283],[-0.015149047353550696,-0.016093347935464856,0.031892068460887116,0.045326684356283,0.0979523557527634]],[[0.07664631322010616,0.01605057520615223,0.042602194598462206,0.043095659393111246,-0.02756159799208612],[0.01605057520615223,0.12306893856632573,0.03943267795353822,0.019117932498522734,-0.04009804834113386],[0.042602194598462206,0.03943267795353822,0.07167474799610704,0.030420143149584727,-0.03682040884824712],[0.043095659393111246,0.019117932498522734,0.030420143149584727,0.026884283954788642,-0.01676189860422705],[-0.02756159799208612,-0.04009804834113386,-0.03682040884824712,-0.01676189860422705,0.03190589647162701]]]}

Resultado de 'testHMM.mq5':

HD      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   LL 47.90226114316213
EO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state probs [[1,1.322031040402482e-33]
KP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KF      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KM      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
EJ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,5.329453688054051e-123]
IP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,8.00195599043147e-30]
KG      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
ES      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,1.045741207369424e-27]
RQ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0.999999902488374,9.751162535898832e-08]]
QH      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state seq [0,1,1,1,1,0,0,1,0,0]

Conclusión

Los HMM son potentes herramientas estadísticas para modelar y analizar datos secuenciales. Su capacidad para capturar los estados ocultos subyacentes que impulsan las secuencias observadas los hace valiosos para tareas que involucran series de tiempo, como datos financieros. A pesar de sus puntos fuertes, los HMM no están exentos de limitaciones. Se basan en el supuesto de Márkov de primer orden, que puede ser demasiado simplista para dependencias complejas. Las demandas computacionales del entrenamiento y la inferencia, especialmente para espacios de estados grandes, y el potencial de sobreajuste son desafíos importantes. Además, seleccionar el número óptimo de estados e inicializar los parámetros del modelo requieren una consideración cuidadosa y pueden afectar el rendimiento. No obstante, los HMM siguen siendo un método fundamental en el modelado de secuencias y ofrecen un marco sólido para muchas aplicaciones prácticas. Con los avances continuos y los enfoques híbridos que combinan HMM con modelos más flexibles, su utilidad continúa evolucionando. Para los profesionales, comprender tanto las capacidades como las limitaciones de los HMM es esencial para aprovechar eficazmente su potencial en el desarrollo del comercio automatizado.

Todo el código descrito en el artículo se adjunta a continuación. Cada uno de los archivos de código fuente se describe en la tabla.

Archivo	Descripción
Mql5\Python\script\saveHMM.py	Demuestra el entrenamiento y el guardado de un modelo oculto de Márkov. Contiene la definición de la función 'hmm2json()'.
Mql5\include\hmmlearn.mqh	Contiene la definición de la clase HMM que permite la importación de HMM entrenados en Python para su uso en MQL5.
Mql5\script\testHMM.mq5	Script MT5 que demuestra cómo cargar un HMM guardado.